1 Introduction
Derivative-Free Global Optimization (DFGO) problems that require significant computational resources can be found in a wide range of fields, including robotics (Hauser, 2017; Wang et al., 2020), engineering design (Lin et al., 2022; Kim et al., 2022b), economics (Liu et al., 2022; Kim et al., 2022a), tourism (Liao et al., 2021; Paulavičius et al., 2023), and many others (Floudas et al., 2013; Moret et al., 2016; Grigaitis et al., 2007; Stripinis et al., 2021). These problems often involve black-box functions that require expensive simulations or experiments for evaluation. For example, Mugunthan et al. (2005) reported that a simulation of chlorinated ethene bio-degradation based on real field data took approximately 2.5 hours to run. Due to these challenges, there is an active global research with numerous references dedicated to addressing these issues. The complexity of real-life design problems, the presence of multiple local optima, various constraints, and the need for optimal solutions make global optimization techniques crucial for solving such problems across different domains.
This paper focuses on addressing a general non-linear programming global optimization potentially black-box problem described as follows:
where, $f:{\mathbb{R}^{n}}\to \mathbb{R}$, $\mathbf{g}:{\mathbb{R}^{n}}\to {\mathbb{R}^{m}}$, and $\mathbf{h}:\hspace{2.5pt}{\mathbb{R}^{n}}\to {\mathbb{R}^{r}}$ represent continuous functions that may exhibit nonlinearity. The domain D is defined as a bound-constrained region
(1)
\[ \begin{aligned}{}\underset{\mathbf{x}\in D}{\min }\hspace{2.5pt}& f(\mathbf{x})\\ {} \text{s.t.}\hspace{2.5pt}& \mathbf{g}(\mathbf{x})\leqslant \mathbf{0},\\ {} & \mathbf{h}(\mathbf{x})=\mathbf{0},\end{aligned}\]
\[ D=[\mathbf{a},\mathbf{b}]=\big\{\mathbf{x}\in {\mathbb{R}^{n}}:\hspace{2.5pt}{a_{j}}\leqslant {x_{j}}\leqslant {b_{j}},\hspace{2.5pt}j=1,\dots ,n\big\}.\]
The feasible region, denoted as ${D^{\mathrm{feas}}}=D\cap \Omega $, consists of points that satisfy all the constraints, where
It is assumed that all the functions involved are Lipschitz continuous, although specific Lipschitz constants are unknown. These functions may exhibit nonlinearity, lack of differentiability, and non-convexity.The algorithm DIRECT, introduced by Jones et al. (1993), has attracted significant attention in the field of computer science and DFGO due to its potential to address a wide range of global optimization problems in various applications. Its ability to handle non-convex problems has motivated researchers and practitioners to explore and utilize the DIRECT algorithm as a practical solution approach. The algorithm offers several advantages that make it a preferred choice among practitioners. One notable advantage is its fast convergence towards an approximate global minimum, as highlighted in the metamodelling work by Jie et al. (2015). By conducting an exhaustive search over the entire domain, the DIRECT algorithm effectively escapes local minima, as demonstrated in several studies (Barmuta et al., 2016; Kancharala and Philen, 2016). Another appealing aspect of the algorithm is its ease of implementation and minimal or non-existent hyper-parameters (Li et al., 2022). Being derivative-free, the algorithm exhibits flexibility in solving black-box optimization problems, as emphasized in Bouadi et al. (2022). Furthermore, the deterministic nature of the algorithm ensures consistent results, as noted in Campana et al. (2016).
Like any algorithm, the DIRECT algorithm also has its weaknesses and limitations, as discussed in Jones and Martins (2021). One notable drawback is the potential slowness in achieving high-accuracy solutions. This can be attributed to the exhaustive search performed by the algorithm, which can be computationally expensive. Another limitation is that DIRECT can spend significant time exploring uninteresting regions of the search domain, thus delaying the discovery of global minima. This behaviour can hinder its efficiency, especially when dealing with complex optimization problems.
To overcome these shortcomings, various techniques (see, e.g. Paulavičius et al., 2020; Stripinis and Paulavičius, 2022a, 2022c, 2023a), including hybrid ones that combine the DIRECT algorithm with other optimization techniques, have been widely adopted in practical applications (Liuzzi et al., 2010, 2016). By integrating DIRECT with complementary methods, such as local search or metaheuristics, these hybrid approaches aim to mitigate the weaknesses of the algorithm and improve its overall performance. This allows for more effective search space exploration and enhances the algorithm’s ability to find optimal solutions within specific requirements.
The objective of this comprehensive review is to assess the practical value of DIRECT-type methods in solving non-convex constrained optimization problems. By conducting a thorough examination of the existing literature, our aim is to highlight the modifications and enhancements proposed by researchers to address the limitations of these methods and improve their applicability in specific practical scenarios. To evaluate the performance and practicality of DIRECT-type methods, we conduct computational comparisons using real-world design problems. However, our evaluation goes beyond the scope of DIRECT-type methods by including State-Of-The-Art (SOTA) evolutionary solution techniques. This broader assessment allows us to gain a comprehensive understanding of the strengths, weaknesses, and limitations of DIRECT-type methods when faced with constrained non-convex optimization problems. Through this detailed analysis, we aim to identify key characteristics, challenges, and potential areas of improvement for DIRECT-type methods. Ultimately, our goal is to provide valuable insights into the practical viability and effectiveness of these methods in various real-world applications.
1.1 New Contributions and the Structure of the Paper
First and foremost, it is essential to emphasize that certain findings from this study have been integrated into our most recent monograph (Stripinis and Paulavičius, 2023a). This monograph provides a comprehensive overview of three decades of progress in the DIRECT field, with a specific emphasis on applications and software tailored for DIRECT-type algorithms. However, it is crucial to note that this paper goes beyond the monograph by detailing the entire research process and presenting significantly expanded findings along with their in-depth analysis.
Outlined below are the distinctive contributions and key differences between the monograph and the present study:
-
1. Comprehensive Systematic Literature Review: The systematic review in our study underwent a more thorough process and analysis, encompassing recent works in the field. This increased scrutiny results in a more comprehensive summary of existing knowledge, making it a valuable reference for both researchers and practitioners seeking in-depth understanding.
-
2. Extended Experimental Exploration: In our experimental investigation, we utilized real-world design problems from the Congress on Evolutionary Computation (CEC) competitions included in the most recent DIRECTGOLib v2.0 and considered a greater number of state-of-the-art (SOTA) algorithms. This expanded experimental analysis delves deeper into practical problems, providing a more comprehensive examination of various subsets.
-
3. Insights and Future Prospects: Beyond presenting findings, this article offers valuable insights and suggestions for future prospects and opportunities in the field of practical applicability of DIRECT-type algorithms. Researchers can leverage this information to guide their research directions and focus on areas that require further investigation.
The remaining sections of this review are organized as follows. Section 2 presents a brief overview of the DIRECT algorithm and its positioning within DFGO. Section 3 offers a systematic review of the literature and a comparative analysis of existing applications of DIRECT-type algorithms. The results of experimental investigations carried out to evaluate the performance of DIRECT-type algorithms on real-world optimization problems are presented in Section 4. Lastly, in Section 5, we summarize the key findings of this review and provide concluding remarks on the current state and future prospects of research on DIRECT-type algorithms.
2 The DIRECT Algorithm and Its Positioning within DFGO
The DIRECT algorithm, initially developed to tackle box-bounded global optimization problems, has gained substantial popularity and widespread adoption in diverse applications. This section briefly explores the original DIRECT algorithm and its positioning within DFGO. For more comprehensive details regarding the modifications of DIRECT, see Jones and Martins (2021).
2.1 Brief Overview of the DIRECT Algorithm
This section provides a brief introduction to the original DIRECT algorithm proposed by Jones et al. (1993). The DIRECT algorithm is specifically designed to handle optimization problems with bound constraints:
The DIRECT algorithm belongs to the class of “divide-and-conquer” methods, as discussed in Al-Dujaili and Suresh (2016), Finkel and Kelley (2006), Paulavičius et al. (2018, 2014), Sergeyev and Kvasov (2006), Stripinis and Paulavičius (2021, 2023b 2024). Assuming defined lower and upper bounds, the algorithm DIRECT normalizes the design variables to the range of $[0,1]$ to transform the search space (D) into a unit hypercube ($\bar{D}$) without loss of generality. The core methodology of DIRECT involves the iterative building of finer and finer partitions of the unit hypercube ($\bar{D}$) into smaller hyper-rectangles, each containing the objective function’s evaluation at its central point. The algorithm forms the partition $\mathcal{P}$, which is defined in iteration k as:
where ${\bar{D}_{k}^{i}}=[{\bar{\mathbf{a}}^{i}},{\bar{\mathbf{b}}^{i}}]=\{\mathbf{x}\in {\mathbb{R}^{n}}:0\leqslant {\bar{a}_{j}^{i}}\leqslant {x_{j}}\leqslant {\bar{b}_{j}^{i}}\leqslant 1,j=1,\dots ,n,\forall i\in {\mathbb{I}_{k}}\}$ and ${\mathbb{I}_{k}}$ is the index set that identifies the current partition ${\mathcal{P}_{k}}$. During each iteration, specific hyper-rectangles ${\bar{D}_{k}^{i}}\subseteq {\mathcal{P}_{k}}$ are chosen for further exploration. These selected hyper-rectangles undergo further subdivision, and the function’s values are assessed at the centre points of the newly created hyper-rectangles. After the subdivision of the selected hyper-rectangles from the current partition ${\mathcal{P}_{k}}$, the next partition ${\mathcal{P}_{k+1}}$ is obtained.
The main steps of the original DIRECT algorithm are illustrated in Fig. 1, while the following subsections will briefly describe them.
2.1.1 Selection Rule
Within the current partition ${\mathcal{P}_{k}}$, a set of hyper-rectangles is selected by means of a so-called identification procedure. During the first iteration, the identification procedure is straightforward, as only one candidate is available, ${\bar{D}_{1}^{1}}$. However, for future iterations, DIRECT determines the goodness of hyper-rectangles based on the lower bound estimates for the objective function $f(\mathbf{x})$ over each hyper-rectangle ${\bar{D}_{k}^{i}}$. The identification procedure basically tends to select more “promising” hyper-rectangles that may contain the global optimum. More specifically, the requirement of “potential optimal hyper-rectangle” (POH) is stated formally in Definition 1 (Jones et al., 1993).
Definition 1 (Potentially optimal hyper-rectangle).
Let ${\mathbf{c}^{i}}$ represent the centre sampling point and ${\delta _{k}^{i}}$ be a measure (distance, size) of the hyper-rectangle ${\bar{D}_{k}^{i}}$. Let $\varepsilon \gt 0$ be a positive constant and ${f_{k}^{\min }}$ be the best value currently known of the objective function. A hyper-rectangle ${\bar{D}_{k}^{j}},j\in {\mathbb{I}_{k}}$ is considered potentially optimal if there exists a rate-of-change (Lipschitz) constant $\tilde{L}\gt 0$ such that where the measure of the hyper-rectangle is given by
The hyper-rectangle ${D_{k}^{j}}$ is considered potentially optimal if its lower Lipschitz bound for the objective function, computed on the left-hand side of (3), is the smallest among all hyper-rectangles in the current partition ${\mathcal{P}_{k}}$ with some positive constant $\tilde{L}$. Additionally, it is necessary that the hyper-rectangle’s lower bound is superior to the best present solution value (${f_{k}^{\min }}$) as indicated in requirement (4). This requirement acts as a threshold, preventing the DIRECT algorithm from wasting function evaluations on excessively small hyper-rectangles that are improbable to result in noteworthy enhancements.
2.1.2 Sampling Rule
The objective function is first evaluated at the midpoint ${\mathbf{c}^{1}}\in {\bar{D}_{1}^{1}}$, regardless of the dimensions of the initial hyper-cube. Afterward, DIRECT picks points for each selected POH (${\bar{D}_{k}^{i}}$) at
where ${\mathbf{e}_{j}}$ denotes the jth Euclidean base vector, ${d_{k}^{i}}$ is one third of the maximum side length of ${\bar{D}_{k}^{i}}$, and ${\mathbb{J}_{k}^{i}}$ the indices of the longest hyper-rectangles (${\bar{D}_{k}^{i}}$) sides. Only the longest side requires two additional points to be sampled, and each POH can have between 2 and $2n$ samples.
2.1.3 Subdivision Rule
The process of dividing the hyper-rectangle within DIRECT involves splitting it into three equal parts along its longest sides in a n-dimensional space. If multiple sides share the longest length, the trisection process begins from the sides with the smallest value of ${w_{j}^{i}}$ and moves towards the side with the highest value. The ${w_{j}^{i}}$ is calculated as the optimal function value sampled along the j dimension, and is determined using the following equation:
The newly created hyper-rectangles have centres that are the points that were newly sampled, while the original centre point becomes the centre of the middle hyper-rectangle. The partitioning strategy of the DIRECT algorithm aims to guarantee that the best function values are contained within the largest hyper-rectangles.
2.1.4 Example of the DIRECT Algorithm
Figure 2 demonstrates the process of DIRECT in its initial three iterations on a two-variable problem. Initially, a single encompassing rectangle (representing the entire unit hyper-cube) is chosen for evaluation. The rectangle is then subdivided into thirds, and the centre points of the new rectangles (represented as empty dots) are evaluated. In the second iteration, only one rectangle is selected and sampled, while in the third iteration, two rectangles are selected, subdivided, and sampled. This process continues iteratively until a predefined limit on the number of iterations or function evaluations is reached.
Fig. 2
Visualization of selection, central sampling, and trisection in DIRECT algorithm (Jones et al., 1993) on the two-dimensional problem.
2.2 Positioning DIRECT-Type Techniques in the Field of DFGO
Global optimization algorithms have been classified according to several taxonomies (Leon, 1966; Archetti and Schoen, 1984; Törn and Žilinskas, 1989). The most recent study in Stork et al. (2022) categorizes algorithms based on key features into six classes: hill-climbing, trajectory, population, surrogate, exact, and hybrid, as summarized in Fig. 3. The hill-climbing and trajectory algorithms are described as a single hiker that initializes and maintains a single solution through the search and focuses mainly on exploitation. While hill-climbing algorithms swiftly converge to a local optimum within the attraction region and typically do not employ an explicit exploration strategy, the trajectory algorithms are supported by defined exploration techniques. Notable standard algorithms in hill-climbing category include the quasi-Newton Broyden-Fletcher-Goldfarb-Shanno (Shanno, 1970), Nelder-Mead simplex (Nelder and Mead, 1965), and $(1+1)$-Evolution strategy (Kellermayer, 1977), while the most popular examples of trajectory algorithms are Tabu search (Glover, 1989), variable neighbourhood search (Mladenović et al., 2008), and simulated annealing (Kirkpatrick et al., 1983).
The algorithms in the population class operate a set of possible solutions, referred to as a population, as opposed to a single solution like in trajectory or hill-climbing algorithms. By keeping a population, these population algorithms can investigate numerous areas of the search space at once, avoiding getting stuck in local optima. Some examples of population-based search algorithms include differential evolution (Storn and Price, 1997), particle swarm optimization (Eberhart and Kennedy, 1995), covariance matrix adaptation strategy (Hansen and Ostermeier, 1996), population-based incremental learning (Baluja, 1994), and a plethora of others (Beheshti and Shamsuddin, 2013).
Surrogate class algorithms are designed to optimize the search by replacing costly objective function evaluations with a simplified, less expensive model to evaluate. Bayesian optimization (Mockus, 1975, 1994) and efficient global optimization (Jones et al., 1998) are popular frameworks for optimizing expensive black-box functions. In addition, surrogate models are frequently used to assist other algorithms, such as evolutionary search strategies (Ong et al., 2005), or multilevel coordinate search (Huyer and Neumaier, 1999).
Original DIRECT, as well as many other pure DIRECT-type algorithms fall into the category of exact algorithms. Algorithms in this class belong to deterministic, systematic, or exhaustive optimization strategies. The performance of many algorithms in this class is exceptional when dealing with discrete or combinatorial domains with a finite number of feasible solutions. In continuous domains, such as DIRECT-type algorithms, they efficiently explore and can identify the global optimum within specified tolerances. A notable property of exact algorithms is their ability to guarantee a global optimal result while utilizing predictable resources such as function evaluations or computation time.
Another category in which DIRECT-type algorithms are situated is the hybrid class algorithms. Within this class, several hybrid DIRECT-type algorithms (Holmstrom et al., 2010; Jones, 2001; Liuzzi et al., 2010, 2016; Paulavičius and Žilinskas, 2009) integrate elements from existing algorithms, mainly belonging to the hill-climbing class methods, to improve convergence speed. Another variant within this class involves automated hybrids that employ optimization or machine learning techniques to determine optimal algorithm designs or compositions. An example of this type is automated algorithm selection (hyper-algorithms), where machine learning and problem-specific information, such as explorative landscape analysis (Kerschke and Trautmann, 2019), are utilized to identify the algorithm most suitable for a given problem. In this context, DIRECT may be a possible choice.
3 Systematic Literature Review on Applications of the DIRECT Algorithm
This section provides an extensive overview of the application of DIRECT-type algorithms in solving real-world optimization problems. We conducted this review systematically examining the literature while adhering to a well-defined methodology to ensure a comprehensive and unbiased analysis (Moher et al., 2009). This methodology, with slight modifications, is widely utilized in various research endeavours (see, for example, Navakauskas and Kazlauskas, 2023; Torkayesh et al., 2023).
Our review protocol encompasses the formulation of research questions, the identification of searched databases, the selection of appropriate search terms, and the establishment of inclusion and exclusion criteria for the selection of relevant studies. By using this systematic approach, our objective is to provide a current and inclusive summary of the existing research landscape related to the applications of DIRECT-type algorithms to solve real-world optimization problems.
3.1 Research Method
An extensive literature review was conducted in the most widely used databases to identify the primary literature on applications of the DIRECT algorithm. The search followed the PRISMA (Preferred Reporting Items for Systematic Reviews and Meta-Analyses) methodology (Moher et al., 2009). This methodology provides a well-defined framework for identifying, screening, and synthesizing published works to gather comprehensive evidence that addresses specific research inquiries. The systematic review protocol is summarized in Fig. 4, and a more detailed description can be found in the following subsections.
3.1.1 Research Questions
The main objective of this paper is to support researchers and practitioners in performing more research by thoroughly analysing the applications of DIRECT-type algorithms. This involves identifying limitations and potential areas for future research within the existing literature and offering suggestions for future studies. Therefore, the central research questions addressed in this systematic review of the literature are the following:
By addressing these research questions, this review aims to provide valuable information and guidance for researchers and practitioners interested in further exploring the applications of DIRECT-type algorithms in various domains and advancing the SOTA in real-world optimization problems.
-
RQ1 In which major real-world domains or industries have DIRECT-type algorithms been applied?
-
RQ2 What types of problems are being addressed by algorithms of type DIRECT?
-
RQ3 What recent advances, modifications or extensions of the DIRECT algorithm have been developed specifically for real-world applications?
3.1.2 Database Selection and Used Keywords
We conducted extensive searches in well-known databases, such as Scopus, Web of Science, IEEE Xplore, ACM Digital Library, and Science Direct, to ensure that we covered all relevant literature. These databases were chosen for their reputation for providing comprehensive citation data and coverage across various fields (Trigueiro de Sousa Junior et al., 2019).
To identify relevant publications for our research, we used specific search strings that included terms such as “DIRECT”, “Optimization”, “Applications”, “Real-world”, “Engineering”, “Jones”, and “Dividing Rectangles”. Our initial database searches used the query string: “DIRECT” AND “Optimization” AND (“Applications” OR “Real-world” OR “Engineering”). The search was set to look for publications that focused on the practical applications of the DIRECT algorithm in real-world engineering scenarios. We used this query in the titles, abstracts, and keywords of articles to ensure that we capture relevant publications.
Furthermore, we expanded our search to include additional criteria across all data. In the field of global optimization, the term “direct” is commonly used to refer to a group of algorithms that belong to a well-known taxonomy (Törn and Žilinskas, 1989). To ensure that the DIRECT algorithm is the exact algorithm we seek, we used a refined query string that included the author of the DIRECT algorithm and the concept of “Dividing Rectangles”, which is commonly associated with the description of the algorithm. The query string for these extended searches in the full text was: AND (“Jones” OR “Dividing Rectangles”).
Some of the databases we considered allowed the search using a document references list. Therefore, in such situations, we restricted the search only to documents that cited the original DIRECT algorithm paper without providing these extra query strings, and the search was performed using all metadata.
Our goal was to collect a comprehensive collection of publications that are highly relevant to our research objectives and cover the applications of the DIRECT algorithm in real-world engineering contexts.
3.1.3 Search and Screening Process
The study selection process for the systematic literature review investigating applications of DIRECT-type algorithms involved four stages, as illustrated in Fig. 4. A literature search was conducted without a specified starting publication date but was limited to publications until November 2023. The search was carried out in five databases, which resulted in a total of 283 records, with Scopus having the highest number of records (117), followed by Web of Science (88), IEEE Xplore (39), Science Direct (24), and ACM Digital Library (15).
Fig. 4
Summary of the literature search process and its findings. The green colour indicates the number of articles that have been added in the corresponding step, while the red color indicates the number that has been removed.
At the beginning, we identified a pool of 283 sources. However, we found 80 duplicate articles that had already been included in the analysis from other sources. In order to narrow down our focus to publications that specifically dealt with applications of the DIRECT algorithm, we conducted a thorough analysis of titles, keywords, and abstracts. As a result, we excluded 108 articles that did not use the DIRECT algorithm in their research, or these articles only considered DIRECT as the baseline competitor.
Among the remaining sources, 49 articles were removed as they focused solely on theoretical studies without practical applications of the DIRECT algorithm. Additionally, eight articles were inaccessible as full articles, which limited our ability to access and evaluate their complete content. Hence, we excluded them from the final analysis.
As part of the bibliography search, we manually searched and included a number of documents. This was done because newly published works are expected to appear with a delay in the databases. Also, we may have missed some important applications during our search process. In total, we identified 56 documents for subsequent analysis, including 18 highly related ones that were discovered during the manual search.
After completion of the literature collection process, we thoroughly reviewed the selected 56 sources. During this review, we found that nine documents simply used DIRECT as a baseline algorithm without providing substantial information beyond its basic application. Consequently, we excluded these articles from the final analysis.
3.1.4 Analysis and Synthesis
To answer the research questions, a thorough examination of the 47 chosen articles was conducted, taking into account various factors. The evaluation was based on six crucial elements related to each article: the type and nature of the problem being addressed, the specific algorithm of type DIRECT utilized, the software used for implementation and the availability of data. These criteria were carefully selected to facilitate a complete understanding of the articles and to enable an in-depth analysis of their contributions to the field of study. Through this process, valuable information is obtained on the applications of the DIRECT algorithm and its impact in various scenarios.
3.2 Findings from the Bibliography Analysis
Over the last thirty years, DIRECT-type algorithms have been extensively studied for solving real-world optimization problems. These algorithms have shown great flexibility and applicability in a wide range of applications and problem domains, as evidenced by a collection of research papers presented in Table 1. Each entry in the table includes essential information, such as the reference, application domain, problem type (PT), solution technique, description of the implementation (IM) used (sequential (Seq) or parallel (Par)), the programming language (PL) used, and the availability of the source or results (SCA). Moreover, it provides researchers and practitioners with essential information on the effectiveness and potential benefits of using these algorithms in different domains of problems.
Table 1
Review of real-world applications of DIRECT-type algorithms in the literature.
| Reference | Application | PT | DIRECT | IM | PL | SCA |
| Dapšys et al. (2023) | Finding initial concentrations of analytes in a mixture from its biosensor response when the latter is corrupted with noise | GLB | Novel | Par | c++ | − |
| Kanayama et al. (2023) | Optimizing optimal atomic cluster structures | GLB | Hybrid | Seq | Unknown | − |
| Ramsahye et al. (2023) | Enhancing connected automated vehicles impact on mixed traffic flow dynamics | GLB | Hybrid | Seq | Unknown | − |
| Jin et al. (2023) | Optimizing the dimensional sections in high-rise steel-concrete composite structures | NLP | Novel | Seq | Matlab | − |
| Alexandrov et al. (2023) | Fitting theoretical light-scattering profiles to an experimental one, analysing polystyrene beads modelled as homogeneous spheres | GLB | Original | Seq | Unknown | − |
| Wang et al. (2023) | Optimizing shifting strategy for multi-gear and multi-mode parallel plug-in hybrid electric vehicles | GLB | Original | Seq | Matlab | − |
| Smith et al. (2023) | Estimating Error Rates in Single Molecule Protein Sequencing Experiments | GLB | Hybrid | Seq | Python | + |
| Li et al. (2022) | Portfolio optimization in the financial market | MOO | Novel | Seq | Python | − |
| Bouadi et al. (2022) | Optimizing sensitivity parameters of automated driving vehicles in an open heterogeneous traffic flow system | GLB | Original | Seq | Matlab | − |
| Abood et al. (2022) | Polydispersed solid sedimentation in wastewater | GLB | Hybrid | Seq | c++ | − |
| Xiao et al. (2020) | Optimizing registration of tissue shift in brain tumour resection | GLB | Hybrid | Seq | Unknown | − |
| Mockus et al. (2017) | Truss optimization | GLB | Novel | Seq | Matlab | − |
| Na et al. (2017) | Optimizing cryogenic natural gas liquefaction | GLH | Novel | Seq | Matlab | − |
| Cao et al. (2017) | Structural damage identification using multiple damage location assurance criteria | MOO | Novel | Seq | Unknown | − |
| Li et al. (2016) | Calibration of a car-following model based on trajectory data | GLB | Hybrid | Seq | Matlab | + |
| Liuzzi et al. (2016) | Protein structural alignment problem | GLB | Hybrid | Seq | Fortran | + |
| Campana et al. (2016) | Reducing DTMB 5415 ship resistance | GLB | Hybrid | Seq | Fortran | + |
| Chen et al. (2016) | Congestion pricing optimization problem | GLB | Hybrid | Seq | Unknown | − |
| Barmuta et al. (2016) | Mono-static radar leakage cancellation optimization | GLB | Original | Seq | Unknown | − |
| Jasper et al. (2016) | Leak detection problems in water distribution systems | MINLP | Novel | Par | c | − |
| Serani et al. (2016) | Reducing DTMB 5415 ship resistance | GLB | Hybrid | Seq | Unknown | − |
| Kancharala and Philen (2016) | Reducing fin oscillations in aerial and underwater vehicles | MOO | Hybrid | Seq | Matlab | − |
| Jie et al. (2015) | Component size optimization of fuel cell vehicle | MINLP | Hybrid | Seq | Unknown | − |
| Liu et al. (2015) | Optimization of maximum equivalent stress in axial compressor blade | GLB | Novel | Seq | Matlab | − |
| Shen et al. (2014) | Optimizing hybrid energy storage system and EV battery cycle life estimation | MOO | Original | Seq | Matlab | − |
| Panday and Bansal (2014) | Reduction of liquid fuel consumption in hybrid electric vehicles | GLB | Original | Seq | Matlab | − |
| Scitovski and Scitovski (2013) | Detection of spatial locations of seismic activity centres | GLB | Hybrid | Seq | Unknown | − |
| Ruf et al. (2012) | Optimizing weight configurations in 14 V automotive power net topologies | MINLP | Novel | Par | Matlab | − |
| Ramanathan et al. (2012) | Reducing NOx emissions in lean-burn SIDI engines using passive ammonia-SCR | GLB | Hybrid | Seq | Unknown | − |
| Di Serafino et al. (2011) | Detection of gravitational waves in astrophysics | GLB | Novel | Seq | Fortran | − |
| Svensson et al. (2011) | Optimizing the parameters of a sheet-metal press line | GLB | Hybrid | Seq | Matlab | − |
| Wang et al. (2011) | Optimizing slider bearing load capacity in thermohydrodynamic lubrication | GLB | Original | Par | Fortran | − |
| Kvasov et al. (2008) | Tuning fuzzy power-system stabilizers for multi-machine systems | GLB | Novel | Seq | Matlab | − |
| Rousseau et al. (2008) | Parameter optimization for plug-in hybrid electric vehicles | GLB | Original | Seq | Matlab | − |
| Menon et al. (2007) | Optimizing a nonlinear-dynamic inversion flight control law for a hypersonic re-entry vehicle | GLB | Hybrid | Seq | Matlab | − |
| Gao and Mi (2007) | Maximize the fuel efficiency in hybrid vehicles | NLP | Novel | Seq | Matlab | − |
| Wachowiak and Peters (2006) | Applying optimization for medical image registration | MINLP | Hybrid | Par | c/c++ | − |
| Wachowiak (2005) | Applying optimization for bio-medical image registration | MINLP | Hybrid | Par | c/c++ | − |
| He et al. (2004) | Parameter estimation in systems biology | GLB | Original | Par | Unknown | − |
| Ljungberg et al. (2004) | Maximizing the detection of epistatic QTL | GLB | Original | Seq | Fortran | − |
| Verstak et al. (2002) | Placement of transmitters in indoor wireless communication systems | GLB | Original | Seq | Unknown | − |
| He and Narayana (2002) | Register magnetic resonance images of brain | GLB | Hybrid | Seq | IDL | − |
| Herrenbauer et al. (2001) | Enhancing mammalian cell productivity with Generalized Predictive Controllers for dissolved oxygen control | GLB | Original | Seq | Matlab | − |
| Zhu and Bogy (2002) | Optimizing the slider air-bearing surface in magnetic hard disk drives | GLB | Original | Seq | Unknown | − |
| Bartholomew-Biggs et al. (2002) | Flight path calculation for aircraft | NLP | Hybrid | Seq | Unknown | − |
| Carter et al. (2001) | Gas transmission pipeline industry | GLH | Hybrid | Seq | Fortran | − |
| Baker et al. (2001) | Configuration design of a high speed civil transport | NLP | Novel | Par | Unknown | − |
3.2.1 Problem Domains
DIRECT-type algorithms have proven to be versatile and efficient in various domains. For example, these algorithms have been used in the financial market to optimize portfolios, allowing investors to maximize their returns while effectively managing risks (Li et al., 2022). Within transportation and traffic, researchers have utilized DIRECT-type algorithms to fine-tune the sensitivity parameters of automated driving vehicles in diverse traffic flow systems, resulting in improved performance and safety for connected automated vehicles. In addition, these algorithms have been employed to optimize shifting strategies for multi-gear and multi-mode parallel plug-in hybrid electric vehicles, ultimately contributing to the advancement of efficient and secure transportation systems. The relevant literature includes Bouadi et al. (2022); Ramsahye et al. (2023); Wang et al. (2023) research in this area. Additionally, DIRECT-type algorithms have shown successful applications in structural engineering (Jin et al., 2023), particularly in truss optimization (Mockus et al., 2017) and optimizing the load capacity of slider bearings in thermohydrodynamic lubrication (Wang et al., 2011). These applications highlight the potential of DIRECT-type algorithms to improve structural designs and improve performance in engineering systems.
In the energy sector, these algorithms have played a crucial role in improving cryogenic natural gas liquefaction processes (Na et al., 2017), hybrid energy storage systems, and battery cycle life estimation for electric vehicles (Shen et al., 2014). By leveraging the power of DIRECT-type algorithms, researchers and engineers have successfully achieved improved energy efficiency, reduced emissions, and optimized energy storage systems.
DIRECT-type algorithms have also found applications in medical imaging and surgery (Wachowiak and Peters, 2006; Wachowiak, 2005), where they have been instrumental in optimizing image registration algorithms, leading to improved precision in medical image analysis. These applications showcase the potential of DIRECT-type algorithms in advancing medical imaging techniques and improving diagnostic and treatment procedures.
The versatility of DIRECT-type algorithms is evident from their vast application in areas such as financial optimization, structural engineering, aerospace (Menon et al., 2007), geophysics (Scitovski and Scitovski, 2013), water and fluid systems (Jasper et al., 2016), molecular biology (Smith et al., 2023), and wireless communication and networking (Verstak et al., 2002). The use of DIRECT-type algorithms in these areas has resulted in significant improvements in decision-making, system performance, and technological advancements.
By analysing the data presented in Table 1 and engaging in the subsequent discussion, we have successfully addressed RQ1 by demonstrating the widespread use of DIRECT-type algorithms in various problem domains, underscoring their versatility and effectiveness.
As optimization research continues to evolve, DIRECT-type solution techniques are expected to find further applications in emerging domains, thus contributing to advancements and innovations in various fields.
3.2.2 Problem Types
The DIRECT algorithm was initially developed to solve global optimization problems with bound constraints (GLB). Despite its initial design for a specific type of problem, the algorithm has demonstrated remarkable versatility and effectiveness, leading to successful extensions that enable it to easily handle a wide range of problem types. In this analysis, we explore the various types of problems that DIRECT-type algorithms have been applied to.
Our study demonstrates the successful application of the algorithm to different problem types, including general nonlinear programming problems (NLP), constrained mixed-integer nonlinear optimization problems (MINLP), multi-objective global optimization problems (MOO), and problems with hidden constraints (GLH). We have identified five main types of problems, namely GLB, GLH, NLP, MINLP, and MOO. The use of DIRECT-type algorithms has expanded to encompass various types of problem beyond box-bounded global optimization.
Through a detailed examination of the data presented in Table 1, we have gained valuable information on RQ2, which delves into the application of DIRECT-type algorithms in various types of problems. However, our analysis highlights that approximately $68\% $ of the studies included in our analysis still utilized DIRECT-type algorithms for global optimization problems restricted only by bound constraints.
3.2.3 Employed DIRECT-Type Algorithms
Our analysis of applications that employ DIRECT-type algorithms has revealed some important findings that provide insight into the current state of utilization and advancements in this field. Although novel DIRECT-type algorithms are continuously being developed, a significant number of applications still rely on the original DIRECT algorithm, as we observed in our study where 13 applications employed the original DIRECT framework. However, recent research, such as the work presented in Stripinis and Paulavičius (2022b), has demonstrated more efficient modifications that exist. Our analysis also identified 13 applications that applied a modified version of the original DIRECT algorithm while retaining its fundamental framework. These modifications mainly comprise adaptations and enhancements tailored to specific problem domains or algorithmic refinements to improve performance.
Our analysis also revealed a recurring trend in the incorporation of DIRECT into hybrid solution techniques, with 21 instances identified. These hybrid DIRECT algorithms integrate the inherent capabilities of the DIRECT framework with other optimization techniques, such as stochastic approaches or local solvers. By combining multiple approaches, these hybrid algorithms take advantage of the complementary strengths of different algorithms for improved optimization capabilities.
Regarding the third research question (RQ3), our findings indicate that real-world applications of DIRECT-type algorithms predominantly involve the use of hybrid techniques. These hybrid techniques combine the strengths of various algorithms to address specific problems that are difficult to solve using a single algorithm alone. The integration of different algorithms into these hybrid approaches offers a more comprehensive and effective solution to complex optimization problems encountered in real-world scenarios.
3.2.4 Implementation Details, Programming Language, and Source Code Availability
Through the analysis of Table 1, noticeable patterns and trends have emerged in terms of implementation, programming language, and availability of source code. The iterative nature of partitioning-based DIRECT-type algorithms often limits the potential for efficient parallelism (Griffin and Kolda, 2010; He et al., 2008, 2009a, 2009b, 2009c; Paulavičius et al., 2013; Stripinis et al., 2021; Watson and Baker, 2001). Consequently, most of the implementations listed in the table are sequential.
However, several cases considered using parallel versions of DIRECT-type algorithms. Typically, parallel applications (Jasper et al., 2016; Ruf et al., 2012; Wachowiak, 2005; Gao and Mi, 2007) were considered due to the substantial cost associated with the evaluation of the models. The authors adopted a straightforward approach to parallel function evaluations for expensive objective functions in the original DIRECT. In contrast, other practical applications employed enhanced DIRECT algorithms, which proved to be more computationally demanding (Baker et al., 2001; Dapšys et al., 2023; He et al., 2004). Two studies (Baker et al., 2001; Dapšys et al., 2023) utilized the “Aggressive” version of the DIRECT algorithm, relaxing the selection of POH criteria and subdividing hyper-rectangles in each iteration of every diameter, leading to improved parallel efficiency. Furthermore, He et al. (2004) proposed a hierarchical parallel scheme for DIRECT, where the initial domain was decomposed into smaller parts and each sub-domain was optimized independently using a master-slave scheme.
The programming languages employed for these implementations exhibit variation, with Matlab being the most frequently mentioned language. In addition, Fortran and C/C++ are utilized in some instances. It is worth noting that some entries in Table 1 indicate that the programming language is unknown, suggesting a lack of available information regarding the specific programming language used in those cases.
Moreover, the present state of sharing experiences within the field is limited and ineffective, posing challenges in reproducibility. Reproducibility is a fundamental aspect of scientific research (López-Ibá nez et al., 2021), and numerous research fields are currently grappling with a reproducibility crisis (Fanelli, 2018). Regarding source code availability, there are only a few instances where authors have made their developments accessible, particularly for implementations in Matlab, Python, and Fortran. Consequently, many promising tools either cease development at the conclusion of a specific project or fail to reach a broader audience of practitioners.
The findings of this analysis underscore the importance of prioritizing source code availability in the field. Openly sharing code has the potential to foster collaboration, improve reproducibility, and propel further advancements in the field. Additionally, offering comprehensive documentation and clear instructions for code implementation and usage can greatly benefit researchers and practitioners seeking to apply these algorithms in their work.
4 Evaluation of Selected Algorithms on Real-World Problem Data Sets
From our examination of the literature, it is evident that the source code for a significant number of applications utilizing DIRECT algorithms is not accessible (see Table 1). This poses a challenge in bridging the systematic and experimental components of the paper. To overcome this limitation, we opted to utilize the 33 practical problems available within the DIRECTGOLib v2.0 (Stripinis et al., 2023), which has recently been extended with two extensive data sets of real-world problems: CEC2011 (Das and Suganthan, 2010) and CEC2020 (Kumar et al., 2020b), many of which feature diverse constraints. To ensure a robust comparison, we carefully selected a set of the most promising DIRECT-type algorithms for global constrained optimization, along with algorithms employed in previous applications. Furthermore, we integrated well-established and widely used state-of-the-art algorithms, some of which demonstrated proficiency in the recent CEC2020 problem set, allowing for a comprehensive comparative analysis.
4.1 Selected Real-World Engineering Problems
Table 2
Details of the selected 32 real-world optimization problems.
| Problem | Dimension | Number of constraints | |
| ID | Name | n | |
| Industrial Chemical Processes | |||
| P01 | Optimal operation of Alkylation unit | 7 | 14 |
| Process Synthesis and Design Problems | |||
| P02 | Process synthesis problem | $\{2,7\}$ | $\{2,9\}$ |
| P03 | Process flow sheeting problem | 3 | 3 |
| P04 | Process design problem | 5 | 3 |
| Mechanical Engineering Problems | |||
| P05 | Multi-product batch plant | 10 | 10 |
| P06 | Weight minimization of a speed reducer | $\{7,7\}$ | $\{11,11\}$ |
| P07 | Optimal design of industrial refrigeration system | 14 | 15 |
| P08 | Tension/compression spring design | $\{3,3,3\}$ | $\{3,3,8\}$ |
| P09 | Pressure vessel design | $\{4,4\}$ | $\{4,6\}$ |
| P10 | Welded beam design | $\{4,4\}$ | $\{5,7\}$ |
| P11 | Truss design problem | $\{2,10\}$ | $\{3,3\}$ |
| P12 | Multiple disk clutch brake design problem | 5 | 7 |
| P13 | Robot gripper problem | 7 | 7 |
| P14 | Hydro-static thrust bearing design problem | 4 | 7 |
| P15 | Four-stage gearbox problem | 22 | 86 |
| P16 | Rolling element bearing | 10 | 9 |
| P17 | Gas transmission compressor design problem | 4 | 1 |
| P18 | Himmelblau’s Function | 5 | 6 |
| P19 | Topology Optimization | 30 | 30 |
| Power Systems and Energy Management | |||
| P20 | Static economic load dispatch problem | $\{6,13,15,40,140\}$ | $\{4,2,4,2,4\}$ |
| P21 | Dynamic economic dispatch problem | $\{120,216\}$ | $\{4,4\}$ |
| P22 | Hydrothermal scheduling problem | $\{96,96,96\}$ | $\{5,6,6\}$ |
| P23 | Wind farm layout problem | 30 | 91 |
| Control and Optimization | |||
| P24 | Tersoff potential function minimization Si (B) | $\{6,12,18\}$ | – |
| P25 | Tersoff potential function minimization Si (C) | $\{6,12,18\}$ | – |
| P26 | Optimal control of a non-linear stirred tank reactor | 1 | – |
| P27 | Bifunctional catalyst blend optimal control problem | 1 | – |
| Molecular Simulation and Material Science | |||
| P28 | Lennard-Jones potential problem | $\{6,12,18\}$ | – |
| Spacecraft Trajectory Optimization | |||
| P29 | Spacecraft trajectory optimization problem | $\{26,22\}$ | – |
| Communication and Radar Systems | |||
| P30 | Spread spectrum radar Polly phase code design | $\{6,12,18\}$ | – |
| P31 | Circular antenna array design problem | 12 | – |
| Parameter Estimation (PE) | |||
| P32 | PE for frequency-modulated sound waves | $\{6,12,18\}$ | – |
| P33 | PE in the general non-linear regression model | $\{3,3,6,6,9,9\}$ | – |
Detailed information regarding the selected problems is presented in Table 2. The table displays various characteristics of these problems, such as the number of decision variables and the number of inequality constraints. The number of decision variables ranges from 1 to 216, while the number of inequality constraints varies from 0 to 91. Several problems have multiple variants, resulting in a total of 63 test scenarios.
We note that DIRECTGOLib v2.0 did not include 36 problems with equality constraints, which were available in the CEC2020 data set. The reason for excluding these problems is that most algorithms struggle to locate feasible points and find them extremely challenging to solve (Kumar et al., 2020b).
4.2 Considered Algorithms in Computational Study
We carefully selected six DIRECT-type algorithms for a thorough computational comparison to solve constrained global optimization problems. Our selection includes two canonical DIRECT-type algorithms, three highly validated DIRECT-type algorithms known for their exceptional performance, and one recently introduced SOTA DIRECT-type algorithm. Performance evaluation of DIRECT-type algorithms has been conducted using six competing algorithms, including well-utilized and high-performing ones from various classes.
4.2.1 DIRECT-Type Algorithms
Canonical DIRECT-Type Algorithms. Following a systematic review, it was observed that the original DIRECT algorithm continues to be commonly used to address real-world problems. Consequently, two canonical algorithms, namely DIRECT-L1and glcSolve, were chosen to represent the original DIRECT algorithm, each employing different constraint-handling techniques. Specifically, DIRECT-L1 uses the exact L1 penalty method while algorithm glcSolve applies the auxiliary function approach.
Benchmark-Approved DIRECT-Type Algorithms. Another DIRECT-type algorithm selected for comparison is the glcCluster algorithm. This algorithm combines the glcSolve algorithm, an adaptive clustering technique, and utilizes the NPSOL local solver. According to a well-established comparison conducted by Rios and Sahinidis (2007), the glcCluster algorithm is considered to be one of the most efficient DFGO algorithms on average. However, recent research conducted by Stripinis et al. (2021) has shown that extensions of DIRECT that employ a two-step selection strategy (Stripinis et al., 2018) are highly competitive and rank among the most efficient solvers of type DIRECT. Based on this finding, we have selected two such techniques, namely DIRECT-GLce-min and DIRECT-GLh, which are based on the DIRECT-GL algorithm. The hybrid algorithm DIRECT-GLce-min includes a special step to find feasible regions, an adaptive auxiliary function method, and the interior-point local solver. On the other hand, the DIRECT-GLh algorithm uses an auxiliary function to handle constraints and incorporates a special step to find a feasible region. The last algorithm was developed primarily for problems with hidden constraints.
Emerging DIRECT-Type Algorithm. The author of the original DIRECT algorithm has recently introduced an extension called simDIRECT (Jones, 2023). This extension boasts impressive capabilities and is suitable for single- and multiple-objectives. It can handle black-box inequality-constrained problems and problems with hidden constraints. However, it should be noted that the algorithm has not been validated using comparative and representative benchmark libraries. The author has only reported initial experience with a few simple optimization problems. Therefore, this paper will present a more detailed analysis of this algorithm on a much more extensive collection of problems of various complexities.
4.2.2 Competing Algorithms
Local Solvers with Random Restarts. First, we opt to include the cobyla algorithm, which uses a trust-region local search method that constructs a linear approximation of the objective function (Powell, 1994). We employed the latter algorithm with randomized restarts.
Evolutionary Computation Methods. In this category, we have ϵsCMAgES, a modified version of the Covariance Matrix Adaptation Evolution Strategy CMA-ES (Kumar et al., 2020a). It incorporates an ϵ-constraint-based ranking and a repair method to handle constraint violations effectively. The other two algorithms within this class are COLSHADE and NNA. The NNA is a dynamic meta-heuristic optimization algorithm inspired by biological nervous systems and artificial neural networks (Sadollah et al., 2018). The COLSHADE is the Differential Evolution (DE) variant (Storn and Price, 1997), improved with an adaptive Levy flight-based mutation to achieve better exploration. Both algorithms combined with the feasible approach to handle the constraint functions (Deb, 2000).
Hybrid Methods. We have also incorporated two hybrid algorithms. The first is LGO-BB, which is a combination of the Lipschitzian-based branch-and-bound algorithm and the Generalized Reduced Gradient (GRG) approach (Holmstrom et al., 2010). This algorithm is one of the most efficient DFGO algorithms on average, according to the study conducted in Rios and Sahinidis (2007). The second method in this category is EA4eig, which utilizes CMA-ES and three different algorithms based on DE with SHBA, LSPR. EA4eig algorithm was declared winner of the CEC2022 competition. We use the penalty function to handle the constraint function in this algorithm.
4.3 Experimental Setup and Termination Criteria
All algorithms used in these studies were implemented using MATLAB. The benchmark suite was evaluated on MATLAB R2023a, running on a PC with the Microsoft Windows 10 operating system, an 8th generation Intel Core i7-8750H processor (6 cores), and 16 GB of RAM.
Due to the unknown global minimums for some of the investigated problems, a fixed limit on the number of function evaluations, ${M_{\max }}={10^{5}}$, was employed. We have applied a time limit, ${T_{\max }}=3600$ seconds, for each run to avoid unexpectedly long algorithm runs or other malfunctions. Once these maximum limits were reached, the algorithms were halted and the best solution found up to that point was recorded. Additionally, to ensure the satisfaction of the constraints, a strict condition was imposed: no constraint violations were allowed. This requirement guarantees that all solutions considered for evaluation and comparison are feasible solutions that adhere to the constraints defined in the optimization problem described by equation (1).
Some of the selected stochastic algorithms (ϵsCMAgES, EA4eig, and COLSHADE) depend on parameter control schemes sensitive to the computational budget available for evaluation. To ensure an unbiased evaluation of the results, we performed additional experiments by decreasing the maximum allowable function evaluation budget to ${M_{\max }}={10^{2}}$, ${M_{\max }}={10^{3}}$, and ${M_{\max }}={10^{4}}$. We executed each stochastic algorithm independently 30 times for a thorough evaluation. This approach helps avoid bias due to a single exceptionally lucky or unlucky algorithmic run. However, it is important to note that repeating non-deterministic methods multiple times in practical applications may not be feasible, especially if the objective function evaluations are computationally expensive. Therefore, we focused on average performance, which is a fair and widely accepted basis for comparing algorithms of different types in the literature. Similarly to the approach used in Rios and Sahinidis (2007), we evaluated the algorithms based on the median metric values derived from the results of 30 different runs.
4.4 Results and Discussions
4.4.1 Comments on the Feasibility Detection
In real-world constraints-related problems, it is common for the feasible region to be much smaller than the entire design space. This makes it challenging to find a feasible solution within a limited number of function evaluations. We evaluated various algorithms for these 37 problems and found that none could achieve feasibility for all the problems. Among the DIRECT-type algorithms, DIRECT-L1, glcSolve, and DIRECT-GLh performed the least effectively, as they lack a dedicated feasibility detection phase. DIRECT-GLh could detect feasible solutions for only $56.76\% $ of the problems. However, this algorithm was primarily designed for problems with hidden constraints and does not utilize its information.
Although most algorithms found feasible solutions for half of the problems in a few hundred function evaluations, it was impossible to achieve the same without using constraint information (DIRECT-GLh), which required more than $2,000$ evaluations. Of all the methods tested, the two evolutionary computation methods (NNA and ϵsCMAgES) were the most successful in finding feasible solutions. The NNA algorithm could not locate feasible solutions for only four problems on average, while ϵsCMAgES failed on one additional problem. Compared to the most successful DIRECT-type algorithm (DIRECT-GLce-min), the algorithm NNA was able to locate feasible solutions for four additional problems. Furthermore, the multi-start algorithm cobyla has a high success rate, providing feasible solutions for $83.78\% $ of the problems within the function evaluation limit.
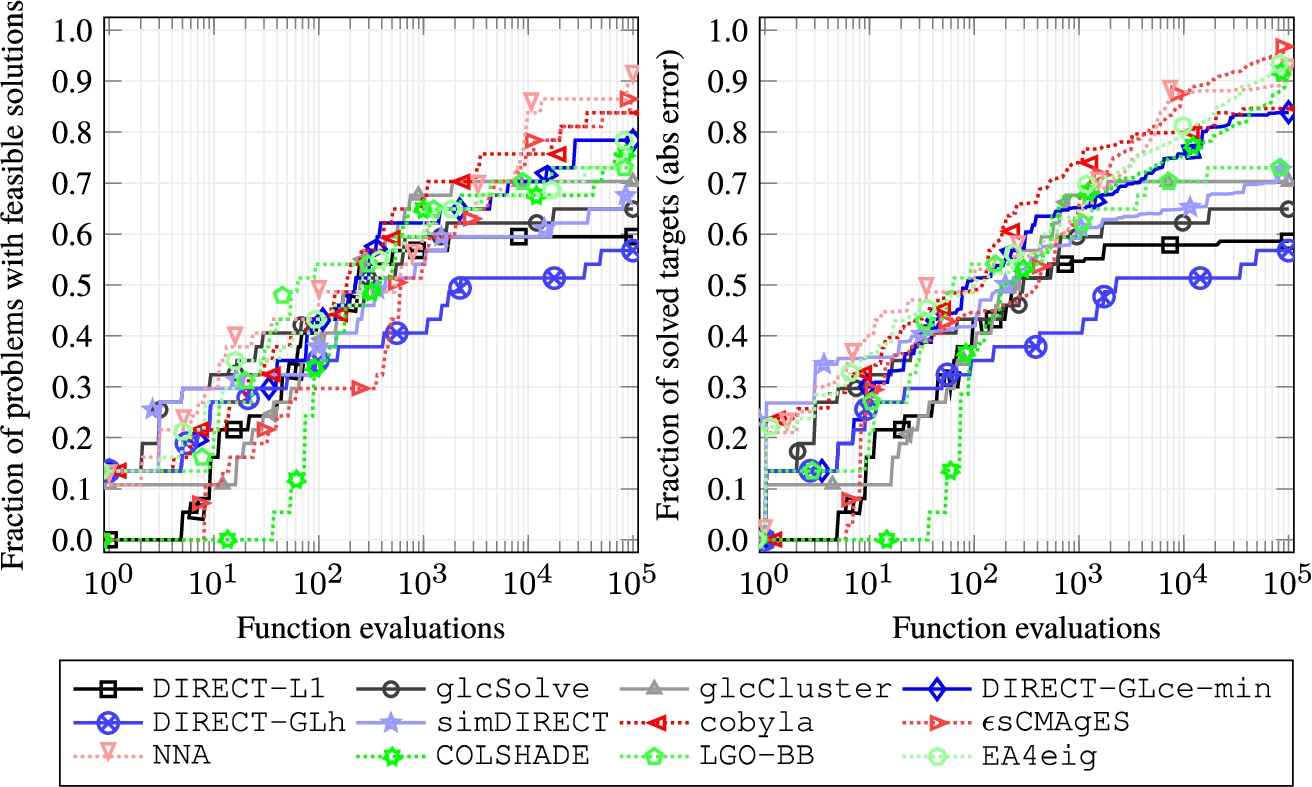
Fig. 5
Left: The fraction of problems (out of 37 problems) for which the algorithms were able to find any feasible solution. Right: Empirical cumulative distribution (ECD) of function evaluations for different target precisions based on the sum of constraint violations.
In our study, we set additional precision targets for the absolute error and analysed the empirical cumulative distribution (ECD) function of the target fraction achieved during evaluations based on the sum of constraint violations. This was done by considering the sum of constraint violations to gain further insights into how algorithms approach the feasible region as the number of function evaluations approaches the limit. The function used for this purpose was defined by the equation:
To evaluate the absolute precision of the algorithms, a total of 51 targets were set, ranging from ${10^{-8}}$ to ${10^{2}}$. This setup is similar to the one utilized in the COCO platform (Hansen et al., 2021). The ECD functions presented on the right side of Fig. 5 provide valuable insight into the performance of the algorithms at different stages of the search process.
Of all the algorithms tested, only four of them achieved more than $\gt 50\% $ of solved targets within 100 function evaluations. Among these algorithms, only one belonged to the DIRECT-type – DIRECT-GLce-min. After conducting a thorough analysis, we found that the NNA algorithm, performed the best when the function evaluation budget was small, that is, less than or equal to 100. However, when the evaluation budget increases, the ϵsCMAgES algorithm demonstrated superior performance. In fact, when the evaluations of the functions reached their maximum, the ϵsCMAgES algorithm outperformed all other competitors with a success rate of $96.82\% $. The EA4eig algorithm came in second place with a success rate of $93.48\% $. The most successful DIRECT-type method (DIRECT-GLce-min) only achieved $83.89\% $ success rate, ranking only sixth.
4.4.2 Evaluating the Impact of Solution Quality
The DIRECT-type algorithm possesses a notable strength in identifying the basin of the global optimum quickly. However, these algorithms may exhibit slower performance in refining solutions to achieve high precision unless solution refinement approaches are implemented (Finkel and Kelley, 2006; Jones and Martins, 2021; Liu et al., 2017; Liu Q. et al., 2015; Stripinis et al., 2018). Consequently, when evaluating the performance of DIRECT-type algorithms, the focus is often on their ability to locate solutions within a certain relative error range rather than to achieve extremely precise solutions, as typically demanded in most CEC competitions (Kumar et al., 2020b). This emphasis comes from the inherent characteristics of DIRECT-type algorithms, which prioritize efficient exploration of the search space and the identification of promising regions rather than placing a heavy emphasis on solution refinement. Consequently, evaluating and applying algorithms of the type DIRECT requires considering specific problem requirements and striking a balance between solution quality and computational efficiency, potentially requiring additional techniques or adaptations to achieve high-precision solutions. For this reason, we evaluate the quality of the solution using rounded numbers with four decimal places.
Table 3
Friedmann mean rank values, using different objective function evaluation budgets.
| Algorithm | ${10^{2}}$ | ${10^{3}}$ | ${10^{4}}$ | ${10^{5}}$ |
| DIRECT-L1 | 6.9127 | 7.6349 | 9.1905 | 9.6429 |
| glcSolve | 5.6349 | 6.5556 | 7.8254 | 8.5397 |
| glcCluster | 7.0238 | 5.9603 | 6.8492 | 7.2937 |
| DIRECT-GLce-min | 7.7222 | 5.1825 | 3.9683 | 4.3651 |
| DIRECT-GLh | 7.3889 | 7.6429 | 7.1984 | 6.8333 |
| simDIRECT | 6.2698 | 6.8730 | 7.5952 | 8.7460 |
| cobyla | 5.5397 | 5.8968 | 6.1825 | 6.5079 |
| ϵsCMAgES | 5.8889 | 5.7619 | 5.3254 | 4.8492 |
| NNA | 5.9841 | 7.5397 | 5.2857 | 5.6349 |
| COLSHADE | 8.8651 | 6.5556 | 6.1111 | 4.6429 |
| LGO-BB | 5.0238 | 5.3730 | 6.5476 | 6.7698 |
| EA4eig | 5.7460 | 7.0238 | 5.9206 | 4.1746 |
| p-value | $\lt {10^{-12}}$ | $\lt {10^{-11}}$ | $\lt {10^{-15}}$ | $\lt {10^{-15}}$ |
To compare the solutions, we performed a statistical analysis using the Friedman rank test (Friedman, 1937) to assess the performance of different algorithms on various computational budgets. The results of this analysis, presented in Table 3, demonstrate significant differences between algorithms, as indicated by the corresponding p-values using a significance level of $5\% $. The algorithms were examined to observe how their relative performance changed as the computational budget increased. A lower rank indicates better performance.
Research findings indicate that algorithms LGO-BB, cobyla, and glcSolve are the top-ranking methods for the smallest budget (${10^{2}}$). However, as the computational budget increases, the ranks of these algorithms gradually decrease, and the DIRECT-L1 and simDIRECT algorithms also join the list of least-performing methods for the largest budget (${10^{5}}$). On the other hand, the algorithms COLSHADE, ϵsCMAgES, and DIRECT-GLh consistently demonstrate improvement within each evaluation budget, and when they reached maximum, the COLSHADE and ϵsCMAgES algorithms had the third and fourth ranks.
The DIRECT-GLce-min algorithm has been shown to be the most efficient DIRECT-type algorithm and emerges as the winner using two evaluation budgets (${10^{3}}$ and ${10^{4}}$). However, when the evaluation budget reaches its maximum, the EA4eig algorithm surpasses the DIRECT-GLce-min algorithm and claims the top ranking. These findings suggest that the choice of algorithm depends on the computational budget available for optimization, and the EA4eig algorithm may provide the best performance for large-budget scenarios.
Performance Comparison Between Problems Constrained by Only Bounds and Those that Additionally Include Inequality Constraints. The performance of optimization algorithms on problems with and without inequality constraints was compared using graphical representations of their Friedman mean ranks in Fig. 6. For problems without inequality constraints, the ϵsCMAgES algorithm performed the best with the smallest evaluation budgets, but the DIRECT-GLce-min algorithm surpassed it by a significant margin when the evaluation budget was larger (${10^{4}}$). When the evaluation budget reached its maximum, the DIRECT-GLce-min and EA4eig algorithms performed similarly, while the ranking of the ϵsCMAgES algorithm dropped to fifth place. The performance of two more algorithms, COLSHADE and DIRECT-GLh, steadily increased and eventually ranked in the third and fourth places accordingly.
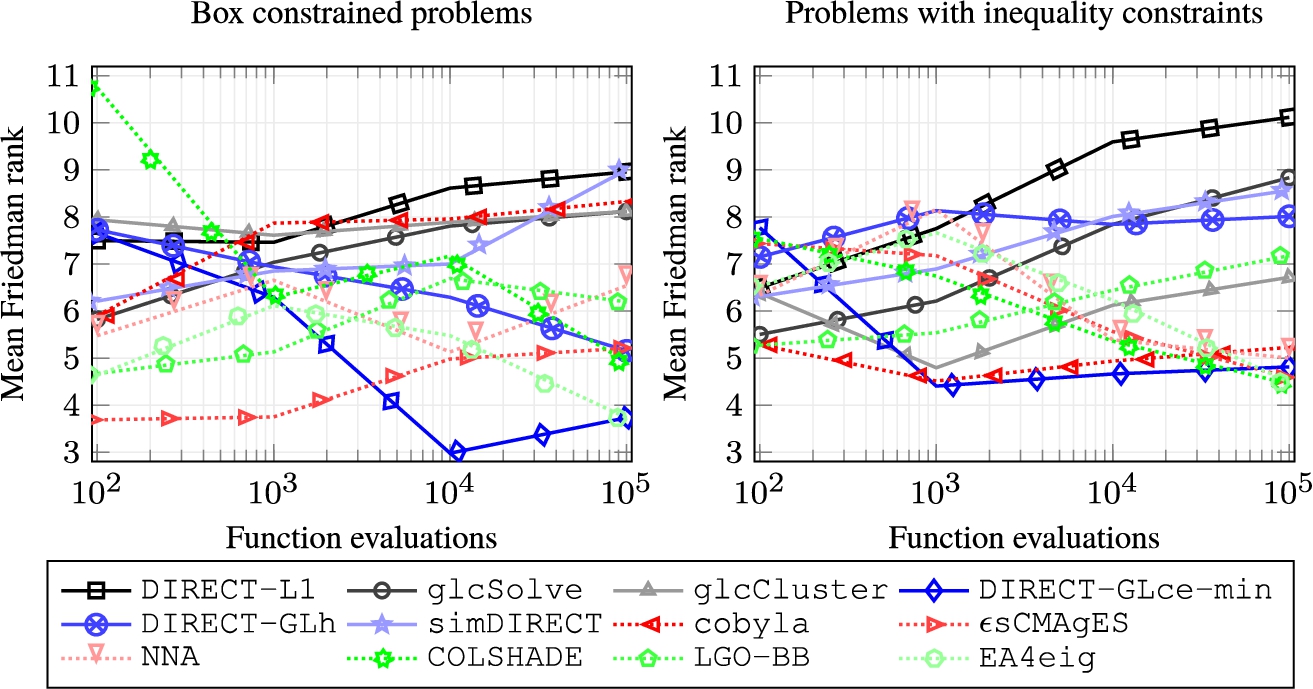
Fig. 6
Graphical comparison of algorithms’ Friedman mean ranks using different function evaluation budgets on problems with and without inequality constraints.
On the other hand, when inequality constraints were introduced, the rankings of the algorithms changed significantly. Although the ϵsCMAgES algorithms performed significantly well on box-constrained problems with small evaluation budgets, it proved to have one of the worst rankings with inequality constraints. In contrast, the algorithm cobyla, one of the worst performers on box-constrained problems, performed very well and remained stable with inequality constraints in all evaluation budgets. Furthermore, the DIRECT-GLce-min algorithm, which is the most efficient DIRECT-type algorithm, was highly competitive with evaluation budgets greater than ${10^{2}}$. However, when the evaluation budget reached its maximum, three algorithms, namely COLSHADE, EA4eig, and ϵsCMAgES slightly outperformed the DIRECT-GLce-min solver.
Performance Comparison on Different Dimensional Sets. In a recent extensive study (Stripinis et al., 2024), it has been found that DIRECT-type algorithms are only competitive on small-dimensional problems. To validate this finding, we divided the problems into two sets, small dimensional ($n\leqslant 12$), and higher dimension ($n\geqslant 13$), and presented graphical representations of the Friedman mean ranks using these two sets in Fig. 7. According to our observations, DIRECT-GLce-min was found to be the most efficient using small-dimensional problems when the evaluation budget was greater than or equal to ${10^{3}}$. The difference between DIRECT-GLce-min and the second-best algorithm, LGO-BB (on ${M_{\max }}={10^{3}}$), and third-best algorithm, ϵsCMAgES (on ${M_{\max }}={10^{4}}$), was quite significant. However, when the evaluation budget reached its maximum, the difference in the Freadman mean rank between the top-performing DIRECT-GLce-min and the second (EA4eig) and third (ϵsCMAgES) best algorithms was minimal.
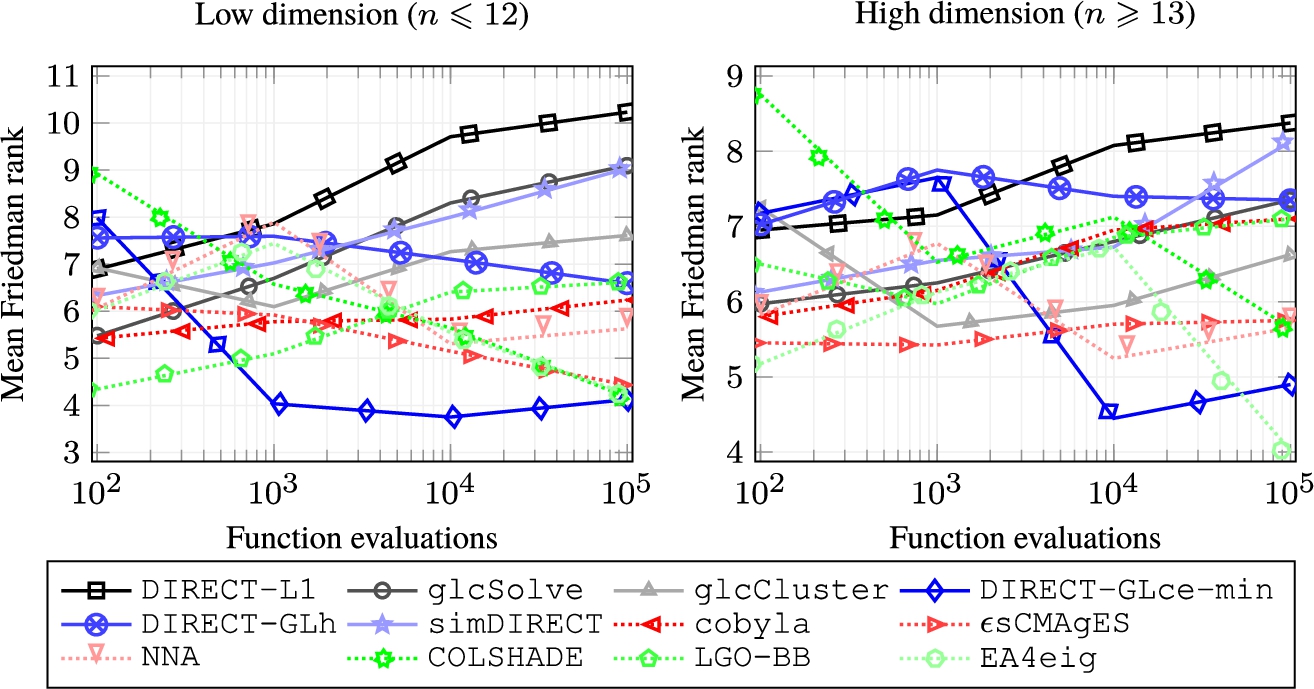
Fig. 7
Graphical comparison of algorithms’ Friedman mean ranks using different function evaluation budgets on problems with different dimensions.
For higher dimensional problems, the difference in Friedman mean ranks was significantly smaller between all algorithms. Only when the evaluation budget was greater than or equal to ${10^{4}}$, the difference in Freidman mean ranks become more spread. Specifically, when the maximum evaluation budget was ${10^{4}}$, the top-performing algorithm with a marginal difference was DIRECT-GLce-min. However, when the maximum evaluation budget was ${10^{5}}$, the EA4eig algorithm showed substantial efficiency and outperformed DIRECT-GLce-min, which ranked second.
4.4.3 Comparing Algorithms Efficiency Based on Function Evaluations
Due to the large number of distinct problems $(63)$ considered in this study, it is not practical to present convergence plots of algorithms for each function and dimension. To overcome this limitation, we employ the ECD function to assess the effectiveness of algorithms in reaching favorable solutions. However, it is important to note that the use of this performance measurement tool is based on the knowledge of problem solutions. To address this requirement, we used the best solutions obtained from this study, rounding them to four decimal places. This allows us to examine how efficiently these solutions can be achieved using various algorithms. For the empirical cumulative distribution (ECD), we establish a total of 51 target values for absolute precision, ranging from ${10^{-4}}$ to ${10^{2}}$.
Fig. 8
ECD of the number of function evaluations for different target precisions based on the best solutions obtained in this study.
The ECD plot in Fig. 8 shows that there is very little difference in algorithm performance with a small evaluation budget (less than or equal to 300). However, as the budget increases, some algorithms perform significantly better, while others do worse. With a larger evaluation budget (500 or more), the DIRECT-type algorithm (DIRECT-GLce-min) demonstrated slightly better performance than any other algorithm and maintained its top performance across all available budgets. However, the DIRECT-GLce-min algorithm was the only DIRECT-type algorithm that showed promising performance compared to six competing algorithms. The closest competitor to DIRECT-GLce-min was the EA4eig algorithm, which on average, solved only about $1\% $ fewer targets within the full evaluation budget. The other five DIRECT-type algorithms showed significantly worse performance. The second and third-best DIRECT-type algorithms, DIRECT-GLh and glcCluster, solved only about $57\% $ of the targets.
5 Conclusion and Discussion
This paper provides a comprehensive examination of the practical application of derivative-free DIRECT-type algorithms to solve real-world optimization problems. The findings of a systematic review of the literature and experimental investigations highlight the efficiency and effectiveness of DIRECT-type algorithms across various domains. While many applications focus on box-bounded problems, there are also successful cases of addressing more complex problems with multiple constraints or multi-objectives. Researchers have proposed modifications to enhance the algorithm’s applicability, with hybrid methods and parallel computing commonly employed. However, the study also reveals limitations in the use of DIRECT-type solution techniques for real-world applications. The lack of shared experiences and the limited availability of developed tools hinder effective comparison, evaluation, and further improvement. This hampers the growth of DIRECT-type systems, as valuable information remains underutilized and poorly disseminated. Furthermore, it is noteworthy that a significant number of applications still rely on the original DIRECT algorithm despite the existence of more advanced and improved alternatives.
This paper also presents an experimental investigation of various DIRECT-type algorithms, including established and emerging ones. The investigation was carried out on a real-world benchmark set, which revealed poor performance of the baseline DIRECT-type algorithms that are still widely used in practical applications. However, recent hybrid extensions of the DIRECT-type algorithm, such as DIRECT-GLce-min, demonstrated highly competitive performance compared to SOTA methods.
Despite the progress made in the field, there is still much work to be done in developing efficient and effective methods for problems with constraints. The experimental investigation also revealed significant limitations of DIRECT-type algorithms, particularly for problems with higher dimensions and finding feasible solutions within given bounds. Future research should focus on addressing these limitations to make DIRECT-type algorithms more attractive and competitive. This requires increased collaboration, knowledge sharing, and the development of comprehensive tools and resources to facilitate the adoption and improvement of DIRECT-type algorithms in practical applications.
Replication and Extension of the Experimental Study
All practical problems are available in the DIRECTGOLib v2.0 repository on GitHub:
Commercial algorithms used in this study can be accessed via the TOMLAB toolbox:
Open-source algorithms used in this study can be accessed:
These resources offer access to the algorithms and data used, making them readily available for use and further research. Authors’ assistance in replication can be obtained upon request.
-
• glcSolve, LGO-BB, and glcCluster: https://tomopt.com
-
• DIRECT-L1, DIRECT-GLce-min, and DIRECT-GLh:
-
• simDIRECT: https://github.com/donaldratnerjones/simDIRECT
-
• cobyla: https://github.com/pdfo/pdfo
-
• COLSHADE and ϵsCMAgES: https://github.com/P-N-Suganthan/2020-RW-Constrained-Optimisation
