1 Introduction
In recent years, productivity and development of today’s organizations have been dependent on some competitive opportunities that arise from competitive environments around the organizations. This is because today’s organizations have changed from the point of view of organizational structure, organizational behaviour, and organizational relationship. An organization can get benefit from its competitive opportunities if its outside environment is fully studied and analysed (Mwesigye and Muhangi,
2015). A typical organization, an educational organization like universities, research centres, higher education centres, etc., responds to the outside environment according to the information and recognition obtained about the outside environment. Higher education organizations of a country play significant roles in the country. Although these organizations may be affected by outside environment seriously, they are effective in national economical and cultural issues (Presmus
et al.,
2003). Based on the literature, outside environment of the higher education sector (in terms of some environmental factors) can seriously influence organizational behaviour in this sector where output and productivity of the employees can be affected by these factors (Robbins and Judge,
2016). Generally, the variables and factors of outside environment of a university are important and the university should be managed and developed according to such environment for achieving the predetermined goals and objectives (Torkzadeh
et al.,
2019). Therefore, we can claim that the environmental factors of an organization, especially organizations from the higher education sector, are important and crucial in all aspects of the organization, specifically its organizational behaviour.
The literature contains numerous studies about the organizational behaviour of general organizations, academic and higher education institutes, and especially the environmental aspect of such behaviour. The studies of Rojas (
2000) and Gita Kumari and Pradhan (
2014) have stated that organizational effectiveness is important for the managers. Torkzadeh and Dehghan Harati (
2015) have concluded that effectiveness is an important index for assessing performance of organizations. They performed the study on the employees of Shiraz University as case study. Ketkar and Sett (
2009) also mentioned that effectiveness can be measured by the employees’ behaviour, financial performance, and operational performance of an organization. Also the works of Nabatchi
et al. (
2007), Zhang and Lee (
2010), and Gita Kumari and Pradhan (
2014) studied the importance of organizational behaviour on productivity and effectiveness of an organization. Robbins and Judge (
2016) studied the importance of organizational behaviour and described it as a set of equipment for understanding, analysing, describing, and managing the behaviour in organizations. According to the study of Kapoor and Jain (
2017), organizational behaviour analyses the impact of people, groups, and structures on improvement and effectiveness of an organization. According to this study, the behaviour in an organization can be studied and analysed in three levels, such as individual, group, and organizational level. Investigating the environmental aspect of organizations and its impact on organizational behaviour is also an important topic which was considered in the studies of Gibson (
2007), Burton and Obel (
2015), and Makolov (
2019). According to the study of Lutans
et al. (
2021), the environmental aspect of organizational behaviour has forced the managers of universities to change their traditional procedures and be more responsible to their inside and outside environments. The studies of Rizvi (
2007) and Mwesigye and Muhangi (
2015) stated that higher education institutes and universities, like other organizations, have been significantly affected by recent developments of the organizational behaviour. The study of Daigle and Cuocco (
2002) is about general responsiveness in higher education. They studied various responsiveness methods in the universities of United States and claim that it is a challenging issue in those universities. Furthermore, Kreysing (
2002) studied the responsiveness and organizational complexity of higher education sector. As a result, they claimed that in order to be more responsive to environmental changes in such organizations, their decentralization level should be increased.
In this study, we focus on the organizational behaviour aspect of higher education sector. This aspect is important in any organization and can help an organization to be successful. The main aim of this study is to analyse the environmental factors which may affect the organizational behaviour in the higher education sector. In this analysis, the aspects, such as importance weights of the factors and their influential impact on each other could be some very important and challenging issues. Therefore, the environmental criteria affecting the organizational behaviour of higher education sector are selected from the literature. We aim to apply the selected criteria and perform a study to determine their effect on the organizational behaviour of higher education sector and prioritize them. This is a new aspect of this field that to the best of our knowledge has not been considered earlier in the literature and can enable the managers to make suitable strategies for managing the organizations. As a solution methodology, some experts from the higher education sector of Iran are selected and are asked to compare the importance of the criteria pair wisely using linguistic terms. Then, in order to respect the uncertain nature of such evaluations, the linguistic terms are converted to interval-valued Pythagorean fuzzy values. Interval-valued Pythagorean fuzzy numbers are used as they keep more information and uncertainty compared to classical fuzzy numbers (see Das and Granados,
2022; Narang
et al.,
2022; Dinçer
et al.,
2023; Younis Al-Zibaree and Konur,
2023; Jafarzadeh Ghoushchi and Sarvi,
2023; Rezazadeh
et al.,
2023). As DEMATEL approach can simultaneously determine importance weight values of the criteria and their influential impact on each other, an interval-valued Pythagorean fuzzy DEMATEL approach is developed for the first time for prioritizing the criteria and performing the causality analysis on them. Finally, the obtained results are interpreted, and some managerial insights are given. In addition, a sensitivity analysis of the proposed approach is performed, and the results are compared to the results obtained by the existing methods of the literature.
The contributions of this study to the literature of the field can be summarized as below:
-
• A real case study is considered and solved.
-
• For the first time, the impact of environmental criteria on organizational behaviour of the higher education sector is studied.
-
• In order to respect the uncertain nature of the problem, opinions of the experts of the field as linguistic terms are converted to interval-valued Pythagorean fuzzy values.
-
• For the first time, interval-valued Pythagorean fuzzy group DEMATEL approach is developed.
The rest of this paper is organized in five sections. In Section
2, some basic concepts of fuzzy sets and numbers are presented. The criteria affecting organizational behaviour of the higher education sector is described in Section
3. As solution approach, an interval-valued Pythagorean fuzzy group DEMATEL approach is developed in Section
4. In continuation, a case study is considered to evaluate the criteria of Section
2, and the numerical results and some remarks about the case study are reported in Section
5. Finally, the conclusions are given in Section
6.
2 Basic Concepts
Zadeh (
1965) introduced fuzzy set theory for the first time. This is a useful theory in order to reflect the uncertain nature of real life systems while modelling them. Therefore, many real life problems are modelled and optimized in a fuzzy based uncertain environment. As the classical fuzzy sets and numbers may have some shortcomings and may not be able to reflect some high degrees of uncertainty, this theory has been developed and modified in the literature (Ali
et al.,
2023; Naseem
et al.,
2023; Mahmoodirad and Niroomand,
2023). For this aim, some newer types of fuzzy sets, such as type-2 fuzzy sets, intuitionistic fuzzy sets, Pythagorean fuzzy sets, etc., have been introduced in the literature (Wang
et al.,
2023; Mishra
et al.,
2023). These newer types of fuzzy sets and numbers reflect more uncertainty of events and parameters.
Pythagorean fuzzy sets and numbers were introduced by Yager (
2013). This type of fuzzy numbers is more flexible and capable to reflect the uncertain nature of an uncertain event. Because of this flexibility and capability, this type of fuzzy numbers are widely used in optimization problems.
Some basic definitions and concepts of Pythagorean fuzzy sets and numbers are given in the rest of this section. These definitions later will be used to construct the solution methodology of this study.
Definition 1 (Otay and Jaller, 2020).
The Pythagorean fuzzy set
$\tilde{P}$ with membership function
${\mu _{\tilde{P}}}(x):X\to [0,1]$ and non-membership function
${\nu _{\tilde{P}}}(x):X\to [0,1]$ with the condition
$0\leqslant {\mu _{\tilde{P}}}{(x)^{2}}+{\nu _{\tilde{P}}}{(x)^{2}}\leqslant 1$ on set
X is defined as below:
Definition 2 (Otay and Jaller, 2020).
The hesitancy degree of the Pythagorean set
$\tilde{P}$ is defined as below:
Definition 3 (Otay and Jaller, 2020).
Considering the Pythagorean fuzzy numbers (PFNs)
$\tilde{X}=\langle {\mu _{1}},{\nu _{1}}\rangle $ and
$\tilde{Y}=\langle {\mu _{2}},{\nu _{2}}\rangle $, and
$\lambda \gt 0$, the following operations can be defined:
Definition 4 (Zhang and Xu, 2014).
Considering the PFNs
$\tilde{X}=\langle {\mu _{1}},{\nu _{1}},{\pi _{\tilde{X}}}\rangle $ and
$\tilde{Y}=\langle {\mu _{2}},{\nu _{2}},{\pi _{\tilde{Y}}}\rangle $, the Euclidean distance of the PFNs is defined as below:
where
${\pi _{\tilde{X}}^{2}}=1-{\mu _{1}^{2}}-{\nu _{1}^{2}}$ is the hesitancy degree of the PFN
$\tilde{X}$.
Definition 5 (Otay and Jaller, 2020).
Considering the interval-valued PFN (IVPFN)
$\tilde{X}=\langle [{\mu _{L}},{\mu _{U}}],[{\nu _{L}},{\nu _{U}}]\rangle $, the hesitancy degrees of its lower and upper points are defined as below, respectively:
Definition 6 (Otay and Jaller, 2020).
Considering the IVPFN
${\tilde{X}_{j}}=\langle [{\mu _{j,L}},{\mu _{j,U}}],[{\nu _{j,L}},{\nu _{j,U}}]\rangle $, where
$j=1,2,\dots ,n$, and the importance weight of
${w_{j}}$, where
${\textstyle\sum _{j=1}^{n}}{w_{j}}=1$, interval-valued Pythagorean fuzzy weighted average (IVPFWA) operator and interval-valued Pythagorean fuzzy weighted geometric (IVPFWG) operator of a set of IVPFNs are defined as below:
Definition 7 (Otay and Jaller, 2020).
The equivalent crisp value (
CR) of the interval-valued PFN (IVPFN)
$\tilde{X}=\langle [{\mu _{L}},{\mu _{U}}],[{\nu _{L}},{\nu _{U}}]\rangle $ is obtained by below formulation.
3 Environmental Criteria Affecting Organizational Behaviour in Higher Education Sector
The environmental aspect of organizational behaviour is an important issue for controlling and effective guidance of the behaviour of members of academic organizations. The managers of academic organizations can recognize and understand the internal behaviour of their organization by focusing on the environmental factors. Assessment of influence of the environmental criteria on the organizational behaviour of academic organizations can be helpful from different points of view, e.g. recognition of the internal behavioural processes of the universities, reaching the goals of universities in organizational behaviour, determining the future goals of universities in organizational behaviour, etc. This might be important to understand the effects of environmental criteria on organizational behaviour in the higher education sector. Therefore, for this aim, the problem of prioritizing and causality analysis of such criteria should be considered. According to the literature of organizational behaviour in higher education sector, the important criteria affecting such organizational behaviour are economic, social, technological, environmental, and professional domain criteria (Torkzadeh
et al.,
2019), where each of these criteria can be divided into several criteria. Based on the literature, Table
1 represents 36 criteria affecting organizational behaviour of the higher education sector.
Table 1
Important criteria selected from the literature for the organizational behaviour assessment problem in academic organizations.
| Criteria index |
Criteria |
Criteria category |
Related references |
| C-1 |
General situation of economy |
Economic criteria |
Voiculet et al. (2010) |
| C-2 |
General life quality |
Economic criteria |
Alcaine (2016) |
| C-3 |
Economic indexes (employment, economic growth, etc.) |
Economic criteria |
Dananjaya and Kuswanto (2015) |
| C-4 |
Income and budget level of country |
Economic criteria |
Voiculet et al. (2010) |
| C-5 |
Economic crises |
Economic criteria |
Alcaine (2016) |
| C-6 |
Governmental (centralized) economy |
Economic criteria |
Alcaine (2016) |
| C-7 |
Internal and foreign investments |
Economic criteria |
Alcaine (2016) |
| C-8 |
Population |
Social criteria |
Voiculet et al. (2010) |
| C-9 |
Social crises |
Social criteria |
Alcaine (2016) |
| C-10 |
Social compatibility |
Social criteria |
Munizu (2010) |
| C-11 |
Social networks |
Social criteria |
O’Brien (2011) |
| C-12 |
Social life style |
Social criteria |
Alcaine (2016) |
| C-13 |
Social solidarity |
Social criteria |
Voiculet et al. (2010) |
| C-14 |
Social behaviour |
Social criteria |
Voiculet et al. (2010) |
| C-15 |
General knowledge of society |
Social criteria |
Voiculet et al. (2010) |
| C-16 |
Social organizations |
Social criteria |
Alcaine (2016) |
| C-17 |
Rules and regulations of the country |
Political criteria |
Voiculet et al. (2010) |
| C-18 |
Political changes |
Political criteria |
Alcaine (2016) |
| C-19 |
International relationships |
Political criteria |
Munizu (2010) |
| C-20 |
Governmental politics |
Political criteria |
Munizu (2010) |
| C-21 |
Political parties |
Political criteria |
Voiculet et al. (2010) |
| C-22 |
General politics of the country |
Political criteria |
Voiculet et al. (2010) |
| C-23 |
IT and ITC developments |
Technological criteria |
Mwesigye and Muhangi (2015) |
| C-24 |
Internet |
Technological criteria |
Beketova (2016) |
| C-25 |
Mobile phone developments |
Technological criteria |
Kirschner and Karpinski (2010) |
| C-26 |
Distance education |
Technological criteria |
Beketova (2016) |
| C-27 |
Science and technology developments |
Technological criteria |
Srikanthan and Dalrymple (2003) |
| C-28 |
Clean technology developments |
Environmental criteria |
Ar (2012) |
| C-29 |
Nature protection |
Environmental criteria |
Ar (2012) |
| C-30 |
Energy efficiency |
Environmental criteria |
Ar (2012) |
| C-31 |
Environmental pollutions |
Environmental criteria |
Ar (2012) |
| C-32 |
Major politics in education |
Professional domain criteria |
Torkzadeh et al. (2019) |
| C-33 |
Relationship with industries |
Professional domain criteria |
Torkzadeh et al. (2019) |
| C-34 |
Competitiveness |
Professional domain criteria |
Voiculet et al. (2010) |
| C-35 |
Innovation and development |
Professional domain criteria |
Voiculet et al. (2010) |
| C-36 |
Essence of higher education |
Professional domain criteria |
Srikanthan and Dalrymple (2003) |
As mentioned earlier, it is an important study to evaluate the effect of the environmental criteria (as mentioned by Table
1) on organizational behaviour of the higher education sector. For this aim, a method for evaluating, prioritizing, and causality analysis of these criteria is needed. For this aim, an interval-valued Pythagorean group DEMATEL approach is developed for the first time in the next section, which performs prioritizing and causality analysis of the criteria of Table
1 on organizational behaviour of higher education sector.
4 Interval-Valued Pythagorean Fuzzy DEMATEL (IVPF-DEMATEL)
In this section, the proposed criteria of Table
1 are analysed and their importance weight values are calculated. There are several methods in the literature that can be used for weight determination of the criteria in MCDM problems (Sahoo and Goswami,
2023). The BWM is a method that determines the criteria weights by comparing the criteria with the best and the worst criteria and then determines all weight values by applying a mathematical model (Rezaei,
2015). The FUCUM (Pamučar
et al.,
2018) is a subjective method of weight determination in MCDM where the relation between consistency and the required number of the comparisons of the criteria are considered. Žižović and Pamucar (
2019) proposed the LBWA method for weight determination purposes. This approach enables the involvement of experts from different fields with the purpose of defining the relations between criteria and providing rational decision making. The DIBR method is another method based on defining the relationship between ranked criteria, i.e. it considers the relationship between adjacent criteria (Pamucar
et al.,
2021).
Here, a solution methodology is proposed in order to evaluate the effect of the environmental criteria on organizational behaviour of the higher education sector as described in Section
3. For this aim, a solution methodology should be applied with the following properties:
-
• to apply the opinions of the experts,
-
• to determine the weight of each criterion,
-
• to assess the impact of given criteria on organizational behaviour of the academic organizations.
For this aim, the DEMATEL approach (see Alinezhad and Khalili,
2019; Nezhad
et al.,
2023) is used. The classical form of the DEMATEL approach is represented by the flowchart of Fig.
1. As mentioned earlier, interval-valued Pythagorean fuzzy values represent more uncertain information compared to Pythagorean fuzzy values and some other types of fuzzy values. Therefore, in this section, the DEMATEL approach is extended to an interval-valued Pythagorean fuzzy form (we call it IVPF-DEMATEL) for evaluating the effect of the environmental criteria on organizational behaviour of higher education sector as described in Section
3.
Fig. 1
Flowchart of the classical DEMATEL approach.
In order to describe the steps of the proposed extended DEMATEL approach with interval-valued Pythagorean fuzzy information (IVPF-DEMATEL), some steps should be followed. These steps are detailed in the rest of this section and depicted in the flowchart of Fig.
2. The notations of this approach are detailed in Table
2 in advance.
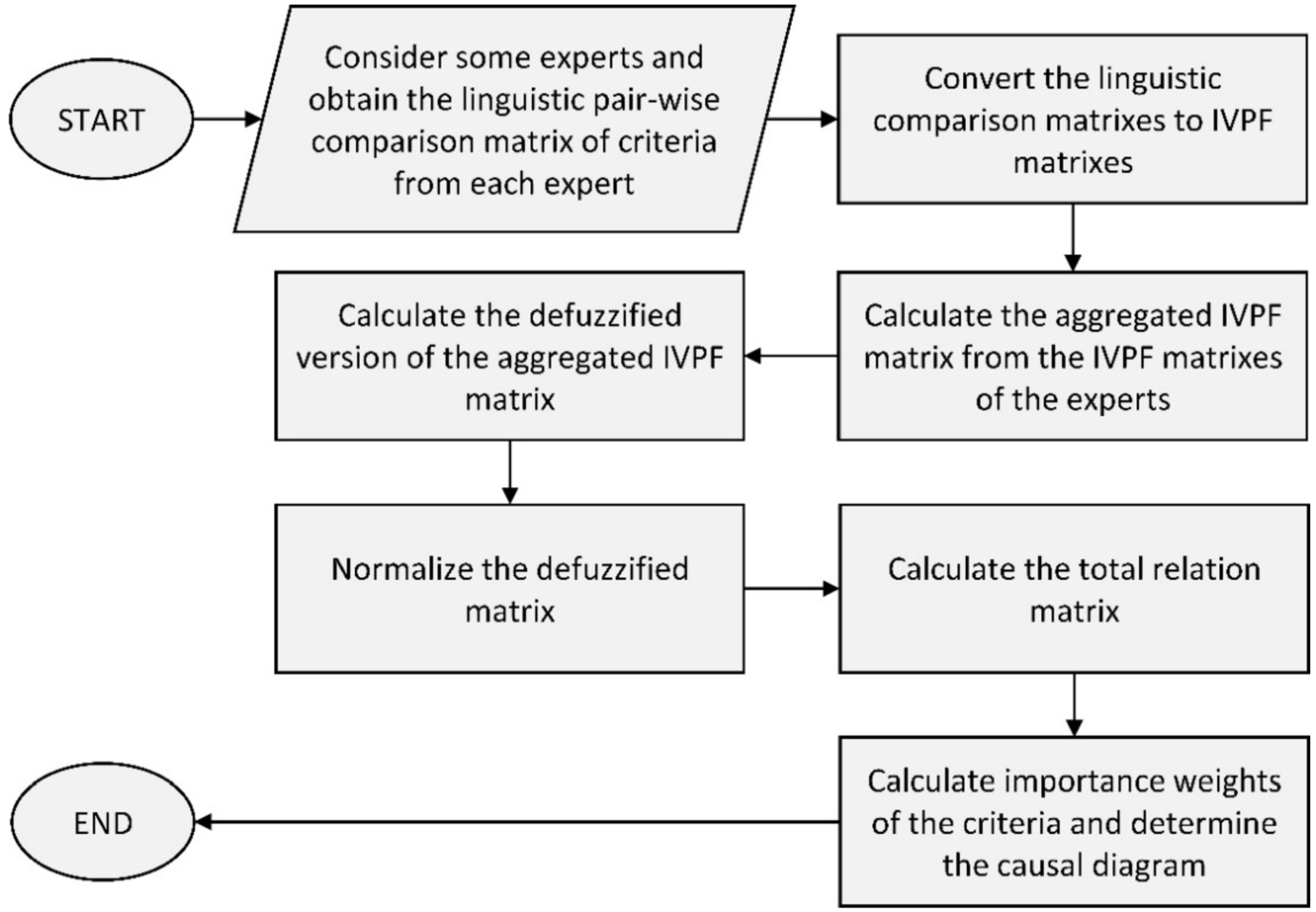
Fig. 2
General framework of the proposed interval-valued Pythagorean fuzzy DEMATEL (IVPF-DEMATEL).
Step 1. A set of criteria (each indexed by $j,k\in \{1,2,\dots ,n\}$) and a set of experts of the field (each indexed by $e\in \{1,2,\dots ,E\}$) are selected.
Table 2
The notations used in the proposed solution methodology.
| Notation |
Description |
| n |
Number of criteria |
| E |
Number of experts |
|
j, k
|
Indexes used for the criteria |
| e |
Index used for the experts |
| ${w_{e}}$ |
Importance weight of expert e
|
| ${\tilde{a}_{jk}^{e}}=\big\langle \big({\mu _{jk,L}^{e}},{\mu _{jk,U}^{e}}\big),\big({\nu _{jk,L}^{e}},{\nu _{jk,U}^{e}}\big)\big\rangle $ |
Equivalent interval-valued Pythagorean fuzzy value for comparing criterion j to k by expert e
|
| $\tilde{{A_{e}}}={[{\tilde{a}_{jk}^{e}}]_{n\times n}}$ |
Interval-valued Pythagorean fuzzy matrix of pairwise comparisons of the criteria |
| ${\tilde{a}_{jk}}=\big\langle ({\mu _{jk,L}},{\mu _{jk,U}}),({\nu _{jk,L}},{\nu _{jk,U}})\big\rangle $ |
Integrated interval-valued Pythagorean fuzzy value for comparing criterion j to k by expert e
|
| $\tilde{A}={[{\tilde{a}_{jk}}]_{n\times n}}$ |
Integrated interval-valued Pythagorean fuzzy matrix of pairwise comparisons of the criteria |
| ${\pi _{jk}^{2}}=\big({\pi _{jk,L}^{2}},{\pi _{jk,U}^{2}}\big)$ |
Interval hesitancy degree of the interval-valued Pythagorean fuzzy value ${\tilde{a}_{jk}^{e}}$
|
| $A={[{a_{jk}}]_{n\times n}}$ |
The crisp matrix which is obtained instead of $\tilde{A}={[{\tilde{a}_{jk}}]_{n\times n}}$
|
| $N={[n{a_{jk}}]_{n\times n}}$ |
The normalized form of the crisp matrix $A={[{a_{jk}}]_{n\times n}}$
|
| $T={[{t_{jk}}]_{n\times n}}$ |
Total-relation matrix |
| ${R_{j}}$ |
Sum of row values for criterion j in the total-relation matrix |
| ${C_{j}}$ |
Sum of column values for criterion j in the total-relation matrix |
| ${\omega _{j}}$ |
The importance weight value of criterion j
|
Step 2. Each expert is requested to complete the linguistic comparison matrix of the criteria (the linguistic terms are shown in the left column of Table
3). Based on the numerical values of Table
3, the linguistic comparison matrix is converted to an interval-valued Pythagorean fuzzy matrix such as
$\tilde{{A_{e}}}={[{\tilde{a}_{jk}^{e}}]_{n\times n}}$ for expert
e, where
${\tilde{a}_{jk}^{e}}=\langle ({\mu _{jk,L}^{e}},{\mu _{jk,U}^{e}}),({\nu _{jk,L}^{e}},{\nu _{jk,U}^{e}})\rangle $ is the equivalent interval-valued Pythagorean fuzzy value for comparing criterion
j to
k (importance or influence of
j to
k).
Step 3. The IVPF matrixes obtained from the experts are integrated into one matrix shown as
$\tilde{A}={[{\tilde{a}_{jk}}]_{n\times n}}$ (where
${\tilde{a}_{jk}}=\langle ({\mu _{jk,L}},{\mu _{jk,U}}),({\nu _{jk,L}},{\nu _{jk,U}})\rangle $) using the IVPFWG operator described in Section
2 as below:
where
${w_{e}}$ is the importance weight of expert
e.
Table 3
Linguistic terms for comparing the criteria in the proposed IVPF-DEMATEL (modified version of Otay and Jaller,
2020).
| Linguistic term |
Equivalent interval-valued Pythagorean fuzzy number $\big\langle ({\mu _{jk,L}^{e}},{\mu _{jk,U}^{e}}),\hspace{2.5pt}({\nu _{jk,L}^{e}},{\nu _{jk,U}^{e}})\big\rangle $
|
| Certainly low influence (CLI) |
$\big\langle (0.00,0.00),(0.90,1.00)\big\rangle $ |
| Very low influence (VLI) |
$\big\langle (0.10,0.20),(0.80,0.90)\big\rangle $ |
| Low influence (LI) |
$\big\langle (0.20,0.35),(0.65,0.80)\big\rangle $ |
| Below average influence (BAI) |
$\big\langle (0.35,0.45),(0.55,0.65)\big\rangle $ |
| Average influence (AI) |
$\big\langle (0.45,0.55),(0.45,0.55)\big\rangle $ |
| Above average influence (AAI) |
$\big\langle (0.55,0.65),(0.35,0.45)\big\rangle $ |
| High influence (HI) |
$\big\langle (0.65,0.80),(0.20,0.35)\big\rangle $ |
| Very high influence (VHI) |
$\big\langle (0.80,0.90),(0.10,0.20)\big\rangle $ |
| Certainly high influence (CHI) |
$\big\langle (0.90,1.00),(0.00,0.00)\big\rangle $ |
| No influence (NI) |
$\big\langle (0.00,0.00),(0.00,0.00)\big\rangle $ |
Step 4. The values of the fuzzy matrix
$\tilde{A}={[{\tilde{a}_{jk}}]_{n\times n}}$ are deffuzified using the below equation:
Therefore, the crisp matrix
$A={[{a_{jk}}]_{n\times n}}$ is obtained instead of
$\tilde{A}={[{\tilde{a}_{jk}}]_{n\times n}}$.
Step 5. Each value of the crisp matrix
$A={[{a_{jk}}]_{n\times n}}$ is normalized by the below equation in order to obtain the normalized matrix
$N={[n{a_{jk}}]_{n\times n}}$:
Step 6. The total-relation matrix (
$T={[{t_{jk}}]_{n\times n}}$) is obtained by below equation:
In equation (
19),
I is the unit matrix, and
${(I-N)^{-1}}$ is the inverse form of matrix
$I-N$.
Step 7. The causal diagram is constructed in this step. For this aim, for each criterion in the total-relation matrix the sum of row values (
${R_{j}}$) and the sum of column values (
${C_{j}}$) are calculated using below equations:
On the causal diagram, a point is depicted for each criterion. The horizontal axis of this diagram shows the importance weights of the criteria, and the vertical axis shows the degree of relation for the criteria. The coordinate of criterion j is obtained as $({R_{j}}+{C_{j}},{R_{j}}-{C_{j}})$. For the case of ${R_{j}}-{C_{j}}\gt 0$, the criterion is effective and is categorized as cause class. For the case of ${R_{j}}-{C_{j}}\lt 0$, the criterion is susceptive and is categorized as effect class.
5 Computational Study
In this section, the solution methodology proposed by Section
4 is implemented to evaluate the environmental criteria influencing the organizational behaviour of academic sector described by Section
3 for the case of higher education sector of Iran. For this aim, the following issues are considered.
-
• Based on Section
3, number of the environmental criteria is
$n=36$, which are detailed in Table
1.
-
• In order to perform the proposed solution methodology, number of the experts is set to $E=3$, therefore, $e=1,2,3$. These experts are selected from the higher education sector of Iran and all of them have at least 5 years of managerial experience in this sector.
-
• Each expert is asked to evaluate the pairwise comparison of the criteria of Table
1 according to the linguistic terms of Table
3. Then each linguistic term of the pairwise comparisons is converted to its equivalent IVPFN using the rules of Table
3. Therefore, three
$36\times 36$ comparison matrixes are obtained, such as
${A_{e}}={[{\tilde{a}_{jk}^{e}}]_{36\times 36}}$, where
$e=1,2,3$.
The proposed solution methodology of Section
4 is coded in MATLAB and is run for the case study on a PC with Core i7 and 2.8 GHz CPU and 16 GB RAM. In the rest of this section, first the results obtained by the proposed solution methodology are presented and discussed, then a comparative study considering the approaches of the literature is performed and the obtained results are presented.
5.1 Results Obtained by the Proposed IVPF-DEMATEL
The proposed IVPF-DEMATEL is applied to evaluate the environmental criteria of the organizational behaviour of the higher education sector described in Section
3 (see Table
1). For this aim, the steps of the IVPF-DEMATEL described in Section
4 are implemented. As mentioned, three experts of the field are selected to evaluate the pairwise influences of the criteria according to the linguistic terms of Table
3. Then according to the conversion of Table
3, the linguistic terms are converted to IVPF values. Therefore, for each expert a comparison matrix of the criteria with IVPF values is obtained. After this step, the IVPF matrixes of the experts are integrated by the IVPFWG operator (using equations (
13)–(
16)), and the obtained integrated matrix is defuzzified by Eq. (
17). It is worth to mention that in this step, the experts are weighted equally as
${w_{1}}={w_{2}}={w_{3}}=\frac{1}{3}$. Then, the obtained crisp matrix is normalized by equation (
18), and after that, the total relation matrix is obtained by Eq. (
19). Finally, in the last step, for each criterion the values of
${R_{j}}$,
${C_{j}}$,
${R_{j}}+{C_{j}}$, and
${R_{j}}-{C_{j}}$ are obtained using equations (
20)–(
21). As mentioned earlier, the value of
${R_{j}}-{C_{j}}$ determines the cause or effect category of the criterion and
${R_{j}}+{C_{j}}$ shows the importance degree of the criterion. Therefore, the importance weight value of criterion
j is shown by
${\omega _{j}}$ and is calculated by the below formulation as a normalized value.
Based on the above-mentioned procedure, the results of applying the proposed IVPF-DEMATEL for evaluating the impact of the criteria of Section
3 (Table
13) on the organizational behaviour of higher education sector, are obtained and represented by Table
4 and Fig.
3.
Table 4
The values of ${R_{j}}$, ${D_{j}}$, ${R_{j}}+{C_{j}}$, and ${R_{j}}-{C_{j}}$ obtained by applying the proposed IVPF-DEMATEL.
| Criterion (j) |
${R_{j}}$ |
${C_{j}}$ |
${R_{j}}+{C_{j}}$ |
${R_{j}}-{C_{j}}$ |
Cause/effect |
Criterion (j) |
${R_{j}}$ |
${C_{j}}$ |
${R_{j}}+{C_{j}}$ |
${R_{j}}-{C_{j}}$ |
Cause/effect |
| C-1 |
2.549 |
2.605 |
5.154 |
−0.056 |
Effect |
C-19 |
3.234 |
2.295 |
5.529 |
0.939 |
Cause |
| C-2 |
2.741 |
2.311 |
5.052 |
0.430 |
Cause |
C-20 |
3.395 |
1.984 |
5.379 |
1.411 |
Cause |
| C-3 |
3.085 |
2.386 |
5.471 |
0.699 |
Cause |
C-21 |
2.965 |
2.321 |
5.286 |
0.644 |
Cause |
| C-4 |
3.162 |
2.350 |
5.512 |
0.812 |
Cause |
C-22 |
3.343 |
2.086 |
5.429 |
1.257 |
Cause |
| C-5 |
3.048 |
2.190 |
5.238 |
0.858 |
Cause |
C-23 |
2.772 |
2.526 |
5.298 |
0.246 |
Cause |
| C-6 |
2.445 |
2.828 |
5.273 |
−0.383 |
Effect |
C-24 |
2.770 |
2.567 |
5.337 |
0.203 |
Cause |
| C-7 |
2.266 |
2.605 |
4.871 |
−0.339 |
Effect |
C-25 |
1.701 |
2.822 |
4.523 |
−1.121 |
Effect |
| C-8 |
2.405 |
2.027 |
4.432 |
0.378 |
Cause |
C-26 |
2.404 |
2.419 |
4.823 |
−0.015 |
Effect |
| C-9 |
2.583 |
2.027 |
4.610 |
0.556 |
Cause |
C-27 |
2.527 |
2.486 |
5.013 |
0.041 |
Cause |
| C-10 |
1.739 |
2.707 |
4.446 |
−0.968 |
Effect |
C-28 |
1.945 |
2.903 |
4.848 |
−0.958 |
Effect |
| C-11 |
2.115 |
2.575 |
4.690 |
−0.460 |
Effect |
C-29 |
1.653 |
2.997 |
4.65 |
−1.344 |
Effect |
| C-12 |
1.742 |
2.699 |
4.441 |
−0.957 |
Effect |
C-30 |
1.626 |
3.028 |
4.654 |
−1.402 |
Effect |
| C-13 |
2.212 |
2.738 |
4.950 |
−0.526 |
Effect |
C-31 |
1.172 |
3.234 |
4.406 |
−2.062 |
Effect |
| C-14 |
2.397 |
2.765 |
5.162 |
−0.368 |
Effect |
C-32 |
2.608 |
2.195 |
4.803 |
0.413 |
Cause |
| C-15 |
2.768 |
2.534 |
5.302 |
0.234 |
Cause |
C-33 |
2.665 |
2.409 |
5.074 |
0.256 |
Cause |
| C-16 |
1.796 |
3.123 |
4.919 |
−1.327 |
Effect |
C-34 |
2.608 |
2.533 |
5.141 |
0.075 |
Cause |
| C-17 |
2.892 |
2.038 |
4.930 |
0.854 |
Cause |
C-35 |
2.574 |
2.539 |
5.113 |
0.035 |
Cause |
| C-18 |
3.434 |
2.068 |
5.502 |
1.366 |
Cause |
C-36 |
2.964 |
2.383 |
5.347 |
0.581 |
Cause |
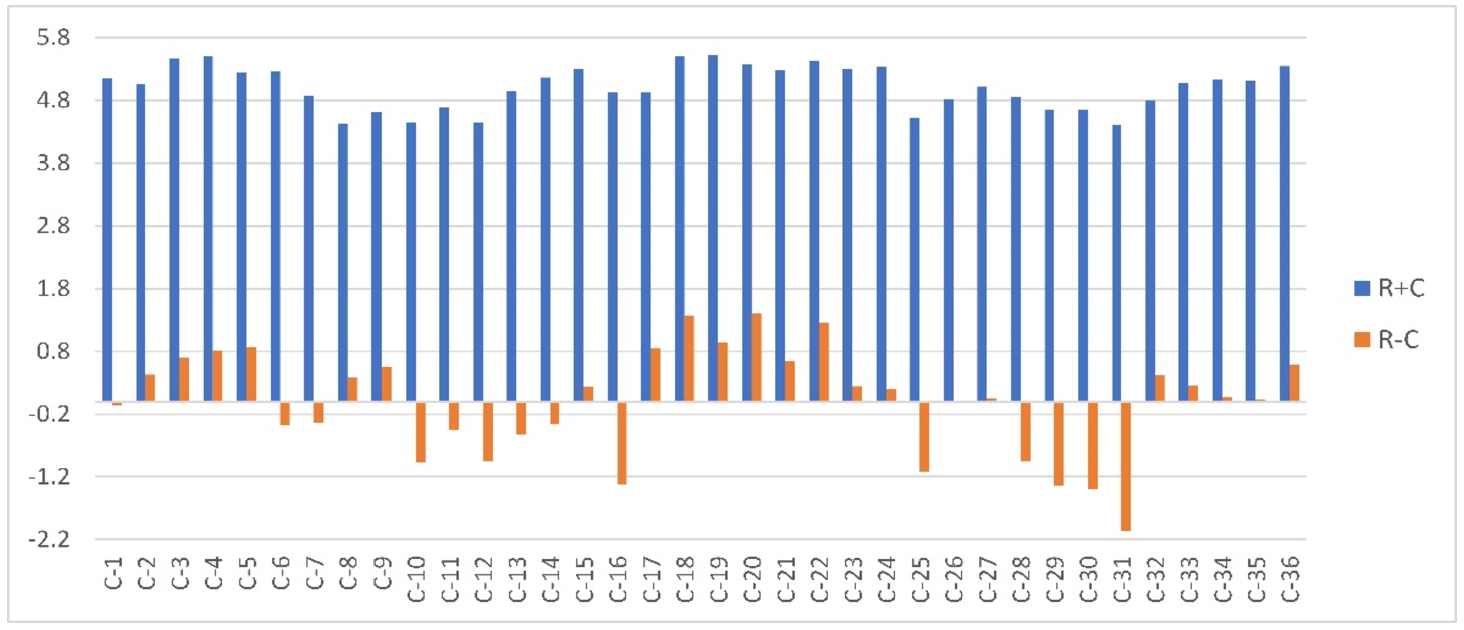
Fig. 3
Cause and effect diagram containing
${R_{j}}+{C_{j}}$ and
${R_{j}}-{C_{j}}$ values of Table
4.
According to the results of Table
4, 21 criteria are placed in the cause category and 15 criteria are placed in the effect category. According to these results, the criteria such as general life quality (C-2), economic indexes (C-3), income and budget level of country (C-4), economic crises (C-5), population (C-8), social crises (C-9), general knowledge of society (C-15), rules and regulations of the country (C-17), political changes (C-18), international relationships (C-19), governmental politics (C-20), political parties (C-21), general politics of the country (C-22), IT and ITC developments (C-23), internet (C-24), science and technology developments (C-27), major politics in education (C-32), relationship with industries (C-33), competitiveness (C-34), innovation and development (C-35), and essence of higher education (C-36) are cause criteria where their influential effect is higher. On the other hand, the criteria such as general situation of economy (C-1), governmental (centralized) economy (C-6), internal and foreign investments (C-7), social compatibility (C-10), social networks (C-11), social life style (C-12), social solidarity (C-13), social behaviour (C-14), social organizations (C-16), mobile phone developments (C-25), distance education (C-26), clean technology developments (C-28), nature protection (C-29), energy efficiency (C-30), and environmental pollutions (C-31) are effect criteria where their influential effect is higher. The cause and effect diagram of the criteria is also depicted in Fig.
3. In this figure, the cause and effect categories of the criteria can be easily noted.
The obtained results can be interpreted in a summarized form. The criteria of the cause category are of the economic, political, and professional domain based criteria. This shows that the organizational behaviour of the higher education sector of Iran is mainly affected by these types of criteria.
Furthermore, the values obtained for
${R_{j}}+{C_{j}}$ show the importance of the criteria. As can be seen from Table
4 and Fig.
3, most of the criteria from the cause category have higher value of
${R_{j}}+{C_{j}}$ compared to the criteria of the effect category. In order to obtain the normalized importance of the criteria (
${\omega _{j}}$), Eq. (
22) is used and the obtained
${\omega _{j}}$ values are presented in Table
5. In this table, according to the values of
${\omega _{j}}$, the criteria are ranked, and their ranking is reported as well. As can be seen, the first ranked criterion is C-19, which is of the cause category, and the last ranked criterion is C-31, which is of the effect category.
Table 5
The importance weight values and the ranking of the criteria obtained by applying the proposed IVPF-DEMATEL.
| Criterion (j) |
${R_{j}}+{C_{j}}$ |
${\omega _{j}}$ |
Ranking |
Criterion (j) |
${R_{j}}+{C_{j}}$ |
${\omega _{j}}$ |
Ranking |
| C-1 |
5.154 |
0.02853 |
15 |
C-19 |
5.529 |
0.03061 |
1 |
| C-2 |
5.052 |
0.02797 |
19 |
C-20 |
5.379 |
0.02978 |
6 |
| C-3 |
5.471 |
0.03029 |
4 |
C-21 |
5.286 |
0.02926 |
11 |
| C-4 |
5.512 |
0.03051 |
2 |
C-22 |
5.429 |
0.03005 |
5 |
| C-5 |
5.238 |
0.02900 |
13 |
C-23 |
5.298 |
0.02933 |
10 |
| C-6 |
5.273 |
0.02919 |
12 |
C-24 |
5.337 |
0.02955 |
8 |
| C-7 |
4.871 |
0.02697 |
24 |
C-25 |
4.523 |
0.02504 |
32 |
| C-8 |
4.432 |
0.02453 |
35 |
C-26 |
4.823 |
0.02670 |
26 |
| C-9 |
4.610 |
0.02552 |
31 |
C-27 |
5.013 |
0.02775 |
20 |
| C-10 |
4.446 |
0.02461 |
33 |
C-28 |
4.848 |
0.02684 |
25 |
| C-11 |
4.690 |
0.02596 |
28 |
C-29 |
4.65 |
0.02574 |
30 |
| C-12 |
4.441 |
0.02458 |
34 |
C-30 |
4.654 |
0.02576 |
29 |
| C-13 |
4.950 |
0.02740 |
21 |
C-31 |
4.406 |
0.02439 |
36 |
| C-14 |
5.162 |
0.02858 |
14 |
C-32 |
4.803 |
0.02659 |
27 |
| C-15 |
5.302 |
0.02935 |
9 |
C-33 |
5.074 |
0.02809 |
18 |
| C-16 |
4.919 |
0.02723 |
23 |
C-34 |
5.141 |
0.02846 |
16 |
| C-17 |
4.930 |
0.02729 |
22 |
C-35 |
5.113 |
0.02830 |
17 |
| C-18 |
5.502 |
0.03046 |
3 |
C-36 |
5.347 |
0.02960 |
7 |
5.2 Impact of the Results and Managerial Insights
The results obtained from the proposed IVPF-DEMATEL and represented in Section
5.1 can be applied by managers of higher education sector in order to manage and improve organizational behaviour of that sector. The following managerial implications and insights can be considered from the obtained results.
-
• In general, managers should concentrate on the cause category of criteria (Fontela and Gabus,
1976).
-
• According to the obtained results, most of economic, political, and professional domain criteria are of the cause category. This means that these criteria should be taken into account more by the managers of the higher education sector of Iran for improving the organizational behaviour of that sector.
-
• The criteria with higher importance weight values like C-19 (international relationships), C-4 (income and budget level of country), C-18 (political changes), C-3 (economic indexes (employment, economic growth, etc.)), etc. are the most important criteria to focus on for the managers in the higher education sector of Iran. This shows that the organizational behaviour of the higher education sector of Iran can be sensitive to international relationships, economic criteria, and political changes.
-
• According to the obtained results, the environmental criteria such as C-28 (clean technology developments), C-29 (nature protection), C-30 (energy efficiency), and C-31 (environmental pollutions) are in the effect category and also obtain least importance weight values. Actually, this class of criteria are out of control of the managers of the higher education sector of Iran and need to be managed by the government directly.
5.3 Sensitivity Analysis
In this section, a sensitivity analysis is performed in order to study the behaviour of the proposed IVPF-DEMATEL approach over some possible variations. Two types of variations can be made in the proposed approach that are explained below.
-
• As in Section
2, two integrating operators of interval-valued Pythagorean fuzzy numbers are defined, such as IVPFWG and IVPFWA, Step 3 of the proposed IVPF-DEMATEL approach can be performed by each of the IVPFWG and IVPFWA operators. Therefore, by applying the operators IVPFWG and IVPFWA, the proposed approach can be titled as IVPFWG-DEMATEL and IVPFWA-DEMATEL, respectively.
-
• Considering each of the IVPFWG-DEMATEL and IVPFWA-DEMATEL approaches, the importance weight values of the experts can be changed. For this aim four experiments of Table
6 are defined.
It is notable to mention that the IVPFWG-DEMATEL approach with the weight values of Experiment 1 has been performed in Section
5.1 and the obtained results have been analysed there. Therefore, in this section, the scenarios of Table
7 are considered for sensitivity analysis of the proposed IVPF-DEMATEL.
Table 6
Different weight combinations of the experts for sensitivity analysis.
| Experiment |
Importance weight (${w_{e}}$) |
| Expert 1 ($e=1$) |
Expert 2 ($e=2$) |
Expert 3 ($e=3$) |
| 1 |
0.33 |
0.33 |
0.33 |
| 2 |
0.60 |
0.30 |
0.10 |
| 3 |
0.10 |
0.60 |
0.30 |
| 4 |
0.30 |
0.1 |
0.60 |
Table 7
Different scenarios defined for sensitivity analysis of the proposed IVPF-DEMATEL.
| Scenario |
Experiment |
Operator |
Note |
| 1 |
1 |
IVPFWG |
The proposed IVPF-DEMATEL is titled as IVPFWG-DEMATEL |
| 2 |
2 |
| 3 |
3 |
| 4 |
4 |
| 5 |
1 |
IVPFWA |
The proposed IVPF-DEMATEL is titled as IVPFWA-DEMATEL |
| 6 |
2 |
| 7 |
3 |
| 8 |
4 |
The results obtained for the scenarios of Table
7 are represented in Table
8, Table
9, and Fig.
4. These results can be analysed from two points of view, such as the difference between cause and effect results among the scenarios, and the difference between the importance weights or rankings of the criteria among the scenarios. According to the results of Table
8, when the IVPFWG-DEMATEL is used, the cause and effect results of scenarios 1 to 4 (changing in the importance weights of the experts) are compared. In this case, only the cause and effect results of 22.22% of the criteria are changed. For other criteria, these results among the scenarios remain unchanged. For the case of IVPFWA-DEMATEL and scenarios 5 to 8, also the cause and effect results of 22.22% criteria are changed. Furthermore, any pair of the scenarios with similar experiment (similar set weight values of the experts) can be compared to investigate the impact of the operators IVPFWG and IVPFWA of the obtained cause and effect results. For this aim, the following results are obtained.
-
• Comparing the results obtained by experiment 1 for the IVPFWG-DEMATEL and the IVPFWA-DEMATEL (scenarios 1 and 5), the cause and effect results for only 2.77% of the criteria are changed.
-
• Comparing the results obtained by experiment 2 for the IVPFWG-DEMATEL and the IVPFWA-DEMATEL (scenarios 2 and 6), the cause and effect results for only 8.33% of the criteria are changed.
-
• Comparing the results obtained by experiment 3 for the IVPFWG-DEMATEL and the IVPFWA-DEMATEL (scenarios 3 and 7), the cause and effect results for only 11.11% of the criteria are changed.
-
• Comparing the results obtained by experiment 4 for the IVPFWG-DEMATEL and the IVPFWA-DEMATEL (scenarios 4 and 8), the cause and effect results for only 13.88% of the criteria are changed.
Table 8
The cause and effect results of the criteria obtained by the proposed IVPF-DEMATEL for all of the scenarios.
| Criterion |
Scenario 1 |
Scenario 2 |
Scenario 3 |
Scenario 4 |
Scenario 5 |
Scenario 6 |
Scenario 7 |
Scenario 8 |
| C-1 |
Effect |
Effect |
Effect |
Cause |
Effect |
Effect |
Effect |
Effect |
| C-2 |
Cause |
Cause |
Cause |
Cause |
Cause |
Effect |
Cause |
Cause |
| C-3 |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
| C-4 |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
| C-5 |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
| C-6 |
Effect |
Cause |
Effect |
Effect |
Effect |
Cause |
Effect |
Effect |
| C-7 |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
| C-8 |
Cause |
Effect |
Cause |
Cause |
Cause |
Effect |
Cause |
Cause |
| C-9 |
Cause |
Effect |
Cause |
Cause |
Cause |
Effect |
Cause |
Cause |
| C-10 |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
| C-11 |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
Cause |
Effect |
| C-12 |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
| C-13 |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
| C-14 |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
| C-15 |
Cause |
Cause |
Cause |
Cause |
Cause |
Effect |
Cause |
Cause |
| C-16 |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
| C-17 |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
| C-18 |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
| C-19 |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
| C-20 |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
| C-21 |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
| C-22 |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
| C-23 |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
| C-24 |
Cause |
Cause |
Cause |
Effect |
Cause |
Cause |
Cause |
Cause |
| C-25 |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
| C-26 |
Effect |
Effect |
Cause |
Cause |
Effect |
Effect |
Effect |
Effect |
| C-27 |
Cause |
Cause |
Effect |
Effect |
Cause |
Cause |
Cause |
Cause |
| C-28 |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
| C-29 |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
| C-30 |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
| C-31 |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
Effect |
| C-32 |
Cause |
Effect |
Cause |
Cause |
Cause |
Effect |
Cause |
Cause |
| C-33 |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
| C-34 |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
Effect |
Cause |
| C-35 |
Cause |
Cause |
Effect |
Cause |
Effect |
Effect |
Effect |
Effect |
| C-36 |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
Cause |
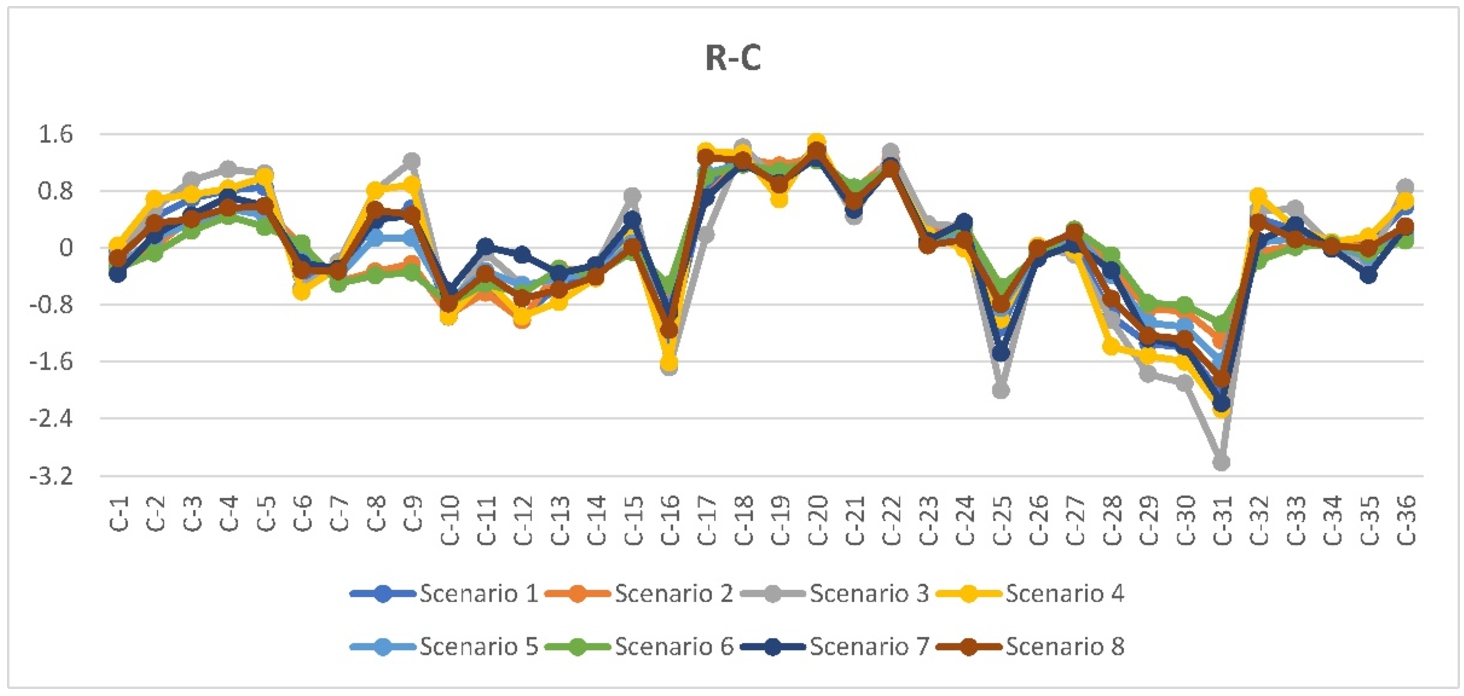
Fig. 4
The graph of ${R_{j}}-{C_{j}}$ values of the criteria obtained by the proposed IVPF-DEMATEL for all of the scenarios.
On the other hand, the results of the scenarios in terms of the ranking of the criteria can be compared to investigate the sensitivity of the proposed IVPF-DEMATEL approach. The importance weight of each criterion in each scenario is obtained by formula (
22). The obtained weight values are used to rank the criteria in each scenario. The obtained importance weight values and associated ranking in each scenario are represented by Table
8. Here, the obtained rankings can be compared using the Jaccard similarity index (JSI) (see Niroomand
et al.,
2019). Thus, for any pair of the rankings a JSI value which is between 0 (indicating no similarity) and 1 (indicating full similarity) is obtained. These values are reported in Table
10. According to these results, the highest JSI is 0.92 which means the rankings of Scenario 5 and Scenario 6 are the most similar rankings. This means that when applying the IVPFWA-DEMATEL approach for experiments 1 and 2, the obtained rankings are more similar than other pairs of scenarios. Also, the lowest JSI is 0.62 which means the rankings of Scenario 3 and Scenario 8 are the least similar rankings. This means that when applying the IVPFWG-DEMATEL approach for Experiment 3 and the IVPFWA-DEMATEL approach for Experiment 4, the obtained rankings are less similar than other pairs of scenarios.
Table 9
The importance weights and ranking of the criteria obtained by the proposed IVPF-DEMATEL for all of the scenarios.
| Criterion (j) |
Scenario 1 |
Scenario 2 |
Scenario 3 |
Scenario 4 |
Scenario 5 |
Scenario 6 |
Scenario 7 |
Scenario 8 |
| ${\omega _{j}}$ |
Ranking |
${\omega _{j}}$ |
Ranking |
${\omega _{j}}$ |
Ranking |
${\omega _{j}}$ |
Ranking |
${\omega _{j}}$ |
Ranking |
${\omega _{j}}$ |
Ranking |
${\omega _{j}}$ |
Ranking |
${\omega _{j}}$ |
Ranking |
| C-1 |
0.02853 |
15 |
0.02905 |
13 |
0.02829 |
14 |
0.02813 |
17 |
0.02745 |
17 |
0.02789 |
18 |
0.02728 |
23 |
0.02741 |
20 |
| C-2 |
0.02797 |
19 |
0.02803 |
20 |
0.02777 |
19 |
0.02791 |
18 |
0.02740 |
19 |
0.02750 |
19 |
0.02737 |
21 |
0.02746 |
18 |
| C-3 |
0.03029 |
4 |
0.03145 |
4 |
0.02979 |
3 |
0.02938 |
6 |
0.02988 |
7 |
0.03098 |
7 |
0.02922 |
6 |
0.02937 |
10 |
| C-4 |
0.03051 |
2 |
0.03188 |
3 |
0.02977 |
4 |
0.02965 |
3 |
0.03071 |
5 |
0.03183 |
5 |
0.03000 |
4 |
0.03009 |
5 |
| C-5 |
0.02900 |
13 |
0.02954 |
12 |
0.02799 |
16 |
0.02916 |
7 |
0.02968 |
8 |
0.03031 |
9 |
0.02914 |
8 |
0.02964 |
8 |
| C-6 |
0.02919 |
12 |
0.02963 |
10 |
0.02938 |
8 |
0.02840 |
12 |
0.02803 |
15 |
0.02845 |
15 |
0.02816 |
16 |
0.02768 |
16 |
| C-7 |
0.02697 |
24 |
0.02597 |
27 |
0.02758 |
23 |
0.02691 |
27 |
0.02505 |
33 |
0.02458 |
32 |
0.02572 |
32 |
0.02524 |
33 |
| C-8 |
0.02453 |
35 |
0.02351 |
33 |
0.02554 |
33 |
0.02512 |
34 |
0.02542 |
31 |
0.02399 |
34 |
0.02592 |
31 |
0.02630 |
29 |
| C-9 |
0.02552 |
31 |
0.02447 |
31 |
0.02703 |
26 |
0.02561 |
33 |
0.02685 |
24 |
0.02525 |
27 |
0.02783 |
18 |
0.02742 |
19 |
| C-10 |
0.02461 |
33 |
0.02283 |
34 |
0.02614 |
31 |
0.02511 |
35 |
0.02398 |
36 |
0.02272 |
36 |
0.02525 |
35 |
0.02414 |
36 |
| C-11 |
0.02596 |
28 |
0.02455 |
30 |
0.02771 |
20 |
0.02583 |
32 |
0.02520 |
32 |
0.02433 |
33 |
0.02661 |
28 |
0.02479 |
34 |
| C-12 |
0.02458 |
34 |
0.02218 |
36 |
0.02766 |
22 |
0.02465 |
36 |
0.02491 |
34 |
0.02325 |
35 |
0.02731 |
22 |
0.02418 |
35 |
| C-13 |
0.02740 |
21 |
0.02714 |
23 |
0.02770 |
21 |
0.02730 |
23 |
0.02646 |
26 |
0.02635 |
24 |
0.02688 |
27 |
0.02632 |
28 |
| C-14 |
0.02858 |
14 |
0.02834 |
19 |
0.02908 |
11 |
0.02786 |
19 |
0.02668 |
25 |
0.02675 |
23 |
0.02727 |
24 |
0.02630 |
30 |
| C-15 |
0.02935 |
9 |
0.02900 |
14 |
0.03038 |
1 |
0.02820 |
16 |
0.02738 |
20 |
0.02745 |
20 |
0.02840 |
15 |
0.02658 |
23 |
| C-16 |
0.02723 |
23 |
0.02654 |
25 |
0.02798 |
17 |
0.02753 |
22 |
0.02768 |
16 |
0.02693 |
22 |
0.02874 |
12 |
0.02747 |
17 |
| C-17 |
0.02729 |
22 |
0.02876 |
17 |
0.02479 |
34 |
0.02914 |
8 |
0.03089 |
4 |
0.03194 |
4 |
0.02894 |
10 |
0.03115 |
3 |
| C-18 |
0.03046 |
3 |
0.03190 |
2 |
0.02908 |
10 |
0.03009 |
1 |
0.03162 |
2 |
0.03258 |
2 |
0.03044 |
2 |
0.03157 |
2 |
| C-19 |
0.03061 |
1 |
0.03209 |
1 |
0.02991 |
2 |
0.02950 |
4 |
0.03111 |
3 |
0.03210 |
3 |
0.03003 |
3 |
0.03088 |
4 |
| C-20 |
0.02978 |
6 |
0.03118 |
5 |
0.02795 |
18 |
0.03001 |
2 |
0.03180 |
1 |
0.03276 |
1 |
0.03051 |
1 |
0.03177 |
1 |
| C-21 |
0.02926 |
11 |
0.03013 |
8 |
0.02864 |
12 |
0.02884 |
10 |
0.02949 |
9 |
0.03039 |
8 |
0.02848 |
14 |
0.02933 |
11 |
| C-22 |
0.03005 |
5 |
0.03111 |
6 |
0.02920 |
9 |
0.02949 |
5 |
0.03008 |
6 |
0.03101 |
6 |
0.02916 |
7 |
0.02987 |
6 |
| C-23 |
0.02933 |
10 |
0.02957 |
11 |
0.02946 |
7 |
0.02863 |
11 |
0.02866 |
14 |
0.02880 |
14 |
0.02883 |
11 |
0.02842 |
13 |
| C-24 |
0.02955 |
8 |
0.03027 |
7 |
0.02973 |
5 |
0.02839 |
13 |
0.02918 |
11 |
0.02950 |
11 |
0.02905 |
9 |
0.02887 |
12 |
| C-25 |
0.02504 |
32 |
0.02447 |
32 |
0.02428 |
36 |
0.02645 |
31 |
0.02486 |
35 |
0.02472 |
30 |
0.02390 |
36 |
0.02602 |
32 |
| C-26 |
0.02670 |
26 |
0.02654 |
24 |
0.02670 |
28 |
0.02671 |
29 |
0.02599 |
27 |
0.02608 |
25 |
0.02569 |
34 |
0.02633 |
27 |
| C-27 |
0.02775 |
20 |
0.02862 |
18 |
0.02704 |
25 |
0.02773 |
21 |
0.02905 |
12 |
0.02950 |
10 |
0.02803 |
17 |
0.02943 |
9 |
| C-28 |
0.02684 |
25 |
0.02760 |
22 |
0.02694 |
27 |
0.02724 |
24 |
0.02941 |
10 |
0.02892 |
13 |
0.02944 |
5 |
0.02971 |
7 |
| C-29 |
0.02574 |
30 |
0.02457 |
29 |
0.02616 |
30 |
0.02676 |
28 |
0.02588 |
28 |
0.02461 |
31 |
0.02695 |
25 |
0.02624 |
31 |
| C-30 |
0.02576 |
29 |
0.02465 |
28 |
0.02597 |
32 |
0.02697 |
26 |
0.02588 |
29 |
0.02486 |
29 |
0.02652 |
29 |
0.02639 |
25 |
| C-31 |
0.02439 |
36 |
0.02252 |
35 |
0.02442 |
35 |
0.02665 |
30 |
0.02693 |
23 |
0.02516 |
28 |
0.02774 |
19 |
0.02799 |
15 |
| C-32 |
0.02659 |
27 |
0.02634 |
26 |
0.02624 |
29 |
0.02715 |
25 |
0.02584 |
30 |
0.02557 |
26 |
0.02572 |
33 |
0.02636 |
26 |
| C-33 |
0.02809 |
18 |
0.02766 |
21 |
0.02857 |
13 |
0.02782 |
20 |
0.02707 |
22 |
0.02719 |
21 |
0.02755 |
20 |
0.02642 |
24 |
| C-34 |
0.02846 |
16 |
0.02888 |
15 |
0.02800 |
15 |
0.02826 |
15 |
0.02743 |
18 |
0.02823 |
16 |
0.02692 |
26 |
0.02712 |
22 |
| C-35 |
0.02830 |
17 |
0.02880 |
16 |
0.02741 |
24 |
0.02837 |
14 |
0.02721 |
21 |
0.02811 |
17 |
0.02622 |
30 |
0.02730 |
21 |
| C-36 |
0.02960 |
7 |
0.03007 |
9 |
0.02956 |
6 |
0.02888 |
9 |
0.02866 |
13 |
0.02920 |
12 |
0.02861 |
13 |
0.02826 |
14 |
To summarizae this section, the proposed approach is sensitive to the importance weight of each expert. Furthermore, this approach is sensitive to the aggregating operator that is used for integrating the pairwise comparison matrixes of the experts.
Table 10
The Jaccard similarity indexes of pair-wise comparison of the criteria rankings obtained by the proposed IVPF-DEMATEL for all of the scenarios.
|
Scenario 1 |
Scenario 2 |
Scenario 3 |
Scenario 4 |
Scenario 5 |
Scenario 6 |
Scenario 7 |
Scenario 8 |
| Scenario 1 |
– |
0.91 |
0.81 |
0.86 |
0.76 |
0.80 |
0.72 |
0.71 |
| Scenario 2 |
– |
– |
0.76 |
0.89 |
0.80 |
0.84 |
0.74 |
0.74 |
| Scenario 3 |
– |
– |
– |
0.72 |
0.68 |
0.67 |
0.67 |
0.62 |
| Scenario 4 |
– |
– |
– |
– |
0.83 |
0.87 |
0.76 |
0.78 |
| Scenario 5 |
– |
– |
– |
– |
– |
0.92 |
0.84 |
0.90 |
| Scenario 6 |
– |
– |
– |
– |
– |
– |
0.79 |
0.87 |
| Scenario 7 |
– |
– |
– |
– |
– |
– |
– |
0.81 |
| Scenario 8 |
– |
– |
– |
– |
– |
– |
– |
− |
5.4 Comparative Study
In this section, the results obtained by the proposed IVPF-DEMATEL in Section
5.1 and Section
5.3 are compared to the approaches of the literature. Otay and Jaller (
2020) proposed an interval-valued Pythagorean fuzzy AHP (IVPF-AHP) which is used in this section for comparison purposes. As the IVPF-AHP approach is sensitive to the IVPFWG and IVPFWA operators, the similar experiments and scenarios as Table
6 and Table
7 are defined for this approach. Therefore, the scenarios of Table
11 are considered.
Table 11
Different scenarios defined for the IVPF-AHP approach.
| Scenario |
Experiment |
Operator |
Note |
| 1 |
1 |
IVPFWG |
The proposed IVPF-AHP is titled as IVPFWG-AHP |
| 2 |
2 |
| 3 |
3 |
| 4 |
4 |
| 5 |
1 |
IVPFWA |
The proposed IVPF-AHP is titled as IVPFWA-AHP |
| 6 |
2 |
| 7 |
3 |
| 8 |
4 |
Table 12
The weights and ranking of the criteria obtained by the IVPF-AHP for all of the scenarios.
| Criterion (j) |
Scenario 1 |
Scenario 2 |
Scenario 3 |
Scenario 4 |
Scenario 5 |
Scenario 6 |
Scenario 7 |
Scenario 8 |
| ${\omega _{j}}$ |
Ranking |
${\omega _{j}}$ |
Ranking |
${\omega _{j}}$ |
Ranking |
${\omega _{j}}$ |
Ranking |
${\omega _{j}}$ |
Ranking |
${\omega _{j}}$ |
Ranking |
${\omega _{j}}$ |
Ranking |
${\omega _{j}}$ |
Ranking |
| C-1 |
0.0313 |
14 |
0.0251 |
19 |
0.0322 |
14 |
0.0322 |
12 |
0.0199 |
20 |
0.0165 |
21 |
0.0225 |
22 |
0.022 |
18 |
| C-2 |
0.033 |
10 |
0.026 |
18 |
0.0314 |
16 |
0.0402 |
9 |
0.0277 |
14 |
0.0214 |
18 |
0.0292 |
14 |
0.0343 |
11 |
| C-3 |
0.0463 |
6 |
0.0461 |
7 |
0.0416 |
6 |
0.0492 |
7 |
0.0382 |
9 |
0.0386 |
10 |
0.0362 |
9 |
0.0392 |
9 |
| C-4 |
0.0481 |
5 |
0.0507 |
5 |
0.0427 |
4 |
0.0516 |
6 |
0.0476 |
7 |
0.0492 |
7 |
0.0438 |
6 |
0.0481 |
7 |
| C-5 |
0.046 |
7 |
0.0429 |
8 |
0.0365 |
9 |
0.0619 |
3 |
0.0521 |
6 |
0.0463 |
8 |
0.0492 |
5 |
0.0585 |
5 |
| C-6 |
0.023 |
22 |
0.029 |
14 |
0.0247 |
20 |
0.0154 |
25 |
0.0223 |
16 |
0.0267 |
15 |
0.0228 |
20 |
0.0171 |
23 |
| C-7 |
0.0169 |
26 |
0.0119 |
26 |
0.0222 |
27 |
0.015 |
26 |
0.0104 |
29 |
0.0076 |
29 |
0.0148 |
30 |
0.0104 |
27 |
| C-8 |
0.0185 |
25 |
0.0093 |
29 |
0.0245 |
21 |
0.0246 |
20 |
0.0198 |
21 |
0.0085 |
28 |
0.0253 |
18 |
0.0307 |
13 |
| C-9 |
0.0235 |
21 |
0.0118 |
27 |
0.0336 |
12 |
0.0285 |
15 |
0.0226 |
15 |
0.0107 |
26 |
0.0309 |
12 |
0.0319 |
12 |
| C-10 |
0.0085 |
31 |
0.0058 |
34 |
0.0147 |
30 |
0.0069 |
31 |
0.0068 |
32 |
0.0046 |
34 |
0.0124 |
32 |
0.0059 |
32 |
| C-11 |
0.013 |
28 |
0.0086 |
30 |
0.0224 |
26 |
0.0109 |
28 |
0.0107 |
28 |
0.0066 |
31 |
0.0192 |
24 |
0.0101 |
28 |
| C-12 |
0.0076 |
32 |
0.0042 |
35 |
0.0181 |
28 |
0.0058 |
32 |
0.008 |
31 |
0.0046 |
35 |
0.0181 |
28 |
0.006 |
31 |
| C-13 |
0.0164 |
27 |
0.0156 |
25 |
0.0233 |
23 |
0.0119 |
27 |
0.0125 |
27 |
0.0116 |
25 |
0.0187 |
27 |
0.0097 |
29 |
| C-14 |
0.0214 |
24 |
0.0183 |
22 |
0.0267 |
18 |
0.0169 |
24 |
0.0135 |
26 |
0.0119 |
24 |
0.0188 |
26 |
0.0113 |
26 |
| C-15 |
0.0306 |
16 |
0.0264 |
17 |
0.0407 |
7 |
0.0229 |
22 |
0.0198 |
22 |
0.0171 |
20 |
0.0284 |
16 |
0.0164 |
24 |
| C-16 |
0.0096 |
30 |
0.0109 |
28 |
0.0142 |
32 |
0.0057 |
33 |
0.0091 |
30 |
0.0098 |
27 |
0.0147 |
31 |
0.0051 |
34 |
| C-17 |
0.0321 |
13 |
0.0355 |
11 |
0.0181 |
29 |
0.0526 |
5 |
0.0648 |
3 |
0.0703 |
4 |
0.0436 |
7 |
0.0731 |
3 |
| C-18 |
0.0648 |
1 |
0.0719 |
1 |
0.0499 |
1 |
0.0651 |
2 |
0.0743 |
2 |
0.0811 |
2 |
0.0602 |
2 |
0.0735 |
2 |
| C-19 |
0.0505 |
4 |
0.0677 |
2 |
0.0426 |
5 |
0.0399 |
10 |
0.06 |
5 |
0.0711 |
3 |
0.0495 |
4 |
0.0532 |
6 |
| C-20 |
0.0564 |
3 |
0.0646 |
4 |
0.0388 |
8 |
0.0672 |
1 |
0.0817 |
1 |
0.0862 |
1 |
0.0652 |
1 |
0.0848 |
1 |
| C-21 |
0.0378 |
9 |
0.0478 |
6 |
0.0347 |
11 |
0.0329 |
11 |
0.0458 |
8 |
0.0545 |
6 |
0.0392 |
8 |
0.0409 |
8 |
| C-22 |
0.0576 |
2 |
0.0653 |
3 |
0.0463 |
3 |
0.0567 |
4 |
0.0622 |
4 |
0.0677 |
5 |
0.0527 |
3 |
0.0607 |
4 |
| C-23 |
0.0326 |
11 |
0.0326 |
12 |
0.032 |
15 |
0.0318 |
13 |
0.028 |
13 |
0.0287 |
12 |
0.0274 |
17 |
0.0274 |
16 |
| C-24 |
0.0324 |
12 |
0.0408 |
9 |
0.0331 |
13 |
0.0241 |
21 |
0.0357 |
10 |
0.0409 |
9 |
0.0344 |
10 |
0.0302 |
14 |
| C-25 |
0.0075 |
33 |
0.0077 |
31 |
0.0066 |
35 |
0.0081 |
29 |
0.0062 |
34 |
0.0073 |
30 |
0.0052 |
36 |
0.0065 |
30 |
| C-26 |
0.0221 |
23 |
0.0194 |
21 |
0.0231 |
24 |
0.0223 |
23 |
0.0179 |
24 |
0.0155 |
22 |
0.0193 |
23 |
0.02 |
21 |
| C-27 |
0.0247 |
20 |
0.0273 |
16 |
0.0229 |
25 |
0.0249 |
19 |
0.035 |
11 |
0.0379 |
11 |
0.0294 |
13 |
0.0348 |
10 |
| C-28 |
0.0107 |
29 |
0.0178 |
24 |
0.0145 |
31 |
0.0072 |
30 |
0.0222 |
17 |
0.0274 |
14 |
0.0242 |
19 |
0.0157 |
25 |
| C-29 |
0.0074 |
34 |
0.0074 |
32 |
0.0096 |
33 |
0.0056 |
34 |
0.0063 |
33 |
0.0057 |
33 |
0.0099 |
33 |
0.0052 |
33 |
| C-30 |
0.0072 |
35 |
0.0074 |
33 |
0.0094 |
34 |
0.0053 |
35 |
0.0061 |
35 |
0.0058 |
32 |
0.0091 |
34 |
0.0048 |
35 |
| C-31 |
0.0037 |
36 |
0.0042 |
36 |
0.0047 |
36 |
0.0024 |
36 |
0.0039 |
36 |
0.0044 |
36 |
0.006 |
35 |
0.0022 |
36 |
| C-32 |
0.0261 |
19 |
0.0182 |
23 |
0.0261 |
19 |
0.0317 |
14 |
0.0174 |
25 |
0.0123 |
23 |
0.019 |
25 |
0.0228 |
17 |
| C-33 |
0.0297 |
17 |
0.0239 |
20 |
0.0358 |
10 |
0.027 |
18 |
0.0208 |
19 |
0.0183 |
19 |
0.029 |
15 |
0.0188 |
22 |
| C-34 |
0.0309 |
15 |
0.0297 |
13 |
0.0314 |
17 |
0.0279 |
16 |
0.0216 |
18 |
0.0227 |
16 |
0.0227 |
21 |
0.0202 |
19 |
| C-35 |
0.0273 |
18 |
0.0276 |
15 |
0.0235 |
22 |
0.0272 |
17 |
0.0197 |
23 |
0.0222 |
17 |
0.0164 |
29 |
0.0202 |
20 |
| C-36 |
0.0449 |
8 |
0.0407 |
10 |
0.0473 |
2 |
0.0404 |
8 |
0.0295 |
12 |
0.0287 |
13 |
0.0325 |
11 |
0.0282 |
15 |
The criteria of Table
1 in Section
3 are evaluated by the above-mentioned IVPF-AHP and the same experts of the field as invited for the proposed IVPF-DEMATEL. The main outputs of the IVPF-AHP are importance weights and ranking of the criteria. These values for all scenarios of Table
11 are obtained and reported in Table
12.
According to the results of Table
12, the importance weight values and ranking of the criteria are sensitive to the variations of the importance weights of the experts and the integrating operators. According to these results, some criteria show less sensitivity and some others show high sensitivity to these variations. The pairwise comparison of the obtained rankings of Table
12 is done in terms of Jaccard similarity index and the obtained JSI values are reported by Table
13. According to the obtained JSI values, the highest similarity is seen between the rankings of scenarios 5 and 6 (experiments 1 and 2 when applying the IVPFWG operator) and 5 and 7 (experiments 1 and 3 when applying the IVPFWA operator) with similar JSI values of 0.91.
Table 13
The Jaccard similarity indexes of pair-wise comparison of the criteria rankings obtained by the proposed IVPF-AHP for all of the scenarios.
|
Scenario 1 |
Scenario 2 |
Scenario 3 |
Scenario 4 |
Scenario 5 |
Scenario 6 |
Scenario 7 |
Scenario 8 |
| Scenario 1 |
– |
0.87 |
0.84 |
0.88 |
0.84 |
0.82 |
0.83 |
0.83 |
| Scenario 2 |
– |
– |
0.77 |
0.80 |
0.83 |
0.91 |
0.80 |
0.80 |
| Scenario 3 |
– |
– |
– |
0.79 |
0.78 |
0.73 |
0.80 |
0.77 |
| Scenario 4 |
– |
– |
– |
– |
0.84 |
0.79 |
0.80 |
0.87 |
| Scenario 5 |
– |
– |
– |
– |
– |
0.89 |
0.91 |
0.89 |
| Scenario 6 |
– |
– |
– |
– |
– |
– |
0.82 |
0.82 |
| Scenario 7 |
– |
– |
– |
– |
– |
– |
– |
0.86 |
| Scenario 8 |
– |
– |
– |
– |
– |
– |
– |
− |
The rankings obtained by the scenarios of the proposed IVPF-DEMATEL are compared to the rankings obtained by the above-mentioned IVPF-AHP. A schematic representation for comparing the obtained rankings is represented by Fig.
5. In this figure, based on Table
7 and Table
11, the scenarios are categorized based on the experiments in such a way that in each experiment four approaches are considered, such as the IVPF-DEMATEL with IVPFWG and IVPFWA operators (called IVPFWG-DEMATEL and IVPFWA-DEMATEL) and IVPF-AHP with IVPFWG and IVPFWA operators (called IVPFWG-AHP and IVPFWA-AHP). Figure
5 shows that the rankings of the mentioned four approaches in Experiment 2 (importance weight combination of
$({w_{1}},{w_{2}},{w_{3}})=(0.60,0.30,0.10))$ have more stability than other experiments. On the other hand, the least stability of rankings appears in Experiment 3 and Experiment 4.
Table 14
The Jaccard similarity indexes of pair-wise comparison of the criteria rankings obtained by the proposed IVPF-DEMATEL and the IVPF-DEMATEL for all of the scenarios.
|
|
IVPF-AHP |
|
|
Scenario 1 |
Scenario 2 |
Scenario 3 |
Scenario 4 |
Scenario 5 |
Scenario 6 |
Scenario 7 |
Scenario 8 |
| IVPF-DEMATEL |
Scenario 1 |
0.80 |
0.83 |
0.78 |
0.73 |
0.74 |
0.79 |
0.72 |
0.70 |
| Scenario 2 |
0.81 |
0.88 |
0.75 |
0.74 |
0.77 |
0.83 |
0.74 |
0.72 |
| Scenario 3 |
0.70 |
0.71 |
0.75 |
0.63 |
0.65 |
0.67 |
0.66 |
0.60 |
| Scenario 4 |
0.81 |
0.87 |
0.74 |
0.75 |
0.77 |
0.83 |
0.75 |
0.73 |
| Scenario 5 |
0.76 |
0.81 |
0.69 |
0.73 |
0.83 |
0.86 |
0.78 |
0.76 |
| Scenario 6 |
0.78 |
0.86 |
0.70 |
0.75 |
0.83 |
0.91 |
0.78 |
0.78 |
| Scenario 7 |
0.72 |
0.74 |
0.67 |
0.67 |
0.76 |
0.76 |
0.76 |
0.68 |
| Scenario 8 |
0.73 |
0.77 |
0.66 |
0.71 |
0.82 |
0.83 |
0.76 |
0.76 |
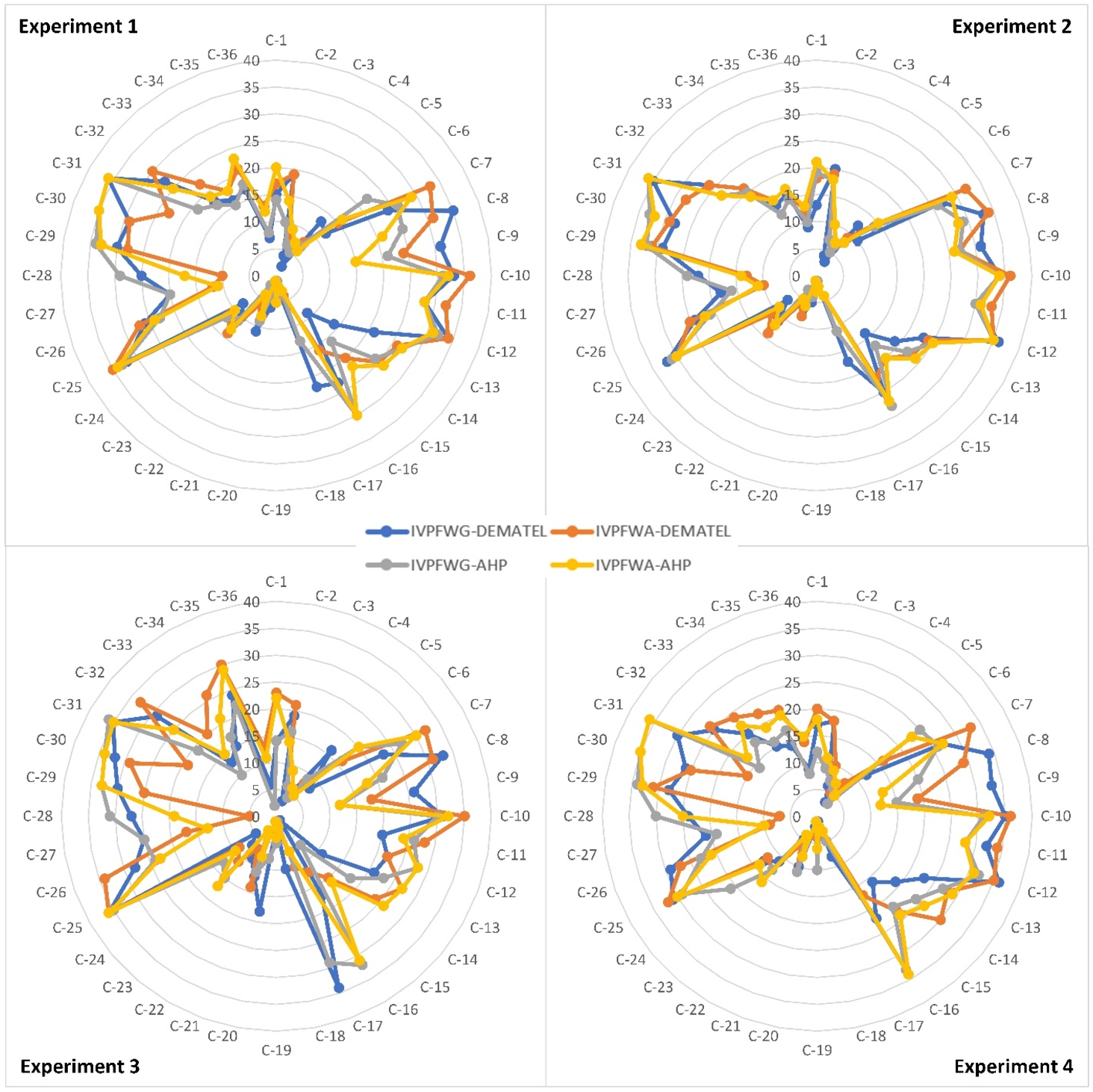
Fig. 5
Schematic representation of the criteria under all scenarios.
Finally, the rankings obtained by the proposed IVPF-DEMATEL and the IVPF-AHP approaches represented in Table
9 and Table
11 are compared. For this aim, for any pair of ranking from these two tables, the Jaccard similarity index (JSI) is calculated. All the JSI values are reported by Table
14. The similarities are higher than 0.63 which is between Scenario 3 of the IVPF-DEMATEL and Scenario 4 of the IVPF-AHP. The main and fair comparisons are done when the same scenario is considered for both approaches. In this case, the JSI values of the main diagonal of the table are considered. Therefore, when considering scenarios 1 to 8 for both approaches, the JSI values of 0.80, 0.88, 0.75, 0.75, 0.83, 0.91, 0.76, and 0.76 are obtained. According to these values, a fair and acceptable similarity exists between the proposed IVPF-DEMATEL and the IVPF-AHP approaches.
6 Conclusion
In this study, some environmental criteria affecting organizational behaviour of the higher education sector were considered. The aim of the study was to analyse and prioritize these factors for giving some insights to the managers. As a solution methodology, first some experts from the higher education sector of Iran were selected and asked to determine pairwise comparison of the criteria. Then, in order to respect the uncertain nature of the comparisons, the linguistic terms were converted to interval-valued Pythagorean fuzzy values. Interval-valued Pythagorean fuzzy numbers were used as they keep more information and uncertainty compared to classical fuzzy numbers. Then, an interval-valued Pythagorean fuzzy DEMATEL approach was developed for the first time for prioritizing the criteria and performing the causality analysis on them. Finally, the obtained results were interpreted, and some managerial insights were given. According to the obtained results, most of the economic, political, and professional domain criteria were selected to be of the cause category. According to the obtained results, the managers can improve the organizational behaviour of their organizations by focusing on the cause category of the criteria. On the other hand, there were some limitations for performing this study. A limitation is selecting suitable and experienced people for criteria comparison step. Another limitation was reflecting the uncertainty that may happen in comparing the criteria that was solved by linguistic terms and their equivalent fuzzy values.
This study can be extended by considering more range of criteria other than the environmental criteria. Also, other types fuzzy sets and numbers can be considered for reflecting the uncertain nature of the problem.

