Abstract
The article presents the tax declaration scheme using blockchain confidential transactions based on the modified ElGamal encryption providing additively-homomorphic property. Transactions are based on the unspent transactions output (UTxO) paradigm allowing to effectively represent digital asset of cryptocurrencies in e-wallets and to perform financial operations. The main actors around transaction are specified, include money senders, receivers, transaction creator, Audit Authority (AA) and Net of users. A general transaction model with M inputs and N outputs is created, providing transaction amount confidentiality and verifiability for all actors with different levels of available information.
The transaction model allows Net to verify the validity of a transaction, having access only to encrypted transaction data. Each money receiver is able to decrypt and verify the actual sum that is transferred by the sender. AA is provided with actual transaction values and is able to supervise the tax payments for business actors. Such information allows to verify the honesty of transaction data for each user role.
The security analysis of the scheme is presented, referencing to ElGamal security assumptions. The coalition attack is formulated and prevention of this attack is proposed. It is shown that transaction creation is effective and requires almost the same resources as multiple ElGamal encryption. In addition to ElGamal encryption of all income and expenses, an additional exponentiation operation with small exponents, representing transferred sums, is needed. AA computation resources are slightly larger, since they have to be adequate for search procedures in the small range from 1 to ${2^{32}}-1=4294967295$ for individual money transfers.
1 Introduction
Recently blockchain technology has been penetrating into business processes monitoring and control (Maupin,
2017), as this technology is based on clear and transparent security foundations. The blockchain technology does not require a Trusted Third Party (TTP) since any user (node) participates in the peer-to-peer blockchain network and is operating according to consensus rules recognized by all. The information is stored and shared on a variety of nodes in many different locations. A node is simply any computer or electronic device, maintaining copies of the blockchain database, named a (hyper)ledger.
The global trends, current tendencies, and frontiers of blockchain technology are reported in Boakye
et al. (
2022), pointing out that blockchain technology research in finance has evolved and is predominated by studies on crowdfunding/equity crowdfunding, entrepreneurial finance, bitcoin, entrepreneurship, fintech, and venture capital. The overview covers 157 articles. However, the interaction of finance activity and tax collection system is not outlined in this study.
The systematic analysis of blockchain in sustainable finance is presented in Ren
et al. (
2023) for the field of renewable finance. Authors indicate that: (1) Blockchain has been widely used in many industries involved in sustainable finance; (2) Blockchain will have a long-term impact on sustainable finance in the fields of smart city and sharing economy fields; (3) Blockchain can be deeply integrated with other technologies to promote the diversified development of sustainable finance. Despite the fact that authors do not reveal specific technologies, the latter proposition is important to justify the solution proposed in this paper, namely integration of tax collection system with blockchain technology, providing transaction confidentiality and verifiability. We are unaware of any solutions of this problem in the literature.
The unspent transaction output (UTxO) and account-based transactions (ABT) are two types of record-keeping methods used by a blockchain network to record provenance of its cryptocurrency and the way cryptocurrency balances are determined. UTxO is also considered a token-based system. Bitcoin, Bitcoin Cash, Zcash, Litecoin, Dogecoin, Dash, etc., are UtxO instances.
The ABT blockchains, such as Ethereum, EOS, Tron, and Ethereum Classic, are focused on smart contracts. In ABT system, the ledger would have accounts for all users of the currency and requires real-time updates of the account balance (Bai
et al.,
2019). This means that we have exponentially growing account information to manage.
The UTxO system can also be used in smart contracts and would enable business models based on asset tokenisation. It would also reduce the large-scale information keeping.
In this paper, we consider an UTxO system, allowing to create e-wallets to the users, thus meeting the user’s needs for offline transactions more effectively, e.g. between users of mobile phones with implemented e-wallets (Sakalauskas
et al.,
2017,
2018; Muleravicius
et al.,
2019). In this case, digital currency is implemented in the customer e-wallet and in the blockchain ledger.
A new and perspective trend in blockchain technology is business process monitoring and control, requiring faster and less expensive transactions, as well as more transparent investment mechanisms using tokens and smart contracts.
However, governments have pointed out that so far there has been a lack of regulation for such activities. Regulation is especially important for tax declaration and honest tax collection. The need for such regulation will also grow, when a new type of blockchain-based cryptocurrency will be issued by Central Banks and named Central Bank Digital Currency (CBDC) (Bouchaud
et al.,
2020).
The overview of tax collection problem is actualized in Phadke
et al. (
2021). But authors do not present technological solutions to this problem. In Dedhia
et al. (
2023) the novel tax tracker application is presented working completely over the blockchain technology, which prioritises decentralised data as its key principle. This solution can solve the transparency problem by showing the use of the tax amount by the government to the users and will keep track of the amount and its allocation for various government projects. But this research does not provide data confidentiality that is important in business processes.
In general, it is natural that in business processes some information is confidential and limited to certain participants. However, it is necessary to define what information can be shared by system users to provide verifiable transactions. This problem can be solved by using a permissioned IBM Hyperledger Fabric or Ethereum blockchain (Paulavičius
et al.,
2019; Mohan,
2019). To simultaneously provide both authentication and confidentiality, a signcryption scheme is used combining signing and encrypting processes which is an important cryptographic primitive (Tseng
et al.,
2022), that can be also be used in blockchain technology. Such networks are more dedicated to consortium activity, and therefore have certain limitations for flexible and effective new users’ growth and involvement. The Ethereum Mainnet, for example, is a public or permissionless blockchain, which, however, does not provide the confidentiality of sensitive business data.
This paper proposes a solution of the regulation for tax collection, when a certain TTP, named Audit Authority (AA), is needed. At the same time, we propose a scheme to provide transaction data confidentiality for other actors, apart from AA. Existing solutions are using range proofs on committed values (Bünz
et al.,
2018). However, range proofs are not adequate for tax collection, since they do not prove the exact amount of transferred money, that is needed for AA.
In Section
2, the overall description of the proposed scheme is presented. In Section
3, introduction to ElGamal encryption is given. The Confidential transaction construction and creation are presented in Sections
4 and
5. In Section
6, security and efficiency analysis is provided. Section
7 gives the conclusions, and at the end the list of references is presented.
2 The Overall Description of the Scheme
We have constructed the following scheme for multiple input and multiple output blockchain transaction. The following actors are defined: the transaction creator Alice, the AA and the network we denote by the Net. The Net is divided into three parts: the Bobs B1, B2, …, BM, transferring money to Alice and providing her with income; the Laries L1, L2, …, LN, receiving money from Alice and thus causing Alice expenses; and other Net nodes verifying the transaction validity, composing and validating blocks, etc.
The presented solution is an integration of several approaches providing trustworthy tax declaration while keeping confidential transactions in blockchain technology. It is known that the trustworthiness of transactions relies on the balance between income (inputs) and expenses (outputs). Bünz
et al. (
2020) presents a method to provide confidentiality and verifiability of transactions to the Net using some modification of ElGamal encryption, ElGamal (
1985). This technique transfers multiplicatively-homomorphic ElGamal encryption to additively-homomorphic encryption. We will use this technique to create a tax declaration scheme.
UTxO transactions rely on the requirement that the sum of all inputs must be equal to the sum of all outputs plus the transaction fee. Change, if it exists, gets sent to the transaction creator as one of the outputs.
Confidentiality means that the transaction data must be encrypted using a secure probabilistic encryption method. The problem is in providing the honesty of transaction with encrypted income and expenses, when, despite the equality of these values, their ciphertexts differ when using the probabilistic encryption. In this case, the balance violation cannot be determined. Moreover, there is a way of cheating by making a transaction with the sum of expenses greater than the sum of actual income, thus “making money out of the air”. The presented solution is provable, secure, transparent, and hence, trustworthy.
Let us consider a transaction, created by Alice, consisting of income and expenses. Any single income or expense is denoted by an integer d representing its value.
Let us assume Alice received income sums
${i_{1}},{i_{2}},\dots ,{i_{M}}$ from several Bobs
${\text{B}_{1}},{\text{B}_{2}},\dots ,{\text{B}_{M}}$, respectively. Then the total income is
$i={i_{1}}+{i_{2}}+\dots ,{i_{M}}$. Alice transfers part of her total income
i to several Laries
${\text{L}_{1}},{\text{L}_{2}},\dots ,{\text{L}_{N}}$ by incurring expenses
${e_{1}},{e_{2}},\dots ,{e_{N}}$, respectively. If the sum of expenses
${e^{\prime }}={e_{1}}+{e_{2}}+\cdots +{e_{N}}$ is less than the total income, then she transfers the change value that we denote by
${e_{N+1}}$, to herself. If the transaction is honest, then the following balance equation must hold
In open blockchain, i.e. in open distributed ledger, all nodes in the Net can verify the balance of the transaction. If it holds, and the transaction is authentic, i.e. signed by eSignatures, then this transaction can be included in the block and validated by the node. The problems of transaction authentication and block validation are not considered in this paper.
The first question is how to share functions between AA and Net?
Secondly, how to provide transaction confidentiality for the Net while ensuring honesty of transactions?
Since AA is a TTP for all the Net, then it is sensible to provide the verification of all actual transaction data to AA. Laries must be able to verify their actual income. Net must be able to verify the balance between income and expenses without any knowledge about the actual values of these data.
Our solution relies on the probabilistic asymmetric ElGamal encryption. In order to realize ElGamal encryption/decryption, public parameters must be shared in the Net. Probabilistic encryption is performed by the sender using receiver’s public key and randomly generated number, thus providing different ciphertexts even for the encryption of the same plaintext. Ciphertext is sent to the receiver, who can decrypt it using the same shared public parameters and his/her private key for obtaining corresponding plaintext. ElGamal encryption has the so-called multiplicatively isomorphic property: the encrypted product of plaintexts is equal to the product of ciphertexts of every corresponding plaintext.
3 ElGamal Encryption
Let
G be a cyclic group of order
q with generator
g. Let
Msg be a message to be encrypted and
m – an image of reversible 1-to-1 function, transforming
Msg to
m in
G. We denote public parameters in ElGamal encryption by
ElGamal cryptosystem is using discrete exponent function (DEF) defined by generator
g in
G and providing the following isomorphic mapping
${\textit{DEF}_{g}}:{Z_{q}}\to G$, where
${Z_{q}}=\{0,1,2,\dots ,q-1\}$ is a ring with addition, subtraction and multiplication operations mod
q. For any integer
$i\in {Z_{q}}$
Private and public key pair (PrK, PuK) is computed using public parameters PP in (
2) and DEF. Encryption is performed using receiver’s PuK, and decryption, correspondingly, with receiver’s PrK. Let
$\text{PrK}=z$ and
$\text{PuK}=\alpha $, then their generation is performed in the following way:
-
1. $\text{PrK}=z$ is an integer generated at random in set
${Z_{q}}$:
-
2. $\text{Puk}=\alpha $ is computed using DEF:
Let Alice encrypt transaction data
d corresponding to single income or expense by receiver’s
$\text{PuK}=\alpha $. Then ciphertext
${c_{\alpha }}=({\varepsilon _{\alpha }},{\delta _{\alpha }})$ is obtained in the following two steps:
Decryption is performed using receiver’s
$\text{PrK}=z$
We denote encryption and decryption functions by
Enc( ) and
Dec( ). Then, formally, encryption and decryption operations are expressed in the following way:
ElGamal encryption has the following multiplicative isomorphic property. Let
${d_{1}},{d_{2}}\in G$. Then, for the encryption of two plaintexts
${d_{1}}$ and
${d_{2}}$, two random numbers
${j_{1}}$,
${j_{2}}$ are generated, yielding two ciphertexts
${c_{1}}$ and
${c_{2}}$:
Encryption of product
${d_{1}}{d_{2}}$ with the random parameter
$j={j_{1}}+{j_{2}}$ mod
q yields a ciphertext
${c_{\alpha ,12}}$ equal to the product of two ciphertexts
${c_{\alpha ,1}}$ and
${c_{\alpha ,2}}$ in
G, i.e.
We will use this isomorphic property after modification in our solution by defining adequate algebraic structures.
4 Confidential Transaction Construction
Let
p be a large strong prime number, expressed by
$p=2q+1$, where
q is a prime number, defining a multiplicative cyclic group
${Z_{p}^{\ast }}=\{1,2,\dots ,p-1\}$ with operations performed mod
p. This group has a subgroup of prime order
q, denoted by
${G_{q}}$ with all elements, except 1, being generators in
${G_{q}}$. From now on, group
G, defined in Section
2, is replaced by group
${G_{q}}$. The operations, defined for group
G in previous section, are computed mod
p unless otherwise stated.
If
g is a generator of
${G_{q}}$, then according to Lagrange theorem and its consequences, the following relation is satisfied
We denote public parameters in ElGamal encryption by
PP generation is performed in the following way:
All actors have their generated public and private key pairs. They share public keys within the Net. Let AA have a public and private key pair that we denote by (
${\text{PrK}_{AA}}=z$,
${\text{PuK}_{AA}}=\alpha $); Alice’s public and private key pair is (
${\text{PrK}_{A}}=x$,
${\text{PuK}_{A}}=a$).
All Laries
${\text{L}_{1}},{\text{L}_{2}},\dots ,{\text{L}_{N}}$ have their key pairs that we denote by (
${\text{PrK}_{Ln}}={y_{n}}$,
${\text{PuK}_{Ln}}={l_{n}}$),
$n=1,2,\dots ,N$. The direct income and expenses encryption does not provide the opportunity to verify transaction balance (1), since, according to (
10) and (
11), encryption is a multiplicative homomorphism of plaintexts. We need to have additively multiplicative homomorphism instead by transforming transaction data by DEF in (
3). Let
${d_{1}}$,
${d_{2}}$ be transaction data. Then they are transformed to new variables
${D_{1}}$,
${D_{2}}$ computed in the following way
We denote the ciphertexts of encrypted exponent values
${D_{1}}$,
${D_{2}}$ by capital letters while lower cases are used otherwise. Then, after encrypting the product
${D_{1}}{D_{2}}=D$ with
${\text{PuK}_{AA}}=\alpha $ according to (
10) and (
11), and when
$j={j_{1}}+{j_{2}}$ mod
q, we obtain
Implicitly, ciphertext can be expressed by the following relations:
Note that all operations in exponents are computed mod
q, since the order of all the elements of the prime order group
${G_{q}}$ (except 1) is equal to
q.
As there is 1-to-1 correspondence between
${d_{1}}$,
${d_{2}}$ and
${D_{1}}$,
${D_{2}}$, and according to (
16), we can state the following properties of ElGamal encryption, if
$j=({j_{1}}+{j_{2}}$) mod
q:
-
1. ElGamal encryption provides the multiplicative isomorphism of plaintexts ${D_{1}}$, ${D_{2}}$ to ciphertexts.
-
2. If initial data ${d_{1}}$, ${d_{2}}$ is exponentially transformed to corresponding data ${D_{1}}$, ${D_{2}}$, then the encryption of ${D_{1}}$, ${D_{2}}$ is the additively-multiplicative encryption of exponents ${d_{1}},{d_{2}}$.
In general, in order to implement an additively-multiplicative isomorphism for encryption, any integer of transaction data
d in
${Z_{q}}$ is transformed to the element
D in
${G_{q}}$ by DEF in (
3).
In order to create Alice’s confidential and verifiable transaction, all her actual income
${i_{1}},{i_{2}},\dots ,{i_{M}}$ must be transformed to the numbers
${I_{1}},{I_{2}},\dots ,{I_{M}}$, and expenses
${e_{1}},{e_{2}},\dots ,{e_{N+1}}$, correspondingly, to the numbers
${E_{1}},{E_{2}},\dots ,{E_{N+1}}$ by (
17). Then the balance equation (
1) can be verified by the following equation:
where addition is replaced by multiplication operation of exponent values of actual incomes and expenses in (
1).
In order to achieve verifiability of transaction, both sets ${I_{1}},{I_{2}},\dots ,{I_{M}}$ and ${E_{1}},{E_{2}},\dots ,{E_{N+1}}$ must be encrypted with the same public key in a special way providing the equality of the sums of random generated numbers for income and expenses. We denote the ciphertexts of encrypted numbers ${I_{1}},{I_{2}},\dots ,{I_{M}}$ with Alice ${\text{PuK}_{A}}=a$ by ${C_{a,{I_{1}}}},{C_{a,{I_{2}}}},\dots ,{C_{a,{I_{M}}}}$. In this case, the following problems have to be solved:
-
P1. How to find the actual values of income ${i_{1}},{i_{2}},\dots ,{i_{M}}$, transformed to ${I_{1}},{I_{2}},\dots ,{I_{M}}$?
-
P2. How to prevent “money making out of the air”, satisfying balance equation (
1)?
-
P3. How to ensure confidential transaction data declaration to AA and data verifiability to the Net?
-
P4. How to implement confidential expenses transfer to Laries, verifiable by AA?
-
P5. How to ensure confidential balance verification for the Net?
The solution to these problems is presented in next section.
5 Confidential and Auditable Transaction Creaton
In the proposed solution, all the information about actual transaction data is available for Alice as a transaction creator and AA as an Audit Authority.
-
P1. Alice receives the following ciphertexts
${C_{\alpha ,{I_{1}}}},{C_{\alpha ,{I_{2}}}},\dots ,{C_{\alpha ,{I_{M}}}}$ from Bobs, and obtains numbers
${I_{1}},{I_{2}},\dots ,{I_{M}}$ corresponding to actual income values
${i_{1}},{i_{2}},\dots ,{i_{M}}$ transformed according to (
17) after their decryption. Since they are in the exponents of generator
g, it is necessary to solve a Discrete Logarithmic Problem (DLP) in
${G_{q}}$, i.e. if
then the discrete logarithm function with base
g must be computed for value
${I_{m}}$
However, in order to provide security of ElGamal encryption (and of most traditional cryptosystems), DLP must be assumed as infeasible for securely generated public parameters, e.g. with prime number
p having 2048 bit length.
Notice that the values of transaction data
d are not so large as compared with the order of exponent ring
${Z_{q}}$. For business processes, it is enough to restrict
d value from 1 to, let us say,
${2^{32}}-1$, i.e.
d can be represented by 32 bits, while
q has at most 2047 bits, if
p is generated by 2048 bit strong prime. Since money receiver Alice knows the exact range of Bobs payments, she can easily verify by (
17) if the decrypted data
D correctly represents required sum
d.
Since AA has much more powerful computation resources, it is not a problem to find transaction data
d from (
17).
-
P2. Prevention has its origin from ring ${Z_{q}}$ property, that it is an additive group, where addition and subtraction operations are performed mod q. For example, let $p=23$, then $q=11$ and ${Z_{q}}=\{0,1,2,\dots ,10\}$. Let ${d_{1}}=1$ and ${d_{2}}=2$, then ${d_{1}}+{d_{2}}=3$ mod 11. But, at the same time, if ${d_{1}}=4$ and ${d_{2}}=10$, then ${d_{1}}+{d_{2}}=14$ mod 11 = 3 mod 11 = 3.
The solution is to dedicate a function for AA in order to verify that all the actual values d in transactions do not exceed $q/2$. It is more than sufficient, since when proposing the solution of P2 we restricted the upper range of d to the value ${2^{32}}-1\ll q/2$.
-
P3. The solution is obtained by generalizing (
15) and (
16) encryption to multiple income and expenses. It is implemented in the following steps:
-
1. Bobs incur their expenses as Alice receives income ${i_{1}},{i_{2}},\dots ,{i_{M}}$, computing values ${I_{1}},{I_{2}},\dots ,{I_{M}}$ and encrypting them using Alice ${\text{PuK}_{A}}=a$ with the random generated numbers ${j_{1}},{j_{2}},\dots ,{j_{M}}$, thus obtaining ciphertexts ${C_{a,{I_{1}}}},{C_{a,{I_{2}}}},\dots ,{C_{a,{I_{M}}}}$. In addition, all Bobs encrypt numbers ${j_{1}},{j_{2}},\dots ,{j_{M}}$, also using Alice ${\text{PuK}_{A}}=a$ and obtaining ciphertexts ${c_{a,{j_{1}}}},{c_{a,{j_{2}}}},\dots ,{c_{a,{j_{M}}}}$. All Bobs send (${C_{a,{I_{1}}}},{C_{a,{I_{2}}}},\dots ,{C_{a,{I_{M}}}}$) and (${c_{a,{j_{1}}}},{c_{a,{j_{2}}}},\dots ,{c_{a,{j_{M}}}}$) to Alice.
-
2. Alice decrypts (${C_{a,{I_{1}}}},{C_{a,{I_{2}}}},\dots ,{C_{a,{I_{M}}}}$) and (${c_{a,{j_{1}}}},{c_{a,{j_{2}}}},\dots ,{c_{a,{j_{M}}}}$) with her $\text{PrK}=x$, thus obtaining ${I_{1}},{I_{2}},\dots ,{I_{M}}$ and ${j_{1}},{j_{2}},\dots ,{j_{M}}$. As it is outlined in P1, the actual values ${i_{1}},{i_{2}},\dots ,{i_{M}}$ are found from ${I_{1}},{I_{2}},\dots ,{I_{M}}$. Alice encrypts ${i_{1}},{i_{2}},\dots ,{i_{M}}$ by AA ${\text{PuK}_{AA}}=\alpha $ and sends obtained ciphertexts (${C_{\alpha ,{I_{1}}}},{C_{\alpha ,{I_{2}}}},\dots ,{C_{\alpha ,{I_{M}}}}$) to AA for auditing.
-
3. Alice defines expenses
${e_{1}},{e_{2}},\dots ,{e_{N+1}}$ and transforms them to
${E_{1}},{E_{2}},\dots ,{E_{N+1}}$, by applying (
17). Alice randomly generates numbers
${j_{E1}},{j_{E2}},\dots ,{j_{EN}}$ and computes number
${j_{E,N+1}}$
In this way, the following relation is satisfied for balance verification
Alice encrypts
${E_{1}},{E_{2}},\dots ,{E_{N+1}}$ using AA
${\text{PuK}_{AA}}=\alpha $ by computing ciphertexts (
${C_{\alpha ,E1}},{C_{\alpha ,E2}},\dots ,{C_{\alpha ,E,N+1}}$) and sends them to AA.
-
4. AA decrypts (${C_{\alpha ,{I_{1}}}},{C_{\alpha ,{I_{2}}}},\dots ,{C_{\alpha ,{I_{M}}}}$) and (${C_{\alpha ,{E_{1}}}},{C_{\alpha ,{E_{2}}}},\dots ,{C_{\alpha ,E,N+1}}$) using its ${\text{PrK}_{AA}}=z$, and finds values ${I_{1}},{I_{2}},\dots ,{I_{M}}$ and ${E_{1}},{E_{2}},\dots ,{E_{N+1}}$. AA finds actual values of income ${i_{1}},{i_{2}},\dots ,{i_{M}}$ and expenses ${e_{1}},{e_{2}},\dots ,{e_{N+1}}$, using the search procedure outlined in P1, and can verify the transaction validity.
Verification passes if:
-
a) for all $m=1,2,\dots ,M$ and $n=1,2,\dots ,N+1$, ${i_{m}}\lt {2^{32}}-1$ and ${e_{n}}\lt {2^{32}}-1$;
-
b) the balance equation (
1) is satisfied.
Data verifiability to the Net is performed by verifying the following equation
If this equation holds, then
and balance equation (
1) is valid. The scheme of transaction declaration and verification is presented in Fig.
1.
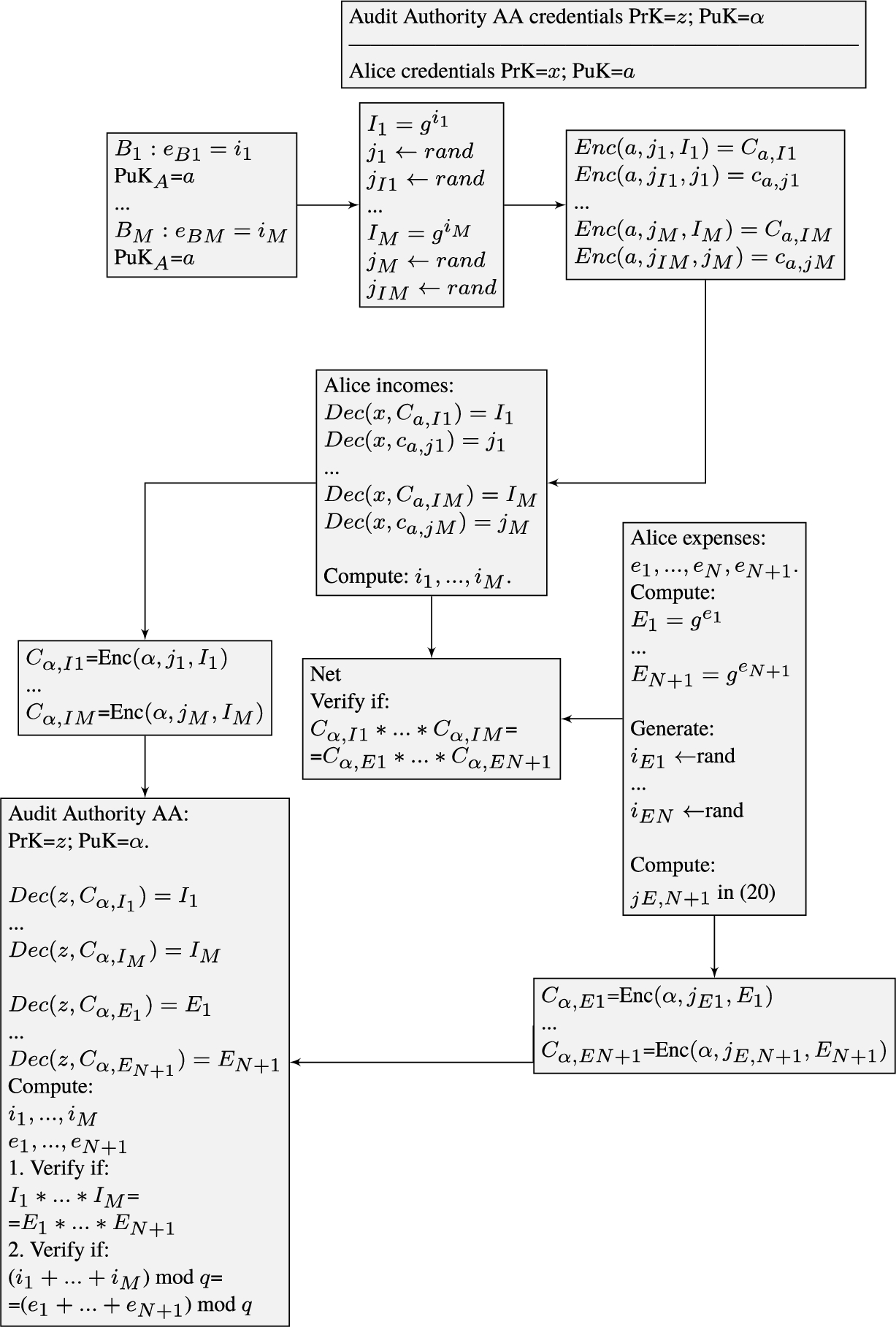
Fig. 1
Alice transaction declaration to AA and Net.
-
P4. Alice must transfer her expenses ${e_{1}},{e_{2}},\dots ,{e_{N}}$ to Laries ${L_{1}},{L_{2}},\dots ,{L_{N}}$ as their income. In order to make a transfer to Larie ${L_{n}}$, she encrypts the transformed expense ${E_{n}}$ using ${\text{PuK}_{Ln}}={l_{n}}$, $n=1,\dots ,N$ with the randomly generated number ${j_{Ln}}$, thus obtaining ciphertext ${C_{ln,En}}$. Alice randomly generates a number ${j_{En}}$ and encrypts the number ${j_{Ln}}$, thus obtaining ciphertext ${c_{ln,jEn}}$. Alice sends ${C_{ln,En}}$ and ${c_{ln,jEn}}$ to ${L_{n}}$.
Larie
${L_{n}}$ decrypts
${C_{ln,En}}$ and
${c_{ln,jEn}}$ using her
${\text{PrK}_{Ln}}={y_{n}}$, and obtains transformed Alice’s expense
${E_{n}}$ and
${j_{Ln}}$. Number
${j_{Ln}}$ will be needed to create Larie’s own transaction by acting in a similar way as Bob
${B_{n}}$ did. Larie computes
${e_{n}}$ and verifies if the obtained sum is correct. If Yes, he assigns
${e_{n}}$ to his income
${i_{Ln}}$ to be declared to AA. Using (
17), Larie computes
and encrypts it using
${\text{PuK}_{AA}}=\alpha $ and random generated number
${j_{ln}}$ obtaining ciphertext
${C_{\alpha ,I{L_{n}}}}$. Larie sends
${C_{\alpha ,I{L_{n}}}}$ to AA.
AA decrypts ${C_{\alpha ,I{L_{n}}}}$ obtains ${I_{{L_{n}}}}$. AA verifies if ${i_{{L_{n}}}}={e_{n}}$, declared by Alice.
The scheme of confidential money transfer from Alice to Larie
${L_{n}}$ is presented in Fig.
2 below.
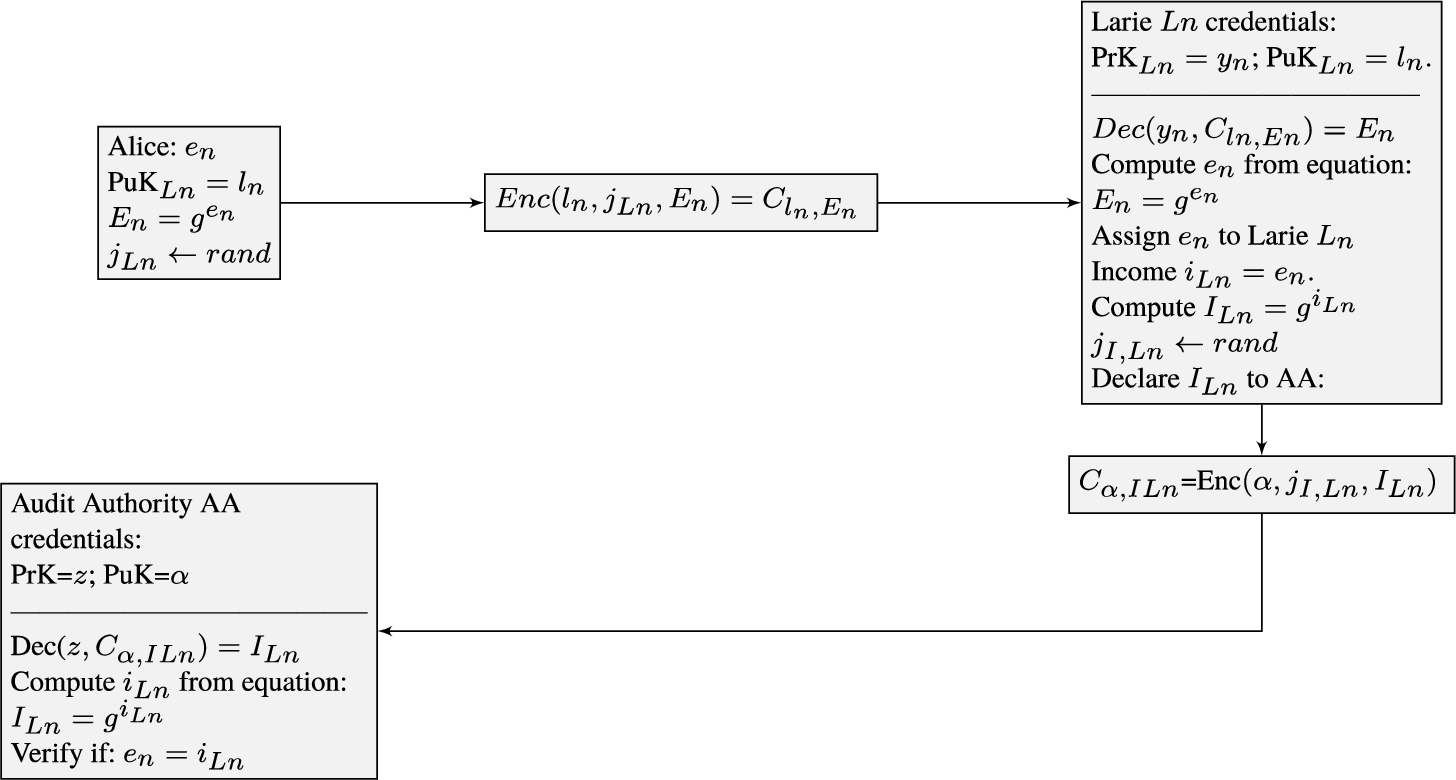
Fig. 2
Alice expense ${e_{n}}$ transfer to Lary ${L_{n}}$ as his income ${i_{{L_{n}}}}={e_{n}}$ verification.
6 Security and Effectivity Analysis
We will show that the presented tax declaration scheme ensures semantic security. It implies that any encrypted information in ciphertext accessible to the eavesdropper can provide only negligible information about the plaintext.
The group
${G_{q}}$, introduced in Section
3, is so-called Schnorr group where the Decissional Diffie-Hellman assumption (DDH) holds (Tsiounis and Yung,
1998). It is proved in the same source that if the DDH assumption holds, then ElGamal achieves semantic security. If DDH assumption holds, then DLP is infeasible in
${G_{q}}$. In this case, the solution of (
3) for finding
i when
${G_{q}}$ and
g is given is infeasible. It means that it is infeasible to find either decryptor’s private key
$\text{PrK}=z$ in (
5) or random secret encryption parameter
j in (6). Since DLP is infeasible, the public key exchange between the parties can be achieved using open communication channels. In order to provide authenticity and integrity of this exchange, the public keys should be digitally signed. We do not consider this technique in this paper.
Let us consider the following issue. If random integer
$j\in {Z_{q}}$ can be found, then the ciphertext
c in (
6) can be decrypted using the following relation
This relation implies the so called coalition attack, when all Bobs and Laries agree to exchange secret numbers numbers
${j_{1}},{j_{2}},\dots ,{j_{M}}$ and
${j_{e1}},{j_{e2}},\dots ,{j_{eN}}$ in order to find a secret number
${j_{E,N+1}}$ from (
20). If this is done, then Alice’s change represented by
${E_{N+1}}$ can be decrypted according to (
23)
In order to prevent this attack, an additional ciphertext is needed. For example, Alice can include the
$N+2$-th expense
${e_{N+2}}$ in order to pay a tax for her transaction to AA.
The efficiency of the implementation of the proposed scheme is almost the same as the efficiency of the implementation of ElGamal encryption. In order to create a transaction, it is necessary to perform an extra exponentiation operation to transform transaction data
d to
D according to (
17). Since we bounded the actual transfer sums up to
${2^{32}}-1=4294967295$, then by using a well-known square and multiply algorithm for all exponentiations, we have the additional number of operations for money transfer as
$O({\log _{2}}d)$. The maximal number of exponentiations for AA is 32.
7 Conclusions
Tax declaration scheme using blockchain confidential transactions based on unspent transactions output (UTxO) paradigm is presented. The main actors are money senders Bobs, Alice (being a receiver and a sender, and a transaction creator), money receivers Laries, Audit Authority AA and the Net. Different information is available for all these actors.
The proposed scheme provides that the Net can only verify the transaction honesty with guarantee that every transaction indirectly satisfies the balance equation (
1) without revealing any feasible information about the actual transaction data. It is guaranteed by the semantic security of the ElGamal encryption, presented in section
5, providing the confidentiality property of transactions for the Net. Actual money transfer values from Alice are available for each Larie, since they can be decrypted by their private keys respectively.
AA is handling all information about the actual transaction income and expenses. AA can also verify that the sum transferred from the sender Alice, as an expense, is equal to the sum received by Larie as an input. Therefore, the expense and income declaration can be monitored. It holds for all related transactions, thus also allowing to monitor tax payments. The efficiency of the implementation of the proposed scheme is almost the same as the efficiency of the implementation of ElGamal encryption. The additional number of operations for money transfer is $O({\log _{2}}d)$. The maximum number of exponentiations for AA is 32.

