1 Introduction
Structures must become stronger, faster, and more versatile, as well as more durable, with a huge increase in the amount of cement used in the process. Most construction projects today use Portland cement concrete, which is the predominant type of concrete. Because of the low cost of construction materials and the ease of maintenance, concrete structures can be built and maintained.
Recent research found that a biomaterial can be used to treat concrete cracks (Van Tittelboom
et al.,
2010; Ramachandran
et al.,
2001). Scientists have discovered that inorganic substances that are deposited by microorganisms inside cement-sand mortar or the pores of concrete can be used for filling cracks (Ghosh
et al.,
2005; Ramakrishnan
et al.,
1999). A concrete structure’s inherent weakness is its vulnerability to cracks that allow water to penetrate, causing corrosion and reducing its durability (Chahal
et al.,
2012).
Ramachandran
et al. (
2001) pioneered microbial concrete, and since then there has been a considerable volume of research on the topic. As ureolytic bacteria are alkali-resistant and nutrition is not necessary for survival for hundreds of years, the researchers examined Bacillus sphaericus, Sporosarcina pasteurii, and Bacillus megaterium (Arunachalam
et al.,
2010; Dhami
et al.,
2013; Achal
et al.,
2011). In some studies, researchers examined the effects of adding bacteria to concrete on its compressive strength and crack healing. The findings reflect that most of them considered bacterial concentrations between 103 to 107 cells/ml when considering strength enhancement. Contrary to crack healing, researchers use higher concentrations of bacterial cells (107–109 cells/ml) (Majumdar
et al.,
2012; Mondal and Ghosh,
2018; De Muynck
et al.,
2008).
The versatility of concrete makes it a popular choice for building materials. Locally available, strong and durable, it is versatile. Despite its capability to resist compression loads to a limit, if the load applied on the concrete exceeds their limit of load resistance, it results in cracks in the concrete, which lowers its strength. Concrete’s serviceability limit is affected by cracks. Concrete may become weaker and less durable as moisture and other chemicals get into it. In addition to that, water absorption is another major issue that reduces the life of concrete. Researchers are currently using bacteria to treat concrete mortar to overcome the problems. The selection of an optimal bacteria concentration and curing day can also pose a problem. Grey Relational Analysis (GRA) can be used in this field to find an optimal solution, since various researchers use it in different fields as an optimization technique (Dagdevir and Ozceyhan,
2021; Güler
et al.,
2021; Roy
et al.,
2016; Si
et al.,
2021). A major drawback of GRA is that it assigns a similar weight to all output characteristics, even though in practice not all output characteristics are equally important (Fangfang,
2021). To overcome the problem, some researchers are using Analytical Hierarchy Process (AHP) along with GRA (Erdoğan and Sayin,
2018; Erdoğan
et al.,
2020). An advantage, as well as a reason for using the AHP method, is that results can be validated by determining the consistency of the model with actual data. A study suggests that comparing pairwise across nine criteria by the AHP method is extremely difficult since it requires a great deal of comparisons
$n(n-1)/2$ (Milićević
et al.,
2007).
The BWM has been shown to be able to resolve certain of the previously listed constraints associated with AHP models (Rezaei,
2015). Compared to AHP’s many pairwise comparisons, BWM does only a small number, such as
$2n-3$. There is a direct correlation between the number of pairwise criteria comparisons and the consistency of the method. Moreover, the BWM does not require a comparison of nine criteria, merely a smaller number of criteria. The AHP model is improved by forming the Best-to-Others (BO) as well as Other-to-Worst (OW) vectors, resulting in fewer pairwise comparisons, and the resulting data are more consistent. The BWM, however, has a problem in determining the optimum weight coefficients when there is a large degree of variation inconsistency. The weight coefficient can be determined by using the average of the intervals as final values in such cases, as proposed by Rezaei (
2015). Despite this, the central part of the interval is not guaranteed to be representative of the optimal weight coefficient value. A better value might lie closer to the right or left end of the interval. The interval weight values do not even cover the optimum values of priority coefficients in the cases of the greater inconsistency of results (Pamučar
et al.,
2018a).
FUCOM uses pairwise comparisons of criteria to determine criteria priority, and it validates results across a wide range of deviations from maximum consistency in order to determine criteria priority (Pamučar
et al.,
2018b). As compared to BWM and AHP tools, FUCOM eliminates some of their weaknesses. When using FUCOM, criteria can be compared in pairs (
$n-1$ comparisons), DMC (Deviation from the Maximum Consistency) can be calculated when comparing comparisons, and transitivity can be recognized throughout pairwise comparisons. There is a subjective effect of DMs on the weighting of criteria in FUCOM, as there is in other subjective models. As such, this refers specifically to the first, as well as second steps of the FUCOM. The FUCOM, in contrast to subjective models, shows minor deviations from the optimum value in the priority value of the criteria. In addition, the FUCOM methodological procedure removes the redundancy caused by comparing criteria pairwise, which is a problem with some subjective methods for priority value determination (Božanić
et al.,
2019; Bozanic
et al.,
2020; Durmić
et al.,
2020). In recent years, FOCUM is being combined with other methods by many researchers to solve problems. For the purpose of selecting the appropriate combination of construction machines to enable mobility, Darko Boana
et al. used a hybrid model of FUCOM and fuzzified RAFSI (Božanić
et al.,
2021). Nunić (
2018) applies a hybrid model of FOCUM-MABAC for evaluating and selecting PVC carpentry manufacturers. Real-world decision-makers often use linguistic variables instead of crisp values to evaluate attributes when they have partial knowledge or little information. Decision-makers are often left with ambiguous, imprecise, or incomplete attribute information as a result of such situations. Inaccuracies such as these can be mathematically represented by fuzzy set theory, introduced by Zadeh (
1975). Since they were created, fuzzy sets have been successfully used to model MCDM problems with imprecise information. A fuzzy full consistency MCDM method was presented by Pamucar and Ecer (
2020). In a hybrid model used by Baig
et al. (
2022) to enhance the resilience of oil supply chains, FOCUM prioritizes vulnerabilities while Fuzzy Quality Function Deployment identifies those capabilities that can ensure their protection. As part of the sustainability plan for urban mobility, Demir
et al. (
2022) used Fuzzy-FOCUM. A hybrid fuzzy FUCOM and neutrosophic fuzzy MARCOS methodology was used to assess alternative fuel vehicles for sustainable road transportation in the United States by Pamucar
et al. (
2021). A fuzzy-focus approach was used by Tang
et al. (
2021) for prioritizing sustainability scenarios for sewage sludge. To determine the drivers for investing in cryptocurrencies, Böyükaslan and Ecer used Fuzzy FUCOM in
2021.
The drawback of fuzzy sets is that, in some circumstances, it can be quite challenging to determine a precise membership mapping for a fuzzy set (Chiao,
2016). An intuitionistic fuzzy set (IFS), which Krassimir and Parvathi proposed in
1986, is a generalized fuzzy set that considers membership and non-membership degrees, as well as hesitation degrees. IFS can handle ambiguous information in a flexible manner (Gong
et al.,
2014). As a result, specialists have been paying more and more attention to the IFS, which is now being used in many other domains, including decision-making (Gong
et al.,
2014). This study addresses a vacuum in the literature, since, as far as the authors are aware, the FUCOM has not yet been used to intuitionistic contexts. In fact, extending FUCOM’s research to the intuitionistic fuzzy environment is motivated in part by this.
In this study, Section
2 discusses IF-FUCOM-GRA, while Section
3 discusses step-by-step methodology with experimental details and results. Results of each method listed in Section
3 are presented in Section
4 in a step-by-step manner. Sections
5 and
6 represent the discussion and conclusion sections, respectively.
2 Intuitionistic Fuzzy Full Consistency Method Grey Relational Analysis (IF-FUCOM-GRA)
IF-FUCOM-AHP has two phases, IF-FUCOM and IF-AHP, which are discussed respectively in Phases I and II. Phase I and Phase II discussed how to analyse criteria and alternatives to determine the priority value of criteria and alternatives. Figure
1 depicts the proposed method’s computational procedure. Figure
1 illustrates how the method is computed.
Phase-1: Intuitionistic Fuzzy Full Consistency Method (IF-FUCOM):
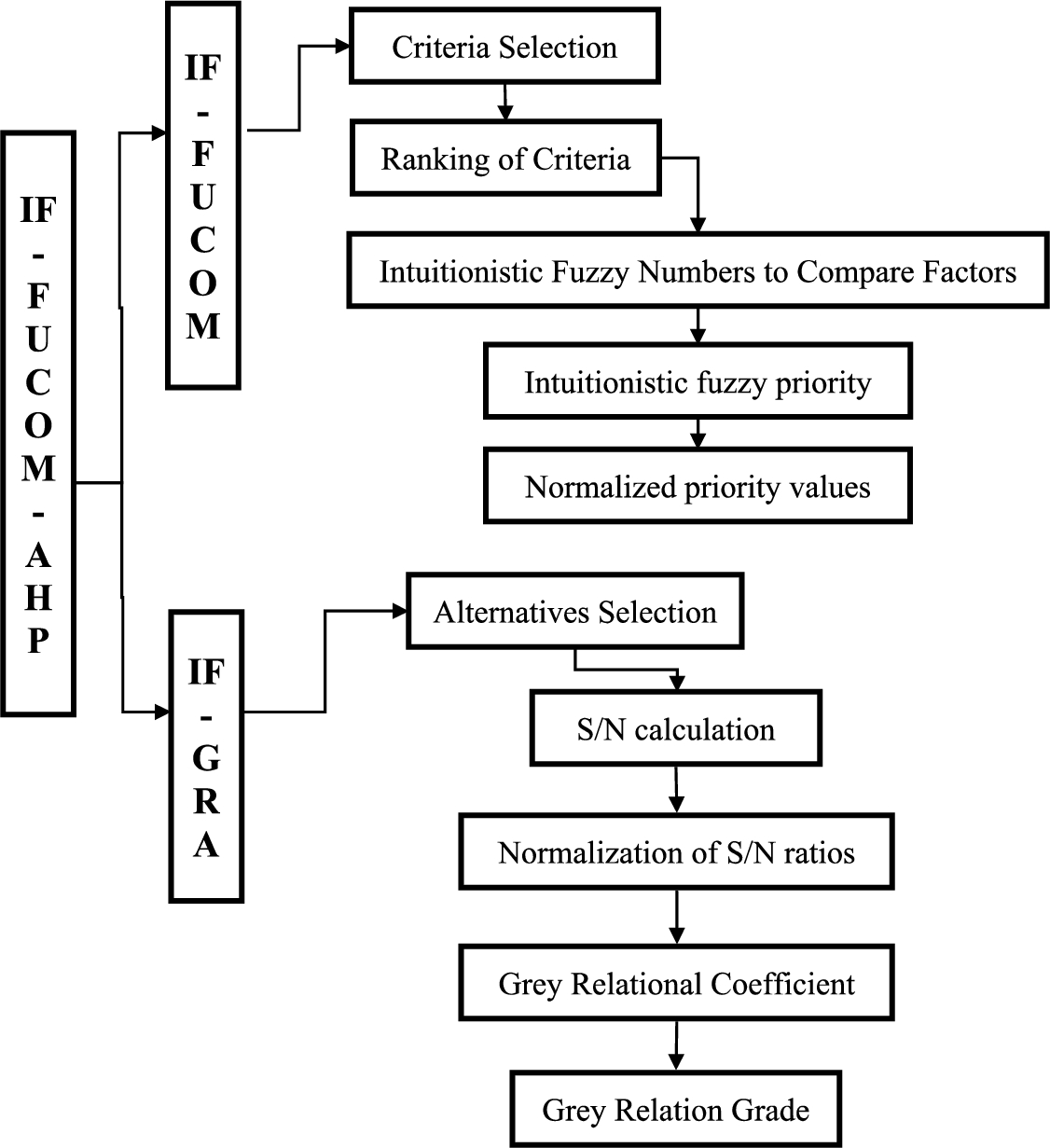
Fig. 1
Total scenario of proposed method.
In order to determine the priority value of criteria, FUCOM is used. It is proposed that a modified fuzzy FUCOM approach is used in the current study called Intuitionistic Fuzzy Full Consistency Method (IF-FUCOM) to find the priority values of each criterion. Five steps make up IF-FUCOM. Following are the steps:
Step-I: Identify the assessment criteria: This consists of n $(r=1(1)q)$ decision criteria, which are represented by $\Omega =\{{\xi _{r}}:r=1(1)q\}$.
Step-II: Determine the ranking of factors: The DMs determine the order of importance of factors based on their opinions. A factor is ranked in ascending order by the weight coefficient that will be assigned to it first, and so on, down to the least significant factor in the equation. The factor whose weight coefficient is expected to be the lowest is ranked last. In the resulting ranking system, ${\xi _{r(1)}}\succ {\xi _{r(2)}}\succ \cdots \succ {\xi _{r(l)}}$ represents the factor rank, where l represents the criterion ranking. A sign of equality replaces “≻” between two or more factors that have the same ranking.
Step-III: Use intuitionistic fuzzy numbers to compare factors: Table
1 is used to compare factors. The factors are compared according to the first ranking factor. The Intuitionistic fuzzy criterion meaning (
${\tilde{p}_{{\xi _{r(l)}}}}$) is then determined for all the factors. In order to compare the remaining factors with the most important factor, a
$(q-1)$ comparison is a necessity. A fuzzy Intuitionistic significance
${\tilde{\mathrm{\wp }}_{l/(l+1)}}$ is derived from equation (
1) by applying the defined significance of factors:
Equation (
2) provides an Intuitionistic fuzzy vector of the relative importance of the decision factors:
Based on the factor of
${\xi _{r(l+1)}}$ rank,
${\tilde{\mathrm{\wp }}_{l/(l+1)}}$ represents the importance that the factor of
${\xi _{r(l)}}$ rank possesses.
Step-IV: Calculate intuitionistic fuzzy priority: here, the Intuitionistic fuzzy priority value coefficients are calculated for factor ${({\tilde{p}_{1}},{\tilde{p}_{2}},\dots ,{\tilde{p}_{q}})^{T}}$. As a final priority coefficient value, the following conditions must be met:
Table 1
Nine-point triangular intuitionistic fuzzy scale (Otay
et al.,
2017).
| Definition |
Intensity of importance $({\delta ^{l}},{\delta ^{m}},{\delta ^{u}};{\delta ^{\prime \hspace{0.1667em}l}},{\delta ^{\prime \hspace{0.1667em}m}},{\delta ^{\prime \hspace{0.1667em}u}})$
|
Reverse of intensity importance $\big(\frac{1}{{\delta ^{u}}},\frac{1}{{\delta ^{m}}},\frac{1}{{\delta ^{l}}};\frac{1}{{\delta ^{\prime \hspace{0.1667em}u}}},\frac{1}{{\delta ^{\prime \hspace{0.1667em}m}}},\frac{1}{{\delta ^{\prime \hspace{0.1667em}l}}}\big)$
|
S.I. |
| EI |
$(1,1,1;1,1,1)$ |
|
1 |
| AI |
$(8,9,9;7,9,9)$ |
|
9 |
| MI |
$(\mu -1,\mu ,\mu +1;\mu -2,\mu ,\mu +2)$ |
$\big(\frac{1}{\mu +1},\frac{1}{\mu },\frac{1}{\mu -1};\frac{1}{\mu +2},\frac{1}{\mu },\frac{1}{\mu -2}\big)$ |
$\mu =3$ |
| STI |
|
|
$\mu =5$ |
| VSI |
|
|
$\mu =7$ |
| Intermediate scale |
|
|
$\mu =2,4,6,8$ |
Condition 1: The weight coefficient ratio between the observed factors (
${\xi _{r(l)}}$ and
${\xi _{r(l+1)}}$) should equal the significance ratio between them (
${\tilde{\mathrm{\wp }}_{l/(l+1)}}$) defined in Step II; in other words, it should satisfy:
Condition 2: Besides satisfying the condition in expression (
3), the coefficients of weights should also qualify as transitive, i.e.
It is also necessary for the final weight coefficient values to satisfy the following condition:
DMC minimum, i.e.
$\nu =0$, can only be satisfied if there is complete transitivity among priority coefficients. Then, it can be said that
$\frac{{\tilde{p}_{l}}}{{\tilde{p}_{l+1}}}-{\tilde{\mathrm{\wp }}_{l/(l+1)}}=0$ and
$\frac{{\tilde{p}_{l}}}{{\tilde{p}_{l+2}}}-{\tilde{\mathrm{\wp }}_{l/(l+1)}}\otimes {\tilde{\mathrm{\wp }}_{(l+1)/(l+2)}}=0$. Accordingly, DMC is
$\nu =0$, when such coefficients are obtained. To satisfy these conditions, the weight coefficients for each criterion
${({\tilde{p}_{1}},{\tilde{p}_{2}},\dots ,{\tilde{p}_{q}})^{T}}$ must satisfy the condition that
$\big|\frac{{\tilde{p}_{l}}}{{\tilde{p}_{l+1}}}-{\tilde{\mathrm{\wp }}_{l/(l+1)}}\big|\leqslant \nu $ and
$\big|\frac{{\tilde{p}_{l}}}{{\tilde{p}_{l+2}}}-{\tilde{\mathrm{\wp }}_{l/(l+1)}}\otimes {\tilde{\mathrm{\wp }}_{(l+1)/(l+2)}}\big|\leqslant \nu $ minimize the value
ν.
The final nonlinear model for computing the ideal Intuitionistic fuzzy values of the relative weights of each factor can then be set to
${({\tilde{p}_{1}},{\tilde{p}_{2}},\dots ,{\tilde{p}_{q}})^{T}}$.
where
${\tilde{p}_{r}}=({p_{r}^{l}},{p_{r}^{m}},{p_{r}^{u}};{p^{\prime \hspace{0.1667em}l}_{r}},{p^{\prime \hspace{0.1667em}m}_{r}},{p^{\prime \hspace{0.1667em}u}_{r}})$ and
${\tilde{\mathrm{\wp }}_{l/(l+1)}}=({\mathrm{\wp }_{l/(l+1)}^{l}},{\mathrm{\wp }_{l/(l+1)}^{m}},{\mathrm{\wp }_{l/(l+1)}^{u}};{\mathrm{\wp }^{\prime \hspace{0.1667em}l}_{l/(l+1)}},{\mathrm{\wp }^{\prime \hspace{0.1667em}m}_{l/(l+1)}},{\mathrm{\wp }^{\prime \hspace{0.1667em}u}_{l/(l+1)}})$.
The highest consistency can only be obtained by following the condition that
$\frac{{\tilde{p}_{l}}}{{\tilde{p}_{l+1}}}-{\tilde{\mathrm{\wp }}_{l/(l+1)}}=0$ and
$\frac{{\tilde{p}_{l}}}{{\tilde{p}_{l+2}}}-{\tilde{\mathrm{\wp }}_{l/(l+1)}}\otimes {\tilde{\mathrm{\wp }}_{(l+1)/(l+2)}}=0$ are both met. In this way, the model (
5) can be re-formulated into an Intuitionistic fuzzy nonlinear model (
6). Intuitionistic fuzzy priority value coefficients are obtained
${({\tilde{p}_{1}},{\tilde{p}_{2}},\dots ,{\tilde{p}_{q}})^{T}}$, if this problem is solved.
where
${\tilde{p}_{j}}=({p_{j}^{l}},{p_{j}^{m}},{p_{j}^{u}};{p^{\prime \hspace{0.1667em}l}_{j}},{p^{\prime \hspace{0.1667em}m}_{j}},{p^{\prime \hspace{0.1667em}u}_{j}})$ and
${\tilde{\mathrm{\wp }}_{l/(l+1)}}=({\mathrm{\wp }_{l/(l+1)}^{l}},{\mathrm{\wp }_{l/(l+1)}^{m}},{\mathrm{\wp }_{l/(l+1)}^{u}};{\mathrm{\wp }^{\prime \hspace{0.1667em}l}_{l/(l+1)}},{\mathrm{\wp }^{\prime \hspace{0.1667em}m}_{l/(l+1)}},{\mathrm{\wp }^{\prime \hspace{0.1667em}u}_{l/(l+1)}})$.
Convert optimal Intuitionistic fuzzy priority value
$({\tilde{p}_{1}^{\ast }},{\tilde{p}_{2}^{\ast }},\dots ,{\tilde{p}_{q}^{\ast }})$, where
${\tilde{p}_{r}^{\ast }}=({p_{r}^{l\ast }},{p_{r}^{m\ast }},{p_{r}^{u\ast }};{p^{\prime \hspace{0.1667em}l\ast }_{r}},{p^{\prime \hspace{0.1667em}m\ast }_{r}},{p^{\prime \hspace{0.1667em}u\ast }_{r}})$, for all
$r=1(1)q$ into crisp value using the formula (
7):
Step-V: Normalized priority values: equation (
8) is used to calculate the normalized priority values of criteria.
Phase-2: Grey Relational Analysis:
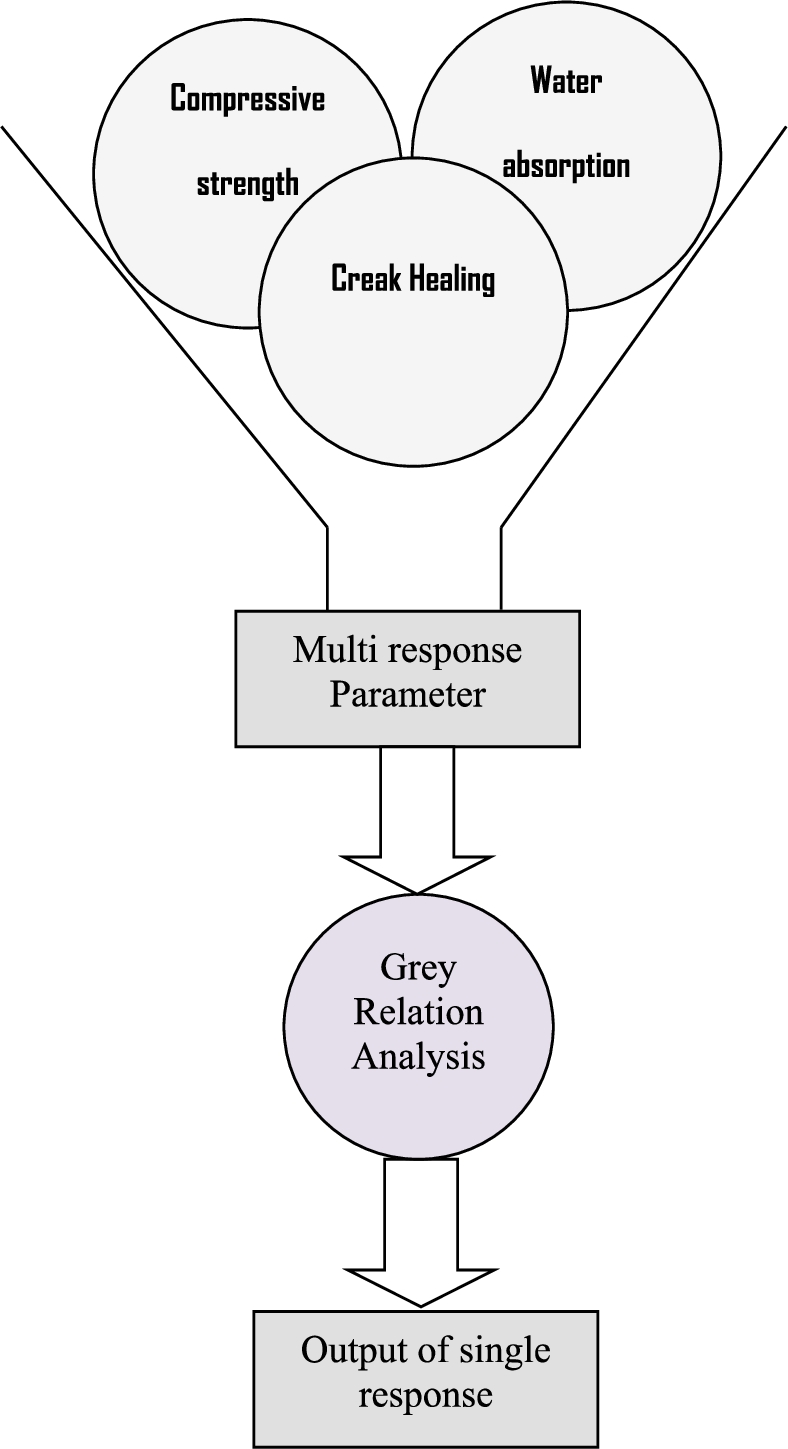
Fig. 2
Graph of a straightforward grey relational analysis.
The grey theory is an immense concept used to explore uncertainty, multi-input, and discrete data. Decision analysis is used to estimate the degree of relation according to the grey relational grade. A multi-objective optimization makes it more complex to analyse the effects and relationships between design factors in experiments at their various levels that result uncertain and insignificant information. In this paper, GRA is proposed for investigating and optimizing the complexity of multi-variable problems by exploiting the concept of information. As shown in Fig.
2, GRA reduces a multi-objective question to a single objective answer (referred to as single relational grade).
The present study is conducted based upon Taguchi’s orthogonal array, which corresponds to nine trails, where every trail is known as a comparison sequence. The GRA places these trails into nine subsystems. The effect of these factors on the outcome variable is assessed through regression analysis. Using GRA, the multi-objective problem is transformed into a single-objective problem by using the parameters corresponding to the greatest weighted grey relational grade.
Step-I: $S/N$ calculation:
Greater, nominal, and lower signal-to-noise ratio analyses are the three possible approaches. For water absorption in this study, smaller-is-better, however, higher-is-better for compressive strength and creak healing. The
$S/N$ ratios of water absorption are calculated by equation (
9), and compressive strength and creak healing by equation (
10).
where,
${\lambda _{k}}$ is the
kth experiment’s observed data and
m is representing the observations’ number.
Step-II: $S/N$ ratio normalization:
To lessen unpredictability, the
$S/N$ ratio of attribute data is modified. Data preparation is the term for this. Pre-processing of the data is needed for grey analysis (Grzenda
et al.,
2012; Kao
et al.,
2008). The following equation (
11) normalizes the original sequence:
However, the data is normalized using equation (
12); the smaller the characteristic, the better.
ζ represents desired value,
${\zeta _{k}^{\ast }}(t)$ indicates normalized value, where
n stands for the number of experiments, and
m for the number of answers, and
$t=1(1)n$;
$k=1(1)n$.
Step-III: Grey Relational Coefficient:
The GRC, a series of information, is used by GRA to assess the relevance of two systems. Equation (
13) can be used to calculate GRC
$({\mu _{k}})$.
where
${\delta _{k}}(t)=\| {\zeta _{k}}(0)-{\zeta _{k}}(t)\| $
${\zeta _{k}}(0)=\hspace{2.5pt}\text{reference value}\hspace{2.5pt}(=1)$;
${\zeta _{k}}(t)$ = specific comparison value, where
τ is the distinguishing coefficient
$0\leqslant \tau \leqslant 1$.
Step-IV: Grey Relation Grade:
In real engineering systems, different parts have different weights based on the circumstances. Then, equation (
14) grades the grey relational coefficient (GRC) (Saaty,
1980).
where
${p_{k}}$ stands for factor
k’s normalized weight. The proposed IF-FUCOM approach yields the weight of each attribute. The higher the value of grey relational grade is, the greater is the desirability.
3 Methodology
The objective of this study is to find the optimal bacterial concentrations and curing days for concrete simultaneously while considering compressive strength (CS), crack healing (CH) and water absorption (WA) as outputs using a novel MCDM technique. During the present investigation, there are six phases. A schematic representation of the detailed methodology is shown in Fig.
3.
Phase-I: The Experimental details include details on the materials, bacteria culture, mixing procedure, compression strength (${\xi _{1}}$), crack healing (${\xi _{2}}$) and water absorption (${\xi _{3}}$) test on mortar surfaces.
Phase-II: The criteria and alternatives were discussed in this phase.
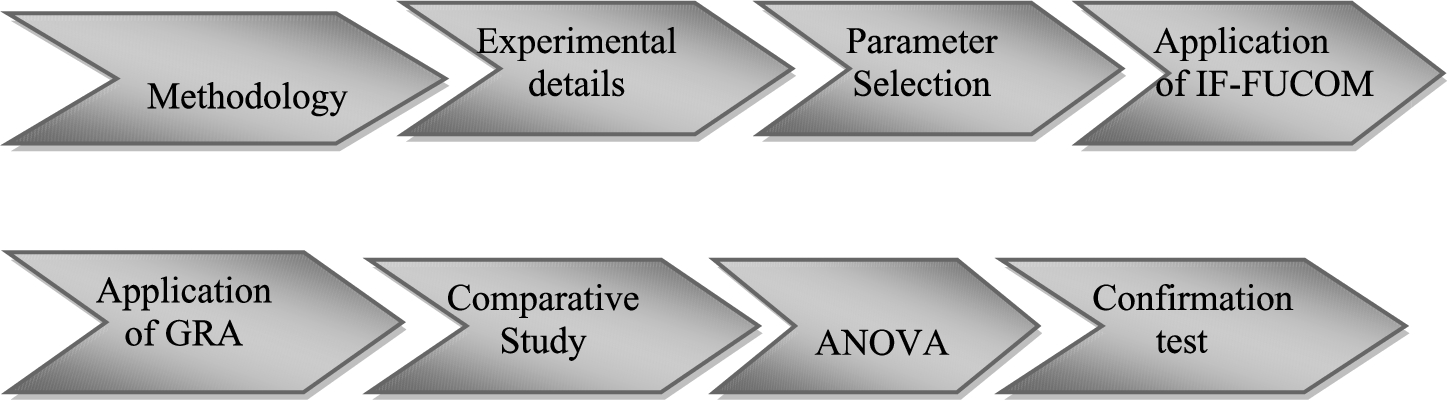
Fig. 3
A diagrammatic representation of the methodology.
Phase-III: Determine the weights of all consideration criteria using the proposed MCDM method.
Phase-IV: Evaluate alternative weights using another existing MCDM technique.
Phase-V: Comparison of the results determined by the proposed MCDM with the existing model.
Phase-VI: An analysis is made of the degree to which each of the chosen parameter values contributes to the output responses.
Phase-VII: Validation tests are run to confirm forecasts and results.
Phase-VIII: Sensitivity analysis investigates how the indicators, which were calculated using the MCDM method, affect the anticipated result.
Phase-I. Experimental details:
This section explains the material choice, the bacteria mixing process, and several tests like compressive strength and water absorption.
Step-I. Materials:
Ordinary Portland Cement (OPC) 43 Grade conforms to IS 8112 : 2013, locally available Fine Aggregate, Bacillus Subtilis and potable water is used in this study. Here cement to sand ratio and water to cement ratio were 1 : 3 and 0.4 (by weight) respectively. For preparing mortar water, distilled water is used. Mortar cubes of dimension 70.6 mm
3 are prepared for both control and bacterial mortar specimens. In fresh water, curing can be conducted at room temperature 27 °C. According to information provided by the manufacturer, OPC cement’s chemical composition and physical properties are presented in Table
2.
Step-II. Bacteria culture:
Table 2
Composition and physical properties of cement.
| Physical properties |
| Colour |
Grey |
| Specific gravity |
3 |
| Chemical constituents (%) |
| Al2O3
|
3.78 |
| SiO2
|
21.5 |
| MgO |
1.79 |
| Fe2O3
|
3.78 |
| CaO |
63.69 |
| SO3
|
3 |
| Na2O |
– |
| K2O |
– |
For this experimental work, selected bacterial sample Bacillus Subtilisis is used in this study. For bacterial culture nutrient broth was made (1.0 gm/lBeef Extract, 5.0 gm/lPeptone, 2.0 gm/lYeast Extract, 5.0 gm/NaCl). Growth conditions of Bacteria are maintained at 37 °C temperature. After 6–7 days, about 10 μl of the nutrient broth is obtained and haemocytometer counting is done. Here, the bacterial concentrations in solution used are ${10^{3}}$ cells/ml, ${10^{5}}$ cells/ml, ${10^{7}}$ cells/ml.
Step-III. The mixing procedure:
Cement and sand is well mixed in 1:3 proportions and a mixture of water and the needed cell concentration is then prepared. After casting and compacting in a vibration machine, specimens are removed and compression tests are performed after 3, 7, 14 and 28 days in air at room temperature (30 °C).
Step-IV. Compressive strength and water absorption test:
Compressive strength and water absorption of control and bacterial mortar cubes are measured in 3, 7 and 28 days after curing. The compressive strength test was done under compression testing machine.
Step-V. Crack healing on mortar surfaces:
A 28-day crack healing test is performed on microbial concrete to determine its self-healing ability at different bacteria concentrations. The crack-measuring instrument measured the crack widths. In this study, crack widths range from 0.11 mm to 1.5 mm; water is used to immerse the cracked specimens and their crack dimensions are recorded after 3, 7 and 28 days.
Phase-II. Parameter Selection:
Table 3
Levels and values of the input parameters.
| Parameters |
Level-1 |
Level-2 |
Level-3 |
| Concentration |
0 |
5 |
7 |
| Days |
3 |
7 |
28 |
The PV of each criterion and alternative will be calculated in the section that follows. In the present study, compressive strength (${\xi _{1}}$), crack healing (${\xi _{2}}$) and water absorption (${\xi _{3}}$) are considered as a set of criteria. Also, nine considering trials, namely, ${10^{7}}$ Concentration with 28 days, ${10^{5}}$ Concentration with 28 days, ${10^{3}}$ Concentration with 28 days, ${10^{7}}$ Concentration with 7 days, ${10^{5}}$ Concentration with 7 days, ${10^{3}}$ Concentration with 7 days, ${10^{7}}$ Concentration with 3 days, ${10^{5}}$ Concentration with 3 days and ${10^{3}}$ Concentration with 3 days as a set of alternatives.
For the present study, the design factors chosen are bacteria concentration and curing day so as to determine their influence on the outcome parameters of compressive strength, crack healing, and water absorption. Table
3 represents the levels of input parameters (bacteria concentration and curing day) that are considered as control factors for the experiment. In Table
4, based on the number of tests, a Taguchi L9 (32) orthogonal array comprising 9 rows has been calculated.
Phase-III. Application of IF-FUCOM:
Table 4
Results of an experiment using ${L_{9}}$ orthogonal arrays.
| Trial No. |
Concentration |
Days |
CS (Map) |
CH (%) |
WA (%) |
| 1 |
${10^{3}}$ |
3 |
30.1206 |
30.3167 |
5.5 |
| 2 |
${10^{3}}$ |
7 |
37.6342 |
50.2262 |
4.66667 |
| 3 |
${10^{3}}$ |
28 |
48.1967 |
60.6335 |
4.25 |
| 4 |
${10^{5}}$ |
3 |
32.7521 |
70.1357 |
5.08333 |
| 5 |
${10^{5}}$ |
7 |
41.2611 |
84.6154 |
4.375 |
| 6 |
${10^{5}}$ |
28 |
52.462 |
90.0452 |
3.79167 |
| 7 |
${10^{7}}$ |
3 |
31.4065 |
94.5701 |
4.91667 |
| 8 |
${10^{7}}$ |
7 |
39.9128 |
98.5 |
4.04167 |
| 9 |
${10^{7}}$ |
28 |
49.4737 |
99.6 |
3.58333 |
Collect all factors based on the literature review, and then send them to three experts, and expert responds. Following the determination of the first-level criteria, the ranking is determined on a second level. Dimensions are ranked in this order:
${\xi _{1}}>{\xi _{2}}>{\xi _{3}}$. In Table
5, the linguistic variables represent the relative importance of the criteria ranked according to decision-makers preferences.
Table 5
A linguistic assessments of the main dimensions.
| Dimensions |
${\xi _{1}}$ |
${\xi _{2}}$ |
${\xi _{3}}$ |
| Linguistic variables |
EI |
MI |
STI |
The fuzzy linguistic scale was used to transform linguistic variables into Intuitionistic fuzzy numbers (IFNs), as shown in Table
6.
Table 6
Evaluations transformed by IFNs.
| Dimensions |
${\xi _{1}}$ |
${\xi _{2}}$ |
${\xi _{3}}$ |
| IFNs |
$(1,1,1;1,1,1)$ |
$(2,3,4;1,3,5)$ |
$(4,5,6;3,5,7)$ |
According to expression (1), the relative importance of the criteria is as follows:
A vector comparative significance is therefore defined as follows:
Three constraints are imposed by equation (
4) based on the conditions of relation transitivity as follows:
Optimization Problem:
Phase-IV. Application of GRA:
To calculate the score, gray relation grading is used after determining the relative weights of each criterion. GRCs are used to calculate gray reasoning grades using equation (
14). GRCs are weighted from 0 to 1. IF-FUCOM decides the weight of each characteristic. A gray relational grade of the higher value indicates greater desirability.
Phase-V. Study of Comparisons:
A comparative research can identify and quantify the relationships between at least two factors by studying different groups that have been exposed to diverse treatments either by choice or circumstance. A relative study is made possible by contrasting two sets of individuals, entities, or circumstances. In the current work, the proposed technique has been contrasted with three sophisticated models.
Model-I: The local weight must be calculated using AHP (Saaty,
1980), and the global weight must be calculated using GRA (Julong,
1989).
Model-II: Identify the local weights of the BWM (Rezaei,
2015) and the GRA (Julong,
1989) alternative, as well as identifying the global weights of the BWM-GRA alternative.
Model-III: Determine the local weight of an alternative GRA (Julong,
1989), the local weight of the FUCOM (Pamučar
et al.,
2018b), then calculate the global weight using a hybrid strategy known as FUCOM GRA.
Here are three mathematical formulations of the models discussed below.
Model-I. AHP result:
The weights of the different criteria are determined by experts within related fields who collaborate in a pairwise comparison between each criterion. This comparison matrix is shown below:
Model-II. BWM result:
For the purpose of weighing the criteria in BWM, relevant experts are asked to identify the most and least significant factors in the case study, along with the best-to-others and other-to-worst vectors. According to expert consensus,
${\xi _{1}}$ and
${\xi _{3}}$ are the best and worst criteria, respectively. The best-to-others and worst-to-others vectors are shown in Tables
7 and
8.
Table 7
Best to others criteria.
| Best to others |
${\xi _{1}}$ |
${\xi _{2}}$ |
${\xi _{3}}$ |
| ${\xi _{1}}$ |
1 |
3 |
7 |
Table 8
Others to worst criteria.
| Others to worst |
${\xi _{3}}$ |
| ${\xi _{1}}$ |
7 |
| ${\xi _{2}}$ |
5 |
| ${\xi _{3}}$ |
1 |
The weight of each criterion can be calculated, as well as the consistency rate, using the non-linear mathematical model.
Model-III. FUCOM result:
The criteria are ranked in order of importance. The ranking is determined by consensus among experts. According to experts, the relation (
17) criteria are ranked. Comparisons are based on a scale of Van Tittelboom
et al. (
2010), Achal
et al. (
2011), which is shown in Table
9.
Table 9
Comparative significance levels for the evaluation criteria.
| ${\xi _{3}}$ |
${\xi _{3}}$ |
${\xi _{3}}$ |
| 1 |
1.08 |
1.25 |
The relative importance of each criterion can be gauged by calculating the comparison importance values based on the obtained importance values ${\theta _{{C_{1}}/{C_{2}}}}=\frac{1.08}{1}=1.08$, ${\theta _{{C_{2}}/{C_{3}}}}=\frac{1.25}{1.08}=1.15740741$ and ${\theta _{{C_{1}}/{C_{3}}}}=1.08\times 1.15740741=1.25$.
The final weight coefficients can be determined by applying expression (
18)
Phase-V. ANOVA:
Statistically, the difference among available scores can be evaluated through Analysis of Variance (ANOVA). In ANOVA, the level of contribution of each of the chosen parameter values over the output responses is analysed (Pattnaik
et al.,
2013). ANOVA results can be used to determine which variables are responsible for the performance of a selected process and to control these variables to obtain a better result. ANOVA cannot provide data analysis, but this statistical method can assess variance of the data.
Phase-VI. Confirmation test:
A confirmation test is done to verify the forecast and the outcome after the
$S/N$ ratio plot is used to estimate the optimal output. The IF-FUCUM-GRG values delivered at the optimal output are predicted by equation (
19):
The group’s reasoning grade
${\vartheta _{\textit{mean}}}$ stands for the overall grade mean,
${\vartheta _{i}}$ for the grade at the best level, and
n is the output regulating parameter.
4 Result
The six parts of the proposed model are described in the results section.
Part-I: Calculate the gray relation coefficient.
Phase-II: In this phase, IF-FUCOM is used to determine weights for the criteria. The weights and rankings of alternatives are determined using IF-FUCOM and GRC.
Phase-III: A comparison of the results offered by novel IF-FUCOM-AHP and some existing methods.
Phase-IV: Next, the ANOVA result is used to determine the influential input parameter.
Phase-V: The percentage significance of input factors can be analysed with ANOVA.
In the following, all phases are discussed in detail.
Phase-I: Result of GRC:
To assess the impact of each parameter, the SN ratio of every trail is computed based on equation (
9) for compressive strength and equation (
10) for crack healing and water absorption. Equations (
11) and (
12) are used to normalize the acquired value of the SN ratio while taking the higher-the-better and smaller-the-better qualities into consideration, respectively. Equation (
13) is used to calculate the GRC after determining the normalized SN ratios for each investigation. Table
10 displays the SN ratios of the output parameters together with the corresponding GRCs.
Phase-II. Result from IF-FUCOM-GRG:
Table 10
SN ratioand GRC associated with output parameter.
| SN RATIO |
GRC |
| CS (Mpa) |
CH (%) |
WA (%) |
CS (Mpa) |
CH (%) |
WA (%) |
| 29.57727237 |
29.63363852 |
−14.8072538 |
0.333333333 |
0.333333333 |
1 |
| 31.51165377 |
34.01860643 |
−13.3801418 |
0.455106149 |
0.464867652 |
0.565946459 |
| 33.66034607 |
35.65425276 |
−12.5677786 |
0.765904066 |
0.545102165 |
0.453817715 |
| 30.30478303 |
36.91878272 |
−14.1229661 |
0.37063052 |
0.629038242 |
0.731129591 |
| 32.31081604 |
38.54898824 |
−12.8195611 |
0.536003016 |
0.784836765 |
0.483508457 |
| 34.39689686 |
39.08921134 |
−11.5766106 |
1 |
0.855012953 |
0.365470817 |
| 29.94039081 |
39.51507697 |
−13.8334212 |
0.350961336 |
0.919850586 |
0.656446929 |
| 32.02224392 |
39.86872461 |
−12.131217 |
0.503674319 |
0.98166898 |
0.410148263 |
| 33.88748783 |
39.96518677 |
−11.0857361 |
0.825498313 |
1 |
0.333333333 |
The IF-FUCOM-GRG result is divided into two parts, namely the result of IF-FUCOM and the result of GRG. All the parts are discussed below.
Step-I. Result from IF-FUCOM:
The best values of the criteria can be found by solving the fuzzy linear model in equation (
11), which is shown.
The weight coefficients for the criteria compressive strength
$({\xi _{1}}$), crack healing (
${\xi _{2}}$) and water absorption (
${\xi _{3}}$) are
$(0.443,0.654,0.866;0.231,0.654,0.943)$,
$(0.212,0.212,0.212;0.192,0.212,0.212)$ and
$(0.0770,0.135,0.231;0.231,0.135,0.353)$, respectively, with a deviation from maximum consistency
$\nu =0.0192$. Lingo 17.0 is used to solve the model (
11).
Next, use equations (
7) to calculate the crisp weights for the criteria compressive strength (
${\xi _{1}}$), crack healing (
${\xi _{2}}$) and water absorption (
${\xi _{3}}$), which are, respectively, 0.637, 0.209, and 0.153.
Use equation (
8) to calculate normalized weights for these three criteria, which are 0.499, 0.245, and 0.256.
The weights of the compressive strength (
${\xi _{1}}$), crack healing (
${\xi _{2}}$) and water absorption (
${\xi _{3}}$) using FUCOM-F (Pamucar and Ecer,
2020) are 0.400, 0.388, and 0.212, respectively, with
$\nu =0.001$. Despite significant discrepancies in the weights of those criteria, all FUCOM-F, as well as IF-FUCOM, algorithms rank each criterion in the same order.
Step-II: Result of IF-FUCOM-GRA:
In GRA, the relative weights of the criteria are obtained by IF-FUCOM. After determining the relative weights of the criteria, the score is calculated using grey relation grading. Using equation (
16), GRCs are used to calculate the different grey reasoning grades. GRCs are weighted from 0 to 1, with
${p_{k}}$ equal to 1.
${p_{1}}$,
${p_{2}}$, and
${p_{3}}$ are used as weighting factors in this study for compressive strength, crack healing, and water absorption, respectively. Gray relational grade (GRG) determined by different MCDM methods are presented in Table
11 for each trial using the L9 orthogonal array data.
Phase-III. Result of Comparative study:
Table 11
Gray relational grade determined by IF-FUCOM.
| Trail No. |
IF-FUCOM-GRG |
Rank |
| 1 |
0.435 |
9 |
| 2 |
0.47365 |
8 |
| 3 |
0.671241 |
3 |
| 4 |
0.479423 |
7 |
| 5 |
0.579442 |
5 |
| 6 |
0.871615 |
1 |
| 7 |
0.516248 |
6 |
| 8 |
0.588762 |
4 |
| 9 |
0.785842 |
2 |
This study validates the result of the proposed model by comparing it to three existing MCDM techniques. There are four steps in this phase. Determine the PV for each criterion using AHP, BWM, and FUCOM methods in the first three steps. As a last step, determine the weights of the alternatives using GRA.
Step-I: Result from AHP:
Calculate the priority value of each criterion using the AHP algorithm as described in Section. The priority value of criteria are
${p_{1}}=0.614$,
${p_{2}}=0.268$,
${p_{3}}=0.117$ and maximum eigen value
${\lambda _{\max }}=3.074$. These values indicate that the most important criterion is CS (
${\xi _{1}}$), while the least important criterion is WA (
${\xi _{3}}$). To determine CI and CR:
Step-II: Result from BWM:
Based on the solution to the above BWM-model (
16), the following criteria weights are optimal:
${p_{1}^{\ast }}=0.66154$,
${p_{2}^{\ast }}=0.26154$,
${p_{3}^{\ast }}=0.07692$ and
$\chi \ast =0.12308$. According to these values, the outputs CS (
${\xi _{1}}$) and WA (
${\xi _{3}}$) are the most important and the least important criteria, respectively. The degree of consistency is as follows:
As suggested by the obtained CR value (0.032996), the obtained criteria weights have a satisfactory degree of consistency.
Step-III: Result from FUCOM:
Based on the solution to the above model (
18), the following criteria weights are optimal:
${p_{1}^{\ast }}=0.3668478$,
${p_{2}^{\ast }}=0.3396739$,
${p_{3}^{\ast }}=0.2934783$ and
$\chi \ast =0.2471142\times {E^{-08}}$. According to these values, the outputs CS (
${\xi _{1}}$) and WA (
${\xi _{3}}$) are the most important and the least important criteria, respectively.
Step-IV: Different Gray relation grade:
In GRA, the relative weights of the criteria are obtained by AHP, BWM, and FUCOM. After determining the relative weights of the criteria, the score is calculated using grey relation grading. Using equation (
16), GRCs are used to calculate the different grey reasoning grades. GRCs are weighted from 0 to 1, with
${p_{k}}$ equal to 1.
${p_{1}}$,
${p_{2}}$, and
${p_{3}}$ are used as weighting factors in this study for compressive strength, crack healing, and water absorption, respectively. Gray relational grade determined by different MCDM methods are presented in Table
12 for each trial using the L9 orthogonal array data.
Phase-IV. ANOVA result:
Table 12
Gray relational grade determined by different MCDM techniques.
| Trail No. |
GRG |
Rank |
AHP-GRG |
Rank |
BWM-GRG |
Rank |
FUCOM-GRG |
Rank |
| 1 |
0.5555556 |
8 |
0.411 |
9 |
0.3846153 |
9 |
0.528986 |
8 |
| 2 |
0.4953068 |
9 |
0.470235 |
8 |
0.4661853 |
7 |
0.490951 |
9 |
| 3 |
0.5882746 |
6 |
0.669449 |
3 |
0.6841493 |
3 |
0.599313 |
6 |
| 4 |
0.5769328 |
7 |
0.481692 |
7 |
0.4659447 |
8 |
0.564204 |
7 |
| 5 |
0.6014494 |
5 |
0.596013 |
5 |
0.5970446 |
5 |
0.605119 |
5 |
| 6 |
0.7401613 |
1 |
0.885904 |
1 |
0.9132704 |
1 |
0.764531 |
1 |
| 7 |
0.6424196 |
3 |
0.538815 |
6 |
0.5232466 |
6 |
0.633852 |
4 |
| 8 |
0.6318305 |
4 |
0.620331 |
4 |
0.621494 |
4 |
0.638589 |
3 |
| 9 |
0.7196105 |
2 |
0.813856 |
2 |
0.8332784 |
2 |
0.740332 |
2 |
The
$S/N$ ratio is used to analyse the IF-FUCOM-GRG data to find the best combination of factors. According to the higher, the better criterion, the optimal combination should correspond to the highest
$S/N$ value on each factor. Results are analysed using Minitab software. Table
13 summarizes the main influences of control factors on mean grey relational grades. As a result of each level of the input control parameter, the
$S/N$ ratio plots of IF-FUCOM-GRG are shown in Fig.
4. Combining the highest factor levels calculated from bacteria concentration at 105 and 28 curing days yields the best factor level combination.
Table 13
IF-FUCOM-GRG response table.
| Parameters |
Level-1 |
Level-2 |
Level-3 |
| Concentration |
0.4932 |
0.6458 |
0.6391 |
| Days |
0.4632 |
0.5516 |
0.7633 |
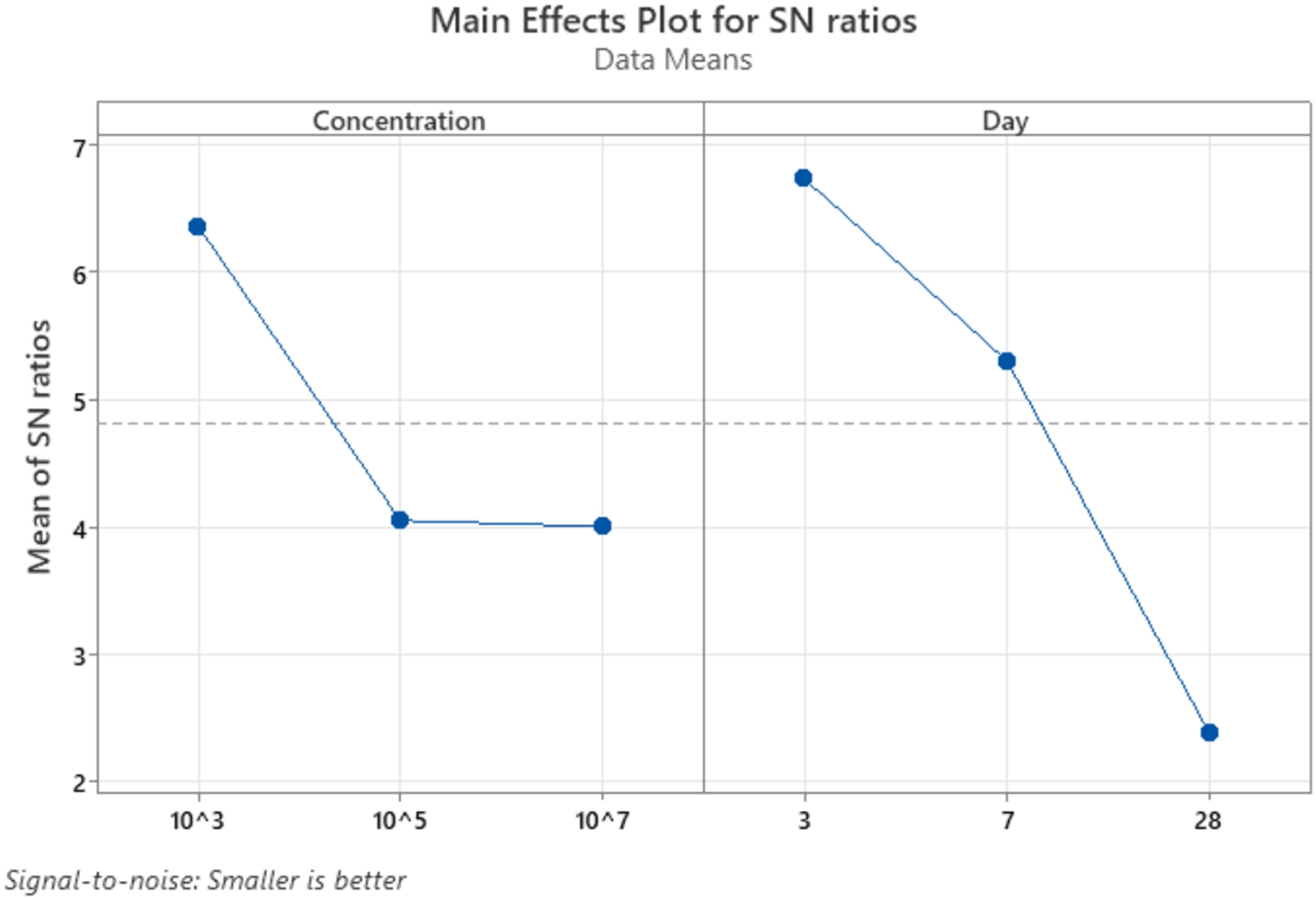
Fig. 4
Response of the IF-FUCOM-GRG SN ratio.
ANOVA is employed to determine whether design elements have a substantial impact on response (Haq
et al.,
2008). ANOVA may examine the percentage importance of input factors. When
$F>4$ (Yang and Tarng,
1998) and a parameter is significant, Fisher’s F-test is employed to evaluate the effect of the parameter on output quality. The ANOVA findings for the IF-FUCOM-GRG are displayed in Table
14. According to the ANOVA results, both input parameters are important for the study, but curing day is more important than bacteria concentration.
Phase-V. Confirmation test result:
Table 14
Results of the ANOVA for the IF-FUCOM-GRG.
| Source |
DF |
Adj SS |
Adj MS |
F-Value |
P-Value |
| Concentration |
2 |
0.044646 |
0.022323 |
11.88 |
0.021 |
| Days |
2 |
0.142686 |
0.071343 |
37.96 |
0.003 |
| Error |
4 |
0.007519 |
0.001880 |
|
|
| Total |
8 |
0.194851 |
|
|
|
In Table
15, the optimal output parameter is tested for actual and predicted IF-FUCOM-GRA values. Equation (
19) predicts the IF-FUCOM-GRA values provided at the optimal output. IF-FUCOM-GRA, as predicted and experimentally determined as an optimum level, are 0.818256 and 0.88929, respectively.
Table 15
Confirmation test table.
|
Optimal input parameter |
|
Predicted |
Experimental |
| Level |
${10^{5}}$ bacteria concentration, 28 curing day |
${10^{5}}$ bacteria concentration, 28 curing day |
| IF-FUCOM-GRA grade |
0.816385 |
0.88929 |
|
$S/N$ ratio |
1.64405 |
1.71291 |

