1 Introduction
Electronic voting introduces a new set of cryptographic properties, to provide confidence to the electors, such as: universal verifiablity, accuracy or mathematically ensured privacy, that are unavailable to traditional voting. It also enables remote voting and multi-device access. Nevertheless, e-voting still fails to gain the trust from the electors and to incentive participation. Most people are reluctant to trust a critical part of democracy to a system they do not fully understand.1
We introduce a voting scheme that makes no use of cryptography without compromising security. Inspired by the work by Shamir (1979), we are able to conceal the vote as fragmented pieces of information. These pieces do not reveal any information about the original vote separately. However, when the pieces are treated as a whole, the vote can be recovered.
Our goal is to create a new, simple, fast and lightweight voting scheme able to engage technology averse and reluctant sectors. The contributions of this paper can be summarized as follows: the voting scheme does not depend on encryption while guaranteeing security; the proposal takes into account that the ballot can be divided into pieces in such a way that any individual pieces does not reveal any vote information; the proposal allows the decentralization of the responsibility of processing the ballots. Overall, our proposal opens the possibility to less conventional electronic voting schemes, looking for other approaches to electronic elections which would reduce reluctance to novice profiles.
The rest of the paper is structured as follows: Section 2 reviews the most relevant literature in electronic voting, Section 4 introduces and fully details our voting protocol, Section 5 analyses the time-complexity of our approach. In Section 6, we review and prove the security properties of our developed scheme. Finally, Section 7 reviews the contributions of our work and concludes the article.
2 Related Work
In this section, we review the most relevant and similar works in the literature and study how they compare with our presented scheme. Electronic voting is a well-established area of research and many approaches have tackled the problem from different angles.
The first scheme we cite is the Three Ballot voting protocol by Rivest (2006). Although this protocol does not consider digital ballots nor remote casting of them, Rivest’s proposal conceals the electors’ votes without the need of any cryptography, and, therefore, it is related to our approach that neither does so.
Rivest proposes the election to be based on paper ballots. These ballots are formed by three sections which the elector fills according to some rules to show her approval, or rejection, of some candidates. When the ballot is correctly filled, its three sections are separated and casted independently. The elector gets a copy of one of these sections as receipt, to ensure all the votes are counted on the final tally. However, the receipt cannot convince anyone of the direction of the vote. This protocol is extended in Rivest and Smith (2007) in order to make it compatible with any kind of election (e.g.: Borda, Ranking, or Condorcet). Unfortunately, both approaches suffer from the so called “Thee Pattern Attack”, where a coercer may buy or influence votes by requiring the electors to fill the ballots in certain anomalous patterns. Later on, the attacker can check for these patterns on the public bulletin that contains the final tally. This attack does not succeed if the ballot is short, since each pattern is likely to occur many times. However, this short ballot assumption restricts the applicable scenarios for these protocols.
Despite this drawback, these two schemes present simple yet powerful voting protocols. They demonstrate that it is possible to ensure voter’s privacy and vote integrity without encrypting the vote. Similarly to Rivest’s protocol, we deconstruct the ballot in several shares that reveal no information until they are all assembled. However, our proposal allows for a complete electronic voting protocol that is compatible with remote voting and lacks the mentioned weakness that would allow a coercer to know the direction of an elector’s vote.
Rivest’s way of concealing the ballot has not been used outside his proposals. Usually the approach has been electronic and heavily based on cryptography. We now review recent solutions to electronic voting considering the techniques used.
2.1 Blind Signatures
Blind signatures were proposed by Chaum (1982), where he presents a method for signing a masked message that cannot be linked to the original content.
In Li et al. (2009), Li et al. introduce a voting system that employs blind signatures to certify the ballot from the multiple authorities involved. The elector obtains a blank ballot from the authentication centre and proceeds to use blind signatures to certify the ballot. Then, the elector removes the blinding factor and the certified ballot is encrypted and sent to a tallying authority. The encryption is used to ensure that the result of the election is kept private until the final tallying. Finally, when the election process finishes, the certification authority reveals the secret key and the tallying authority decrypts, counts and records the votes.
In Nguyen and Dang (2013) the authors present another scheme that uses blind signatures for ballot certification and dynamic ballots to ensure elector’s privacy. Electors register using their personal identification to obtain a digital certificate. Then, to get the signature from the privacy authority, the elector hides his unique id through blind signatures, and sends it together with the serial number of the certificate. To avoid man in the middle attacks, they employ triple DES to encrypt sensible communications. Once the user gets the signature that entitles him to vote, he crafts a dynamic ballot (Cetinkaya and Doganaksoy, 2006) and cast it to the ballot and casting centre. The ballot is encrypted and the elector is required to provide plain-text equivalence tests to proof that the unique identifications are valid.
Another protocol that also employs blind signatures to certify the ballots is described in Larriba et al. (2020). In their work, the authors focus on the efficiency to propose a time-efficient voting scheme that only requires two authorities. In this protocol the elector builds the ballot according some fixed structure. This ballot is blindly signed by an authority that cannot reveal the direction of the vote. The signed ballot is then sent to the authority that plays the role of the polling station. Unless both authorities collude, the method holds all the desired properties.
Plenty of other voting schemes exploit the properties of blind signatures since they provide a flexible method for signing votes and avoiding double voting without compromising elector’s privacy (e.g.: Thi and Dang, 2013; Aziz, 2019; Cruz and Kaji, 2017). Although we also use blind signatures in our scheme, unlike many of the protocols, we do not use them to hide the ballot from unauthorized access.
2.2 Homomorphic Cryptography
Homomorphic cryptography allows us to operate with ciphertexts, and obtain, after decryption, the same results as we would obtain working with plain text. This allows to work with sensitive data without needing to know the actual content of the encrypted message. Indeed, blind signatures benefit from the homomorphic cryptography to achieve secure signing. However, please note that homomorphic cryptography allows for many features such as aggregation or proofs-of-inclusion. Many voting protocols employ homomorphic cryptography, usually to aggregate encrypted votes and only decrypt the final result.
In Cramer et al. (1997), the author presents a voting scheme for Yes/No elections based on homomorphic properties. The votes, which are codified as 1 or −1, are encrypted using a threshold El Gamal cryptosystem (ElGamal, 1985). Encrypted votes are then aggregated, since they can be summed as integers, and a final encrypted result is computed. At the end of the election, authorities collaborate to recover the secret key and decrypt the final result.
In Yang et al. (2017, 2018), Yang et al. introduce a homomorphic voting scheme compatible with range voting. Range voting requires electors to assign a numerical score to all candidates for single seat elections. The candidate with the higher score wins. In this system, the votes are structured, and encrypted, as elements in a matrix in which rows represent candidates and columns represent the assigned score. Since votes for the same candidates are placed in the same rows of the matrix, they can be summed altogether to get the final results per candidate. At the end of the election, authorities collaborate to recover the secret key and decrypt the final matrix that agglutinates all the votes.
2.3 Ring Signatures
Ring signatures are a special kind of digital signature that allow any user to sign as a member of a collective instead of an individual. The verifier can check that the user who wants to sign belongs to a given group, but cannot identify the signer among the group members.
Tornos et al. (2014) propose a voting scheme that provides signer ambiguity by using ring signatures. A single registration authority is employed to handle proper identification of electors. After the identification process, electors use ring signatures to sign their valid votes privately. To prevent double-voting, they use linking tags in the ring signatures. These tags do not reveal personal information about the signer but prevent her from voting more than once using different rings of users.
In Chen et al. (2008), a voting protocol with custom ring signatures is presented. They propose a ring signature scheme that can only be verified by some designated individuals. These verifiers cannot convince a third party of the integrity of a ring signature without revealing their private key. For the encryption of the vote they employ a threshold scheme in which authorities have to collaborate to recover the secret key at the end of the election. To prevent double voting, electors are required to link the vote with a commitment of their private key. This commitment does not reveal any information about the private key, but prevents malicious electors from voting multiple times. If two, or more, votes with the same commitment are detected, only the one with the latest timestamp will be considered.
2.4 Blockchain
Blockchain technology provides a decentralized technology to store and share information. Multiple electronic voting schemes have used blockchain to carry out the election process since they provide a distributed public ledger than can be consulted by anyone. While blockchain is not a cryptographic scheme by itself, and all of these systems use other cryptographic primitives to achieve privacy, it is still a differentiating factor that suffices to make a distinction when studying these protocols.
In Yang et al. (2020), the authors propose a voting protocol for range voting that uses blockchain to structure the election process. In this scheme, each candidate receives a score (e.g.: token on the chain) from the electors and the candidate with the highest score wins the election. To preserve elector’s privacy, they employ an encryption system based on El Gamal and group-based encryption. They employ the homomorphic properties of El Gamal to compute the final tally without compromising individual electors.
In Gao et al. (2019), the authors present an e-voting protocol based on blockchain technology, which also provides anti-quantum resistance properties. To achieve this, they base their method on an NP-complete problem (Niederreiter, 1985) instead of using traditional public key cryptography. Their protocol is equipped with an audit function that allows to detect fraudulent voters while respecting their privacy.
In Larriba et al. (2021), the authors propose a blockchain based scheme that introduces traditional parties inside the election process to raise confidence on the system. To protect elector’s privacy, they employ ring signatures, and to prevent double voting, they employ key images. Key images act as receipts of ring signatures that prevent the malicious elector from creating multiple signatures, without compromising her identity.
In the voting scheme presented here, we do not employ blockchain. However, the public bulletin that is used to communicate the election results, could be implemented using blockchain technology.
2.5 System Comparison
Besides the literature review here introduced, we also present a comparison between the reviewed systems. The purpose of this comparison is twofold. First, it allows the reader to directly assess the presented systems. Secondly, it provides a common baseline to later compare the performance of our system, SUVS.
Nonetheless, comparing different systems is not a trivial task. These schemes are based on different cryptographic primitives, with different architectures that involve a custom number of involved parties. The authors not always report, or at least with the same level of detail, the asymptotical complexity of their works. Therefore, we chose the average number of messages sent in the protocol as basic unit for the comparison. Messaging between electors and parties is accessible to minutely measure and network delays can surpass computational times. The results of our analysis are depicted in Table 1.
Table 1
Table representing the number of messages sent by the elector and the system. In the table: when the number of authorities is not fixed, they are represented as j in the table. v represents the number of processed votes. The ∗ symbol represents systems that are deployed employing blockchain technology.
| Elector’s messages | Total messages | Cryptographic primitives | |
| Chaum (1982) | 2 | $2v$ | Blind signatures |
| Li et al. (2009) | 5 | $3v$ | Blind signatures |
| Nguyen and Dang (2013) | 4 | $7v$ | Blind signatures |
| Larriba et al. (2020) | 3 | $2v+1$ | Blind signatures |
| Cramer et al. (1997) | 1 | $v+j$ | Homomorphic prop. |
| Yang et al. (2017, 2018) | 2 | $2(v+j)$ | Homomorphic prop. |
| Tornos et al. (2014) | 3 | $3v+1$ | Ring signatures |
| Chen et al. (2008) | 2 | $2+v+2j$ | Ring signatures |
| Yang et al. (2020)* | 2 | $2j$ | Homomorphic prop. |
| Gao et al. (2019)* | 2 | v | Ring signatures |
| Larriba et al. (2021)* | 2 | $2+v$ | Ring signatures |
3 Background
In this section we introduce the fundamental cryptographic primitives that are employed in our protocol.
3.1 Shamir Secret Sharing Scheme
The reconstructive approach is based on Shamir’s $(j,d)$-secret sharing work (Shamir, 1979). This scheme allows to share a secret C among j players, in such a way that any subset of $d+1$ players can recover C. The secret is encoded as the independent term of a polynomial $q(x)$ and the pieces of information distributed among players are points of the aforementioned polynomial. Any subset $d+1$ can interpolate their set of points to recover C. Polynomial evaluation operations, as depicted in equation (1), are carried out under modular arithmetic of a prime p:
Given a sufficient set of points $({x_{i}},{y_{i}})$, in order to interpolate the polynomial $q(x)$, we suggest Lagrange’s method. The interpolation is depicted in equation (2), and equation (3) computes the Lagrange’s bases:
where:
Please note that employing Shamir’s secret sharing scheme requires the use of modular arithmetic, however, it does not imply the use of encryption.
3.2 Perfect Secrecy
Perfect secrecy notion directly derives from information-theory (Shannon, 1949). It implies, as represented in equation (4), that a priori probability of a given message m, in the space of all possible messages $\mathcal{M}$, is equal to the a posteriori probability of the message given the ciphertext c, in the space of all possible ciphertexts $\mathcal{C}$.
and, thus, that the ciphertexts reveal no information about the message. All messages are equiprobable for a given ciphertext, making the scheme secure since the attacker has no method to obtain additional information, even with selected ciphertexts.
Table 2
Notation employed in the article.
| Symbol | References to |
| v | Number of processed votes |
| j | Number of parties |
| C | Secret vote |
| p | Prime number |
| $q(x)$ | Polynomial defined over ${\mathbb{F}_{p}}$ |
| d | Degree of $q(x)$ |
| l | Number of generated points |
| v | RSA public view key |
| n | RSA modulus |
| s | RSA secret key |
| b | Election ballot |
| ${\textit{SP}_{i}}$ | Non-overlapping set of points |
4 Our Proposal
We devote this section to describe our proposal for a Secure Unencrypted Voting Scheme (SUVS). We present a protocol that requires minimum interaction from the elector and protects the vote using a constructive approach which does not require to encrypt/decrypt the votes. A summary of the notation used along this section can be found in Table 2.
The process is based on the generation of some pieces of information, which separately do not reveal any information about the elector and her vote, but, when combined, these pieces of information reveal the vote.
Our system consists on three different entities: the electors who cast their individual votes; an identification authority (IA) in charge of crediting valid electors and (blindly) certify the ballots; and the parties, whose purpose is twofold: first they represent themselves as an option in the election, and, second, they are responsible of recovering, validating and tallying the casted votes. These entities employ a Public Bulletin Board (PBB) to communicate public information regarding the election. As for the PBB implementation, we note that today multiple blockchain technologies provide the methods to implement a public and distributed bulletin.
SUVS consists on five sequential phases: the system setup; the ballot crafting; the ballot certification; the vote casting; and the tallying phase. Along these phases, the elector generates a private polynomial that acts as her own ballot. The polynomial enables the elector to conceal her vote as set of points and to cast it in the corresponding phase. We take advantage of the properties of polynomial interpolation, which make the recovery of the vote impossible if not all the points are known. In the last phase, parties collaborate to recover the secret polynomial, and its associated vote, from the received points. A scheme of the protocol’s interactions is depicted on Fig. 1. Example 1 illustrate all the processes previous to the final tallying. Now, we describe in detail each one of the phases that define our method.
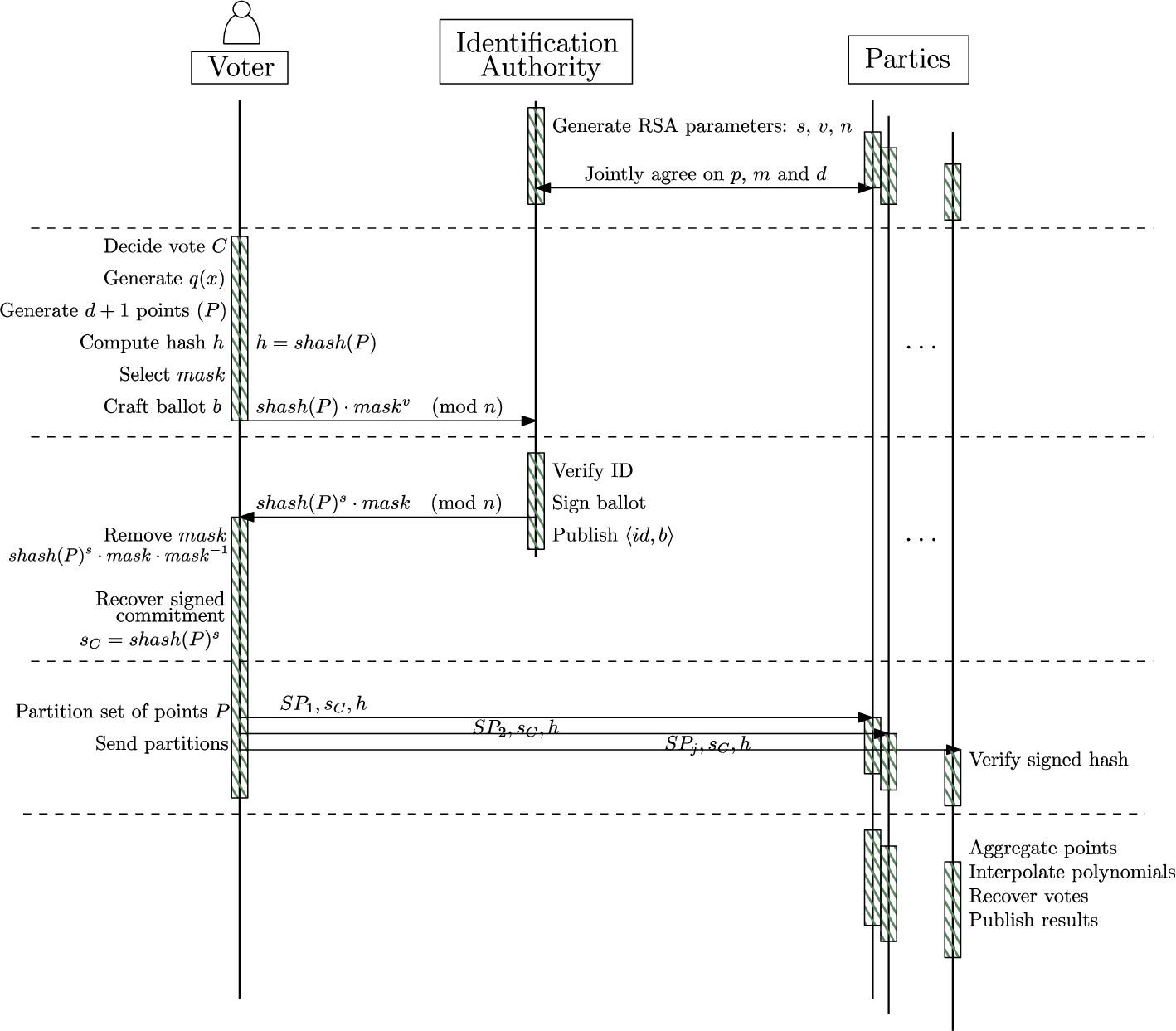
Fig. 1
Scheme representing the election phases, its associated agents and their message interchange.
4.1 System Setup
Before the election process, it is required to arrange and configure the methods that will be used to sign the electors’ ballots. The IA is responsible of the elector identification and ballot certification. For this purpose, the IA must generate the parameters to setup a digital signature scheme.
We employ blind signatures to prevent double voting without compromising electors’ privacy. This allow us to certify ballots from valid electors without being able to link the votes with their identity.
We consider in the description of our proposal a RSA cryptographic scheme to implement blind signatures because of its homomorphic properties under modular exponentiation.2 To carry out the blind signatures, the elector uses the public component of the IA signature key v and public RSA modulus n which will be used to certify the ballots.
The IA also states the hash function to be used, sets up the degree d of the polynomials to create, set the maximum number of points the user can generate l, being $l>d$, as well as generates the prime p under which modulo operations will be carried out. Please note that the degree of the polynomial d must be, at least, equal to $j-1$, being j the number of involved parties on the election. This enforces the collaboration of all parties to recover the polynomial. Apart from this consideration, increasing d does not provide greater security. Please note that l is included as a security measure to prevent users generating too many points. Because of the polynomial’s degree d being public, this could give some small set of malicious parties the ability to collude and recover the votes before the tallying phase. While the integrity of the vote is preserved, it would affect the democracy of the scheme.
At the end of the setup phase, the IA publicly distributes v, n, d and p so that every elector can craft her own ballot.
4.2 Ballot Crafting
Once an elector has decided on her vote, she encodes it as an integer C. Then, she proceeds to generate a d-degree polynomial as shown in equation (5):
such that the independent term contains the encoded vote C. Please note that it is not necessary for all the coefficients to be non-null to deal with a d-grade polynomial. Also note that coefficients must be smaller than the prime p.
Then, the elector samples from the polynomial a minimum of $d+1$ points (to a maximum of l points, see equation (6)). For the sake of clarity, we assume in the rest of the article the user generated minimum $d+1$ points. When necessary, we will order the set of points P taking into account the first coordinate, in order to transform, unequivocally, any set into a sequence of points.
Note that anybody who knows P can interpolate the original polynomial $q(x)$, and therefore recover the vote.
The set is, actually, the ballot to be casted, which will be split in shares to be sent to the parties. In order to allow the reconstruction of the split vote, the elector digests the sorted set of points P using the hash function selected in the system set up phase. Please note the importance of the points being sorted for the hash function to produce consistent outputs. For this reason, we define a function $\textit{shash}$, that sorts, accordingly, the received input before applying the hash. The output of the $\textit{shash}$ functions acts as a commitment of the points. This commitment acts as a receipt that ensures the set P has not been tampered and demonstrates the validity of the ballot when signed.
4.3 Ballot Certification
In order to prevent double voting, each elector sends her ballot to the IA to be certified. In order to prevent the possibility of matching the ballot with the elector, our proposal blinds the ballots before sending them to the authority.
To do so, the elector selects a random invertible mask, considers the verification key v published by the IA and computes the ballot b as shown in equation (7):
which is sent to the IA together with her identification through a secure channel.
The IA checks if the identification is valid and the elector is on the census of registered voters. If the identification is correct, the IA proceeds to sign the ballot as referenced in equation (8):
(8)
\[\begin{aligned}{}{b^{s}}& \equiv {\big(\textit{shash}(P)\cdot {\textit{mask}^{v}}\big)^{s}}\hspace{1em}(\mathrm{mod}\hspace{2.5pt}n),\\ {} {b^{s}}& \equiv \textit{shash}{(P)^{s}}\cdot {\big({\textit{mask}^{v}}\big)^{s}}\hspace{1em}(\mathrm{mod}\hspace{2.5pt}n),\\ {} {b^{s}}& \equiv \textit{shash}{(P)^{s}}\cdot \textit{mask}\hspace{1em}(\mathrm{mod}\hspace{2.5pt}n).\end{aligned}\]Please note that, unless the IA gets to know the mask, the IA cannot never be aware of what message it is actually certifying. After the signature process, the IA replies the elector through a secure channel with the signed ballot. The IA also publishes on the PBB a tuple of the form $\langle id,b=\textit{shash}{(P)\cdot {\textit{mask}^{v}})^{s}}\rangle $. The purpose of this publication is twofold: first, it allows the elector to check that her ballot was received as intended. Second, it proves that every ballot comes from a valid identity from the public census.
The elector receives the signed ballot and proceeds to recover the signed commitment which will certify her vote. Note that the elector is the only one who knows the mask and its inverse. Thus, the elector obtains the signed commitment as indicated in equation (9):
By following these steps, the elector obtains the certified (signed) commitment that will be used in the next phases. These steps are detailed on Algorithm 1. Note that, despite requiring her identity in order to sign the ballot, the IA has no means to link the commitment with the elector. Also note that the elector is able to check if the signed ballot was tampered during the way, because she is able to independently verify the integrity of the signed commitment.
4.4 Vote Casting
In this phase, the elector has a set P that can be used to recover her vote and the signed commitment of the set $\textit{hash}{(P)^{s}}$, which identifies her vote as a valid one.
To finally cast the vote, the elector sends a partition of P (shares of the ballot) together with the certified commitment to all the parties implied in the election tallying. Note that a basic property of polynomial interpolation states the impossibility to recover a d degree polynomial with d or less points of such polynomial. This allows to send different shares of information to different parties with certainty that no information of the original vote will be revealed unless all the parties collaborate to do so.
Thus, taking into account that k parties are implied in the election, the elector partitions P into k non-overlapping subsets ${\textit{SP}_{i}}$, such that P results as the ordered merge of the ${\textit{SP}_{i}}$ subsets. See equation (10):
Each one of the parties receive a share ${\textit{SP}_{i}}$ of P together with the hash and the certified hash: $\textit{shash}(P),\textit{shash}{(P)^{s}}\hspace{2.5pt}(\mathrm{mod}\hspace{2.5pt}n)$. Please note that the certified hash operates as digital signature of the hash, and that both are sent and needed to check its validity. Also note that the elector can freely decide which subset is sent to each party.
We also note that it is possible to reduce the number of shares to put aside from the process those parties which receive no share of the elector’s ballot. Note also that this does not affect the validity of the vote, but the transparency of the process. However, we force that every party receives one share. By doing this, we ensure that the vote requires the collaboration of all the parties to be recovered. Thus, no subset of malicious parties will be able to recover the vote before the tallying phase.
When all the subsets are sent, the vote has been cast. Note that, unlike what happens in the ballot certification phase, no personal information goes along with the shares of the vote. Thus, parties have no means to associate the received shares with an elector’s identity.3 The casting process is depicted on Algorithm 2.
4.5 Tallying
Once the election is over, no new votes are accepted. The parties can proceed to reconstruct the votes and compute the final tally.
In the first place, the parties consider the certification that accompanies the shares to find the set of shares (each one of them received by a different party) that allow to reconstruct each ballot P. Note that the original sequence can be easily obtained, by ordering the set P, and that is possible to check the validity of the certification.
A set of points P such that its certified commitment $\textit{shash}{(P)^{s}}\hspace{2.5pt}(\mathrm{mod}\hspace{2.5pt}n)$ is not correct, or that its cardinality exceeds the defined maximum $(|P|>l)$, is discarded. Parties can now, individually, use the points in P to recover the original polynomial $q(x)$ which contains the vote as its independent term C. To recover a polynomial from a set of points:
that, when $q(x)$ is interpolated, allow to recover the encoded vote C as illustrated in equation (13).
\[ P=\big\{{p_{1}}=({x_{1}},{y_{1}}),{p_{2}}=({x_{2}},{y_{2}}),\dots ,{p_{j}}=({x_{j}},{y_{j}})\big\},\]
we suggest to use Lagrange’s polynomials (see equations (11) and (12)):
where:
(12)
\[ {l_{i}}(x)=\prod \limits_{\substack{0\leqslant k\leqslant j\\ {} k\ne i}}\frac{x-{x_{k}}}{{x_{i}}-{x_{k}}},\]Please note that the interpolation operations are not carried out modulo p. When we forced, on the ballot crafting, the coefficients of the polynomial ${a_{d}}$ to be smaller than p, we made sure that we would interpolate the exact same polynomial without the need of modular arithmetic. Otherwise, we could interpolate a different polynomial, congruent mod p, but with a different encoded vote C.
The parties publish on the PBB, a 3-tuple per vote containing: the certification of the ballot (i.e. the signed commitment); the ballot itself (i.e. the set of points P that conceal the ballot); and the reconstructed vote C. The final tally obtained by each party can also be published. The PBB is available to everyone to check that their votes have been counted as intended, and to verify the integrity of the final tally. Algorithm 3 contains the steps to compute the final tally.
Example 1.
In order to depict the process, let us consider an election with three competing candidates. To setup the system, the IA generates a RSA signature key with, respectively, $\langle v,n\rangle $ and $\langle d\rangle $ as public and private keys. Neither the particular values of the key, nor the hash function h used provide special information in this example and will be referenced as is. Finally, the authority publishes that the degree to use is $d=4$ and the modulus $p=47$.
Once the system has been set up and the values published to the electors, in order to prepare the ballot, each user encodes her vote as an integer modulus p. Let this be $C=23$ in this example. Then the elector randomly generates her polynomial with the codification of her vote as the independent term. Let in this example the polynomial be the following:
that is now used to generate five random points. Let these points ordered with respect to the first coordinate be the following:
This set of values is actually the ballot the elector will split into pieces. To obtain a commitment of the ballot, the elector computes $\textit{shash}(P)$ and masks the digest using a private invertible integer modulus n:
the results are then sent to the authority together with her identification in order to be blindly signed. Note that there is no way the authority can guess the direction of the vote since it just receives the masked commitment.
Once the usual checks are carried out, the authority computes the certificate signing the commitment using its signature private key:
As explained above, the elector can easily obtain the certificate of the ballot as:
The ballot is then split into three disjoint pieces (the number of candidates), for instance:
which are sent to the respective candidates together with the certified commitment. Note that it is impossible for the candidates to obtain the direction of the vote unless they all agree to share the points in order to interpolate the polynomial. Note also that it is also infeasible any candidate to tamper with the ballot since it has not information to do so.
In order to rebuild the ballot, the candidates use the certified commitment to select the pieces of the same ballot, check its integrity and interpolate the polynomial using whichever available method.
5 SUVS Complexity
We devote this section to analyse the time-complexity of our voting scheme. We prove that our protocol is highly efficient and requires minimal effort for the involved parties. We differentiate between the computational complexity related to each individual elector and the complexity of the whole system to process all votes.
We chose bit operation as the unit in our time-complexity analysis. As usual, n denotes the input of the operands and $\log n$ denote its number of bits.
To certify and cast a vote, the elector needs to carry out a series of steps: generate a polynomial, sample some points, compute a hash function, select some subsets, etc. However, we neglect some of these steps in the time-complexity analysis because of two main reasons: most of them can be performed off-line before the actual election process starts, and they are not relevant in terms of time-complexity analysis because other operations dominate the overall complexity. For example, the sort of a sequence, or hash, of length j is not comparable to the magnitude of $\log n$. Therefore, its complexity can be neglected when compared with the rest of operations.
We only consider the mask generation and multiplication and exponentiation operations. They are the most costful operations and dominate the time-complexity functions:
-
• Mask generation. The user must generate a mask and search for its inverse to certify the ballot. To find the inverse, the Euclid’s algorithm which has a complexity of $\mathcal{O}({\log ^{2}}n)$ bit operations is used. Only one iteration of the algorithm is needed to find an invertible mask, otherwise it would mean that we broke RSA (we found a factor of n).
-
• Modular exponentiation. To craft the ballot the user must perform a modular exponentiation (see Line 7 on Algorithm 1), which has a cost of $\mathcal{O}({\log ^{3}}n)$ bit operations.
-
• Modular multiplication. In addition to the exponentiation, a modular multiplication is also required on Section 4.3. This operation has cost of $\mathcal{O}({\log ^{2}}n)$ bit operations.
Then, the complete time-complexity for an elector to cast a vote can be expressed as:
We now consider the complexity of the whole system. To process a vote, SUVS must apply a blind signature to the ballot, and, at the end of the election it must interpolate a polynomial from a set of points. We do not consider the compilation of the shares with the same certified commitment in the complexity analysis, shares can be indexed and compiled in constant time.
-
• Ballot certification requires one modular exponentiation, which has a cost of $\mathcal{O}({\log ^{3}}n)$ bit operations.
-
• Interpolation using Lagrange’s polynomial requires a linear number of non-modular operations. Addition and subtraction present a time-complexity of $\mathcal{O}(\log n)$, while multiplication and division have a complexity of $\mathcal{O}({\log ^{2}}n)$ bit operations. These operations are affected by the number of shares j (equivalent to the number of parties), as can be observed in Section 4.5. The complexity of this step can be expressed as ${(j(\mathcal{O}({\log ^{2}}n)+\mathcal{O}(\log n)))^{2}}={j^{2}}(\mathcal{O}({\log ^{4}}n)+\mathcal{O}(2{\log ^{3}}n)+\mathcal{O}({\log ^{2}}n))$. However, since j is known to be a low and bounded number, we can treat it as a constant and simplify it in the complexity as $\mathcal{O}({\log ^{4}}n)+\mathcal{O}(2{\log ^{3}}n)+\mathcal{O}({\log ^{2}}n)\approx \mathcal{O}({\log ^{4}}n)$.
Thus, the total time-complexity of our scheme scales linearly with the number of processed votes v and can be expressed as:
Please also note that the complete number messages sent by the elector in SUVS can be expressed as $1+j$. While the total number of messages interchanged between the involved parties is simply j. These figures compare well with the results presented in Section 2.5 and shows that the message complexity of SUVS is not affected by the fact of not encrypting the votes. Also note that while additional messages can be required for the user, these are non-blocking communications. The elector sends the shares and does not requires any additional communication. No future steps are delayed by this aspect.
6 Security Analysis
We now analyse the security properties of our presented voting scheme. We enumerate the desired properties of a secure election protocol, proving that our system meets them. Please note that the security of our scheme (except for the signature step) does fall under the information-theory paradigm. Therefore, and unlike other computational security-based schemes, we do not need security parameters. Once some basic constraints are achieved (e.g. $d\geqslant j-1$), the overall security does not rely on larger values to become more secure.
Verifiability
Verifiability is a property that ensures that an elector can verify the integrity of her vote at any given phase (casting, recording or tallying). If the audit is extended to any individual (elector or not), then is called universal verifiability.
Proof.
In order to prove the lemma we will prove, first, that after the identification stage, the elector can verify that her vote was not tampered with during the certification of the commitment, and, second, that at the end of the voting process, any vote was correctly recorded and tallied.
First, we note that during the process of commitment certification, the elector is the only one who knows the mask that conceals the commitment. Therefore, only she can remove the mask and apply the public key of the identification authority check if the commitment was correctly certified or it was somehow modified. She also can check on the PBB that the masked commitment received by the IA has not been tampered with.
Second, regarding universal verifiability, any individual (elector included) can consult on the PBB all the individual votes, that is: their set of points, and their certified commitment. This information is enough for any interested party to check the validity and integrity of the votes.
Thus, our method allows anyone to compute the tally, verifying the validity of all the individual votes, and, therefore, auditing the election process. □
Privacy
Privacy implies the impossibility of linking an elector’s identity with the direction of her vote, even when some authorities or parties implied in the process maliciously participate.
Proof.
To prove this, we will prove, first, that the identification authority cannot compute the direction of any elector’s vote, and, second, that parties can neither do so.
First, note that the elector mask that conceals the commitment of the vote is a private election, the identification authority does not have information to unmask the commitment, and, therefore, the authority cannot gain knowledge of the elector’s commitment. Thus, the identification authority has no way to relate elector’s identification to her final vote, once the PBB is made public.
Second, we note that the parties do not receive any personal information from the elector. Hence, they can not relate the vote in any way. □
Democracy
Democracy guarantees that only valid and registered electors are able to cast a vote, and that they only can vote once.
In our protocol, the IA responsibility is twofold: it verifies elector’s identification to check that they are eligible, and, prevents double voting by using blind signatures.
Please note that even if the IA acted maliciously, democracy would be ensured. The received ballots and their associated identity on the public census are published on the PBB for everyone to review. The malicious IA could not forge invalid votes or link valid ones to their elector. However, in a different scenario, an attacker could try to bypass IA’s certification and forge the employed blind signature scheme.
Proof.
For a vote to be considered valid, it must be accompanied by a certified commitment. This certification is carried out by the IA through a blind signature scheme based on RSA. Assuming that the Discrete Logarithm Problem (DLP) has no efficient solution for meticulously selected parameters, the attacker has no means, apart from bruteforce, to break the signature scheme. □
Accuracy
Accuracy requires the final tally to match the actual outcome of the election. In order to achieve this: all valid votes must be counted; no invalid votes are considered; and no cast vote can be modified.
□
Proof.
We prove the statement in three independent sections:
-
1. Valid votes are counted: Parties are responsible of processing all valid received votes. Both individual and universal verifiability (Lemma 1) guarantee that electors can check that all valid votes are included in the final tally.
-
2. No invalid votes are considered: In order for a vote to be considered valid, it needs to be correctly certified. As proved in Lemma 3, the creation of fake votes is unfeasible. Thanks to verifiability, electors can also audit the results and check that all individual votes are valid.
-
3. Vote modification: Any modification to any of the unencrypted shares of a vote will be detected because it will make the certified commitment not match the shares. As long as the hash function used remains secure, no tampering of the votes will succeed.
Robustness
Robustness ensures that no coalition of electors and/or parties would be able to disrupt the election process. We first prove that our method is robust with the only condition that one party remains honest. Then, we prove that it is unfeasible a coalition of users could tamper with new votes.
Proof.
We note that parties must cooperate to interpolate the polynomials and recover the final votes. If at least one contendant party remains honest, the remaining parties have no way to interpolate the polynomial and access the vote. Of course, at a cost of a high reputational loss, a set of parties can misbehave or refuse to cooperate, in which case the election would have no tally. □
Lemma 6.
It is unfeasible that, according to SUVS protocol, a coalition of electors could tamper with new votes.
Proof.
We note that a coalition of malicious electors could take profit of the multiplicative properties of modular exponentiation, and use their certified commitments in order to obtain a new tampered one ${h_{t}}$. Nevertheless, as long as the chosen hash function remains secure, it is unfeasible to obtain a set of points ${P_{t}}$, such that $\textit{shash}(P)={h_{t}}$, and such that the polynomial interpolated using ${P_{t}}$ codifies in its independent term a valid vote. □
Perfect Secrecy
Perfect secrecy, as defined in Section 3, provides security by uncertainty. The concealing of the vote by partition SUVS is based on provided security derived entirely from information theory, creating a system where partial information does not reveal anything about the scheme’s secrets.
As stated in Lemma 2, there is no mechanism to relate an elector to her vote. By providing perfect secrecy, we also ensure that, even in post-quantum scenarios, it is impossible to reveal any information on any vote unless all the parties are malicious or compromised.
Proof.
If an attacker gains knowledge about all the shares of a vote but one, there is no way he could interpolate the polynomial generated by the user and, therefore, gain access to the direction of the vote.
Note also that, under modular arithmetics, there exists a combinatorial number of d-degree polynomials consistent with d points. This implies that, even if the attacker could find a polynomial that covers the points and encodes a valid vote, he could never be sure which one was the original vote encoded by the elector. □
Malicious Elector Resistance
A malicious elector may try to craft a ballot in order to achieve double voting.
Proof.
SUVS defines the form of the ballot as:
In order to achieve double voting, a malicious elector could generate two different sets of points ${P_{1}}$, ${P_{2}}$ and craft the ballot as follows:
\[ b=\textit{shash}({P_{1}})\cdot \textit{shash}({P_{2}})\cdot {\textit{mask}^{v}}\hspace{1em}\mathrm{mod}\hspace{2.5pt}n.\]
To the IA, the resulting ballot looks the same as a valid one. So it signs the ballot and returns it to the malicious elector. Then, the malicious elector proceeds to remove the mask
\[ \textit{shash}{({P_{1}})^{s}}\cdot \textit{shash}{({P_{2}})^{s}}\cdot \textit{mask}\cdot {\textit{mask}^{-1}}=\textit{shash}{({P_{1}})^{s}}\cdot \textit{shash}{({P_{2}})^{s}}\hspace{1em}\mathrm{mod}\hspace{2.5pt}n.\]
Nonetheless, the malicious user cannot separate $\textit{shash}{({P_{1}})^{s}}$ and $\textit{shash}{({P_{2}})^{s}}$ since s is not known by the users. The malicious user would not only not be able to double vote, she would lose the ability to cast a single vote. □7 Conclusions
In this paper, we present a new voting protocol whose security is based on the partition of the ballot. To our knowledge, our proposal is the first electronic voting scheme that properly does not encrypt the vote. The responsibility of recovering the votes is distributed among the set of parties involved on the election, who are responsible to compute the final tally of the election. The protocol we propose does not allow the parties to modify the votes for their own benefit, and universal verifiability helps the electors to audit the final tally and ensures a fair election.
The system we propose requires minimal interactions from the electors and scales linearly with the number of processed votes. Thanks to the flexibility of the vote codification, our proposal is compatible with almost any kind of election. We believe these facts, alongside the simplicity of the scheme, make the protocol easy to understand and implement, which are essential features to contribute in the development and deployment of this technology.
As future work, we will study on how to reduce the number of shares the elector distributes among the parties without affecting the reliability and trustworthiness of the system. In such a way, if an elector does not trust a certain party, she can decide to arrange and send the shares of the ballot without considering it. The incorporation of alternative identification methods that would make unnecessary to include an identification authority in the protocol is, of course, of interest.
