For the convenience of presentation, in this section, the relevant theories are introduced.
2.1 Fuzzy Relation and Its Developments
To analyse the incompatibility between fuzzy preference relations and the bounded rationality, this section introduces the fuzzy preference relation and its developments. We begin with the concept of binary relation.
For two sets of evaluations on alternatives x and y, $X=\{{x_{1}},{x_{2}},\dots \}$ and $Y=\{{y_{1}},{y_{2}},\dots \}$, the product set $X\times Y$ is $\{({x_{i}},{y_{\xi }})|{x_{i}}\in X,{y_{\xi }}\in Y\}$, where $({x_{i}},{y_{\xi }})$ is an ordering pair. Any subset of $X\times Y$ is a binary relation. For a fixed relation “R”, if an ordering pair $({x_{i}},{y_{\xi }})$ belongs to the relation “R”, alternative ${x_{i}}$ is regarded to have a relation “R” with alternative ${y_{\xi }}$. Given a set of two supply chain suppliers $X=\{{x_{1}},{x_{2}}\}$, the product set $X\times X$ is $\{({x_{1}},{x_{1}}),({x_{1}},{x_{2}}),({x_{2}},{x_{1}}),({x_{2}},{x_{2}})\}$. Let the binary relation “R” be “better”. If the supplier ${x_{1}}$ is better than the supplier ${x_{2}}$, then the ordering pair $({x_{1}},{x_{2}})$ belongs to the relation “R”. Likewise, if the ordering pair $({x_{1}},{x_{2}})$ belongs to the relation “R”, it means that the supplier ${x_{1}}$ is better than the supplier ${x_{2}}$.
In the above Example
1, if we know that
${x_{1}}$ is better than
${x_{2}}$, it can be inferred that the ordering pair
$({x_{1}},{x_{2}})$ must belong to “
R”. However, because of the complexity of practical management activities,
${x_{1}}$ is usually partly better than
${x_{2}}$. In this situation, we cannot say that the ordering pair
$({x_{1}},{x_{2}})$ totally belongs to “
R”. To model such situations, Zadeh (
1971) used the fuzzy theory to define the fuzzy relation (or fuzzy binary relation) where the degree of
$({x_{i}},{y_{\xi }})$ belonging to the relation “
R” was a membership degree
${\mu _{R}}({x_{i}},{y_{\xi }})\in [0,1]$. Particularly, when
${\mu _{R}}({x_{i}},{y_{\xi }})$ is 0,
$({x_{i}},{y_{\xi }})$ does not belong to “
R”; when
${\mu _{R}}({x_{i}},{y_{\xi }})$ is 1,
$({x_{i}},{y_{\xi }})$ belongs to “
R”. In other words, the binary relation is a special case of the fuzzy relation where the membership degree
${\mu _{R}}({x_{i}},{y_{\xi }})$ is 0 or 1.
For fuzzy relations, they have four properties, namely, reflexivity, symmetry, transitivity, and reciprocity (Zadeh,
1971; Bezdek
et al.,
1978). The reflexivity means
${\mu _{R}}({x_{i}},{x_{i}})=1$, which is related to the partial ordering. If
${\mu _{R}}({x_{i}},{x_{i}})=0$, the partial ordering could not be set up. The symmetry means
${\mu _{R}}({x_{i}},{y_{\xi }})={\mu _{R}}({y_{\xi }},{x_{i}})$. There is a mass of rules of the transitivity, satisfying different requirements in different situations (Wang,
1997; Herrera-Viedma
et al.,
2004; Chang
et al.,
2019). The main role of transitivity is to avoid the inconsistency that might cause errors and paradoxes. The reciprocity is
${\mu _{R}}({x_{i}},{y_{\xi }})+{\mu _{R}}({y_{\xi }},{x_{i}})=1$ $({x_{i}}\ne {y_{\xi }})$, meaning that the degree of
${x_{i}}$ dominating
${y_{\xi }}$ plus the degree of
${y_{\xi }}$ dominating
${x_{i}}$ must be 1.
Different combinations of these four properties yielded different developments of the fuzzy relation. These developments could be divided into two categories. Regarding the first group, Zadeh (
1971) proposed a few concepts which mainly focused on transitivity, symmetry, and reflexivity. The fuzzy ordering was the fuzzy relation having transitivity. The fuzzy preordering was the fuzzy ordering having reflexivity. The similarity relation was the fuzzy preordering satisfying the symmetry. The fuzzy partial ordering was the fuzzy preordering which was anti-symmetric. The fuzzy linear ordering was the fuzzy partial ordering satisfying
${x_{i}}\ne {y_{\xi }}\Rightarrow {\mu _{R}}({x_{i}},{y_{\xi }})>0$ or
${\mu _{R}}({y_{\xi }},{x_{i}})>0$. The fuzzy weak ordering was the fuzzy preordering having
${x_{i}}\ne {y_{\xi }}\Rightarrow {\mu _{R}}({x_{i}},{y_{\xi }})>0$ or
${\mu _{R}}({y_{\xi }},{x_{i}})>0$. In the second group, the reciprocity and the necessity of transitivity were investigated. Bezdek
et al. (
1978) proposed the reciprocal property and defined the reciprocal fuzzy relation which was irreflexive and reciprocal. Orlovsky (
1978) proposed the fuzzy non-strict preference relation which was a reflexive but not necessarily a transitive fuzzy relation. Tanino (
1984) introduced the fuzzy preference ordering which was reciprocal and transitive. Based on the fuzzy non-strict preference relation, Parreiras
et al. (
2012) defined the nonreciprocal property and introduced a nonreciprocal fuzzy preference relation. Motivated by Nakamura (
1986), we give Fig.
1 to clearly illustrate the relations of these developments of the fuzzy relation.
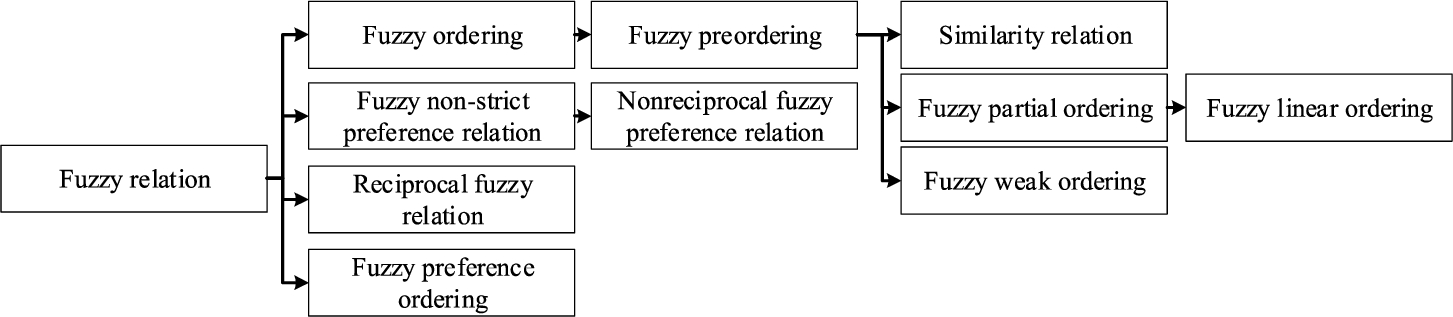
Fig. 1
The relations of the developments of the fuzzy relation.
Among the developments of fuzzy relations, the fuzzy preference ordering attracted the attention of many researchers. Different kinds of uncertainty were considered to improve the fuzzy preference ordering. Xu (
2007) proposed the intuitionistic preference relation considering the membership and non-membership degrees. Liao
et al. (
2014) introduced the hesitant fuzzy preference relation which could express experts’ hesitancy degrees. There were triangular fuzzy reciprocal preference relation (Meng
et al.,
2017) in which the membership function was a triangular fuzzy number and interval fuzzy preference relation (Meng
et al.,
2019) using intervals to express uncertainty. Zhang
et al. (
2019) presented the
q-rung orthopair fuzzy preference relation to deal with the problems that the membership degree plus non-membership degree is larger than 1. Gong
et al. (
2020) proposed the linear uncertain preference relation. The use of fuzzy relations in decision making facilitated its developments in theory (Wan
et al.,
2017; Ferrera-Cedeño
et al.,
2019; Zhang
et al.,
2021). Known from Section
2.2., experts are usually bounded rational. However, as far as we know, few studies discussed the suitability of the four properties within the context of bounded rationality.
2.2 Bounded Rationality Theory
In the traditional economic theory, there is a postulate of economic man, that experts are familiar with, who has related knowledge and a stable system of preference (Simon,
1955). This economic man postulate requires experts to have high rationality, and thus it is also called the global rationality postulate (Simon,
1955). The postulate of economic man simplifies the analysis of real problems by mathematical models. In real situations, especially in economic and management realms, practical issues might be complex. Usually, an expert is only proficient in one or two areas. Facing practical issues that involve many areas like the law and marketing, experts might not have enough knowledge, which causes the cognitive limitation of experts. Besides, experts’ computation ability is limited. When there is a large amount of data, experts might not be able to process the whole data, resulting in the weak estimation of the result of a decision. Because the cognition levels of experts are limited by their knowledge, it is hard for them to satisfy the global rationality postulate. In this situation, the simplification of real problems by the postulate of economic man might cause unreasonable results.
To make the postulate of economic man compatible with experts’ abilities, Simon (
1955) first proposed the concept of bounded rationality. Different from the global rationality postulate which restricts human behaviours, the bounded rationality theory aims to give a reasonable explanation for experts’ realistic behaviours from the aspects of human cognition and psychology. To achieve this goal, decision processes and methods were simplified from the perspective of the gross characteristics of human choice (Simon,
1955) and the broad features of the environment (Simon,
1956). A few interesting notions, such as the satisfactory solutions (Simon,
1955), were proposed based on the bounded rationality theory.
Motivated by the bounded rationality theory, a mass of researches has been done, which can be grouped into two categories. The first group considered probability models with the bounded rationality theory. Mattsson and Weibull (
2002) reviewed the development of the game theory with the bounded rationality and proposed a probabilistic choice model with bounded rationality. Sterman
et al. (
2007) combined the bounded rationality theory with disequilibrium dynamics to create a dynamic behavioural game model. Huang
et al. (
2013) used a special queue model, where customers’ waiting time cannot be accurately estimated, to capture the bounded rationality, and concluded that if the bounded rationality was ignored, there was a “
significant revenue and welfare loss”. The second group focused on the fuzzy theory. Angus (
2016) found that, in addition to the probability theory, it was also necessary to consider the fuzzy theory together with the bounded rationality theory. Wang and Fu (
2014) used a nonlinear scalarization technique to model bounded rationality in generalized abstract fuzzy economies. Wu and Zhao (
2014) proposed the fuzzy choice functions of fuzzy preference relations under the circumstance of bounded rationality. Chang
et al. (
2019) considered the transitivity of fuzzy preference relations with bounded rationality and proposed the triangular bounded consistency of fuzzy preference relations. Furthermore, the bounded rationality theory has achieved several applications in terms of organization management (Simon,
1991), transportation system design (Cascetta
et al.,
2015), stock management (Sterman,
1989), policy advice (Caballero and Lunday,
2020), hotel selection (Wang
et al.,
2020), and the analysis of customers’ behaviours in service operations systems (He
et al.,
2020).
For the existing researches on fuzzy preference relations under the bounded rationality circumstance (Wang and Fu,
2014; Wu and Zhao,
2014), the core idea was to use formulas and constraints to express the bounded rationality, which was similar to Lipman’s idea (
1991). However, they ignored a key problem that the original properties of fuzzy preference relations might not be compatible with the bounded rationality. This incompatibility might cause systematic and inherent errors when using existing methods (Wang and Fu,
2014; Wu and Zhao,
2014). In Section
3, we will further analyse this incompatibility in detail.

