In this section, theoretical problems regarding the quality of the same LS (basic structure and structure with restriction) for all districts are evaluated and the new quality measure is proposed.
3.1 Basic Structure of LSs
To illustrate the problem of a summary
Q entities in X are P, let us evaluate the truth value of the sentence
the most of patients are old for each district. The fuzzy set
old is a linguistic term on a domain of attribute
age (see e.g. Fig.
5). The quantifier
most of is expressed by Eq. (
4). In Table
1, there is an example of the numbers of patients in three districts, belonging to sets
young,
middle-aged and
old. For the simplicity reason (which do not affect generality), all the patients belong to one of these sets with the degree equal to 1. In this case,
${\textstyle\sum _{i=1}^{n}}{\mu _{P}}(x)$ (expressing the cardinality of a fuzzy set
P) assigns a natural number.
Table 1
Example of a truth value of summary on districts with different number of entities.
|
District D1 |
District D2 |
District D3 |
| Cardinality of set young
|
3 |
110 |
150 |
| Cardinality of set middle–aged
|
3 |
120 |
140 |
| Cardinality of set old
|
15 |
540 |
160 |
| Truth value for summary the most of patients are old by (5) |
0.7143 |
0.7013 |
0 |
District
D1 has a higher truth value than district
D2, which means a slightly darker hue on a map. But, a higher concern should be focused on
D2, instead of on
D1. Thus, we should include the data distribution among districts to emphasize
D2 on a map. It has a significantly higher number of patients which should be reflected in the summary, while a lower number of patients should reduce the relevance (alarm) of a summary. Theoretically, not a single record in a district might be recorded, which leads to undefined operation
$0/0$ in Eq. (
5), i.e.
$n=0$. For this case, we adopt
$0/0=0$.
The first (and simple) option is considering the proportion index
p as a weight of the summary, i.e.
where
n is the number of districts. The proportion can be expressed as
where
${N_{i}}$ is the number of patients in district
i,
${N_{i}}\leqslant \max \{{N_{1}},\dots ,{N_{n}}\}$ causing
${p_{i}}\in [0,1]$,
$i=1,\dots ,n$. If
$\max \{{N_{1}},\dots ,{N_{n}}\}=0$, not a single case is recorded and therefore interpreting summaries on a map is irrelevant. For simplicity, we denoted
${v_{LS{b_{i}}}}={v_{i}}$. Instead of the number of patients, the ratio of patients to the number of inhabitants in districts can be used. Firstly, it does not solve this problem. Secondly, many inhabitants might have a temporal address somewhere else. Assigning weights is a widely applied approach, but we should be careful. Discussions related to weights can be found in e.g. (Dujmović,
2018; Zadrożny
et al.,
2008).
Next, $\overline{{v_{i}}}(\mathbf{X})={v_{i}}(\mathbf{X})$ holds only for a district where ${N_{i}}=\max \{{N_{1}},\dots ,{N_{n}}\}$. However, a high truth value for a district of a bit lower number of cases is attenuated, which is problematic.
Apparently, we should emphasize a summary for districts where both the truth value and proportion of data are high, and reduce the relevance of summaries when these two values are low. This observation leads to the aggregation by functions known as uninorms.
Uninorms generalize t-norms and t-conorms using the fact that these two classes of aggregation functions are defined by the same axioms of associativity, commutativity, monotonicity, and the presence of a neutral element. It means that uninorms consider neutral element
e inside the unit interval (Beliakov
et al.,
2007).
A uninorm is a bi-variate aggregation function
$U:{[0,1]^{2}}\to [0,1]$ which is associative, commutative, and has a neutral element
$e\in ]0,1[$. For
$e\in \{0,1\}$ we have the limiting cases of t-conorm and t-norm. Next,
-
• $\forall (x,y)\in {[0,e]^{2}}\hspace{10pt}U(x,y)=e{T_{u}}(\frac{x}{e},\frac{y}{e})$ has a conjunctive behaviour;
-
• $\forall (x,y)\in {[e,1]^{2}}\hspace{10pt}U(x,y)=e+(1-e){S_{u}}(\frac{x-e}{1-e},\frac{y-e}{1-e})$ has a disjunctive behaviour;
-
• $\forall (x,y)\in [0,e]\times [e,1]\cup [e,1]\times [0,e]\hspace{2.5pt}\min (x,y)\leqslant U(x,y)\leqslant \max (x,y)$ has an averaging behaviour,
where
${T_{u}}$ stands for t-norm and
${S_{u}}$ for t-conorm. This function is explained graphically in Fig.
2. When applying strict t-norm and strict t-conorm, we get the downward and upward reinforcement property, respectively (Beliakov
et al.,
2007).
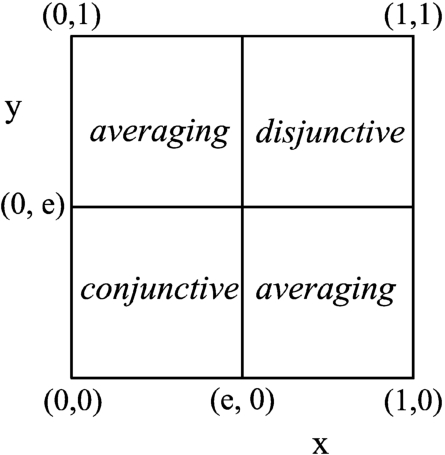
Fig. 2
The graphical interpretation of a uninorm function.
Representative uninorms are continuous everywhere except for the corners $(0,1)$ and $(1,0)$. For conjunctive uninorm holds $U(0,1)=0$ (annihilator $a=0$), whereas for disjunctive uninorm holds $U(0,1)=1$ (annihilator $a=1$). The former case might solve the problem with the quality of summaries. Due to commutativity, the same observation holds for $U(1,0)$. The presence of annihilator prevents uninorms from being strict on the whole unit square, i.e. they are strict on $]0,1{[^{2}}$.
An important family of parametrized representative uninorms is (Fodor
et al.,
1997; Klement
et al.,
1996):
where
$\lambda \in ]0,\infty [$ and either
${U_{\lambda }}(0,1)=0$ or
${U_{\lambda }}(0,1)=1$, the neutral element is
${e_{\lambda }}=\frac{1}{1+\lambda }$. Taking
$\lambda =1$, we get the well-known
$3-\textstyle\prod $ function (Yager and Rybalov,
1996)
where
$e=0.5$ and convention
$0/0=0$ holds for the conjunctive uninorm.
This function can meet the needs for aggregating the truth value (consider
${v_{i}}=x$) and data proportion (consider
${p_{i}}=y$). When
${p_{i}}=0$, the validity is also 0 (the validity of a summary on empty set is 0, when adopting
$0/0=0$ in Eq. (
5)). When
${v_{i}}=0$, the solution should be 0, regardless of value
${p_{i}}$. These observations hold for the
$3-\textstyle\prod $ function.
Moving back to the example in Table
1, we get
${p_{1}}=0.0273$,
${p_{2}}=1$,
${p_{3}}=0.5844$ by Eq. (
8) and therefore we get by Eq. (
7)
$\overline{{v_{1}}}=0.019$,
$\overline{{v_{2}}}=0.7013$ and
$\overline{{v_{3}}}=0$. The resulting relevance by Eq. (
10) of summary for district
D1 is 0.0649 (averaging function), for district
D2 is 1 (disjunctive function), and for district
D3 is 0. District
D2 is emphasized because a truth value and the proportion of entities influencing a truth value are higher than 0.5. District
D1 is attenuated by the averaging behaviour of validity higher than 0.5 and the proportion lower than 0.5. District
D3 gets the value of 0 as the validity of summary is 0 (0 is an annihilator for the conjunctive behaviour).
On the other hand, due to discontinuity in the proximity of (0, 1) this function is unstable, especially for the imprecision of input data, i.e. $U(1,\epsilon )=1$ for any $\epsilon >0$ like 0.001. A simple solution is replacing 1 (for truth value and proportion) with 0.999 to get the average of 0.999 and 0.001. Anyway, we have searched for a better solution.
The next option is aggregating a truth value and data proportion by the ordinal sums, which are an extension for semigroups (Clifford,
1954) or for posets (Birkhoff,
1967). In the framework of fuzzy sets theory, they were considered to build new t-norms/t-conorms from the scaled versions of existing ones (Klement
et al.,
2000). The ordinal sum of conjunctive and disjunctive functions has been proposed by De Baets and Mesiar (
2002) as follows.
For an
n-ary aggregation function
$B:{[0,1]^{n}}\to [0,1]$ and
$[a,b]\subset \mathbb{R}$, denote
${B_{[a,b]}}(\mathbf{x})=a+(b-a)\cdot B(\frac{\mathbf{x}-a}{b-a})$. Then
${B_{[a,b]}}$ is an n-ary aggregation function on
$[a,b]$. For
${B_{1}},\dots ,{B_{k}}:{[0,1]^{n}}\to [0,1]$,
$k\geqslant 2$, and
$0\leqslant {a_{0}}<{a_{1}}<\cdots <{a_{k}}=1$. Let
${A_{i}}:{[{a_{i-1}},{a_{i}}]^{n}}\to [{a_{i-1}},{a_{i}}]$ be given by
${A_{i}}={({B_{i}})_{[{a_{i-1}},{a_{i}}]}}$. Then the ordinal sum
$A:{[0,1]^{n}}\to [0,1]$,
$A=(\langle {a_{i-1}},{a_{i}},{A_{i}}\rangle )|i=1,\dots ,k$ given by De Baets and Mesiar (
2002):
is an aggregation function on
$[0,1]$. If all
${B_{1}},\dots ,{B_{k}}$ are t-norms (t-conorms, copulas, means) then also
A is a t-norm (t-conorm, copula, mean) (De Baets and Mesiar,
2002).
Analogously,
$A(\mathbf{x})={\textstyle\sum _{i=1}^{k}}({a_{i}}-{a_{i-1}})\cdot {B_{i}}(1\wedge (0\vee \frac{\mathbf{x}-{a_{i-1}}}{{a_{i}}-{a_{i-1}}}))$. For our purposes,
$n=k=2$ is considered. Denoting
${a_{1}}=a({a_{0}}=0,{a_{2}}=1)$, we have two next forms of ordinal sums (Hudec
et al.,
2021):
(i)
${B_{1}},{B_{2}}:{[0,1]^{2}}\to [0,1]$,
(ii)
${A_{1}}:{[0,a]^{2}}\to [0,a]$,
${A_{2}}:{[a,1]^{2}}\to [a,1]$,
Functions
${B_{i}}$ cover subsquares of the unit square. In order to be inside the respective subsquares, conjunction between the attribute values (considering the separation point
a) and 1, and disjunction between the values and 0 is applied. Observe that the function
A covers the conjunctive part
${A_{1}}(x,y)$ when
x and
y are lower or equal to
a, i.e.
$a\wedge x=x$, and
$a\wedge y=y$. Then, for
${A_{2}}$ we get
$a\vee x=a$ and
$a\vee y=a$. As a consequence
$(a\vee a)-a=0$. More details are in De Baets and Mesiar (
2002), Hudec
et al. (
2021).
Then:
-
• if $(x,y)\in {[0,a]^{2}}$, $A(x,y)=a\cdot {B_{1}}(\frac{x}{a},\frac{y}{a})={A_{1}}(x,y)$,
-
• if $(x,y)\in {[a,1]^{2}}$, $A(x,y)=a+(1-a)\cdot {B_{2}}(\frac{x-a}{1-a},\frac{y-a}{1-a})={A_{2}}(x,y)$,
-
• if $(x,y)\in [0,a]\times [a,1]$, $A(x,y)=a\cdot {B_{1}}(\frac{x}{a},1)+(1-a)\cdot {B_{2}}(0,\frac{y-a}{1-a})={A_{1}}(x,a)+{A_{2}}(a,y)-a$,
-
• if $(x,y)\in [a,1]\times [0,a]$, $A(x,y)=a\cdot {B_{1}}(1,\frac{y}{a})+(1-a)\cdot {B_{2}}(\frac{x-a}{1-a},0)={A_{1}}(a,y)+{A_{2}}(x,a)-a$.
The next task is the suitable variation of conjunctive, disjunctive, and averaging functions in ordinal sums. In this work, we need upward reinforcement when both values are high, downward reinforcement when both are low and averaging behaviour when one measure is high and another is low. In addition, we need the stability in the ϵ neighbour of $(0,1)$ and $(1,0)$.
The option is a strict t-norm for the conjunctive part, strict t-conorm for the disjunctive part and a logically neutral averaging function (arithmetic mean), because we do not consider inclinations towards conjunctive or disjunctive areas provided by, e.g. geometric and quadratic mean, respectively.
The representative function of strict behaviour is product t-norm (expressed as ${C_{P}}(x,y)=xy$), whereas its dual t-conorm is a probabilistic sum (expressed as ${D_{P}}(x,y)=x+y-xy$).
The result for
$A(0.5,0.5)$, when
$a=0.5$ should be 0.5 for conjunctive, averaging and disjunctive function (see Fig.
3). In order to keep the expected value on this point, the product t-norm on
${[0,0.5]^{2}}$ is expressed as (Hudec
et al.,
2021):
Analogously, strict t-conorm on
${[0.5,1]^{2}}$ is expressed as:
Finally, the aggregation on the averaging part is expressed as:
From the logic perspective, the arithmetic mean and its variants thereof (weighted arithmetic mean and the like) are the logically neutral averaging functions, with the
ORNESS measure equal to 0.5. The other functions either incline towards conjunction
$(\textit{ORNESS}<0.5)$ or disjunction
$(\textit{ORNESS}>0.5)$ (Dujmović,
2018). Applying the other averaging functions will increase the complexity. This is the reason, why we applied arithmetic mean. However, the other averaging functions could be examined in the future work.
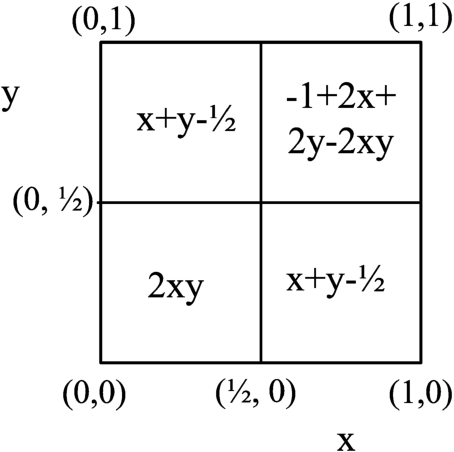
Fig. 3
The graphical interpretation of ordinal sums for product t-norm (
14), probabilistic sum t-conorm (
15) and arithmetic mean (
16) (Hudec
et al.,
2021).
Considering again the example in Table
1 (consider
$x=v$ – truth value and
$y=p$ – proportion), the resulting quality of the summary (
$\overline{v}$) for district
D1 is 0.2413 (an example of averaging behaviour), for district
D2 is 1 (an example of disjunctive behaviour), and for district
D3 is 0 (due to restriction put on summary). We get the expected results. Moreover, we get
$A(1,0.001)=0.501$, which is an averaging behaviour. Next, when the proportion is 0, the truth value gets the same value. It is worth noting that, when a truth value is 0, the solution should be zero. This is not a problem, because quality measures should be activated when a truth value is greater than zero.
The downward and dual upward reinforcement behaviour is also a property of nilpotent t-norms and t-conorms, respectively. The representative functions are the Łukasiewicz t-norm and its dual Łukasiewicz t-conorm. In order to keep the expected value on edges of subinterval
${[a,1]^{2}}$ when
$a=0.5$, the Łukasiewicz t-conorm on
${[0.5,1]^{2}}$ is expressed as (Hudec
et al.,
2021)
When the truth value and proportion are higher than 0.75, the solution is equal to 1. Thus, we cannot distinguish between two summaries, for which the truth value and proportion are $(0.75,0.76)$ and $(0.95,1)$, respectively. Considering this fact and the need for providing continued hues on maps, the option is a strict t-norm and its dual t-conorm.
3.2 The Structure with Restriction
In summary
Q R entities in X are P, when, for instance, two of
${10^{6}}$ entities satisfy
R and only the same two entities satisfy
P (Eq. (
6)), the truth value gets value 1, but it is based on outliers (Hudec
et al.,
2018). To overcome this problem, Wu
et al. (
2010) proposed a coverage measure that expresses the proportion of entities included in both
R and
P to avoid summaries on outliers. We refer this measure here. The ratio of included entities in a summary is
where
n is the number of records and
${m_{i}}=\left\{\begin{array}{l@{\hskip4.0pt}l}1\hspace{1em}& \text{for}\hspace{2.5pt}{\mu _{P}}({x_{i}})>0\wedge {\mu _{R}}({x_{i}})>0,\\ {} 0\hspace{1em}& \text{otherwise}.\end{array}\right.$
Since a summary of the structure (Eq. (
6)) covers a subset of the entire database,
${i_{c}}$ is considerably smaller than 1. Thus, the following function converts this ratio into the degree of sufficient coverage (Wu
et al.,
2010)
where the suggested values for parameters
${r_{1}}$ and
${r_{2}}$ depend on the length of the summary (the number of attributes in
R and
P).
To illustrate these calculations, let us have 2000 records,
${r_{1}}=0.02$ and
${r_{2}}=0.15$ (i.e. when 15% of data are included in the
R and
S parts, it is considered as a fully relevant coverage). Next, we have three summarized sentences
${S_{1}}$,
${S_{2}}$ and
${S_{3}}$ covering 175, 320 and 13 records, respectively. The ratio of included records and coverage are shown in Table
2. Summary
${S_{2}}$ fully covers the relevant subset of data, whereas summary
${S_{3}}$ should be excluded, even when its validity is equal to 1.
Table 2
Example of a ratio of included records and coverage.
| Included records |
${i_{c}}$ (Eq. (18)) |
coverage (Eq. (19)) |
| 175 |
0.0875 |
0.5377 |
| 320 |
0.1600 |
1 |
| 13 |
0.0065 |
0 |
The method for calculating a truth value of conjunction of summary and its antonym based on the Sugeno integral (Jain and Keller,
2015) also solves this problem (Wilbik
et al.,
2020).
The same problem as for a basic structure of a summary holds here. Even though quality measures filter summaries on outliers, the distinction among subsets of different sizes should be reflected on the map. Districts, where the number of patients is higher, should be emphasized when the truth value of a summary and data coverage are high. In addition, we have a truth value of a summary, data coverage, and proportion. Hence, we should aggregate these three measures.
The truth value and coverage are measures for evaluating different summaries on the same data set. As both should be satisfied, we aggregate them by t-norm function (Hudec,
2017). In the next step, we apply ordinal sums (see Eqs. (
14), (
15), (
16)).

