1 Introduction
McLennan, Manning, and Tuft presented a mnemonic variant of password security that uses game positions as passwords. Their proposal is called “Game Changer Password System,” or GCPS for short (McLennan
et al.,
2017).
The idea behind the GCPS is that “
a number of different games are presented on the screen, similar to viewing a screen full of movie options in Netflix, allowing users to select the game first and then to enter his or her password in the game selected” (McLennan
et al.,
2017). For example, a user first selects a Chess game, then puts a black king (BK) on position a7, followed by a black rook (BR) on e6, a white knight (WN) on c4, and finally, a white pawn (WP) on g3. Such a combination can be transcribed as a textual password, e.g. ‘BKa7BRe6WNc4WPg3’.
The proposed system’s main innovative and essential element are passwords based on graphical presentations familiar to users, i.e. games. Graphical background significantly improves the memorability of such passwords (Kiesel
et al.,
2017). Another advantage is that users find the GCPS system fun to use, and the effect is shown in a relatively high recall rate (>75%).
However, the security analysis of the system has shown the initial design is vulnerable to brute force attacks and that needs to be addressed before the actual implementation (Brumen,
2019). Because of the “hotspot” problem (Constantinides
et al.,
2021), it is also susceptible to specialized dictionary attacks. The main weakness of the original proposal is the limited number of pieces and position on the chessboard on which these pieces can be placed. However, this weakness is due to the design of original games used, not the GCPS as such (Brumen,
2019). A version that would be both brute force and dictionary attack resistant would require several modifications, including increasing the search space and the number of layers.
The authors of the original proposal did foresee such an improvement. Still, their tests for memorability of GCPS-based passwords were conducted using a simple setup without any layering. Additionally, the passwords employed in the study contained very few game pieces, thus not properly addressing the possibility of a brute force and/or a dictionary attack.
The initial proposal needs to be re-validated, particularly in terms of the additional two aspects: memorability, its (claimed) most significant advantage, and usability. Hence, the research question of this paper is whether the modified Game Changer Password System (such that it limits the feasibility of a brute force and dictionary attack) is still producing memorable and usable passwords.
The rest of the paper is organized as follows. The following section elaborates on a layered game changer password system based on a “Battleship” game and discusses its resilience against attacks. In Section
3, we present the experimental setup, while the results are discussed in Section
4. The paper is concluded with final remarks in Section
5.
2 The Layered “Battleship” Game Changer Password System
McLennan
et al. (
2017) described the main idea behind the Game Password Changer System as: “
$\dots \mathit{passwords}$ [
that]
are stored in game positions. This approach involves giving up the idea of passwords as alphanumeric strings and replacing such strings with iconic codes that are stored on the virtual game positions of different games”. Authors chose chess and Monopoly as an example and originally proposed variants where users selected (only) two or four pieces. Such passwords were shown to be vulnerable to guessing attacks due to the small search space.
To improve the search space, we propose a game called “Battleship” (also known as “Convoy” and “Sinking ships”). Battleship is a two-player game based on guessing. It dates to the beginning of the 20th century and is played on two
$n\times n$ grids (usually
$10\times 10$). Before the start of the game, each player randomly allocates
i boats on her grid. Five ships
$(i=5)$ of varying lengths are most typically used in the game, each occupying a specific position on the field. A typical setting contains five ships of the following lengths: 5, 4, 3, 3, 2. Each of the fields is identified by coordinates made up of numbers and letters. Ships may be positioned horizontally or vertically, but should not overlap, as only a single ship can occupy one coordinate location. Since ships are not allowed to touch, they also cannot occupy adjacent coordinate locations. While playing the game, the players alternately call the coordinates (e.g. “B-4”) and try to “sink” the opponent’s ships by guessing their location. Each time a player manages to land a hit on their opponent’s boat, the opponent must proclaim a hit and announce which boat has been damaged. When all the coordinates corresponding to a particular ship are hit, that boat is sunk. When all the player’s ships are sunken, the game is over (see Fig.
1).
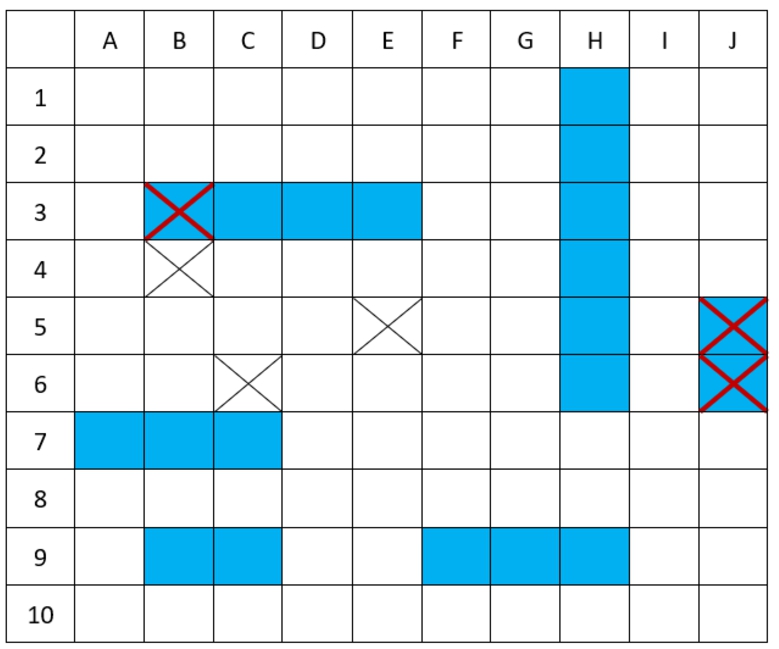
Fig. 1
An example of battleship game setting.
This particular game was also selected because “brain games” increase memorability, particularly the “pattern memory” game (Moser
et al.,
2015), which is based on the same principle as “Battleship.”
Our modified “Battleship” GCPS is representative of drawmetric (pure recall-based) schemes (Stobert and Biddle,
2013; Adama
et al.,
2021) in which a user places their “password” on an empty
$n\times n$ grid. Most of the pure recall-based schemes’ memorability does not exceed 80% (Al-Ameen
et al.,
2015), as is also the case with the original GPCS.
An advantage of this game over the initially selected chess and Monopoly is its design, which allows for a more extensive search space from which to create a password. Another advantage is the ease with which the search space can then be increased without disrupting users and their familiarity with the game.
The search space from which a password can be created depends on the grid size (i.e. the number of coordinate locations), the number of ships, and their sizes. Unfortunately, the Battleship game so far remains unstudied from a complexity standpoint, i.e. an exact formula for a number of possible combinations is unknown (Demaine,
2001). Fortunately, though, the Battleship problem is an NP problem (Sevenster,
2004).
The upper bound of the search space of a Battlefield game is needed to estimate the brute force resilience against an algorithm creating passwords drawn from such a space. Here we expand on the initial idea by Lugo (
2009). Let us first assume we start with two ships
w and
z of various sizes. Then, we can define the length of ship
w as
m, and the length of ship
z as
l in such a way that both lengths are different from one another (
$m\ne l$). Finally, the two ships are placed on an
$n\times n$ grid.
The number of ways to place the ship
w of length
m is:
There are
$(n-m+1)n$ ways to place the ship vertically (
n columns, each having
$n-m+1$ possible placements) and
$n(n-m+1)$ ways to put the ship horizontally (
n rows, each having
$n-m+1$ possible arrangements).
Similarly, the number of ways to place the ship
z of length
l ship is:
The total number of combinations to place the two ships should be the product of these, minus the possible intersections or adjacencies:
We have to consider the possibility that the ships could intersect or be adjacent. If the two ships intersect, either:
-
– one is horizontal, and one is vertical, and the intersection is a single square, or
-
– both have the same orientation, and the two ships lie in the same row or column, and the intersection is either a single or multiple squares.
If they are adjacent, either:
-
– they are adjacent left-to-right, i.e. for any pair of two ship’s coordinates $({x_{w}},{y_{w}})$ and $({x_{z}},{y_{z}})$, there is at least one such pair of coordinates where ${x_{w}}={x_{z}}+1$ and ${y_{w}}={y_{z}}$, or
-
– they are adjacent top-to-bottom, i.e. for any pair of two ship’s coordinates $({x_{w}},{y_{w}})$ and $({x_{z}},{y_{z}})$, there is at least one such pair of coordinates where ${y_{w}}={y_{z}}+1$ and ${x_{w}}={x_{z}}$, or
-
– they are adjacent diagonally, i.e. for any pair of two ship’s coordinates $({x_{w}},{y_{w}})$ and $({x_{z}},{y_{z}})$, there is one such pair of coordinates where either ${y_{w}}={y_{z}}+1$ and ${x_{w}}={x_{z}}+1$ or ${y_{w}}={y_{z}}-1$ and ${x_{w}}={x_{z}}-1$.
Obviously, the shorter the ships (low
l and
m), the more combinations there are and the less possibility there is for intersections and adjacencies.
An additional feature, the ship’s orientation, adds to the complexity by a constant of 2. Namely, each ship can have two directions, as shown in Fig.
2: a ship 5-units long occupying the exact locations D4–H4 can point either to the left or right.
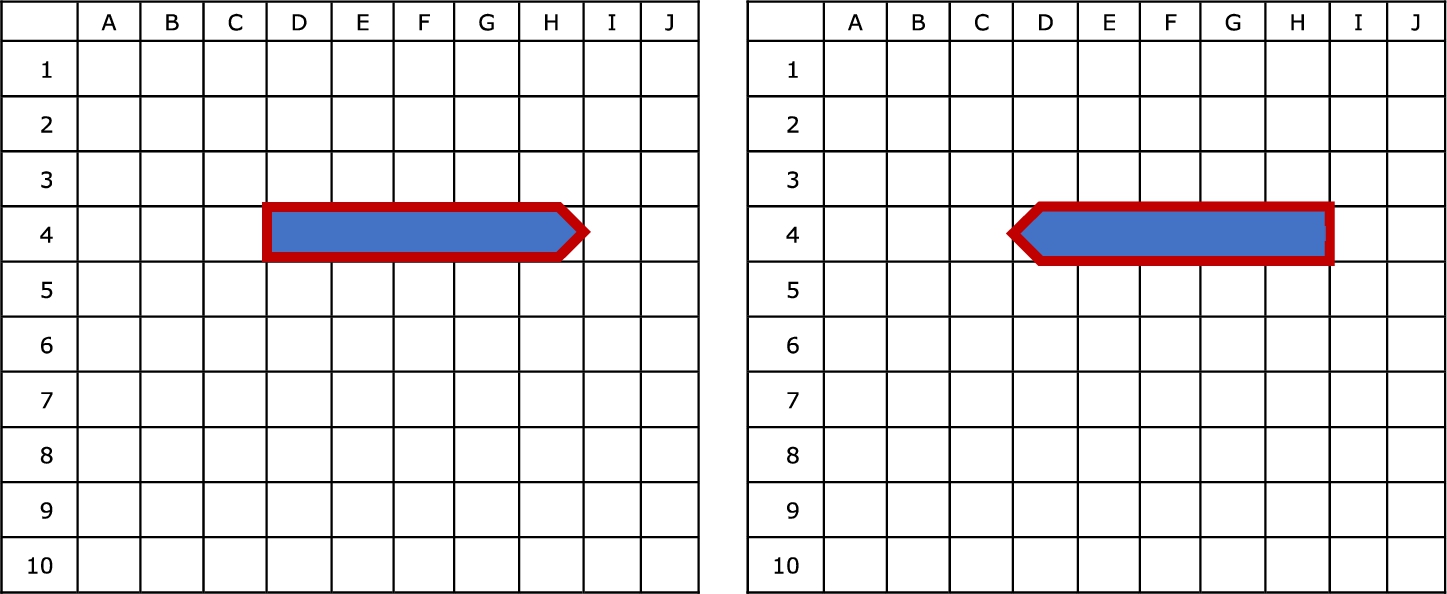
Fig. 2
(a) right and (b) left-pointing ship occupying precisely the exact locations.
The exact number of intersections and adjacencies depends on the chosen positions of each ship and their lengths. Unfortunately, as mentioned, the equation does not exist. In every case, the number of configurations with that intersection and adjacency structure is a polynomial in m, l, and $n\times n$.
Let
m and
l be (chosen, fixed) constants and let
n vary; then the leading term of Eq. (
3) (i.e. when
$m=l=1$) is
$2\times 2\times {n^{2}}\times {n^{2}}=4\times {n^{4}}$. Essentially, if we consider the upper bound, there are
$2\times {n^{2}}$ ways to place each ship and
$4\times {n^{4}}$ to place two ships. Therefore, a general formula to compute the number of possible combinations to position
i ships is
${(2\times {n^{2}})^{i}}$. As such, the upper bound for placing
$i=5$ ships is therefore
${2^{5}}\times {n^{2\times 5}}=32\times {n^{10}}$. For the special case when
$n=10$, the upper bound is
$3.2\times {10^{11}}$. The upper bound applies to the situation in which no Battleship rules are observed: the ships can be adjacent or overlapping or even placed partially outside the grid.
The actual number of possible placements is less than this. Fortunately, Thielemann (
2016) solved the problem by dynamic programming, and the source code is freely available. We calculated the number of possible combinations for a few examples, and the results are presented in Table
1.
Table 1
Number of possible combinations for a $10\times 10$ grid.
| Example |
# of ships of lengths |
Total # of ships |
Possible combinations |
| $m=2$ |
$m=3$ |
$m=4$ |
$m=5$ |
| #1 |
1 |
2 |
1 |
1 |
5 |
$1.9\times {10^{9}}$ |
| #2 |
2 |
1 |
1 |
1 |
5 |
$2.7\times {10^{9}}$ |
| #3 |
3 |
1 |
1 |
0 |
5 |
$2.5\times {10^{9}}$ |
| #4 |
1 |
1 |
2 |
1 |
5 |
$1.3\times {10^{9}}$ |
| #5 |
3 |
2 |
1 |
1 |
7 |
$6.4\times {10^{11}}$ |
| #6 |
2 |
2 |
1 |
1 |
6 |
$4.9\times {10^{10}}$ |
The calculation of the extreme upper bound, data from Table
1, and the analysis conducted in Brumen (
2019) all clearly indicate that the search space for the Battlefield setting is not nearly enough for the initially proposed GCPS system to be brute force attack resilient.
Namely, a search space containing a minimum of
${95^{11}}$ possible combinations is required. Base 95 corresponds to the size of a pool consisting of small (25) and capital (25) letters, digits (10), and a set of special characters (∼35). Potent 11 corresponds to 11 characters, yielding the total search space size of
$5.7\times {10^{21}}$ (equivalent to an 11-character random password). Passwords having 11 and beyond (independent and randomly drawn) characters are considered safe (Brumen and Taneski,
2015); 8-character passwords with a search space of
$6.6\times {10^{15}}$ are a minimum (Grassi
et al.,
2017).
Hence, as correctly identified by the inventors of the GCPS, layering is required. They had initially proposed but not elaborated on a possible security improvement of the system they called “layering,” i.e. using a sequence of several games to construct a password. The layering of two games would increase the possible search space. Using the numbers from example #6 in Table
1, layering two Battleship settings would increase the search space to
${(4.9\times {10^{10}})^{2}}=2.4\times {10^{21}}$ all possible combinations. Hence, a password constructed by such a two-layer Battleship setting would be considered brute-force resilient.
However, layering needs to be appropriately implemented, or else it gives only a false sense of security. For example, the password from Fig.
1 could read: “2H.B9-3H.F9-3H.A7-2V.J5-4H.B3-5H.H1”, where the first number in the block represents the size of the ship, the second letter represents the orientation of the ship (H = horizontal, V = vertical), and the number and letter following the period represent coordinates of the leftmost (or topmost) ship’s block. Note that in this setting, the sequence of placing the ships on the board is essential. The same setting as in Fig.
1 would yield another password by placing ships in reverse order, i.e. “5H.H1-4H.B3-2V.J5-3H.A7-3H.F9-2H.B9”.
Suppose we have two identical settings as described in the previous paragraph, and two passwords are used to implement the layering. The corresponding MD5 hashes computed for the first and second passwords are ‘323af404e22f688d63179bb6342de18b’ and ‘522384195addf91fd8a83defe95d8bae’. An attacker would create a password guess in each step, e.g. “5H.G1-4H.B2-2V.J4-3H.A7-3H.F9-2H.B9” and compute a corresponding hash: ‘98ef3267b095d62bd59c67ab8f1cbc49’, then compare her hash with both hashes at once rather than only one at a time. This can be accomplished in a single (parallel) step, requiring only a few additional CPU/GPU instructions (Brumen,
2019). The layering would only work if both passwords were considered (and implemented) as a single long password, e.g. ‘2H.B9-3H.F9-3H.A7-2V.J5-4H.B3-5H.H1-5H.H1-4H.B3-2V.J5-3H.A7-3H.F9-2H.B9’. This solution is not optimal from the “Security by design principle” (Norman,
2014) perspective, which mandates that security issues should be resolved at the design time and not assumed to be handled at the implementation phase. Requiring two passwords instead of one and using the same or similar passwords is a much bigger problem for alphanumeric passwords than game-based ones. Namely, if layering is used, it is quite hard to have a Battleship password and a Chess password that are the same or even similar.
However, the memorability and usability of such a password system must be verified. As mentioned, McLennan, Manning, and Tuft have initially proposed but not elaborated on a possible security improvement of the GCPS by using a sequence of several games to construct a password. They neither checked the memorability nor usability of such a layered system. Their results describe the memorability and usability of a simplified brute-force susceptible version. However, layering increases the memory burden on users because they need to memorize two settings instead of one. Additionally, it also increases the time necessary to enter the password correctly because users need to enter two of them instead of only one.
The problem with passwords is optimizing the triangle “security-memorability-usability”; by improving one aspect, the other two degrade.
We designed an experiment that closely followed the experiment executed in the original proposal to check the memorability and usability aspects of the Layered Battleship Game Changer Password System (LB-GCPS). The experiment will be presented in the next section.
3 Experiment: Memorability and Usability of Layered Battleship Game Changer Password System (LB-GCPS)
We designed the experiment by following the guidelines of the evaluation framework given in Bošnjak and Brumen (
2020). The guidelines affect the results, interpretation, validity, and quality of the study. Thirty parameters were proposed for evaluating a graphical password system’s vulnerability to shoulder surfing attacks; however, the goal of this study is different. Hence we used only the parameters applicable to our research questions and objectives of the present study. The parameters are grouped into two sets. The first set relates to the graphical password method design, and the second is about the experiment itself. Since the original design was proposed by McLennan
et al. (
2017), we considered the weaknesses identified in Brumen (
2019) and proposed a sound attack-resistant solution presented in the previous section. We paid particular attention to the second set of parameters regarding the experimental setup (i.e. efficiency, memorability, interaction method, constraints, participants’ profile, internal and external validity) within our experiment design.
The experiment was conducted in several phases after the design and testing of the supporting application was finished. Firstly, we recruited our participants. Secondly, the participants were given instructions on how to take part in the investigation. Thirdly, usability and memorability were measured using an online application in three iterations (initial, after a week, and after two weeks). Lastly, additional data was collected from the participants in the form of an online survey.
3.1 Recruitment Procedure
The study aimed to check the usability and memorability of a brute-force attack-resistant game changer password system, a Layered Battleship GCPS. Thus, the proof-of-concept was developed to check if game changer based graphical authentication systems can be implemented at high enough security levels yet maintain sufficient usability and memorability of the passwords.
For these reasons, we employed snowball sampling (Biernacki and Waldorf,
1981) as a convenience method to obtain a representative sample that we could use to study this phenomenon. We used emails and social media to recruit participants from among authors’ contacts and then to recruit them further or recommend additional participants in our experiment. Our goal was to recruit about 30 participants to avoid some inherent snowball sampling problems and take advantage of its simplicity (Heckathorn,
2002). At the same time, we avoided the time-consuming recruitment of more participants. Since a pilot study is sufficient for proving that the concept is working (or not), we were not inclined to conduct a full-scale usability study typically needed when deploying a more mature solution.
3.2 Participants and Their Profile
Initially, we recruited 44 participants. Since the experiment was designed in three iterations and lasted a total of 14 days, 33 participants successfully completed all three phases ($N=44$ for the 1st phase, $N=39$ for the 2nd phase, and $N=33$ for the 3rd phase). We report the profile for only the participants who completed all stages successfully.
Of our 33 respondents, 10 were female (30.3%), and 23 were male (69.7%). The vast majority of respondents ($n=20$, 60.6%) were between 20–30 years old, 11 (33.3%) were between 31–45 years old, and two (6.1%) were over 46 years old.
The respondents varied in their levels of education. Most respondents (15, 45.4%) had finished some form of college education (12–14 years of schooling), followed by 13 respondents (39.4%) who had completed high school education (12 years of education). Three participants (3%) held a university degree (15+ years of education), and one (3%) participant held a doctorate of science degree. One respondent did not complete their high school education (3%).
We also asked participants about their employment status. The largest group was comprised of employed participants (24, 72.7%), followed by a group of 8 students (24.2%) and one unemployed (3%).
Based on the data from the Statistical Office (SURS,
2020), the population’s male to female ratio is 0.958 to 1, compared to our 2.3 : 1. The educational levels in the population are also much lower than in our sample. In the general population, 22.7% of persons have primary school level or less, 52.8% completed secondary education, and only 24.5% held some college degree or more. 60.7% are active (employed, unemployed) in the population, and 39.3% are inactive, compared to 76%/24% of the sample.
Comparing the descriptive statistics of our sample with the population data, we liberally conclude without any additional statistical tests that the sample is not representative of the population (of Slovenia). As mentioned, the full representativeness of the population was not a requirement for our pilot study. We further discuss this in the limitations section.
3.3 Participants Training and Instructions
An online application was developed for the experiment. The supervision of the experiment flow was implemented through the application’s logic. No additional supervision steps were taken, and no training took place. Because of that, we paid particular attention to the instructions and rules.
Recruitment letters were sent either via email or social media platforms. The rules were outlined in the welcome message sent to the participants. The rules were as follows:
-
– Participants must be of age and have a basic knowledge of using computers.
-
– Participants must have normal or corrected-to-normal eyesight.
-
– Under no circumstances may the password be written down or otherwise stored in digital or physical form.
-
– Text passwords must be different from those used for any other user accounts.
-
– The password must not be associated with their names, surnames, and other personal details, such as dates of important events, places, pet names, friends, and alike.
Descriptions and instructions were provided to the participants via the messages displayed in the online app.
-
– The aim of the study (“studying a novel graphical password scheme”) was briefly explained,
-
– The general scope of the study was provided, revealing that two authentication schemes, classical textual and a novel graphical one, would be compared with Battleship game, and
-
– A general description of the experiment flow was given: “registration” phase (creating textual and two graphical passwords) immediately followed by “measurement” phase (using the created passwords). The participants were told that the experiment would repeat in two steps in the following two weeks without further details. The experiment flow was finished with the participants completing an online survey.
To avoid introducing bias, the participants were not informed of the following details:
-
– The entry of textual and graphic passwords would repeat twice following the initial session (we did inform the participants that they will be asked to take part “sometime later,” but omitted any details),
-
– The exact time lag between iterations would be seven and 14 days from the start of the experiment,
-
– Participants would have to remember the passwords created during the registration phase, both for immediate use and delayed use after 7/14 days,
-
– The input time would be measured for every iteration of each entry,
-
– Each correct and incorrect entry of both types of passwords would be recorded, along with the number of attempts needed to enter the correct password, and
-
– Users would be blocked after the third wrong attempt and notified that they entered the password incorrectly three times (the password is then displayed to the user to remember it for use in the next iteration).
All of the above rules were visible to the participants throughout the entire experiment. Brief instructions for what was expected from the participants in each step were also displayed during the individual stages.
3.4 Ethical Considerations and Mitigation Measures
Due to the involvement of persons and a potential threat to their private data, we considered the ethical issues with great caution.
We required all the participants to be of age (18+). We assured this by personally checking the persons’ names against our knowledge of their age. For participants we did not know in person, we checked their registered names, surnames, and email addresses on the web. We found a person’s company profile, articles, photos, or social media accounts to verify their age for all the participants. We had no means of verifying if their web presence is valid. However, we assessed the risks associated with this as low.
We requested full consent from potential participants before they could enroll in the study. For this reason, we included the instruction text in the messages sent via emails during the recruitment phase and the registration phase. The consent text was clearly visible on the first landing page of the experiment and before the registration. Users had to click the “I consent” button before they were allowed to proceed.
A potential high-impact danger arose from a possibility that a participant would (re)use one of her existing textual passwords to register for our experiment, and such a password would be leaked. For this reason, we explicitly asked the participants to use a novel, never before used password specially crafted for the experiment. However, we had no control over this beyond checking that first and last names do not appear within the password as a substring. We first stored the participants’ passwords in an encrypted form in a database using the AES encryption algorithm and a randomly generated 20-character mixed-type password to mitigate the risk. Secondly, we made sure the server running the app was updated with the latest security patches. The application URL address was not listed anywhere except in the messages sent to the participants who initially agreed to participate. HTML code to avoid indexing by search engines and internet crawlers was included. Thirdly, we logged the access to the database and the server and inspected the access log files daily for any anomalies. None were detected. Lastly, all the passwords were purged on the last day of the experiment. Since the experiment was running on a virtual machine, we de-mounted it and permanently deleted all the associated files. For the entire duration of the experiment, only the second author had access to the server and the application. We assessed the risk of exposing the participants’ passwords as low.
Another low-risk problem was identified with the storage of other personal data, such as the first and last name and email address and the fact that a given person was involved in our study. Here, due to low risk and low impact in the case of a potential breach, we decided not to encrypt the data but to purge it at the end of the experiment. The only data retained was the transaction ID, trial number (how many tries a participant needed), entry type (text/graphical), which password was entered (textual or one of the two possible graphical passwords), the time to enter the password, whether the password was correct, which iteration it was, and the numerical user ID. Sample data is presented in Fig.
3.
Fig. 3
Data retained after the experiment.
The risks and the measures described in this section were presented and fully disclosed to the participants as a part of the consent text.
3.5 Experiment Procedure
The experiment was supported by a web-based application running on a virtual machine within the authors’ domain. The application was developed for desktop and tablet browsers. It was tested using a small group of colleagues for clarity, guidance, input, and other essential aspects of the experiment. Log files were examined to check for any problems. Minor modifications were made to the user interface, and the instructions were written more clearly where potential issues were identified.
The core of the experiment was divided into three iterations. The first iteration started immediately after the participants consented to take part in the study. It was composed of two phases, the registration phase and the replication phase. The other two iterations only consisted of the replication phase; the last iteration also included the final survey. The 2nd and 3rd iterations followed one and two weeks after the initial iteration, respectively. This way, we were able to account for the memory decay associated with forgetting the passwords. The whole experiment procedure is depicted in Fig.
4.
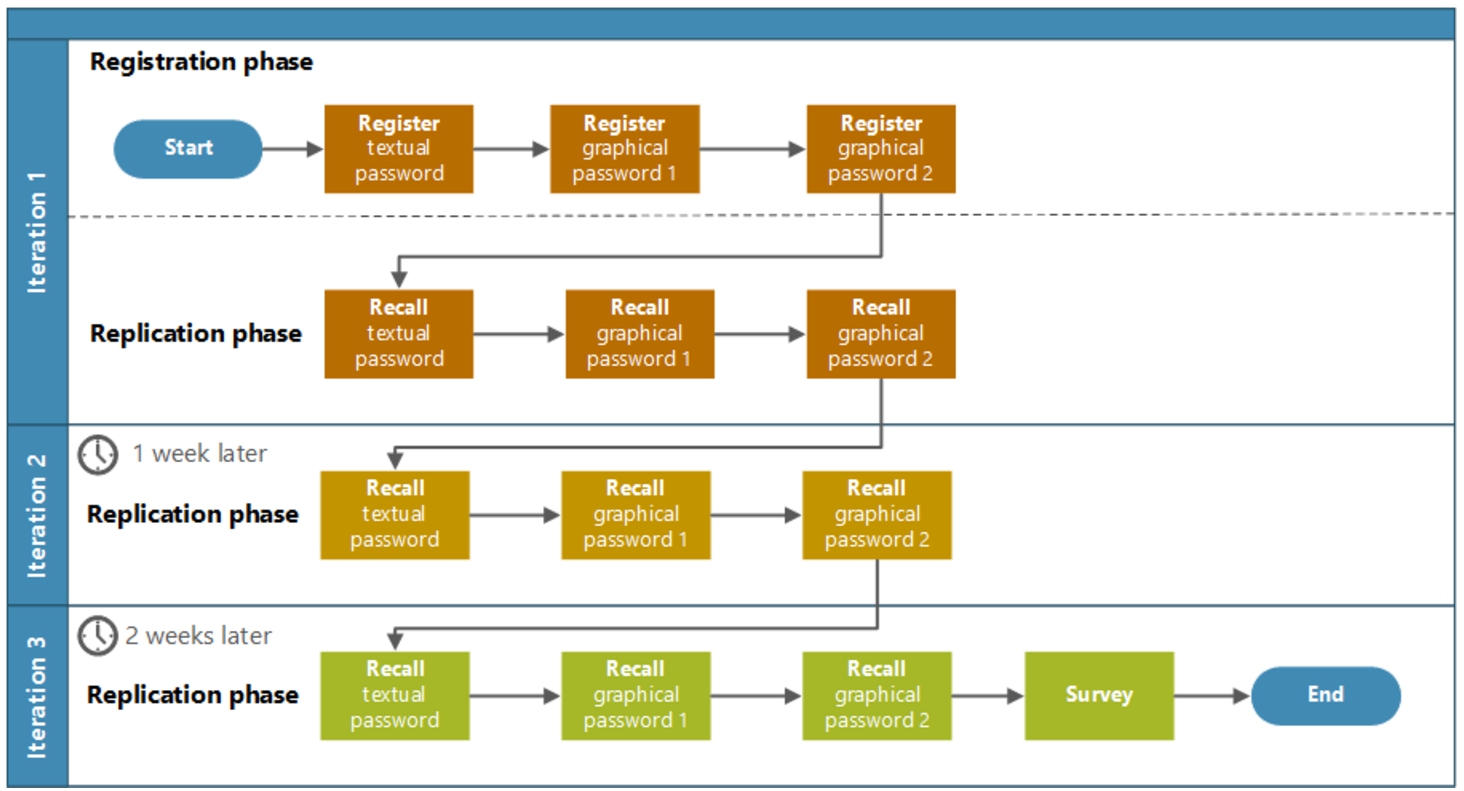
Fig. 4
Process of the experiment.
Each of the phases and iterations was supported by the application logic guiding the participants through the process.
3.5.1 Registration Phase
Step 1: After the consent page, the participant was presented with a registration “home” page where she could initially only click on the “textual password” button. A form with the following fields was to be completed: first name, last name, email address, password, and confirm password. An instruction was presented, warning the user not to select a password associated with any personal details. The password had to consist of 11 characters, including lower and upper case letters, numbers, and a special symbol. The password fields were protected so that only asterisks (*) were displayed when typing. An eye icon (AKIS) was shown on the side of the field to disclose the characters upon clicking.
Entering a password that was not consistent with the composition rules produced a warning, and users were required to comply by repeating the process.
Step 2: A participant was taken to the creation of the first graphical password. As mentioned, Layered Battleship GCPS was designed with two layers, so two graphical passwords needed to be created independently.
Firstly, an empty
$10\times 10$ grid was displayed. To the side of the grid, available ships were shown for the user to choose from (see Fig.
5a). A user first had to click on a boat, then on the grid. Then, the direction of the ship needed to be determined. This was done by moving the mouse in the desired direction (Fig.
5b). Another click fixed the ship and indicated that the ship was used (Fig.
5c). Additional click or a right-click offered a possibility to delete the ship or to change its direction, respectively.
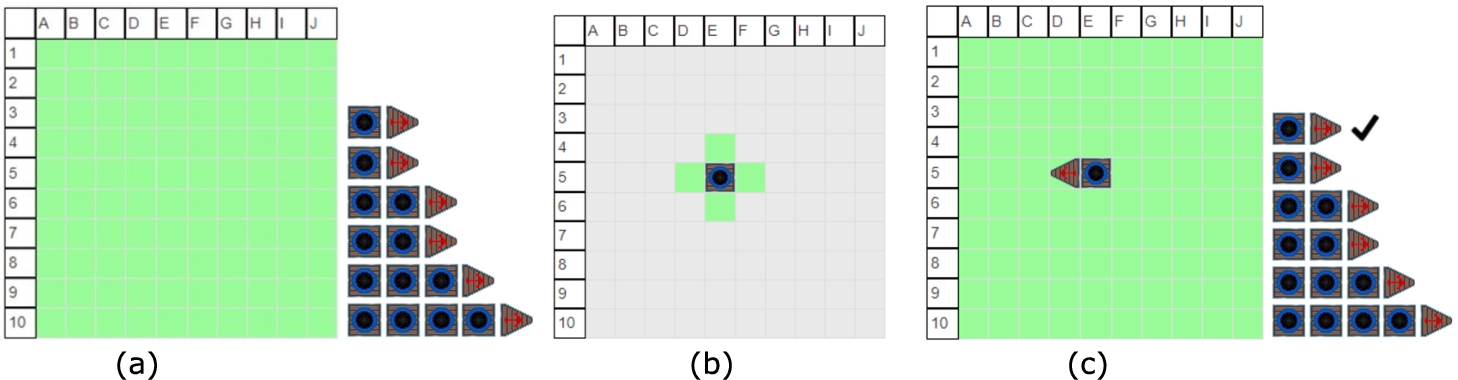
Fig. 5
Creating a password using the Battleship board.
Once all the ships were used, users clicked on the “Register” button, and the registration of the first graphical password was complete.
Step 3: Here, Step 2 was repeated for the second graphical password. The participants were reminded that the second password must be different from the first one. Application logic checked for compliance with this rule.
3.5.2 Replication Phase
The replication phase followed immediately after the registration in the first iteration. This phase required the participants to reproduce (recall from the memory and re-enter) the password they created during the registration phase.
The user interface was the same as in the registration phase, except there was no need for the user to enter their personal details, such as names and email addresses. Minor modifications were introduced, such as the button’s name changing from “Register” to “Login”. Iterations 2 and 3 followed seven and 14 days after the first one, respectively.
During the replication phase, we measured the times needed to recall and enter a password. We had two alternatives to measure the login times. Firstly, they could be measured from when the user starts entering the password (the first click or key pressed) to the moment she clicks to confirm her choice (or hits the enter button). The second option was to time the difference from when the user lands on the website until she finishes logging in.
We decided to measure the time when the user lands on the page to enter either a text or graphic password until the “Login” button is pressed. Firstly, we opted for this method of measuring the time because we wanted to find out how long the whole process of entering a password takes, including recalling the password for a particular type of password. Usually, before entering a password, a user first tries to recall what password she has set before entering it. It is essential to measure the same time for both types of passwords, i.e. from the moment the website is displayed to the user. Secondly, most of the literature, including the original GCPS, used the same measurement method. Hence, our results are comparable to others.
Participants were given three chances to enter the password correctly, simulating the three-and-out rule typically implemented in the operating environment (where an account is locked on a third unsuccessful attempt and the user needs to unlock it using another communication channel). We measured the number of attempts necessary for the participant to enter the password successfully. In the case of three unsuccessful attempts, we displayed the passwords to the participants to remember them for the next iteration, simulating a procedure during which the users can reset their passwords if they forgot the original one.
4 Results and Evaluation of the Layered Battleship Game Changer Password System
During our experiment, we measured two Layered Battleship Game Changer Password System parameters: memorability and usability. The third parameter of a password system, security (resistance against brute force attack), was considered during the design phase (elaborated and presented in Section
2).
The memorability was measured in terms of the percentage of users who successfully authenticated in each iteration. The usability was measured in seconds it took a user to complete the login process, including the password recall from memory. We checked for any differences among participants regarding sex, educational level, and employment status to verify the internal validity of our study. We compared our LB-GCPS to the base scheme, plaintext passwords, and the original GCPS scheme to check for external validity.
4.1 Memorability
The measurements of memorability of textual and graphical passwords are presented in Table
2 and Table
3, respectively.
Table 2
Recall rates for textual passwords.
| Iteration |
Successful in attempt 1 |
Successful in attempt 2 |
Successful in attempt 3 |
Not successful |
Overall success |
| # |
N |
N |
% |
N |
% |
N |
% |
N |
% |
N |
% |
| 1 |
44 |
34 |
77 |
6 |
14 |
1 |
2 |
3 |
7 |
41 |
93 |
| 2 |
39 |
15 |
39 |
7 |
18 |
3 |
8 |
14 |
36 |
25 |
64 |
| 3 |
33 |
15 |
46 |
4 |
12 |
1 |
3 |
13 |
39 |
20 |
61 |
Table 3
Recall rates for graphical passwords.
| Iteration |
Successful in attempt 1 |
Successful in attempt 2 |
Successful in attempt 3 |
Not successful |
Overall success |
| # |
N |
N |
% |
N |
% |
N |
% |
N |
% |
N |
% |
| 1 |
P1: |
35 |
80 |
5 |
11 |
0 |
0 |
|
|
|
|
|
P2: |
37 |
84 |
4 |
9 |
0 |
0 |
|
|
|
|
|
44 |
35 |
80 |
3 |
7 |
0 |
0 |
6 |
14 |
38 |
86 |
| 2 |
P1: |
19 |
49 |
8 |
21 |
8 |
21 |
|
|
|
|
|
P2: |
23 |
59 |
5 |
13 |
10 |
26 |
|
|
|
|
|
39 |
19 |
49 |
5 |
13 |
4 |
10 |
11 |
28 |
28 |
72 |
| 3 |
P1: |
20 |
61 |
5 |
15 |
6 |
18 |
|
|
|
|
|
P2: |
24 |
73 |
3 |
9 |
5 |
15 |
|
|
|
|
|
33 |
20 |
61 |
3 |
9 |
3 |
9 |
7 |
21 |
26 |
79 |
In Table
2 and Table
3, each row corresponds to an iteration. In iteration 1, the replication phase followed immediately after the registration phase, i.e. only a few moments after a participant came up with a password; iterations 2 and 3 followed one and two weeks after the 1st iteration, respectively. In the columns, we list the success rates for each attempt; each user only had three possibilities to enter a password correctly. Additionally, we present the number and the rates of unsuccessful attempts and overall success.
In Table
3, each iteration is represented by three rows. The first two rows show the rates for participants entering the first and the second graphical password, respectively. The third row shows the combined rates of entering both passwords (in)correctly. For example, in iteration 2, attempt 3, out of 39 participants, eight (21%) users correctly entered the first and ten (26%) users, the second password. However, only four users (10%) entered both passwords correctly. Since the LB-GCPS requires both passwords to be entered correctly, the first two lines are only for reference.
Using the Pearson Chi-Square test for associations, we found no significant associations between the recall level and sex (${\chi _{\text{sex}}}(1)=0.002$, $p=0.963$), education levels (${\chi _{\text{edu}}}(4)=2.714$, $p=0.607$), and employment status (${\chi _{\text{emp}}}(2)=0.487$, $p=0.485$) for textual passwords. Similarly, no significant associations were found for the graphical passwords (${\chi _{\text{sex}}}(1)=0.013$, $p=0.911$; ${\chi _{\text{edu}}}(4)=1.640$, $p=0.802$; ${\chi _{\text{emp}}}(2)=4.080$, $p=0.130$).
To check whether the changes in recall rates were significant, we used the Pearson Chi-square goodness-of-fit test or the Fisher’s exact test when the chi-square assumption was violated. For textual passwords, the success rate in the 2nd iteration dropped from 93% to 64%. The drop is statistically significant (${\chi _{\text{it2-it1}}}(1)=50.81$, ${p_{\mathit{exact}}}<0.0005$). In the 3rd iteration, there was a further statistically significant drop to 61% (${\chi _{\text{it3-it1}}}(1)=53.508$, ${p_{\mathit{exact}}}<0.0005$). The drop from the 2nd to the 3rd iteration from 64% to 61% was not statistically significant (${\chi _{\text{it2-it3}}}(1)=0.19$, $p=0.717$). For graphical passwords, only the drop from the 1st to the 2nd iteration from 86% to 72% was statistically significant (${\chi _{\text{it2-it1}}}(1)=7.094$, $p=0.008$). Neither the raise from the 2nd to the 3rd, nor the drop from the 3rd to the 1st iteration was statistically significant (${\chi _{\text{it2-it3}}}(1)=0.792$, $p=0.373$; ${\chi _{\text{it1-it3}}}(1)=1.608$, ${p_{\mathit{exact}}}=0.308$).
Additionally, we checked whether there was any significant memorability advantage of the layered graphical passwords compared to the textual ones. In the first iteration, textual passwords had memorability of 93% compared to 86% of the graphical ones. However, the difference is not statistically significant (${\chi _{\text{t1-g1}}}(1)=3.220$, ${p_{\mathit{exact}}}=0.121$). The same holds for the 64% compared to 72% in the second iteration (${\chi _{\text{t2-g2}}}(1)=1.003$, $p=0.317$). However, in the 3rd iteration, the graphical passwords are significantly more memorable than the textual ones (${\chi _{\text{t3-g3}}}(1)=4.569$, $p=0.033$).
4.2 Usability
The usability measurements in terms of the time needed to enter a password are presented in Table
4. Here, we list the times only for the correct entries. For example, if a participant entered the password unsuccessfully in the first attempt, but succeeded in the second, the first and second attempts’ total time is typically double the average.
Table 4
Times to enter a password (in seconds).
| Entry method |
Iteration #1 |
Iteration #2 |
Iteration #3 |
Average |
| Textual |
15.4 |
16.2 |
14.5 |
15.4 |
| Graphical #1 |
21.1 |
20.2 |
19.3 |
20.1 |
| Graphical #2 |
18.6 |
19.2 |
18.3 |
19.0 |
| Graphical – combined |
41.6 |
39.4 |
37.6 |
39.5 |
| Ratio textual to graphical |
1 : 2.7 |
1 : 2.4 |
1 : 2.6 |
1 : 2.6 |
The average time to enter a textual password using our web application was about 15.4 seconds. For a single graphical password, it was about 20 seconds; for both graphical passwords, it took a participant on average 40 seconds to enter.
We checked whether the average values to enter the passwords are statistically different between the iterations. To decide between the parametric and non-parametric tests, we ran the Shapiro-Wilk test of normality. All nine datasets on time to enter (three iterations per one textual and two graphical passwords) were normally distributed, with statistics running from 0.947 to 0.987 $(p=0.106\dots p=0.953)$.
We first ran ANOVA with repeated measures on the times for textual passwords. A repeated-measures ANOVA with sphericity assumed (based on Mauchly’s test: M(2) = 5.667, $p=0.059$) determined that mean times to enter textual passwords did not differ statistically significantly between time (iteration) points (F(2, 64) = 2.005, $p=0.143$).
The same test on graphical passwords determined that mean times to enter the first graphical password did not differ statistically significantly between time (iteration) points (F(2, 64) = 2.309, $p=0.108$; Mauchly’s test: M(2) = 1.653, $p=0.438$). The same holds for the second graphical passwords (F(2, 64) = 0.582, $p=0.562$; Mauchly’s test: M(2) = 3.114, $p=0.211$).
However, the times to enter textual passwords differed statistically significantly from graphical passwords (F(5, 160) = 10.665, $p<0.0005$; Mauchly’s test: M(14) = 17.473, $p=0.233$). We only checked the difference between the textual and the second graphical password because the latter has lower means.
The results show that entering textual passwords is significantly faster than entering graphical ones by about 20%. The time to enter the passwords did not improve through the iterations, either for textual or graphical passwords.
Importantly, in LB-GCPS, two layers of graphical passwords are used, effectively doubling the time needed to enter the entire password. It is more than twice faster to enter a textual password than a layered graphical one.
4.3 Hotspot Susceptibility
As with the original proposal, we found that the layered battleship GCPS is vulnerable to the hotspot problem. We measured how many times each position was occupied by a graphical element (a ship). Participants were least likely to place their ships on positions spanning rows 4 and 7, columns G and H, and to a lesser extent, rows 3 and 8, and columns I, F and G.
From Fig.
6, it can be seen that participants most frequently have put a graphic element into one of the corners, followed by positions near the corners or on the sides of the board.
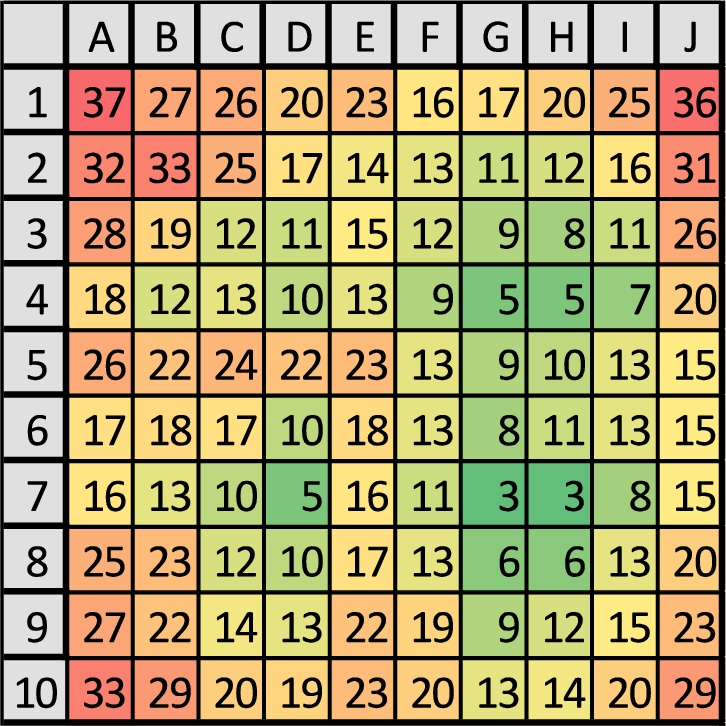
Fig. 6
Heatmap of the distributions of the graphical elements.
To mitigate this problem, a “password checker” would have to be implemented (Vu
et al.,
2007). Such a checker would prevent users from selecting frequent spots and simple passwords (e.g. many pieces in the corners or at the sides, elements arranged in obvious patterns, etc.), that is, from preventing hotspot problems (Thorpe and van Oorschot,
2007). The evidence shows a strong need to implement the password checker; it should not be optional. Other hotspot mitigation strategies such as users’ sociocultural experiences (Constantinides
et al.,
2021) and gamification of the password creation process (Raptis
et al.,
2021) have also been explored in the context of graphical passwords. Future studies should investigate whether and to what extent such findings can be applied to GCPS and other game-based password systems.
4.4 Comparison of LB-GCPS to the Original Chess GCPS
In the original paper, McLennan, Manning, and Tuft proposed a GCPS and presented the results of an experiment with Monopoly and chess as the underlying games. Since the original proposal was vulnerable to brute-force attacks, we only compare our results to the original version with four chess pieces, which is most attack-resilient. They reported an overall recall rate of 83% in the group of younger adults (high school students and older adults performed worse, at 67% and 60%, respectively). Similarly, Tao and Adams report a comparable recall rate of 78% using a single setting of a Chinese game “Go” (Tao and Adams,
2008). Another study investigated chess-based passwords that reported recall rates as high as 100% for passwords of length 8 and more even up to a week after the initial study (Zhu
et al.,
2018). Although the memorability analysis was conducted on a rather small sample, thus limiting the study’s internal validity, the results are nonetheless promising for game-based systems.
The reported recall rate of 83% in the original GCPS is not significantly different from the recall rates in our iterations (I1: ${\chi _{\text{g1-original}}}(1)=0.362$, $p=0.548$; I2: ${\chi _{\text{g2-original}}}(1)=3.531$, $p=0.06$; I3: ${\chi _{\text{g3-original}}}(1)=0.422$, $p=0.516$). The result is interesting because it suggests that remembering more elaborate game settings with more pieces does not necessarily mean a much higher memory burden for the users. The result also shows that layering is not the factor that causes lower recall rates.
What is also noticeable from our measurements is that the recall rates are pretty stable between the iterations, which is also in line with the findings of the original paper.
The recall times in our experiment are also comparable to the “reaction times” reported in the original paper. Our average measured time is about 20 seconds, while their reaction times are reported at between 17 and 27 seconds in the comparable group of younger adults. Again, similar results are reported for the chess-based CMAPS (Zhu
et al.,
2018). However, the comparison must take into consideration different devices used. Our participants used PCs while the original setup employed iPod Touch and iPad Minis (27 and 17 seconds, respectively). Unfortunately, due to original data not being available, we could not run any statistical test to check for the statistical significance of the differences.
However, layering in our experiment effectively doubled the times needed to enter both parts of the graphical password.
4.5 Participants’ Perceptions on Using Graphical Passwords
As mentioned, we surveyed the users $(N=33)$ about their perceptions of using graphical passwords. We firstly asked about the length of their typical mostly used passwords. The responses are worrying: 12 users (36%) used passwords between 5 and 8 characters, 20 users had passwords between 9 and 12 characters long (61%), and only one user used longer passwords.
Next, we asked the users how many times a year they forget their password. There were 22 (67%) who forget their password several times a year, followed by eight (24%) respondents with the answer “at least once a month,”; the remaining three users answered “weekly”, “never”, “several times per month” each. Forgetting a password is thus not a rare occasion.
We wanted to know whether the general requirements to enter the layered graphical and 11-character textual passwords were too demanding. Regarding the layered graphical password, the majority, 26 respondents (76%), replied with “no”, and only the minority, 8 (24%), thought it was too demanding. Interestingly, 21 users (64%) responded that an 11-character password is too high of a demand.
Next, we asked which feature of graphical passwords they liked the most. Out of seven choices, they were able to select three. Most respondents chose memorability (11), followed by innovativeness (9) and simplicity (8). Other possibilities (in order) were: “none of the above”, “speed of entry”, “user interface”, and “applicability for a wider use”.
The final block of questions was about the participants’ impressions on using graphical passwords. We measured their responses using a 5-point Likert scale. Knowing that the answers are ordinal and not scalar, we report the average values for reference only.
Table 5
Participants’ perceptions of using graphical passwords.
|
1 –Completely disagree |
2 –Disagree |
3 – Neither agree nor disagree |
4 – Agree |
5 –Completely agree |
$\overline{x}$ |
|
N |
% |
N |
% |
N |
% |
N |
% |
N |
% |
|
| Not difficult to use |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
21 |
26 |
79 |
4.8 |
| Does not take a long time to enter |
6 |
18 |
11 |
33 |
10 |
30 |
5 |
15 |
1 |
3 |
2.5 |
| Not cumbersome to use |
0 |
0 |
1 |
3 |
4 |
12 |
9 |
27 |
19 |
58 |
4.4 |
| Instructions were clear |
0 |
0 |
0 |
0 |
6 |
18 |
10 |
30 |
17 |
52 |
4.3 |
| Graphical password is easier to remember than textual |
0 |
0 |
2 |
6 |
4 |
12 |
11 |
33 |
16 |
49 |
4.2 |
| User interface was intuitive |
0 |
0 |
0 |
0 |
4 |
12 |
8 |
24 |
21 |
64 |
4.5 |
| Could be used by anyone |
0 |
0 |
1 |
3 |
5 |
15 |
18 |
55 |
9 |
27 |
4.1 |
| Graphical passwords feel safer than textual |
0 |
0 |
0 |
0 |
0 |
0 |
6 |
18 |
27 |
82 |
4.8 |
| Useful |
0 |
0 |
1 |
3 |
11 |
33 |
9 |
27 |
12 |
36 |
3.9 |
| Thrilled |
|
|
3 |
9 |
11 |
33 |
13 |
39 |
6 |
18 |
3.7 |
| Would like to use elsewhere |
4 |
12 |
3 |
9 |
11 |
33 |
12 |
36 |
3 |
9 |
3.2 |
| Would recommend to others |
4 |
12 |
3 |
9 |
16 |
49 |
8 |
24 |
2 |
6 |
3.0 |
Data from Table
5 confirm our measurements and the related work on graphical passwords. The results are pretty in line with findings from McLennan
et al. (
2017). Our participants, too, felt it is not difficult or cumbersome to use graphical passwords, and they liked the user interface. They commended the intuitiveness of the graphical password system, probably because participants are familiar with the underlying game.
However, it takes a long time to enter the password. That is possibly why our participants were not entirely thrilled with the system, would be less likely to use it elsewhere, and recommend it to others.
4.6 Limitations
We paid particular attention to the experimental details during our study to make our results as valid as possible. However, due to the nature of the research and the available resources, the findings have some limitations.
Firstly, the respondents we recruited are not representative of the population. They are younger and more educated and have some experience using authentication schemes. The time to enter either textual or graphical passwords is probably longer in the general population. Nevertheless, our reported times to enter the password are in line with the previous findings (which, in turn, again used a younger-than-population sample).
Secondly, we were comparing the usability and memorability of LB-GCPS against well-established textual passwords. Participants use textual passwords almost daily, and they are well familiar with the user interface. We exposed them to an entirely new authentication scheme with minimal instructions on how to use it. Despite the participants finding the user interface intuitive, it was a new system they needed to adapt to. Hence, usability measurements are biased towards textual passwords due to their widespread use. We can speculate that more prolonged use of graphical passwords would shorten the time to enter them, especially on touch devices.
Thirdly, our results apply only to PC-based settings. Based on our limited resources, we were not able to conduct the research using touch-based devices. The comparisons with the base GCPS scheme on usability are thus not directly applicable. Nevertheless, with about 20 seconds to enter a graphical password, our results are on the same scale as the original and related studies.
Finally, our study mimicked the experimental design of the original proposal by McLennan, Manning, and Tuft. Although this choice was made to increase our external validity by allowing for direct comparisons with the GCPS, the limitations of the original experimental design were also inherited. Namely, we did not investigate all relevant attack vectors, such as smudge and shoulder surfing attacks (Bošnjak and Brumen,
2020), which were empirically demonstrated to be more dangerous for graphical authentication schemes. Future studies should examine the LB-GCPS in the context of these potential security vulnerabilities.
5 Conclusion
The innovative and unique Game Changer Password System, as initially proposed in McLennan
et al. (
2017), was shown to have some security weaknesses and be prone to simple brute force and dictionary attacks (Brumen,
2019). The authors of the initial solution proposed layering to increase brute force and dictionary attack resilience. The layering introduces an additional layer of passwords. If properly implemented, it increases the overall length of a password, and with that, the system’s resilience against the attacks. The authors of the initial proposal have conducted an experiment and have shown that the system produces memorable and useful passwords; however, layering has neither been used nor its effects have been measured. In the present study, we fill this knowledge gap by measuring the impact of layering on the usability and memorability of the proposed graphical-based password system.
The findings regarding memorability are surprising. There is no significantly observable decrease in the recall rate of a layered design. Participants were able to recall two unrelated graphical passwords just as well as a single one. This is a unique finding in the studies of graphical passwords.
Additionally, the recall rate is high, at around 80%, and may still be improved (Woods and Siponen,
2019). This finding is in line with the results of other studies of graphical passwords.
The results regarding usability are expected: because of layering, the amount of time needed to enter two graphical passwords is doubled, from about 20 seconds per single password to about 40 for both. Compared to textual passwords, a single textual password is entered about 20% faster than a graphical. Participants felt that the increased time to enter a graphical password made it much less useful. Hence, they were less likely to use it elsewhere and recommend it to others. However, trust is essential in systems with elevated security requirements (Larriba
et al.,
2021). Namely, users’ motivation is the primary drive to accept a new password system.
Our study has again shown that optimizing the password security–memorability–usability triangle is hard to achieve without compromising one of its cornerstones. This finding is consistent with past studies of graphical and hybrid authentication schemes, which demonstrated that a tradeoff must be made (Nizamani
et al.,
2021). For now, it seems, textual passwords remain at the optimum in general applications.
Nevertheless, game changer password systems are a promising direction. Additional research is needed to find a better balance between the memorability and usability of the game-based passwords and their resilience to brute force and dictionary attacks.
The graphical passwords in general and the GCPS (or LB-GCPS) in particular can be used in special cases in which entry speed is not the primary factor or high resilience against brute-force attacks is not required.

