1 Introduction
The issue of measuring inequality in a system found extensive treatment in the literature. One interesting approach is based on entropic measures. Starting from the pioneering work by Shannon (
1948) on the mathematical theory of communication, the concept of entropy has found a rapid development and diffusion in many scientific communities. Notable examples are statistics (see, e.g. Kullback and Leibler,
1951), statistical mechanics (see, e.g. Jaynes,
1957), economy (see, e.g. Theil,
1967) and ecology (see, e.g. Phillips
et al.,
2006), just to name a few.
Recent efforts have been dedicated mainly to introduce new entropies as the cumulative residual entropy (see, Rao
et al.,
2004) or the cumulative past entropy (see, Di Crescenzo and Longobardi,
2009). In the meantime, and mainly motivated by economic problems, the notion of random entropy has emerged in terms of a normalization of a random process. The random entropy shares the same functional form as the classical entropy but is related to a random process (D’Amico and Di Biase,
2010). This more general entropy was called by the author Dynamic Theil Entropy. Nevertheless, we refer to it as Random Entropy, to avoid any possible misunderstanding with other dynamic entropies which are expressed as deterministic functions as in Di Crescenzo and Longobardi (
2002), Asadi and Zohrevand (
2007) and Calì
et al. (
2020).
The Random Entropy allows to quantify uncertainty in a random system evolving in time and encompasses recent approaches and measures introduced in Curiel and Bishop (
2016). In this paper, we consider the general model considered in a previous work (D’Amico
et al.,
2019) and we present a software that permits the calculation of the inequality in a general system composed by a number of interacting individuals. Any individual moves among several communities in time and according to its membership, and depending on that of the other individuals, produces an attribute. The dynamic of individuals among the communities is described according to a piecewise homogeneous Markov chain which requires the identification of an unknown number of change-points (i.e. where the Markov chain changes its dynamic). Conditional on the occupancy of the communities, the individuals produce an attribute in quantities expressed by a multivariate probability distribution where the dependence structure is managed by a copula function. Finally, using a Monte Carlo algorithm, we show how to compute the moments of the Random Entropy.
The main innovation brought by this research is the building of the software
Randentropy. It contemplates different aspects that were only partially considered in other research papers. Indeed, different studies deal with software and packages related to multi-state models of Markovian type. For example, in Ferguson
et al. (
2012) the authors consider a package for computing marginal and conditional occupation probabilities for Markov and non-Markov multi-state models, including the censoring problem and the use of covariates. In Jackson
et al. (
2011), multi-state models for panel data observed continuously and generally based on the Markov assumption have been instead considered. The possibility to obtain a time-varying model is considered using piecewise-constant time-dependent covariates. Contrarily to these studies, our software gives different transition probability matrices according to the change-point detection methodology presented in Polansky (
2007), which is based only on observations of the Markov process and not on additional covariates. Moreover, once the piecewise homogeneous Markov chain is identified, the software provides sequences of dependent random vectors denoting the ownership of an attribute by the individuals of the system. Thus, the system becomes a multivariate Markov reward process on which the Random Entropy is evaluated. To our knowledge, our software is the only one that computes the Random Entropy and does it in a very general framework that encompasses recent contributions presenting diversity measurement based on (deterministic) entropy where the migration of individuals among the communities is not allowed, see Marcon and Hérault (
2015a). Of potential interest is also the use of the software
Randentropy to problems approached with the traditional concept of entropy, see e.g. Behrendt
et al. (
2019) and Saad and Ruai (
2019).
The subsequent sections of this paper present the general mathematical model, relevant scenarios of application and the software main characteristics, both the CLI (Command Line Interface) and GUI (Graphical User Interface) are described.
2 Theory
The main function driving the development of the software we are presenting here (i.e.
Randentropy) refers to the computation of a measure of inequality on the distribution of a given attribute among a set of
N individuals. The quantity of this attribute depends on a discriminatory criterion, according to whom the individual belongs to a given group. Accordingly to the nomenclature mainly derived within the ecology community, but preserving its general validity also in other domains, we denote the set of individuals as a meta-community that is partitioned in several interacting groups called communities. This description is the same adopted in Marcon and Hérault (
2015b).
Let denote the meta-community by
$\mathcal{C}$ and the number of its members by
N. Each individual
c $\in \mathcal{C}$ belongs, at any time
$t\in \mathbb{N}$, to one of
D different communities that form the meta-community
$\mathcal{C}$. The variable
${x^{c}}(t)$ with values in
$E=\{1,2,\dots ,D\}$ denotes the community to which the individual
c belongs to at time
t. Every time the individual is a member of a given community, it owns a quantity of the personal attribute denoted by
${s^{c}}(t)$. The considered system is stochastic, in the sense that each individual passes through different communities randomly in the course of time and, as a consequence, the personal attributes evolve over time randomly. In this way, the proposed approach is more general as compared to that proposed by Marcon and Hérault (
2015b), where the possibility for members to migrate from a community to another is not permitted.
The sequence of the visited communities by any individual $c\in \mathcal{C}$, that is ${\{{x^{c}}(t)\}_{t\in \mathbb{N}}}$, is assumed to be a realization of a stochastic processes ${\textbf{X}^{c}}:={({X^{c}}(t))_{t\in \mathbb{N}}}$. Thus, the sequences of individual’s attribute, that is ${\{{s^{c}}(t)\}_{t\in \mathbb{N}}}$, evolve randomly, too. We will denote, from now on, the stochastic process describing the evolution of individuals’ attribute as ${\textbf{S}^{c}}:={({S^{c}}(t))_{t\in \mathbb{N}}}$. The processes ${\textbf{X}^{c}}$ and ${\textbf{S}^{c}}$ evolve jointly, meaning that: the evolution of the process ${\textbf{S}^{c}}$ is driven by the stochastic process ${\textbf{X}^{c}}$, which controls it. A precise description of this mechanism follows.
Firstly, we assume an independence assumption between the dynamics of the individuals. Thus, the community process for every individual will be denoted simply by $\mathbf{X}=\mathbf{X}(t)$, and the reference to specific individual $c\in \mathcal{C}$ is dropped.
Moreover, we assume that
$\mathbf{X}=\mathbf{X}(t)$ is distributed according to a piecewise homogeneous Markov chain (PHMC). The process
X is a PHMC taking values in the finite set
E, if a positive number of change-points
k, a sequence
${\tau _{0}}=0<\cdots <{\tau _{k}}$ of increasing times and a sequence
${^{(0)}}\textbf{P},\dots {,^{(k)}}\textbf{P}$ of stochastic matrices (such that for any
$l\in \mathbb{N},l\leqslant k$) exist, it ensues that: for any
$t\in \{{\tau _{l}},\dots ,{\tau _{l+1}}-1\}$ and any
$i,j\in $ E the following Markov property holds:
The symbols ${i_{0:(t-1)}}=({i_{0}},\dots ,{i_{t-1}})\in {E^{t}}$, $X(0:(t-1))=(X(0),\dots ,X(t-1))$ and $\{{\tau _{l}},\dots ,{\tau _{l+1}}-1\}$ represents the time interval, enclosed between the lth and the $l+1$th change-point where the dynamics at community-level are fixed and described by the transition probability matrix ${^{(l)}}\textbf{P}={{\{^{(l)}}{p_{ij}}\}_{i,j\in E}}$.
Intuitively, the term piecewise refers to the existence of some points in time where the dynamic changes consistently. These times are called change-points. They break up the timeline into several sub-periods within whom the Markov process is homogeneous.
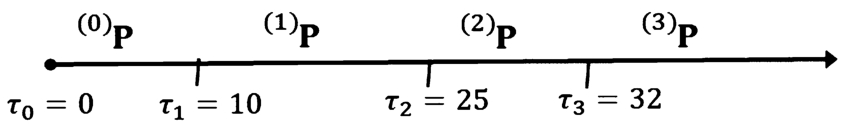
Fig. 1
Example of three change-points.
However, for the sake of clarity of presentation, consider the example illustrated in Fig.
1 where three change-points are considered at times
${\tau _{1}}=10$,
${\tau _{2}}=25$,
${\tau _{3}}=32$. For every time
$t\in \{{\tau _{0}},\dots ,{\tau _{1}}-1\}=\{0,\dots ,9\}$ the dynamic of the process is given by the transition probability matrix
${^{(0)}}\textbf{P}$, thus it results that
$\forall t\in \{0,\dots ,9\}$:
At any time point
t during the interval
$\{{\tau _{1}},\dots ,{\tau _{2}}-1\}=\{10,\dots ,24\}$ it results that
A similar argument applies to the dynamic during the intervals
$\{{\tau _{2}},\dots ,{\tau _{3}}-1\}=\{10,\dots ,24\}$ and
$\{{\tau _{3}},\dots \}=\{32,\dots \}$ where the dynamics are given by the matrices
${^{(2)}}\textbf{P}$ and
${^{(3)}}\textbf{P}$, respectively.
Next step concerns the specification of the processes describing the personal attributes, i.e. ${\textbf{S}^{c}}$. We consider a meta-community where the personal attributes of the individuals can be considered to be dependent among each others.
This strategy is pursued first by assuming that the marginal distributions of the attributes of the individuals allocated in the same community at a given time share the same probability distribution function. Formally, let
${F_{x}}$ be the conditional distribution of attribute
${S^{c}}(t)$ knowing the community
${X^{c}}(t)=x$ of the individual
$c\in \mathcal{C}$, then
where, for a given random variable
A, the symbol
$\mathcal{D}(A)$ denotes its probability distribution.
Before presenting our second main assumption we need to present the concept of copula which will be a key issue in the model and software.
An
N-dimensional copula
C is any function
$C:{[0,1]^{N}}\to [0,1]$, grounded and
N-increasing whose marginals satisfy
From the above definition of the copula, it is understandable that if we consider a set of univariate cumulative distribution functions
${F_{1}},{F_{2}},\dots ,{F_{N}}$, the function
$C({F_{1}},{F_{2}},\dots ,{F_{N}})$ is a multivariate distribution function with marginal distributions
${F_{i}}$,
$i=1,\dots ,N$.
Additionally, a dependence structure is introduced through the application of a copula function. This is formally done advancing the second main assumption stating that: the conditional joint distribution of
$({S^{1}}(t),\dots ,{S^{N}}(t))$ knowing
$({X^{1}}(t)={x^{1}},\dots ,{X^{N}}(t)={x^{N}})$ is given by
where
${C_{\theta }}$ is the copula, with dependence parameter
θ. According to the considered copula function,
θ may also be a vector of parameters.
A notable example of copula function is the Normal (or Gaussian) copula. Let
R be a correlation matrix and denote by
${\Phi _{\mathbf{R}}}$ the standardized multivariate normal distribution with correlation matrix
R. The Gaussian copula is defined according to:
where the vector
$({u_{1}},\dots ,{u_{N}})$ belongs to the unit cube
${[0,1]^{N}}$ and
${\Phi ^{-1}}(\cdot )$ is the inverse of the standard normal cumulative distribution function.
In general, the corresponding density of the copula is
and in the Gaussian case it assumes the well known form
where
${K_{i}}={\Phi ^{-1}}({u_{i}})$, see e.g. Durante and Sempi (
2016).
Here, the parameters are represented by the correlation matrix R.
As we are interested in measuring the inequality of the distribution of attributes in the meta-community, we need to introduce a measure of inequality. In particular, the measure of inequality we consider allows the user to face with stochastic processes. The measure is based on the Theil entropy (see Theil,
1967), closely related to the Shannon entropy (see Shannon,
1948). Given a probability distribution
the Theil index,
$T(\textbf{p})$ of
$\textbf{p}$, is defined as the Kullback–Leibler (KL) divergence
$\mathbb{K}(\textbf{p}|\textbf{u})$ between
$\textbf{p}$ and the uniform distribution
$\textbf{u}$, or equivalently, as the difference between
$\log (N)$ and the Shannon entropy
$\xi (\textbf{p})$. Precisely,
where
$\xi (\textbf{p})=-{\textstyle\sum _{i=1}^{N}}{p^{i}}\log {p^{i}}$. The usual convention that if
${p^{i}}=0$ for some
i, the value of the corresponding expression
$0\log (0)$ is set to be 0, is considered.
The definition of Theil index has been extended for stochastic processes by D’Amico and Di Biase (
2010) and successively applied and further investigated in D’Amico
et al. (
2012) and in D’Amico
et al. (
2014) for an additive decomposition of this index. The random extension of the Theil index is, indeed, introduced.
Let
$s{h^{c}}(t)$ be the share of the attribute held by individual
$c\in \mathcal{C}$ at time
$t\in \mathbb{N}$. It is defined as the proportion of its own attribute
${S^{c}}(t)$ relative to the sum of the attribute over all individuals, i.e.
The vector of shares of attributes at time
t,
$sh(t):={(s{h^{c}}(t))_{c\in \mathcal{C}}}$ defines a probability distribution on the set of countries
$\mathcal{C}$. Note that
$\textbf{sh}:=(sh{(t)_{t\in \mathbb{N}}})$ is a stochastic process that depends on the stochastic processes
${\textbf{S}^{c}}$, controlled by
${\mathbf{X}^{c}}$.
We denote the Random Entropy in the meta-community by the stochastic process
$\textit{DT}(\textbf{sh}(t))$, defined according to the following equation
In this case also, if
$s{h^{c}}(t)=0$ for some
c and
t, the value of the corresponding expression
$0\log (N\cdot 0)$ is set to be 0.
An explicit formula for the expected value of
$\textit{DT}(\textbf{sh}(t))$ has been provided in D’Amico
et al. (
2019). Nevertheless, that formula can only be effectively implemented for small sized meta-communities and number of communities. In the contrary case, a Monte Carlo simulation approach can be successfully implemented. The proposed algorithm simulates repeatedly the trajectories of all individuals according to the underlying Markov model, providing the sequence of communities to which each individual belongs in time. Moreover, the personal attributes are simulated by using the copula function with marginal distribution for each individual dependent on the community of membership. The expected value of the Random Entropy can be estimated by averaging, for each time, over all simulated attributes in the meta-community.
The whole computational procedure is made of several steps, thus, to simplify the readability of the reported pseudocode (see Algorithm
1), we are omitting some of the preliminary tasks, such as: the identification of the number
K and dislocation in time of the change points
${\{{\tau _{k}}\}_{k=1}^{K}}$; the corresponding estimation of the transition probability matrices
${\hspace{0.1667em}^{(l)}}\textbf{P}={\{{\hspace{0.1667em}^{(l)}}{p_{ij}}\}_{i,j\in E}}$; the cdf’s
$\{{F_{x}},x\in E\}$ of attribute depending on the community
x; and the identifiability of the copula function
${C_{\theta }}$. Obviously, the software
Randentropy is designed to solve all the aforementioned tasks, including the implementation of the Monte Carlo algorithm which represents the very last step of the computation.

Algorithm 1
Monte Carlo Simulation of the Random Entropy
For easiness of notation we adopt the following vectorial notation along the Algorithm
1:
-
• $X(t,c)={X^{c}}(t)$ denotes the community to which the individual c belongs to at time t. Thus, $X(\cdot \hspace{0.1667em},\cdot )$ is a matrix whose values are element of E. Its i-th row $X(i,\cdot )$ provides the meta-community configuration at time i, that is, the allocation of the individuals at that time among the communities. Instead, the j-th column of the matrix ($X(\cdot ,j)$) gives the trajectory of the individual j in time, that is, the sequence of communities it visited in time;
-
• $s(t,c)=s{h^{c}}(t)$ denotes the attribute held by individual c at time h. Thus, $s(\cdot \hspace{0.1667em},\cdot )$ is a matrix whose values are non-negative real numbers. Its i-th row $s(i,\cdot )$ provides the share of the attribute owned by the individuals of the meta-community at time i; it represents a probability distribution. The j-th column of the matrix $s(\cdot \hspace{0.1667em},j)$ shows instead the evolution in time of the share of the attribute owned by the individual j;
-
• $DT(t)=\textit{DT}(\textbf{sh}(t))$ denotes the value of the Random Entropy at time t in the meta-community. Specifically, it gives the Theil’s entropy computed on the probability distribution $s(t,\cdot )$ which represents a realization of the Random Entropy in a given simulation;
-
• M denotes the horizon time of the simulation.
The Algorithm
1 generates a vector of observations
$({u_{1}},\dots ,{u_{N}})$ from random variables having Uniform
$U(0,1)$ marginals and sharing the
N-dimensional Copula
${C_{\theta }}$. To do this, first a vector
$({v_{1}},\dots ,{v_{N}})$ is generated from
N independent uniform distributions over
$[0,1]$ and then their conditional distributions are assessed using the copula, in fact the quantity
gives the conditional cumulative distribution function of a uniform random variable
${U_{b}}$ given the values of the previous
$b-1$ variables, i.e.
The computation of
${u_{b}}={C_{\theta }^{-1}}({v_{b}}|({u_{1}},\dots ,{u_{b-1}}))$ produces the number
${u_{b}}\in [0,1]$ that is dependent on
$({u_{1}},\dots ,{u_{b-1}})$. The value
${u_{b}}$ is then used to generate the attribute of individual
b through the inverse of the cumulative distribution function of the specific community to which the individual belongs to at time
h, i.e.
In this way, the resulting individual attributes at any time
h show a dependence to each other which is due to the copula function.
The result of Algorithm
1 is a sequence of values
$\{\textit{DT}(h)\}$,
$h=1,\dots ,M$. Now, if we execute the cited algorithm
L times, we can denote by
$\{{\textit{DT}^{(l)}}(h)\}$,
$h=1,\dots ,M$ the result of the simulation at the
l-th repetition. Then, we are able to provide an estimation of the expected value of the Random Entropy by the average value in the
L simulation, i.e.
4 Computational Details and Applications
The software we are presenting here has been engineered so that the main computational kernel is included in a single python module named
randentropymod (Storchi,
2020). The cited module contains two classes:
randentropykernel and
changepoint. The two classes are devoted to the Markov reward approach computation, and to the change-point estimation, respectively. The full software bundle is then composed by two Command Line Interfaces (CLIs):
randentropy.py and
randentropy_qt.py, and a single Graphical User Interface (GUI) based on PyQt5 Summerfield (
2007) (i.e. the Python binding of the cross-platform GUI toolkit).
While the two mentioned CLIs have been specifically developed to perform separately the Markov reward computation (i.e. randentropy.py) and the change-point estimation (i.e. changepoint.py), the GUI has a wider ability. Indeed, the GUI may be used to perform both the change-point estimation as well as the Markov reward computation, and clearly also to easily visualize and explore the obtained results.
The full software suite has been developed within the Linux OS environment. However, once the needed packages are downloaded and installed, it should work, without restrictions, also under Mac OS and Windows thanks to the intrinsic portability nature of the Python programming language. The Python packages, in addition to the aforementioned PyQT5, strictly needed to run the code are:
Numpy (see Dubois
et al.,
1996) and
Scipy (Jones
et al.,
2001) used to engineered the numerical tasks,
matplotlib for the plots and data visualization (see Hunter,
2007).
4.1 The Randentropykernel Class and Related CLI
As already stated, the
randentropykernel class is devoted to the computation of the Random Entropy which is based on the Markov model with dependent rewards as described in Section
2. The class is made of several methods as the one to specify the community matrix (i.e.
set_community) and the attributes matrix (i.e.
set_attributes), which correspond to the matrices
$X(\cdot \hspace{0.1667em},\cdot )$ and
$s(\cdot \hspace{0.1667em},\cdot )$ used in the algorithm, respectively. There are clearly various methods to tune the computation behaviour such as: set the number of Monte Carlo simulation steps (i.e.
set_num_of_mc_iterations), or the simulated time period
set_simulated_time. Finally, the user has the ability to enable or disable the copula function via the
set_usecopula method, and clearly to perform the main computation calling the
run_computation method. The software makes use of a Gaussian (or Normal) Copula which is probably the most frequently used copula in the applications. Nevertheless, Algorithm
1 is general and holds for any copula function, and since the software is open source, any researcher can adapt it to consider a different copula. Once the computation is completed, the user can retrieve all the results: the first and the second-order moments of the Random Entropy using
get_entropy and
get_entropy_sigma, respectively.
The
randentropy.py is the CLI that is naturally bonded to the mentioned class. As can be seen from Fig.
2, the user has the possibility to specify two input matrices (i.e. to specify both their locations and names): the first one representing the community matrix, while the second is the Attributes one. The mentioned matrices may be stored both on a MatLab file or on a CSV style one.
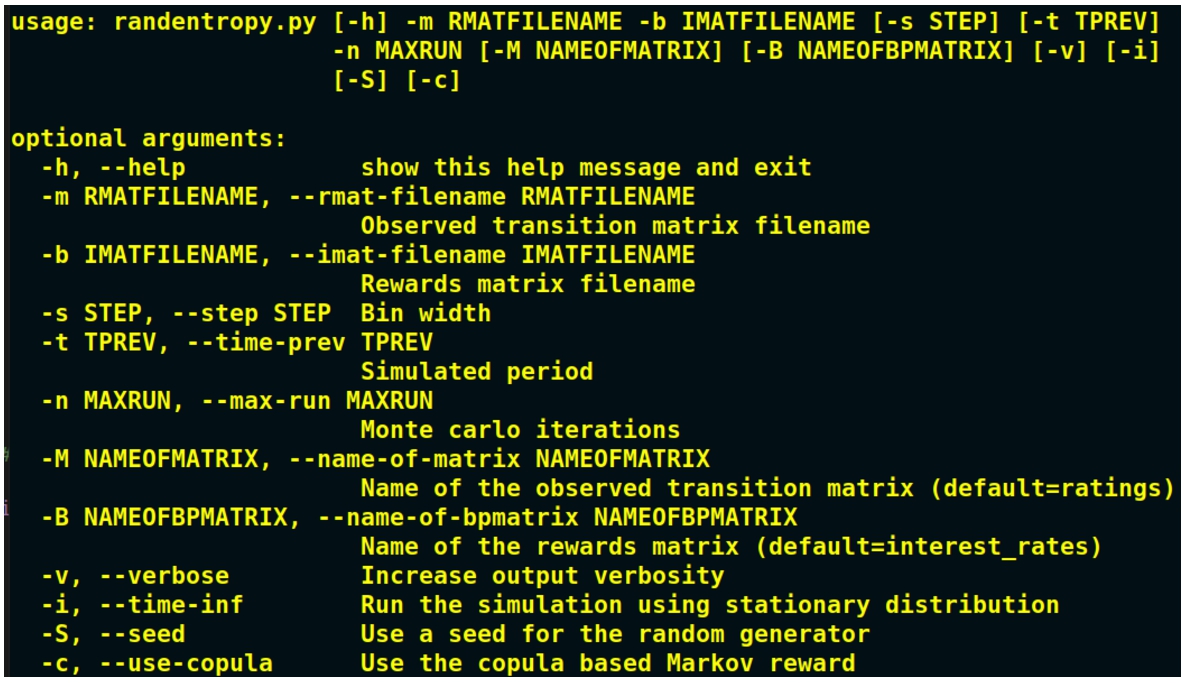
Fig. 2
CLI for the Markov reward approach.
Evidently, the CLI options reported in Fig.
2 reflect the cited
randentropykernel capabilities. Then,
-s allows for the bin width specification, needed to estimate the probability distribution of the attribute given the community membership. Secondly,
-t enables the user to specify the simulated period, and
-n refers to the number of Monte Carlo iterations. Optionally, the
-i flag allows the user to run the simulation after computing the stationary distribution.
It is finally somehow interesting to report here that: in case one wants to perform the simulation using the stationary distribution
π of the Markov chain
$\mathbf{X}=\mathbf{X}(t)$ we need to solve a linear matrix equation
$ax=b$. To solve the given equation one can compute the value of
x that minimizes the Euclidean 2-norm
$\| b-ax{\| ^{2}}$. This has been done by applying a specific function within Numpy libraries (see Dubois
et al.,
1996).
4.2 The Changepoint Class and Related CLI
As already stated within the
randentropymod module there is also the
changepoint class. The cited class, and thus the related CLI, is devoted to detect the position of
k change-points, where
$k=1,2,3$. In particular, the code finds the positions of the change-points by maximizing the likelihood function of the observed trajectories of the members within their communities. At the same time, the Λ test is carried out in order to assess statistically significant differences among the transition probability matrices found. Additional details on this statistical test are available in Polansky (
2007) and D’Amico
et al. (
2019).
The most relevant methods within the class are needed to specify the transition matrix (i.e. set_community) and the number of change-points to be detected (i.e. set_num_of_cps). Once the initial settings have been specified, the main computation starts using the compute_cps method. Finally, the calculated x change-points can be retrieved using the get_cp1_found, get_cp2_found and get_cp3_found, respectively, for the first, second and third change-point.
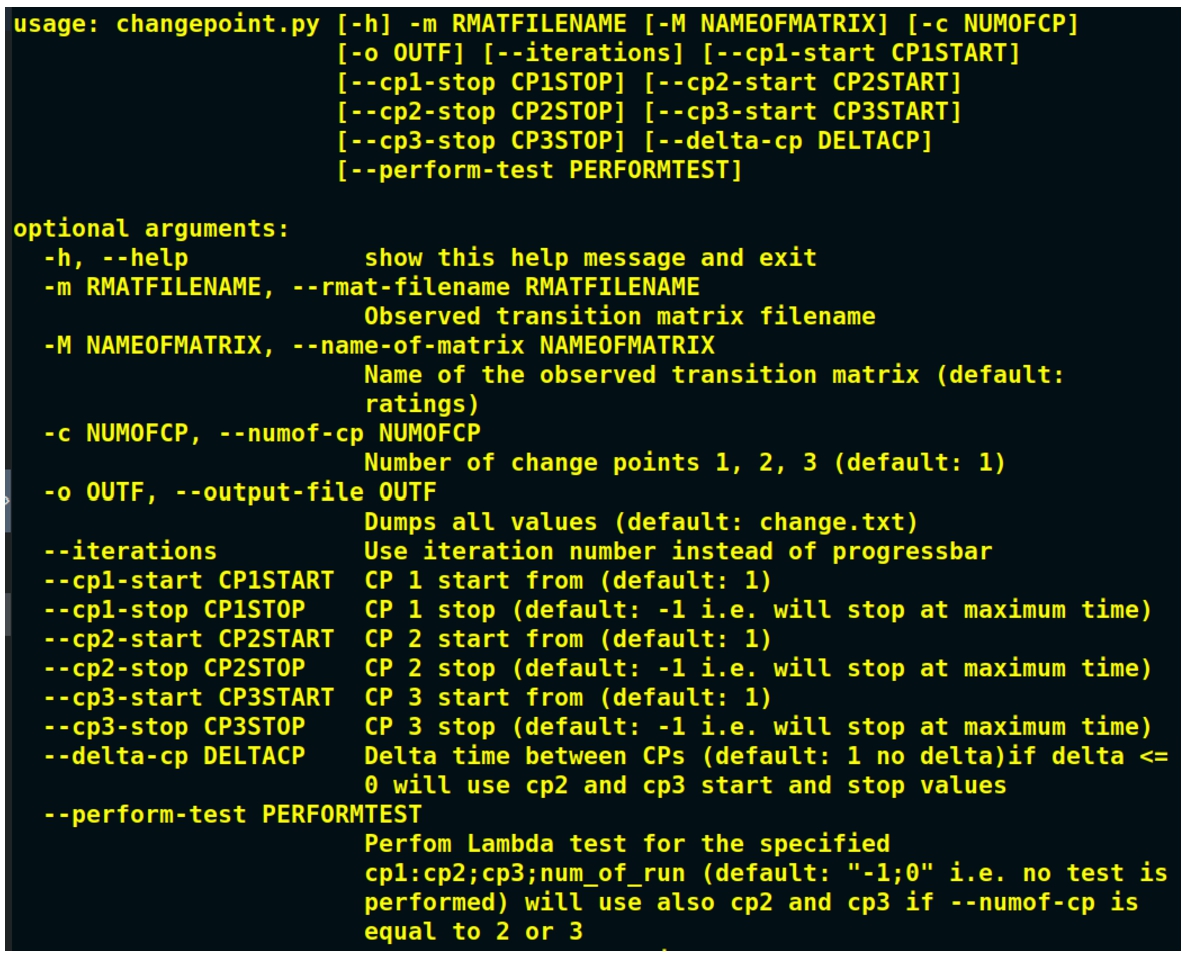
Fig. 3
CLI for change-point detection algorithm.
Once again the CLI options, reported in Fig.
3, as expected, reflect the class capabilities. Thus, to run the code, the input transition matrix has to be specified, in terms of a Matlab or a CSV filename, as well as the matrix name within the file (options
-m and
-M, respectively). The number of change-points to be considered has to be defined as well (i.e. using the
-c option), otherwise the code will run assuming a single change-point. Optionally, an output filename, where all the results are written, can be specified using the
-o/–output-file option.
Finally, we introduced some methods, and clearly the relative CLI options that can be used also to distribute the computational burden among several processes, thus CPUs. Indeed, while working with a huge amount of data it can be convenient to specify a range of time within which the algorithm is carried out, or to use a specific time distance between two change-points. Thus, the user has the ability to define a range of time for the first change-point (the same applies for the others) via the set_cp1_start_stop method. Similarly, using the set_delta_cp method, one can specify the delta time to be considered among the change-points.
4.3 Graphical User Interface
All the previously illustrated functionalities have been integrated also on a GUI (Graphical User Interface). The GUI has been implemented using PyQT5, a comprehensive set of Python bindings for Qt v5 (PyQT,
2012). While we implemented two different CLIs, to fully cover the various aspects implemented within the
randentropymod, the GUI is unique and can be access via the
randentropy_qt.py file (Storchi,
2020).
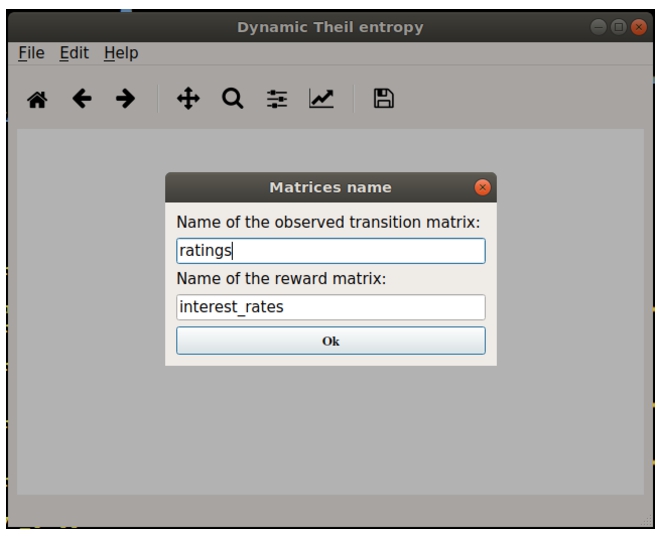
Fig. 4
Dialog to specify the input matrices.
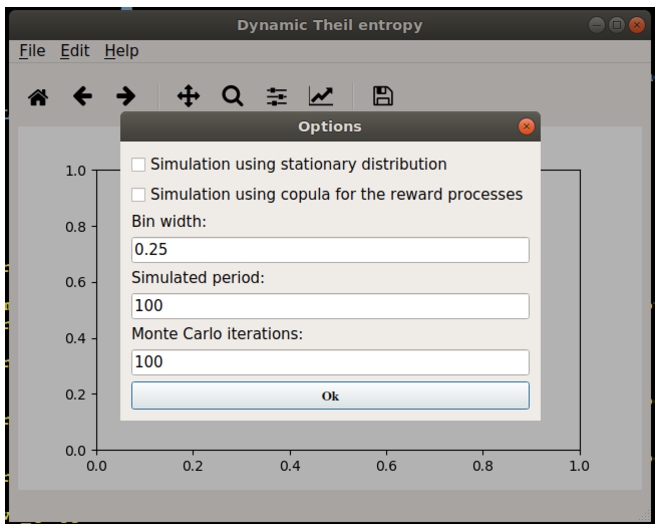
Fig. 5
Dialog to specify the the input parameters related to the Monte Carlo simulation.
The computation starts after choosing an input file, it can be both a Matlab, as well as a CSV, containing two matrices. The first matrix has to contain the data of the variable which is supposed to evolve according to a Homogeneous Markov Chain (HMC) (e.g. in the financial application the variable consists on the sovereign credit ratings, see Section
3.1). As a matter of fact, the first matrix is expected to be named “ratings” by default (see Fig.
4). The second matrix has to refer to the reward process describing the attribute which is driven by the HMC. In the case of the financial application, as illustrated in Section
3.1, this is the credit spread. As the code directly computes the credit spread starting from the interest rates, the second matrix directly collects the interest rate data. Indeed, by default, this matrix within the file is expected to be named “interest_rates” (see Fig.
4).
Once the two matrices have been specified, the user may start the computation:
Edit -> Run. The use is prompted with a dialog window, reported in Fig.
5, where there is the ability to specify: the bin width to estimate the empirical distributions (one for each ordered variable of the first matrix), the simulated period and the number of Monte Carlo iterations.
Alternatively, the user can flag “Simulation using stationary distribution” to compute the asymptotic values of the Random Theil’s Entropy. After clicking the button
OK, the program will start the computation, and when it finishes, it returns the plot of the Dynamic inequality (Fig.
6) that the user has the ability to interact with and to save as a graphical file (i.e. PNG, PDF, PS, and more).
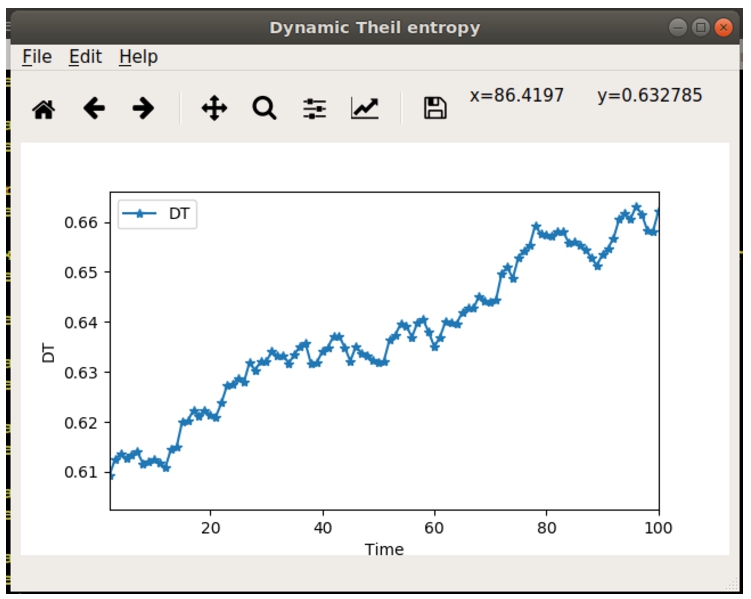
Fig. 6
Output: dynamic inequality.
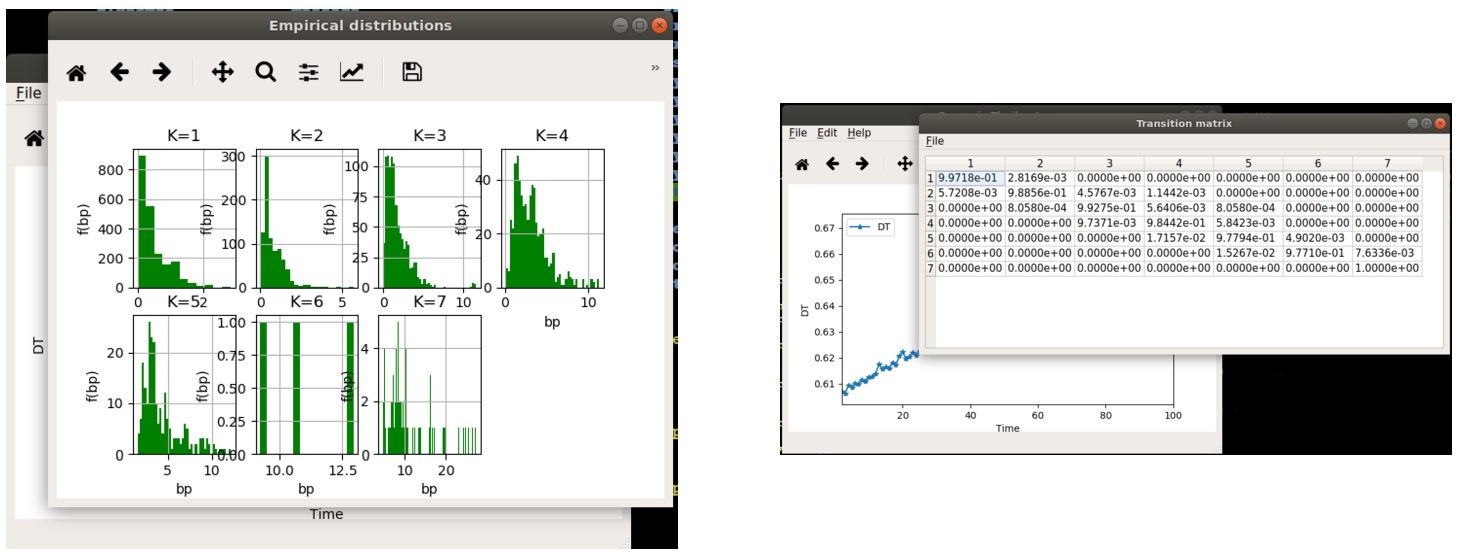
Fig. 7
Histogram of the CS empirical distribution/transition probability matrix.
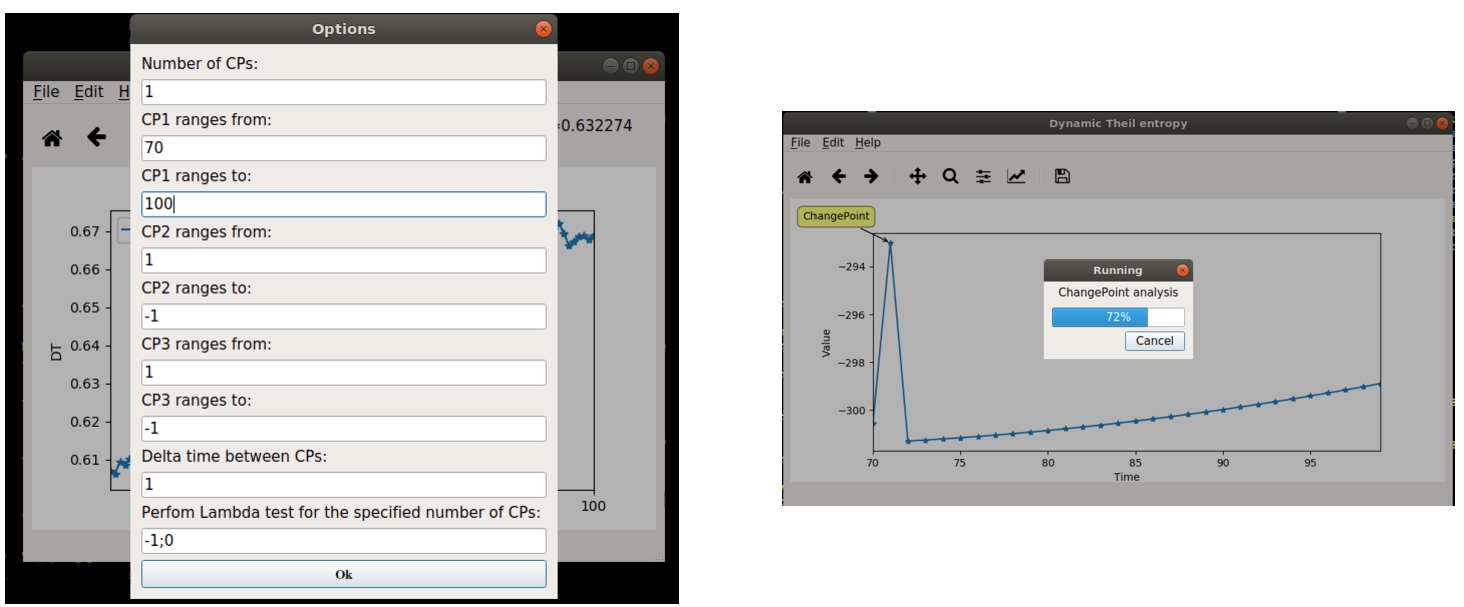
Fig. 8
Options required for change-point detection.
Subsequently, by clicking on
Edit -> Plot CS distributions the user can plot the histograms of the empirical distributions of the attribute. Moreover, by clicking on
Edit –> View Transition matrix the transition probability matrix, estimated on the sequences of visited communities, is shown (Fig.
7).
Finally, with
Edit -> RunChangePoint one can run the change-point detection algorithm. As described for the CLI, the code runs after the specification of: the number of change-points to be detected and the corresponding Λ test (see Fig.
8); the range of time where the algorithm is carried out and, eventually, the distance between two subsequent change-points.
In the case reported in Fig.
8, a single change-point is detected within a range of time spreading between
$t=70$ and
$t=100$.
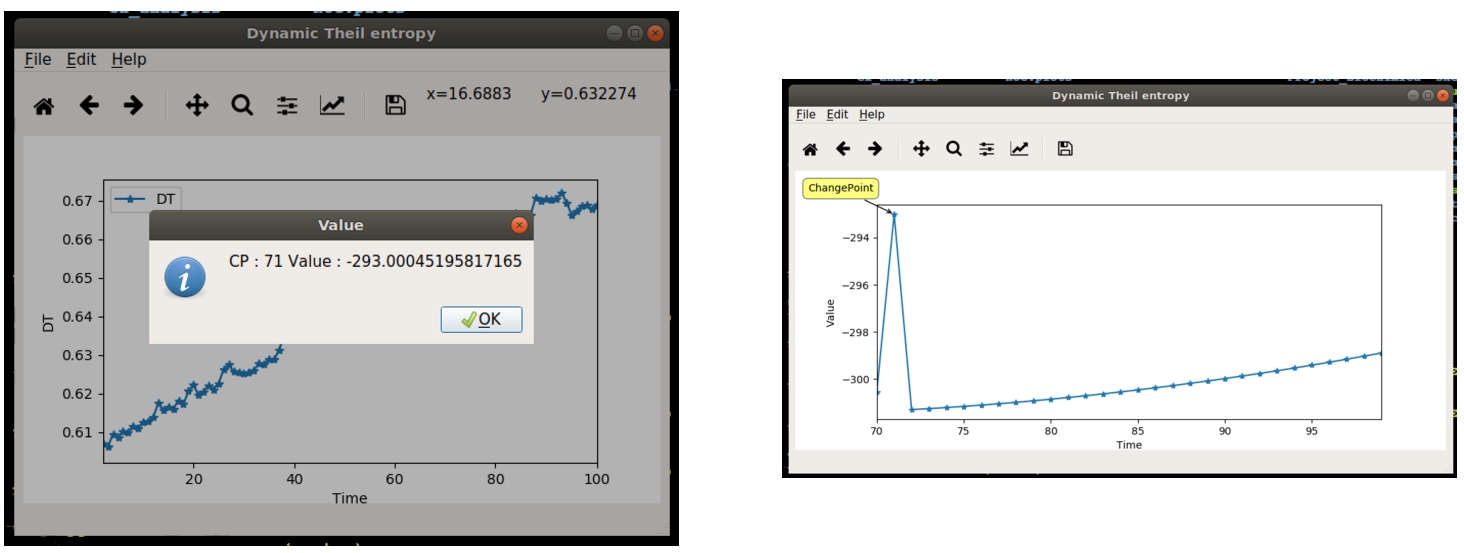
Fig. 9
Output of the change-point detection algorithm.
After confirming the chosen options, the computation starts and the GUI returns the plot of the likelihood function estimated on the community data (see in Fig.
9), together with the value of the maximum likelihood function, and the corresponding position of the calculated change-point. Evidently, also in this case, the resulting plot can be saved into a standard graphical file format.
4.4 Testing Financial Inequality in an Economic Area
Finally, we will show how the described CLIs and GUI can be used to predict the financial inequality in the European Economic Area according to the theoretical model proposed in D’Amico
et al. (
2018a,
2018b). In this specific case, the meta-community coincides with all the countries within the European Community. Thus, each rating class, as assigned by rating agencies, can be seen as a community, in which the countries are allocated at every time step. Clearly, as also already stated in the previous section, the credit spread represents the personal attributes held by each country.
The results we are here reporting have been obtained using the monthly rating, attributed by the Standard & Poor’s agency, to the 26 European countries (UK and Cyprus have been excluded in the current meta-community sample) from January 1998 to December 2016 (see, D’Amico
et al.,
2018a, for extra details on the data-set we are here considering).
To detect the position of a change-point, within the considered horizon time, we compute the maximum value of the likelihood function considered as a function of the position of the change point. Finally, we fix the change point as the value that maximizes the likelihood function. In the proposed software one can use both the
changepoint.py CLI as well as the GUI:
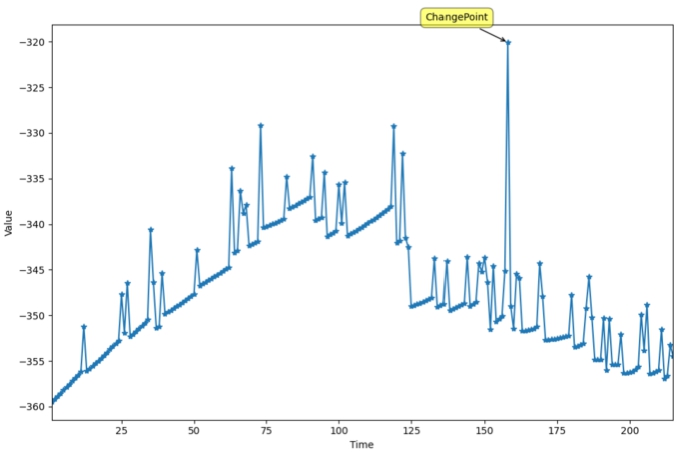
Fig. 10
GUI results for the change-point detection, see text for details.
The result is reported in Fig.
10, where the likelihood function is computed depending on the position of the change point (measured on the
X-axis). The software detects a change-point at time 158 (the maximum value of the likelihood function). The value 158 corresponds to a change point detected in January 2012. Indeed, at the beginning of 2012 the value of the total credit spread in Europe had a peak of about 10.000 basis points (bp) and this growth was driven by the rise of the securities yield of Greece (2.924 bp), Ireland (1.245 bp) and Portugal (1.385 bp), see D’Amico
et al. (
2018b) for more detail about the evolution of financial variables. Similarly, for the interested reader, financial examples with multiple change-points can be found in D’Amico
et al. (
2019)
It is relevant to notice that the software (i.e. the
changepoint.py CLI) also provides an indication related to the choice of the best model as it computes the Bayesian information criterion (BIC) to balance the improvement in the goodness of fit test obtained by increasing the number of the parameters obtained by an increase in the number of change points. Precisely, the BIC is evaluated according to the relation
k is the number of change points,
n is the size of the sample,
D is the cardinality of the state space of the Markov chain, thus,
$D\cdot (D-1)\cdot (k+1)$ is the total number of parameters. The quantity
${\textstyle\sum _{r=0}^{k}}L({\tau _{r}},{\tau _{r+1}})$ is the likelihood function conditional on the estimated change points. The best model can be selected by minimizing the value of the
$\textit{BIC}(k)$ with respect to
k. The application of the BIC to our financial data provides interesting practical results that can be summarized as follows. First, we set
$k=1$ and we obtain a value of the change point equal to 158 months. The corresponding log-likelihood function assumes the maximum value of −320.06 and a BIC equal to 1129.10. Second, we set
$k=2$ to understand if two change points better describe our data. In this case, the optimal change points are identified at times 73 and 119. The corresponding log-likelihood function assumes the maximum value of −311.12 which shows an increasing ability of the model with two change points to fit the data but the BIC value increases to 1623.29. Thus, the model with a single change point was found as the most suitable having least BIC value.
Equivalently, a user can forecast the financial inequality in an economic area and its evolution in time via the
randentropy.py (or the GUI):
where the forecast period has been set to 36 months, using 1000 Monte Carlo simulations. The final result, reported in Fig.
11, shows a similar trend for both the GUI and CLI, with some clear differences related to the implicit randomness of the Monte Carlo procedure (clearly the user can easily avoid this difference selecting a fixed random seed using the – seed option, or equivalently via the
set_use_a_seed method within the
randentropykernel class). The results entail a sharp increase in short-term financial inequality, as measured in term of credit spread, which is expected to persist in the first 10 months of the forecast. Then, the rise is expected to be less pronounced until the reaching of its maximum value around month 20. Immediately afterwards, a slight decrease is expected to be observed.
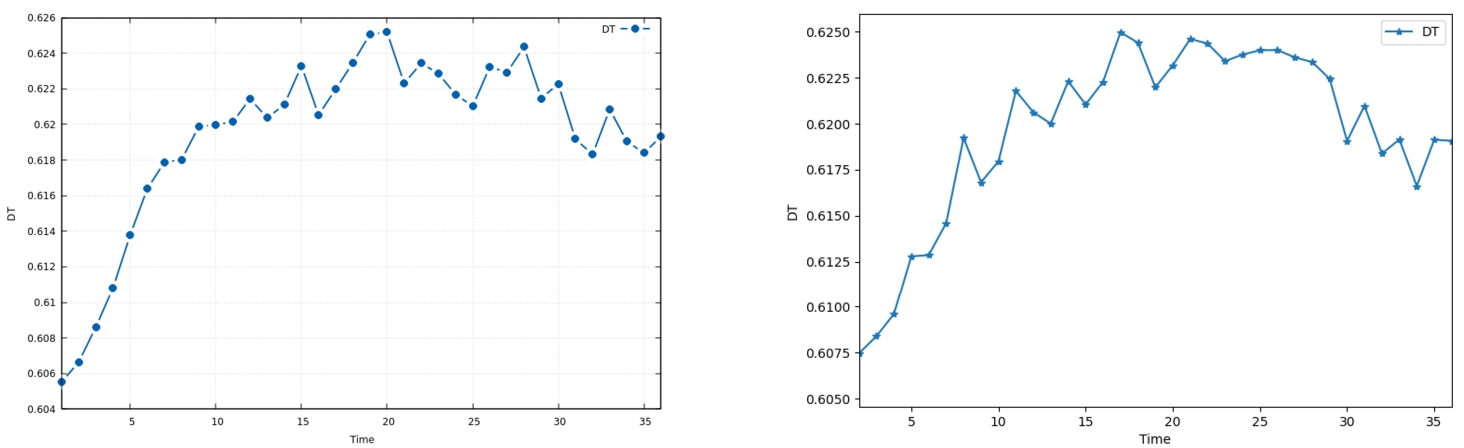
Fig. 11
Random Entropy. Results obtained using the CLI are reported on the left panel, while the ones obtained using the GUI have been reported on the right panel.
As a final remark, it is somehow important to underline that, evidently, a user has the capability of building its own code, to perform the same or similar computations just described, accessing directly the functionalities implemented within the randentropymod Python 3.x module.

