1 Introduction
Spray painting is a technique where a special device is utilized to spray a coating, mainly paint, ink, varnish etc. through the air onto a finished surface. During this operation, compressed gas, usually air is employed to atomize and direct the paint particles towards the surface. It has now become an indispensable process in many industries, like automobile, fabrication, pipe, cookware, aerospace and defense (Haugan,
1974). However, the industrial paint mainly in the form of volatile organic compounds is extremely hazardous to human body after atomization. Airtight spraying room and poor ventilation conditions also make the working environment of manual spray painters extremely deleterious. Manual spray painting also causes non-uniform and imperfect coating, wastage of paint, high cycle time, low flexibility, poor repeatability, difficulty in painting complicated inaccessible part features, etc.
With rapid industrialization and rise in automation, painting robots have gradually evolved out as an effective substitute to manual spray painting operation ensuring reduced human effort with better working environment, increased consistency, higher productivity, increased flexibility, lower power consumption and minimum paint wastage (Muzan
et al.,
2012). The paramount outcome of Industry 4.0 is to select and deploy an intelligent spray painting robot combining massive data, cloud computing, solid safety, intelligent sensors, the Internet of Things (IoT), and other significant technologically advanced features. Digitalization and closed-loop solutions provided by Industry 4.0 would enable the spray painting robots to optimize their painting operations while minimizing the paint used and energy consumed. Furthermore, deploying a suitable spray painting robot in the era of Industry 4.0 would eliminate paint shear, poor finishing quality, recurrent flushing, undesirable downtime, etc. Consequently, the use of digitalization technologies would aid in careful monitoring of paint quality, predicting machine failure and paint lines, resulting in improving performance and efficiency of spray painting robots. Usually, paint robots are of two types, i.e. hydraulic and electronic. Hydraulic robots are robust in construction, offer high load capacity and provide simple solutions for fulfilling explosion-proof standards as power cables to electronic servo motors are eliminated. They are also low cost alternatives to their electronic counterparts. With respect to speed, repeatability and flexibility, electronic paint robots are far superior to hydraulic robots. These electronic robots are highly accurate, and can deliver consistent, seemingly identical results with respect to thickness and uniform coatings. While eliminating the risk of human error, when paired with other automatic painting equipment they can maximize the efficiency of spray painting operation. Although their initial cost is quite high, they require less mechanical maintenance due to their modular design. With the help of suitable software, algorithms, sensors and cameras, they can recognize which parts of the products to paint using right amount of paint for a flawless finish. However, both these paint robot types require proper preventive maintenance and intervention of technically knowledgeable support staff for their operations and selection of some of the specific operational parameters. For spray painting operation, a five or six-axis (degree of freedom) robot capable of complex arm and wrist motions is usually preferred. Among these axes, three are for the base motions and the remaining are for applicator orientation (Gujela
et al.,
2015). Degree of freedom is the number of independent parameters needed to completely specify the configuration of a mechanism. The number of axes configured in a robot is directly related to its degree of freedom. For a simple straight-forward operation, like material handling or pick-n-place task, a simple four axis robot is sufficient. However, if its application is constrained within a small confined space with its arm requiring a lot of twisting and turning, a six axis robot would be a good choice. The number of axes thus depends on its application. More axes provide better flexibility, provided that the cost permits. Hence, while considering and solving an industrial robot selection problem, the most important decision is to evaluate what kind of applications and what kind of processes the robot is used for.
In order to fulfill the requirements of present-day manufacturing industries, selection of spray painting robots has now become much varied due to availability of plenty of alternatives with varying configurations and complexities. Sometimes, the end users are so fascinated with a particular robot that they do not examine whether the required parts can be painted more quickly and inexpensively with a less costly alternative. Many a time, a robot is selected for a painting operation without sufficient analysis of the application requirements. Thus, while selecting a robot for a given painting task, due consideration needs to be provided on its various specifications and capabilities, like space requirement, ability to paint dissimilar parts at high production rate, speed, purchase cost including additional expenses of integrating it into the paint system, cycle time, simplicity of programming, repeatability, work envelop, payload, mechanical weight, etc. (Khouja and Offodile,
1994). Thus, it can be propounded that identification of the most appropriate robot from a pool of available alternatives with respect to a set of conflicting evaluation criteria resembles a typical multi-criteria decision making (MCDM) problem (Tashtoush
et al.,
2015; Bader and Rahimifard,
2020). In this paper, a spray painting robot selection problem for an automobile industry is solved while integrating step-wise weight assessment ratio analysis (SWARA) and combined compromise solution (CoCoSo) methods. Based on the opinions of a group of decision makers, subjective weights assigned to the considered criteria are estimated using SWARA method, while CoCoSo method helps in deriving the ranking order of the alternative spray painting robots for the given task.
This paper is organized as follows: Based on the literature review, the corresponding research gap is identified in Section
2. Section
3 provides the mathematical details of SWARA and CoCoSo methods. A real-time spray painting robot selection problem is solved in Section
4 along with a comparative analysis of the ranking performance of SWARA-CoCoSo method against other integrated MCDM techniques. Conclusions are drawn in Section
5.
2 Survey of the Literature
It has already been mentioned that selection of a spray painting robot from an array of alternatives available in the market for a given painting task is a typical MCDM problem. Presence of conflicting evaluation criteria (like high speed with low power consumption, high efficiency with reduced initial capital investment, etc.) often makes this problem more complex. Due to availability of a large number of MCDM techniques and ardent need to accurately resolve this problem, solving robot selection problems for diverse industrial applications with the help of MCDM techniques has already caught the interest of the past researchers. Table
1 provides a list of different MCDM techniques applied for industrial robot selection along with the corresponding evaluation criteria and weight measurement techniques considered.
It is interestingly noticed that a plethora of MCDM techniques, like weighted sum method (WSM), weighted product model (WPM), weighted aggregated sum product assessment (WASPAS), multi-objective optimization on the basis of ratio analysis (MOORA), multiplicative MOORA (MULTIMOORA), simple multi-attribute rating technique (SMART), analytic hierarchy process (AHP), technique for order of preference by similarity to ideal solution (TOPSIS), VIKOR (Vlse Kriterijumska Optimizacija I Kompromisno Resenje), elimination et choice translating reality (ELECTRE), graph theory and matrix approach (GTMA), preference ranking organization method for enrichment evaluation (PROMETHEE), grey relational analysis (GRA), range of value (ROV), polygons area method (PAM), complex proportional assessment (COPRAS), additive ratio assessment (ARAS), evaluation based on distance from average solution (EDAS), TODIM (TOmada de Decisao Interativa Multicriterio), multi-attributive border approximation area comparison (MABAC), etc. have been adopted in this direction.
The AHP and best worst method (BWM) are the subjective techniques, and entropy method and criteria importance through intercriteria correlation (CRITIC) are the objective techniques mainly deployed for assigning relative importance to the considered robot selection criteria. It can be noted from Table
1 that those MCDM tools have principally been applied to identify industrial robots for pick-n-place (while avoiding certain predefined obstacles), assembly, arc welding and packaging operations. Robots have also been selected to provide support during milling and numerical control machining operations.
Table 1
A comprehensive list of past researches on industrial robot selection.
| Author(s) |
Application |
Criteria |
Weight measurement |
MCDM |
| Chatterjee et al. (2010) |
Pick-n-place operation |
Load capacity, maximum tip speed, repeatability, memory capacity, manipulator reach, velocity, vendor’s service quality, program flexibility, cost |
AHP, subjective judgment |
VIKOR, ELECTRE |
| Athawale and Chakraborty (2011) |
Pick-n-place operation |
Load capacity, repeatability, maximum tip speed, memory capacity, manipulator reach |
AHP |
WSM, WPM, AHP, TOPSIS, GTMA, VIKOR, ELECTRE, PROMETHEE, GRA, ROV |
| Rehman and Ahamri (2013a) |
Packaging |
Velocity, load capacity, repeatability, program flexibility, purchase cost, installation cost |
AHP |
ELECTRE |
| Athawale et al. (2012) |
Pick-n-place operation |
Load capacity, maximum tip speed, repeatability, memory capacity, manipulator reach, velocity, cost, vendor’s service quality, program flexibility |
AHP |
VIKOR |
| Rehman and Ahamri (2013b) |
Packaging |
Velocity, load capacity, repeatability, program flexibility, purchase cost, installation cost |
AHP |
TOPSIS |
| Azimi et al. (2014) |
NC machine support, pick-n-place operation |
Cost, handling coefficient, load capacity, repeatability, velocity, maximum tip speed, memory capacity, manipulator reach |
AHP |
WSM, WPM, TOPSIS, VIKOR, PAM |
| Omoniwa (2014) |
Pick-n-place operation |
Repeatability, load capacity, maximum tip speed, memory capacity, manipulator reach, cost, handling capacity, velocity |
– |
GRA |
| Sen et al. (2015) |
Pick-n-place operation |
Velocity, load capacity, cost, repeatability, maximum tip speed, memory capacity, manipulator reach |
AHP |
PROMETHEE-II |
| Karande et al. (2016) |
Pick-n-place operation |
Load capacity, repeatability, maximum tip speed, memory capacity, manipulator reach, cost, handling coefficient, velocity |
AHP |
WSM, WPM, MOORA, WASPAS, MULTIMOORA |
| Sen et al. (2016) |
Pick-n-place operation |
Load capacity, repeatability, maximum tip speed, memory capacity, manipulator reach, velocity, cost |
AHP |
TODIM |
| Breaz et al. (2017) |
Milling |
Load capacity, reach, weight, repeatability, power consumption, dexterity, service |
AHP |
AHP |
| Mathew et al. (2017) |
Pick-n-place operation |
Load capacity, repeatability, maximum tip speed, memory capacity, manipulator reach |
AHP |
WASPAS |
| Mondal et al. (2017) |
Pick-n-place operation |
Load capacity, repeatability, maximum tip speed, memory capacity, manipulator reach |
AHP |
COPRAS |
| Simion et al. (2018) |
Arc welding |
Motion, repeatability, allowable loading moment, payload, robot mass, reach, power rating, cost, flexibility |
AHP |
AHP |
| Yalçin and Uncu (2019) |
Manufacturing Pick-n-place operation |
Load capacity, repeatability, vertical reach, degree of freedom, maximum tip speed, memory capacity, manipulator reach, man-machine interface, program flexibility, vendor’s service contract, cost |
AHP |
EDAS |
| Suszyński and Rogalewicz (2020) |
Assembly |
Lifting capacity, weight, working range, repeatability, range of movement, cost, velocity |
AHP |
AHP, TOPSIS, SMART |
| Agarwal et al. (2021) |
Arc welding |
Payload, horizontal reach, vertical reach, repeatability, weight, power rating, cost, flexibility, safety, welding performance, maintainability, ease of programming |
Entropy |
MABAC |
| Goswami et al. (2021) |
Pick-n-place operation |
Velocity, load capacity, cost, repeatability, maximum tip speed, memory capacity, manipulator reach |
CRITIC |
TOPSIS-ARAS, COPRAS-ARAS |
| Rashid et al. (2021) |
Manufacturing |
Load capacity, repeatability, velocity ratio, degree of freedom |
BWM |
EDAS |
| Chodha et al. (2021) |
Arc welding |
Mechanical weight, repeatability, payload, maximum reach, average power consumption |
Entropy method |
TOPSIS |
| This paper |
Spray painting |
Payload, cost, repeatability, speed, reach, robot mass, power consumption |
SWARA |
CoCoSo |
The review of literature in Table
1 reveals that until date, no endeavor has been put forward by the past researchers in identifying candidate robots for spray painting operations in manufacturing industries. On the other hand, applications of SWARA as a subjective criteria weight measurement tool and CoCoSo as a ranking tool for alternatives have not been explored towards industrial robot selection. There is also a lack of studies related to comparative analysis of different MCDM techniques while solving industrial robot selection problems. Athawale and Chakraborty (
2011) only exhaustively compared the ranking performance of various MCDM techniques, like WSM, WPM, AHP, TOPSIS, GTMA, VIKOR, ELECTRE, PROMETHEE, GRA and ROV for an industrial pick-n-place robot selection problem. Keeping in view the identified research gaps, this paper proposes an integrated application of SWARA and CoCoSo methods for identifying the most suitable robot for spray painting operations in an automobile industry.
While solving a given MCDM problem with m alternatives and n evaluation criteria, both AHP and SWARA methods can subjectively estimate the corresponding criteria weights. They employ pair-wise comparisons to express relative importance of the decision making elements in a hierarchy, which is known as comparative importance of average value in SWARA method. The AHP method requires a significantly large number of pair-wise comparisons against SWARA method, which has a relatively small, i.e.
$(n-1)$ comparisons. Thus, for a high-dimensional problem, in AHP method, the number of pair-wise comparisons proportionately increases, adversely influencing consistency of the derived solutions. But AHP method employs an effective procedure to check consistency of the pair-wise comparisons, which helps in identifying biasness in decision making. The SWARA method does not have such a procedure. In AHP method, for performing pair-wise comparisons, a 9-point scale is usually adopted. On the contrary, in SWARA method, the decision makers have more freedom to express their judgments using a wider scale (any value between 0 and 1). A smaller number of pair-wise comparisons and easiness in expressing judgments along with its capability to rank criteria and determine their weights makes SWARA a more demanding approach in prioritizing sustainability assessment indicators of energy system (Zolfani and Saparauskas,
2013) and failures in solar panel systems (Ghoushchi
et al.,
2020), solving personnel selection problem (Karabašević
et al.,
2015), assessing sustainable third party reverse logistic provider (Mishra and Rani,
2021), selecting landfill site (Majeed and Breesam,
2021), etc. On the other hand, CoCoSo method integrates WSM and WPM methods to determine sum of weighted comparability sequence and power of weighted comparability sequence while deriving an aggregated performance score for ranking of the alternatives under consideration. It has found successful applications in solving supplier (Yazdani
et al.,
2019a) and cloud service provider (Lai
et al.,
2020) selection problems, and studying machinability properties of graphene nanocomposites (Kumar and Verma,
2021). In this paper, the effectiveness of SWARA-CoCoSo method in solving spray painting robot selection problem in real-time manufacturing environment is validated using Spearman’s rank correlation coefficients against SWARA-TOPSIS, SWARA-VIKOR, SWARA-COPRAS, SWARA-PROMETHEE and SWARA-MOORA methods. Similarly, its effectiveness is also proved with respect to AHP-CoCoSo, PIPRECIA (pivot pairwise relative criteria importance assessment)-CoCoSo, BWM-CoCoSo and FUCOM (full consistency method)-CoCoSo techniques. The SWARA-CoCoSo approach has already been adopted in solving location selection problem for logistics center (Ulutaş
et al.,
2020), renewable energy resource selection problem (Rani
et al.,
2021), identifying barriers for adoption of IoT in manufacturing sector (Cui
et al.,
2021), etc.
4 Spray Painting Robot Selection Using SWARA-CoCoSo Method
In order to apply SWARA-CoCoSo method in solving an industrial spray painting robot selection problem, 12 alternative robot models from six different manufacturers are considered here. They all have six degrees of freedom. Their operational performance is then assessed with respect to seven evaluation criteria, i.e. payload (P) (kg), mechanical weight (M) (kg), speed (S) (m/sec), repeatability (RE) (mm), reach (RC) (mm), cost (C) (USD) and power consumption (PC) (kVA). Among them, P, S and RC are beneficial attributes having their higher values, while M, RE, C and PC are non-beneficial (cost) attributes requiring their lower values. Payload is the weight including weight of the end arm tooling and weight of the product (spray gun and paint) that a robot can lift. Although its higher value is always recommended, its extreme value may adversely affect the performance of a robot by slowing down its speed and increasing the cycle time. Choosing a robot not only depends on its payload, but also it requires a comprehensive consideration of other important criteria. Robot’s own mechanical weight plays an important role when it needs to be mounted on a conveying system for automated spray painting operation. Excessive payload and higher mechanical weight increase the inertia of a spray painting robot, abating its performance. Speed can be defined as the rate at which the spray painting operation is performed and is directly related to the productivity of the robotic system. Speed mainly depends on the cycle time that the given task needs to complete with due consideration of both acceleration and deceleration of a robot from one point to another. Repeatability is the capacity of a robot to consistently perform the same task with minimum deviation. It ensures defect-free painting of the components/parts. Generally, its value between 0.02 mm and 0.05 mm is highly desirable. If the application process is relatively rough, such as packaging, palletizing, etc., the robot needs not to have high precision. Reach can be defined as the distance from the centre of a robot to the fullest extension of its arm, determining the work envelop of a given robot. Cost is related to the total capital invested for procurement of a robot for a specific painting task and power consumption measures the total electric power required to operate it. Lower power consumption provides cost savings as it is treated as an input to the device. Table
2 provides the initial decision matrix, consisting of 12 alternatives and seven criteria, considered in this paper for solving the spray painting robot selection problem using SWARA-CoCoSo method. The information regarding the technical specifications of the considered spray painting robots is collected from the catalogues/websites of the concerned robot manufacturers.
Table 2
Spray painting robot alternatives and evaluation criteria.
| Alternative |
Criteria |
| Manufacturer |
Model |
P |
M |
S |
RE |
RC |
C |
PC |
| Kawasaki |
KF121 |
12 |
770 |
1.2 |
0.5 |
2668 |
52186 |
5.1 |
|
KJ264 |
15 |
540 |
1.5 |
0.5 |
2640 |
58137 |
7.3 |
|
| ABB |
IRB 5500-22 |
13 |
780 |
1.4 |
0.15 |
2975 |
20167 |
6.2 |
|
IRB 5510 |
13 |
767 |
1.4 |
0.15 |
2600 |
12550 |
5.3 |
| YASKAWA |
Motoman MPX-3500 |
15 |
590 |
2 |
0.15 |
2700 |
39000 |
3 |
|
Motoman EPX-2800 |
20 |
650 |
2 |
0.5 |
2779 |
44000 |
5 |
| Haosheng |
HS-6-1722 |
20 |
220 |
2 |
0.06 |
1722 |
54000 |
4.4 |
|
HS-6-1640 |
10 |
185 |
2 |
0.05 |
1640 |
50000 |
5.7 |
| Fanuc |
P-250iB/15 |
15 |
530 |
1.8 |
0.2 |
2800 |
22500 |
4.4 |
|
P-350iA/45 |
45 |
590 |
1.8 |
0.1 |
2606 |
25000 |
3.1 |
| Yooheart |
HY1010A-143 |
10 |
170 |
1.6 |
0.06 |
1430 |
23000 |
3 |
|
HY1050A-200 |
50 |
520 |
1.6 |
0.08 |
2000 |
25000 |
8 |
To estimate subjective weights of the considered criteria using SWARA method, they are first sorted with respect to their expected relative significance based on unanimous opinions of a group of decision makers while fulfilling the basic requirements of spray painting operation. Three experts were called for meetings, and after mutual discussion and brainstorming, relative significances of the considered criteria were estimated. The first expert is a managing director having 25 years of administrative experience in spray painting division of a large aerosol company. The second expert is a quality control manager with 12 years job experience in powder coating quality control. On the other hand, the third expert is a project manager and has more than 15 years experience in managing paint and wall covering functions on contracts and product submittals. Among these criteria, maximum importance is assigned to the procurement cost of a spray painting robot, followed by its payload capacity. On the other hand, mechanical weight of the robot has the least significance. Thus, the order of preference for the evaluation criteria is set as
$\text{C}\to \text{P}\to \text{PC}\to \text{RE}\to \text{RC}\to \text{S}\to \text{M}$. Table
3 depicts the criteria weight calculations using SWARA method. In this table, the concerned group of decision makers expresses the relative importance of
jth criterion in relation to
$(j-1)$th criterion, leading to the estimation of comparative importance of average value
$({s_{j}})$. Now, using Eqs. (
3)–(
4), values of coefficient
$({k_{j}})$ and recalculated weight
$({q_{j}})$ are respectively calculated. Finally, the relative criteria weights are computed applying Eq. (
5). It can be unveiled that according to the set preference order of the criteria, C has the maximum priority weight, followed by P, while M is the least important criterion.
Table 3
Calculation of criteria weights using SWARA method.
| Criteria |
${s_{j}}$ |
${k_{j}}$ |
${q_{j}}$ |
${w_{j}}$ |
| C |
|
1 |
1.00 |
0.28 |
| P |
0.4 |
1.4 |
0.71 |
0.20 |
| PC |
0.35 |
1.35 |
0.53 |
0.15 |
| RE |
0.25 |
1.25 |
0.42 |
0.12 |
| RC |
0.2 |
1.2 |
0.35 |
0.10 |
| S |
0.15 |
1.15 |
0.31 |
0.09 |
| M |
0.1 |
1.1 |
0.28 |
0.08 |
Table 4
Ranking of spray painting robots using SWARA-CoCoSo method (for $\lambda =0.5$).
| Model |
${S_{i}}$ |
${P_{i}}$ |
${k_{ia}}$ |
${k_{ib}}$ |
${k_{ic}}$ |
${k_{i}}$ |
Rank |
| KF121 |
0.2150 |
3.7341 |
0.0549 |
2.1343 |
0.5244 |
1.2990 |
12 |
| KJ264 |
0.1895 |
4.2238 |
0.0613 |
2.1311 |
0.5861 |
1.3508 |
11 |
| IRB 5500-22 |
0.5180 |
5.2567 |
0.0802 |
4.1409 |
0.7669 |
2.2966 |
8 |
| IRB 5510 |
0.5693 |
6.0680 |
0.0922 |
4.6284 |
0.8814 |
2.5892 |
5 |
| Motoman MPX-3500 |
0.5830 |
6.3058 |
0.0957 |
4.7645 |
0.9148 |
2.6722 |
3 |
| Motoman EPX-2800 |
0.4212 |
5.2748 |
0.0791 |
3.6347 |
0.7564 |
2.0915 |
10 |
| HS-6-1722 |
0.4831 |
6.0575 |
0.0909 |
4.1709 |
0.8686 |
2.4006 |
7 |
| HS-6-1640 |
0.4206 |
5.3244 |
0.0798 |
3.6449 |
0.7629 |
2.1013 |
9 |
| P-250iB/15 |
0.6208 |
6.3912 |
0.0974 |
4.9871 |
0.9312 |
2.7729 |
2 |
| P-350iA/45 |
0.8007 |
6.7296 |
0.1046 |
6.0267 |
1.0000 |
3.2346 |
1 |
| HY1010A-143 |
0.6081 |
4.8665 |
0.0761 |
4.5118 |
0.7270 |
2.4011 |
6 |
| HY1050A-200 |
0.6315 |
5.6850 |
0.0878 |
4.8543 |
0.8388 |
2.6366 |
4 |
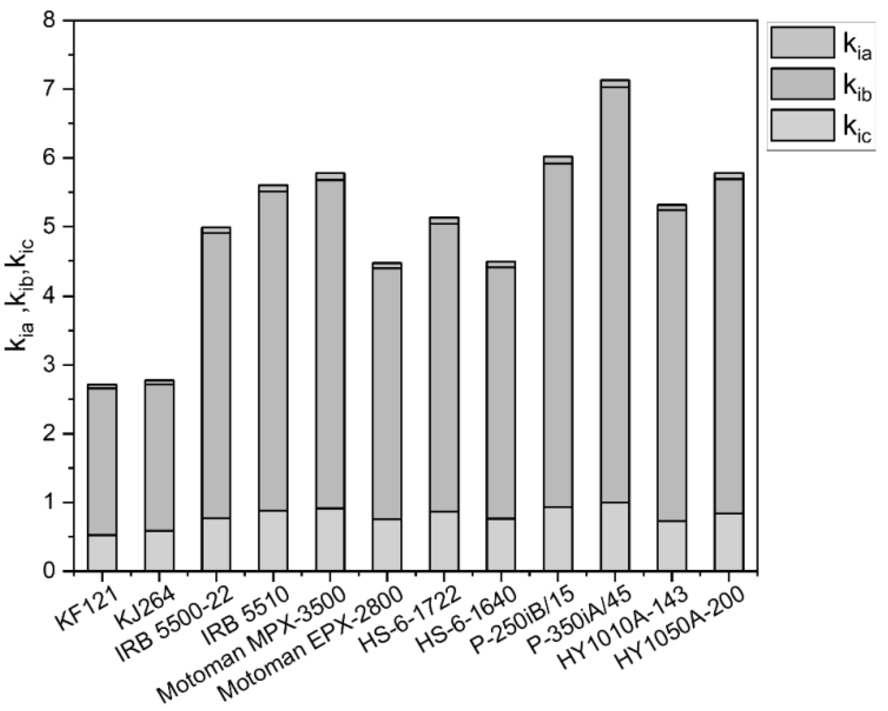
Fig. 1
Ranking of spray painting robots based on their appraisal scores.
Following the procedural steps of CoCoSo method, the initial decision matrix of Table
2 needs to be linearly normalized to transform all of its elements within a range of 0 to 1, considering the type of the evaluation criterion involved in the spray painting robot selection problem. In Table
4, the corresponding values of sum of weighted comparability sequence
$({S_{i}})$ and power of weighted comparability sequence
$({P_{i}})$ are determined for all the alternative robots, employing Eqs. (
9) and (
10) respectively. Using this information, the corresponding values of three different appraisal scores are estimated which are aggregated together to derive the final appraisal scores for all the considered spray painting robots. It can be clearly noticed from Table
4 that Fanuc P-350iA/45 model occupies the top position in the ranking list with the maximum appraisal score, followed by P-250iB/15 model of the same manufacturer. On the other hand, minimum preference would be assigned to Kawasaki KF121 model for the given spray painting operation. The ranking positions of these robots are pictorially represented in Fig.
1. Relatively high payload and speed, moderate reach and mechanical weight, and relatively low repeatability, cost and power consumption justify the selection of Fanuc P-350iA/45 model as the most suitable spray painting robot. It is interesting to note here that while calculating the appraisal scores (i.e.
${k_{ic}}$ in Eq. (
13)), value of the corresponding tuning parameter
$(\lambda )$ may play an important role in influencing the final selection decision. The behaviour of SWARA-CoCoSo method while ranking the candidate robots for varying values of
λ is studied in Fig.
2. It can be observed from this figure that for all the possible values of
λ, the positions of the top two and last two spray painting robots in the derived ranking lists remain unaltered, although there are marginal deviations in the positions of the intermediately ranked robots. Thus, it can be propounded that the proposed SWARA-CoCoSo method is quite robust, being almost unaffected by the changing
λ values.
To understand the impact of
λ on the ranking pattern of SWARA-CoCoSo method, a robustness study is carried out where the value of
λ is varied between 0 and 1 with 0.01 increments to generate 101 independent trials. The rank awarded to each robot for each
λ value is presented in Fig.
3(a). It is observed that except for ranks 6–9, other ranks remain constant even with changes in
λ. The relative rank shares of different alternatives (robots) are provided in Fig.
3(b). It is noticed that there is 0% change in the top 5 and bottom 3 robot rankings. However, the robot rankings between ranks 6–9 are marginally affected by changes in
λ value. Between ranks 8–9, there is 11% variation, whereas, for ranks 6–7, it is only 4%. The results of this robustness test indicate that SWARA-CoCoSo is almost insensitive to changes in
λ and thus, parameter tuning can be overlooked for low-dimensional MCDM problems. The ranking pattern may be affected with
λ value for high-dimensional MCDM problems. Thus, it is recommended for future studies that the default value for
λ should be considered as 0.5 while solving MCDM problems. Thus, SWARA-CoCoSo is a viable tool for such real-working optimal robot selection scenarios.
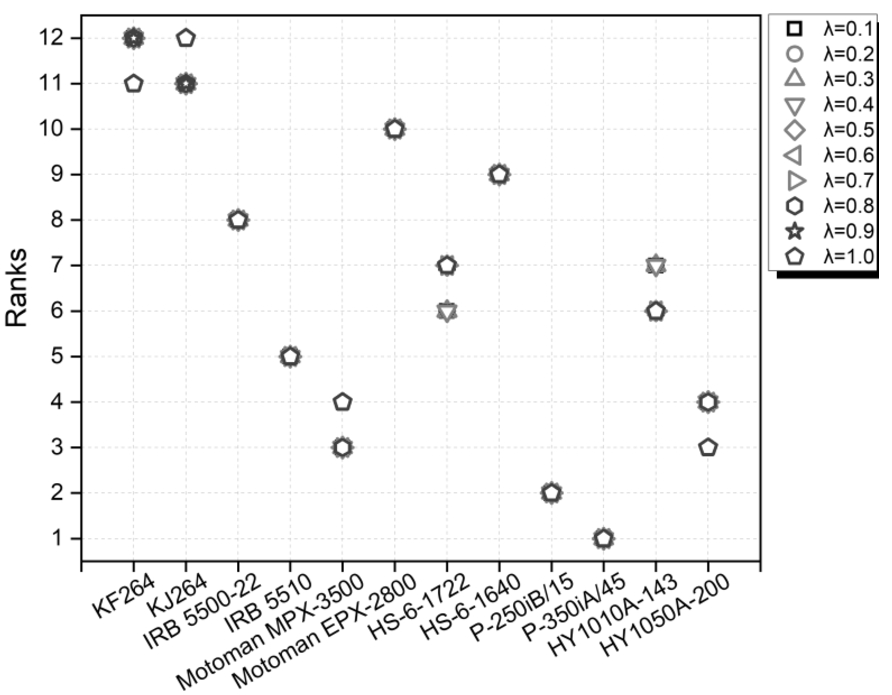
Fig. 2
Rankings of alternative robots for varying λ values.
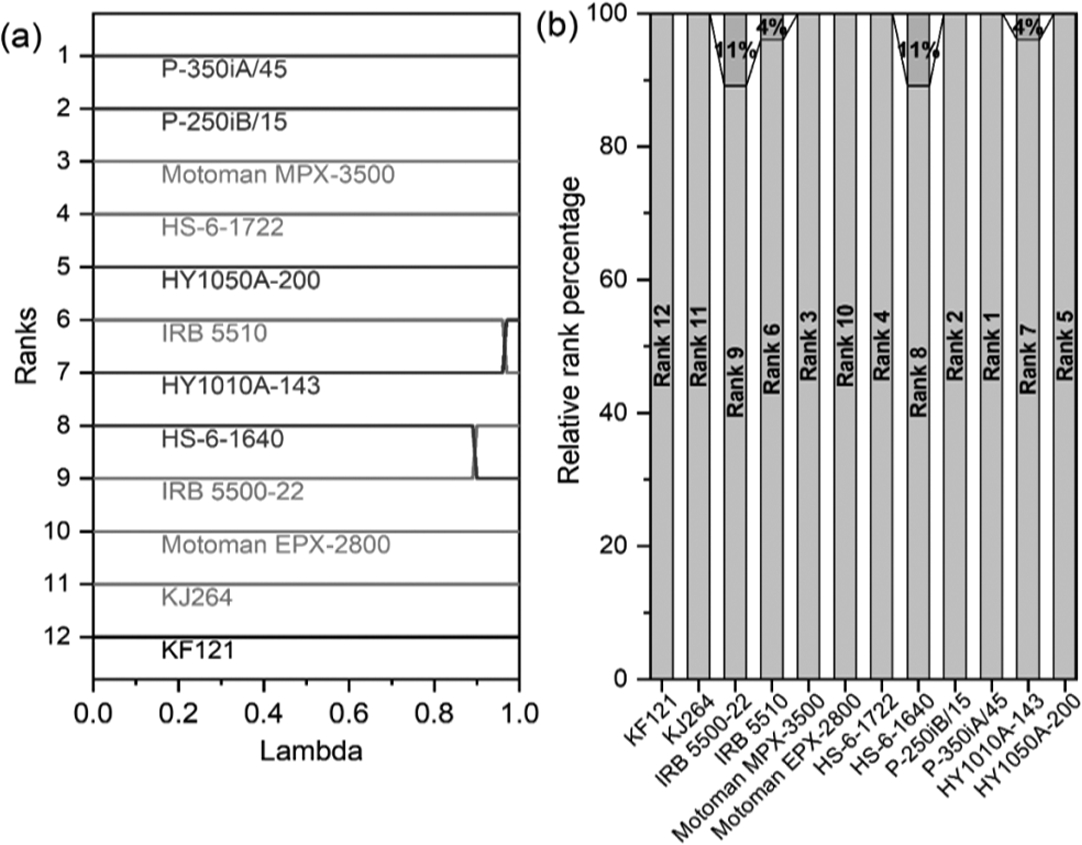
Fig. 3
(a) Variation of ranks by SWARA-CoCoSo with respect to change in λ for each robot, and (b) Relative share of ranks for each robot for 101 SWARA-CoCoSo trials for $\lambda =0$ to 1.
Table 5
Ranking of robots using different integrated MCDM techniques.
| Model |
SWARA-CoCoSo |
SWARA-TOPSIS |
SWARA-VIKOR |
SWARA-COPRAS |
SWARA-PROMETHEE |
SWARA-MOORA |
| KF121 |
12 |
11 |
11 |
12 |
11 |
11 |
| KJ264 |
11 |
12 |
12 |
11 |
12 |
12 |
| IRB 5500-22 |
8 |
6 |
7 |
7 |
7 |
7 |
| IRB 5510 |
5 |
3 |
5 |
4 |
6 |
5 |
| Motoman MPX-3500 |
3 |
7 |
4 |
6 |
5 |
6 |
| Motoman EPX-2800 |
10 |
10 |
8 |
10 |
9 |
10 |
| HS-6-1722 |
7 |
8 |
10 |
8 |
8 |
8 |
| HS-6-1640 |
9 |
9 |
9 |
9 |
10 |
9 |
| P-250iB/15 |
2 |
5 |
3 |
5 |
3 |
4 |
| P-350iA/45 |
1 |
1 |
1 |
1 |
1 |
1 |
| HY1010A-143 |
6 |
4 |
6 |
2 |
4 |
3 |
| HY1050A-200 |
4 |
2 |
2 |
3 |
2 |
2 |
| r |
|
0.5400 |
−0.9227 |
0.8400 |
0.8500 |
0.9400 |
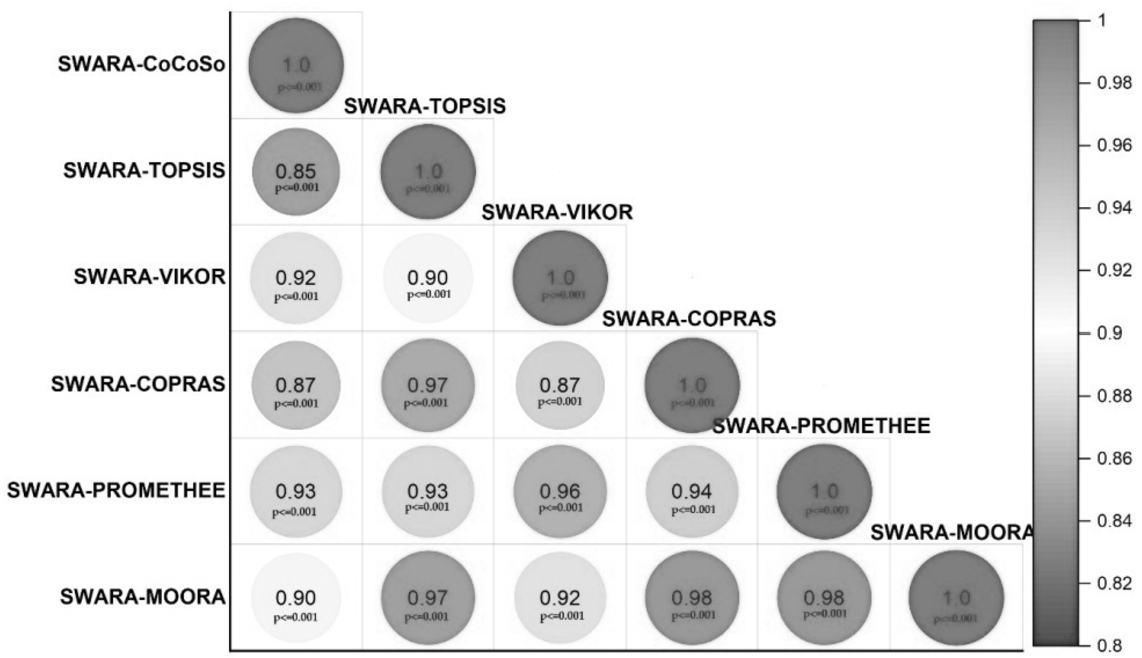
Fig. 4
Spearman’s rank correlations for different integrated MCDM techniques.
Now, to validate the effectiveness of SWARA-CoCoSo method in accurately ranking the candidate alternative spray painting robots, its performance is contrasted with other popular MCDM techniques, like TOPSIS (Behzadian
et al.,
2012), VIKOR (Opricovic and Tzeng,
2004), COPRAS (Zavadskas
et al.,
2008), PROMETHEE (Brans and Vincke,
1985) and MOORA (Brauers
et al.,
2008) methods. In this comparative analysis, the criteria weighting technique, i.e. SWARA remains the same. Table
5 provides the ranking results for all the considered integrated approaches and the corresponding Spearman’s rank correlation values are plotted in Fig.
4 (
p-values for almost all the cases <0.001). For all the MCDM techniques integrated with SWARA method, Fanuc P-350iA/45 model is identified as the most preferred choice. On the other hand, the worst chosen robot alternative is from one of the models manufactured by Kawasaki. It can be revealed from Fig.
4 that the ranking pattern of the alternative spray painting robots derived using SWARA-CoCoSo is almost similar to that of SWARA-TOPSIS, SWARA-VIKOR, SWARA-CORPAS, SWARA-PROMETHEE and SWARA-MOORA methods. High correlation coefficients
$(r)$ between the utility (performance) scores of SWARA-CoCoSo and other integrated MCDM techniques (shown in the last row of Table
5) reassure this observation. In VIKOR, the alternatives are ranked based on ascending values of its utility score, whereas, in other methods (CoCoSo, TOPSIS, COPRAS, PROMETHEE and MOORA), alternatives are ranked using descending values of their utility scores. This is the reason of obtaining negative
r value between SWARA-CoCoSo and SWARA-VIKOR methods. Slight variations in the rankings of the intermediately positioned robots exist only due to differences in the mathematical treatments involved in these methods.
Table 6
Criteria weights using other subjective weighting methods.
| Criteria |
SWARA |
AHP |
PIPRECIA |
BWM |
FUCOM |
| C |
0.28 |
0.35 |
0.30 |
0.1865 |
0.1921 |
| P |
0.20 |
0.23 |
0.23 |
0.1553 |
0.1529 |
| PC |
0.15 |
0.17 |
0.17 |
0.1366 |
0.1518 |
| RE |
0.12 |
0.16 |
0.12 |
0.1358 |
0.1366 |
| RC |
0.1 |
0.04 |
0.08 |
0.1353 |
0.1258 |
| S |
0.09 |
0.03 |
0.05 |
0.1294 |
0.1251 |
| M |
0.08 |
0.03 |
0.03 |
0.1211 |
0.1157 |
Table 7
CoCoSo-based ranking of robots with other subjective weighting methods.
| Model |
SWARA-CoCoSo |
AHP-CoCoSo |
PIPRECIA-CoCoSo |
BWM-CoCoSo |
FUCOM-CoCoSo |
| KF121 |
12 |
11 |
11 |
12 |
12 |
| KJ264 |
11 |
12 |
12 |
11 |
11 |
| IRB 5500-22 |
8 |
7 |
7 |
9 |
8 |
| IRB 5510 |
5 |
3 |
4 |
6 |
7 |
| Motoman MPX-3500 |
3 |
6 |
5 |
3 |
3 |
| Motoman EPX-2800 |
10 |
10 |
9 |
10 |
10 |
| HS-6-1722 |
7 |
8 |
8 |
4 |
4 |
| HS-6-1640 |
9 |
9 |
10 |
8 |
9 |
| P-250iB/15 |
2 |
4 |
3 |
2 |
2 |
| P-350iA/45 |
1 |
1 |
1 |
1 |
1 |
| HY1010A-143 |
6 |
5 |
6 |
7 |
6 |
| HY1050A-200 |
4 |
2 |
2 |
5 |
5 |
To further prove the effectiveness of SWARA-CoCoSo method in ranking of the alternative spray painting robots, weights of the seven evaluation criteria are further estimated using other subjective weighting techniques, like AHP (Saaty,
1977), PIPRECIA (Stanujkic
et al.,
2015), BWM (Rezaei,
2015) and FUCOM (Pamučar
et al.,
2018), keeping in mind the preference order of those criteria. These weight values are provided in Table
6. The rankings of all the robots are now derived in Table
7 while integrating those subjective weighting techniques with CoCoSo method. Fig.
5 plots the values of Spearman’s rank correlations for SWARA-CoCoSo, AHP-CoCoSo, PIPRECIA-CoCoSo, BWM-CoCoSo and FUCOM-CoCoSo methods (
p-values for almost all the cases <0.001). The rankings of the candidate spray painting robots obtained using these combined methodologies are also almost similar. As the corresponding criteria weights are estimated subjectively using those techniques by a group of decision makers based on a specific preference order, it is expected that there may be insignificant deviations in the weight values, minimally affecting the derived ranking orders. Hence, it can be concluded that SWARA-CoCoSo method, having simple computational steps, can be effectively deployed in identifying the most apposite robot for the given spray painting task.
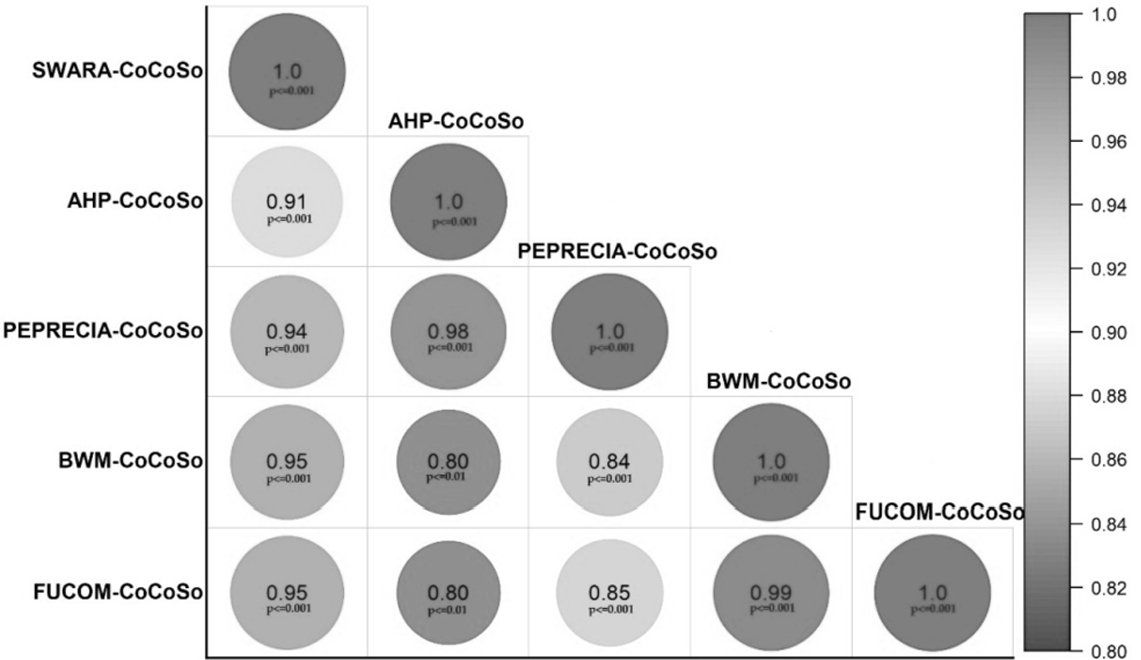
Fig. 5
Spearman’s rank correlations for CoCoSo integrated with other weighting techniques.
It is worthwhile to mention here that while solving any decision making problem, the priority weights assigned to the considered criteria play important roles in ranking of the alternatives. This spray painting robot selection problem is finally solved using TOPSIS, VIKOR, COPRAS, PROMETHEE and MOORA methods while assigning weights to the criteria using AHP and entropy (Li
et al.,
2011) methods. In AHP method, the weights allotted to the evaluation criteria are
${w_{C}}=0.35$,
${w_{P}}=0.23$,
${w_{PC}}=0.17$,
${w_{RE}}=0.16$,
${w_{RC}}=0.04$,
${w_{S}}=0.03$ and
${w_{W}}=0.03$, whereas, in entropy method (based on randomness of data in the decision matrix), the corresponding weights are
${w_{C}}=0.1437$,
${w_{P}}=0.1371$,
${w_{PC}}=0.1478$,
${w_{RE}}=0.1268$,
${w_{RC}}=0.1499$,
${w_{S}}=0.1509$ and
${w_{W}}=0.1438$. Table
8 provides the ranks of the alternative spray painting robots for both the cases (rankings based on entropy method are shown in parentheses). It can be interestingly noticed that for all the MCDM methods, the position of the top ranked spray painting robot remains unchanged. The worst chosen robot is one from the models manufactured by Kawasaki. It thus proves the capability of all the adopted MCDM techniques in correctly identifying the best and worst spray painting robots for a problem with smaller numbers of alternatives and criteria.
Table 8
Ranks of robots using TOPSIS, VIKOR, COPRAS, PROMETHEE and MOORA methods.
| Model |
TOPSIS |
VIKOR |
COPRAS |
PROMETHEE |
MOORA |
| KF121 |
11(11) |
11(12) |
12(12) |
11(12) |
12(12) |
| KJ264 |
12(12) |
12(11) |
11(11) |
12(11) |
11(11) |
| IRB 5500-22 |
6(9) |
7(10) |
6(9) |
7(4) |
6(9) |
| IRB 5510 |
3(8) |
4(8) |
4(8) |
6(8) |
4(8) |
| Motoman MPX-3500 |
7(6) |
6(2) |
7(6) |
5(6) |
7(6) |
| Motoman EPX-2800 |
10(10) |
8(5) |
10(10) |
9(7) |
10(10) |
| HS-6-1722 |
8(4) |
10(4) |
8(4) |
8(10) |
8(4) |
| HS-6-1640 |
9(7) |
9(6) |
9(7) |
10(9) |
9(7) |
| P-250iB/15 |
5(5) |
3(3) |
5(5) |
3(5) |
5(5) |
| P-350iA/45 |
1(1) |
1(1) |
1(1) |
1(1) |
1(1) |
| HY1010A-143 |
4(3) |
5(7) |
3(3) |
4(3) |
3(3) |
| HY1050A-200 |
2(2) |
2(9) |
2(2) |
2(2) |
2(2) |
5 Conclusion
In this paper, SWARA method is first applied to determine subjective weights of the considered evaluation criteria (set in a given preference order) and these weights are subsequently employed along with CoCoSo method for ranking of the alternative spray painting robots. The calculation steps involved in both these methods are easy to comprehend and implement. Based on a set preference order, SWARA method identifies cost as the most significant criterion, while application of CoCoSo method selects Fanuc P-350iA/45 as the most suitable robot for the given spray painting task, followed by P-250iB/15 model. Kawasaki KF121 model is the worst preferred choice. The proposed method is quite robust being insensitive with respect to variations in the corresponding tuning parameter value for low-dimensional MCDM problems. A comparative analysis of its ranking performance against other popular MCDM techniques proves its effectiveness in accurately ranking the robot alternatives. It is also observed that SWARA method behaves similarly as compared to other subjective criteria weighting techniques. Thus, this integrated approach can be considered as a viable tool for ranking of alternatives for real-time manufacturing-related problems taking into account opinions of the experts in a group decision making environment. The limitations of SWARA method are that it does not evaluate relationships between the considered attributes and reliability of the expert judgments may be uncertain due to inaccurate information. On the other hand, in CoCoSo method, the hybrid integration operator basically combines benefits of arithmetic average integration operator with geometric average integration operator. This integration, however, considers three subordinate compromise scores having significant variances affecting the final selection decision. In CoCoSo method, determination of a compromise value of λ is also a contentious task. The ranking performance of this approach may be contrasted with other MCDM tools, like ELECTRE, ARAS, MABAC, multi-attributive real-ideal comparative analysis (MARICA), measurement of alternatives and ranking according to compromise solution (MARCOS), etc., methods. As another future scope of this paper, the alternative spray painting robots may be ranked while estimating objective criteria weights based on randomness of the data in the initial decision matrix. But in this case, the preference order of the evaluation criteria may be distorted. Integration of CoSoSo method with fuzzy sets, interval values, neutrosophic and intuitionistic fuzzy sets, etc., is highly recommended to improve the solution accuracy of the decision making task. As it is not feasible to manually solve high-dimensional MCDM problems using this integrated approach, development of a software prototype (decision support system) is thus strongly encouraged.

