2 Notion of T-SF Sets: Preliminaries
T-SF sets contribute a magnificent model to comprehensively manage the equivocation and indefiniteness accompanied by multiple criteria evaluation and assessment activities. Herein, this section intends to describe preliminary notations related to T-SF sets. Throughout this work, the notations μ, η, ν, and γ represent grades of positive membership, neutral membership (i.e. abstinence), negative membership, and refusal membership, respectively, in the unit interval $[0,1]$. Relevant concepts can give assistance to construct the initiated T-SF REGIME method.
Definition 1 (Cuong, 2014).
Let a finite nonempty set
U represent the domain of discourse containing an element
u. A picture fuzzy set
P in
U is stated precisely like this:
where
${\gamma _{P}}(u)=1-{\mu _{P}}(u)-{\eta _{P}}(u)-{\nu _{P}}(u)$. The triplet (
${\mu _{P}}(u),{\eta _{P}}(u),{\nu _{P}}(u)$) is stipulated as a picture fuzzy number.
Definition 2 (Gündoğdu and Kahraman, 2019).
A spherical fuzzy set
S in
U is listed below:
where
${\gamma _{T}}(u)=\sqrt{1-{({\mu _{S}}(u))^{2}}-{({\eta _{S}}(u))^{2}}-{({\nu _{S}}(u))^{2}}}$. The triplet (
${\mu _{S}}(u),{\eta _{S}}(u),{\nu _{S}}(u)$) is explicated as a spherical fuzzy number.
Definition 3 (Mahmood et al., 2019).
A T-SF set
T in
U is delineated as shown:
where
${\gamma _{T}}(u)=\sqrt[z]{1-{({\mu _{T}}(u))^{z}}-{({\eta _{T}}(u))^{z}}-{({\nu _{T}}(u))^{z}}}$, and
$z\in {Z^{+}}$ (
${Z^{+}}$: a collection of positive integers). The triplet (
${\mu _{T}}(u),{\eta _{T}}(u),{\nu _{T}}(u)$) is named a T-SF number, denoted as
$t(u)$.
If
$z=1$, the T-SF set
T in Eq. (
3) reduces to the picture fuzzy set
P in Eq. (
1). If
$z=2$, the T-SF set
T in Eq. (
3) reduces to the spherical fuzzy set
S in Eq. (
2). From this basis, picture fuzzy sets and spherical fuzzy sets are referred to as the special cases of the concepts of T-SF sets. On the flip-side, if
${\eta _{T}}(u)=0$, the T-SF set
T condenses into a q-rung orthopair fuzzy version. And by the same token, making allowance for the precondition that
${\eta _{T}}(u)=0$, the T-SF set
T reduces to intuitionistic, Pythagorean, and Fermatean fuzzy sets if
$z=1,2,3$, respectively. Therefore, the theory of T-spherical fuzziness can be referred to as a generalized configuration with respect to the well-received non-standard fuzzy sets.
Definition 4 (Mahmood et al., 2019).
The score value
$\textit{Sv}(t(u))$ and the accuracy value
$\textit{Av}(t(u))$ of a T-SF number
$t(u)$ are portrayed precisely in this manner:
where
$\textit{Sv}(t(u))\in [-1,1]$ and
$\textit{Av}(t(u))\in [0,1]$.
The notions of $\textit{Sv}(t(u))$ and $\textit{Av}(t(u))$ can facilitate the establishment of a comparison rule of T-SF numbers. The greater the score value $\textit{Sv}(t(u))$ is, the higher the T-SF number $t(u)$ will be. In the same fashion, the greater the accuracy value $\textit{Av}(t(u))$ is, the higher the $t(u)$ will be. By way of explanation, let $t({u_{1}})$ and $t({u_{2}})$ denote two T-SF numbers. The following rules can be employed to compare $t({u_{1}})$ and $t({u_{2}})$:
-
1. If $\textit{Sv}(t({u_{1}}))>\textit{Sv}(t({u_{2}}))$, then $t({u_{1}})$ is higher than $t({u_{2}})$;
-
2. If $\textit{Sv}(t({u_{1}}))=\textit{Sv}(t({u_{2}}))$, then:
-
a) If $\textit{Av}(t({u_{1}}))>\textit{Av}(t({u_{2}}))$, then $t({u_{1}})$ is higher than $t({u_{2}})$;
-
b) If $\textit{Av}(t({u_{1}}))=\textit{Av}(t({u_{2}}))$, then $t({u_{1}})$ is equal to $t({u_{2}})$.
However, the grades of neutral membership
${\eta _{T}}(u)$ and refusal membership
${\gamma _{T}}(u)$ are not involved in the specification of
$\textit{Sv}(t(u))$. Furthermore, the grade of refusal membership
${\gamma _{T}}(u)$ is not contained in the specification of
$\textit{Av}(t(u))$. On the grounds of this, the aforesaid comparison rule would lose some decision information contained in T-SF numbers. In an attempt to avoid loss of influential information, Zeng
et al. (
2019) initiated a new formulation of T-SF score functions and stated several useful properties for the sake of comparing T-SF numbers. Zeng
et al. (
2019) took advantage of a curve function with the format
$\textit{Cf}(x)={e^{x}}/({e^{x}}+1)$ whose range is always in the open interval
$(0,1)$. Moreover, it is recognized that
$\textit{Cf}(x)+\textit{Cf}(-x)=0$, which follows directly that
$\textit{Cf}(0)=0.5$. In particular, the curve function
$\textit{Cf}(x)$ is rigorously upswing in domain of real numbers. Supported by the curve function
$\textit{Cf}(x)$, Zeng
et al. (
2019) propounded an efficacious score function
$\textit{Sf}(t(u))$ of a T-SF number
$t(u)$ in
U.
Definition 5 (Zeng et al., 2019).
The score function
$\textit{Sf}(t(u))$ is delineated as shown:
where
$\textit{Sf}(t(u))\in [-1,1]$. Moreover,
$\textit{Sf}(t(u))$ reduces a score value for picture fuzzy and spherical fuzzy contexts if
$z=1,2$, respectively. When
${\eta _{T}}(u)=0$,
$\textit{Sf}(t(u))$ reduces a score value for intuitionistic, Pythagorean, and Fermatean fuzzy contexts if
$z=1,2,3$, respectively.
3 Proposed T-SF REGIME Methodology
This section makes an effort to develop a novel T-SF REGIME method for managing multiple-criteria choice issues under intricate uncertain circumstances. This section designs some beneficial concepts to plan an approach for determining predominance relationships among the T-SF evaluation values of given alternatives. An efficacious T-SF REGIME procedure is evolved to help decision makers arrive at a choice.
The proposed T-SF REGIME method consists of five phases: (i) organization of a multiple-criteria choice problem, (ii) establishment of score function-based superiority criteria, (iii) determination of the superiority measurements, (iv) identification of the REGIME matrix and guide indices, and (v) construction of the eventual partial/complete ranking. The research focuses in the five phases are depicted in the T-SF REGIME framework of the evolved methodology. The analytical framework of the advanced T-SF REGIME is portrayed in Fig.
1. In the first phase, this paper constitutes a multiple-criteria choice issue under complicated T-SF uncertainty. In the second phase, this paper utilizes a beneficial score function to differentiate T-SF information for pinpointing the superiority criteria. In the third phase, the developed approach aims to exploit the score function-based collection of superiority criteria to delineate the notions of a superiority index and a superiority identifier. In the fourth phase, this paper utilizes the sign of the contrast between score functions to form a REGIME matrix and then generate a guide index. In the final phase, this study produces the T-SF REGIME I and II prioritization mechanisms in the expectation of yielding partial-preference and complete-preference predominance rankings, respectively, for choice options. To draw as a logical conclusion about the T-SF REGIME I eventual predominance ranks, this study launches the conception of a superiority-based Boolean matrix and a guide-based Boolean matrix. This paper unfolds the notions of net superiority identifiers and net guide indices for deducing the T-SF REGIME II ranking among choice options. At the beginning, a multiple-criteria choice task would be constituted in T-SF decision circumstances.
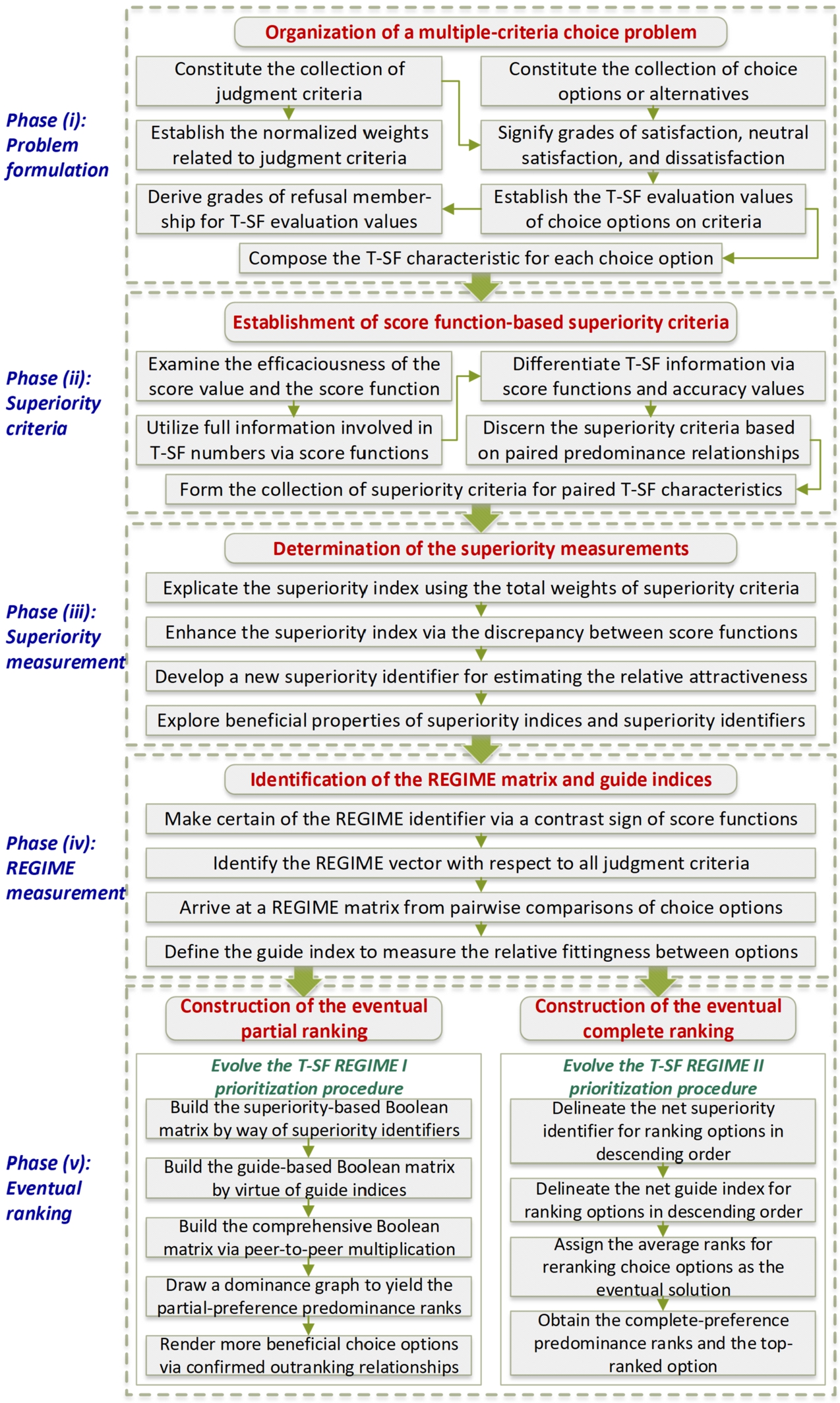
Fig. 1
The framework of the evolved T-SF REGIME methodology.
Consider the mathematical description of a multiple-criteria choice analysis task in the first phase. Let
$A=\{{a_{1}},{a_{2}},\dots ,{a_{m}}\}$ expound a collection of
m (⩾2) choice options or alternatives. Moreover, let
$C=\{{c_{1}},{c_{2}},\dots ,{c_{n}}\}$ represent a collection of
n (⩾2) judgment criteria that elucidate factors and characteristics for evaluating the choice options from which decision makers are choosing. The weight
${w_{j}}\in [0,1]$ associated with each judgment criterion
${c_{j}}\in C$ fulfills the normalized condition
${\textstyle\sum _{j=1}^{n}}{w_{j}}=1$. In a fundamental manner, the measures concerning performance ratings of choice options can be determined using a satisfaction survey through a questionnaire designed to understand what the decision maker thinks about these alternatives in terms of each criterion. In the uncertain contexts with T-spherical fuzziness, the T-SF evaluation value
${t_{ij}}$ of a choice option
${a_{i}}\in A$ in conjunction with a judgment criterion
${c_{j}}\in C$ is precisely stated via a T-SF number (
${\mu _{ij}},{\eta _{ij}},{\nu _{ij}}$) that is constituted by the grade of satisfaction
${\mu _{ij}}$, grade of neutral satisfaction
${\eta _{ij}}$, and grade of dissatisfaction
${\nu _{ij}}$. Moreover, the corresponding grade of refusal membership is given by
${\gamma _{ij}}=\sqrt[z]{1-{({\mu _{ij}})^{z}}-{({\eta _{ij}})^{z}}-{({\nu _{ij}})^{z}}}$. The T-SF characteristic
${T_{i}}$ of
${a_{i}}$ for
$z\in {Z^{+}}$ is expressed in this manner:
The REGIME mechanism exploits a comparison of any two choice options in pairs. Next, an eventual predominance ranking of all available options is co-ascertained through the mutual comparisons of alternatives. With the purpose of building a new mechanism of the proposed T-SF REGIME method, this paper would first launch an identification approach of a regime. There is usually no obvious single dominant choice option in practical decision-making affairs. Therefore, one needs a better way to proceed with T-SF evaluation values in pairwise comparisons that focus on differences between choice options with respect to the judgment criteria. The score function exhibited by Zeng
et al. (
2019) can fully utilize the information about grades of positive, neutral, negative, and refusal memberships that quantify belongingness of a judgment criterion in the domain of discourse to a T-SF characteristic. Let us examine the effectiveness of the score function
$\textit{Sf}({t_{ij}})$ in comparison with the score value
$\textit{Sv}({t_{ij}})$ through the agency of the subsequent example.
Example 1.
Consider that two T-SF evaluation values
${t_{ij}}=(0.6,0.4,0.5)$ and
${t_{{i^{\prime }}j}}=(0.6,0.1,0.5)$ with
$z=3$. By virtue of Eq. (
4), it was received that
$\textit{Sv}({t_{ij}})=0.{6^{3}}-0.{5^{3}}=0.0910$ and
$\textit{Sv}({t_{{i^{\prime }}j}})=0.{6^{3}}-0.{5^{3}}=0.0910$. Next, the grades of refusal membership corresponding to
${t_{ij}}$ and
${t_{{i^{\prime }}j}}$ were separately computed as follows:
${\gamma _{ij}}=\sqrt[3]{1-0.{6^{3}}-0.{4^{3}}-0.{5^{3}}}=0.8411$ and
${\gamma _{{i^{\prime }}j}}=\sqrt[3]{1-0.{6^{3}}-0.{1^{3}}-0.{5^{3}}}=0.8698$. With the aid of Eq. (
6), it was obtained that:
Obviously, due to
$\textit{Sv}({t_{ij}})=\textit{Sv}({t_{{i^{\prime }}j}})$, failure to discriminate between the superiority degrees of
${t_{ij}}$ and
${t_{{i^{\prime }}j}}$ leads to the decreased usefulness of the score value as stated by Definition
4. In contrast, the employment of the score function as attested by Definition
5 was able to differentiate between the superiority degrees of
${t_{ij}}$ and
${t_{{i^{\prime }}j}}$ because
$\textit{Sf}({t_{ij}})<\textit{Sf}({t_{{i^{\prime }}j}})$. This example has demonstrated the effectuality of the score function due to the fact that the specification of
$\textit{Sf}({t_{ij}})$ can utilize full information contained in T-SF evaluation values.
The research focus in the second phase is the differentiation of T-SF evaluation values for discerning the superiority criteria. For the most part, one can determine a predominance relationship portrayed by the rationale of “the higher, the better”. A T-SF evaluation value is considered to be superior to another T-SF evaluation value in case that the corresponding score function is more significant. When two T-SF evaluation values have an identical score function value, the corresponding accuracy values would be exploited to examine the superiority of these T-SF evaluations. That is, a T-SF evaluation value is regarded to be more significant to another T-SF evaluation value if its accuracy value is larger. Considering two T-SF evaluation values of choice options ${a_{i}},{a_{{i^{\prime }}}}\in A$ in conjunction with a judgment criterion ${c_{j}}\in C$, the comparison rule concerned with ${t_{ij}}$ and ${t_{{i^{\prime }}j}}$ is elucidated as follows:
-
1. If $\textit{Sf}({t_{ij}})>\textit{Sf}({t_{{i^{\prime }}j}})$, then ${t_{ij}}$ is superior to ${t_{{i^{\prime }}j}}$;
-
2. If $\textit{Sf}({t_{ij}})=\textit{Sf}({t_{{i^{\prime }}j}})$, then:
-
a) If $\textit{Av}({t_{ij}})>\textit{Av}({t_{{i^{\prime }}j}})$, then ${t_{ij}}$ is superior to ${t_{{i^{\prime }}j}}$;
-
b) If $\textit{Av}({t_{ij}})=\textit{Av}({t_{{i^{\prime }}j}})$, then the superiority of ${t_{ij}}$ and ${t_{{i^{\prime }}j}}$ becomes equal.
Definition 6.
Consider two T-SF characteristics
${T_{i}}$ and
${T_{{i^{\prime }}}}$ of the choice options
${a_{i}},{a_{{i^{\prime }}}}\in A$, where
${T_{i}}=\{\langle {c_{j}},{t_{ij}}\rangle \mid {c_{j}}\in C\}$ and
${T_{{i^{\prime }}}}=\{\langle {c_{j}},{t_{{i^{\prime }}j}}\rangle \mid {c_{j}}\in C\}$. Let
$\textit{Cs}({T_{i}},{T_{{i^{\prime }}}})$ denote a collection of superiority criteria in which
${T_{i}}$ is at least as good as
${T_{{i^{\prime }}}}$; it is identified along these lines:
Theorem 1.
The complement of $\textit{Cs}({T_{i}},{T_{{i^{\prime }}}})$, which is named a collection of inferiority criteria, contains all judgment criteria for which ${T_{i}}$ performs worse than ${T_{{i^{\prime }}}}$. The collection of inferiority criteria $Ci({T_{i}},{T_{{i^{\prime }}}})$ is written like this:
Without loss of generality, assume that the equalities $\textit{Sf}({t_{ij}})=\textit{Sf}({t_{{i^{\prime }}j}})$ and $\textit{Av}({t_{ij}})=\textit{Av}({t_{{i^{\prime }}j}})$ will not happen at the same time for each ${c_{j}}\in C$. Then, the collection of superiority criteria $\textit{Cs}({T_{i}},{T_{{i^{\prime }}}})$ satisfies the following properties:
-
(T1.1) $\textit{Cs}({T_{i}},{T_{{i^{\prime }}}})\cap \textit{Cs}({T_{{i^{\prime }}}},{T_{i}})=\varnothing $;
-
(T1.2) $\textit{Cs}({T_{i}},{T_{{i^{\prime }}}})\cup \textit{Cs}({T_{{i^{\prime }}}},{T_{i}})=C$;
-
(T1.3) $\textit{Cs}({T_{{i^{\prime }}}},{T_{i}})=C\setminus \textit{Cs}({T_{i}},{T_{{i^{\prime }}}})$ (i.e. the set difference of C and $\textit{Cs}({T_{i}},{T_{{i^{\prime }}}})$);
-
(T1.4) $\textit{Cs}({T_{i}},{T_{{i^{\prime }}}})=Ci({T_{{i^{\prime }}}},{T_{i}})$.
Proof.
Because two equalities
$\textit{Sf}({t_{ij}})=\textit{Sf}({t_{{i^{\prime }}j}})$ and
$\textit{Av}({t_{ij}})=\textit{Av}({t_{{i^{\prime }}j}})$ do not happen simultaneously for a specific criterion
${c_{j}}$, it can be received that:
Clearly, it is deduced that
$\textit{Cs}({T_{i}},{T_{{i^{\prime }}}})\cap \textit{Cs}({T_{{i^{\prime }}}},{T_{i}})=\varnothing $ and
$\textit{Cs}({T_{i}},{T_{{i^{\prime }}}})\cup \textit{Cs}({T_{{i^{\prime }}}},{T_{i}})=C$; moreover, the latter leads to the relative complement of
$\textit{Cs}({T_{i}},{T_{{i^{\prime }}}})$ in conjunction with the set
C, written
$C\setminus \textit{Cs}({T_{i}},{T_{{i^{\prime }}}})$. The set of elements in
C that are not in
$\textit{Cs}({T_{i}},{T_{{i^{\prime }}}})$ is derived by
$\textit{Cs}({T_{{i^{\prime }}}},{T_{i}})=C\setminus \textit{Cs}({T_{i}},{T_{{i^{\prime }}}})$. Thus, (T1.1)–(T1.3) are valid. (T1.4) can be easily concluded because:
Thus, the theorem is proved. □
Example 2.
Consider a collection of judgment criteria
$C=\{{c_{1}},{c_{2}},{c_{3}},{c_{4}}\}$ and two T-SF characteristics
${T_{i}}$ and
${T_{{i^{\prime }}}}$ of the choice options
${a_{i}},{a_{{i^{\prime }}}}\in A$. Herein,
${T_{i}}$ and
${T_{{i^{\prime }}}}$ are given by:
In accordance with Eq. (
6), the following score functions were acquired:
$\textit{Sf}({t_{i1}})=0.5626$,
$\textit{Sf}({t_{i2}})=0.5829$,
$\textit{Sf}({t_{i3}})=-0.2547$,
$\textit{Sf}({t_{i4}})=0.4339$,
$\textit{Sf}({t_{{i^{\prime }}1}})=-0.0638$,
$\textit{Sf}({t_{{i^{\prime }}2}})=0.7042$,
$\textit{Sf}({t_{{i^{\prime }}3}})=0.0632$, and
$\textit{Sf}({t_{{i^{\prime }}4}})=0.2685$. It was acquired that
$\textit{Cs}({T_{i}},{T_{{i^{\prime }}}})=\{{c_{1}},{c_{4}}\}$ and
$Ci({T_{i}},{T_{{i^{\prime }}}})=\{{c_{2}},{c_{3}}\}$, using Eqs. (
8) and (
9), respectively. Based on (T1.3),
$\textit{Cs}({T_{{i^{\prime }}}},{T_{i}})=C\setminus \textit{Cs}({T_{i}},{T_{{i^{\prime }}}})=\{{c_{2}},{c_{3}}\}$. Finally, it was gained that
$Ci({T_{{i^{\prime }}}},{T_{i}})=\textit{Cs}({T_{i}},{T_{{i^{\prime }}}})=\{{c_{1}},{c_{4}}\}$ by way of (T1.4).
Consider the third phase of the superiority measurements in the evolved T-SF REGIME methodology. A significant concept in the classical REGIME mechanism would be the superiority index. This index manifests an extent to which a choice option ${a_{i}}$ is superior or equal to ${a_{{i^{\prime }}}}$ merely as the relevant judgment criteria is involved in the collection of superiority criteria $\textit{Cs}({T_{i}},{T_{{i^{\prime }}}})$. In the framework of REGIME, the superiority index is explicated using the sum of weights contingent upon the superiority criteria contained in $\textit{Cs}({T_{i}},{T_{{i^{\prime }}}})$. This index can simply estimate the relative attractiveness of ${a_{i}}$ over ${a_{{i^{\prime }}}}$ in a rather unsophisticated manner. Nonetheless, this treatment of superiority measurements may ignore the essential nature of T-SF data. The extent of the discrepancy between $\textit{Sf}({t_{ij}})$ and $\textit{Sf}({t_{{i^{\prime }}j}})$ should be taken under advisement. That is, a more efficacious approach to proceeding with T-SF information in the proposed REGIME mechanism is to focus on differences between $\textit{Sf}({t_{ij}})$ and $\textit{Sf}({t_{{i^{\prime }}j}})$ by means of mutual comparisons, more specifically, by adding the products of the difference $\textit{Sf}({t_{ij}})-\textit{Sf}({t_{{i^{\prime }}j}})$ and the weight ${w_{j}}$ for ${c_{j}}\in \textit{Cs}({T_{i}},{T_{{i^{\prime }}}})$. This improved way delivers a new and creative superiority identifier that can be carried out with a focus on arriving at consequences about the relative attractiveness between choice options.
Definition 7.
Consider the normalized weight
${w_{j}}$ and the T-SF characteristics
${T_{i}}$ and
${T_{{i^{\prime }}}}$. In accordance with the score functions
$\textit{Sf}({t_{ij}})$ and
$\textit{Sf}({t_{{i^{\prime }}j}})$ along with the collection of superiority criteria
$\textit{Cs}({T_{i}},{T_{{i^{\prime }}}})$, the superiority index
$Si({T_{i}},{T_{{i^{\prime }}}})$ and the superiority identifier
$\textit{SI}({T_{i}},{T_{{i^{\prime }}}})$ in connection with
${a_{i}}$ over
${a_{{i^{\prime }}}}$ are elucidated along these lines:
Theorem 2.
The superiority index $Si({T_{i}},{T_{{i^{\prime }}}})$ and the superiority identifier $\textit{SI}({T_{i}},{T_{{i^{\prime }}}})$ fulfill the subsequent conditions:
-
(T2.1) $0\leqslant Si({T_{i}},{T_{{i^{\prime }}}})\leqslant 1$;
-
(T2.2) $0\leqslant \textit{SI}({T_{i}},{T_{{i^{\prime }}}})\leqslant 2$.
Proof.
Based on (T1.2), it can be recognized that
$\textit{Cs}({T_{i}},{T_{{i^{\prime }}}})$ is a subset of the collection of judgment criteria
C; thus,
$\textit{Cs}({T_{i}},{T_{{i^{\prime }}}})\subset C$ in mathematics. In line with the normalized condition, it is deduced that
$0\leqslant {\textstyle\sum _{{c_{j}}\in \textit{Cs}({T_{i}},{T_{{i^{\prime }}}})}}{w_{j}}\leqslant {\textstyle\sum _{{c_{j}}\in C}}{w_{j}}=1$, which brings about
$0\leqslant Si({T_{i}},{T_{{i^{\prime }}}})\leqslant 1$. Next, based on Definition
5, the ranges of
$\textit{Sf}({t_{ij}})$ and
$\textit{Sf}({t_{{i^{\prime }}j}})$ are bounded in the interval [
$-1,1$], which indicates explicitly that
$0\leqslant |\textit{Sf}({t_{ij}})-\textit{Sf}({t_{{i^{\prime }}j}})|\leqslant 2$. From Definition
6, it leads us to understand that
$\textit{Sf}({t_{ij}})\geqslant \textit{Sf}({t_{{i^{\prime }}j}})$ for each
${c_{j}}\in \textit{Cs}({T_{i}},{T_{{i^{\prime }}}})$, which follows that
$0\leqslant \textit{Sf}({t_{ij}})-\textit{Sf}({t_{{i^{\prime }}j}})\leqslant 2$ for
${c_{j}}\in \textit{Cs}({T_{i}},{T_{{i^{\prime }}}})$. By reason of the normalized condition of
${w_{j}}$, it concludes that
$0\leqslant {\textstyle\sum _{{c_{j}}\in \textit{Cs}({T_{i}},{T_{{i^{\prime }}}})}}{w_{j}}(\textit{Sf}({t_{ij}})-\textit{Sf}({t_{{i^{\prime }}j}}))\leqslant 2$. Therefore, (T2.1) and (T2.2) are correct. The theorem is proved. □
Next, consider the fourth phase of the REGIME matrix formation and the determination of guide indices in the current methodology. In particular, the guide index is employed to measure the relative fittingness between choice options. In accordance with the score functions of T-SF evaluation values, this paper builds the REGIME identifier and the REGIME vector for arriving at a REGIME matrix from paired juxtapositions of choice options in conjunction with judgment criteria, as described below.
Definition 8.
Consider the T-SF evaluation values
${t_{ij}}$ and
${t_{{i^{\prime }}j}}$ contained in the T-SF characteristics
${T_{i}}$ and
${T_{{i^{\prime }}}}$, respectively. The REGIME identifier
$\textit{Ri}({t_{ij}},{t_{{i^{\prime }}j}})$ is demarcated as a sign of the contrast outcomes through score functions in this manner:
The REGIME vector
$\textit{Rv}({T_{i}},{T_{{i^{\prime }}}})$ is composed of
$\textit{Ri}({t_{ij}},{t_{{i^{\prime }}j}})$ across all
${c_{j}}\in C$ like this:
The REGIME matrix
$\textit{Rm}$ is established by taking together the REGIME vectors for all ordered couples of choice options (
${a_{i}},{a_{{i^{\prime }}}}$) (for
$i\ne {i^{\prime }}$):
Theorem 3.
The REGIME identifier $\textit{Ri}({t_{ij}},{t_{{i^{\prime }}j}})$ in the REGIME matrix Rm possesses the property of $\textit{Ri}({t_{ij}},{t_{{i^{\prime }}j}})+\textit{Ri}({t_{{i^{\prime }}j}},{t_{ij}})=0$ for all ordered couples of $({a_{i}},{a_{{i^{\prime }}}})$ $(i\ne {i^{\prime }})$ in connection with each ${c_{j}}\in C$.
Proof.
Based on Eq. (
12), it readily draws as a logical conclusion that
$\textit{Ri}({t_{ij}},{t_{{i^{\prime }}j}})+\textit{Ri}({t_{{i^{\prime }}j}},{t_{ij}})=0$. In particular, one half of the number of arrays in the REGIME matrix
$\textit{Rm}$ can be deduced from the other half by reason of
$\textit{Ri}({t_{{i^{\prime }}j}},{t_{ij}})=-\textit{Ri}({t_{ij}},{t_{{i^{\prime }}j}})$. Therefore, the arrays in
$\textit{Rm}$ are not independent from each other. The theorem is proved. □
Definition 9.
Considering the normalized weight
${w_{j}}$ for each
${c_{j}}\in C$, the guide index
$\textit{GI}({T_{i}},{T_{{i^{\prime }}}})$ is determined through the utility of the REGIME identifier
$\textit{Ri}({t_{ij}},{t_{{i^{\prime }}j}})$ like this:
Theorem 4.
The guide index $\textit{GI}({T_{i}},{T_{{i^{\prime }}}})$ and its relevant concept meet some properties:
-
(T4.1) $-1\leqslant \textit{GI}({T_{i}},{T_{{i^{\prime }}}})\leqslant 1$;
-
(T4.2) $\textit{GI}({T_{i}},{T_{{i^{\prime }}}})+\textit{GI}({T_{{i^{\prime }}}},{T_{i}})=0$;
-
(T4.3) ${\textstyle\sum _{j=1}^{n}}{w_{j}}|\textit{Ri}({t_{ij}},{t_{{i^{\prime }}j}})|=1$ if $\textit{Sf}({t_{ij}})\ne \textit{Sf}({t_{{i^{\prime }}j}})$.
Proof.
As per the fact that
${\textstyle\sum _{j=1}^{n}}{w_{j}}=1$ and
$\textit{Ri}({t_{ij}},{t_{{i^{\prime }}j}})\in \{-1,0,1\}$, one readily obtains
$-1\leqslant \textit{GI}({T_{i}},{T_{{i^{\prime }}}})\leqslant 1$. Next, based on Theorem
3, it is known that
$\textit{Ri}({t_{ij}},{t_{{i^{\prime }}j}})+\textit{Ri}({t_{{i^{\prime }}j}},{t_{ij}})=0$, which brings about
$\textit{GI}({T_{i}},{T_{{i^{\prime }}}})+\textit{GI}({T_{{i^{\prime }}}},{T_{i}})={\textstyle\sum _{j=1}^{n}}{w_{j}}\cdot (\textit{Ri}({t_{ij}},{t_{{i^{\prime }}j}})+\textit{Ri}({t_{{i^{\prime }}j}},{t_{ij}}))=0$. Herein, (T4.1) and (T4.2) are valid. At last, the presupposition
$\textit{Sf}({t_{ij}})\ne \textit{Sf}({t_{{i^{\prime }}j}})$ leads to either
$\textit{Ri}({t_{ij}},{t_{{i^{\prime }}j}})=1$ or
$\textit{Ri}({t_{ij}},{t_{{i^{\prime }}j}})=-1$. In either case, one has
$|\textit{Ri}({t_{ij}},{t_{{i^{\prime }}j}})|=1$, which indicates that
${\textstyle\sum _{j=1}^{n}}{w_{j}}|\textit{Ri}({t_{ij}},{t_{{i^{\prime }}j}})|=1$, i.e. (T4.3) is correct. The theorem is proved. □
In the final phase, this paper first establishes the T-SF REGIME I prioritization procedure as a means of achieving partial-preference predominance ranks for choice options. Specifically, this paper attempts to constitute two Boolean matrices on the grounds of superiority identifiers and guide indices separately for generating eventual predominance ranks of all available options. First, on the basis of the superiority identifiers $\textit{SI}({T_{i}},{T_{{i^{\prime }}}})$ and $\textit{SI}({T_{{i^{\prime }}}},{T_{i}})$, decision makers or analysts may conclude that the choice option ${a_{i}}$ is preferred to ${a_{{i^{\prime }}}}$ when $\textit{SI}({T_{i}}$, ${T_{{i^{\prime }}}})\geqslant \textit{SI}({T_{{i^{\prime }}}},{T_{i}})$. By contrast, decision makers or analysts may conclude that ${a_{i}}$ is less preferred to ${a_{{i^{\prime }}}}$ when $\textit{SI}({T_{i}},{T_{{i^{\prime }}}})<\textit{SI}({T_{{i^{\prime }}}},{T_{i}})$. Depending on comparison outcomes of the superiority identifier $\textit{SI}({T_{i}},{T_{{i^{\prime }}}})$ and its counter version $\textit{SI}({T_{{i^{\prime }}}},{T_{i}})$, this paper delineates the superiority-based Boolean matrix $\textit{Bs}$ as below.
Definition 10.
Given the superiority identifier
$\textit{SI}({T_{i}},{T_{{i^{\prime }}}})$ for choice options
${a_{i}},{a_{{i^{\prime }}}}\in A$, the superiority-based Boolean matrix
$\textit{Bs}$ involving an entry
$\textit{Bs}({a_{i}},{a_{{i^{\prime }}}})$ (for
$i\ne {i^{\prime }}$) would be designated via comparisons of
$\textit{SI}({T_{i}},{T_{{i^{\prime }}}})$ with
$\textit{SI}({T_{{i^{\prime }}}},{T_{i}})$ in this manner:
Theorem 5.
For all ${a_{i}},{a_{{i^{\prime }}}}\in A$, the entry $\textit{Bs}({a_{i}},{a_{{i^{\prime }}}})$ in the superiority-based Boolean matrix Bs possesses the following properties:
-
(T5.1) $\textit{Bs}({a_{i}},{a_{{i^{\prime }}}})+\textit{Bs}({a_{{i^{\prime }}}},{a_{i}})=1$ if $\textit{SI}({T_{i}},{T_{{i^{\prime }}}})\ne \textit{SI}({T_{{i^{\prime }}}},{T_{i}})$;
-
(T5.2) $\textit{Bs}({a_{i}},{a_{{i^{\prime }}}})+\textit{Bs}({a_{{i^{\prime }}}},{a_{i}})=0$ if $\textit{SI}({T_{i}},{T_{{i^{\prime }}}})=\textit{SI}({T_{{i^{\prime }}}},{T_{i}})$;
-
(T5.3) ${\textstyle\sum _{{i^{\prime }}=1,{i^{\prime }}\ne i}^{m}}{\textstyle\sum _{i=1,i\ne {i^{\prime }}}^{m}}\textit{Bs}({a_{i}},{a_{{i^{\prime }}}})=m(m-1)/2$ if $\textit{SI}({T_{i}},{T_{{i^{\prime }}}})\ne \textit{SI}({T_{{i^{\prime }}}},{T_{i}})$.
Proof.
When
$\textit{SI}({T_{i}},{T_{{i^{\prime }}}})>\textit{SI}({T_{{i^{\prime }}}},{T_{i}})$, it is recognized
$\textit{Bs}({a_{i}},{a_{{i^{\prime }}}})=1$ and
$\textit{Bs}({a_{{i^{\prime }}}},{a_{i}})=0$. On the contrary,
$\textit{Bs}({a_{i}},{a_{{i^{\prime }}}})=0$ and
$\textit{Bs}({a_{{i^{\prime }}}},{a_{i}})=1$ when
$\textit{SI}({T_{i}},{T_{{i^{\prime }}}})<\textit{SI}({T_{{i^{\prime }}}},{T_{i}})$. Thus, one obtains
$\textit{Bs}({a_{i}},{a_{{i^{\prime }}}})+\textit{Bs}({a_{{i^{\prime }}}},{a_{i}})=1$. Next, the condition
$\textit{SI}({T_{i}},{T_{{i^{\prime }}}})=\textit{SI}({T_{{i^{\prime }}}},{T_{i}})$ gives rise to
$\textit{Bs}({a_{i}},{a_{{i^{\prime }}}})=0$ and
$\textit{Bs}({a_{{i^{\prime }}}},{a_{i}})=0$. Hence, one yields
$\textit{Bs}({a_{i}},{a_{{i^{\prime }}}})+\textit{Bs}({a_{{i^{\prime }}}},{a_{i}})=0$. From above, (T5.1) and (T5.2) are correct. (T5.3) can be proved in view of the fact that:
Thus, the theorem is proved. □
Definition 11.
Given a guide index
$\textit{GI}({T_{i}},{T_{{i^{\prime }}}})$ for choice options
${a_{i}},{a_{{i^{\prime }}}}\in A$, the guide-based Boolean matrix
$\textit{Bg}$ involving an entry
$\textit{Bg}({a_{i}},{a_{{i^{\prime }}}})$ (for
$i\ne {i^{\prime }}$) would be designated via comparisons of
$\textit{GI}({T_{i}},{T_{{i^{\prime }}}})$ and
$\textit{GI}({T_{{i^{\prime }}}},{T_{i}})$ in this manner:
Theorem 6.
For all ${a_{i}},{a_{{i^{\prime }}}}\in A$, the entry $\textit{Bg}({a_{i}},{a_{{i^{\prime }}}})$ in the guide-based Boolean matrix Bg possesses the following properties:
-
(T6.1) $\textit{Bg}({a_{i}},{a_{{i^{\prime }}}})+\textit{Bg}({a_{{i^{\prime }}}},{a_{i}})=1$ if $\textit{GI}({T_{i}},{T_{{i^{\prime }}}})\ne \textit{GI}({T_{{i^{\prime }}}},{T_{i}})$;
-
(T6.2) $\textit{Bg}({a_{i}},{a_{{i^{\prime }}}})+\textit{Bg}({a_{{i^{\prime }}}},{a_{i}})=0$ (i.e. $\textit{Bg}({a_{i}},{a_{{i^{\prime }}}})=\textit{Bg}({a_{{i^{\prime }}}},{a_{i}})=0$) if $\textit{GI}({T_{i}},{T_{{i^{\prime }}}})=\textit{GI}({T_{{i^{\prime }}}},{T_{i}})$;
-
(T6.3) ${\textstyle\sum _{{i^{\prime }}=1,{i^{\prime }}\ne i}^{m}}{\textstyle\sum _{i=1,i\ne {i^{\prime }}}^{m}}\textit{Bg}({a_{i}},{a_{{i^{\prime }}}})=m(m-1)/2$ if $\textit{GI}({T_{i}},{T_{{i^{\prime }}}})\ne \textit{GI}({T_{{i^{\prime }}}},{T_{i}})$.
Proof.
The proving process would be analogous to the proof in Theorem
5. □
By applying a peer-to-peer multiplication operation in conjunction with the entries in
$\textit{Bs}$ and
$\textit{Bg}$, the comprehensive Boolean matrix
$\textit{Bc}$ is identified along these lines:
The unit entries in the comprehensive Boolean matrix $\textit{Bc}$ give a description of the confirmed predominance relationships between choice options. The outcome $\textit{Bc}({a_{i}},{a_{{i^{\prime }}}})=1$ indicates that ${a_{i}}$ is preferred to ${a_{{i^{\prime }}}}$ from both perspectives of superiority identifiers and guide indices. In contrast, the outcome $\textit{Bc}({a_{i}},{a_{{i^{\prime }}}})=0$ mentions that ${a_{i}}$ is indifferent to or less preferred to ${a_{{i^{\prime }}}}$ based on superiority identifiers and guide indices. The partial-preference predominance ranks of choice options can be determined by virtue of the entry $\textit{Bc}({a_{i}},{a_{{i^{\prime }}}})$ in $\textit{Bc}$, which renders the T-SF REGIME I ranking conclusion.
However, the use of the Boolean matrices $\textit{Bs}$, $\textit{Bg}$, and $\textit{Bc}$ would sometimes bring about certain difficulties, because no concrete outcome can be concluded concerning the complete predominance ranking among choice options. The characteristic of a net regime analysis would be the circumvention of such difficulties by determining a net superiority identifier and a net guide index for linear ranking outcomes. Such an approach can draw a definite conclusion about the complete predominance ranking of choice options. This is the subject of the T-SF REGIME II prioritization procedure.
The proposed T-SF REGIME II approach delineates the net superiority identifier
${N_{\textit{SI}}}({a_{i}})$ which measures the degree to which the relative attractiveness of a choice option
${a_{i}}$ over the other competing options exceeds the relative attractiveness of the other competing options over
${a_{i}}$. Concurrently, the current T-SF REGIME II approach elucidates the net guide index
${N_{\textit{GI}}}({a_{i}})$ which measures the degree to which the relative fittingness of
${a_{i}}$ over the other competing options exceeds the relative fittingness of the other competing options over
${a_{i}}$. These net measurements are capable of generating a complete-preference predominance ranking among choice options for decision aiding in intricate T-SF contexts. To be specific, the net superiority identifier
${N_{\textit{GI}}}({a_{i}})$ of
${a_{i}}$ with relevance to the other choice options is mathematically denoted as follows:
Additionally, the net guide index
${N_{\textit{GI}}}({a_{i}})$ of
${a_{i}}$ in connection with the other choice options is represented in this manner:
Obviously, a choice option ${a_{i}}$ enjoys a greater preference with a higher ${N_{\textit{SI}}}({a_{i}})$ and a higher ${N_{\textit{SI}}}({a_{i}})$. Following the above rationale, the eventual choice option must satisfy the conditions that its net superiority identifier should be at a maximum and its net guide index at a maximum simultaneously. If both these conditions are not fulfilled, the alternative that possesses the highest average rank would be selected as an eventual solution. Furthermore, the complete-preference predominance ranks can be rendered by reranking choice options in accordance with the average ranks.
The initiated T-SF REGIME I and II methods for manipulating a multiple-criteria choice problem in uncertain contexts with T-spherical fuzziness are devised systematically as Algorithms I and II, respectively, described below. The two algorithms consist of five phases, including formulating a multiple-criteria choice problem in Phase (i), constructing score function-based superiority criteria in Phase (ii), ascertaining the superiority measurements in Phase (iii), pinpointing the REGIME matrix and guide indices in Phase (iv), and generating the eventual partial/complete ranking in Phase (v).
Algorithm I: T-SF REGIME I method
$\underline{\textit{Phase}\hspace{2.5pt}(i):\hspace{2.5pt}\textit{Steps I.1--I.3}}$
Step I.1. Designate the collection of choice options $A=\{{a_{1}},{a_{2}},\dots ,{a_{m}}\}$ and the collection of judgment criteria $C=\{{c_{1}},{c_{2}},\dots ,{c_{n}}\}$.
Step I.2. Signify the normalized weight ${w_{j}}$ in conjunction with each ${c_{j}}\in C$ and the T-SF evaluation value ${t_{ij}}=({\mu _{ij}},{\eta _{ij}},{\nu _{ij}})$ along with the refusal membership ${\gamma _{ij}}$.
Step I.3. Compose the T-SF characteristic
${T_{i}}=\{\langle {c_{j}},({\mu _{ij}},{\eta _{ij}},{\nu _{ij}})\rangle \mid 0\leqslant {({\mu _{ij}})^{z}}+{({\eta _{ij}})^{z}}+{({\nu _{ij}})^{z}}\leqslant 1\hspace{2.5pt}\forall {c_{j}}\in C\}$ in Eq. (
7) associated with each
${a_{j}}\in A$ for
$z\in {Z^{+}}$.
$\underline{\textit{Phase}\hspace{2.5pt}(\textit{ii}):\hspace{2.5pt}\textit{Steps I.4 and I.5}}$
Step I.4. Utilize Eqs. (
6) and (
5) to compute the score function
$\textit{Sf}({t_{ij}})$ and the accuracy value
$\textit{Av}({t_{ij}})$, respectively, of each T-SF evaluation value
${t_{ij}}$ embedded in
${T_{i}}$.
Step I.5. Obtain the superiority criteria in which
${T_{i}}$ is at least as good as
${T_{{i^{\prime }}}}$ based on score functions and build the collection of superiority criteria
$\textit{Cs}({T_{i}},{T_{{i^{\prime }}}})$ using Eq. (
8).
$\underline{\textit{Phase}\hspace{2.5pt}(\textit{iii}):\hspace{2.5pt}\textit{Steps I.6 and I.7}}$
Step I.6. Compute the discrepancy between $\textit{Sf}({t_{ij}})$ and $\textit{Sf}({t_{{i^{\prime }}j}})$ for any two choice options ${a_{i}},{a_{{i^{\prime }}}}\in A$ in terms of each superiority criterion ${c_{j}}\in \textit{Cs}({T_{i}},{T_{{i^{\prime }}}})$.
Step I.7. Make use of the normalized weight
${w_{j}}$ to determine the superiority identifier
$\textit{SI}({T_{i}},{T_{{i^{\prime }}}})$ in connection with
${a_{i}}$ over
${a_{{i^{\prime }}}}$ using Eq. (
11).
$\underline{\textit{Phase}\hspace{2.5pt}(\textit{iv}):\hspace{2.5pt}\textit{Steps I.8 and I.9}}$
Step I.8. Apply Eq. (
12) to generate the REGIME identifier
$\textit{Ri}({t_{ij}},{t_{{i^{\prime }}j}})$ to establish the REGIME matrix
$\textit{Rm}$ in Eq. (
14) for all ordered couples of choice options.
Step I.9. Fuse the normalized weight
${w_{j}}$ and the REGIME identifier
$\textit{Ri}({t_{ij}},{t_{{i^{\prime }}j}})$ to derive the guide index
$\textit{GI}({T_{i}},{T_{{i^{\prime }}}})$ relative to
${a_{i}}$ over
${a_{{i^{\prime }}}}$ using Eq. (
15).
$\underline{\textit{Phase}\hspace{2.5pt}(v):\hspace{2.5pt}\textit{Steps I.10--I.13}}$
Step I.10. Exploit Eq. (
16) to gain an entry
$\textit{Bs}({a_{i}},{a_{{i^{\prime }}}})$ based on superiority identifiers for building the superiority-based Boolean matrix
$\textit{Bs}$ in Eq. (
17).
Step I.11. Use Eq. (
18) to acquire an entry
$\textit{Bg}({a_{i}},{a_{{i^{\prime }}}})$ through the utility of guide indices for setting up the guide-based Boolean matrix
$\textit{Bg}$ in Eq. (
19).
Step I.12. Employ Eq. (
20) to derive an entry
$\textit{Bc}({a_{i}},{a_{{i^{\prime }}}})$ using a peer-to-peer multiplication operation for constructing the comprehensive Boolean matrix
$\textit{Bc}$ in Eq. (
21).
Step I.13. Confirm the partial-preference predominance rank regarding ${a_{i}}$ over ${a_{{i^{\prime }}}}$ if $\textit{Bc}({a_{i}},{a_{{i^{\prime }}}})=1$. Sketch a dominance graph for yielding evidently beneficial choice options.
Algorithm II: T-SF REGIME II method
$\underline{\textit{Phases}\hspace{2.5pt}(i)\text{--}(\textit{iv}):\hspace{2.5pt}\textit{Steps II.1--II.9}}$
Steps II.1–II.9. See Steps I.1–I.9 in Algorithm I.
$\underline{\textit{Phase}\hspace{2.5pt}(v):\hspace{2.5pt}\textit{Steps II.10--II.12}}$
Step II.10. Derive the net superiority identifier
${N_{\textit{SI}}}({a_{i}})$ of
${a_{i}}$ relating to the other choice options using Eq. (
22), and then rank all
m options according to
${N_{\textit{SI}}}({a_{i}})$ in descending order.
Step II.11. Delineate the net guide index
${N_{\textit{GI}}}({a_{i}})$ of
${a_{i}}$ with relevance to the other choice options using Eq. (
23), and then rank all
m options depending on
${N_{\textit{GI}}}({a_{i}})$ in descending order.
Step II.12. Select the top-ranked option as the eventual solution if it enjoys the maximal net superiority identifier and the maximal net guide index, otherwise select an option having the highest average rank. The complete-preference predominance ranks are yielded by reranking options based on the average ranks.
In comparison with the prevailing decision-making methods predicated on a variety of aggregation operators, such as various multiple-criteria evaluation approaches in Ali
et al. (
2020), Chen
et al. (
2021), Garg
et al. (
2021), Guleria and Bajaj (
2021), Khan
et al. (
2021b), Liu
et al. (
2021a), Liu
et al. (
2021b), Munir
et al. (
2020), and Munir
et al. (
2021), the T-SF REGIME architecture and techniques propounded by this research are simpler, easier to use, and more efficacious. The initiated T-SF REGIME methodology in this study possesses a comprehensive theoretical basis; but in terms of execution procedures, it is quite simple and conforms to human intuitive judgments. For analysts or decision makers, the principles of the REGIME method are easy to understand and accept. Moreover, abstract theoretical foundations can be realized through the developed notions and measurements, such as the superiority index, superiority identifier, REGIME identifier, and guide index. The decision maker can exploit systematic algorithms, i.e. T-SF REGIME I and II, to manage real-world multiple-criteria choice problems in highly complex and uncertain environments. In a nutshell, the most significant advantage of the propounded algorithms is highly intellectual but still easily understandable to use. The advanced methodology is designed to be easy for an untrained decision maker to manipulate, and it will facilitate the determination of eventual partial- and complete-preference predominance rankings of choice options in an uncomplicated and effectual manner.
5 Conclusions
The T-SF theory has the productive competence and technological capability to manipulate ambiguous and equivocal decision information in a complex real-world environment. In particular, on the subject of fuzzy community, the T-SF model contains a comprehensive account of several beneficial non-standard fuzzy configurations, such as intuitionistic fuzziness, Pythagorean fuzziness, Fermatean fuzziness, q-rung orthopair fuzziness, picture fuzziness, and spherical fuzziness. The three motivations were the major driving forces to propound the T-SF REGIME methodology, consisting of: (1) high demand for utilizing the T-SF theory in specialized decision analysis, (2) technical gap of the current REGIME methods and techniques, and (3) lack of T-SF versions of the REGIME framework.
This study has made some noteworthy academic contributions to decision-making practice under complicated uncertainties, including the advancement of the REGIME-based technique, the beneficial measurement system in T-SF settings, superiority indices and identifiers for relative attractiveness, REGIME identifiers and guide indices for relative fittingness, and the efficacious T-SF REGIME I and II procedures for decision support. Consider that the REGIME method is a well-established approach to a multiple-criteria evaluation process and choice analysis; however, fresh enrichments of REGIME-based techniques have not been discussed in T-SF decision situations. In this regard, this paper has unfolded a novel and creative T-SF REGIME methodology through the utility of an advisable measurement system in T-SF uncertain circumstances. This paper has utilized an efficacious score function to differentiate T-SF information in a thorough manner. Moreover, the superiority criteria have been recognized judging by score functions and accuracy values; the resulting outcomes have been used to determine the superiority index and the superiority identifier for ascertaining the relative attractiveness between the T-SF characteristics. Furthermore, this paper has identified the REGIME identifier and the REGIME vector to constitute the REGIME matrix and the guide index for ascertaining the relative fittingness between T-SF characteristics. Two effectual prioritization procedures have been inaugurated to generate the T-SF REGIME I and II predominance rankings regarding all choice options. The core notions in the T-SF REGIME I mechanism contain the superiority-based Boolean matrix, guide-based Boolean matrix, and comprehensive Boolean matrix. The core notions in the T-SF REGIME II mechanism involve the net superiority identifier and net guide index. The investigation toward the selection problem of companies for constructing food processing plants has exhibited the usefulness and superior points of employing the advanced T-SF REGIME methodology in tackling pragmatic decision issues.
However, the proposed T-SF REGIME methodology is subject to one major theoretical limitation. This paper has made an important contribution by strengthening the REGIME method aiming to empower it to manipulate T-FS uncertain information. The initiated T-FS version of the REGIME method has been validated to be an advantageous approach to multiple-criteria choice analysis within intricate equivocal environments. The technological applicability has been also illustrated in the selection problem of companies for erecting food processing plants. Nevertheless, decision makers or analysts might recognize some of the research limitations on the propounded methodology. The major limitation of the developed techniques is the early defuzzification of T-SF evaluation values by way of the score function advanced by Zeng
et al. (
2019). After constructing T-SF characteristics in the first phase of the T-SF REGIME framework, the T-SF evaluation values are then converted to the scalar value using the score function; moreover, the sequential phases are performed by the agency of the exploitation of such crisp forms. The specification of score functions can exploit enough information contained in T-SF evaluation values because of the utilization of grades of positive, neutral, negative, and refusal memberships. However, the T-SF evaluation values are defuzzied in a very early stage, which might make the T-SF REGIME method questionable in the process of evaluation, because perhaps certain information might be lost in practicality. In this regard, the initiated Algorithms I and II might result in a small amount of information not being considered in addressing a multiple-criteria choice problem in uncertain contexts, which is the main research limitation faced by the T-SF REGIME methodology.
Another consideration should be mentioned concerning the application of T-SF sets, namely, the data collection issue. The T-SF theory has been progressively concerned owing to its great ability for treating much complicated and obscure decision situation. However, a critical challenge for the T-SF theory to put into practice is how to collect evaluations from the decision maker and convert them into T-SF information. In most cases, the decision maker may be not familiar with the notion of T-SF sets. Thus, the decision maker may not know what T-SF evaluation values mean. Accordingly, the data collection process would be very challenging in case an analyst would like to collect evaluations from the decision maker. Therefore, how to reasonably produce T-SF evaluation values originating out of the decision maker’s discernments and appraisals is an issue worthy of mention. This study suggests an approach to generating T-SF evaluation values by employing a linguistic rating system, i.e. using the scale for the linguistic variables. For example, Mathew
et al. (
2020) presented two nine-point rating scales and an eleven-point rating scale that can be exploited by decision makers to quantify their subjective judgments and assessments. By the same token, Farrokhizadeh
et al. (
2021) and Jin
et al. (
2021) also provided useful nine-point rating scales for facilitating data collection. These linguistic variables can be easily converted into spherical fuzzy or T-SF numbers. With the advent of linguistic rating scales involving spherical fuzziness, linguistic terms can be quantified by transforming them to spherical fuzzy numbers, which leads to convenient construction of T-SF evaluation values.
Furthermore, this paper proposes some future research work directions that are promising and appropriate. First, the proposed notions and measurements (e.g. the superiority index, superiority identifier, REGIME identifier, and guide index) can furnish theoretical bases to create other decision-making models and support mechanisms. For example, by expanding Garg and Rani’s (
2021) intuitionistic fuzzy MULTIMOORA (i.e. MULTIplicative form for Multiple Objective Optimization based on a Ratio Analysis) technique, our proposals can be incorporated into the MULTIMOORA scheme to adapt to T-SF decision contexts. By the same token, the proposed measurements can be exploited in the procedure of the ORESTE (i.e. Organisation, Rangement Et Synthèse de données relaTionnElles) approach for facilitating an advancement of ORESTE in T-SF circumstances. Secondly, in addition to multiple-criteria choice analysis, the procedures for the T-SF REGIME I and II prioritization can be recognized as a significant enhancement tool for exploring group decision analyses, sorting approaches, design and evaluation strategies, etc. By way of illustration, the sine-trigonometric operations presented by Garg (
2021b) can be generalized to T-SF environments and then combined in the T-SF REGIME mechanism for group decision-making processes. Finally, the evolved T-SF REGIME methodology can be continuously modified and developed for adapting to different decision circumstances. To give an instance, Garg’s (
2021a) initiated possibility degree measure derived from the q-rung orthopair fuzzy model is suggested to be exploited and extended in the evolved T-SF REGIME methodology. These improvements and modifications can offer the most appropriate and functional approaches regarding the exact engineering, management science, economics, and business problem.

