Abstract
In the family of Intelligent Transportation Systems (ITS), Multimodal Transport Systems (MMTS) have placed themselves as a mainstream transportation mean of our time as a feasible integrative transportation process. The Global Economy progressed with the help of transportation. The volume of goods and distances covered have doubled in the last ten years, so there is a high demand of an optimized transportation, fast but with low costs, saving resources but also safe, with low or zero emissions. Thus, it is important to have an overview of existing research in this field, to know what has already been done and what is to be studied next. The main objective is to explore a beneficent selection of the existing research, methods and information in the field of multimodal transportation research, to identify industry needs and research gaps and provide context for future research. The selective survey covers multimodal transport design and optimization in terms of: cost, time, and network topology. The multimodal transport theoretical aspects, context and resources are also covering various aspects. The survey‘s selection includes currently existing best methods and solvers for Intelligent Transportation Systems (ITS). The gap between theory and real-world applications should be further solved in order to optimize the global multimodal transportation system.
1 Introduction
The current context of World Globalization has raised many difficult problems regarding the transportation of goods. The products are hauled over large distances of land and water, and more often have to travel by more than one means of transport: by ships, planes, trucks (see Van Schijndel and Dinwoodie,
2000); all these lead to the Multimodal Transportation Systems (MMTS).
In contrast with classical, single mean transportation, multi-modal transportation has multiple constraints, for example, Litman (
2017) names different optimization processes as parcel loading, and transfer between transports. In a context of today’s global warming and increased pollution, it is a necessity to also globally reduce gas emission. The environmental goal correlated with the economical performance could be reached through several ways including an optimized transport planning and using appropriate resources.
In the literature review on Multimodal freight transportation planning conducted by SteadieSeifi
et al. (
2014), several strategic planning issues within multi-modal freight transportation and tactical planning problems are shown. Complex operational planning for real-time requirements of multimodal operators, carriers and shippers, not previously addressed at strategic and tactical levels, are described. The main models with related solvers and proposed future research are included. A detailed review, with an analysis of the optimization-based decision-making models for the problem of
Disaster Recovery Planning of Transportation Networks (DRPTN), is provided by Zamanifar and Hartmann (
2020). The authors described the phases of optimization-based decision-making models and investigate their methodologies. Nevertheless, the authors identified some challenges and opportunities, discussed research improvement and made suggestions for possible future research.
A recent systematic review about dynamic pricing techniques for
Intelligent Transportation System (ITS) in smart cities was published by Saharan
et al. (
2020). The authors included existing ITS techniques with pertinent overviews and discussions about problems related to electric vehicles (EVs) used for reducing the peak loads and congestion, at the same time increasing the mobility.
The current work overviews the multimodal transport. Section
2 presents prerequisites related to the multimodal transport and the context around it. Section
3 follows presenting the characteristics and the challenges related to the transport. Further on, methods of planning (Section
4) and optimization (Section
5) in terms of time (Section
5.1), cost (Section
5.2) and network topology (Section
5.3) are presented. Existing unimodal transport models and solvers with possible future extension to multimodal features are included in Section
6. Section
7 draws the important conclusions about multimodal transport.
2 What is Multimodal Transportation?
The multimodal transport is defined by the UN Convention on International Multimodal Transport of Goods as follows.
Definition 1 (See Peplowska-Dabrowska and Nawrot, 2019).
The multimodal transport is the transport of goods from one place to another, usually located in a different country, by at least two means of transportation.
Mathematical formalization. The transportation problem was first formalized by Monge (
1781) and extended by Kantorovich (
1942). Today there are mathematical optimization techniques as, for example, Newton, Quasi-Newton methods and Gauss-Newton techniques already used or to be further used in relation with transportation, e.g. in assignment models to calibrate the traffic and transit; see: Karballaeezadeh
et al. (
2020), Ticala and Balog (
2008), Kamel
et al. (
2019).
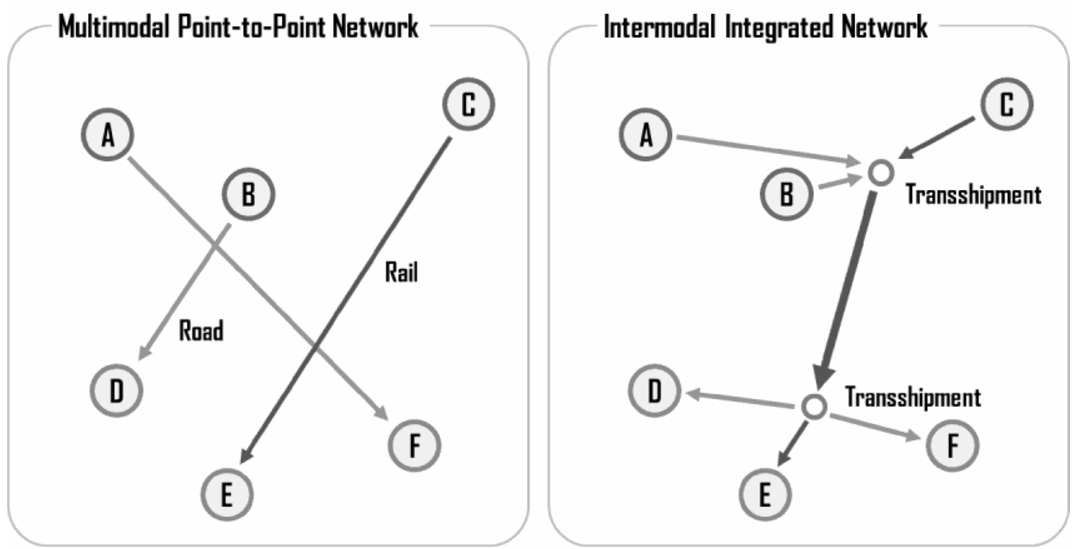
Fig. 1
The difference between a multimodal point-to-point network and a multimodal integrated network, see Rodrigue (
2020).
Optimization. A classical transportation of goods implies direct links and one mode of transportation (Fig.
1 left), a shortest path route, from a sender to a receiver of goods, see Zografos and Androutsopoulos (
2008); the multimodal transport (Fig.
1 right), implies complex links and more than one mode of transportation. Optimization of classical transportation routes is a fairly easy and intensely studied topic. There are already existing state-of-the-art algorithms, like Dijkstra’s Algorithm (see Jianya,
1999), or Clarke-Wright technique as in Golden
et al. (
1977). These approaches use a single mean of transport, a single warehouse and one or more clients (or receivers).
Real-life scenarios. In the complex reality, goods can be transported in any direction, for example, inside a country there are couriers delivering from any side of the country to another side; using just trucks to perform a complete task would be impossible, as the problem has
$O({n^{2}})$ complexity for
n cities to reach. Optimizing this case means designing a system with a central warehouse or hub, where all the goods are unloaded, sorted according to the destination and finally loaded on the respective trucks and dispatched towards the destination. This optimization alone reduces the required number of trucks (the same truck makes a round trip from each city to the central hub) (Zhang
et al.,
2013).
But what about the
larger countries, or about
international transport? The multimodal transportation has the advantage of moving a huge amount of goods, in the hundreds of thousands of tons at once, via large ships, over very large distances (Fig.
1).
3 Characteristics and Challenges of Multimodal Transportation
This section focuses on the challenges of the multimodal transportation, both for
passengers (Section
3.1) and
freight (Section
3.2). The majority of received goods are moved by many transportation modes, e.g. ships, airplanes, trucks. In the first stages of the transport, the sorting hubs collect all the goods from different senders, establish their destination and assign them a way of dispatch. Routes may be calculated at this step to assess the most economical ones, both in cost and time. Goods with the same route are grouped and loaded on the same shipment mode.
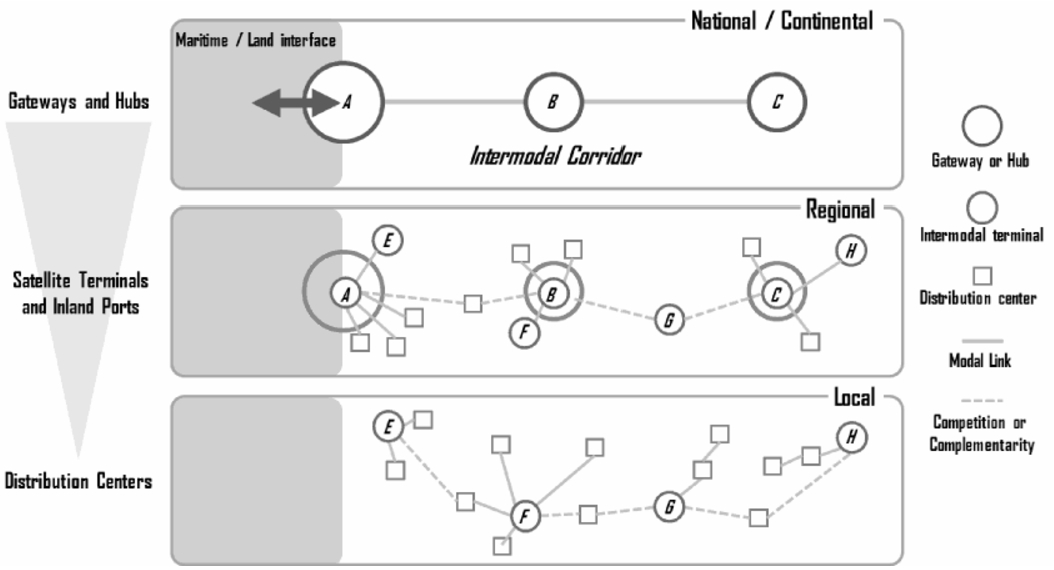
Fig. 2
Overview: diverse scales of multimodal transport, from continental to local (Rodrigue,
2020).
Figure
2 shows the direct
consequence: when reaching the end of a route, for each transportation mode there must be a sorting/dispatching hub. These operations of unloading, sorting, grouping and dispatching are repeated at every hub and with a highly time consuming action. As a consequence, the intermediate hubs have to be very organized so as to limit the time spent at that point, and also their number has to be kept low enough. As a disadvantage, the very large number of shipping hubs will dramatically increase the transport cost, due to the number of transport units used.
Based on these features, several challenges arise: How can we make shipping from A to B cheaper, quicker, and with the least environmental impact? How can we calculate the optimum number of hubs with maximum benefits? What is the optimal way of transporting goods between hubs while avoiding their weaknesses?
> Real-life scenarios.
–
HAZMAT: transport Security Vulnerability Assessment (SVA) by Reniers and Dullaert (
2013). The hazardous materials HAZMAT transport SVA assesses the relative security risk levels of the different modes of hazardous freight transport models, e.g. road, inland waterways, pipelines or railway. The policymakers could use this tool to assess the user-friendly security in multi-modal transport. The HAZMAT model follows:
-
– The routes are split into smaller segments.
-
– The probability scores of security-related risks in which dangerous freight is involved and possibly causing fatalities in the surrounding population, are determined for each segment.
-
– The impact of injury scenarios are computed in terms of the number of people within the 1% lethal distance of the incident centre.
-
– Based on these probability and impact scores, transport route security risk levels are determined.
-
– The transshipment risks are considered for determining the final transport route security risk levels.
The intermodal risk is determined on the minimum security risk path, considering only the risks of the individual segments of a transport route and include also the number of intermodal transshipment.
The risk with the transshipment is defined as: ${R_{t}}={R_{nt}}(1+x(nts))$ where ${R_{t}}$ is the security with the transshipment, ${R_{nt}}$ is the security risk without transshipment, x is the weight factor for importance of transshipment risks, compared with the transportation risks and $nts$ is the number of transshipment. The model was implemented with CPLEX studio and OPL; it was successfully tested on two multimodal networks with highways and railways.
–
New Delhi, Indian busy urban area MMTS by Kumar
et al. (
2013). In 2021 the Delhi population will be around 23 million, therefore public transit should be integrated. In Kumar
et al. (
2013) MMTS focuses on reducing congestion on roads and improving transfers and interchanges between modes. Delhi’s public transport will grow from a 60% of the total number of vehicular trips to at least at 80% in 2021; 15 million trips per day by 2021 in the Integrated Rail-cum-Bus Transit, plus 9 million by other modes are estimated. The Delhi public transport model is illustrated, evaluated and its performance is discussed in Kumar
et al. (
2013).
The performance of the MMTS is quantified using the following measures.
-
– Travel Time Ratio (TTR): a large TTR value leads to a less competitive public transport, e.g. $\textit{TTR}\in [1,5]$;
-
– Level of Service (LS) is a ratio of Out-of-Vehicle Travel Time (OVTT) to In-Vehicle Travel Time (IVTT); a large LS measure leads to a less attractive public transport, e.g. $\textit{LS}\in [1.2,5.0]$;
-
– Inter-connectivity Ratio (IR) is the ratio of access and egress time to the total trip time; $\textit{IR}\in [0,1]$;
-
– Passenger Waiting Index (PWI) is the ratio of mean passenger waiting time to transport services’ frequency; the number of boarding passengers is less or equal to the available space in the transport mode; $\textit{PWI}\in [0,1]$;
-
– Running Index (RI) is the ratio of total service time to total travel time; a large RI leads to a decreased efficiency of the system; $\textit{RI}\in [0,1]$;
In particular, for the New Delhi case study: $\textit{TTR}=1.3$ shows a competitive public transport; LS, the mean $\textit{OVTT}/\textit{IVTT}>1$, thus people spend more time out-of-vehicle than in-vehicle; $\textit{IR}\in [0.2,0.5]$ value shows that inter-connectivity between transportation modes should be improved; $\textit{PWI}=0.825$ for the metro is recommended as the mean passenger waiting time is similar to metro’s frequency; $\textit{RI}=0.7681$, indicates that passenger satisfaction should be improved.
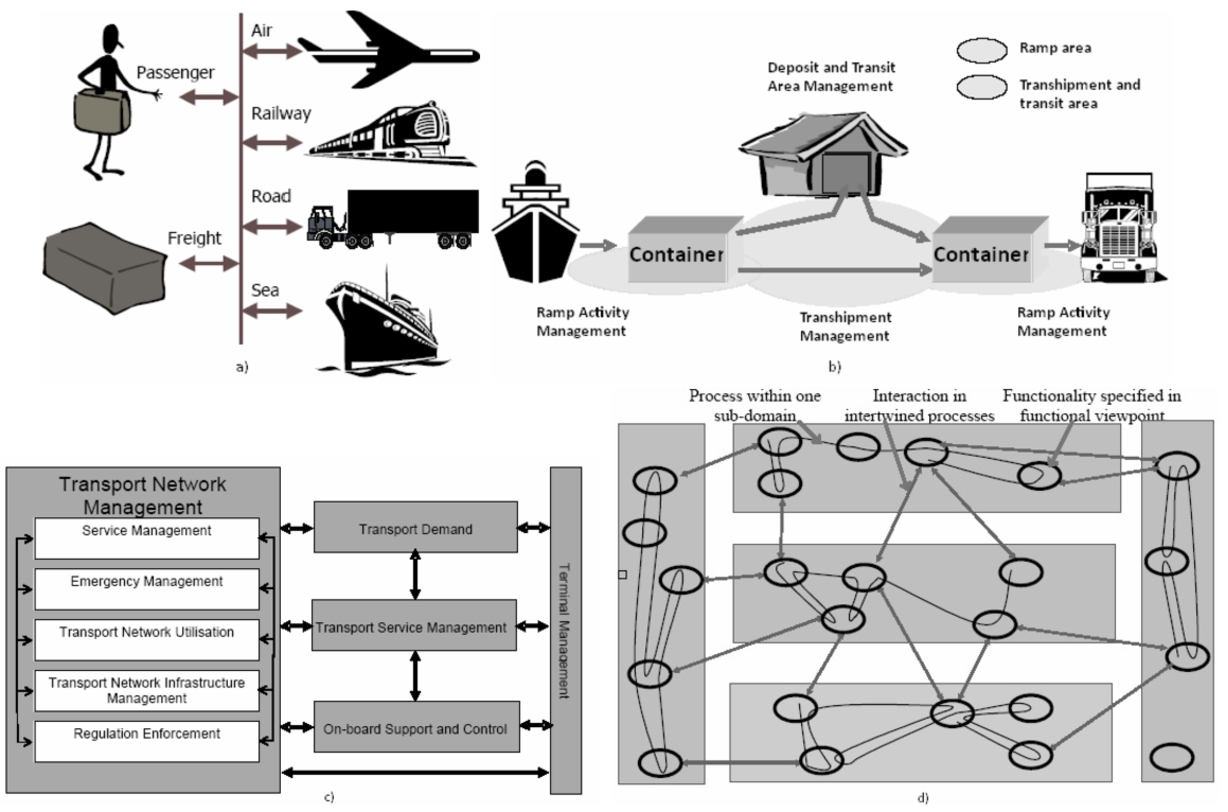
Fig. 3
ARKTRANS: the Norwegian framework for MMTS (Natvig
et al.,
2006): a) MMTS components; b) Functionality required related to transhipment and storage; c) Reference model and upper level functional decomposition of the Transport Network Management; d) Intertwined processes, a theoretical example.
–
ARKTRANS. The Norwegian MMTS framework architecture by Natvig
et al. (
2006) and Natvig and Vennesland (
2010). The framework offers an overview of all the major systems running in Norway that will hopefully further contribute to new and improved solutions. The transport, whether sea, air or railway, have similar needs and challenges with respect to communication, information, management, planning and costs.
Figure
3 illustrates: a) specific multimodal components, b) an example of functionality between components, c) an example of the Transport Network Management, d) and how a transport process includes functionality from sub-domains and how processes are intertwined; thus transport services work together and efficiently exchange information. Furthermore, the main
MMTS specifications of the ARKTRANS frameworks could serve as a guide for other similar frameworks.
-
– A reference model with detailed sub-domains and the roles of the stakeholders;
-
– A functional view with detailed functionality of sub-domains;
-
– A behaviour view with detailed scenarios & interactions between sub-domains;
-
– An information view with detailed models for freight transport & MMTS route information.
The detailed technical aspects conclude this list. A beneficent interaction within all MMTS process leads to an efficient multimodal transport framework. Overall conclusions specify that MMTS is especially suited for long distances; a major MMTS feature is the total travel time; the access, egress and transfer times could be reduced if there is an integrated MMTS, e.g. park and bicycles facilities, and card access on transit systems.
Other Frameworks. Frameworks for multimodal transport security and various policy applications are described in detail in the book by Szyliowicz
et al. (
2016). Other related
frameworks and security challenges, for both passengers and freight and security and policy applications around the world, are analysed in the book by Wiseman and Giat (
2016).
3.1 Passenger Multimodal Transportation
> Theoretical approaches.
– Designs for chains and networks by Bockstael-Blok (
2003). As the author describes it: “The objective of this research is: Develop a design approach for improving inter-organizational multimodal passenger transport systems from a chain perspective”. The article raises some interesting aspects, like balancing the positive and negative impacts of mobility, a holistic approach for modes of transportation not necessarily reducing the number of kilometres for passengers, but improving the number of vehicle-kilometres, resulting in a more efficient usage of the resources (infrastructure, fuel).
–
A highly conceptual approach by Chiabaut (
2015). It is applied to a very idealized network. The authors aim to combine different transport modes by extending the concept of Macroscopic Fundamental Diagram (MFD) and therefore, the efficiency of the global transportation system can be assessed. This approach can be applied to a wide range of cases. Although it is an idealized analysis, it provides knowledge about how to compute the overall performance of a multimodal transportation network and methods to compare different traffic management strategies.
> Real-life scenarios.
–
A multiobjective linear programming model for passenger pre-trip planning in Greece by Aifadopoulou
et al. (
2007). As a case study, trips in Greece using public transport were studied through an integrated web based information gateway. The introduced algorithm (with polynomial complexity) computes the compatibility of various modes based on user preferences, respective intermodal stations, and identifies the feasible paths. It was structured to check and certificate optimality; validation on how constrains impact the computational complexity linear model was made; and it focuses on a decomposition strategy. Hub selection is significant for compatibility and viability of MMTS; it leads to identify parameters in order to increase compatibility of MMTS services and fees.
–
A detailed analysis of the Rhein-Ruhr area by Schöharting
et al. (
2003). The authors identified the
Rhein-Ruhr area as a network of corridors (or mega-corridor). Good practices are featured and analysed with the aim of putting the
Rhein-Ruhr area on the “map” of good examples to follow.
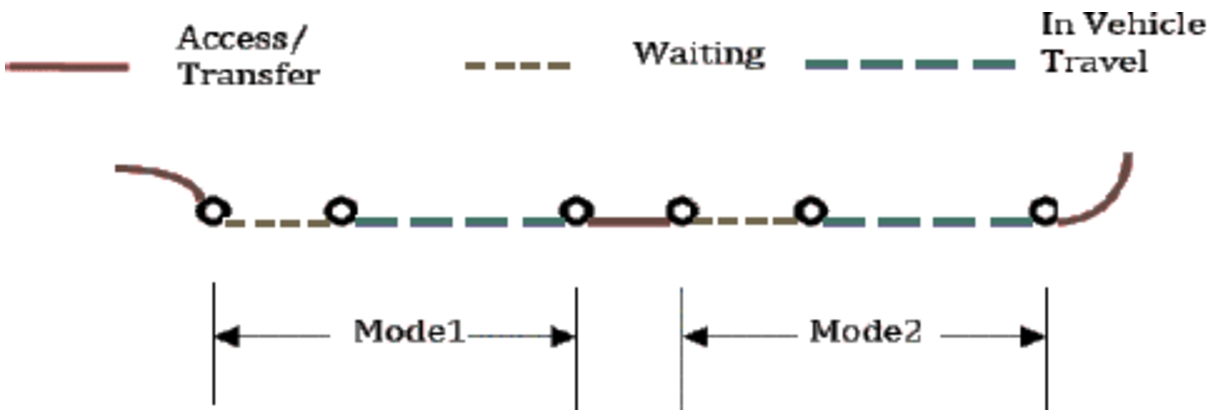
Fig. 4
Passenger Multimodal Transportation: example of a “waiting time model” (Bouzir
et al.,
2014).
–
A “waiting time model”: case study Tunisian Great Sahel by Bouzir
et al. (
2014). The model based on multiple variables was developed in order to optimize waiting time in stations. A case study was based on a survey in the Tunisian Great Sahel. Multiple Correspondence Analysis (MCA) and the General Linear Model were technically used. The new model from Fig.
4 depends on the following features: the travel cost, purpose and frequencies while using MMTS, and is based on the age of respondents.
The main results of the case study follow.
-
– The MMTS combination including bus & tram needs a longer waiting time than other transportation modes;
-
– Young people wait longer for transport services; they use public transport more often than workers; tourists wait more than daily passengers;
-
– MMTS trips, including waiting time of taxis, are shorter when two transport services are included;
-
– The semi-collective transportation seems beneficent as it reduces waiting time; the semi-public transport with just one transportation mode, e.g. taxi, cancels reduced waiting time;
-
– The travel cost has a major influence in the overall waiting time.
The waiting time within public transportation is a direct consequence of the quality of the transportation service.
–
TRANSFER model-multimodal network in large cities by Carlier
et al. (
2005). The model was introduced for analysis of the multimodal network in large cities, as well as route generation. Building Park and Ride (P&R) keeps automobiles outside city centre. More P&R locations are planned for car drivers as they could park there and transfer to public transport to further arrive in the city centre. The main advantage is that it makes public and/or alternative transport more appealing to passengers.
As any other model, it could be successful if MMTS became more attractive than unimodal transport, e.g. car-only trip. The access and egress are also quantified. Here, MMTS are represented as supernetworks where unimodal networks are interconnected by transfer links, the possibility of transfer and related time and costs. TRANSFER components include the following:
-
– A multimodal route-set generation module based on network features and passenger preferences;
-
– An assignment module to distribute transport flows among routes;
-
– A path-size route-choice algorithm to avoid overlap among the routes in a route set.
The superbuilder tool was developed, combining some unimodal networks & transfering data in order to generate a multimodal supernetwork with features of unimodal networks and most relevant transfer possibilities.
–
Transfer points with specific features by Sun
et al. (
2015). The authors analyse age-related transfer speed, the effect of the time of day, the effect of a single person in relation to others, crowding and the use of smart cards. The authors detailed the following: passenger behaviour related to transfer between MTTS modes; correctness of data in order to make a feasible model for passenger transport when complex real-world configurations are provided; efficient using of the Smart card data within MMTS. An overall conclusion includes the fact that passengers are faster in the morning whether or not it is crowded; children and seniors transfer more slowly than adults but children outperform adults in relation to overpasses; further models will have to support pedestrian behaviour and convenient facility design.
3.2 Freight Multimodal Transportation
–
A case study for least-developed economies where different problems arise, is presented by Islam
et al. (
2006), where the situation of Bangladesh is explored from the point of view of infrastructure, as well as local bureaucracy. In order to evaluate the extent of integration of seaport container terminals in supply chains, Panayides and Song (
2008) define and develop specific measures. Optimizing the integration of said container terminals can improve the flow of freight, limiting time waste and delays.
–
A case study: shipments focusing on a major iron and steel manufacturer from NW Australia and it’s iron ore shipments to NE China, are presented by Beresford
et al. (
2011). They studied multiple routes and transport options and even punctual optimization (like congested traffic at a specific moment). Their studies suggest that for long shipments, port variations and inland transport variations have only marginal overall differences, so several combinations of transport and handling methods may successfully coexist. A counter-intuitive conclusion is that just one company controls the entire supply chain, as the bulk cargo market is subject to frequent changes of the prices under global economic conditions.
Others. In Yuen and Thai (
2017) Supply Chain Integration with barriers for the maritime logistics industry is discussed. The authors identified a list of barriers from interviews and literature reviews, but also from 172 surveys sent to container shipping companies. Five factors that cause most of these barriers were also identified. Collaborations are also discussed by Stank
et al. (
2001). An integrated mathematical model of optimal location for transshipment facility in a single source-destination vessel scheduling and transportation-inventory problem was proposed by Al-Yakoob and Sherali (
2018). The authors’ hybrid proposal finds a set of cost-effective facility locations and that the use of these locations reduces costs (e.g. daily vessels operations, chartering and penalties costs).
4 Multimodal Transport Planning
Multiple facets of planning multimodal transport exist, making it more difficult. For example, in a large city, somebody might suddenly decide to engage in a long distance travel. This implies an ad-hoc computation of the route and means of transport to be used, according to the individual personal preferences, e.g. not using metro system due to motion-sickness. Planning such a transport means using any available means at the specific time; the factors to consider could include: time, cost, weather, waiting time in hubs, etc. What does planning a diverse transport system for a large city imply? The designer must compute the available resources, the requirements and even the schedules/working hours of different companies.
In the planning phase, the designer could suggest the transport means (buses, trams, etc.) in order to obtain an economic and eco-friendly system. An Introduction in Multimodal Transportation Planning book was published by Litman (
2017) in which he summarizes the basic principles for multimodal transportation planning for people. He studies transport options for pedestrians, like sidewalk design, bicycles, ride-sharing and public transit systems. He also has very good explanations for multimodal transport planning process, impact to be considered that is often overlooked and different traffic models, like the Four-Step Traffic Model. The first stage of planning a multimodal transport system is to understand its complexities. A complete and accurate model has to be created and analysed.
> Planning MMTS with uncertainties and limitations.
–
Fuzzy cross-efficiency Data Envelopment Analysis by Dotoli
et al. (
2016). The planning of efficient multimodal transports using a fuzzy cross-efficiency Data Envelopment Analysis technique is presented by Dotoli
et al. (
2016). Other approaches like uncertainty conditions with complex traits and high discriminative power are described. They prove the effectiveness of their approach while studying the optimal transport planning and computing the boundaries of the multi-modal transport. In Sumalee
et al. (
2011) the multi-modal transport network with demand uncertainties and adverse weather conditions includes formulation of the fixed point problem; other future and existing related developments include works by Ticala (
2017) and Xu and Gao (
2009).
–
Metaheuristics for real-time decisions by Mutlu
et al. (
2017). The planning part of multimodal transport with various limitations is reviewed by Mutlu
et al. (
2017). They discuss problems like real-time decisions in the context of short-term planning, restructuring and re-configuring logistic strategies, and collaborative planning (Fig.
5). Appropriate solution methods and intuitive meta-heuristic approaches to rapidly act upon changes are suggested.
> Passenger & freight flows Planning for Multimodal transport.
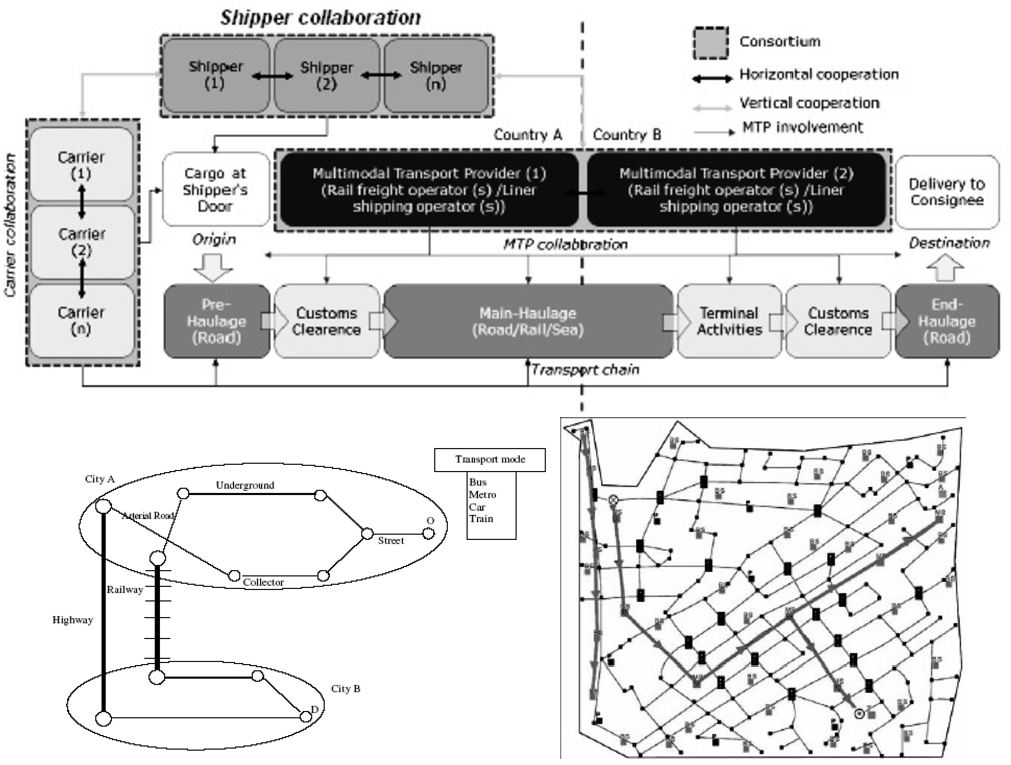
Fig. 5
Freight Transport Network, Multimodal Freight Transportation (MTP) Collaborations, as in Mutlu
et al. (
2017) (upper); Network levels and transport modes (left); using Multimodal Routing Algorithm to find the optimum path: the number of paths, transfers and total time (right), see Bielli
et al. (
2006)
–
Multi-Agents Systems for MMTS planning by Greulich
et al. (
2013). As the name suggests, the implementation uses intelligent agents representing various stakeholders and considers the effects of passenger behaviour.
–
Genetic Local Search tested in the Java Island, Indonesia by Yamada
et al. (
2007). The research revealed that a procedure based on
Genetic Local Search outperforms in order to find the best combination of alternatives.
> Multi-modal systems.
–
A multimodal travel system by Bielli
et al. (
2006). The authors focused on the network object modelling (Fig.
5). This enables to use the model for computing a shortest path while also integrating multimodal options. They also implement and test a solution for the problem of long-run planning in such systems.
–
Syncromodal Transport Planning by Mes and Iacob (
2016). It is a multimodal planning where the best possible combination of transport modes is selected for each package and is discussed in depth. The syncromodal algorithm is implemented in a 4PL service provider in the Netherlands and managed to obtain a 10.1% cost reduction and a 14.2% reduction in
$C{O_{2}}$.
–
A multimodal transport path sequence: AND/OR graphs facilitate planning by Wang
et al. (
2020b). It proposes a triple-phase generate route method for a feasible multimodal transport path sequence, based on AND/OR graphs. Energy consumption evaluates the multimodal transport energy efficiency. A biobjective optimization model for both energy consumption and route risk is solved with an ant-based technique. The research is limited by the graph complexity; the simulation shows valid and promising results.
> Traffic Flow Risk Analysis and Predictions.
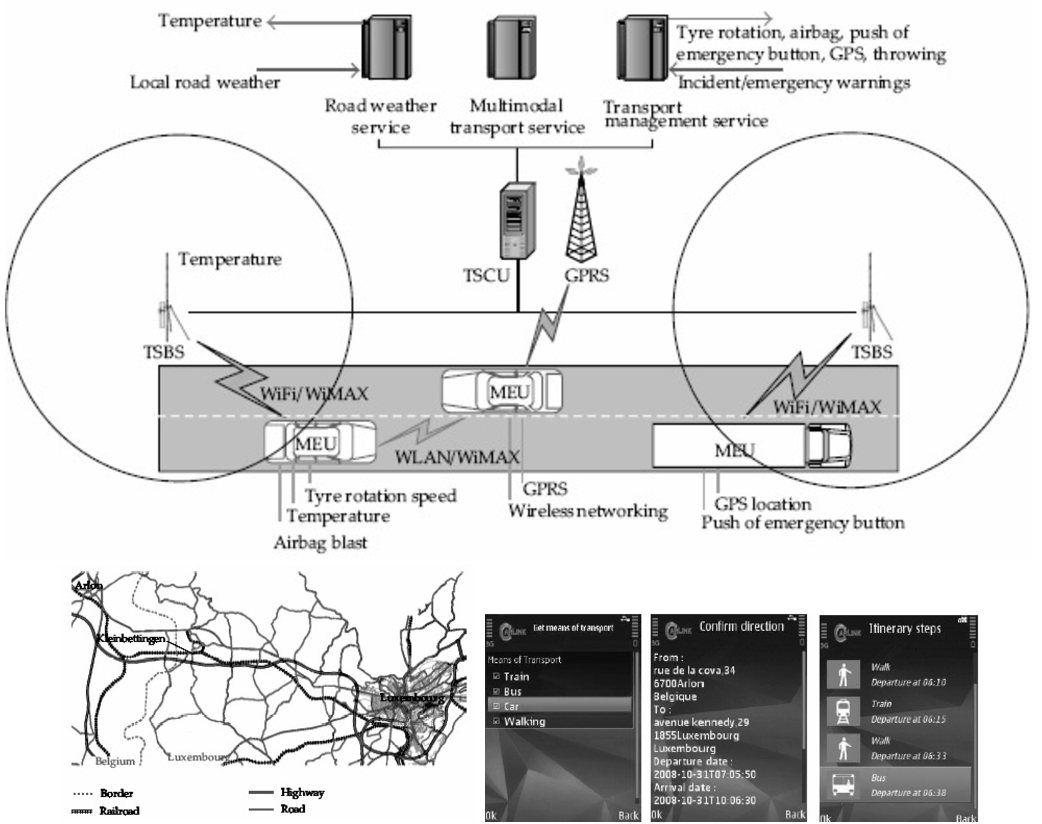
Fig. 6
European Carlink framework for distributed time-dependant transport networks; a validation within a route from Arlon to Luxembourg and a related mobile application representations (Bock,
2010).
–
Fuzziness approach for risk analysis by Stanković
et al. (
2020). A fuzzy Measurement Alternatives and Ranking according to the Compromise Solution, fuzzy MARCOS for Road Traffic Risk Analysis was proposed. The method defines reference points, determined relationships between alternatives & fuzzy ideal/anti-ideal values and defined utility degree of alternatives in relation to the fuzzy ideal and fuzzy anti-ideal solutions. A case study on a road network of 7.4 km was made. The method supported multi-criteria decision-making, within uncertain environments and its results, in terms of risk, could be further used for improving road safety. Other similar efficient method used to cope with multi-criteria optimization is described in Dzemyda and Petkus (
2001). As a plus, parallel processes, see e.g. Dzemyda (
1996), are effective to optimize objective functions.
–
A Best-worst method & triangular fuzzy sets by Moslem
et al. (
2020). It is used for ranking and prioritizing critical driver uncertain behaviour criteria for road safety. The case study uses data from Budapest city: on how drivers perceived road safety issues.
–
Intelligent transportation system-Bird Swarm Optimizer by Zhang and Lin (
2020). It includes an Improved Bird Swarm Optimizer used to predict traffic flows; the prediction results are evaluated and an accurate prediction is obtained; the model has positive significance to prevent urban traffic congestion.
5 Optimization of Multimodal Transport
A distributed approach for time-dependant transport networks integrated in the multimodal transport service of the European Carlink platform and validated in real scenarios, was proposed by Galvez-Fernandez
et al. (
2009) (Fig.
6). A real-life validation is included for a specific route from a Belgian city Arlon to Luxembourg.
In the related mobile application implementation within MTS of the Carlink Platform, the requests are sent to the MTS and the users get the shortest path between two selected locations. A framework for selecting an optimal multi-modal route was designed by Kengpol
et al. (
2014) based on a multimodal transport cost-model, CO
2 emissions and even the integrated quantitative risk assessment. This complex optimization targets to minimize transportation costs, transportation time, risk and CO
2 emission all at once. Multi-node, Multi-mode, Multi-path Integrated Optimization Problems using Hybrid heuristics in the work of Kai
et al. (
2010) are studied. They propose an integrated
Particle Swarm Optimization (
PSO)-
Ant Colony Optimization (
ACO) double-layer optimization algorithm.
Hierarchical network structures of transport networks and how the main mechanisms lead to these network structures are the main interests of van Nes (
2002). Optimizing Containerized Transport across multiple choice Multimodal Networks using Dynamic Programming was proposed and successfully tested on a real problem by Hao and Yue (
2016). Route Optimisation Problem using Genetic Algorithms (GA) was proposed by Jing
et al. (
2012); the same technique was used to solve a Multi-Objective Transport System by Khan
et al. (
2019) and could be further extended for the multimodal transport. GA was also used by Kozan and Preston (
1999) to optimize the time for container handling/transfer, and, respectively, the time at the port, by speeding up the handling of operations.
5.1 Time Optimization of Multimodal Transport
–
Running time &
Rescheduling; solver: Ant Colony Optimization. Zidi and Maouche (
2006) propose an Ant-Colony Optimization (ACO) approach for the rescheduling of multimodal transport networks. The ant-colony approach is best in this case (rescheduling) as it is able to work from a given state and only adapt the solution to new conditions. Rescheduling is a must, as the system is subject to disturbances (traffic jams, collisions, strikes) which cannot be accounted for at the beginning of the transport, but are very likely to introduce delays or other discrepancies. Furthermore, Zidi
et al. (
2006), plans the public transportation system, by using the ant-colony optimization when the theoretical schedule cannot be followed; this approach overcomes the inherent overloading with information of the operators when some problematic situations occur.
–
Transport time between nodes; solver: Genetic Algorithms &
K-shortest path. Zeng
et al. (
2009) take into consideration the transport time between nodes, time needed for mode change and possible delays. They also present a model that aims to minimize transport and transfer costs, built on a GA based K-shortest-paths.
–
Real-time system. We cannot discuss time optimizations without including (Bock,
2010) article about “real-time control of freight forwarder transportation networks”. The architecture is depicted in Fig.
7. His approach integrates multimodal transportation and multiple transshipments. The real-time system is continually optimized in order to adapt it to the current status of the live data.
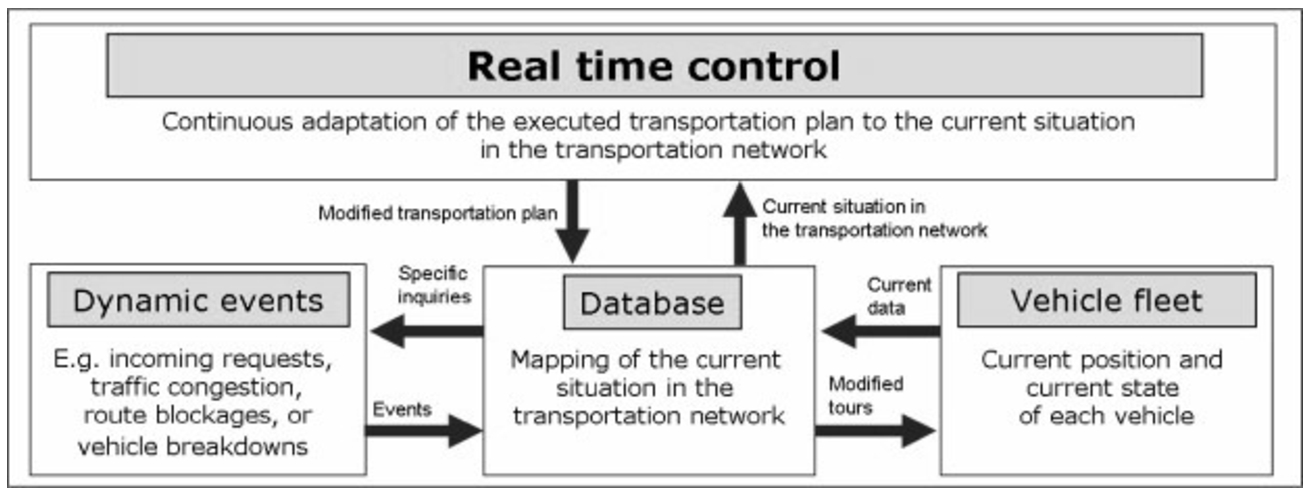
Fig. 7
Information flow in a real-time control system of transportation networks (Bock,
2010).
5.2 Cost Optimization of Multimodal Transport
From the perspective of the multimodal logistics provider, cost may be the second most important aspect, immediately after customer satisfaction. This is why cost optimization is one of the concerns of every CEO.
–
Cost Optimization with specific criteria using Mixed Integer Linear Programming by Sitek and Wikarek (
2012). The authors included a mathematical model of a multilevel cost-optimization by
Mixed Integer Linear Programming (
MILP). They analyse and integrate in their algorithm, as optimization criteria, factors such as costs of:
Production, Transport, Distribution and
Environmental Protection. Furthermore, all these multiple factors are used by Sitek and Wikarek (
2012) as optimization criteria into the MILP algorithm, where more criteria are included: timing, volume and capacity. The tests for showing the possibilities of practical decision support and optimization of the supply chain have been performed on sample data.
–
Cost Optimization including emissions &
economies of terminal using Genetic Algorithms by Zhang
et al. (
2013). The authors discussed the environmental costs and introduced a modelling optimization approach for terminal networks, integrating the costs of CO
2 emissions and economies of terminals. Their proposed algorithm is composed of two levels: the upper level uses genetic algorithms to search for the optimal terminal network configurations; the lower level performs multi-commodity flow assignment over a multimodal network. This model is applied to the Dutch container terminal network.
5.3 Network Planning and Optimization of Multimodal Transport
–
Multiple means into a multimodal system by van Nes (
2002). It underlines that a change is needed in today’s transportation system, in order to address problems like accessibility of city centres, traffic congestion, but most of all, the environmental impact. In this regard, combining multiple means into a truly multimodal system has the ability to capitalize on each subsystem’s strengths and limit their weaknesses. Negative factors such as the obligation to transfer, although not very pleasant for the passengers, can have many long-term economical and environmental benefits. So, high quality travel information is crucial.
–
Abstract perspective of multimodal transport network system by Zhang
et al. (
2011). Here the necessity of seamless multimodal traveller information systems is shown; therefore a multimodal transport network system and a test for the model in a study for the Eindhoven region was included.
–
Environmental impact constraint when planning by Zhang
et al. (
2013) and economic development are the two reasons why Yamada
et al. (
2009) say that it is crucial to develop and design efficient multimodal networks. They employ a heuristic approach for a complex algorithm with road transport, sea links and freight terminals. The model is successfully applied in network planning in the Philippines.
–
Supernetwork equilibrium for supply chain–multimodal transport by Yamada and Febri (
2015). A 2 level approach using particle swarm optimization is presented. The upper level is solved using particle swarm optimization, while the lower-level decision use a supply chain–multimodal transport supernetwork equilibrium.
–
Emergencies solved with an immune affinity model by Hu (
2011). The paper proposes a transportation scheduling approach based on immune affinity model. The paper concludes that container multimodal transportation will play an important role in emergency relief, due to the exploitation of the different system’s strengths.
–
Practical traffic assignment model for a multimodal transport system with low-mobility groups by Zhang
et al. (
2020). Here a route choice equilibrium for specific vehicle and non-vehicle travel times at intersections design is proposed. Validation and verification is made employing a case study: Wenling city in China. Some limitations of the models include ignoring modal choice equilibrium, uncertainty of travel and missing a detailed analysis due to insufficient data.
–
Bayesian model for transport options by Arentze (
2013). A Bayesian method to learn user preferences and to provide personalized advice regarding transport options in short time is presented; a new sequential attribute processing and an efficient parameter sampling is provided.
–
Limit cruising-for-parking constraint when planning by Zheng and Geroliminis (
2016). It aims to limit cruising-for-parking; the model is based on the
Macroscopic Fundamental Diagram (MFD) for both single and bi-modal transport, by car and bus, in order to reduce costs.
6 Future Possible Extensions from Unimodal to Multimodal Transport
As transportation quickly expands worldwide, some existing unimodal transport problems and their solvers could be furthermore extended while including specific requirements to solve multimodal transport problems. Some of these problems are further described briefly.
A. Supply Chain Networks. One of the two-stage supply chain network is considered here to optimize the cost from a manufacturer, to a given number of customers while using a set of distribution centres (Fig.
8).
Models & Solvers: Supply chain for further Multimodal extension.
-
– Multi-Objective Goal Programming by Roy
et al. (
2017). The mathematical model of Two-Stage Multi-Objective Transportation Problem (MOTP) with the use of a utility function for selecting the goals of the objective functions and numeric tests are included; real-world uncertainty with the use of grey parameters (reduced to numbers) are also involved. As for the metrics within objective functions, usually Euclidean distances are used, but today, for urban related ITS, for example, it could be a plus to use city-block distances as in Redondo
et al. (
2012), where an evolutionary multimodal optimization technique with suitable parameters obtains better results than existing techniques.
-
– Genetic Algorithm. Pop
et al. (
2016) proposes a heuristic-genetic approach with a hybrid based GA for the capacitated fixed-charge problem. Their algorithm was tested on benchmark instances and found to obtain competitive results with other state-of-the-art algorithms.
-
– Other heuristics. Chen
et al. (
2017) studies an
Uncertain Bicriteria Solid Transportation problem; Moreno
et al. (
2016) employs a heuristic approach for the multiperiod location-transportation problem. Several versions of supply-chain problem including efficient reverse distribution system, secure and green features alongside related solvers are presented by Pop
et al. (
2014,
2016,
2019). A parallel fast solver where the search domain of solutions is efficiently reduced at each iteration was proposed by Cosma
et al. (
2020) for the two-stage transportation problem with fixed charges. It was identified as a very competitive approach when compared to existing ones using the literature dataset.
B. (Generalized) Vehicle Routing Problem. For a given set of vehicles and clients, the (G)VRP problem is to determine the optimal set of routes, see Toth and Vigo (
2002). This is one of most studied combinatorial set of problems. Lee
et al. (
2019) consider an integrative three-echelon supply chain: Vehicle Routing and Truck Scheduling Problem with a Cross-Docking System; this promising logistics strategy distributes products by eliminating storage and order-picking while using warehouse: directly from inbound to outbound vehicles; a cost optimization EEA-based method was proposed which outperforms existing solvers.
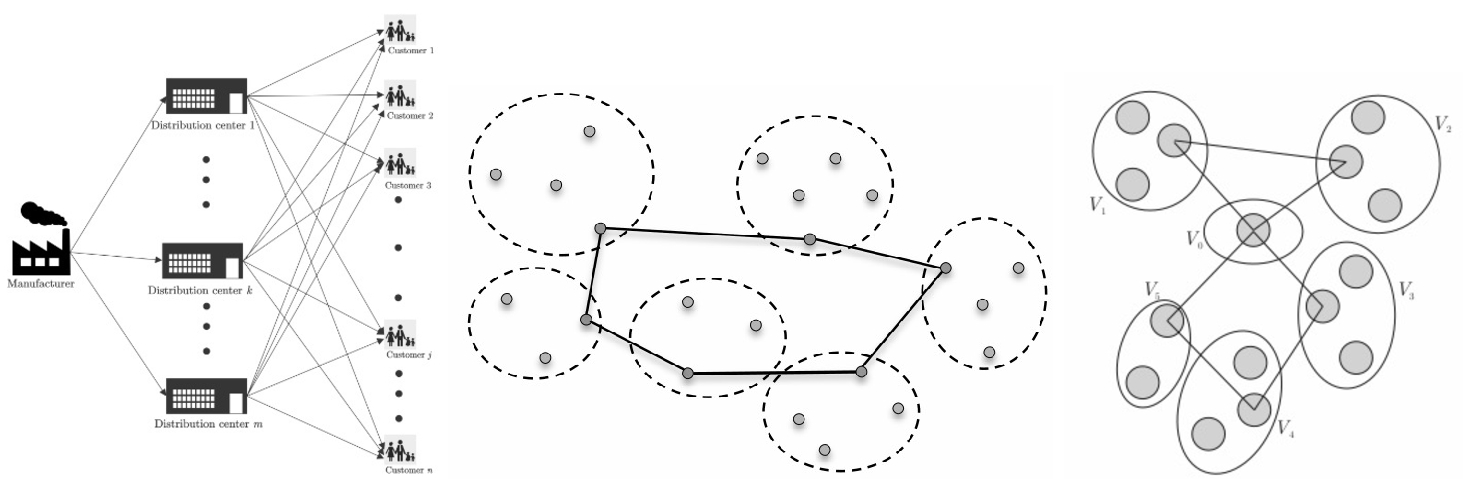
Fig. 8
Examples of feasible solutions for supply chain in order (Pop
et al.,
2014), GTSP (Helsgaun,
2015) and GVRP (Pop
et al.,
2011).
Due to its effectiveness many variations of the VRP were built on the basic VRP with extra features, e.g. the Generalized VRP (GVRP), Fig.
8. VRP with time windows and VRP pick-up and delivery problems, e.g. solved by Vaira and Kurasova (
2014) with GA insertion operators, can be further extended to related complex problem.
A version of GVRP includes designing optimal delivery or collection routes, subject to capacity restrictions, from a given depot to a number of locations organized in clusters, with exactly one node visited from each cluster. See Ghiani and Improta (
2000), Pop
et al. (
2013) for more details.
Models & Solvers: (G)VRP for further Multimodal extension.
-
– Capacitated VRP implies that the vehicles have fixed capacities and the locations have fixed demands in time, see Toth and Vigo (
2002);
-
– VRP & Multiple Depots involves more depots from which each customer can be served as in Crevier
et al. (
2007);
-
– Heterogeneous Fixed Fleet VRP uses a heterogeneous (different types) fleet of vehicles as in Taillard (
1999);
-
– Multi-Commodity VRP deals with more commodities per vehicle, which has a set of compartments in which only one commodity can be loaded, the same as in Repoussis
et al. (
2006);
-
– Tabu Search and hybridization. Various heuristics have been developed for solving the VRP including: an algorithm based on Tabu Search, adaptive memory and column generation described by Taillard (
1999). Tarantilis
et al. (
2004) implemented a threshold accepting procedure where a worse solution is accepted only if it is within a given threshold. A multi-start adaptive memory procedure combined with Path Relinking and a modified Tabu Search was developed by Li
et al. (
2010).
-
– Iterated Local Search based & Set Partitioning. (Subramanian
et al.,
2012) described a hybrid algorithm composed by an Iterated Local Search based heuristic and Set Partitioning formulation.
-
– Bio-inspired algorithms. Matei
et al. (
2015) propose an improved immigration memetic algorithm which combines the power of genetic algorithms with the advantages of local search. The article describes the advantages of the immigrational approach on the overall quality of the algorithm (result quality and run-time speed). Diverse versions of the Genetic Algorithms for solving the current problem are presented by Matei and Pop (
2010) and Petrovan
et al. (
2019). Ant colony methods were used to solve Generalized VRP by Pop
et al. (
2009a,
2009b) and Pintea
et al. (
2011).
-
– Heuristics. Leuveano
et al. (
2019) proposed a heuristic to find optimum inventory replenishment decision when solving transportation & quality problems into a Just-in-Time (JIT) environment. An vendor-buyer lot-sizing model was proposed; parameter study was included and both capacitated and incapacitated cases were studied. Some advantages of the proposals follow: it obtains feasible solution for inventory replenishment decisions; improves transport payload, reduces defectiveness of products and improves quality-related costs.
C. (Generalized) Travelling Salesman Problem. Since 1988, this is one of the most studied problems, and the problem of Applegate
et al. (
2006) from which the (G)VRP evolved. It is considered a particular case of GVRP when the capacity of the vehicles is infinite, and no intermediary return to the depot is required (Fig.
8). Some GTSP versions use a node from each cluster in a route solution, e.g. a city-node from a county-cluster. (G)TSP libraries (see TSP library,
2020; TSP data instances,
2020; GTSP Library,
2020) are continuously updated mainly based on Geographical Information Systems (GIS) as in Crisan
et al. (
2020a), Crisan
et al. (
2016), Crisan
et al. (
2017) and TSP world-wide countries instances (
2020). Integer solvers, e.g. NEOS-Concorde integer TSP solver (
2020), are feasible for TSP, but solving large-scale real-life problems requires updated strategies.
Models & Solvers (G)TSP for further Multimodal extension.
An
abstract Formalization of Multimodal Transportation, as a concept, is presented by Ayed
et al. (
2008). ITS could be expanded by using multi-objective facility location problem models and solvers including heuristics, e.g. Lancinskas
et al. (
2016).
The graph theory is applied within an algorithm in order to optimize routes and route guidance. The authors try to insert their approach into the Carlink project in order to assess its performance. Cosma
et al. (
2018) propose an efficient Hybrid Iterated local Search heuristic procedure to obtain high-quality solutions in a reasonable running-time.
7 Conclusions
The current selective survey presents a review of real-world problems, applications and optimization in the integrative multimodal transportation. Transportation is a key element of today’s society and a very important engine for economic growth. Some areas (like food, medical supplies) raise transportation to strategic importance, and thus indispensable.
The multimodal transport comes with diverse challenges, e.g. related to security, resource saving and reduction of emissions. In the context of today’s accelerated global warming, it is more important than ever to do everything to reduce pollution as much as possible. An example is the green multi-modal transport organization approach presented by Wang
et al. (
2020a), where the China-Europe railway network is validated, reducing the transportation time, increasing energy conservation and lowering carbon emissions by 40%, when compared with the classical unimodal water transport.
Uncertainties will coexist with the multimodal transportation problem, and as recent (Sharma
et al.,
2020) research shows, while using road, rail and air transportation, soft sets, for example, could be used to model these uncertainties related to the transportation attributes (cost, distance and duration of transport). Multi-criteria shortest path optimization, including time, travel cost and route length, for the NP-complete bus routing problem as in Widuch (
2013) could be further extended for complex ITS problems.
Multimodal transportation research nowadays is a challenge that is being continued, on both theory (e.g. solving complex vehicle routing problem) and applicability, in order to obtain feasible models and solvers for various transportation means on complex conditions, with general and specific attributes.

