3.1 General Overview
Figure
1 shows the proposed architecture for the described new control mechanism. At the highest level, managers are defining processes ① using any of the existing process description technologies, such as BPMN or YAWL. Industrial production processes are usually very large and complex, including many activities and tasks which may be partially related (or not). Besides, some technologies enable defining quality indicators for tasks’ outputs, so the activity execution may be rejected if those indicators are not met. Process definitions at this level (named as prosumer level, as managers act as producers and consumers in the proposed technology) are typically graphic, and only relations among tasks and quality measurements are described.
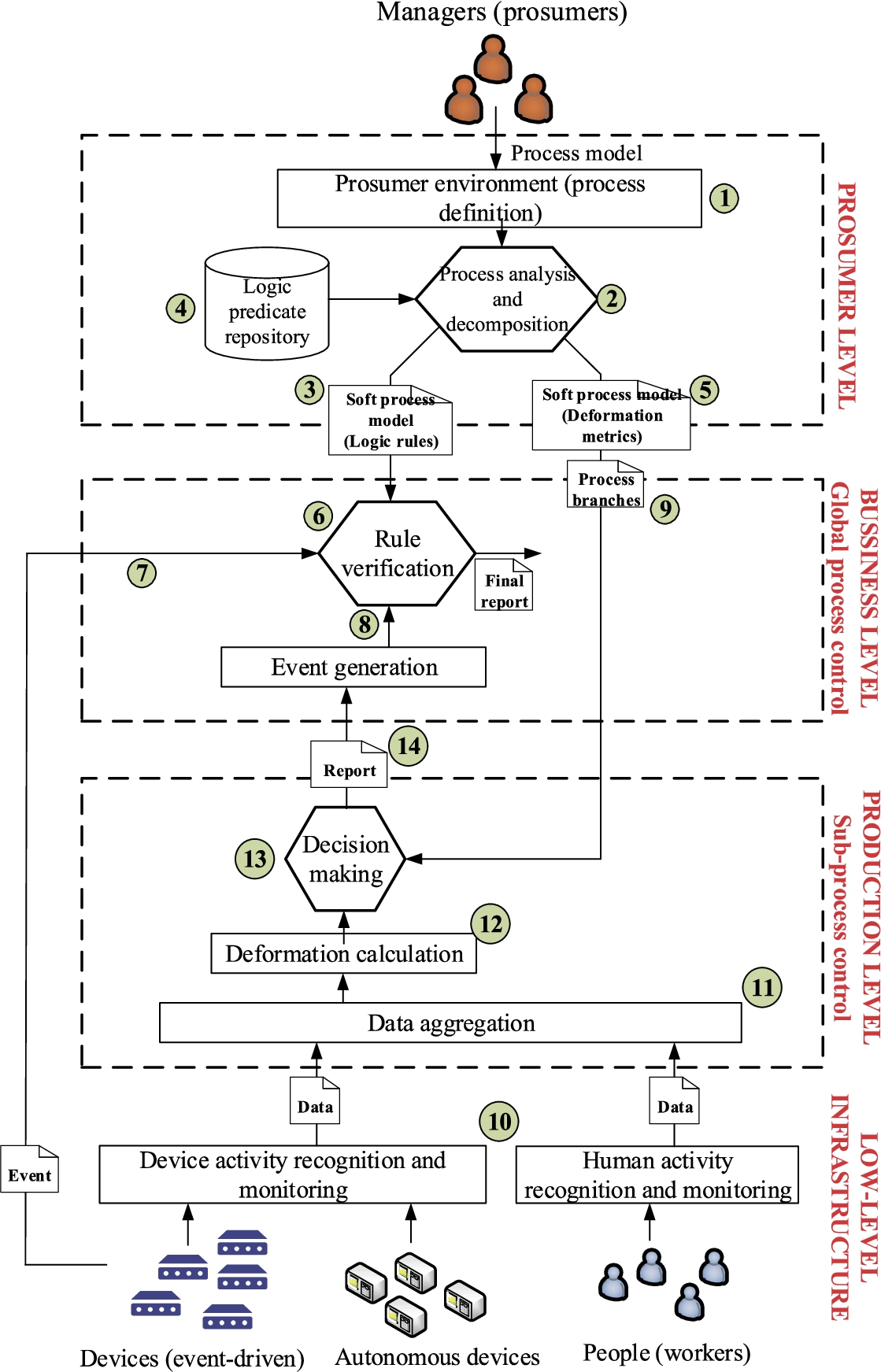
Fig. 1
Proposed architecture for new supervisory control solution in Industry 4.0 scenarios.
The process model based on standard technologies (hereinafter we are considering YAWL language) is then analysed and decomposed ② to “soft” and relax the model. The idea is to transform a hard or rigid process definition where deformations and variations are not expressed (and, then, not accepted by the control solution) into a soft model ③ where global quality and organization restriction are equivalent but dynamic changes, variations and deformation are admissible.
To perform this transformation, a specific engine ② analyses the YAWL process model and identifies the key branches or subprocesses whose exterior structure cannot be modified. For example, a subprocess generating a subproduct as output which is the input of a second subprocess must be executed strictly before the second subprocess. However, tasks inside both subprocesses could be executed in any order, and the same subproduct is created.
After this analysis and decomposition procedure, two different soft process descriptions are generated. The first one is a global description based on logic rules ③. To generate this description, each subprocess is represented by a discrete state. And the global state map is regulated by a set of logical rules extracted and instantiated from a logic predicate repository ④, where different general conditions are stored (temporal order, necessary conditions, etc.). Those logical rules represent the minimum restrictions that the production process must fulfill, but all additional restrictions artificially introduced by the limitations or graphic process representations are removed. The second one is a set of reports ⑤ where deformation metrics about each subprocess are indicated. Quality indicators about each task are considered together and three global metrics for the whole subprocess are obtained: stiffness, strength and ductility.
The global soft description is transferred to a verification engine ⑥, where logical rules are validated (or not) at real-time. This global understanding about the process takes place at business level, where information from managers (process models) and from autonomous hardware platforms are matched to determine if production processes are being correctly executed or not. This verification engine takes as input two information sources: events directly generated by hardware devices ⑦ following an event-driven paradigm; and events generated ⑧ by control component in lower layers (the production layer). These events are employed to validate logical rules and determine if minimum conditions to consider the process execution is valid are being met.
All reports about subprocesses ⑨ are transferred to a lower level (the production level), where low-level (physical) information is collected to evaluate if process deformation is above the proposed global metrics. To do that, information from different recognition technologies (human-oriented, device-oriented, etc.) is collected ⑩. These recognition technologies are not addressed in this paper, as any of the previously existing mechanisms may be integrated (Bordel
et al.,
2019; Bordel and Alcarria,
2017). All information sources are integrated ⑪ to perform a global evaluation of process deformation. To obtain those global metrics a mathematical algorithm ⑫ is employed. This algorithm is deducted by understanding production processes as discrete flexible solids in a generalized phase space. Dynamic behaviour of autonomous devices is represented as external forces acting on the solid (process) and deforming it. Using different deformation functions (and the provided deformation metrics), it is evaluated if the final process execution is similar enough to the model to be considered as a valid execution or not. A decision-making engine ⑬ performs these functions. A report ⑭ and event-like result (whose format may be adapted in an event generation module) is sent to the rule verification engine ⑥ (as one of the information sources described before).
3.2 Process Description at Prosumer Level
Using YAWL language, managers may define processes in a very easy manner with graphic instruments (see Fig.
2). At the highest level (prosumer level) managers (prosumers) are defining a complex production process or workflow
W. This workflow is an ordered sequence
T of
${M_{T}}$ tasks, connected through
${M_{E}}$ oriented edges,
E (
1). Each task
${t_{i}}\in $ is labelled with a discrete timestamp
${n_{i}}$ indicating the planned temporal order for the workflow. On the other hand, each edge
${e_{i}}\in E$ is labelled with a collection
$S{P_{i}}$ indicating the list of subproducts flowing (as input and/or outputs) between tasks along the edge (
2). Labelling applications
${\lambda _{T}}$ and
${\lambda _{E}}$ are employed to relate labels and edges and tasks. To learn which tasks
${t_{i}}$ are connected through oriented edges
${e_{i}}$, and incidence application
${\gamma _{W}}$ is defined (
3). This application relates each edge
${e_{i}}$ with the order pair of tasks
${t_{i}},{t_{j}}$ this edge connects. The edge is outgoing from
${t_{i}}$ and incoming in
${t_{j}}$:
Besides, in YAWL, tasks may be labelled with a list
${\mathfrak{I}_{i}}$ of
${M_{I}}$ quality indicators
${\mathrm{\coprod }_{i}^{j}}$, employed to accept or reject the actual tasks execution (
4). These indicators may refer maximum delays, jitter, errors in physical dimensions, etc. A labelling application
${\lambda _{\mathit{ind}}}$ is employed to relate indicators and tasks (
5). This list must be exhaustive: every possible indicator must be present in every task. If an indicator does not apply to a particular task, this value in the list should be empty but still present.
Moreover, bifurcation conditions can be considered in YAWL process definitions (see Fig.
2). These conditions are modelled as lists
${\mathcal{C}_{i}}$ of semantic annotations associated to edges through a label application
${\lambda _{\mathit{cond}}}$ (
6). These annotations
${c_{i}^{j}}$ are logical predicates referred to output characteristics, time, etc. This whole process description (including all labels), then, is analysed and decomposed in a specific engine. The first step is to calculate the key process branches or subprocesses
${\omega _{i}}$ (
7):

Fig. 2
Graphic representation of a YAWL process.
A key subprocess is characterized by only one input point (only one task receives inputs from the physical world) and only one output point (only one task generates a physical service or product). Besides, relations among tasks within the subprocess do not have associated subproducts
${\textit{SP}_{i}}=\varnothing $, but input and output edges to the subprocess do have associated subproducts. Inside a subproduct, then, the temporal order is artificially induced by YAWL language, as it requires all tasks to be connected in sequences. But the process does not require tasks to be executed in that order and it could be altered. When a key subprocess is detected, it is extracted to an independent report to be analysed separately using deformation metrics, and in the global description the subprocess is replaced by a state
${s_{j}}$, taken from a set
${\Sigma _{W}}$ of possible states for this workflow. And a transaction relation
${\rho _{W}}$ is built to connect all states
${s_{j}}$ according to restrictions in the original process (
8). Algorithm
1 describes the proposed mechanism to calculate subprocess and new states and the transaction relation.
On the other hand, annotations
${\mathcal{C}_{i}}\hspace{2.5pt}$ must be transformed into logic predicates referred to states
${s_{j}}$ and/or the discrete timestamps
${n_{i}}$. To do that, a semantic algorithm may be employed. This algorithm is not described in this paper, but similar solutions may be found in the state of the art [8]. To do that, a repository of generic logic predicates is considered. These generic predicates are instanced according to annotations
${\mathcal{C}_{i}}\hspace{2.5pt}$ to generate a set
$\mathcal{R}$ of atomic propositions
${r_{i}}$ or logical rules. An interpretation function
${L_{W}}$ is finally defined, indicating what predicates from
$\mathcal{R}$ are true for each state
${s_{j}}$ (
8).
The set of states
${\Sigma _{W}}$ and both the interpretation
${L_{W}}$ and the transaction
${\rho _{W}}$ applications define a Kripke structure
K (
9) which is transferred to the business layer for further processing. This Kripke structure is formally defined if only one additional element is considered: the set of states from which the workflow may be initiated
${\Sigma _{\mathit{init}}}$.

Algorithm 1
Key subprocess identification and Kripke structure creation
A second element is generated in the analysis and decomposition engine. For each key subprocess
${\omega _{i}}$, each task
${t_{i}}$ is labelled with an exhaustive set of indicators
${\mathfrak{I}_{i}}$. These indicators are split into two different vectors
${\mathfrak{I}_{i}^{a}}$ and
${\mathfrak{I}_{i}^{r}}$ (
10). On the one hand, absolute indicators
${\mathfrak{I}_{i}^{a}}$ referring state variables (such as time, temperature, etc.) are preserved (including empty positions). On the other hand, relative indicators
${\mathfrak{I}_{i}^{r}}$ referring tolerances, errors, etc. are processed to calculate three basic and global deformation metrics: stiffness, strength and ductility.
-
• Stiffness (F) represents the ability of a process to resist to deformations. In other words, it presents how much a process may absorb variations in the input parameters and conditions and still keep the planned values in the state variables.
-
• Strength (G) represents the ability of a process to prevent unsatisfactory executions. It describes how resistant the internal organization of the process is, producing correct executions even if inputs and/or state variables suffer great changes with respect to the original model.
-
• Ductility (D) represents the ability of a process to be deformed and, still, produce correct executions. This parameter indicates how flexible a process is, so even large changes in the state variables are considered as valid executions.
Stiffness is related to security margins and safeguards between consecutive tasks in the process model (
11). As these security margins are larger, it is easier for the process to resist to global deformations, as the effect of inputs on the first tasks are absorbed by security margins. Function calculating the stiffness of a process
${\sigma _{f}}$ must, then, be strictly increasing: linear, logarithmic or exponential functions could be employed depending on the scenario.
Strength is related to the number of restrictions and indicators in the list
${\mathfrak{I}_{i}^{r}}$ (
12). As more restrictions are considered, the process is more probable to generate an unsatisfactory execution. Besides, if we consider all restrictions as independent effects, the probability of unsatisfactory executions grows up exponentially with the number of restrictions. Then, function calculating the process strength
${\sigma _{f}}$ is exponentially decreasing.
Finally, ductility is obtained from the tolerances and relative errors in the list
${\mathfrak{I}_{i}^{r}}$ (
13). As tolerances go up, processes can be deformed at a higher level, but the process execution is still valid. Then, the function calculating the ductility of the process
${\sigma _{d}}$ is strictly increasing: linear, logarithmic or exponential functions could be employed depending on the scenario
Then, the subprocess descriptions $\{{\omega _{i}}\}$ together with the vector $\{{\mathcal{I}_{i}^{a}}\}$ and the deformation indicators $\{{({F_{i}},{G_{i}},{D_{i}})_{i}}\}$ are transferred to the production layer for further processing.
3.3 Global Process Control and Rule Validation at Business Level
At business level, a Kripke structure (
9) describing the process model is received. On the other hand, from this level, the control solution is viewed as a discrete event system (DES),
$\mathfrak{Z}$ (
14). Where
X is the set of possible states in the system;
$\mathcal{E}$ is the finite set of events;
f is the transition function indicating the next state for a given current state and a received event (
15); Γ is the function indicating what events are active for a given state (
16) and
$\mathcal{P}(\mathcal{E})$ is the power set of
$\mathcal{E}$;
${X_{0}}$ is the initial state of the system and
${X_{m}}$ is the set of market states (of allowed final states).
In this DES,
${\mathcal{E}^{\ast }}$ is the Kleene closure of
$\mathcal{E}$ which is the set of all possible string in the system (including the empty string); being a string the juxtaposition of states in
X describing the evolution of the system; i.e.
${\mathcal{E}^{\ast }}$ is the set of all possible evolutions the system may follow. Two different languages (sets of strings) can be defined, then. The language marked (
17)
${\mathcal{L}_{m}}$ contains all strings that finished with a marked state. The language generated (
18)
${\mathcal{L}_{g}}$ contains all possible strings, i.e. all possible system evolution although they may be not acceptable. In traditional supervisory control systems, the underlaying event-driven infrastructure is assumed to be fully controllable (all events are controllable) or partially controllable (where only some events are uncontrollable). However, in future Industry 4.0 all events tend to be uncontrollable (as devices and people are totally dynamic and autonomous). In that case, common supervisory control theory is not applicable, as its objective is to avoid certain undesired controllable events (and, in Industry 4.0, they are all incontrollable). On the contrary, the objective of the proposed supervisory mechanism is to create reports when undesired states are reached.
Moreover, in this scenario, events and states in the low-level platform are unknown and, probably, infinite. Then, supervisory control cannot be performed directly over the workers and hardware devices, but over the Kripke structure. Actually, this structure is a fair Kripke structure are two additional conditions are met in every process model:
-
• Justice or weak fairness requirements: Many states ${s_{j}}$ activate the same logical predicate.
-
• Compassion or strong fairness requirements: If many states ${s_{j}}$ have the same logical predicate; many states ${s_{k}}$ do not activate that logical predicate.
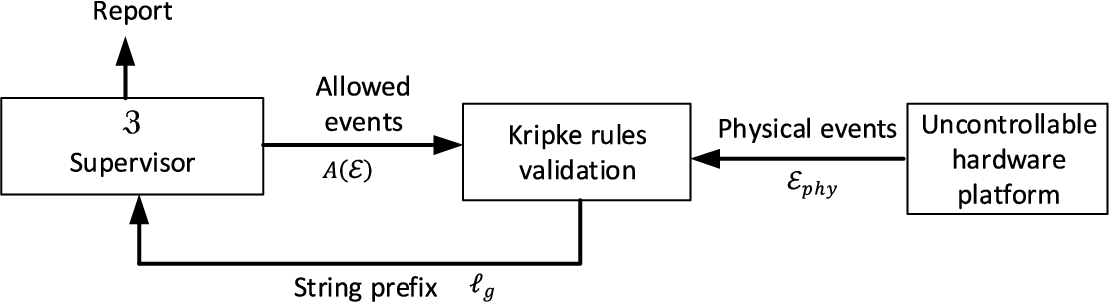
Fig. 3
Supervisory control solution.
In that way, a two-level verification is performed in the “rule verification engine” (see Fig.
3). In this solution, states
$\mathcal{E}$ in DES
$\mathfrak{Z}$ and in the Kripke structure
K are the same, although the state set
${\Sigma _{W}}$ in the Kripke structure includes a special state
${s_{\mathit{null}}}$ to represent unknown states (
19). This state
${s_{\mathit{null}}}$ does not activate any logical predicate (
20). The initial states are the same (
21). Discrete events
ε in the DES
$\mathfrak{Z}$ are words
${\ell _{g}}$ of the language general
${\mathcal{L}_{m}}(\mathfrak{Z})$ (where the empty string corresponds to the unknown state in the Kripke structure), describing the states the Kripke structure has reached (
22) before the current state
${s_{\mathit{current}}}$. Then, the transition function in the DES may be easily constructed from the transaction relation in
K (
23):
In those conditions, the proposed supervisory control algorithm operates as follows. First, physical events
${\mathcal{E}_{\mathit{phy}}}$ (obtained through the event generation module from physical information and reports) are employed to determine in the Kripke structure which states
${s_{j}}$ are allowed in the production process (several of them, because of the justice and compassion requirements). This action is performed using the interpretation function (
24). If only one state is allowed, a new DES event
${\varepsilon _{i}}$ is generated, juxtaposing the new event to the previous string prefix
${\ell _{g}^{i}}$ (
25). This information is introduced as strings’ prefix in the DES
$\mathfrak{Z}$, and the supervisory control module determines which future states
$A(\mathcal{E})$ are allowed by the business model (
26) and, eventually, reports if the executed process is incompatible with business requirements (
27). Algorithm
2 describes the proposed control solution.

Algorithm 2
Supervisory control
Different solutions to validate logic rules have been reported (Leucker,
2017), any of them may be integrated into the proposed mechanism.
3.4 Subprocess Control Using Deformation Functions at Production Level
Finally, at production level, a collection of labelled key subprocess
$\{{\omega _{i}}\}$ and deformation metrics
$\{{({F_{i}},{G_{i}},{D_{i}})_{i}}\}$ are received. At this point, every task
${t_{i}}$ in any subprocess
${\omega _{i}}$ is totally defined by the set of absolute quality indicators
${\mathfrak{I}_{i}^{a}}$. This set is a
${M_{I-A}}$-dimensional vector which, eventually, can be represented as a point in a generalized
${M_{I-A}}$-dimensional phase space. To do that, it is enough to consider the position vector
$\overrightarrow{{x_{i}}}$ of that point (
28) in a general Euclidian space. Besides, in the most common case, every subprocess
${\omega _{i}}$ is composed of a very large set of tasks, so if the same procedure is repeated for every task, finally the whole subprocess is represented as a point cloud in the phase space. This point cloud may be understood as a discrete solid
${\Omega _{i}}$ in the phase space (
29). This solid, moreover, is flexible, as from the beginning we have assumed that tasks inside each subprocess may be altered (see Fig.
4). In this context,
${M_{{\omega _{i}}}}$ is the number of tasks in the subprocess
${\omega _{i}}$. In those conditions, the subprocess execution may be understood as a function
${T_{D}}$ (
30) applied over the solid
${\Omega _{i}}$ to be transformed into a new and deformed solid
${\Omega _{i}^{\ast }}$ in the original phase space (see Fig.
5). Rotations, extrusions, and any other deformation could appear.
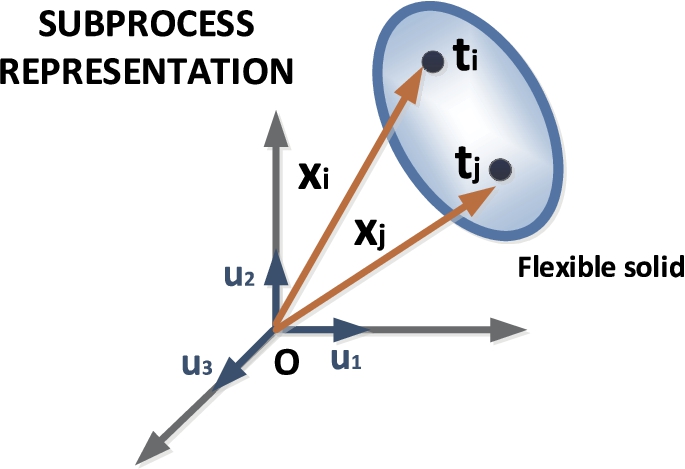
Fig. 4
Subprocess representation in a general phase space.
The question to address, then, is if the suffered deformation is high enough to consider whether the execution is unsatisfactory or not.
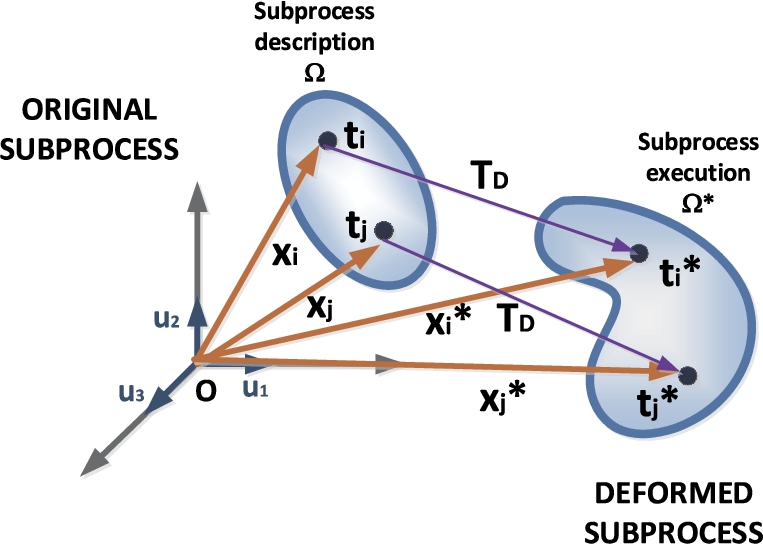
Fig. 5
Subprocess representation in a general phase space.
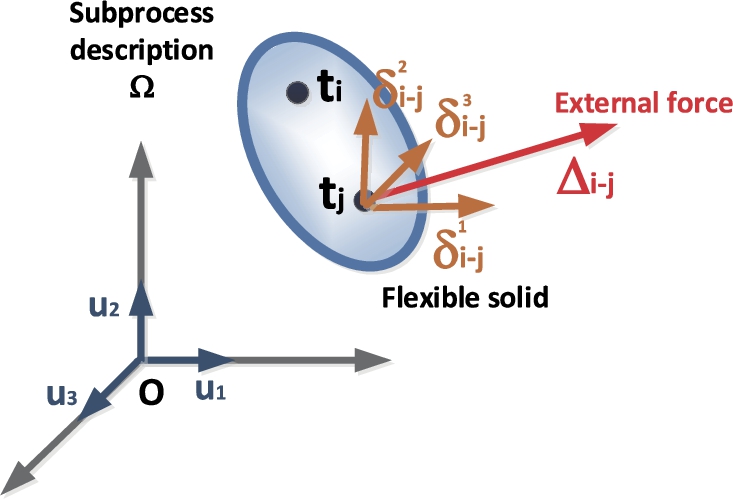
Fig. 6
External forces acting on the flexible solid in the phase space.
In the proposed model, a set of external forces
${\Delta _{i-k}}$ (
31) is actuating on the solid
${\Omega _{i}}$ in the point
${t_{k}}$. These forces represent the dynamic, variable, and anarchic behaviour of autonomous devices and humans, which tend to deform the original process model (see Fig.
6). If forces were acting only in one dimension
${\delta _{i-k}^{j}}$, the global deformation suffered in that dimension
${\Phi _{i-k}^{j}}$ could be easily calculated through the Hook law (
32); where
${F_{i}}$ is the stiffness parameter calculated in the prosumer layer. Although it is not completely correct in terms of physical meaning, we are generalizing this law by taking modular functions, so the global aggregated deformation in all directions of the phase space may be also estimated through the Hook law (
33) and, even, the global deformation for the entire solid, by integrating along the entire solid’s surface (
34). Considering, now, ductility
${D_{i}}$ and strength
${G_{i}}$ we can extend the common Hook law to include inelastic areas and break zones (where executions are considered unsatisfactory). This new deformation function includes three different branches (
35), see Fig.
7.
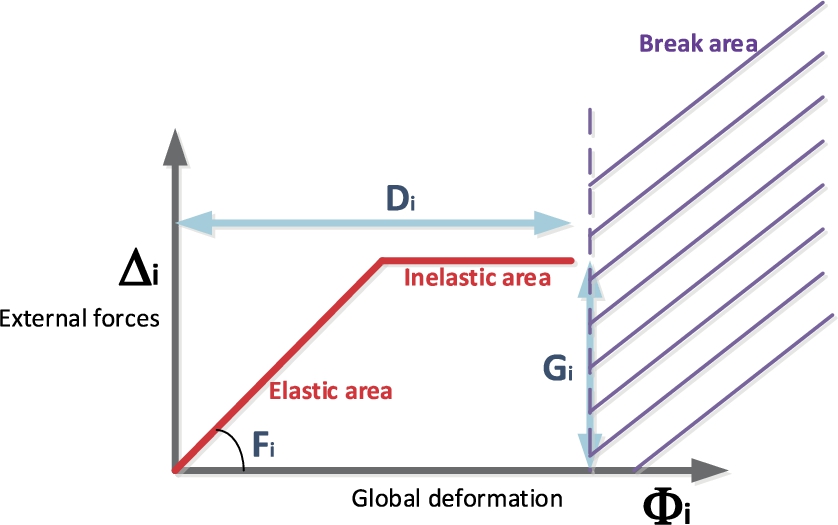
Fig. 7
Generalized Hook law for process verification.
As can be seen in Fig.
7, it is not necessary to evaluate the external forces
${\Delta _{i}}$ to learn if global subprocess deformation is too high to consider the execution is valid. These forces are extremely complicated to analyse, as almost no data about them is available. On the contrary, global deformation
${\Phi _{i}}$ can be evaluated through the absolute quality indicators
${\mathfrak{I}_{i}^{a}}$, which are monitored through the recognition technologies at low-level. For every deformation value
${\Phi _{i}}$ in the break area, the execution is considered unsatisfactory. Otherwise, it is considered valid. For deformation values in the elastic area, external forces are only deforming the process in a transitory manner, i.e. only some tasks are affected (those which are directly affected by forces). Security margins are absorbing the secondary effects over other tasks, and no permanent global deformation is suffered. On the contrary, when deformation values are in the inelastic area, security margins are not enough to compensate the external forces, and permanent and global deformation appear. Nevertheless, executions are still valid although deformed. Moreover, two contradictory situations must be considered before deformation calculation.
On the one hand, in the inelastic area, small variations in the estimated global deformation ${\Phi _{i}}$ may cause the subprocess execution to be rejected. So, high precision algorithm to perform those analyses are needed. On the other hand, Industry 4.0 scenarios present real-time requirements, so algorithms must be fast and efficient, and complex high-precision mechanisms must be employed.
Thus, we proposed a two phases deformation evaluation: in the first step, a very simple algorithm where all state variables and quality indicators are considered independent is employed; only if this algorithm places the global deformation in the inelastic area, a second step where a complex and much more precise algorithm is employed would be triggered.
To calculate the first and approximate global deformation
${\Phi _{i}^{ind}}$ of the subprocess
${\omega _{i}}$ after an execution, we are considering all quality indicators
${\mathfrak{I}_{i}^{a}}$ to be totally independent. Then, deformation
${\phi _{i-k}^{j}}$ along each indicator and on each task can be calculated independently. This calculation is based on the ratio between the planned value for each quality indicator
${\mathrm{\coprod }_{i-a}^{j}}$, and the final obtained result
${\mathrm{\coprod }_{i-a}^{j,\ast }}$ (
36). Using this radio, deformation
${\phi _{i-k}^{j}}$ can be obtained through different expressions: unitary deformation (
37), Almansi deformation (
38), Green deformation (
39), Hencky deformation (
40) or any other application specific algorithm. Each one of these expressions is adequate for a range of deformation values (see Table
2). Then, we are always initially calculating the unitary deformation, and, after that, we can recalculate the value using a more adequate expression if needed.
As can be seen in Table
2, using the unitary deformation we can evaluate the subprocess rotation and absolute deformation. Then, for processes where rotation and large deformation values are present, Hencky function is the most precise calculation method. Equally, for null rotation and large deformation values, specific logarithmic algorithms and expressions may be proposed depending on the scenario. Finally, for small values of deformation we can use the Green or Almansi function (as desired) if rotation is present, or the unitary deformation if no rotation and small deformation values are observed.
After calculating the global deformation
${\Phi _{i}}$ for the subprocess, if this value is in the elastic area, the execution is accepted. If the subprocess execution is in the break area the execution is rejected; and if the value is in the inelastic area, a more precise evaluation is needed. In this more precise calculation mechanism, we are assuming the realistic scenario, where quality indicators are dependent on each other. Then, deformation parameters are obtained through the deformation tensor
${\Psi _{i-k}}$ (
41), where differential expressions are approximated using numerical expressions (
42). Basically, for initial task we are employing the previous expressions (
37)–(
40) to start the calculation algorithm. Other tasks are evaluated through the backward differences. There exists also a tensor expression for Almansi deformation (
43) and for Green–Lagrange deformation (
44) which can be employed for depending on the scenario under study (selecting that which is closer to reality in all cases).

Algorithm 3
Deformation evaluation
Table 2
Different deformation calculation expressions.
| Rotation |
Deformation: Large |
Deformation: Small
$(0.1<|{\phi _{i-k}^{j}}|<10)$
|
Yes
$(|{\phi _{i-k}^{j}}-{\phi _{i-k+1}^{j}}|<{10^{-4}}\hspace{2.5pt}\forall \hspace{0.1667em}k)$
|
Hencky deformation
${\phi _{i-k}^{j}}=\ln ({\mu _{i-k}^{j}})$
|
Green deformation
${\phi _{i-k}^{j}}=\frac{1}{2}\big({({\mu _{i-k}^{j}})^{2}}-1\big)$
|
|
|
Almasi deformation
${\phi _{i-k}^{j}}=\frac{1}{2}\Big(1-\frac{1}{{({\mu _{i-k}^{j}})^{2}}}\Big)$
|
| No |
Ad hoc logarithmic definitions |
Unitary deformation
${\phi _{i-k}^{j}}={\mu _{i-k}^{j}}-1$
|
Module calculation (
34), in this case, will refer to the tensor module calculation; contrary to the previous case where vector module was employed.
With this much more precise value, the caused deformation is finally evaluated. If it remains in the inelastic area, the execution is approved. In the contrary event, the execution is rejected. Algorithm
3 describes the entire described solution at production level.

