1 Introduction
Multi-attribute decision making method (MADM) and multi-attribute group decision making method (MAGDM) are two essential research directions in the field of modern management decision making. The practical issue of MADM or MAGDM is that decision makers are often confronted with inaccurate description. The complexity of the human brain means that even rational decision makers can be influenced by emotional factors to make vague expressions in the decision-making process. Just as the word “beautiful” is an imprecise expression of fuzzy things, which is prevalent in realistic society. The way to express this reality scientifically has become an important problem for scientists. Thinking about this phenomenon, Zadeh (1965) proposed the concept of fuzzy sets in 1965 to study the inexact phenomena mentioned above by using membership functions. It can be said without exaggeration that fuzzy set is the cornerstone for the research and development of decision making and control. Since then, many researchers have dedicated themselves to the study of fuzziness and uncertainty, greatly developing the fuzzy sets. In 1986, Atanassov (1986) put forward Intuitionistic Fuzzy Sets (IFSs), in which subordinate and non-subordinate functions are integrated to describe uncertain things. In addition, Cuong (2014) introduced degree of neutral subordinate on the basis of IFSs and proposed the concept of picture fuzzy sets (PFSs) in 2014. In addition, many other sets for describing uncertain problems have been proposed and extensively studied (Liu Y. et al., 2019; Zhang et al., 2017; Zhang Z. et al., 2019). However, picture fuzzy set is still irreplaceable and unique in investigating the issues of MADM and MAGDM. Specifically, PFSs have four expressions of membership degree including the positive subordinate degree, neutral subordinate degree, negative subordinate degree and refusal subordinate degree, which is a very detailed breakdown of decision makers’ attitudes, corresponding to four descriptions (affirmative, adiaphorous, averse and refusal) when decision makers make a decision (Liang et al., 2018). Because of its excellent characteristics, many scholars use picture fuzzy sets to study decision problems. Ma et al. (2019) gave complex fuzzy sets and extended the range of membership function values. Obviously, compared with other kinds of fuzzy sets, PFSs can delineate the conduct of decision-makers in more detail and are closer to human thinking and cognition of fuzzy things. Therefore, it has more advantages in solving multi-attribute decision making (MADM). Liang et al. (2018) evaluated the cleaner production for gold mines with picture fuzzy information. Meksavang et al. (2019) researched for the selection of sustainable suppliers. Wang et al. (2018) studied the risk evaluation of construction project with PFSs. Khan et al. (2019) invented logarithmic aggregation operators of Picture Fuzzy Numbers to solve MADM problems. Ju et al. (2019) used extended GRP method to study the location of charging stations for electric vehicles under picture fuzzy environment. Sindhu et al. (2019) developed a linear programming model with PFSs. Liu and Zhang (2018) put forward picture fuzzy linguistic set and some aggregation operator based on picture fuzzy information, such as, A-PFLWAA. Wei (2017) also gave some picture fuzzy aggregation operators.
As mentioned above, many great scholars put forward all kinds of methods to study MADM problems, such as MABAC (the distance between the alternatives and the boundary approximation area was defined and introduced by Pamucar and Cirovic (2015) in 2015), VIKOR (a compromising method which was introduced by Opricovic and Tzeng (2004) in 1998), MOORA (proposed by Brauers and Zavadskas (2006) in 1986), TODIM (brought forward by Gomes and Lima (1992) in 1992), EDAS (it was used for calculating the distance of each alternative from the optimal one and presented by Keshavarz Ghorabaee et al. (2015) in 2015) and so on. Among them, the TODIM method is distinctive, which makes use of piecewise function to denote the distance between two schemes. What’s more, it is more authentic to take the different attitudes of decision makers towards gains and losses on decision making into consideration by introducing parameter in the process of evaluation. Liang et al. (2020) utilized TODIM to introduce the risk appetite on three-way decisions. Wu Y.N. et al. (2019) investigated the investment selection of meeting the requirements of rooftop distributed photovoltaic projects for industrial and commercial households with TODIM. Biswas and Sarkar (2019) put forward a kind of methodology based on TODIM. Liang et al. (2019) proposed a mixture TODIM method to assess the risk level of the targets. Zhang Y.X. et al. (2019) explored water safety evaluation on the strength of the TODIM method. Zhang Y.X. et al. (2019) integrated maximizing deviation, FANP and TODIM method. Renet al. (2017) studied TODIM under probabilistic dual hesitant fuzzy environment. Zhu et al. (2019) used grey relational analysis to count the dominance degree. Yuan et al. (2019) got through the ranking of risk level of CFPP investment with TODIM. Liu et al. (2019) generalized TODIM and TOPSIS methods to distance measure. Wu and Zhang (2019) used TODIM under intuitionistic fuzzy environment to obtain the results of product ranking. Wei (2018) accomplished the TODIM in picture fuzzy environment. Mishra and Rani (2018) designed TODIM technique to solve problems in interval-valued IFSs. Zhang et al. (2019) utilized sentiment analysis as well as classical TODIM to evaluate and rank products online in an intuitionistic fuzzy environment. Yu et al. (2017) combined the classical TODIM method with unbalanced hesitant fuzzy linguistic term sets to analyse multi-criteria group decision making. Liang Y.Y. et al. (2019) ameliorated the conventional TODIM with a weight determination method which was based on incomplete weight information. Wang et al. (2019) applied a novel function to TODIM. Liu and Teng (2019) acquired weights by means of probabilistic linguistic information, which extend the TODIM. Tian et al. (2019) developed the traditional TODIM by using Cumulative Prospect Theory (CPT).
The TODIM method based on CPT combines the advantages of traditional TODIM and CPT, providing a more reliable method for studying uncertain decision-making, and makes up for the shortcomings of traditional TODIM method. Unfortunately, we hardly find the use of improved TODIM method based on Cumulative Prospect Theory to study the multi-attribute group decision making (MAGDM) problem in picture fuzzy environment. Hence, the heart of this article is to build a more practical model to resolve the problem of picture fuzzy MAGDM. For achieving this goal, this article pays attention to the psychology of decision makers through a more realistic way to analyse and brings in the entropy weight method to obtain the original weighting vector of attributes, eliminating the subjectivity of the information of attribute weight directly given by the decision maker.
The primary research ideas of this paper are as follows: Section 2 recommends and sorts out the basic knowledge to be used in this paper briefly. In the Section 3, the improved TODIM method is applied to work out the problem of picture fuzzy MAGDM. Section 4 demonstrates the application of the new method and compares it with other approaches to guarantee the availability. Finally, we draw the corresponding conclusions based on the research in this paper, which are shown in Section 5.
2 Preliminary Knowledge
In this topic, we review a number of fundamental concepts and methods in regard to picture fuzzy sets as well as extend TODIM based on CPT (Cumulative Prospect Theory).
2.1 PictureFuzzy Sets and Picture Fuzzy Numbers
Definition 1 (See Garg, 2017).
For a non-empty set O, Picture Fuzzy Set (PFS) is defined by
where ${\alpha _{L}}(o)\in [0,1]$ is well-known as degree of positive membership of L, ${\varphi _{L}}(o)\in [0,1]$ is well-known as degree of negative membership of L, ${\beta _{L}}(o)\in [0,1]$ is well-known as degree of neutral membership of L. In the meantime, ${\alpha _{L}}(o)$, ${\beta _{L}}(o)$ and ${\varphi _{L}}(o)$ satisfy the relation of “ $0\leqslant {\alpha _{L}}(o)+{\beta _{L}}(o)+{\varphi _{L}}(o)\leqslant 1$, $\forall o\in O$”. Then the refusal membership of o in L can be calculated by Eq. ( 2)
(1)
\[ L(\mathrm{o})=\big\{\big\langle o,{\alpha _{L}}(o),{\beta _{L}}(o),{\varphi _{L}}(o)\big\rangle \hspace{0.1667em}\big|\hspace{0.1667em}o\in O\big\},\]For convenience, we define the corresponding Picture Fuzzy Number (PFN) $L=({\alpha _{L}},{\beta _{L}},{\varphi _{L}})$. And now, let’s introduce some algorithms.
Definition 2 (See Meksavang et al., 2019).
Let $\delta =({\alpha _{\delta }},{\beta _{\delta }},{\varphi _{\delta }})$ and $\varepsilon =({\alpha _{\varepsilon }},{\beta _{\varepsilon }},{\varphi _{\varepsilon }})$ represent two PFNs, respectively, then
-
(1) $\delta \oplus \varepsilon =({\alpha _{\delta }}+{\alpha _{\varepsilon }}-{\alpha _{\delta }}{\alpha _{\varepsilon }},{\beta _{\delta }}{\beta _{\varepsilon }},{\varphi _{\delta }}{\varphi _{\varepsilon }})$;
-
(2) $\delta \otimes \varepsilon =({\alpha _{\delta }}{\alpha _{\varepsilon }},{\beta _{\delta }}+{\beta _{\varepsilon }}-{\beta _{\delta }}{\beta _{\varepsilon }},{\varphi _{\delta }}+{\varphi _{\varepsilon }}-{\varphi _{\delta }}{\varphi _{\varepsilon }})$;
-
(3) $\omega \cdot \delta =(1-{(1-{\alpha _{\delta }})^{\omega }},{({\beta _{\delta }})^{\omega }},{({\varphi _{\delta }})^{\omega }})$, $\omega >0$;
-
(4) ${\delta ^{\omega }}=({({\alpha _{\delta }})^{\omega }},1-{(1-{\beta _{\delta }})^{\omega }},1-{(1-{\varphi _{\delta }})^{\omega }})$, $\omega >0$;
-
(5) $\overline{\delta }=({\varphi _{\delta }},{\beta _{\delta }},{\alpha _{\delta }})$.
Definition 3 (See Wei, 2018).
Definition 4 (See Liang et al., 2018).
If $\delta =({\alpha _{\delta }},{\beta _{\delta }},{\varphi _{\delta }})$ and $\varepsilon =({\alpha _{\varepsilon }},{\beta _{\varepsilon }},{\varphi _{\varepsilon }})$ are two PFNs, respectively, their relationships of size are as follows:
Definition 5 (See Meksavang et al., 2019).
Let $\delta =({\alpha _{\delta }},{\beta _{\delta }},{\varphi _{\delta }})$ and $\varepsilon =({\alpha _{\varepsilon }},{\beta _{\varepsilon }},{\varphi _{\varepsilon }})$ represent two PFNs, respectively, then their distance is counted by:
(5)
\[\begin{array}{r@{\hskip4.0pt}c@{\hskip4.0pt}l}\displaystyle d(\delta ,\varepsilon )& \displaystyle =& \displaystyle \frac{1}{4}(|{\alpha _{\delta }}-{\alpha _{\varepsilon }}|+|{\beta _{\delta }}-{\beta _{\varepsilon }}|+|{\varphi _{\delta }}-{\varphi _{\varepsilon }}|+|{z_{\delta }}-{z_{\varepsilon }}|)\\ {} & & \displaystyle +\frac{1}{2}\max (|{\alpha _{\delta }}-{\alpha _{\varepsilon }}|+|{\beta _{\delta }}-{\beta _{\varepsilon }}|+|{\varphi _{\delta }}-{\varphi _{\varepsilon }}|+|{z_{\delta }}-{z_{\varepsilon }}|).\end{array}\]2.2 Extended TODIM Method Based on Cumulative Prospect Theory
The original TODIM, which was proposed by Gomes and Lima (1992), utilizes the dominance degree of each alternative over the other alternatives to select the optimal project. At present, this method has extensive use in Multiple Attribute Decision Making (MADM) and other areas. Nonetheless, this method is unable to acquire the weight of attributes, using the weighting function. So, XU, TIAN, and GU improved classical TODIM and demonstrated extended TODIM on the Basis of Cumulative Prospect Theory. Meanwhile, they show the application of extended TODIM in real-valued MADM. In what follows, we introduce this extended TODIM method.
In the following decision matrix N, the alternatives and attributes are displayed in accordance with decision maker’s view.
\[ N=\left[\begin{array}{c@{\hskip4.0pt}c@{\hskip4.0pt}c@{\hskip4.0pt}c@{\hskip4.0pt}c@{\hskip4.0pt}c}{n_{11}}\hspace{1em}& {n_{12}}\hspace{1em}& \cdots \hspace{1em}& {n_{1r}}\hspace{1em}& \cdots \hspace{1em}& {n_{1g}}\\ {} {n_{21}}\hspace{1em}& {n_{22}}\hspace{1em}& \cdots \hspace{1em}& {n_{2r}}\hspace{1em}& \cdots \hspace{1em}& {n_{2g}}\\ {} \vdots \hspace{1em}& \vdots \hspace{1em}& \ddots \hspace{1em}& \vdots \hspace{1em}& \ddots \hspace{1em}& \vdots \\ {} {n_{s1}}\hspace{1em}& {n_{s2}}\hspace{1em}& \cdots \hspace{1em}& {n_{sr}}\hspace{1em}& \cdots \hspace{1em}& {n_{sg}}\\ {} \vdots \hspace{1em}& \vdots \hspace{1em}& \ddots \hspace{1em}& \vdots \hspace{1em}& \ddots \hspace{1em}& \vdots \\ {} {n_{f1}}\hspace{1em}& {n_{f2}}\hspace{1em}& \cdots \hspace{1em}& {n_{fr}}\hspace{1em}& \cdots \hspace{1em}& {n_{fg}}\end{array}\right]={({n_{sr}})_{f\times g}},\]
$\lambda =({\lambda _{1}},{\lambda _{2}},\dots ,{\lambda _{g}})$ represents the weighting vector of attributes, which satisfies ${\textstyle\sum _{r=1}^{g}}{\lambda _{r}}=1$.
Step 1. The converted probability of the alternative ${V_{i}}$ to ${V_{k}}$ will be computed according to (6) or (7), where $i,k\in f$ and $i\ne k$.
When ${n_{ir}}-{n_{kr}}\geqslant 0$, the converted probability weight is calculated by (6):
Otherwise, the converted probability weight is calculated by ( 7):
where ζ and ξ are the parameters describing the curvature of the weighting function.
Step 2. Eq. (8) is used to determine the relative weight ${\eta _{ikr}^{\ast }}({\lambda _{r}})$ of the alternative ${V_{i}}$ to ${V_{k}}$.
where ${\eta _{ikr}}({\lambda _{r}})$ represents the converted probability weight of the rth attribute for the alternative ${V_{i}}$, which is equal to ${\eta _{ikr}^{+}}({\lambda _{r}})$ when ${n_{ir}}\geqslant {n_{kr}}$, or equal to ${\eta _{ikr}^{-}}({\lambda _{r}})$ according to (7).
(8)
\[ {\eta _{ikr}^{\ast }}({\lambda _{r}})={\eta _{ikr}}({\lambda _{r}})\big/\max \big\{{\eta _{ikr}}({\lambda _{p}})\hspace{0.1667em}\big|\hspace{0.1667em}p\in g\big\},\hspace{1em}r\in g,\hspace{2.5pt}\forall (i,k),\]
Step 3. Figure out the relative prospect dominance of alternative ${V_{i}}$ to ${V_{k}}$ underneath the attribute r with (9):
where α, β and θ are the parameters.
(9)
\[ {\vartheta _{r}}({V_{i}},{V_{k}})=\left\{\begin{array}{l@{\hskip4.0pt}l}{\eta _{ikr}^{\ast }}({\lambda _{r}})\cdot {({n_{ir}}-{n_{kr}})^{\beta }}/{\textstyle\textstyle\sum _{r=1}^{g}}{\eta _{ikr}^{\ast }}({\lambda _{r}}),\hspace{1em}& \text{if}\hspace{5pt}{n_{ir}}>{n_{kr}},\\ {} 0,\hspace{1em}& \text{if}\hspace{5pt}{n_{ir}}={n_{kr}},\\ {} -\theta ({\textstyle\textstyle\sum _{r=1}^{g}}{\eta _{ikr}^{\ast }}({\lambda _{r}}))\cdot {({n_{kr}}-{n_{ir}})^{\alpha }}/{\eta _{ikr}^{\ast }}({\lambda _{r}}),\hspace{1em}& \text{if}\hspace{5pt}{n_{ir}}<{n_{kr}},\end{array}\right.\]
Step 4. Determine the dominance degree of the alternative ${V_{i}}$ over the others, which is calculated as Eq. (10).
Step 5. Acquire the overall dominance degree of the alternative ${V_{i}}$ from Eq. (11).
Step 6. Rank the overall dominance degree $\psi ({V_{i}})$, $i\in f$. The alternative with the bigger $\psi ({V_{i}})$ value is considered the better choice.
3 Extended TODIM for Picture Fuzzy MAGDM Based on Cumulative Prospect Theory
Let $V=\{{V_{1}},{V_{2}},\dots ,{V_{f}}\}$ and $D=\{{D_{1}},{D_{2}},\dots ,{D_{g}}\}$ be the sets of alternatives and attributes, respectively, and the information about the attribute weights is unknown. Now, there are n decision makers, integrated into the set of decision makers $M=\{{M_{1}},{M_{2}},\dots ,{M_{n}}\}$, whose weight vector is $\chi =({\chi _{1}},{\chi _{2}},\dots ,{\chi _{n}})$, ${\chi _{t}}\geqslant 0$, $(t=1,2,\dots ,n)$, ${\textstyle\sum _{t=1}^{n}}{\chi _{t}}=1$.
${N^{t}}={({n_{sr}^{t}})_{f\times g}}={({\alpha _{sr}^{t}},{\beta _{sr}^{t}},{\varphi _{sr}^{t}})_{f\times g}}$ is the decision matrix under picture fuzzy environment of the tth decider, where ${\alpha _{sr}^{t}}$ indicates the positive subordinate degree of the tth decision maker, ${\beta _{sr}^{t}}$ expresses the neutral subordinate degree of the tth decision maker, ${\varphi _{sr}^{t}}$ expresses the negative subordinate degree of the tth decision maker, ${\alpha _{sr}^{t}},{\beta _{sr}^{t}},{\varphi _{sr}^{t}}\in [0,1]$ and $0\leqslant {\alpha _{sr}^{t}}+{\beta _{sr}^{t}}+{\varphi _{sr}^{t}}\leqslant 1$, $s=1,2,\dots ,f$, $r=1,2,\dots ,g$, $t=1,2,\dots ,n$.
In the following, we introduce Picture Fuzzy MAGDM using extended TODIM. The framework is shown in Fig. 1.
Step 1. Transform the cost attributes into the benefit attributes by using Eq. (12).
(12)
\[\begin{aligned}{}& {U^{t}}={\big({u_{sr}^{t}}\big)_{f\times g}},\hspace{1em}s=1,2,\dots ,f,\hspace{2.5pt}r=1,2,\dots ,g,\hspace{2.5pt}t=1,2,\dots ,n,\\ {} & {u_{sr}^{t}}=\big({\mu _{sr}^{t}},{\nu _{sr}^{t}},{\rho _{sr}^{t}}\big)=\left\{\begin{array}{l@{\hskip4.0pt}l}{n_{sr}^{t}}=({\alpha _{sr}^{t}},{\beta _{sr}^{t}},{\varphi _{sr}^{t}}),\hspace{1em}& {D_{r}}\hspace{2.5pt}\text{is a benefit attribute}\hspace{2.5pt},\\ {} {\overline{n}_{sr}^{t}}=({\varphi _{sr}^{t}},{\beta _{sr}^{t}},{\alpha _{sr}^{t}}),\hspace{1em}& {D_{r}}\hspace{2.5pt}\text{is a cost attribute}\hspace{2.5pt}.\end{array}\right.\end{aligned}\]
Step 2. Calculate score matrix ${C^{t}}={({c_{sr}^{t}})_{f\times g}}$ for each normalized decision maker using Eq. (13), and integrate these score matrices for different decision maker into one group score matrix $Y={({y_{sr}})_{f\times g}}$ using Eq. (14).
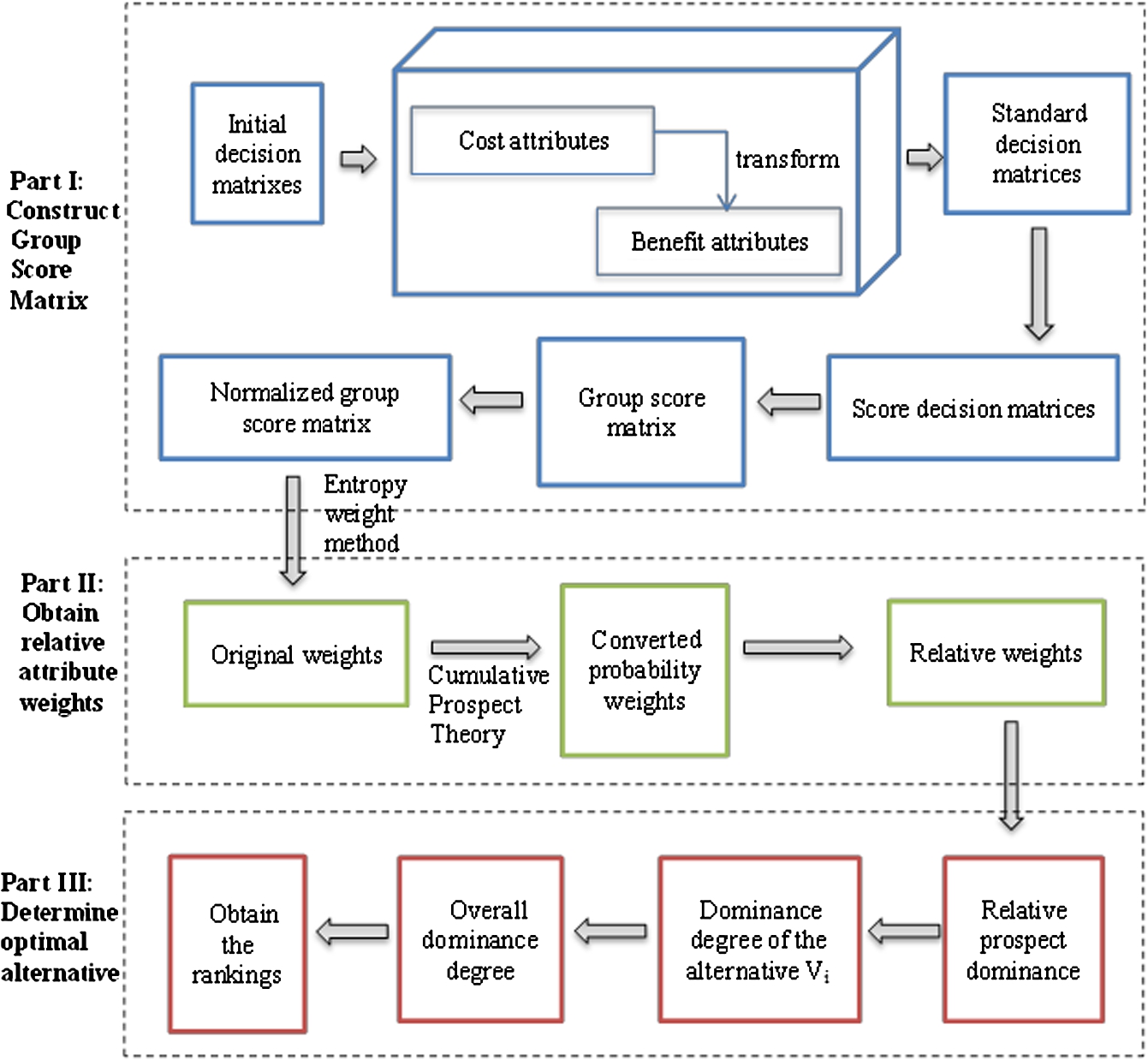
Fig. 1.
The flow chart of extended TODIM for picture fuzzy MAGDM based on cumulative prospect theory.
Step 3. Use Eq. (15) to normalize the group score matrix and obtain the normalized matrix $X={({x_{sr}})_{f\times g}}$.
Step 4. Utilize the Entropy Weight Method to obtain the original weight attributes $\lambda =({\lambda _{1}},{\lambda _{2}},\dots ,{\lambda _{n}})$, ${\lambda _{r}}\geqslant 0$, which is calculated as (16) and (17):
Step 5. The converted probability of the alternative ${V_{i}}$ to ${V_{k}}$ will be computed according to (18) or (19), where $i,k\in f$ and $i\ne k$.
When ${x_{ir}}-{x_{kr}}\geqslant 0$, the converted probability weight is calculated by (18):
Otherwise, the converted probability weight is calculated by ( 19):
where ζ and ξ are the parameters describing the curvature of the weighting function.
Step 6. Eq. (20) is used to determine the relative weight ${\eta _{ikr}^{\ast }}({\lambda _{r}})$ of the alternative ${V_{i}}$ to ${V_{k}}$.
where ${\eta _{ikr}}({\lambda _{r}})$ represents the converted probability weight of the rth attribute for the alternative ${V_{i}}$, which is equal to ${\eta _{ikr}^{+}}({\lambda _{r}})$ when ${x_{ir}}\geqslant {x_{kr}}$, or equal to ${\eta _{ikr}^{-}}({\lambda _{r}})$ according to Eq. (19).
(20)
\[ {\eta _{ikr}^{\ast }}({\lambda _{r}})={\eta _{ikr}}({\lambda _{r}})\big/\max \big\{{\eta _{ikr}}({\lambda _{p}})\big|p\in g\big\},\hspace{1em}r\in g,\hspace{2.5pt}\forall (i,k),\]
Step 7. Determine the dominance degree of the alternative ${V_{i}}$ over the others, which is calculated as Eq. (21):
where
(21)
\[ \pi ({V_{i}})={\sum \limits_{k=1}^{f}}{\sum \limits_{r=1}^{g}}{\vartheta _{r}}({V_{i}},{V_{k}}),\hspace{1em}i=1,2,\dots ,f,\](22)
\[ {\vartheta _{r}}({V_{i}},{V_{k}})=\left\{\begin{array}{l@{\hskip4.0pt}l}{\eta _{ikr}^{\ast }}({\lambda _{r}})\cdot {({x_{ir}}-{x_{kr}})^{\beta }}/{\textstyle\textstyle\sum _{r=1}^{g}}{\eta _{ikr}^{\ast }}({\lambda _{r}}),\hspace{1em}& \text{if}\hspace{5pt}{x_{ir}}>{x_{kr}},\\ {} 0,\hspace{1em}& \text{if}\hspace{5pt}{x_{ir}}={x_{kr}},\\ {} -\theta ({\textstyle\textstyle\sum _{r=1}^{g}}{\eta _{ikr}^{\ast }}({\lambda _{r}}))\cdot {({x_{kr}}-{x_{ir}})^{\alpha }}/{\eta _{ikr}^{\ast }}({\lambda _{r}}),\hspace{1em}& \text{if}\hspace{5pt}{x_{ir}}<{x_{kr}}.\end{array}\right.\]The ${\vartheta _{r}}({V_{i}},{V_{k}})$ indicates the relative prospect dominance of alternative ${V_{i}}$ to ${V_{k}}$ under the attribute r, and α, β and θ are the parameters.
Step 8. Acquire the overall dominance degree of the alternative ${V_{i}}$ from Eq. (23).
Step 9. Rank the overall dominance degree $\psi ({V_{i}})$, $i\in f$. The alternative with the bigger $\psi ({V_{i}})$ value is considered a better choice.
4 Numerical Instance
4.1 Numerical Example for Picture Fuzzy MAGDM
China’s accession to the world trade organization has continued for ten years, the retail circulation market has gradually opened to foreign investment, so that China’s local retail enterprises are facing the challenge of international retail giants. In the past period of time, with the continuous improvement of China’s urbanization level, community business has been developing vigorously. As a new type of business organization, community supermarket has become the focus of many retail manufacturers. However, many supermarkets are blind in site selection and lack scientific site selection research, which leads to high cost input and low benefit level, and eventually they are eliminated by the market. How to scientifically study and draw the relationship between the factors influencing the reasonable location of the supermarket, related to the future development of retail enterprises imminent problem. With the spring of Internet economy, the competition of real economy is more and more fierce. The supermarket location selection could be regarded as a MAGDM problem (Gao et al., 2020; Lu et al., 2019; Wang P. et al., 2019; Wei et al., 2019a). Therefore, it is crucial for a supermarket to select the best location that may result in prodigious effectiveness. Now, for the management of a supermarket, there are four site locations ${V_{i}}$ ( $i=1,2,3,4$) from which to choose. And the management adopts five attributes to assess these four alternatives: (1) ${D_{1}}$ is the shop rent, (2) ${D_{2}}$ is the population density, (3) ${D_{3}}$ is the consumption level, (4) ${D_{4}}$ is the intensity of competitive rivalry, (5) ${D_{5}}$ is the transportation convenience. Among them, ${D_{1}}$ and ${D_{4}}$ are cost attributes, and the others are benefit attributes. The four store location plans are going to be evaluated by three experts (whose weighting vector is $\chi ={({\chi _{1}},{\chi _{2}},{\chi _{3}})^{T}}={(0.43,0.22,0.35)^{T}}$) using PFNs under five attributes. Then, the picture fuzzy decision matrices which are given by the three experts are shown below (see Tables 1– 3).
Table 1
Decision matrix ${N^{1}}$ given by the first expert.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${_{{V_{1}}}}$ | $(0.28,0.06,0.54)$ | $(0.86,0.03,0.11)$ | $(0.55,0.13,0.26)$ | $(0.24,0.08,0.63)$ | $(0.56,0.18,0.22)$ |
| ${_{{V_{2}}}}$ | $(0.26,0.19,0.48)$ | $(0.53,0.12,0.03)$ | $(0.52,0.18,0.21)$ | $(0.21,0.16,0.53)$ | $(0.75,0.05,0.12)$ |
| ${_{{V_{3}}}}$ | $(0.15,0.02,0.72)$ | $(0.74,0.06,0.05)$ | $(0.70,0.04,0.13)$ | $(0.17,0.04,0.74)$ | $(0.61,0.21,0.08)$ |
| ${_{{V_{4}}}}$ | $(0.22,0.13,0.58)$ | $(0.69,0.21,0.08)$ | $(0.64,0.16,0.08)$ | $(0.16,0.24,0.59)$ | $(0.46,0.31,0.13)$ |
Table 2
Decision matrix ${N^{2}}$ given by the second expert.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${_{{V_{1}}}}$ | $(0.28,0.06,0.62)$ | $(0.87,0.03,0.09)$ | $(0.71,0.05,0.20)$ | $(0.33,0.14,0.49)$ | $(0.58,0.14,0.16)$ |
| ${_{{V_{2}}}}$ | $(0.22,0.16,0.52)$ | $(0.47,0.14,0.26)$ | $(0.62,0.13,0.25)$ | $(0.12,0.22,0.48)$ | $(0.65,0.13,0.15)$ |
| ${_{{V_{3}}}}$ | $(0.19,0.11,0.67)$ | $(0.69,0.05,0.21)$ | $(0.84,0.02,0.13)$ | $(0.09,0.23,0.62)$ | $(0.63,0.05,0.25)$ |
| ${_{{V_{4}}}}$ | $(0.02,0.08,0.74)$ | $(0.62,0.12,0.04)$ | $(0.58,0.26,0.14)$ | $(0.24,0.02,0.71)$ | $(0.52,0.17,0.24)$ |
Table 3
Decision matrix ${N^{3}}$ given by the third expert.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${_{{V_{1}}}}$ | $(0.14,0.28,0.52)$ | $(0.68,0.02,0.16)$ | $(0.67,0.06,0.23)$ | $(0.21,0.09,0.66)$ | $(0.47,0.11,0.26)$ |
| ${_{{V_{2}}}}$ | $(0.13,0.15,0.68)$ | $(0.58,0.24,0.16)$ | $(0.43,0.38,0.12)$ | $(0.15,0.26,0.48)$ | $(0.65,0.08,0.16)$ |
| ${_{{V_{3}}}}$ | $(0.11,0.03,0.77)$ | $(0.73,0.09,0.13)$ | $(0.65,0.12,0.22)$ | $(0.16,0.08,0.72)$ | $(0.59,0.04,0.35)$ |
| ${_{{V_{4}}}}$ | $(0.21,0.09,0.66)$ | $(0.56,0.07,0.26)$ | $(0.49,0.21,0.26)$ | $(0.28,0.03,0.54)$ | $(0.53,0.22,0.23)$ |
In the rest of the paper, we introduce using the suggested approach in this article obtaining the optimal location.
Table 4
Normalized decision matrix ${U^{1}}$ given by the first expert.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${_{{V_{1}}}}$ | $(0.54,0.06,0.28)$ | $(0.86,0.03,0.11)$ | $(0.55,0.13,0.26)$ | $(0.63,0.08,0.24)$ | $(0.56,0.18,0.22)$ |
| ${_{{V_{2}}}}$ | $(0.48,0.19,0.26)$ | $(0.53,0.12,0.03)$ | $(0.52,0.18,0.21)$ | $(0.53,0.16,0.21)$ | $(0.75,0.05,0.12)$ |
| ${_{{V_{3}}}}$ | $(0.72,0.02,0.15)$ | $(0.74,0.06,0.05)$ | $(0.70,0.04,0.13)$ | $(0.74,0.04,0.17)$ | $(0.61,0.21,0.08)$ |
| ${_{{V_{4}}}}$ | $(0.58,0.13,0.22)$ | $(0.69,0.21,0.08)$ | $(0.64,0.16,0.08)$ | $(0.59,0.24,0.16)$ | $(0.46,0.31,0.13)$ |
Table 5
Normalized decision matrix ${U^{2}}$ given by the second expert.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${_{{V_{1}}}}$ | $(0.62,0.06,0.28)$ | $(0.87,0.03,0.09)$ | $(0.71,0.05,0.20)$ | $(0.49,0.14,0.33)$ | $(0.58,0.14,0.16)$ |
| ${_{{V_{2}}}}$ | $(0.52,0.16,0.22)$ | $(0.47,0.14,0.26)$ | $(0.62,0.13,0.25)$ | $(0.48,0.22,0.12)$ | $(0.65,0.13,0.15)$ |
| ${_{{V_{3}}}}$ | $(0.67,0.11,0.19)$ | $(0.69,0.05,0.21)$ | $(0.84,0.02,0.13)$ | $(0.62,0.23,0.09)$ | $(0.63,0.05,0.25)$ |
| ${_{{V_{4}}}}$ | $(0.74,0.08,0.02)$ | $(0.62,0.12,0.04)$ | $(0.58,0.26,0.14)$ | $(0.71,0.02,0.24)$ | $(0.52,0.17,0.24)$ |
Step 2. Calculate score matrix ${C^{t}}={({c_{sr}^{t}})_{4\times 5}}$ for each normalized decision maker using Eq. (13), and it is shown in Table 7 to Table 9. Then, integrate these score matrices for different decision maker into one group score matrix $Y={({y_{sr}})_{4\times 5}}$ using Eq. (14). The result is shown in Table 10.
Table 6
Normalized decision matrix ${U^{3}}$ given by the third expert.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${_{{V_{1}}}}$ | $(0.52,0.28,0.14)$ | $(0.68,0.02,0.16)$ | $(0.67,0.06,0.23)$ | $(0.66,0.09,0.21)$ | $(0.47,0.11,0.26)$ |
| ${_{{V_{2}}}}$ | $(0.68,0.15,0.13)$ | $(0.58,0.24,0.16)$ | $(0.43,0.38,0.12)$ | $(0.48,0.26,0.15)$ | $(0.65,0.08,0.16)$ |
| ${_{{V_{3}}}}$ | $(0.77,0.03,0.11)$ | $(0.73,0.09,0.13)$ | $(0.65,0.12,0.22)$ | $(0.72,0.08,0.16)$ | $(0.59,0.04,0.35)$ |
| ${_{{V_{4}}}}$ | $(0.66,0.09,0.21)$ | $(0.56,0.07,0.26)$ | $(0.49,0.21,0.26)$ | $(0.54,0.03,0.28)$ | $(0.53,0.22,0.23)$ |
Table 7
Score matrix ${C^{1}}$ given by the first expert.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${_{{V_{1}}}}$ | 0.6300 | 0.8750 | 0.6450 | 0.6950 | 0.6700 |
| ${_{{V_{2}}}}$ | 0.6100 | 0.7500 | 0.6550 | 0.6600 | 0.8150 |
| ${_{{V_{3}}}}$ | 0.7850 | 0.8450 | 0.7850 | 0.7850 | 0.7650 |
| ${_{{V_{4}}}}$ | 0.6800 | 0.8050 | 0.7800 | 0.7150 | 0.6650 |
Table 8
Score matrix ${C^{2}}$ given by the second expert.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${_{{V_{1}}}}$ | 0.6700 | 0.8900 | 0.7550 | 0.5800 | 0.7100 |
| ${_{{V_{2}}}}$ | 0.6500 | 0.6050 | 0.6850 | 0.6800 | 0.7500 |
| ${_{{V_{3}}}}$ | 0.7400 | 0.7400 | 0.8550 | 0.7650 | 0.6900 |
| ${_{{V_{4}}}}$ | 0.8600 | 0.7900 | 0.7200 | 0.7350 | 0.6400 |
Table 9
Score matrix ${C^{3}}$ given by the third expert.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${_{{V_{1}}}}$ | 0.6900 | 0.7600 | 0.7200 | 0.7250 | 0.6050 |
| ${_{{V_{2}}}}$ | 0.7750 | 0.7100 | 0.6550 | 0.6650 | 0.7450 |
| ${_{{V_{3}}}}$ | 0.8300 | 0.8000 | 0.7150 | 0.7800 | 0.6200 |
| ${_{{V_{4}}}}$ | 0.7250 | 0.6500 | 0.6150 | 0.6300 | 0.6500 |
Step 3. Use Eq. (15) to normalize the group score matrix and obtain the normalized matrix $X={({x_{sr}})_{4\times 5}}$ shown in Table 11.
Table 10
Groupscore matrix Y.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${_{{V_{1}}}}$ | 0.6598 | 0.8381 | 0.6955 | 0.6802 | 0.6561 |
| ${_{{V_{2}}}}$ | 0.6766 | 0.7041 | 0.6616 | 0.6662 | 0.7762 |
| ${_{{V_{3}}}}$ | 0.7909 | 0.8062 | 0.7759 | 0.7789 | 0.6978 |
| ${_{{V_{4}}}}$ | 0.7354 | 0.7475 | 0.7091 | 0.6897 | 0.6543 |
Step 4. Utilize Eq. (16) and (17) to obtain the original weighting vector of attributes $\lambda =(0.2368,0.2054,0.1546,0.1765,0.2266)$.
Table 11
Normalized Group score matrix X.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${_{{V_{1}}}}$ | 0.2305 | 0.2707 | 0.2447 | 0.2416 | 0.2356 |
| ${_{{V_{2}}}}$ | 0.2363 | 0.2274 | 0.2328 | 0.2367 | 0.2788 |
| ${_{{V_{3}}}}$ | 0.2763 | 0.2604 | 0.2730 | 0.2767 | 0.2506 |
| ${_{{V_{4}}}}$ | 0.2569 | 0.2414 | 0.2495 | 0.2450 | 0.2350 |
Step 5. Compute the converted probability of the alternative ${V_{i}}$ to ${V_{k}}$ according to (18) or (19). The result is shown in Tables 12 to 15 ( $\zeta =0.61$, $\xi =0.69$, which derive from the experiment of Kahneman, 1992).
Table 12
The converted probability of the alternative ${V_{1}}$ to others.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${_{{\eta _{12}}}}$ | 0.2842 | 0.2642 | 0.2303 | 0.2455 | 0.2768 |
| ${_{{\eta _{13}}}}$ | 0.2842 | 0.2642 | 0.2207 | 0.2387 | 0.2768 |
| ${_{{\eta _{14}}}}$ | 0.2842 | 0.2642 | 0.2207 | 0.2387 | 0.2771 |
Table 13
The converted probability of the alternative ${V_{2}}$ to others.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${_{{\eta _{21}}}}$ | 0.2831 | 0.2611 | 0.2207 | 0.2387 | 0.2771 |
| ${_{{\eta _{23}}}}$ | 0.2842 | 0.2611 | 0.2207 | 0.2387 | 0.2771 |
| ${_{{\eta _{24}}}}$ | 0.2842 | 0.2611 | 0.2207 | 0.2387 | 0.2771 |
Table 14
The converted probability of the alternative ${V_{3}}$ to others.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${_{{\eta _{31}}}}$ | 0.2831 | 0.2611 | 0.2303 | 0.2455 | 0.2771 |
| ${_{{\eta _{32}}}}$ | 0.2831 | 0.2642 | 0.2303 | 0.2455 | 0.2768 |
| ${_{{\eta _{34}}}}$ | 0.2831 | 0.2642 | 0.2303 | 0.2455 | 0.2771 |
Step 6. Determine the relative weight ${\eta _{ikr}^{\ast }}({\lambda _{r}})$ of the alternative ${V_{i}}$ to ${V_{k}}$ by using Eq. (20). The result is shown in Tables 16 to 19.
Table 15
The converted probability of the alternative ${V_{4}}$ to others.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${_{{\eta _{41}}}}$ | 0.2831 | 0.2611 | 0.2303 | 0.2455 | 0.2768 |
| ${_{{\eta _{42}}}}$ | 0.2831 | 0.2642 | 0.2303 | 0.2455 | 0.2768 |
| ${_{{\eta _{43}}}}$ | 0.2842 | 0.2611 | 0.2207 | 0.2387 | 0.2768 |
Table 16
The relative weight of the alternative ${V_{1}}$ to others.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${_{{\eta _{12}^{\ast }}}}$ | 1.0000 | 0.9296 | 0.8103 | 0.8639 | 0.9742 |
| ${_{{\eta _{13}^{\ast }}}}$ | 1.0000 | 0.9296 | 0.7765 | 0.8400 | 0.9742 |
| ${_{{\eta _{14}^{\ast }}}}$ | 1.0000 | 0.9296 | 0.7765 | 0.8400 | 0.9751 |
Table 17
The relative weight of the alternative ${V_{2}}$ to others.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${_{{\eta _{21}^{\ast }}}}$ | 1.0000 | 0.9223 | 0.7794 | 0.8431 | 0.9788 |
| ${_{{\eta _{23}^{\ast }}}}$ | 1.0000 | 0.9189 | 0.7765 | 0.8400 | 0.9751 |
| ${_{{\eta _{24}^{\ast }}}}$ | 1.0000 | 0.9189 | 0.7765 | 0.8400 | 0.9751 |
Table 18
The relative weight of the alternative ${V_{3}}$ to others.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${_{{\eta _{31}^{\ast }}}}$ | 1.0000 | 0.9223 | 0.8133 | 0.8671 | 0.9788 |
| ${_{{\eta _{32}^{\ast }}}}$ | 1.0000 | 0.9330 | 0.8133 | 0.8671 | 0.9779 |
| ${_{{\eta _{34}^{\ast }}}}$ | 1.0000 | 0.9330 | 0.8133 | 0.8671 | 0.9788 |
Step 7. Determine the relative prospect dominance ${\vartheta _{r}}({V_{i}},{V_{k}})$ and the dominance degree of the alternative ${V_{i}}$ ( $i=1,2,3,4$) over the others, which are calculated as in Eq. (22) and (21), respectively. The result is shown in Tables 20 to 23. ( $\alpha =0.88$, $\beta =0.88$, $\theta =2.25$, which derive from the experiment of Kahneman, 1992).
Table 19
The relative weight of the alternative ${V_{4}}$ to others.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${_{{\eta _{41}^{\ast }}}}$ | 1.0000 | 0.9223 | 0.8133 | 0.8671 | 0.9779 |
| ${_{{\eta _{42}^{\ast }}}}$ | 1.0000 | 0.9330 | 0.8133 | 0.8671 | 0.9779 |
| ${_{{\eta _{43}^{\ast }}}}$ | 1.0000 | 0.9189 | 0.7765 | 0.8400 | 0.9742 |
Table 20
The relative prospect dominance of the alternative ${V_{1}}$ to others.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${\vartheta _{12}}$ | −0.1117 | 0.0128 | 0.0036 | 0.0018 | −0.6653 |
| ${\vartheta _{13}}$ | −0.6741 | 0.0037 | −0.5687 | −0.6344 | −0.2589 |
| ${\vartheta _{14}}$ | −0.4153 | 0.0092 | −0.1190 | −0.0805 | 0.0003 |
Table 21
The relative prospect dominance of the alternative ${V_{2}}$ to others.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${\vartheta _{21}}$ | 0.0024 | −0.6960 | −0.2647 | −0.1138 | 0.0136 |
| ${\vartheta _{23}}$ | −0.5964 | −0.5483 | −0.7729 | −0.7117 | 0.0093 |
| ${\vartheta _{24}}$ | −0.3323 | −0.2581 | −0.3566 | −0.1791 | 0.0138 |
Table 22
The relative prospect dominance of the alternative ${V_{3}}$ to others.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${\vartheta _{31}}$ | 0.0145 | −0.1994 | 0.0077 | 0.0099 | 0.0053 |
| ${\vartheta _{32}}$ | 0.0128 | 0.0101 | 0.0105 | 0.0111 | −0.4568 |
| ${\vartheta _{34}}$ | 0.0068 | 0.0062 | 0.0065 | 0.0091 | 0.0055 |
Step 8. Acquire the overall dominance degree of the alternative ${V_{i}}$ ( $i=1,2,3,4$) from Eq. (23).
Table 23
The relative prospect dominance of the alternative ${V_{4}}$ to others.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${\vartheta _{41}}$ | 0.0089 | −0.4996 | 0.0016 | 0.0013 | −0.0164 |
| ${\vartheta _{42}}$ | 0.0071 | 0.0047 | 0.0048 | 0.0028 | −0.6735 |
| ${\vartheta _{43}}$ | −0.3158 | −0.3370 | −0.4820 | −0.5792 | −0.2680 |
4.2 Comparative Analysis
In the following, we take into account the classical TODIM method (Wei, 2018), the VIKOR method (Meksavang et al., 2019), the picture fuzzy weighted cross-entropy method (Wei, 2016), the projection model (Wei et al., 2018), the MULTIMOORA method (Lin et al., 2020) and the EDAS method (Li et al., 2019) to test the efficiency of the improved TODIM, respectively.
4.2.1 Comparison with the Classical TODIM
Firstly, we take into account the classical TODIM (Wei, 2018) to verify the usability of the improved TODIM method proposed in this article. The final results of these two methods have a certain similarity that ${V_{3}}$ is confirmed to be the optimal alternative. However, there are some pivotal differences between the new improved TODIM method and the classical TODIM method. The new method provides a more detailed description of the mental processes of decision makers. In addition, beyond all questions, the introduction of weight calculation method further deepens the scientificity of the new method. The relevant process and results are shown as follows.
Step 1. We can use the same method to process data, like Section 4.1 from step 1 to step 4, obtaining the weighting vector of attributes $\lambda =(0.2368,0.2054,0.1546,0.1765,0.2266)$ and normalized Group score matrix X shown in Table 11.
Step 2. Determine the dominance degree using Eq. (24). And the result is shown in Tables 24 to 27.
(24)
\[ {\vartheta _{r}}({V_{i}},{V_{k}})=\left\{\begin{array}{l@{\hskip4.0pt}l}\sqrt{{\lambda _{r}}\cdot ({x_{ir}}-{x_{kr}})/{\textstyle\textstyle\sum _{r=1}^{g}}{\lambda _{r}}},\hspace{1em}& \text{if}\hspace{5pt}{x_{ir}}>{x_{kr}},\\ {} 0,\hspace{1em}& \text{if}\hspace{5pt}{x_{ir}}={x_{kr}},\\ {} -\theta \sqrt{({\textstyle\textstyle\sum _{r=1}^{g}}{\lambda _{r}})\cdot ({x_{kr}}-{x_{ir}})/{\lambda _{r}}},\hspace{1em}& \text{if}\hspace{5pt}{x_{ir}}<{x_{kr}}.\end{array}\right.\]Table 24
The dominance degree of the alternative ${V_{1}}$ to others.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${\vartheta _{12}}$ | −0.7268 | 0.0459 | 0.0209 | 0.0144 | −2.0175 |
| ${\vartheta _{13}}$ | −2.0330 | 0.0224 | −1.9784 | −2.0601 | −1.1886 |
| ${\vartheta _{14}}$ | −1.5436 | 0.0377 | −0.8134 | −0.6376 | 0.0059 |
Table 25
The dominance degree of the alternative ${V_{2}}$ to others.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${\vartheta _{21}}$ | 0.0181 | −2.1221 | −1.2833 | −0.7775 | 0.0481 |
| ${\vartheta _{23}}$ | −1.8986 | −1.8523 | −2.3581 | −2.2019 | 0.0389 |
| ${\vartheta _{24}}$ | −1.3618 | −1.2072 | −1.5194 | −1.0055 | 0.0485 |
Table 26
The dominance degree of the alternative ${V_{3}}$ to others.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${\vartheta _{31}}$ | 0.0507 | −1.0356 | 0.0322 | 0.0383 | 0.0284 |
| ${\vartheta _{32}}$ | 0.0473 | 0.0400 | 0.0384 | 0.0409 | −1.6303 |
| ${\vartheta _{34}}$ | 0.0330 | 0.0304 | 0.0293 | 0.0364 | 0.0290 |
Step 3. Acquire the overall dominance degree of the alternative ${V_{i}}$ ( $i=1,2,3,4$) from Eq. (23).
Table 27
The dominance degree of the alternative ${V_{4}}$ to others.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${\vartheta _{41}}$ | 0.0385 | −1.7453 | 0.0132 | 0.0118 | −0.2469 |
| ${\vartheta _{42}}$ | 0.0339 | 0.0261 | 0.0247 | 0.0187 | −2.0326 |
| ${\vartheta _{43}}$ | −1.3230 | −1.4048 | −1.8034 | −1.9590 | −1.2140 |
Step 4. Rank the overall dominance degree $\psi ({V_{i}})$, $i=1,2,3,4$.
So, the alternative ${V_{3}}$ is the best one.
4.2.2 Comparison with the VIKOR Method
In the VIKOR (Meksavang et al., 2019) method, the collective picture fuzzy evaluation matrix is shown in Table 28. The positive ideal in different attributes is as follows: ${u_{1}^{+}}=(0.7290,0.0335,0.1418)$, ${u_{2}^{+}}=(0.8160,0.0260,0.1200)$, ${u_{3}^{+}}=(0.7243,0.0504,0.1563)$, ${u_{4}^{+}}=(0.7099,0.0749,0.1447)$, ${u_{5}^{+}}=(0.6971,0.0727,0.1394)$ and the negative is: ${u_{1}^{-}}=(0.5523,0.1029,0.2197)$, ${u_{2}^{-}}=(0.5360,0.1582,0.0867)$, ${u_{3}^{-}}=(0.5158,0.2177,0.1794)$, ${u_{4}^{-}}=(0.5021,0.2034,0.1650)$, ${u_{5}^{-}}=(0.4988,0.2409,0.1817)$. The distance from each scheme to the perfect point is shown in Table 29. And the values ${S_{i}}$ ( $i=1,2,3,4$) and ${R_{i}}$ ( $i=1,2,3,4$) are as follows: ${S_{1}}=0.6600$, ${S_{2}}=1.0086$, ${S_{3}}=0.2474$, ${S_{4}}=0.8842$; ${R_{1}}=0.2368$, ${R_{2}}=0.3642$, ${R_{3}}=0.1326$, ${R_{4}}=0.2699$. The ${Q_{i}}$ ( $i=1,2,3,4$) index is as follows: ${Q_{1}}=0.4959$, ${Q_{2}}=1$, ${Q_{3}}=0$, ${Q_{4}}=0.7147$, ${Q_{3}}<{Q_{1}}<{Q_{4}}<{Q_{2}}$. Therefore, there is ${V_{3}}>{V_{1}}>{V_{4}}>{V_{2}}$. The alternative ${V_{3}}$ is the optimal one.
Table 28
The collective picture fuzzy evaluation matrix U.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${_{{V_{1}}}}$ | $(0.5523,0.1029,0.2197)$ | $(0.8160,0.0260,0.1200)$ | $(0.6335,0.0804,0.2351)$ | $(0.6145,0.0943,0.2457)$ | $(0.5352,0.1434,0.2175)$ |
| ${_{{V_{2}}}}$ | $(0.5689,0.1684,0.1966)$ | $(0.5360,0.1582,0.0867)$ | $(0.5158,0.2177,0.1794)$ | $(0.5021,0.2034,0.1650)$ | $(0.6971,0.0727,0.1394)$ |
| ${_{{V_{3}}}}$ | $(0.7290,0.0335,0.1418)$ | $(0.7261,0.0664,0.0958)$ | $(0.7243,0.0504,0.1563)$ | $(0.7099,0.0749,0.1447)$ | $(0.6077,0.0857,0.1723)$ |
| ${_{{V_{4}}}}$ | $(0.6490,0.1027,0.1277)$ | $(0.6335,0.1264,0.1038)$ | $(0.5793,0.1958,0.1367)$ | $(0.6045,0.0671,0.2128)$ | $(0.4988,0.2409,0.1817)$ |
Table 29
The distance from each scheme to the perfect point.
| ${D_{1}}$ | ${D_{2}}$ | ${D_{3}}$ | ${D_{4}}$ | ${D_{5}}$ | |
| ${_{{V_{1}}}}$ | 0.2650 | 0.0000 | 0.1631 | 0.1805 | 0.2430 |
| ${_{{V_{2}}}}$ | 0.2846 | 0.4700 | 0.3127 | 0.3117 | 0.0000 |
| ${_{{V_{3}}}}$ | 0.0000 | 0.1712 | 0.0000 | 0.0000 | 0.1342 |
| ${_{{V_{4}}}}$ | 0.1411 | 0.2981 | 0.2468 | 0.1699 | 0.3157 |
4.2.3 Comparison with the Picture Fuzzy Weighted Cross-Entropy Method
In this part, we list the vital process of picture fuzzy weighted cross-entropy method (Wei, 2016). According to the principle of maximum positive membership degree and minimum negative as well as neutral membership degree, we can get the information of the ideal alternative
\[ {V^{+}}=\left(\hspace{-0.1667em}\begin{array}{l}(0.7290,0.0335,0.1277),(0.8160,0.0260,0.0867),(0.7243,0.0504,0.1367),\\ {} (0.7099,0.0671,0.1447),(0.6971,0.0727,0.1394)\end{array}\hspace{-0.1667em}\hspace{-0.1667em}\right).\]
Meanwhile, the picture fuzzy weighted cross-entropy between ${V_{i}}$ ( $i=1,2,3,4$) and ${V^{+}}$ is as following: $C({V_{1}},{V^{+}})=0.0179$, $C({V_{2}},{V^{+}})=0.0373$, $C({V_{3}},{V^{+}})=0.0034$, $C({V_{4}},{V^{+}})=0.0271$. The smallest picture fuzzy weighted cross-entropy $C({V_{3}},{V^{+}})$ corresponds with the best alternative ${V_{3}}$.4.2.4 Comparison with the Projection Model
The following describes the key information about the projection model (Wei et al., 2018). In accordance to the identical principle with picture fuzzy weighted cross-entropy method,
\[ {V^{+}}=\left(\hspace{-0.1667em}\begin{array}{l}(0.7290,0.0335,0.1277),(0.8160,0.0260,0.0867),(0.7243,0.0504,0.1367),\\ {} (0.7099,0.0671,0.1447),(0.6971,0.0727,0.1394)\end{array}\hspace{-0.1667em}\hspace{-0.1667em}\right)\]
is considered as the ideal alternative. The projection ${V_{i}}$ ( $i=1,2,3,4$) on ${V^{+}}$ can easily be obtained. The results are shown as follows: ${\mathrm{Prj}_{{V^{+}}}}({V_{1}})=0.3000$, ${\mathrm{Prj}_{{V^{+}}}}({V_{2}})=0.2758$, ${\mathrm{Prj}_{{V^{+}}}}({V_{3}})=0.3253$, ${\mathrm{Prj}_{{V^{+}}}}({V_{4}})=0.2846$. The alternative ${V_{3}}$ with biggest ${\mathrm{Prj}_{{V^{+}}}}({V_{3}})$ is the best one.4.2.5 Comparison with the MULTIMOORA Method
The main idea of the MULTIMOORA method (Lin et al., 2020) is to dispose of the fundamental information in different way. Finally, ranking value matrix and the corresponding ranking order matrix come into being. The ranking value matrix is
\[T=\begin{array}{l}\hspace{34.14322pt}\begin{array}{c@{\hskip4.0pt}c@{\hskip4.0pt}c}{T_{1}}\hspace{2em}\hspace{2.5pt}& {T_{2}}\hspace{2em}\hspace{2.5pt}\hspace{2.5pt}& {T_{3}}\end{array}\\ {} \begin{array}{c}{V_{1}}\\ {} {V_{2}}\\ {} {V_{3}}\\ {} {V_{4}}\end{array}\left(\begin{array}{c@{\hskip4.0pt}c@{\hskip4.0pt}c}0.4200\hspace{1em}& 0.2368\hspace{1em}& 1.2911\\ {} 0.4174\hspace{1em}& 0.2557\hspace{1em}& 1.2778\\ {} 0.5545\hspace{1em}& 0.0750\hspace{1em}& 1.4190\\ {} 0.4408\hspace{1em}& 0.2266\hspace{1em}& 1.2999\end{array}\right)\end{array}\]
and the ranking order matrix is
\[G=\begin{array}{l}\hspace{22.76228pt}\begin{array}{c@{\hskip4.0pt}c@{\hskip4.0pt}c}{G_{1}}\hspace{2.5pt}& {G_{2}}\hspace{2.5pt}& {G_{3}}\end{array}\\ {} \begin{array}{c}{V_{1}}\\ {} {V_{2}}\\ {} {V_{3}}\\ {} {V_{4}}\end{array}\left(\begin{array}{c@{\hskip4.0pt}c@{\hskip4.0pt}c}3\hspace{1em}& 3\hspace{1em}& 3\\ {} 4\hspace{1em}& 4\hspace{1em}& 4\\ {} 1\hspace{1em}& 1\hspace{1em}& 1\\ {} 2\hspace{1em}& 2\hspace{1em}& 2\end{array}\right)\end{array}.\]
Based on these two matrices, we can figure out the final ranking score of alternative ${V_{i}}$ ( $i=1,2,3,4$): $B({V_{1}})=0.0204$, $B({V_{2}})=-0.1486$, $B({V_{3}})=0.4369$, $B({V_{4}})=0.1833$. Therefore, the ranking result is ${V_{3}}>{V_{4}}>{V_{1}}>{V_{2}}$ and the alternative ${V_{3}}$ is first-rank.4.2.6 Comparison with the EDAS Method
4.2.7 Contrastive Analysis
We put all the results from different methods together in Table 31. Either way, the alternative ${V_{3}}$ is always the best one, which fully proves the reliability of the new proposed method. Furthermore, the improved picture fuzzy TODIM method, which has unparalleled superiority in meticulously describing the decision maker’s psychological states, is proposed in this paper for further improvement of TODIM method based on CPT. In addition, the improved picture fuzzy TODIM method gives logical method to obtain the attribute weights, eliminating the subjectivity of the information of attribute weight directly given by the decision maker. Therefore, it is more widely applicable in handling the MAGDM issues.
Table 31
The comparison.
| Method | The ranking result |
| Classical TODIM | ${V_{3}}>{V_{4}}>{V_{1}}>{V_{2}}$ |
| VIKOR | ${V_{3}}>{V_{1}}>{V_{4}}>{V_{2}}$ |
| Picture fuzzy weighted cross-entropy | ${V_{3}}>{V_{1}}>{V_{4}}>{V_{2}}$ |
| Projection model | ${V_{3}}>{V_{1}}>{V_{4}}>{V_{2}}$ |
| MULTIMOORA | ${V_{3}}>{V_{4}}>{V_{1}}>{V_{2}}$ |
| EDAS | ${V_{3}}>{V_{1}}>{V_{4}}>{V_{2}}$ |
| Improved TODIM | ${V_{3}}>{V_{4}}>{V_{1}}>{V_{2}}$ |
5 Conclusions
The TODIM method just focuses on MADM in real number, and doesn’t distinguish positive and negative attributes. Moreover, it supposes that the initial attributes weight vector is directly afforded by the expert. In this article, we expound the application of extended TODIM based on Cumulative Prospect Theory under picture fuzzy multiple attribute group decision making. First of all, we briefly sort out the basic knowledge (e.g. PFSs and PFNs) and introduce the extended TODIM. In addition, we adopt information entropy, which is used to identify the attributes weighting vector, to improve the availability of the TODIM method. At last, we exercise the improved TODIM into a numerical case and testify the effectiveness of this new method by means of comparing its results with other methods’ results. In years to come, the improved TODIM method should saturate numerous other fields and uncertainty environments ( Deng and Gao, 2019; Gao et al., 2019; He et al., 2019; Li and Lu, 2019; Lu and Wei, 2019; Wang J. et al., 2019; Wang, 2019; Wei et al., 2019b; Wu et al., 2019a, 2019b). And we will also continue to explore the application of this proposed TODIM method in other fields (Lu et al., 2020; Wang et al., 2020; Wei Y. et al., 2020) and seek more scientific methods to solve the multi-attribute group decision problems (Liu and Liu, 2019; Liu and Wang, 2014; Liu et al., 2018).
