Abstract
Emotion recognition from facial expressions has gained much interest over the last few decades. In the literature, the common approach, used for facial emotion recognition (FER), consists of these steps: image pre-processing, face detection, facial feature extraction, and facial expression classification (recognition). We have developed a method for FER that is absolutely different from this common approach. Our method is based on the dimensional model of emotions as well as on using the kriging predictor of Fractional Brownian Vector Field. The classification problem, related to the recognition of facial emotions, is formulated and solved. The relationship of different emotions is estimated by expert psychologists by putting different emotions as the points on the plane. The goal is to get an estimate of a new picture emotion on the plane by kriging and determine which emotion, identified by psychologists, is the closest one. Seven basic emotions (Joy, Sadness, Surprise, Disgust, Anger, Fear, and Neutral) have been chosen. The accuracy of classification into seven classes has been obtained approximately 50%, if we make a decision on the basis of the closest basic emotion. It has been ascertained that the kriging predictor is suitable for facial emotion recognition in the case of small sets of pictures. More sophisticated classification strategies may increase the accuracy, when grouping of the basic emotions is applied.
1 Introduction
Recently, a fast growth of emotion recognition research has been observed in various types of communication such as text (Shivhare and Khethawat,
2012; Calvo and Kim,
2013; Ramalingam
et al.,
2018), speech (Tamulevičius
et al.,
2017,
2019; Sailunaz
et al.,
2018), body gestures (Stathopoulou and Tsihrintzis,
2011; Metcalfe
et al.,
2019), and facial expressions (Revina and Emmanuel,
2018; Ko,
2018; Shao and Qian,
2019; Sharma
et al.,
2019).
Facial expressions are one of the most important means of interpersonal communication, since a facial expression says a lot without speaking. Therefore, research on facial emotions has received much attention in recent decades in applications in the perceptual and cognitive sciences (Purificación and Pablo,
2019). Facial emotion recognition (FER) is widely used in distinct areas such as: neurology (Adolphs and Anderson,
2018; Metcalfe
et al.,
2019), clinical psychology (Su
et al.,
2017), artificial intelligence (Ranade
et al.,
2018), intelligent security (Wang and Fang,
2008), robotics manufacturing (Weiguo
et al.,
2004), behavioural sciences (Vorontsova and Labunskaya,
2020), multimedia (Mariappan
et al.,
2012), educational software (Ferdig and Mishra,
2004; Filella
et al.,
2016), etc.
In the literature, the common approach to facial emotion recognition consists of these steps: image pre-processing (noise reduction, normalization), face detection, facial feature extraction, and facial expression classification (recognition). Numerous techniques have been made for FER by using different methods in these steps (Bhardwaj and Dixit,
2016; Deshmukh
et al.,
2017; Ko,
2018; Revina and Emmanuel,
2018; Shao and Qian,
2019; Sharma
et al.,
2019). In the literature, recognition accuracy of this approach varies from approximately 48% to 98% (Deshmukh
et al.,
2017; Revina and Emmanuel,
2018; Shao and Qian,
2019; Nonis
et al.,
2019; Sharma
et al.,
2019). However, the common approach has some drawbacks (Shao and Qian,
2019): a) recognition accuracy is highly dependent on the methods used and the data set analysed; b) methods are often difficult, because of many unknown parameters and/or long computation time.
Recently, deep-learning-based algorithms have been employed for feature extraction, classification, and recognition tasks. The convolutional neural networks and the recurrent neural networks have been applied in many studies including object recognition, face recognition, and facial emotion recognition as well. However, deep-learning-based techniques are available with big data (Nonis
et al.,
2019). A brief review of conventional FER approaches as well as deep-learning-based FER methods is presented in Ko (
2018). It is shown that the average recognition accuracy of six conventional FER approaches is equal to 63.2% and the average recognition accuracy of six deep-learning-based FER approaches is 72.65%, i.e. deep-learning based approaches outperform conventional approaches. In Gan
et al. (
2019), a novel FER framework via convolutional neural networks with soft labels that associate multiple emotions to each expression image is proposed. Investigations are made on the FER-2013 (35 887 face images) (Goodfellow
et al.,
2013), SFEW (1766 images) (Dhall
et al.,
2015) and RAF (15 339 images) (Li
et al.,
2017) databases, and the proposed method achieves accuracy of 73.73%, 55.73% and 86.31%, respectively.
In this paper, we focus on emotion recognition by facial expression. We have developed an approach, based on the two-dimensional model of emotions as well as using the kriging predictor of Fractional Brownian Vector Field (Motion) (FBVF). The classification problem, related to the recognition of facial emotions, is formulated and solved. The relationship of different emotions is estimated by expert psychologists by putting different emotions as the points on the plane. The kriging predictor allows us to get an estimate of a new picture emotion on the plane. Then, we determine which emotion, identified by psychologists, is the closest one. Seven emotions (Joy, Sadness, Surprise, Disgust, Anger, Fear, and Neutral) have been chosen for recognition.
The advantage of our method is that it is focused on small data sets. In the literature, seven basic emotions (e.g. Joy, Sadness, Surprise, Disgust, Anger, Fear, and Neutral) are usually used. However, sometimes specific emotions are measured. In this case, classical databases with basic emotions cannot be used for training of classifier. If we have little data for the study and cannot adapt other databases, then methods such as CNN will not give good accuracy with a small data set. This is an advantage of the kriging method. Our approach can be easily extended to other emotions.
2 Computational Models of Emotions
Emotions can be expressed in a variety of ways, such as facial expressions and gestures, speech, and written text. There are two models to recognize emotions: the categorical model and the dimensional one. In the first model, emotions are described with a discrete number of classes, affective adjectives, and, in the second model, emotions are characterized by several perpendicular axes, i.e. by defining where they lie in a two, three or higher dimensional space (Grekow,
2018). The review of these models is made in Sreeja and Mahalakshmi (
2017), Grekow (
2018).
There are many attempts in the literature to visualize similarities of emotions. This allows them to be compared not only qualitatively but also quantitatively. Such visualizations, namely the quantitative correspondence of emotions to points on the 2D plane, are reviewed below. We rely on this in the proposed new method of recognizing and classifying facial emotions.
2.1 Categorical Models of Emotions
Emotions are recognized with the help of words that denote emotions or class tags (Sreeja and Mahalakshmi,
2017). The categorical model either uses some basic emotion classes (Ekman,
1992; Johnson-Laird and Oatley,
1989; Grekow,
2018) or domain-specific expressive classes (Sreeja and Mahalakshmi,
2017). A various set of emotions may be required for different fields, for instance, in the area of instruction and education (D’mello and Graesser,
2007), five classes such as
Boredom,
Confusion,
Joy,
Flow, and
Frustration are proposed to describe affective states of students.
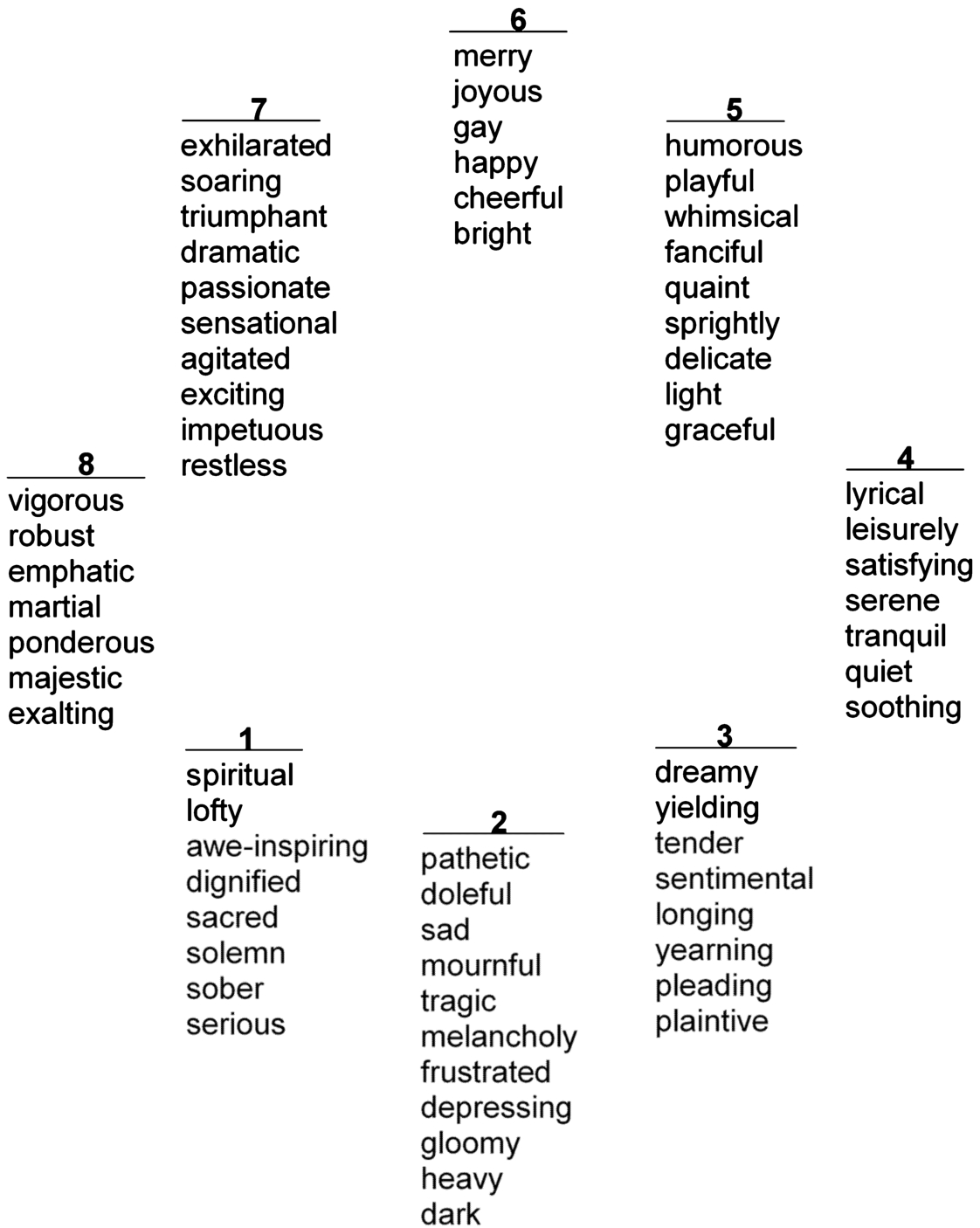
Fig. 1
Hevner’s adjectives arranged into 8 groups (Hevner,
1936).
Regarding categorical models of emotions, there are a lot of concepts about class quantity and grouping methods in the literature. Hevner was one of the first researchers who focused on finding and grouping terms pertaining to emotions (Hevner,
1936). He created a list of 66 adjectives arranged into eight groups distributed on a circle (Fig.
1). Adjectives inside a group are close to each other, and the opposite groups on the circle are the furthest apart by emotion. Farnsworth (
1954) and Schubert (
2003) modified Hevner’s model by decreasing the number of adjectives to 50 and 46, grouped them into nine groups. Recently, many researchers have been using the concept of six basic emotions (
Happiness,
Sadness,
Anger,
Fear,
Disgust, and
Surprise) presented by Ekman (
1992,
1999), which was developed for facial expression. Ekman described features that enabled differentiating six basic emotions. Johnson-Laird and Oatley (
1989) indicated a smaller group of basic emotions:
Happiness,
Sadness,
Anger,
Fear, and
Disgust. In Hu and Downie (
2007), five mood clusters were used for song classification. In Hu
et al. (
2008), etc., a deficiency of this categorical model was indicated, i.e. a semantic overlap among five clusters was noticed, because some clusters were quite similar. In Grekow (
2018), a set of 4 basic emotions:
Happy,
Angry,
Sad and
Relaxed, corresponding to the four quarters of Russell’s model (Russell,
1980), were used for the analysis of music recordings using the categorical model. More categories of emotions, used by various researchers, are indicated in Sreeja and Mahalakshmi (
2017).
The main disadvantage of the categorical model is that it has poorer resolution by using categories than the dimensional model. The number of emotions and their shades met in various types of communication is much richer than the limited number of categories of emotions in the model. The smaller the number of groups in the categorical model, the greater the simplification of the description of emotions (Grekow,
2018).
2.2 Dimensional Models of Emotions
Emotions can be defined according to one or more dimensions. For example, Wilhelm Max Wundt, the father of modern psychology, proposed to describe emotions by three dimensions: pleasurable versus unpleasurable, arousing versus subduing, and strain versus relaxation (Wundt,
1897).
In the dimensional model, emotions are identified according to their location in a space with a small number of emotional dimensions. In this way, the human emotion is represented as a point on an emotion space (Grekow,
2018). Since all emotions can be understood as changing values of the emotional dimensions, the dimensional model, in contrast to the categorical one, enables us to analyse the larger number of emotions and their shades. Commonly emotions are defined in a two (valence and arousal) or three (valence, arousal, and power/dominance) dimensional space. The valence dimension (emotional pleasantness) describes the positivity or negativity of an emotion and ranges from unpleasant feelings to a pleasant feeling (sense of happiness). The arousal dimension (physiological activation) denotes the level of excitement that the emotion depicts, and it ranges from
Sleepiness or
Boredom to high
Excitement. The dominance (power, influence) dimension represents a sense of control or freedom to act. For example, while
Fear and
Anger are unpleasant emotions,
Anger is a dominant emotion, and
Fear is a submissive one (Mehrabian,
1980,
1996; Grekow,
2018).
The two-dimensional models such as the Russell’s circumplex model (Russell,
1980) (Section
2.2.1), Thayer’s model (Thayer,
1989) (Section
2.2.2), the vector model (Bradley
et al.,
1992) (Section
2.2.3), the Positive Affect – Negative Affect (PANA) model (Watson and Tellegen,
1985; Watson
et al.,
1999) (Section
2.2.4), Whissell’s model (Whissell,
1989) (Section
2.2.5), and Plutchik’s wheel of emotions (Plutchik and Kellerman,
1980; Plutchik,
2001) (Section
2.2.6) are the most prevalent in emotion research. Among the three-dimensional models, Plutchik’s cone-shaped model (Plutchik and Kellerman,
1980; Plutchik,
2001) (Section
2.2.6), the Pleasure–Arousal–Dominance (PAD) model (Mehrabian and Russell,
1974) (Section
2.2.7), and Lövheim cube of emotion (Lövheim,
2011) (Section
2.2.8) are the most dominant and commonly used in emotion recognition field. Researchers have noticed that, in particular cases, two or three dimensions cannot adequately describe human emotions. Consequently, four or more dimensions are necessary to identify affective states. The number of dimensions, required to represent emotions, depends on the problem the researcher is solving (Fontaine
et al.,
2007; Cambria
et al.,
2012). The Hourglass Model (Cambria
et al.,
2012) (Section
2.2.9) is an interesting combination of the categorical and four-dimensional models.
The description of emotions by using dimensions has some advantages. Dimensions ensure a unique identification and a wide range of the emotion concepts. It is possible to identify fine emotion concepts (shades of an emotion) that differ only to a small extent. Thus, a dimensional model of emotions is a useful representation capturing all relevant emotions and providing a means for measuring the similarity between emotional states (Sreeja and Mahalakshmi,
2017). The categorical model is more general and simplified in describing emotions, and the dimensional model is more detailed and able to detect shades of emotions (Grekow,
2018).
2.2.1 Russell’s Circumplex Model
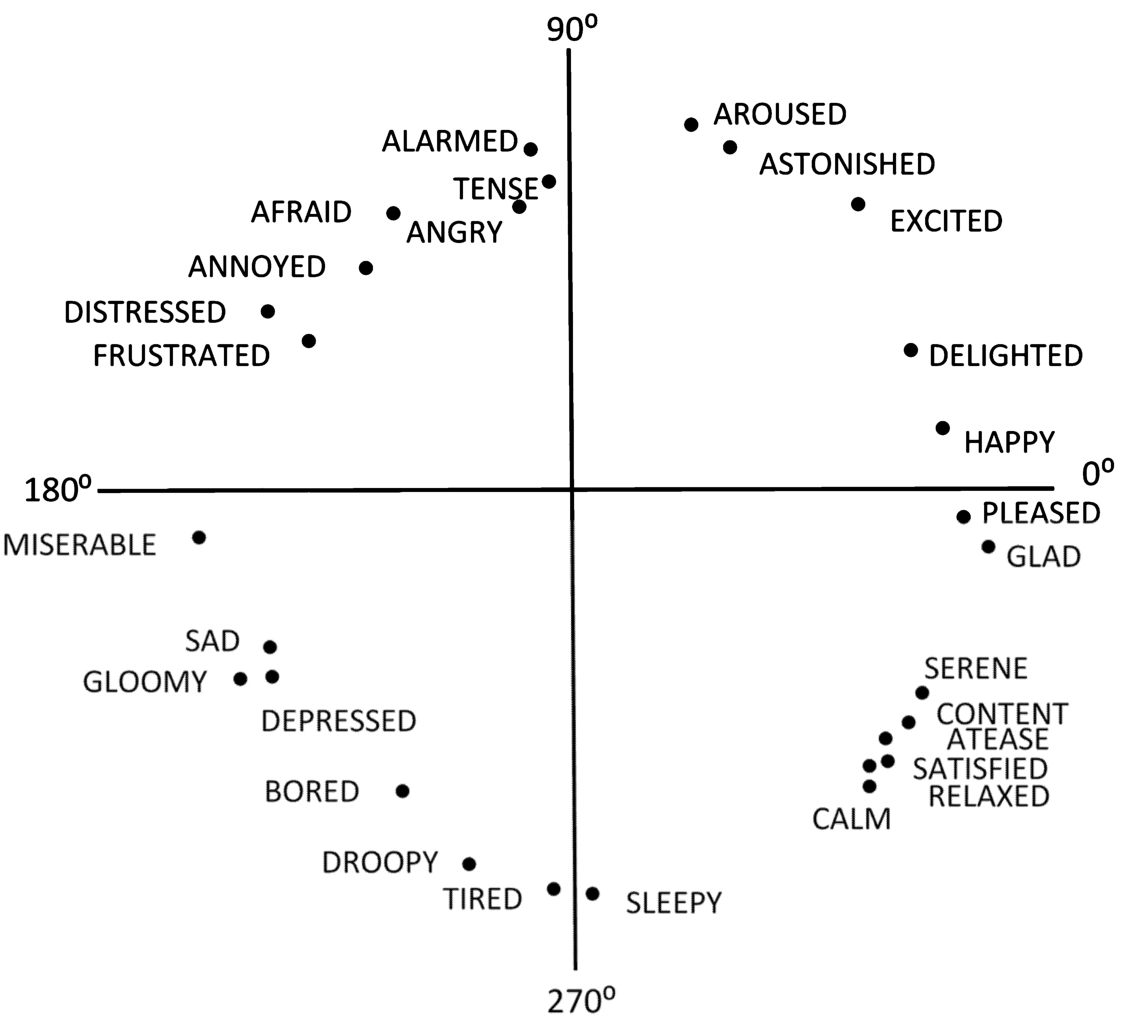
Fig. 2
Russell’s circumplex model (Russell,
1980).
The first two-dimensional model was developed by Russell (
1980) and is known as the Russell’s circumplex model (the circumplex model of affect) (Fig.
2). Russell identified two main dimensions of an emotion: arousal (physiological activation) and valence (emotional pleasantness). Arousal can be treated as high or low and valence may be positive or negative.
The circumplex model is formed by dividing a plane by two perpendicular axes. Valence represents the horizontal axis (negative values to the left, positive ones to the right) and arousal represents the vertical axis (low values at the bottom, high ones at the top). Emotions are mapped as points in a circumplex shape. The centre of this circle represents a neutral value of valence and a medium level of arousal, i.e. the centre point depicts a neutral emotional state. In this model, all emotions can be represented as points at any values of valence and arousal or at a neutral value of one or both of these dimensions.
The four basic categories of emotions can be highlighted regarding the quarters of Russell’s model as follows: 1)
Happy – high valence, high arousal (top-right), 2)
Angry – low valence, high arousal (top-left), 3)
Sad – low valence, low arousal (bottom-left), 4)
Relaxed – high valence, low arousal (bottom-right) (Wilson
et al.,
2016; Grekow,
2018).
2.2.2 Thayer’s Model
Thayer’s model (Thayer,
1989) is a modification of Russell’s circumplex model. Thayer proposed to describe emotions by two separate arousal dimensions: energetic arousal and tense arousal, also named energy and stress, correspondingly. Valence is supposed to be a varying combination of these two aforementioned dimensions. For example, in Thayer’s model,
Satisfaction and
Tenderness take up a position in a part of low energy-low stress;
Astonishment,
Surprise position in high energy-low stress part;
Anger,
Fear belong to a high energy – high stress part, and
Depression,
Sadness take up a position in a part of low energy-high stress, correspondingly. Figure
3 presents a visual perception of both Russell’s circumplex model and Thayer’s one.
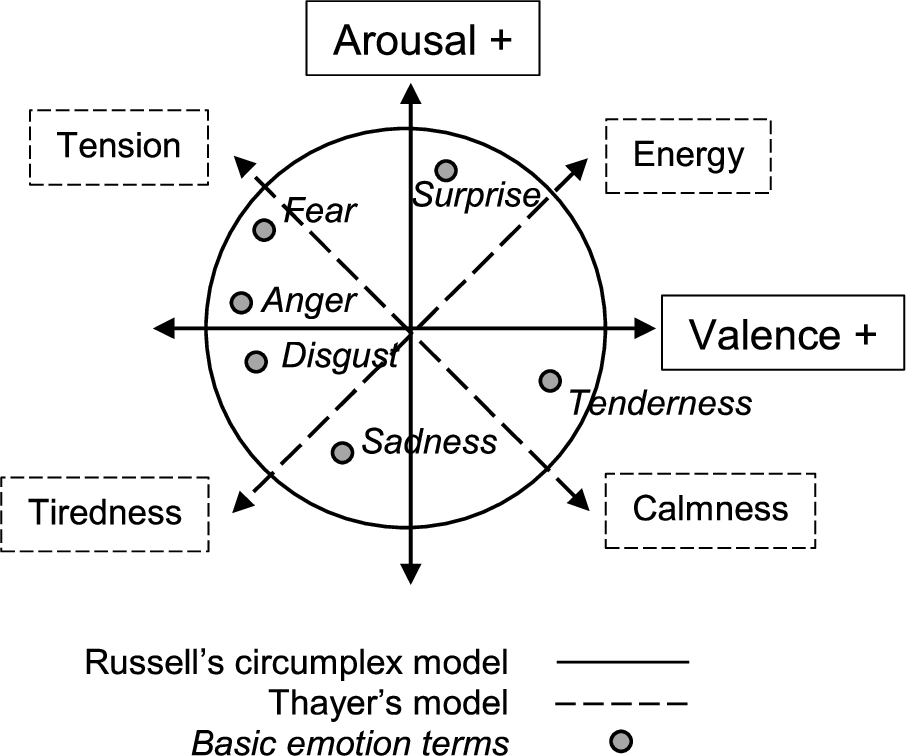
Fig. 3
Schematic diagram of the two-dimensional models of emotions with common basic emotion categories overlaid (Eerola and Vuoskoski,
2011).
2.2.3 Vector Model
The vector model of emotion (Bradley
et al.,
1992) holds that emotions are structured in terms of valence and arousal, but they are not continuously related or evenly distributed along these dimensions (Wilson
et al.,
2016). This model assumes that there is an underlying dimension of arousal and a binary choice of valence that determines a direction in which a particular emotion lies. Thus, two vectors are obtained. Both of them start at zero arousal and neutral valence and proceed as straight lines, one in a positive, and one in a negative valence direction (Rubin and Talarico,
2009). Figure
4 exhibits the Russell’s circumplex (left) and vector (right) models assuming valence is varying in the interval
$[-3;3]$, and the values of arousal belong to the interval
$[1;7]$. Squares filled with a C or a V represent predictions of where emotions should occur according to the Russell’s circumplex model or a vector model, respectively (Rubin and Talarico,
2009; Wilson
et al.,
2016). Briefly, the circumplex model assumes that emotions are spread in a circular space with dimensions of valence and arousal, pattern centred on neutral valence and medium arousal. In the vector model, emotions of higher arousal tend to be defined by their valence, whereas emotions of lower arousal tend to be more neutral in respect of valence (Rubin and Talarico,
2009).
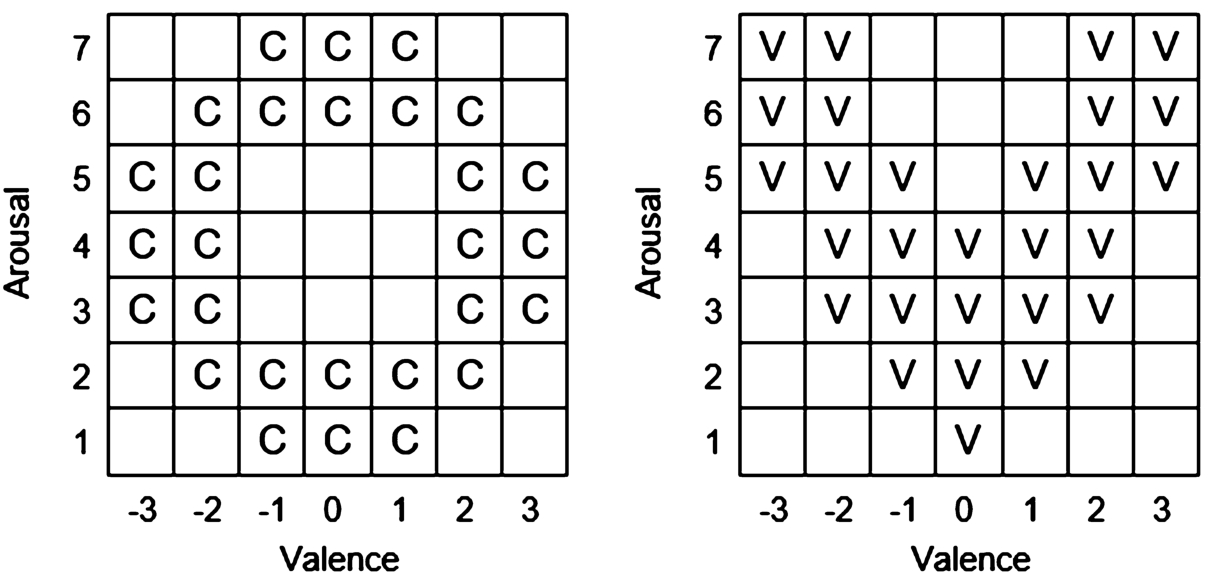
Fig. 4
Instantiations of the Russell’s circumplex (left) and vector (right) two-dimensional models (Wilson
et al.,
2016).
2.2.4 The Positive Affect – Negative Affect (PANA) Model
The Positive Affect – Negative Affect (also known as Positive Activation – Negative Activation) (PANA) model (Watson and Tellegen,
1985; Watson
et al.,
1999) characterizes emotions at the most general level. Figure
5 accurately generalizes the relations among the affective states. Terms of affect within the same octant are highly positively correlated, meanwhile, the ones in adjacent octants are moderately positively correlated. Terms 90° apart are substantially unrelated to one another, whereas those 180° apart are opposite in meaning and highly negatively correlated.
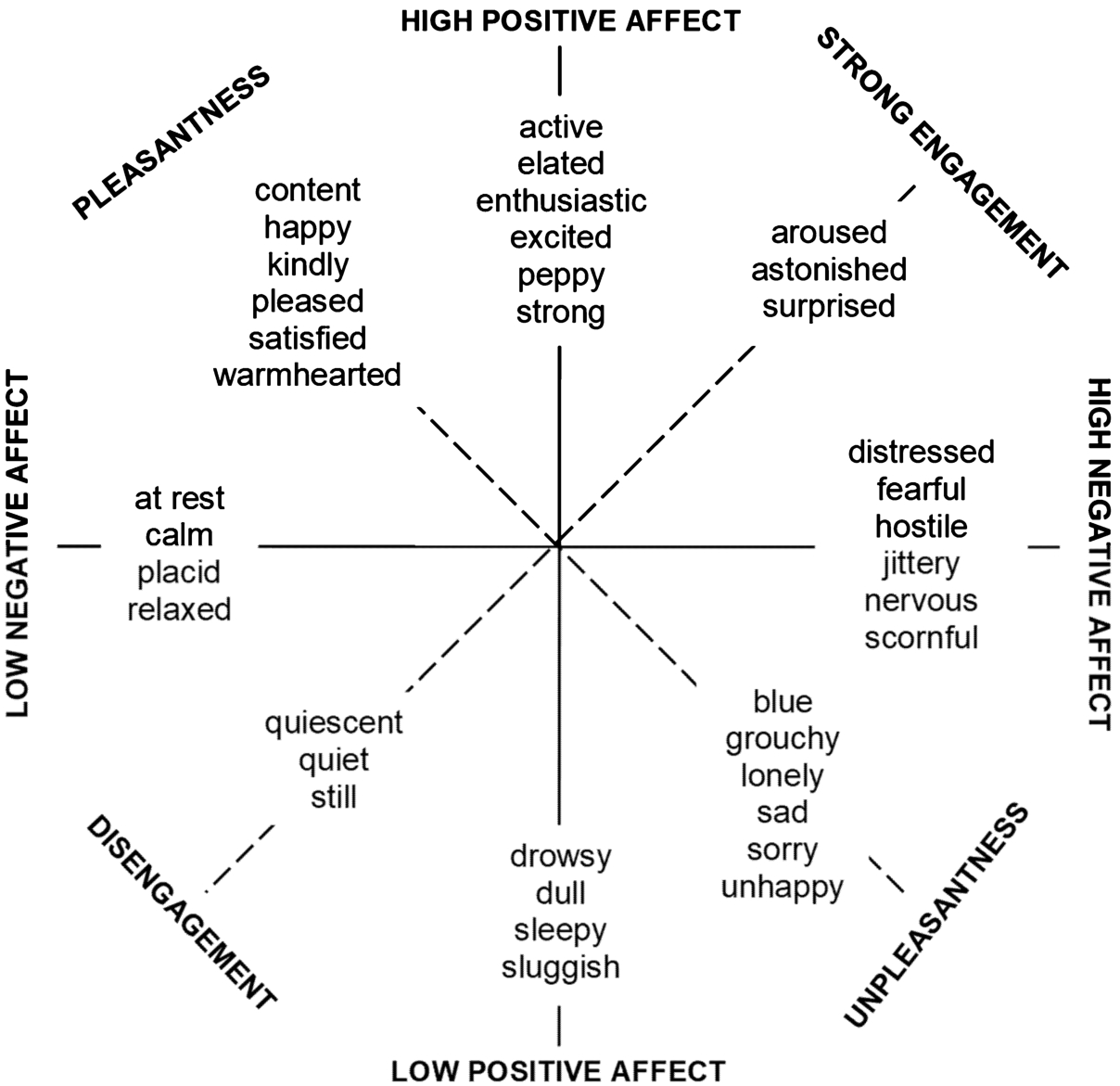
Fig. 5
The basic two-factor structure of affect (Watson and Tellegen,
1985).
Figure
5 schematically depicts the two-dimensional (two-factor) affective spaces. In the basic two-factor space, the axes are displayed as solid lines. The horizontal and vertical axes represent Negative Affect and Positive Affect, respectively. The first factor, Positive Affect (PA), represents the extent (from low to high) to which a person shows enthusiasm in life. The second factor, Negative Affect (NA), is the extent to which a person is feeling upset or unpleasantly aroused. At first sight, the terms Positive Affect and Negative Affect can be perceived as opposite ones, i.e. negatively correlated. However, they are independent and uncorrelated dimensions. We can notice from Fig.
5 that many affective states are not pure markers of either Positive or Negative Affect as these concepts are described above. For instance, the Pleasantness includes terms representing a mixture of high Positive Affect and low Negative Affect, and Unpleasantness contains emotions between high Negative Affect and low Positive Affect. Terms denoting Strong Engagement have moderately high values of both factors PA and NA, whereas emotions representing Disengagement reflect low values of each dimension PA and NA. Thus, Fig.
5 also depicts an alternative rotational scheme that is indicated by the dotted lines. The first factor (dimension) represents the Pleasantness-Unpleasantness (valence), while the second factor (dimension) represents Strong Engagement-Disengagement (arousal).
Thus, the PANA model is commonly understood as a 45-degree rotation of the Russell’s circumplex model as it is a circle and the dimensions of valence and arousal lay at a 45-degree rotation over the PANA model axes NA and PA, respectively (Watson and Tellegen,
1985). In Rubin and Talarico (
2009), it is noticed that the PANA model is more similar to the vector model than a circumplex one. The similarity between the PANA and vector models is explained as follows. In the vector model, low arousal emotions are more likely to be neutral and high arousal ones are differentiated by their valence. Most affective states cluster in the high Positive Affect and high Negative Affect octants (Watson and Tellegen,
1985; Watson
et al.,
1999). This corresponds to the prediction of the vector model, i.e. an absence of high arousal and neutral valence emotions. In conclusion, the PANA model can be employed while exploring emotions of high levels of activation like in the vector model (Rubin and Talarico,
2009).
2.2.5 Whissell’s Model
Similarly to the Russell’s circumplex model, Whissell represents emotions in a two-dimensional continuous space, the dimensions of which are evaluation and activation (Whissell,
1989). The evaluation dimension is a measure of human feelings, from negative to positive. The activation dimension measures whether a human is less or more likely to take some action under the emotional state, from passive to active. Whissell has made up the Dictionary of Affect in Language by assigning a pair of values to each of the approximately 9000 words with affective connotations. Figure
6 depicts the position of some of these words in the two-dimensional circular space (Cambria
et al.,
2012).
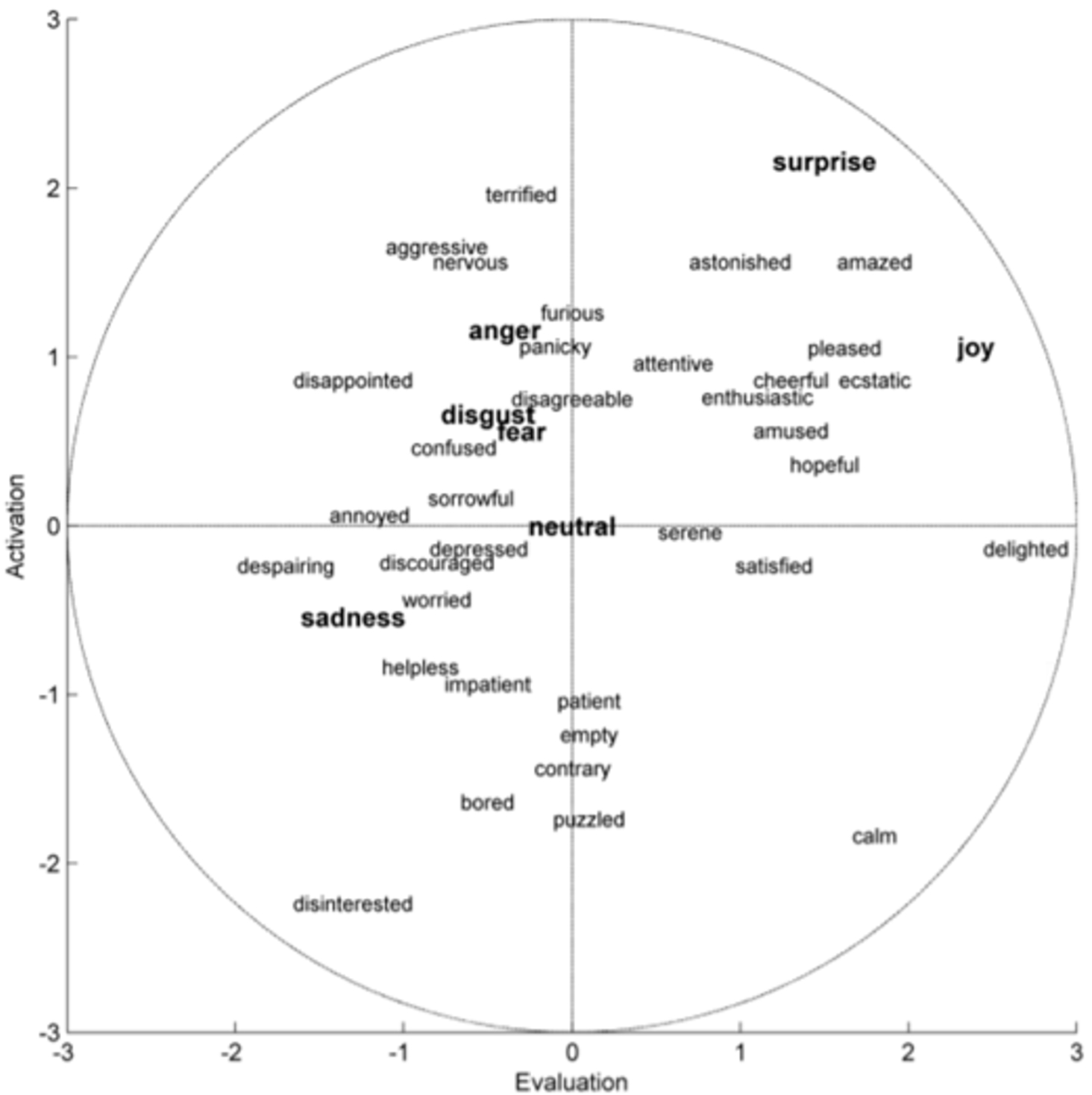
Fig. 6
The two-dimensional representation of emotions by the Whissell’s model (Cambria
et al.,
2012).
2.2.6 Plutchik’s Model (Plutchik’s Wheel of Emotions)
In 1980, Robert Plutchik created a wheel of emotions seeking to illustrate different emotions and their relationship. He proposed a two-dimensional wheel model and a three-dimensional cone-shaped model (Plutchik and Kellerman,
1980; Plutchik,
2001).
In order to make the wheel of emotions, Plutchik used eight primary bipolar emotions such as
Joy versus
Sadness,
Anger versus
Fear,
Trust versus
Disgust, and
Surprise versus
Anticipation, as well as eight advanced, derivative emotions (
Optimism,
Love,
Submission,
Awe,
Disapproval,
Remorse,
Contempt, and
Aggressiveness), each composed of two basic ones. This circumplex two-dimensional model combines the idea of an emotion circle with a colour wheel. With the help of colours, primary emotions are presented at different intensities (for instance,
Joy can be expressed as
Ecstasy or
Serenity) and can be mixed with one another to form different emotions, for example,
Love is a mixture of
Joy and
Trust. Emotions, obtained from two basic emotions, are shown in blank spaces. In this two-dimensional model, the vertical dimension represents intensity and the radial dimension represents degrees of similarity among the emotions (Cambria
et al.,
2012). The three-dimensional model depicts relations between emotions as following: the cone’s vertical dimension represents intensity, and the circle represents degrees of similarity among the emotions (Maupome and Isyutina,
2013). Both models are shown in Fig.
7.
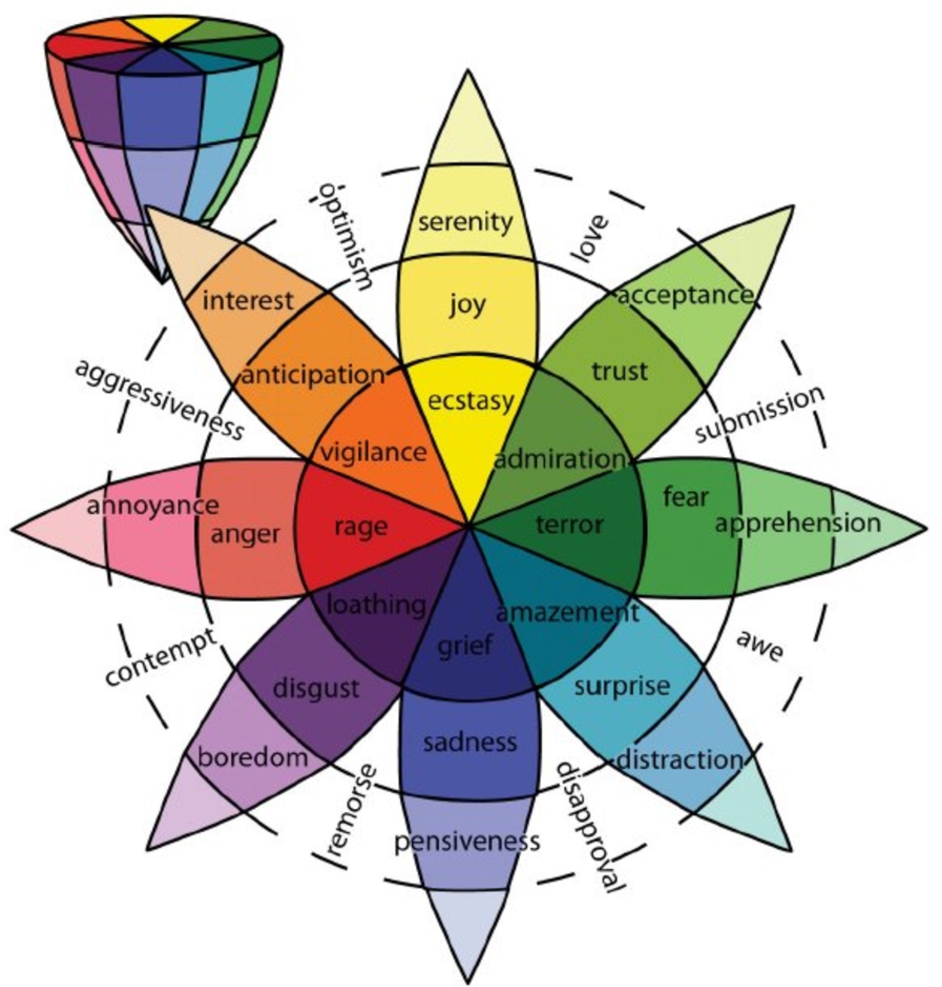
Fig. 7
Plutchik’s two-dimensional wheel of emotions and the cone-shaped model, three-dimensional wheel of emotions, demonstrating relationships between basic and derivative emotions (Maupome and Isyutina,
2013).
2.2.7 The Pleasure-Arousal-Dominance (PAD) Model
The Mehrabian and Russell’s Pleasure-Arousal-Dominance (PAD) model (Mehrabian and Russell,
1974) was developed seeking to describe and measure a human emotional reaction to the environment. This model identifies emotions by using three dimensions such as pleasure, arousal, and dominance. Pleasure represents positive (pleasant) and negative (unpleasant) emotions, i.e. this dimension measures how pleasant an emotion is. For example,
Joy is a pleasant emotion, and
Sadness is unpleasant one. Arousal shows a level of energy and stimulation, i.e. measures the intensity of an emotion. For instance,
Joy,
Serenity, and
Ecstasy are pleasant emotions, however,
Ecstasy has a higher intensity and
Serenity has a lower arousal state in comparison with
Joy. Dominance represents a sense of control or freedom to act. For example, while
Fear and
Anger are unpleasant emotions,
Anger is a much more dominant emotion than
Fear (Mehrabian,
1980,
1996; Grekow,
2018). The PAD model is similar to the Russell’s model, since two dimensions, arousal and pleasure that resembles valence, are the same. These models differ because of the third dominance dimension that is been used to perceive whether a human feels in control of the state or not (Sreeja and Mahalakshmi,
2017).
2.2.8 Lövheim Cube of Emotion
In 2011, Lövheim revealed that the monoamines such as serotonin, dopamine and noradrenaline greatly influence human mood, emotion and behaviour. He proposed a three-dimensional model for monoamine neurotransmitters and emotions. In this model, the monoamine systems are represented as orthogonal axes and the eight basic emotions, labelled according to Silvan Tomkins, are placed in the eight corners of a cube. According to Lövheim model, for instance,
Joy is produced by the combination of high serotonin, high dopamine and low noradrenaline (Fig.
8). As neither the serotonin nor the dopamine axis is identical to the valence dimension, the cube seems somewhat rotated in comparison to aforementioned models. This model may help perceive human emotions, psychiatric illness and the effects of psychotropic drugs (Lövheim,
2011).
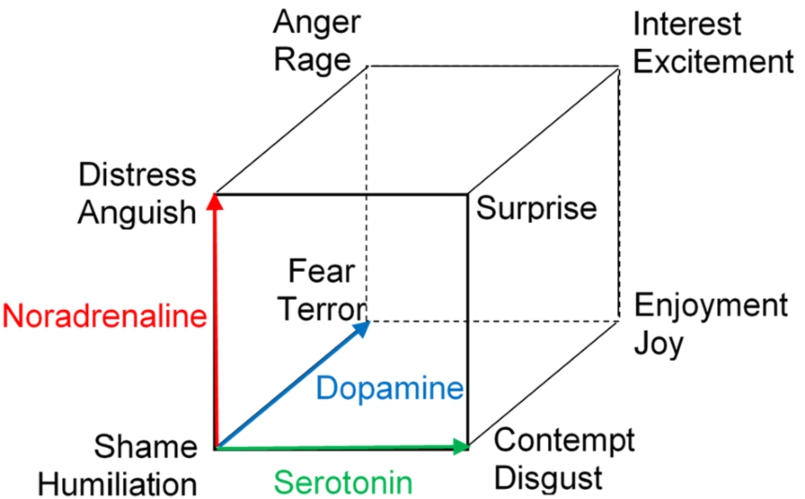
Fig. 8
Lövheim cube of emotion (Lövheim,
2011).
2.2.9 The Hourglass Model
Cambria
et al. (
2012) proposed a biologically inspired and psychologically motivated emotion categorization model that combines categorical and dimensional approaches. The model represents emotions both through labels and through four affective dimensions (Cambria
et al.,
2012). This model, also called the Hourglass of Emotions, reinterprets Plutchik’s model (Plutchik,
2001) by organizing primary emotions (
Joy,
Sadness,
Anger,
Fear,
Trust,
Disgust,
Surprise,
Anticipation) around four independent but concomitant affective dimensions such as pleasantness, attention, sensitivity, and aptitude, whose different levels of activation make up the total emotional state of the mind.
These dimensions measure how much: the user is amused by interaction modalities (pleasantness), the user is interested in interaction contents (attention), the user is comfortable with interaction dynamics (sensitivity), and the user is confident in interaction benefits (aptitude). Each dimension is characterized by six levels of activation (measuring the strength of an emotion). These levels are also labelled as a set of 24 emotions (Plutchik,
2001). Therefore, the model specifies the affective information associated with the text both in a dimensional and in a discrete form. The model has an hourglass shape because emotions are represented according to their strength (from strongly positive to null to strongly negative) (Fig.
9).
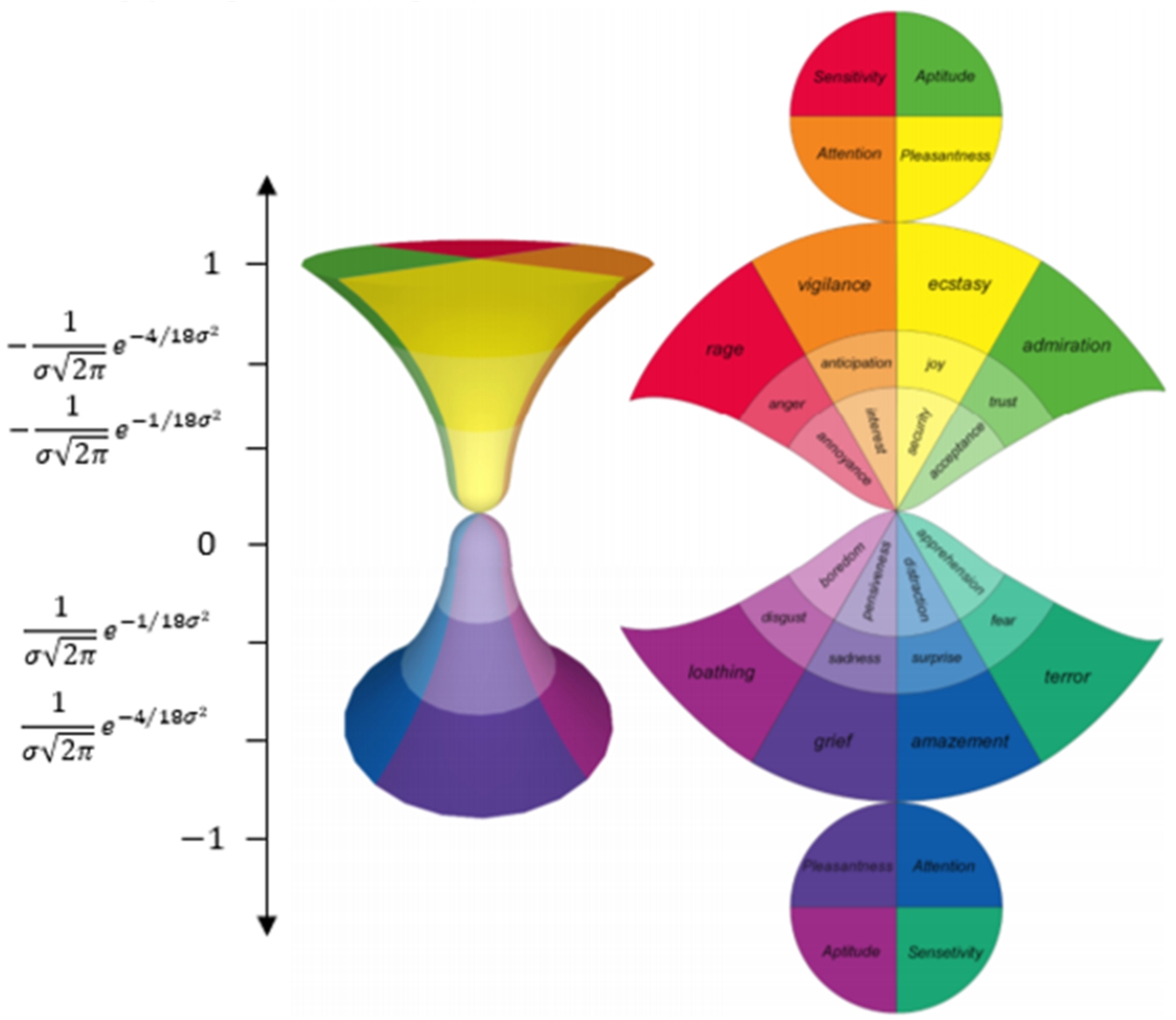
Fig. 9
The 3D model and the net of the hourglass of emotions (Cambria
et al.,
2012).
2.2.10 2D Visualization of a Set of Emotions
In our research, the two-dimensional circumplex space model of emotions (Fig.
10), based on the Russell’s model (Russell,
1980) and Scherer’s structure of the semantic space for emotions (Scherer,
2005) as well as employing numerical proximities of human emotions (Gobron
et al.,
2010), is used for facial emotion recognition. Figure
10 is taken from Paltoglou and Thelwall (
2013). Its obtainment is described below. A set of emotions is visualized on a 2D plane, giving a particular place for each emotion.
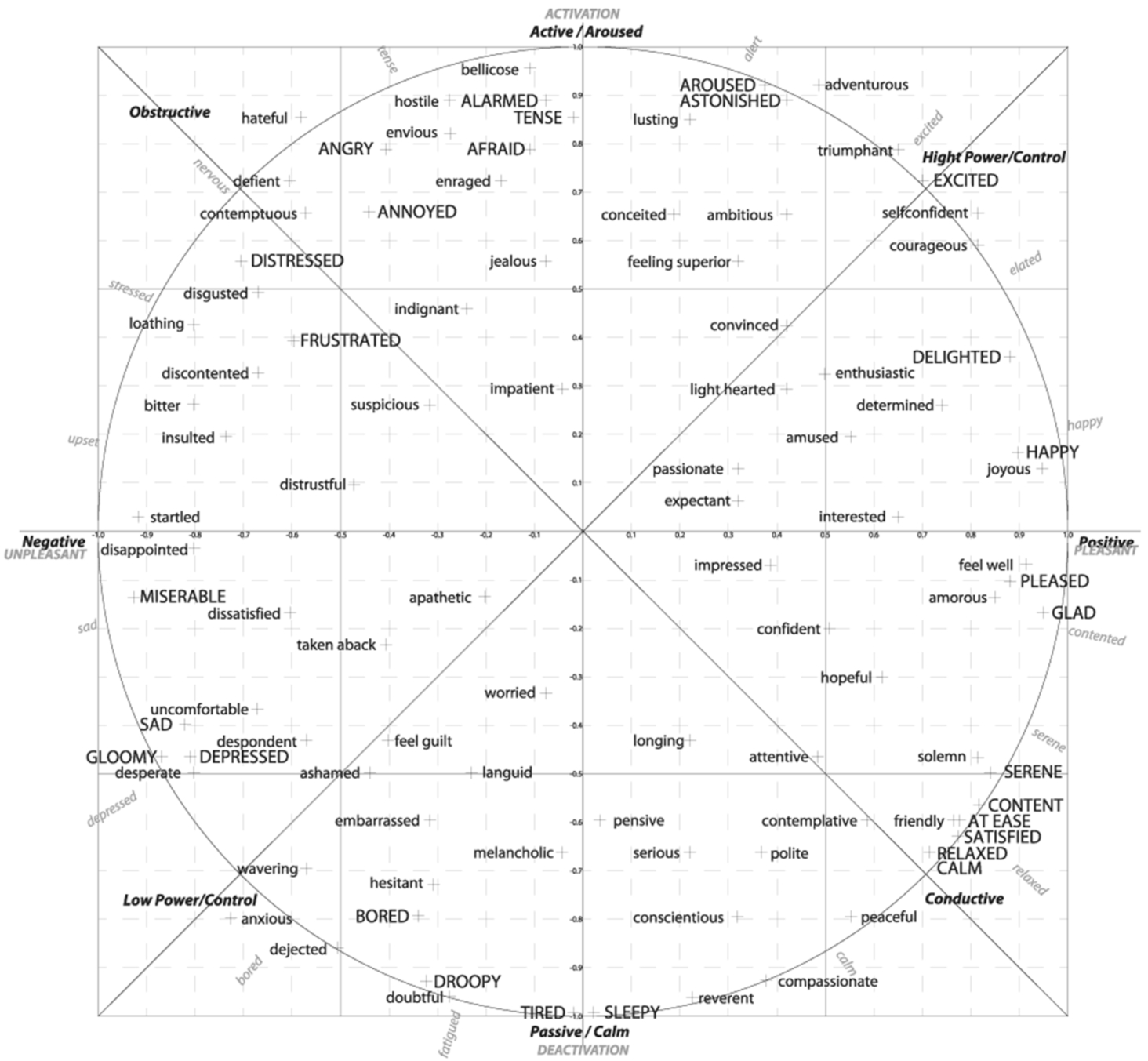
Fig. 10
The two-dimensional circumplex space model of emotions. Upper-case notation denotes the terms used by Russell, lower-case notation denotes the terms used by Scherer. Figure is taken from Paltoglou and Thelwall (
2013).
Figure
10 illustrates the alternative two-dimensional structures of the semantic space for emotions. In Scherer (
2005), a number of frequently used and theoretically interesting emotion categories were arranged in a two-dimensional space that is formed (constructed) by goal conduciveness versus goal obstructiveness on the one hand and high versus low control/power on the other. Scherer used the Russell’s circumplex model that locates emotions by a circumplex way in the two-dimensional valence – arousal space. In Fig.
10, upper-case notation denotes the terms used by Russell (
1980). Onto this representation, Scherer superimposed the two-dimensional structure based on similarity ratings of 80 German emotion terms (lower-case terms, translated to English). The exact location of the terms (emotions) in a two-dimensional space is indicated by the plus (+) sign. It was noticed that this simple superposition yielded a remarkably good fit (Scherer,
2005).
In Fig.
10, every emotion is represented as a point that has two coordinates: valence and arousal. The coordinates of the mapped emotions (values of valence and arousal) are taken from Gobron
et al. (
2010) and are given in Paltoglou and Thelwall (
2013). The valence parameter is determined by using the four parameters (two lexical, two language), derived from the data mining model that is based on a very large database (4.2 million samples). The arousal parameter is based on the intensity of the vocabulary. The valence and arousal values were generated from lexical and language classifiers and the probabilistic emotion generator (the Poisson distribution is used). A statistically good correlation with James Russell’s circumplex model of emotion was obtained. The control mechanism was based on Ekman’s Facial Action Coding System (FACS) action units (Ekman and Friesen,
1978).
The Russell’s circumplex model is widely used in various areas of emotion recognition. Gobron
et al. transferred lexical and language parameters, extracted from database, into coherent intensities of valence and arousal, i.e. parameters of Russell’s circumplex model. Paltoglou and Thelwall (
2013) employed these values of valence and arousal to the emotion recognition from segments of a written text in blog posts. We have decided to use this two-dimensional model of emotions (Fig.
10) and the derived emotion coordinates for the facial emotion recognition. To our knowledge, it has not been done before.
3 Kriging Predictor
Recently, Fractional Brownian Vector Field (Motion) (FBVF) has been very popular among mathematicians and physicists (Yancong and Ruidong,
2011; Tan
et al.,
2015). The created model for FER is based on modelling valence and arousal dimensions in Russell’s model by the two-dimensional FBVF. Hereinafter, these dimensions are called coordinates as well.
Stochastic model of facial emotions on pictures should incorporate uncertainty about quantities in unobserved points and to quantify the uncertainty associated with the kriging estimator. Namely, the emotion at each facial picture is considered as a realization of FBVF $Z(X,\omega )$, $Z:{R^{n}}\otimes \Omega \to {R^{2}}$,
which for every point in the variables space
$X\in {R^{n}}$ is a measurable function of random event
$\omega \in (\Omega ,\Sigma ,P)$ in some probability space (Pozniak
et al.,
2019). As it is unknown which of all function variables will be preponderant, consider them as equivalent, thus, calculate a distance between measurement points, which now is symmetric with respect to the miscellaneous variables. Usually it is assumed the FBVF has a constant mean vector and covariance matrix at each point:
Thus, assume, the set
$\mathbb{X}=\{{X_{1}},\dots ,{X_{N}}\}$ of observed mutually disjoint vectors
${X_{i}}\in {R^{n}}$,
$1\leqslant i\leqslant N$,
$N>1$,
$n\geqslant 1$, where each vector represents one facial picture, is fixed, and data of measurement
$Y={({Y_{1}},{Y_{2}},\dots ,{Y_{N}})^{T}}$ of the response vector surface, representing the emotion dimensions, at points of
$\mathbb{X}$ is known,
${Y_{i}}=Z({X_{i}},\omega )$. Hence, the matrix of fractional Euclidean distances is computed as well:
Degree
d is a perfect parameter of FBVF as well, which can be estimated according to observation data. The maximal likelihood estimate
$\hat{d}$ ensuring asymptotically efficient and unbiased estimator can be estimated by minimization of logarithmic likelihood function:
Novelty of our method is as follows: 1) We evaluate the Hurst parameter d by the maximum likelihood method; 2) We use a posteriori expectations and covariance matrix for kriging prediction of emotion model dimensions (coordinates); 3) We apply kriging predictor to FER in pictures.
Assume one has to predict the value of response vector surface
Z at some point
$X\in {R^{n}}$. Kriging gives us a way of anticipating, with some probability, a result associated with values of the parameters that have never been met before, or have been lost, to “store” the existing information (the experimental measurements), and propagate it to any situation where no measurement has been made. According to gentle introduction to kriging (Jones,
2001) and (Pozniak
et al.,
2019), it is defined by the kriging predictor which is defined as the conditional mean of FBVF:
where
a is a distance vector, the elements of which are fractional Euclidean distances between a new (testing) data point and all the training data points.
This prediction is stochastic, its uncertainty is described by the conditional variance:
where the likelihood estimate of covariance matrix is applied:
Regarding the kriging model, the resent novelty is the introduction of
$d\ne 1$ that expanded the possibilities of the model. So far, only
$d=1$ was known in Dzemyda (
2001). It is proved in Pozniak and Sakalauskas (
2017) that the kernel matrix and the associated covariance matrix is positively defined, when
$0\leqslant d<1$ for any number of features and sample size. From the continuity of the likelihood function it follows that when there are more features (such as pixels) than the sample size (number of pictures), the covariance matrix can be positively defined when
$d>1$, as well.
In this paper, the kriging predictor has been employed for emotion recognition from facial expression and explored experimentally because the kriging predictor performs simple calculations and has only one unknown parameter d, as well as because this method works very well with small data sets.
4 Data Set
Warsaw set of emotional facial expression pictures (WSEFEP) (Olszanowski
et al.,
2015) has been used in the experiments. This set contains 210 high-quality pictures (photos) of 30 individuals (14 men and 16 women). They display six basic emotions (
Joy,
Sadness,
Surprise,
Disgust,
Anger,
Fear) and
Neutral display. Examples of each basic emotion displayed by one woman are shown in Fig.
11.
The original size of these pictures was
$1725\times 1168$ pixels. In order to avoid the redundant information (background, hair, clothes, etc.), pictures were cropped and resized to
$505\times 632$ pixels (Fig.
12). Brows, eyes, nose, lips, cheeks, jaws, and chin are the key features that describe an emotional facial expression in obtained pictures.
Each picture has been digitized, i.e. a data point consists of colour parameters of pixels, and, therefore, it is of very large dimensionality. The number of pictures (data points) is $N=210$. The images have $505\times 632$ colour pixels (RGB), therefore their dimensionality is $n=957480$.

Fig. 11
Examples of each basic emotion displayed by one woman (original pictures).

Fig. 12
Examples of each basic emotion displayed by one woman (cropped and resized pictures).
5 Analysis of the Kriging Predictor Algorithm
Before presenting the kriging algorithm, some mathematical notations are introduced below. Suppose that the analysed data set $\mathbb{X}=\{{X_{1}},\dots ,{X_{N}}\}$ consists of N n-dimensional points ${X_{i}}=({x_{i1}},\dots ,{x_{in}})$, $i=\overline{1,N}$ (${X_{i}}\in {R^{n}}$). The data point ${X_{i}}$ corresponds to the ith picture in the picture set. Seven emotions (Joy, Sadness, Surprise, Disgust, Anger, Fear, and Neutral) are displayed in these pictures. For the sake of simplicity, the neutral state is attributed to the emotion as well. In this paper, for short, an emotion, identified from the facial expression shown in a particular picture, is called a picture emotion.
Since the two-dimensional circumplex space model of emotions (Fig.
10) is used for facial emotion recognition in the investigations, every emotion is represented as a point that has two coordinates: valence and arousal. The coordinates of the seven basic emotions (values of valence and arousal) are taken from Gobron
et al. (
2010) and are given in Paltoglou and Thelwall (
2013). These coordinates are presented in Table
1.
Table 1
The valence and arousal coordinates of seven basic emotions in the two-dimensional circumplex emotion space.
|
Emotion |
Joy |
Sadness |
Surprise |
Disgust |
Anger |
Fear |
Neutral |
| Coordinates |
|
|
|
|
|
|
|
|
| Valence |
|
0.95 |
−0.81 |
0.2 |
−0.67 |
−0.4 |
−0.12 |
0 |
| Arousal |
|
0.14 |
−0.4 |
0.9 |
0.49 |
0.79 |
0.79 |
0 |
As a picture emotion is known in advance, each data point
${X_{i}}$ is related to an emotion point
${Y_{i}}=({y_{i1}},{y_{i2}})$ that describes the
ith picture emotion. Seven different combinations of (
${y_{i1}},{y_{i2}}$) are obtained (Table
1). In other words,
${y_{i1}}$ and
${y_{i2}}$ mean the valence and arousal coordinates, respectively, of the
ith picture emotion in the two-dimensional circumplex emotion space (Fig.
10). Then, for the whole data set
$\mathbb{X}$, two column vectors
${y_{1}}$ and
${y_{2}}$, the size of which is
$[N\times 1]$, are comprised. The column vector
${y_{1}}$ consists of the valence coordinates of the emotion points
${Y_{i}}$,
$i=\overline{1,N}$, and the column vector
${y_{2}}$ consists of the arousal coordinates of these points, i.e.
${y_{1}}={({y_{11}},{y_{21}},\dots ,{y_{N1}})^{T}}$ and
${y_{2}}={({y_{12}},{y_{22}},\dots ,{y_{N2}})^{T}}$.
The kriging predictor algorithm is as follows:
-
1. The Euclidean distance matrix D between all the data points ${X_{i}}$, $i=\overline{1,N}$ (from training data set) is calculated.
-
2. This matrix is normalized by dividing each element from the largest one.
-
3. Denote the Hurst parameter by d, where d is a real number, $d>0$.
-
4. Elements of the normalized distance matrix D are raised to the power of ($2d$). Denote this new fractional distance matrix as A, i.e. $A={D^{2d}}$.
-
5. The kriging prediction of a new (testing) picture emotion is made by using a posteriori expectation:
Here,
${A^{-1}}$ is the inverse matrix of
A,
E is a unit column vector of size
$[N\times 1]$, and
a $[N\times 1]$ is a distance vector, the elements of which are fractional Euclidean distances between a new (testing) data point and all the training data points. A new (testing) data point corresponds to a new picture whose emotion is being predicted. The training data points describe pictures whose emotions are known in advance. The meaning of
${y_{1}}$ and
${y_{2}}$ are described above. Outputs
${z_{1}}$ and
${z_{2}}$ correspond to the first and the second prediction parameter, respectively. In regard to the emotion model, employed in this research (Fig.
10), values of
${z_{1}}$ and
${z_{2}}$ mean the first (valence) and the second (arousal) coordinates, respectively, of the predicted emotion of a testing picture in the two-dimensional circumplex space.
The kriging predictor algorithm has only one unknown parameter
d. The first investigation is performed seeking to find the optimal value of
d. At first, the
maximum likelihood (
ML)
function of picture emotion features
${y_{1}}$ and
${y_{2}}$ is determined as follows:
where
$\| A\| $ is an absolute value of the matrix
A determinant, and
$|C|$ is a determinant of a posteriori covariance symmetric matrix
$C=\Big(\begin{array}{c@{\hskip4.0pt}c}{c_{11}}\hspace{1em}& {c_{12}}\\ {} {c_{21}}\hspace{1em}& {c_{22}}\end{array}\Big)$, elements of which are calculated as follows:
In the next step, values of the ML function
f are calculated for various values of the parameter
d, i.e.
$d\in [0.01;1.05]$. As a result, the dependence of the ML function
f on the parameter
d is obtained (Fig.
13). Figure
13 shows that this function is concave upward and has one local minimum as
$d=0.83$ for the considered example.
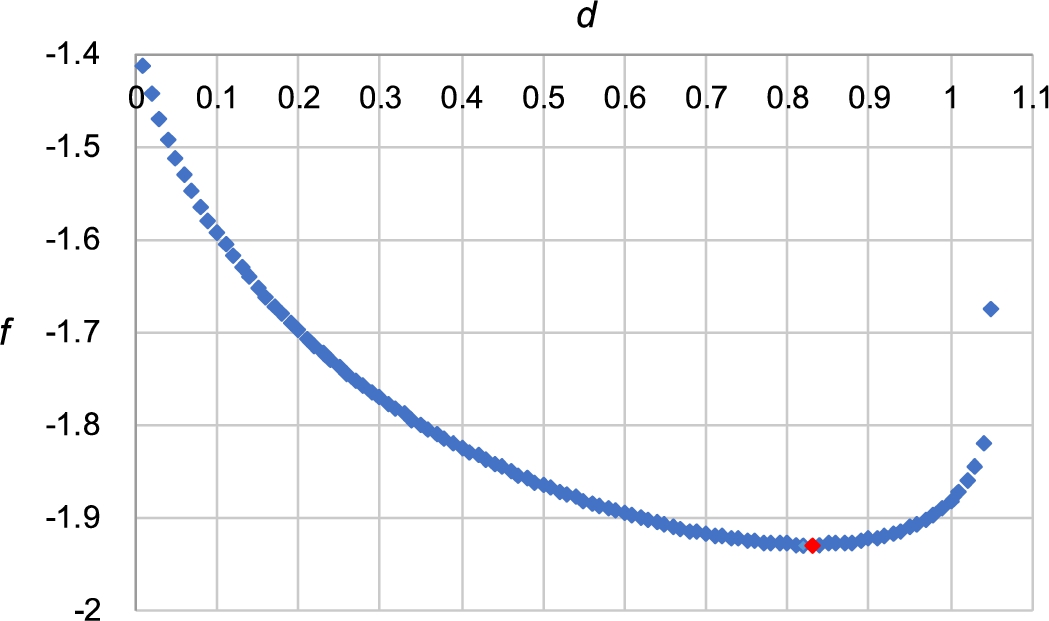
Fig. 13
Dependence of the maximum likelihood function f on the parameter d.
6 Experimental Exploration of the Kriging Predictor for Facial Emotion Recognition
The first investigation is pursued in order to recognize an emotion of a particular picture and evaluate the result obtained, as well as to verify that the optimal value $\hat{d}=0.83$ has been assessed properly.
In fact, we have a problem of classification into seven classes. Let the analysed picture data set
$\mathbb{X}$ of size
N be divided into two groups: testing and training data so that the testing data consist of only one picture and the training data are comprised of the remaining ones. In this way,
$N=210$ experiments have been done. In the
ith experiment, the
ith picture emotion (
$i=\overline{1,N}$) is identified. A classifier training leads to a kriging predictor training. According to formula (
5), two coordinates (
${z_{1}}$ (valence) and
${z_{2}}$ (arousal)) of this picture emotion are predicted by kriging and this picture emotion is mapped as a new point in the two-dimensional circumplex space. Then, a classification of the
ith picture emotion is made. The task is to find out which of the seven basic emotions (Table
1) is the nearest one to the
ith picture emotion, mapped in the emotion model (Fig.
10, Fig.
14). For this purpose, a measure of proximity, based on the Euclidean distances, is used. These distances are calculated between the mapped picture emotion and all the basic emotions (Table
1). The emotion that has the smallest distance to the analysed picture emotion is supposed to be the most suitable to identify the picture emotion. As a result, we get an emotion class to which the testing
ith picture emotion belongs.
The efficiency of classifier will be estimated after such a run through all
N experiments with picking different
ith pictures for testing (
N runs). Since the true picture emotions are known in advance, it is possible to find out how many picture emotions from the whole picture set (
$N=210$) are classified (recognized) successfully. Classification accuracy (CA) is calculated as the ratio of the number of correctly classified picture emotions to the total number of pictures as follows:
Figure
15 illustrates the dependence of the picture emotion classification accuracy (CA) (%) on the parameter
d, as
$d\in [0.1;1.05]$. It is obvious from this figure that the best accuracy, i.e.
$\mathrm{CA}\in [49\% ;50\% ]$, is obtained as
$d\in [0.68;0.92]$. When the optimal value of the parameter
d is chosen, i.e.
$\hat{d}=0.83$, the classification accuracy is 50%. Since the best classification results are obtained as
$d\in [0.68;0.92]$ and the optimal value of the parameter
d belongs to this range as well, i.e.
$\hat{d}=0.83\in [0.68;0.92]$, it means that the optimal value
$\hat{d}=0.83$ has been established properly by the ML method.
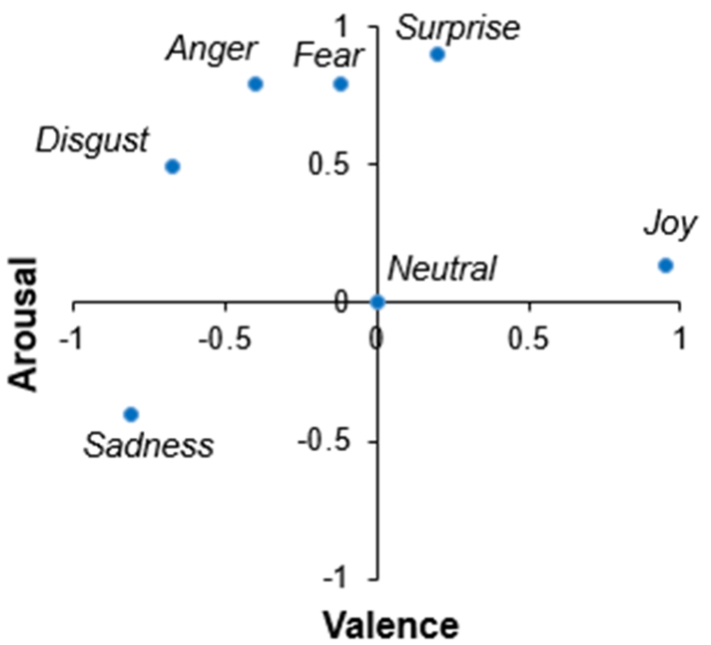
Fig. 14
The basic emotions, depicted in the analysed model of emotions. The coordinates of points are given in Table
1.
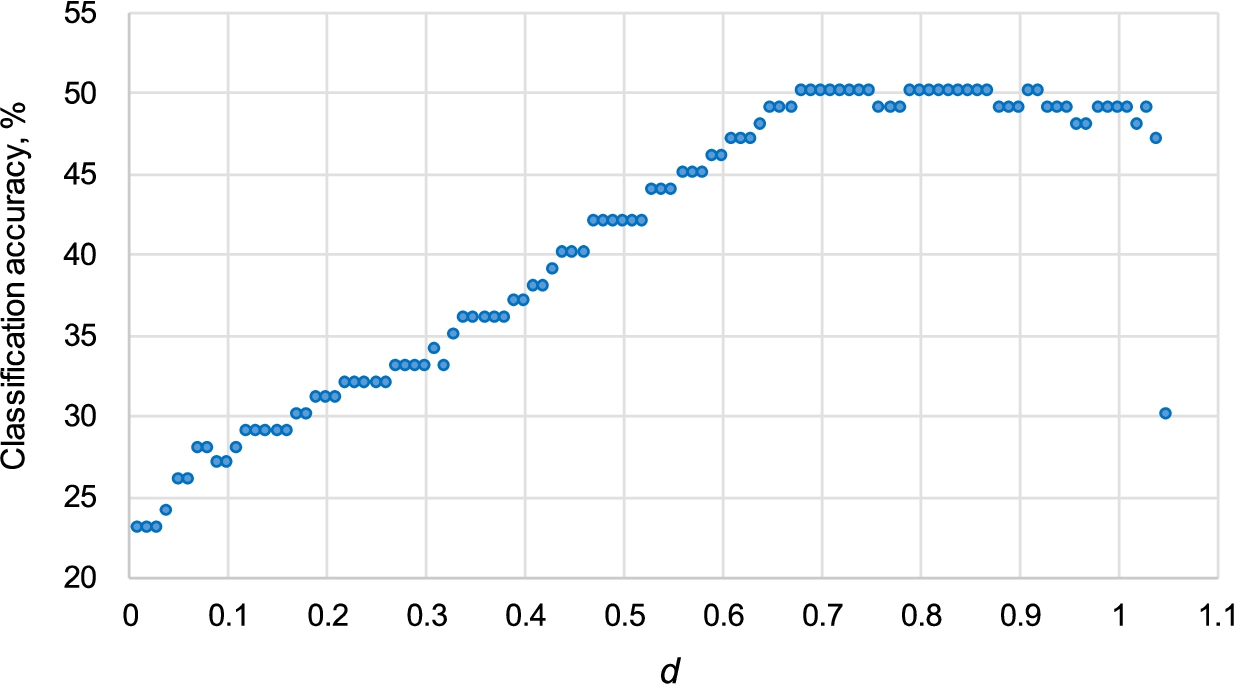
Fig. 15
The dependence of the picture emotion classification accuracy on the parameter d.
Figure
16 shows the mapping of predicted coordinates (valence and arousal) of all the 210 picture emotions in the two-dimensional circumplex space. It is obvious that
Joy is predicted most precisely. However, the remaining emotions overlap quite strongly.
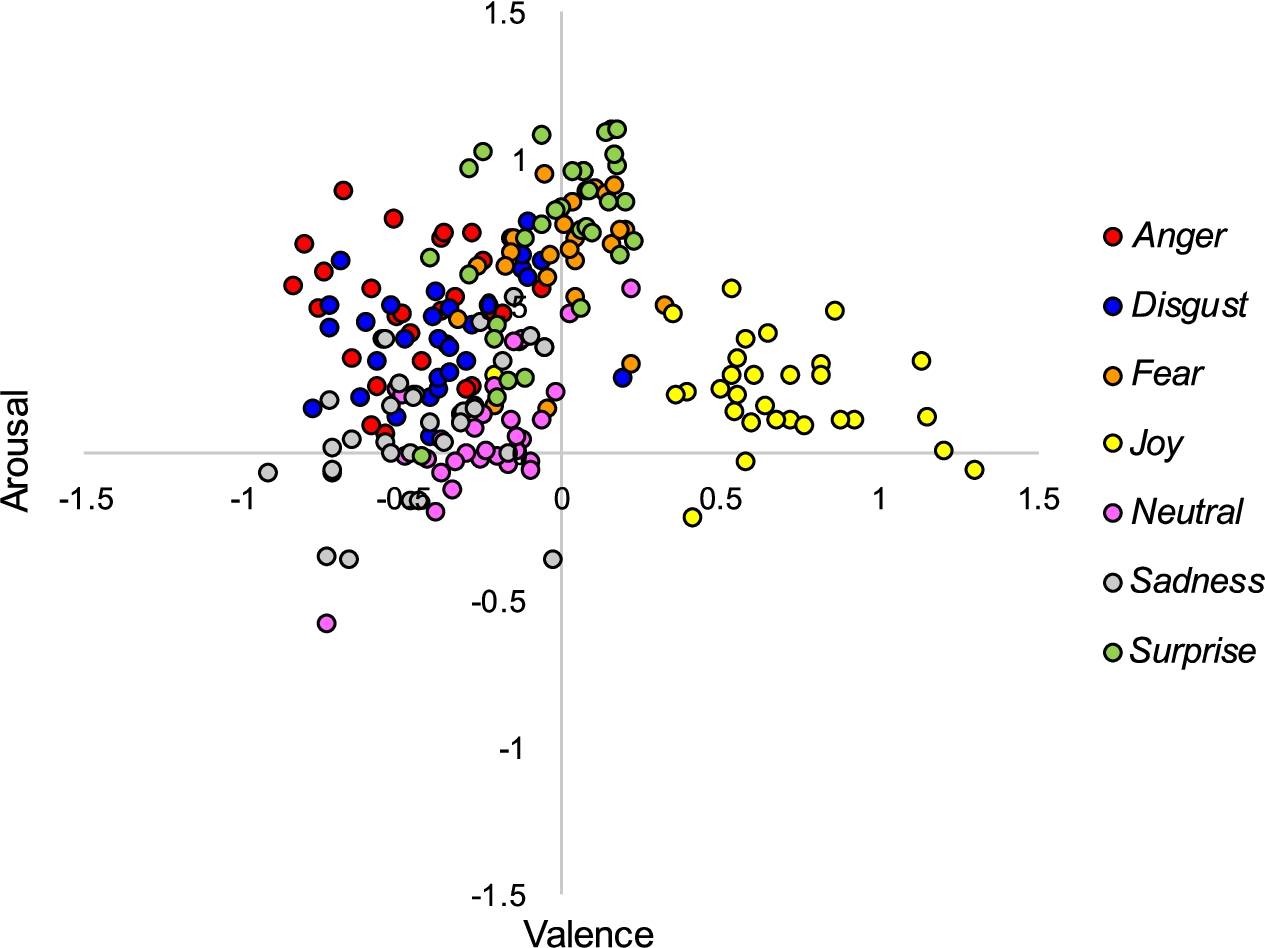
Fig. 16
The mapping of predicted coordinates of all the 210 picture emotions in the two-dimensional circumplex space.
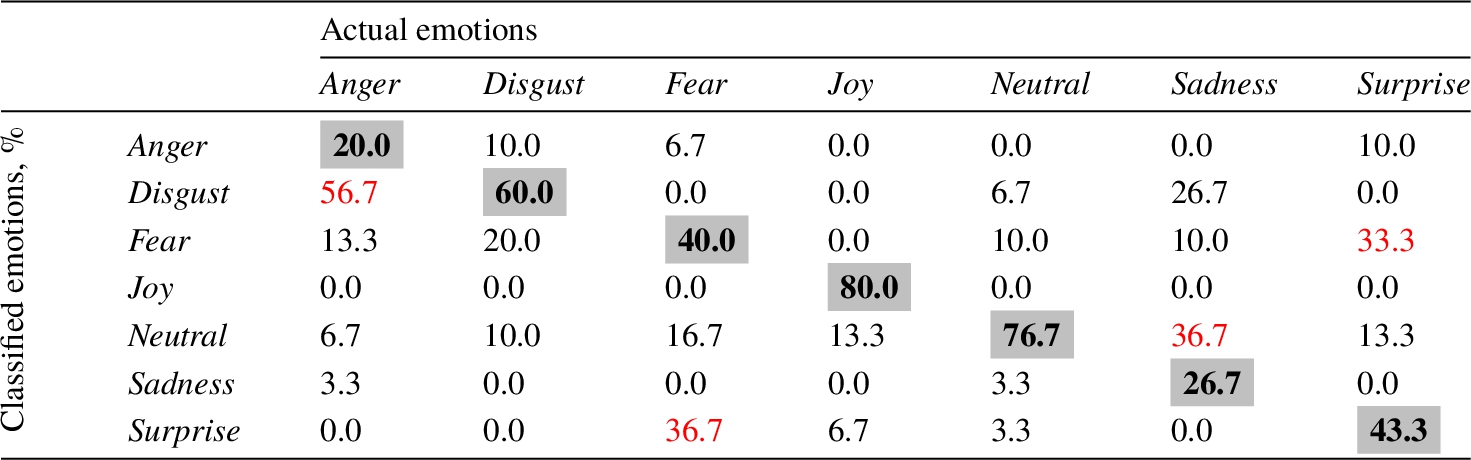
For deeper analysis of this classification, a confusion matrix of the seven basic emotions is given in Table
2. The highest true positive rates were observed for
Joy (80%),
Neutral (76.7%), and
Disgust (60%). The highest false positive rates (the numbers are written in red) were observed for
Anger (56.7% of pictures with
Anger emotion were classified as
Disgust),
Fear (36.7% as
Surprise),
Sadness (36.7% as
Neutral), and
Surprise (33.3% as
Fear).
Table 2
Confusion matrix of the seven basic emotions.
The second investigation is similar to the first one because the
ith picture emotion (
$i=\overline{1,N}$) is identified, as well. However, in the 2nd investigation, differently from the 1st one, several basic emotions are combined into one group. At first, the three basic emotions, such as
Fear,
Anger, and
Disgust, are combined into one group. It is reasonable to do this, because all the three emotions have the coordinates of negative valence and high arousal, i.e. they all are located in the second quarter of the analysed model of emotions (Fig.
14). In this case, we have a problem of classification into five classes: {
Fear,
Anger,
Disgust}, {
Surprise}, {
Joy}, {
Neutral}, and {
Sadness}. Subsequently, the four emotions, i.e.
Fear,
Anger,
Disgust, and
Surprise, are grouped together. The decision to add the fourth emotion, i.e.
Surprise, to the previous 3-emotion group is made because of the similarity of pictures with the
Surprise and
Fear emotions (see Fig.
12), as well as because
Surprise and
Fear are in a very near neighbourhood in the two-dimensional model of emotions (Fig.
14). For this reason, the picture emotion
Surprise is very often classified as
Fear and vice versa. So, we have a problem of classification into four classes: {
Fear,
Anger,
Disgust,
Surprise}, {
Joy}, {
Neutral}, and {
Sadness}. Since the true picture emotions and emotion groups created are known in advance, the classification accuracy of the picture emotion set (size
N) can be calculated. It is said that the picture emotion is identified rightly if the true picture emotion or emotion group (this picture emotion belongs to) is coincident with the identified one (emotion or group). Averaged values of the classification accuracy (%), when
$d\in [0.7;0.9]$, are as follows:
$\mathrm{CA}=50\% $, when emotions are not grouped, in the case of 3-emotion group,
$\mathrm{CA}=64\% $, and, in the case of 4-emotion group,
$\mathrm{CA}=76\% $. In this way, the classification accuracy is achieved rather well, i.e.
$76\% $, when 4 emotions are grouped together.
7 Conclusions
Facial emotion recognition (FER) is an important topic in computer vision and artificial intelligence. We have developed the method for FER, based on the dimensional model of emotions as well as using the kriging predictor of Fractional Brownian Vector Field. The classification problem, related to the recognition of facial emotions, is formulated and solved. We use the knowledge of expert psychologists about the similarity of various emotions in the plane. The goal is to get an estimate of a new picture emotion on the plane by kriging and determine which emotion, identified by psychologists, is the closest one. Seven basic emotions (Joy, Sadness, Surprise, Disgust, Anger, Fear, and Neutral) have been chosen. The experimental exploration has shown that the best classification accuracy corresponds to the optimal value of Hurst parameter, estimated by the maximum likelihood method. The accuracy of classification into seven classes has been obtained approximately 50%, if we make a decision on the basis of the closest basic emotion. It has been ascertained that the kriging predictor is suitable for facial emotion recognition in the case of small sets of pictures. More sophisticated classification strategies may increase the accuracy, when grouping of the basic emotions is applied.

