Processing math: 53%
  1. Home
  2. Issues
  3. Volume 32, Issue 4 (2021)
  4. Score-Based Multiple Criteria Decision M ...

Informatica


Score-Based Multiple Criteria Decision Making Process by Using P-Rung Orthopair Fuzzy Sets
Volume 32, Issue 4 (2021), pp. 709–739
Pub. online: 20 December 2021      Type: Research Article     
Received
1 June 2019
Accepted
1 March 2020
Published
20 December 2021

Abstract

A p-rung orthopair fuzzy set (p-ROFS) describes a generalization of intuitionistic fuzzy set and Pythagorean fuzzy set in the case where we face a larger representation space of acceptable membership grades, and moreover, it gives a decision maker more flexibility in expressing his/her real preferences. Under the p-rung orthopair fuzzy environment, we are going to propose a novel and parametrized score function of p-ROFSs by incorporating the idea of weighted average of the degree of membership and non-membership functions. In view of this fact, this study is further undertaken to investigate and present different properties of the proposed score function for p-ROFSs. Moreover, we indicate that this ranking technique reduces some of the drawbacks of the existing ones. Eventually, we develop an approach based on the above-mentioned ranking technique to deal with multiple criteria decision making problems with p-rung orthopair fuzzy information.

1 Introduction

Fuzzy set (Zadeh, 1965) was first introduced for assigning each criterion to a vague or an uncertain information with the help of membership degree which ranges between 0 and 1. Then, intuitionistic fuzzy set (IFS) (Atanassov, 1986) was proposed to take into account both membership and non-membership degrees such that their sum is less than or equal to 1. This property is used to describe an object which satisfies a criterion more definitively and further precisely compared with that in fuzzy environment (Cong, 2014; Si et al., 2019).
Since the sum of both satisfaction and dissatisfaction degrees of an IFS is not always less than or equal to 1, it would be interesting to consider the sum of their square to be less than or equal to 1. In this regard, the concept of IFS clearly fails to deal with such a situation. In order to clarify this fact, we suppose that an expert would like to express his/her preference in a decision making situation where the degree of an object satisfying a criterion is √32, and the degree of dissatisfying is 12. In this case, we easily see that √32+12⩾1, that is, the current case is not able to be properly described by the use of IFS concept. Instead, the satisfaction of (√32)2+(12)2⩽1 shows the need of employing another concept for describing the latter-mentioned case, and that concept is nothing else except the concept of Pythagorean fuzzy set (PFS) (Yager, 2013).
Besides that, we may consider a more general situation in which an expert would like to express his/her preference by the degree of an object satisfying a criterion as 3√72, and the degree of dissatisfying is 12. Then, it is easily seen that 3√72+12⩾1 and also (3√72)2+(12)2⩾1 which indicate that the current case cannot be described with the help of concepts of IFS and PFS. This is while, (3√72)3+(12)3⩽1. Thus, such an implication makes clear the need of defining a more general concept than the IFS and the PFS concepts. Indeed, this fact made a study of introducing a more general concept than that of IFS and PFS which is called p-rung orthopair fuzzy set (p-ROFS) (Yager, 2017).
The p-ROFS concept describes the degree of an object satisfying a criterion together with the degree of dissatisfying such that the sum of p-power of both satisfaction and dissatisfaction degrees is less than or equal to 1. It can be easily deduced that the space of p-ROFS membership grades is greater than those of Pythagorean and intuitionistic membership grades. That is, any Pythagorean or intuitionistic membership grade is also a p-ROFS membership grade, but in general, all p-ROFS membership grades are not in the forms of Pythagorean or intuitionistic membership grades. This obviously implies that we are able to implement the concept of p-ROFS in the cases where we do not allow to implement the concepts of PFS or IFS.
Apart from the above-mentioned advantages, an immediate and very interesting benefit of p-ROFS definition is that it provides the experts with greater freedom in modelling the forms of imprecise information.
There exist a large number of researches that deal mainly with the concept of p-ROFS which has been applied in many different contexts. Liu and Wang (2018) introduced and investigated the p-rung orthopair fuzzy weighted averaging operator and the p-rung orthpair fuzzy weighted geometric operator. Moreover, the p-rung orthopair fuzzy Bonferroni mean and the p-rung orthopair fuzzy Heronian mean were proposed respectively by Liu and Liu (2018) and Wei et al. (2018). Subsequently, the p-rung orthopair fuzzy Archimedean Bonferroni mean operators were developed by Liu and Wang (2019). Besides the latter-mentioned application of p-ROFSs, there is an increasing demand and a growing number of researches for other application fields, for instance, Du (2018) proposed Minkowski-type distance measures for p-ROFS by emphasizing on their application in decision making, and Zhang C. et al. (2019, in press) dealt with additive and multiplicative consistency analysis for p-ROF preference relation.
One of the leading topics of the recent development of p-ROFSs has been the focus on the ranking function which plays an essential role in the decision making problems. The pioneer works in this regard are those proposed by Yager (2017) and Wei et al. (2018) in which non-algorithmic ranking techniques for p-ROFSs are described. As it will be demonstrated later, Yager’s (2017) and Wei et al.’s (2018) score functions cannot differentiate many p-ROFNs in some situations. The other is that given by Liu and Wang (2018) as an algorithmic ranking technique which uses both score and accuracy functions of p-ROFSs. By taking the impact of membership and non-membership degrees together with the hesitation information into account, Peng et al. (2018) introduced another algorithmic ranking technique for p-ROFSs. Anyway, both Liu and Wang’s (2018) and Peng et al.’s (2018) techniques are in algorithmic form and they need definitely more computations than the non-algorithmic techniques. Moreover, since Liu and Wang’s (2018) technique does not consider the influence of abstention, the information of p-ROFS may be lost. Furthermore, the curve function f(x)=exp(x)exp(x)+1 which appears in Peng et al.’s (2018) technique leads to more complexity in the evaluation of the score function.
Regarding the above-mentioned deficiencies of the existing p-ROFS ranking techniques, we are motivated here to investigate an effective score function for p-ROFSs in the form of non-algorithmic ranking technique which is constructed by considering the impact of membership and non-membership degrees together with the hesitation information.
The present contribution is organized as follows: Introduction of p-ROFS concept and a brief review of some preliminaries are given in Section 2. Section 3 deals with reviewing three kinds of p-ROFS ranking orders, and then this section continues with introducing an innovative score function for p-ROFSs which possesses different properties. Section 4 is devoted to the application of p-ROFS score function in multiple criteria decision making (MCDM) problems by emphasizing the superiority of the proposed score function over the other existing ones. Finally, this article concludes in Section 5.

2 The p-Rung Orthopair Fuzzy Set (p-ROFS)

Throughout this section, we are willing to firstly review the concepts of IFS and PFS, and then we will focus mainly on the concept of p-rung orthopair fuzzy set (p-ROFS) and its essential set and algebraical operations.
Definition 1 (See Atanassov, 1986).
Let X be the universe of discourse. An intuitionistic fuzzy set (IFS) on X is defined in terms of
AIFS={⟨x,μAIFS(x),νAIFS(x)⟩:x∈X},
in which μAIFS and νAIFS denote the membership and non-membership functions of AIFS such that for any x∈X it holds 0⩽μAIFS(x)+νAIFS(x)⩽1.
Definition 2 (See Zhang and Xu, 2014).
Let X be the universe of discourse. A Pythagorean fuzzy set (PFS) on X is defined in terms of
APFS={⟨x,μAPFS(x),νAPFS(x)⟩:x∈X},
in which μAPFS and νAPFS denote the membership and non-membership functions of APFS such that for any x∈X it holds 0⩽μ2APFS(x)+ν2APFS(x)⩽1.
Now, if we are interested in describing a situation in which an expert would like to express his/her preference by the degree of an object satisfying a criterion as 3√72, and the degree of dissatisfying as 12, then we immediately find that none of the existing concepts of IFS and PFS can explain such a situation because of 3√72+12⩽̸1 and (3√72)2+(12)2⩽̸1. This impulses Yager (2017) to define a more general concept than the IFS and the PFS concepts which is not only able to improve such a shortcoming, but it is also well-obeyed in this case.
Definition 3 (See Yager, 2017).
Let X be the universe of discourse. A p-rung orthopair fuzzy set (p-ROFS) on X is defined in terms of
Ap-ROFS={⟨x,μAp-ROFS(x),νAp-ROFS(x)⟩:x∈X},
in which μAp-ROFS and νAp-ROFS denote the membership and non-membership functions of Ap-ROFS such that for any x∈X it holds 0⩽μpAp-ROFS(x)+νpAp-ROFS(x)⩽1 where p∈[1,∞).
Moreover, for notational convenience, we name (μAp-ROFS(x),νAp-ROFS(x)) a p-rung orthopair fuzzy number (p-ROFN), and it is simply indicated hereafter by (μAp-ROFN,νAp-ROFN).
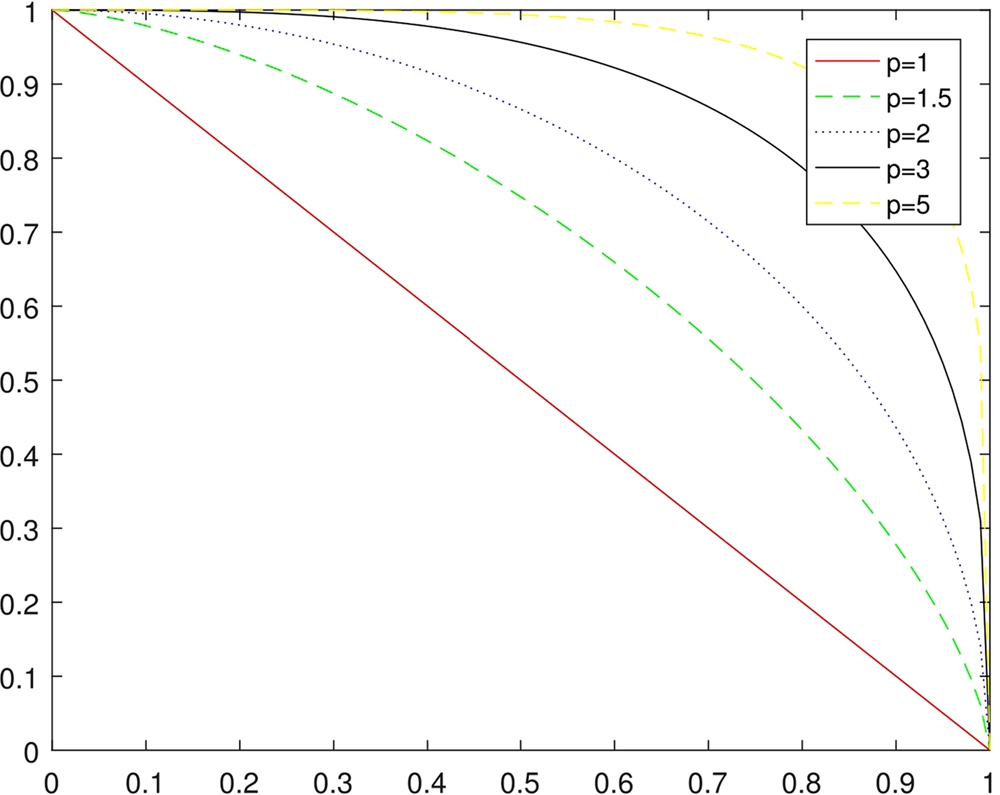
infor412_g001.jpg
Fig. 1.
Comparison of spaces of p-ROFSs for the parameters p=1,1.5,2,3,5.
As can be seen from Fig. 1, the intuitionistic membership degrees are those points being located in the area of the graph x+y⩽1, and the Pythagorean membership degrees are those points being located in the area of the graph x2+y2⩽1. This is while, the p-rung orthopair membership degrees are those points being located in the area of the graph xp+yp⩽1 where p∈[1,∞). This implies that the p-rung orthopair membership degrees provide us with a wider representation of non-standard membership degrees than the intuitionistic and the Pythagorean membership degrees. Indeed, any intuitionistic fuzzy number (IFN) and Pythagorean fuzzy number (PFN) can be considered as a p-ROFN, but the reverse is not held, that is, all p-ROFNs are not always IFNs or PFNs.
In what follows, we are interested in reviewing a number of set and algebraical operations on p-ROFNs.
Definition 4 (See Yager, 2017).
For any p-ROFNs Ap-ROFN and Bp-ROFN, the following operations are defined:
(1)
Acp-ROFN=(μAcp-ROFN,νAcp-ROFN)=(νAp-ROFN,μAp-ROFN),
(2)
Ap-ROFN∩Bp-ROFN=(μAp-ROFN∩Bp-ROFN,νAp-ROFN∪Bp-ROFN)=(min{μAp-ROFN,μBp-ROFN},max{νAp-ROFN,νBp-ROFN}),
(3)
Ap-ROFN∪Bp-ROFN=(μAp-ROFN∪Bp-ROFN,νAp-ROFN∩Bp-ROFN)=(max{μAp-ROFN,μBp-ROFN},min{νAp-ROFN,νBp-ROFN}).
In an analogous manner similar to IFNs and PFNs, the subset relation of p-ROFNs is defined as the following:
Definition 5 (See Yager, 2017).
For any p-ROFNs Ap-ROFN and Bp-ROFN, we indicate that Ap-ROFN⊆Bp-ROFN if and only if μAp-ROFN⩽μBp-ROFN together with νAp-ROFN⩾νBp-ROFN.
Definition 6 (See Yager, 2017).
For any p-ROFNs Ap-ROFN and Bp-ROFN, the following operations are defined:
(4)
Ap-ROFN⊕Bp-ROFN=(μAp-ROFN⊕Bp-ROFN,νAp-ROFN⊗Bp-ROFN)=([1−(1−μpAp-ROFN)(1−μpBp-ROFN)]1p,[νpAp-ROFNνpBp-ROFN]1p),
(5)
Ap-ROFN⊗Bp-ROFN=(μAp-ROFN⊗Bp-ROFN,νAp-ROFN⊕Bp-ROFN)=([μpAp-ROFNμpBp-ROFN]1p,[1−(1−νpAp-ROFN)(1−νpBp-ROFN)]1p).
An immediate consequence from the above definition is that
(6)
kAp-ROFN=(μkAp-ROFN,νkAp-ROFN)=([1−(1−μpAp-ROFN)k]1p,[(νpAp-ROFN)k]1p),
(7)
Akp-ROFN=(μAkp-ROFN,νAkp-ROFN)=([(μpAp-ROFN)k]1p,[1−(1−νpAp-ROFN)k]1p),
for any k>0.

3 Ranking Techniques of p-ROFNs

Throughout the present section, we first review the existing ranking techniques of p-ROFN, and in the second stage, we propose a new parametrical score function for p-ROFNs by taking both the membership and the hesitation degree of a p-ROFN into account.

3.1 Non-Algorithmic Ranking Technique

Assume that Ap-ROFN=(μAp-ROFN,νAp-ROFN) denotes a p-ROFN where μAp-ROFN indicates the proposal, and νAp-ROFN stands for the disagreement. It was Yager (2017) who first defined the following ranking technique for p-ROFNs:
Definition 7 (See Yager, 2017).
For any p-ROFN Ap-ROFN, Yager’s score function is constructed as
(8)
ScY(Ap-ROFN)=μpAp-ROFN−νpAp-ROFN,
where p∈[1,∞), and also −1⩽ScY(Ap-ROFN)⩽1.
With the help of this setting, we are able to present the comparison rule between the two p-ROFNs Ap-ROFN=(μAp-ROFN,νAp-ROFN) and Bp-ROFN=(μBp-ROFN,νBp-ROFN) as the following:
  • • if ScY(Ap-ROFN)<ScY(Bp-ROFN), then Ap-ROFN is considered smaller than Bp-ROFN and denoted by Ap-ROFN≺YBp-ROFN;
  • • if ScY(Ap-ROFN)=ScY(Bp-ROFN), then we get Ap-ROFN≃YBp-ROFN.
There exists another p-ROFN score function introduced by Wei et al. (2018) which behaves much like the Yager’s (2017) score function.
Definition 8 (See Wei et al., 2018).
For any p-ROFN Ap-ROFN, Wei et al.’s score function is constructed as
(9)
ScW(Ap-ROFN)=12(1+μpAp-ROFN−νpAp-ROFN),
where p∈[1,∞), and also 0⩽ScW(Ap-ROFN)⩽1.
With the help of this setting, we are able to present another comparison rule between the two p-ROFNs Ap-ROFN=(μAp-ROFN,νAp-ROFN) and Bp-ROFN=(μBp-ROFN,νBp-ROFN) as the following:
  • • if ScW(Ap-ROFN)<ScW(Bp-ROFN), then Ap-ROFN is considered smaller than Bp-ROFN and denoted by Ap-ROFN≺WBp-ROFN;
  • • if ScW(Ap-ROFN)=ScW(Bp-ROFN), then we get Ap-ROFN≃WBp-ROFN.

3.2 Algorithmic Ranking Techniques

Following Yager’s ( 2017) non-algorithmic ranking technique for p-ROFNs, Liu and Wang (2018) presented an algorithmic ranking technique by considering both score and accuracy functions of p-ROFNs.
Definition 9 (See Liu and Wang, 2018).
For any p-ROFN Ap-ROFN, the score and accuracy functions are respectively defined by
(10)
ScLW(Ap-ROFN)=μpAp-ROFN−νpAp-ROFN,
(11)
AccLW(Ap-ROFN)=μpAp-ROFN+νpAp-ROFN,
where p∈[1,∞), and moreover, −1⩽ScLW(Ap-ROFN)⩽1 and 0⩽AccLW(Ap-ROFN)⩽1.
Using this setting, the comparison rule between the two p-ROFNs Ap-ROFN=(μAp-ROFN,νAp-ROFN) and Bp-ROFN=(μBp-ROFN,νBp-ROFN) is considered as the following:
  • • if ScLW(Ap-ROFN)<ScLW(Bp-ROFN), then Ap-ROFN is considered smaller than Bp-ROFN and denoted by Ap-ROFN≺LWBp-ROFN;
  • • if ScLW(Ap-ROFN)=ScLW(Bp-ROFN), then
    • – if AccLW(Ap-ROFN)=AccLW(Bp-ROFN), hence we result that μAp-ROFN=μBp-ROFN together with νAp-ROFN=νBp-ROFN, that is, Ap-ROFN≃LWBp-ROFN;
    • – if AccLW(Ap-ROFN)<AccLW(Bp-ROFN), hence we get Ap-ROFN≺LWBp-ROFN.
As can be observed from equations (8) and (10), Yager’s (2017) and Liu and Wang’s (2018) score functions have the same construction. To simplify the next considerations, we will denote both of them with the notation ScYLW instead.
In continuation of Liu and Wang’s ( 2018) technique, Peng et al. (2018) introduced a ranking technique by taking the impact of membership and non-membership degrees together with the hesitation information into consideration.
Definition 10 (See Peng et al., 2018).
For any p-ROFN Ap-ROFN, the score function is defined by
(12)
ScPDG(Ap-ROFN)=μpAp-ROFN−νpAp-ROFN+(exp(μpAp-ROFN−νpAp-ROFN)exp(μpAp-ROFN−νpAp-ROFN)+1)πp(Ap-ROFN),
where p∈[1,∞), and moreover, −1⩽ScPDG(Ap-ROFN)⩽1 and πp(Ap-ROFN)=1−μpAp-ROFN−νpAp-ROFN.
Based on the above score function ScPDG and the hesitation information π, Peng et al. (2018) proposed an algorithmic ranking technique as the following:
For any two p-ROFNs Ap-ROFN=(μAp-ROFN,νAp-ROFN) and Bp-ROFN=(μBp-ROFN,νBp-ROFN), we deduce that
  • • if ScPDG(Ap-ROFN)<ScPDG(Bp-ROFN), then Ap-ROFN is considered smaller than Bp-ROFN and denoted by Ap-ROFN≺PDGBp-ROFN;
  • • if ScPDG(Ap-ROFN)=ScPDG(Bp-ROFN), then
    • – if π(Ap-ROFN)=π(Bp-ROFN), hence it results that μAp-ROFN=μBp-ROFN together with νAp-ROFN=νBp-ROFN, that is, Ap-ROFN≃PDGBp-ROFN;
    • – if π(Ap-ROFN)<π(Bp-ROFN), hence we have Ap-ROFN≻PDGBp-ROFN.
In view of this setting, Peng et al. (2018) demonstrated that the above-defined ranking technique ScPDG is monotonically increasing according to μAp-ROFN and monotonically decreasing according to νAp-ROFN.
Furthermore, Peng et al. (2018) indicated that
  • • ScPDG(Ap-ROFN)=−1 if and only if Ap-ROFN=(μAp-ROFN=0,νAp-ROFN=1);
  • • ScPDG(Ap-ROFN)=1 if and only if Ap-ROFN=(μAp-ROFN=1,νAp-ROFN=0).
Keeping the relation given in Definition 7 in the mind, Peng et al. (2018) showed that:
Theorem 1 (See Peng et al., 2018).
For any two p-ROFNs Ap-ROFN and Bp-ROFN, Peng et al.’s (2018) ranking order satisfies
(13)
ScPDG(Ap-ROFN)<ScPDG(Bp-ROFN)if and only ifAp-ROFN≺YBp-ROFNthat isμAp-ROFN<μBp-ROFNandνAp-ROFN>νBp-ROFN.
We are now in a position to provide a brief summary of advantages and disadvantages of the ranking techniques described above:
  • • Following from the non-algorithmic techniques of Yager (2017) and Wei et al. (2018) given respectively by (8) and (9), we easily find that Yager’s (2017) and Wei et al.’s (2018) score functions cannot differentiate many p-ROFNs in some situations. For instance, in the case where q=2 together with Ap-ROFN=(0.1,0.3) and Bp-ROFN=(0.2,√0.12), we obtain that ScY(Ap-ROFN)=ScY(Bp-ROFN)=−0.08 and ScW(Ap-ROFN)=ScW(Bp-ROFN)=−0.08 which are not reasonable.
  • • Both Liu and Wang’s ( 2018) and Peng et al.’s (2018) techniques are algorithmic in nature and require more computations than a non-algorithmic technique. More precisely, the information of p-ROFN may be lost when Liu and Wang’s (2018) technique is implemented and this is due to the fact that it does not consider the influence of abstention. Moreover, from the curve function f(x)=exp(x)exp(x)+1 in Peng et al.’s (2018) technique, we easily find that it causes more complexity in the evaluation of the score function.
On the basis of the above-mentioned deficiencies of the existing techniques, we still believe that an effective score function in the form of non-algorithmic ranking technique should be constructed by considering the impact of membership and non-membership degrees together with the hesitation information.

3.3 Innovative Non-Algorithmic Ranking Technique

Definition 11.
For any p-ROFN Ap-ROFN, the innovative score function is defined by
(14)
ScF(Ap-ROFN)=μpAp-ROFN+λ(1−μpAp-ROFN−νpAp-ROFN)
or equivalently
(15)
ScF(Ap-ROFN)=μpAp-ROFN+λπp(Ap-ROFN),
where 0<λ<1.
It is interesting to note that the score function ScF might be re-formulated as
(16)
ScF(Ap-ROFN)=μpAp-ROFN+λ(1−μpAp-ROFN−νpAp-ROFN)=μpAp-ROFN+λ−λμpAp-ROFN−λνpAp-ROFN=(1−λ)μpAp-ROFN+λ(1−νpAp-ROFN),
where 0<λ<1.
Remark 1.
In view of relation ( 16), the parameter λ corresponding to μpAp-ROFN and (1−νpAp-ROFN) represents the attitudinal characters of ScF. That is, whenever λ turns out to be larger from 0 to 1, then the term μpAp-ROFN gets less attention, and conversely, the term (1−νpAp-ROFN) gets more attention.
From another point of view, the score function ScF gives the average of hesitation degree between membership degree μpAp-ROFN and non-membership degree νpAp-ROFN. In this regard, the different values of λ indicate the integration of subjective and objective decision making information. These findings are quite straightforward by using the insights gained from the next section.
However, such a consideration in defining a parametrized score function is quite common and reasonable, and it can be found in Zhang et al. (2018, 2019), Garg (2016) and so on.
The formula ( 16) is nothing else, except for the certainty degree of Ap-ROFN which is denoted by the interval [μpAp-ROFN,1−νpAp-ROFN]. Needless to say that this interval follows from the fact that μpAp-ROFN+νpAp-ROFN⩽1 which results in μpAp-ROFN⩽1−νpAp-ROFN.
It is also of some interest to note that the above-introduced innovative score function ScF inherits the terms of membership degree μAp-ROFN, non-membership degree νAp-ROFN and hesitation information π(Ap-ROFN).
It is easily seen from Definition 11 that
  • • ScF(Ap-ROFN)=0 if and only if Ap-ROFN=(μAp-ROFN=0,νAp-ROFN=1);
  • • ScF(Ap-ROFN)=1 if and only if Ap-ROFN=(μAp-ROFN=1,νAp-ROFN=0).
Let us now investigate a number of other properties of innovative score function ScF which are given below.
Theorem 2.
For any p-ROFN Ap-ROFN, the innovative score function ScF(Ap-ROFN) given by (14) belongs to the interval [μpAp-ROFN,1−νpAp-ROFN).
Proof.
For any p-ROFN Ap-ROFN, it holds that μpAp-ROFN+νpAp-ROFN⩽1 or 1−μpAp-ROFN−νpAp-ROFN⩾0. If we consider 0<λ<1, then
λ(1−μpAp-ROFN−νpAp-ROFN)⩾0,μpAp-ROFN+λ(1−μpAp-ROFN−νpAp-ROFN)⩾μpAp-ROFN,
which implies that ScF(Ap-ROFN)⩾μpAp-ROFN.
On the other hand, from the fact that 0<λ<1, we get
ScF(Ap-ROFN)=μpAp-ROFN+λ(1−μpAp-ROFN−νpAp-ROFN)<μpAp-ROFN+(1−μpAp-ROFN−νpAp-ROFN)=1−νpAp-ROFN.
Therefore, we result in μpAp-ROFN⩽ScF(Ap-ROFN)<1−νpAp-ROFN. □
Corollary 1.
For any p-ROFN Ap-ROFN, the innovative score function ScF(Ap-ROFN) given by (14) satisfies ScF(Ap-ROFN)∈[0,1).
Proof.
The proof comes from the fact that 0⩽μpAp-ROFN⩽ScF(Ap-ROFN)<1−νpAp-ROFN⩽1. □
Theorem 3.
For any two p-ROFNs Ap-ROFN and Bp-ROFN, we conclude that
(17)
Ap-ROFN⪯YBp-ROFNif and only ifScF(Ap-ROFN)⩽ScF(Bp-ROFN).
Proof.
(Necessity) The relation Ap-ROFN⪯YBp-ROFN holds true if and only if
(18)
μAp-ROFN⩽μBp-ROFN,
(19)
νAp-ROFN⩾νBp-ROFN.
From the relation (18), we get that μpAp-ROFN⩽μpBp-ROFN for any p∈[1,∞), and consequently, (1−λ)μpAp-ROFN⩽(1−λ)μpBp-ROFN for any 0<λ<1.
From the relation ( 19), it results that νpAp-ROFN⩾νpBp-ROFN for any p∈[1,∞), and consequently, 1−νpAp-ROFN⩽1−νpBp-ROFN or λ(1−νpAp-ROFN)⩽λ(1−νpBp-ROFN) for any 0<λ<1.
Taking all the above relations into account, we get
(1−λ)μpAp-ROFN+λ(1−νpAp-ROFN)⩽(1−λ)μpBp-ROFN+λ(1−νpBp-ROFN),μpAp-ROFN+λ(1−μpAp-ROFN−νpAp-ROFN)⩽μpBp-ROFN+λ(1−μpBp-ROFN−νpBp-ROFN),
which implies that
ScF(Ap-ROFN)⩽ScF(Bp-ROFN).
(Sufficiency) Let
ScF(Bp-ROFN)−ScF(Ap-ROFN)=μpBp-ROFN+λ(1−μpBp-ROFN−νpBp-ROFN)−μpAp-ROFN−λ(1−μpAp-ROFN−νpAp-ROFN)=(μpBp-ROFN−μpAp-ROFN)+λ(1−μpBp-ROFN−νpBp-ROFN−1+μpAp-ROFN+νpAp-ROFN)=(1−λ)(μpBp-ROFN−μpAp-ROFN)+λ(νpAp-ROFN−νpBp-ROFN).
Now, it is obvious that ScF(Bp-ROFN)−ScF(Ap-ROFN)⩾0 if (1−λ)(μpBp-ROFN−μpAp-ROFN)+λ(νpAp-ROFN−νpBp-ROFN)⩾0 for any 0<λ<1, that is,
μpBp-ROFN−μpAp-ROFN⩾0,νpAp-ROFN−νpBp-ROFN⩾0,
for any p∈[1,∞). Consequently, we deduce that μAp-ROFN⩽μBp-ROFN and νAp-ROFN⩾νBp-ROFN which implies that Ap-ROFN⪯YBp-ROFN. □
Theorem 4.
For any p-ROFN Ap-ROFN=(μAp-ROFN,νAp-ROFN) and its corresponding complement Acp-ROFN=(νAp-ROFN,μAp-ROFN), we deduce that
(20)
ScF(Ap-ROFN)+ScF(Acp-ROFN)⩽1.
Proof.
From definition of the innovative score function ScF, we have
ScF(Ap-ROFN)+ScF(Acp-ROFN)=μpAp-ROFN+λ(1−μpAp-ROFN−νpAp-ROFN)+μpAcp-ROFN+λ(1−μpAcp-ROFN−νpAcp-ROFN)=μpAp-ROFN+λ(1−μpAp-ROFN−νpAp-ROFN)+νpAp-ROFN+λ(1−νpAp-ROFN−μpAp-ROFN)=(1−2λ)(μpAp-ROFN+νpAp-ROFN)+2λ.
Now, from the relation μpAp-ROFN+νpAp-ROFN⩽1, we get that
ScF(Ap-ROFN)+ScF(Acp-ROFN)⩽(1−2λ)+2λ=1.
□
As a result, it is interesting to remark that in the case where λ=12, it holds that
(21)
ScF(Ap-ROFN)+ScF(Acp-ROFN)=1.
Theorem 5.
For any p-ROFN Ap-ROFN, the innovative score function ScF(Ap-ROFN) given by (14) is a monotonically increasing function of μAp-ROFN and a monotonically decreasing function of νAp-ROFN.
Proof.
The proof is immediately apparent from calculating the first partial derivatives of ScF(Ap-ROFN)=μpAp-ROFN+λ(1−μpAp-ROFN−νpAp-ROFN) according to μAp-ROFN and νAp-ROFN where
∂ScF(Ap-ROFN)∂μAp-ROFN=pμp−1Ap-ROFN+λ(−pμp−1Ap-ROFN)=pμp−1Ap-ROFN(1−λ)⩾0;∂ScF(Ap-ROFN)∂νAp-ROFN=λ(−pνp−1Ap-ROFN)=−λ(pνp−1Ap-ROFN)⩽0,
for any 0<λ<1. □
Theorem 6.
For any p-ROFN Ap-ROFN, the innovative score function ScF(Ap-ROFN)=μpAp-ROFN+λ(1−μpAp-ROFN−νpAp-ROFN) is anincreasing function of λ, where 0<λ<1.
Proof.
The result now follows from the fact that
∂ScF(Ap-ROFN)∂λ=1−μpAp-ROFN−νpAp-ROFN=πp(Ap-ROFN)⩾0.
□

3.4 Comparison of the Proposed and Existing Score Functions

In this part of the contribution, we re-consider once again the comparison results given in Peng et al. (2018) together with the corresponding results of the proposed score function ScF. All the results are summarized in Tables 1– 6.
Needless to say that what we expect from Remark 1 is that by increasing the value of λ from 0 to 1, the precedence of that p-ROFN, which has the larger membership degree μp∗p-ROFN, reduces, and further, the precedence of that p-ROFN, which has the smaller non-membership degree νp∗p-ROFN (or has the larger degree (1−νp∗p-ROFN)), enlarges. This is exactly what we observe from Tables 2, 4, and 6. For instance, if we consider the p-ROFNs in Tables 1 and 2 in the form of A:=Ap-ROFN=(√0.22,0.7) and B:=Bp-ROFN=(0.3,0.6), we clearly see that μpAp-ROFN>μpBp-ROFN and (1−νpAp-ROFN)<(1−νpBp-ROFN). Therefore, we expect that by increasing the value of λ from 0 to 1, the precedence of Ap-ROFN decreases, and moreover, the precedence of Bp-ROFN increases. Indeed, this is what we see in Table 2. The other results in Tables 3– 6 are consistent with the above-mentioned fact.
Table 1
The ranking results of the existing score functions.
p-ROFN p ScY (Yager, 2017) Ranking ScW (Wei et al., 2018) Ranking
A:=Ap-ROFN=(√0.22,0.7) p=1 ScY(A)=−0.2310 ScW(A)=0.3845
B:=Bp-ROFN=(0.3,0.6) ScY(B)=−0.3000 A>B ScW(B)=0.3500 A>B
p=2 ScY(A)=−0.2700 ScW(A)=0.3650
ScY(B)=−0.2700 A=B ScW(B)=0.3650 A=B
p=3 ScY(A)=−0.2398 ScW(A)=0.3801
ScY(B)=−0.1890 A<B ScW(B)=0.4055 A<B
ScLW (Liu and Wang, 2018) Ranking ScPDG (Peng et al., 2018) Ranking
ScLW(A)=−0.2310 ScPDG(A)=−0.2212
ScLW(B)=−0.3000 A>B ScPDG(B)=−0.3074 A>B
ScLW(A)=−0.2700 (Using AccLW) ScPDG(A)=−0.2895
ScLW(B)=−0.2700 A>B ScPDG(B)=−0.2247 A<B
ScLW(B)=−0.2398 ScPDG(A)=−0.2729
ScLW(B)=−0.1890 A<B ScPDG(B)=−0.3069 A>B
Table 2
The ranking results of the proposed score function ScF corresponding to the values of λ from 0 to 1.
p-ROFN p λ ScF Ranking
A:=Ap-ROFN=(√0.22,0.7) p=1 λ=0 ScF(A)=∗
B:=Bp-ROFN=(0.3,0.6) ScF(B)=∗ ∗
p=2 ScF(A)=0.2200
ScF(B)=0.0900 A>B
p=3 ScF(A)=0.1032
ScF(B)=0.0270 A>B
p=1 λ=0.1 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.2490
ScF(B)=0.1450 A>B
p=3 ScF(A)=0.1586
ScF(B)=0.1027 A>B
p=1 λ=0.2 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.2780
ScF(B)=0.2000 A>B
p=3 ScF(A)=0.2140
ScF(B)=0.1784 A>B
p=1 λ=0.3 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.3070
ScF(B)=0.2550 A>B
p=3 ScF(A)=0.2693
ScF(B)=0.2541 A>B
p=1 λ=0.4 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.3360
ScF(B)=0.3100 A>B
p=3 ScF(A)=0.3247
ScF(B)=0.3298 A<B
p=1 λ=0.5 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.3651
ScF(B)=0.3650 A>B
p=3 ScF(A)=0.3801
ScF(B)=0.4055 A<B
p=1 λ=0.6 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.3940
ScF(B)=0.4200 A<B
p=3 ScF(A)=0.4355
ScF(B)=0.4812 A<B
p=1 λ=0.7 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.4230
ScF(B)=0.4750 A<B
p=3 ScF(A)=0.4909
ScF(B)=0.5569 A<B
p=1 λ=0.8 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.4520
ScF(B)=0.5300 A<B
p=3 ScF(A)=0.5462
ScF(B)=0.6326 A<B
p=1 λ=0.9 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.4810
ScF(B)=0.5850 A<B
p=3 ScF(A)=0.6016
ScF(B)=0.7083 A<B
p=1 λ=1 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.5100
ScF(B)=0.6400 A<B
p=3 ScF(A)=0.6570
ScF(B)=0.7840 A<B
Table 3
The ranking results of the existing score functions.
p-ROFN p ScY (Yager, 2017) Ranking ScW (Wei et al., 2018) Ranking
A:=Ap-ROFN=(0.6,0.3) p=1 ScY(A)=0.3000 ScW(A)=0.6500
B:=Bp-ROFN=(0.5,0.2) ScY(B)=0.3000 A=B ScW(B)=0.6500 (UsingAccLW)A=B
p=2 ScY(A)=0.2700 ScW(A)=0.6350
ScY(B)=0.2100 A>B ScW(B)=0.6050 A>B
p=3 ScY(A)=0.1890 ScW(A)=0.5945
ScY(B)=0.1170 A>B ScW(B)=0.5585 A>B
ScLW (Liu and Wang, 2018) Ranking ScPDG (Peng et al., 2018) Ranking
ScLW(A)=0.3000 ScPDG(A)=0.3074
ScLW(B)=0.3000 A>B ScPDG(B)=0.3233 A<B
ScLW(A)=0.2700 (Using AccLW) ScPDG(A)=0.3069
ScLW(B)=0.2100 A>B ScPDG(B)=0.2471 A>B
ScLW(B)=0.1890 ScPDG(A)=0.2247
ScLW(B)=0.1170 A>B ScPDG(B)=0.1423 A>B
Table 4
The ranking results of the proposed score function ScF corresponding to the values of λ from 0 to 1.
p-ROFN p λ ScF Ranking
A:=Ap-ROFN=(0.6,0.3) p=1 λ=0 ScF(A)=∗
B:=Bp-ROFN=(0.5,0.2) ScF(B)=∗ ∗
p=2 ScF(A)=0.3600
ScF(B)=0.2500 A>B
p=3 ScF(A)=0.2160
ScF(B)=0.1250 A>B
p=1 λ=0.1 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.4150
ScF(B)=0.3210 A>B
p=3 ScF(A)=0.2917
ScF(B)=0.2117 A>B
p=1 λ=0.2 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.4700
ScF(B)=0.3920 A>B
p=3 ScF(A)=0.3674
ScF(B)=0.2984 A>B
p=1 λ=0.3 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.5250
ScF(B)=0.4630 A>B
p=3 ScF(A)=0.4431
ScF(B)=0.3851 A>B
p=1 λ=0.4 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.5800
ScF(B)=0.5340 A>B
p=3 ScF(A)=0.5188
ScF(B)=0.4718 A>B
p=1 λ=0.5 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.6350
ScF(B)=0.6050 A>B
p=3 ScF(A)=0.5945
ScF(B)=0.5585 A>B
p=1 λ=0.6 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.6900
ScF(B)=0.6760 A>B
p=3 ScF(A)=0.6702
ScF(B)=0.6452 A>B
p=1 λ=0.7 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.7450
ScF(B)=0.7470 A<B
p=3 ScF(A)=0.7459
ScF(B)=0.7319 A>B
p=1 λ=0.8 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.8000
ScF(B)=0.8180 A<B
p=3 ScF(A)=0.8216
ScF(B)=0.8186 A>B
p=1 λ=0.9 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.8550
ScF(B)=0.8890 A<B
p=3 ScF(A)=0.8973
ScF(B)=0.9053 A>B
p=1 λ=1 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.9100
ScF(B)=0.9600 A<B
p=3 ScF(A)=0.9730
ScF(B)=0.9920 A<B
Table 5
The ranking results of the existing score functions.
p-ROFN p ScY (Yager, 2017) Ranking ScW (Wei et al., 2018) Ranking
A:=Ap-ROFN=(0.4,0.1) p=1 ScY(A)=0.3000 ScW(A)=0.6500
B:=Bp-ROFN=(√0.1501,0.01) ScY(A)=0.3774 A<B ScW(A)=0.6887 A<B
p=2 ScY(A)=0.1500 ScW(A)=0.5750
ScY(B)=0.1500 A=B ScW(B)=0.5750 A=B
p=3 ScY(A)=0.0630 ScW(A)=0.5315
ScY(B)=0.0582 A>B ScW(B)=0.5291 A>B
ScLW (Liu and Wang, 2018) Ranking ScPDG (Peng et al., 2018) Ranking
ScLW(A)=0.3000 ScPDG(A)=0.3372
ScLW(B)=0.3774 A<B ScPDG(B)=0.4336 A<B
ScLW(A)=0.1500 (Using AccLW) ScPDG(A)=0.1811
ScLW(B)=0.1500 A>B ScPDG(B)=0.1818 A<B
ScLW(A)=0.0630 (Using AccLW) ScPDG(A)=0.0777
ScLW(B)=0.0582 A>B ScPDG(B)=0.0718 A>B
Table 6
The ranking results of the proposed score function ScF corresponding to the values of λ from 0 to 1.
p-ROFN p λ ScF Ranking
A:=Ap-ROFN=(0.4,0.1) p=1 λ=0 ScF(A)=∗
B:=Bp-ROFN=(√0.1501,0.01) ScF(B)=∗ ∗
p=2 ScF(A)=0.1600
ScF(B)=0.1501 A>B
p=3 ScF(A)=0.0640
ScF(B)=0.0582 A>B
p=1 λ=0.1 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.2430
ScF(B)=0.2351 A>B
p=3 ScF(A)=0.1575
ScF(B)=0.1523 A>B
p=1 λ=0.2 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.3260
ScF(B)=0.3201 A>B
p=3 ScF(A)=0.2510
ScF(B)=0.2465 A>B
p=1 λ=0.3 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.4090
ScF(B)=0.4050 A>B
p=3 ScF(A)=0.3445
ScF(B)=0.3407 A>B
p=1 λ=0.4 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.4920
ScF(B)=0.4900 A>B
p=3 ScF(A)=0.4380
ScF(B)=0.4349 A<B
p=1 λ=0.5 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.5751
ScF(B)=0.5750 A>B
p=3 ScF(A)=0.5315
ScF(B)=0.5291 A>B
p=1 λ=0.6 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.6580
ScF(B)=0.6600 A<B
p=3 ScF(A)=0.6250
ScF(B)=0.6233 A>B
p=1 λ=0.7 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.7410
ScF(B)=0.7450 A<B
p=3 ScF(A)=0.7185
ScF(B)=0.7174 A>B
p=1 λ=0.8 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.8240
ScF(B)=0.8299 A<B
p=3 ScF(A)=0.8120
ScF(B)=0.8116 A>B
p=1 λ=0.9 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.9070
ScF(B)=0.9149 A<B
p=3 ScF(A)=0.9055
ScF(B)=0.9058 A<B
p=1 λ=1 ScF(A)=∗
ScF(B)=∗ ∗
p=2 ScF(A)=0.9900
ScF(B)=0.9999 A<B
p=3 ScF(A)=0.9990
ScF(B)=1.0000 A<B
The findings from Tables 1– 6 are summarized below:
  • • The first collection of p-ROFNs demonstrates that Ap-ROFN=(√0.22,0.7) is not a p(=1)-ROFN (because √0.22+0.7⩽̸1 which means that Ap-ROFN=(√0.22,0.7) is not an IFN), and clearly, no score function should return value in this case. This is while, all the existing score-based comparison techniques of ScY (Yager, 2017), ScW (Wei et al., 2018), ScLW (Liu and Wang, 2018) and ScPDG (Peng et al., 2018) return some values which are not obviously reasonable. Actually, such a case verifies the superiority of the proposed score function over the existing ones, and the proposed score function can effectively solve the deficiencies of all the above-mentioned score-based comparison techniques.
  • • In spite of the existing score-based comparison techniques ScY (Yager, 2017), ScW (Wei et al., 2018), ScLW (Liu and Wang, 2018) and ScPDG (Peng et al., 2018), the proposed score function ScF enables the decision maker to achieve greater insight and perform fine tuning of the selection process by choosing an appropriate value for the attitudinal character λ∈[0,1].
In summary, the proposed score function ScF is more reliable and preferable than the other existing score functions where they are unable to discriminate reasonably between the pairs of p-ROFNs in some situations.

4 MCDM Method Based on the Score Function of p-ROFNs

Multiple criteria decision making (MCDM) is an active research area, and there exist a large number of researches ( Farhadinia, 2014, 2016a, 2016b; Farhadinia and Herrera-Viedma, 2018; Farhadinia and Xu, 2017) in which the decision maker is going to provide a list of alternatives ranking in accordance with a given set of criteria.
In this part of the manuscript, we are facing a MCDM problem in which decision making is made by the use of a ranking procedure of p-ROFNs.
Suppose that X={x1,x2,…,xm} describes a set of alternatives, and the set of criteria is in the form of C={c1,c2,…,cn}. Furthermore, we denote the associated weight vector of criteria by w=(w1,w2,…,wn) such that 0⩽wj⩽1 (j=1,2,…,n) with the property ∑nj=1wj=1. Assume that a decision maker group is organized to evaluate the characteristics of each alternative with respect to each criterion with the help of p-ROFN concept. In this regard, the p-rung orthopair fuzzy decision matrix will be
(22)
D=[D(ij)p-ROFN]m×n=[(μD(ij)p-ROFN,νD(ij)p-ROFN)]m×n,
where 0⩽μpD(ij)p-ROFN+νpD(ij)p-ROFN⩽1 for any p∈[1,∞).
Now, with the help of Vlsekriterijumska Optimizacija I Kompromisno Resenje (VIKOR) technique (Liou et al., 2011) and Technique for Order of Preference by Similarity to the Ideal Solution (TOPSIS) (Lai et al., 1994) together with implementing the innovative score function of p-ROFNs, we will be able to describe a MCDM algorithm as the following:
Step 1.
Determine the best and the worst values with respect to all criteria which are denoted respectively by the p-ROFNs f+j and f−j:
(For the benefit criteria)
(23)
f+j=(max1⩽i⩽m{μD(ij)p-ROFN},min1⩽i⩽m{νD(ij)p-ROFN}),
(24)
f−j=(min1⩽i⩽m{μD(ij)p-ROFN},max1⩽i⩽m{νD(ij)p-ROFN}).
(For the cost criteria)
(25)
f+j=(min1⩽i⩽m{μD(ij)p-ROFN},max1⩽i⩽m{νD(ij)p-ROFN}),
(26)
f−j=(max1⩽i⩽m{μD(ij)p-ROFN},min1⩽i⩽m{νD(ij)p-ROFN}).
Step 2.
Construct the score matrix SD=[Sc(D(ij)p-ROFN)]m×n, and define the n-array vectors:
(27)
S+D=[max1⩽i⩽m{Sc(D(ij)p-ROFN)}]nj=1,
(28)
S−D=[min1⩽i⩽m{Sc(D(ij)p-ROFN)}]nj=1.
Step 3.
Construct the following normalized nearest-best and farthest-worst solution matrices:
(29)
SnearD:=[SnearD(ij)]m×n=[MIN(S+D(j)−Sc(D(ij)p-ROFN)S+D(j)−S−D(j))]m×n,
(30)
SfarD:=[SfarD(ij)]m×n=[MIN(Sc(D(ij)p-ROFN)−S−D(j)S+D(j)−S−D(j))]m×n,
where SnearD(ij),SfarD(ij)∈[0,1], and moreover, MIN(x)=min{x,1x}.
Step 4.
Keeping the above normalized nearest-best and farthest-worst solution matrices together with the weighting vector w=(w1,w2,…,wn) in mind, we are able to calculate the group utility and the individual regret for each alternative xi (i=1,2,…,m) in both best and worst cases:
(Best case)
(31)
Sbesti:=n∑j=1wj×SnearD(ij),
(32)
Rbesti:=max1⩽j⩽n{wj×SnearD(ij)}.
(Worst case)
(33)
Sworsti:=n∑j=1wj×SfarD(ij),
(34)
Rworsti:=min1⩽j⩽n{wj×SfarD(ij)}.
Step 5.
Construct the normalized nearest-best group utility and nearest-best individual regret values, respectively, of alternative xi (i=1,2,…,m):
(35)
¯¯Si=MIN(Sbesti−S_best¯Sbest−S_best),
(36)
¯¯Ri=MIN(Rbesti−R_best¯Rbest−R_best),
where
¯Sbest:=max1⩽i⩽m{Sbesti},S_best:=min1⩽i⩽m{Sbesti},¯Rbest:=max1⩽i⩽m{Rbesti},R_best:=min1⩽i⩽m{Rbesti},
and construct the normalized farthest-worst group utility and farthest-worst individual regret values, respectively, of alternative xi (i=1,2,…,m):
(37)
S__i=MIN(Sworsti−S_worst¯Sworst−S_worst),
(38)
R__i=MIN(Rworsti−R_worst¯Rworst−R_worst),
where
\begin{aligned}{}& {\overline{S}^{\mathit{worst}}}:=\underset{1\leqslant i\leqslant m}{\max }\big\{{S_{i}^{\mathit{worst}}}\big\},\\ {} & {\underline{S}^{\mathit{worst}}}:=\underset{1\leqslant i\leqslant m}{\min }\big\{{S_{i}^{\mathit{worst}}}\big\},\\ {} & {\overline{R}^{\mathit{worst}}}:=\underset{1\leqslant i\leqslant m}{\max }\big\{{R_{i}^{\mathit{worst}}}\big\},\\ {} & {\underline{R}^{\mathit{worst}}}:=\underset{1\leqslant i\leqslant m}{\min }\big\{{R_{i}^{\mathit{worst}}}\big\},\end{aligned}
in which \operatorname{MIN}(x)=\min \{x,\frac{1}{x}\}.
Step 6.
Construct the nearest-best and farthest-worst score values of alternative {x_{i}} (i=1,2,\dots ,m), respectively, as follows:
(39)
\begin{aligned}{}& {\overline{\overline{C}}_{i}}=\alpha {\overline{\overline{S}}_{i}}+(1-\alpha ){\overline{\overline{R}}_{i}},\end{aligned}
(40)
\begin{aligned}{}& {\underline{\underline{C}}_{i}}=\alpha {\underline{\underline{S}}_{\hspace{0.1667em}i}}+(1-\alpha ){\underline{\underline{R}}_{\hspace{0.1667em}i}},\end{aligned}
where {\overline{\overline{C}}_{i}},{\underline{\underline{C}}_{i}}\in [0,1] for any 1\leqslant i\leqslant m, and α indicates the strategy of maximum group utility while (1-\alpha ) indicates the strategy of minimum individual regret. Here, we suppose that \alpha =0.5.
Step 7.
Compute the relative closeness degree of each alternative {x_{i}} (i=1,2,\dots ,m) in the form of
(41)
C{C_{i}}=\frac{{\underline{\underline{C}}_{i}}}{{\overline{\overline{C}}_{i}}+{\underline{\underline{C}}_{i}}},
where the smaller value of the relative closeness degree indicates the better preference order of alternative {x_{i}}.
Before going more into detail, we summarize again the superiorities of the above-mentioned MCDM algorithm compared to the existing approaches being based independently on VIKOR or TOPSIS techniques:
  • * The proposed MCDM algorithm implements the innovative score function S{c_{F}} of p-ROFNs whose results are more reasonable than that of existing ones;
  • * By employing the new transformation function MIN, we are able to prevent violence of division by zero which occurs in the traditional version of VIKOR techniques;
  • * The proposed MCDM algorithm ranks the alternatives based on the combination of VIKOR and TOPSIS outputs.
Example 1 (Adopted from Chen et al., 2016).
We are going to investigate here a MCDM problem that deals with the supplier selection in supply chain management with p-ROFN information, in which five alternatives of suppliers {x_{i}} ( i=1,2,\dots ,5) are assessed by the use of four benefit criteria {c_{1}}: Quality, {c_{2}}: Service, {c_{3}}: Delivery and {c_{4}}: Price. Suppose that the weight vector of criteria is w=({w_{1}}=0.25,{w_{2}}=0.40,{w_{3}}=20,{w_{4}}=0.15).
We assume that the decision values are described by p-ROFNs in the form of the decision matrix:
\begin{array}{r@{\hskip4.0pt}c@{\hskip4.0pt}l}\displaystyle D& \displaystyle =& \displaystyle {\big[{D_{\text{p-ROFN}\hspace{2.5pt}}^{(ij)}}\big]_{5\times 4}}={\big[({\mu _{{D_{\text{p-ROFN}\hspace{2.5pt}}^{(ij)}}}},{\nu _{{D_{\text{p-ROFN}\hspace{2.5pt}}^{(ij)}}}})\big]_{5\times 4}}\\ {} & \displaystyle =& \displaystyle \left|\begin{array}{c@{\hskip4.0pt}c@{\hskip4.0pt}c@{\hskip4.0pt}c}\langle 0.6,0.3\rangle \hspace{1em}& \langle 0.5,0.2\rangle \hspace{1em}& \langle 0.2,0.5\rangle \hspace{1em}& \langle 0.1,0.6\rangle \\ {} \langle \textbf{0.8, 0.3}\hspace{2.5pt}\rangle \hspace{1em}& \langle 0.8,0.1\rangle \hspace{1em}& \langle 0.6,0.1\rangle \hspace{1em}& \langle 0.3,0.4\rangle \\ {} \langle 0.6,0.3\rangle \hspace{1em}& \langle 0.4,0.3\rangle \hspace{1em}& \langle 0.4,0.2\rangle \hspace{1em}& \langle 0.5,0.2\rangle \\ {} \langle \textbf{0.9, 0.2}\hspace{2.5pt}\rangle \hspace{1em}& \langle 0.5,0.2\rangle \hspace{1em}& \langle 0.2,0.3\rangle \hspace{1em}& \langle 0.1,0.5\rangle \\ {} \langle 0.7,0.1\rangle \hspace{1em}& \langle 0.3,0.2\rangle \hspace{1em}& \langle 0.6,0.2\rangle \hspace{1em}& \langle 0.4,0.2\rangle \end{array}\right|.\end{array}
Needless to say that the above decision matrix is not in the form of an intuitionistic fuzzy matrix as considered in Chen et al. (2016) because the entries ({\mu _{{D_{\text{p-ROFN}\hspace{2.5pt}}^{(21)}}}},{\nu _{{D_{\text{p-ROFN}\hspace{2.5pt}}^{(21)}}}}) and ({\mu _{{D_{\text{p-ROFN}\hspace{2.5pt}}^{(41)}}}},{\nu _{{D_{\text{p-ROFN}\hspace{2.5pt}}^{(41)}}}}) are not IFNs.
Step 1. We determine the best and the worst values in correspondence with all benefit criteria as the following:
\begin{aligned}{}& \big\{{f_{1}^{+}},{f_{2}^{+}},{f_{3}^{+}},{f_{4}^{+}}\big\}=\big\{(0.9,0.1),(0.8,0.1),(0.6,0.1),(0.5,0.2)\big\},\\ {} & \big\{{f_{1}^{-}},{f_{2}^{-}},{f_{3}^{-}},{f_{4}^{-}}\big\}=\big\{(0.6,0.3),(0.3,0.3),(0.2,0.5),(0.1,0.6)\big\}.\end{aligned}
Step 2. By keeping the score functions S{c_{YLW}}, S{c_{\mathit{PDG}}} and S{c_{F}} given respectively by (10), (12) and (14) into account, we are able to construct the score matrices
{S_{D\text{-}\hspace{2.5pt}\mathit{YLW}}}={\big[S{c_{\mathit{YLW}}}\big({D_{\text{p-ROFN}\hspace{2.5pt}}^{(ij)}}\big)\big]_{5\times 4}}=\left|\begin{array}{c@{\hskip4.0pt}c@{\hskip4.0pt}c@{\hskip4.0pt}c}0.2700\hspace{1em}& 0.2100\hspace{1em}& -0.2100\hspace{1em}& -0.3500\\ {} 0.5500\hspace{1em}& 0.6300\hspace{1em}& 0.3500\hspace{1em}& -0.0700\\ {} 0.2700\hspace{1em}& 0.0700\hspace{1em}& 0.1200\hspace{1em}& 0.2100\\ {} 0.7700\hspace{1em}& 0.2100\hspace{1em}& -0.0500\hspace{1em}& -0.2400\\ {} 0.4800\hspace{1em}& 0.0500\hspace{1em}& 0.3200\hspace{1em}& 0.1200\end{array}\right|
for p=2;
{S_{D\text{-}\hspace{2.5pt}\mathit{YLW}}}={\big[S{c_{\mathit{YLW}}}\big({D_{\text{p-ROFN}\hspace{2.5pt}}^{(ij)}}\big)\big]_{5\times 4}}=\left|\begin{array}{c@{\hskip4.0pt}c@{\hskip4.0pt}c@{\hskip4.0pt}c}0.1890\hspace{1em}& 0.1170\hspace{1em}& -0.1170\hspace{1em}& -0.2150\\ {} 0.4850\hspace{1em}& 0.5110\hspace{1em}& 0.2150\hspace{1em}& -0.0370\\ {} 0.1890\hspace{1em}& 0.0370\hspace{1em}& 0.0560\hspace{1em}& 0.1170\\ {} 0.7210\hspace{1em}& 0.1170\hspace{1em}& -0.0190\hspace{1em}& -0.1240\\ {} 0.3420\hspace{1em}& 0.0190\hspace{1em}& 0.2080\hspace{1em}& 0.0560\end{array}\right|
for p=3;
{S_{D\text{-}\hspace{2.5pt}\mathit{PDG}}}={\big[S{c_{\mathit{PDG}}}\big({D_{\text{p-ROFN}\hspace{2.5pt}}^{(ij)}}\big)\big]_{5\times 4}}=\left|\begin{array}{c@{\hskip4.0pt}c@{\hskip4.0pt}c@{\hskip4.0pt}c}0.5819\hspace{1em}& 0.6021\hspace{1em}& 0.1079\hspace{1em}& -0.0896\\ {} 0.7212\hspace{1em}& 0.8584\hspace{1em}& 0.7196\hspace{1em}& 0.2919\\ {} 0.5819\hspace{1em}& 0.4581\hspace{1em}& 0.5440\hspace{1em}& 0.6021\\ {} 0.8725\hspace{1em}& 0.6021\hspace{1em}& 0.3741\hspace{1em}& 0.0858\\ {} 0.7889\hspace{1em}& 0.4959\hspace{1em}& 0.6676\hspace{1em}& 0.5440\end{array}\right|
for p=2;
{S_{D\text{-}\hspace{2.5pt}\mathit{PDG}}}={\big[S{c_{\mathit{PDG}}}\big({D_{\text{p-ROFN}\hspace{2.5pt}}^{(ij)}}\big)\big]_{5\times 4}}=\left|\begin{array}{c@{\hskip4.0pt}c@{\hskip4.0pt}c@{\hskip4.0pt}c}0.6032\hspace{1em}& 0.5758\hspace{1em}& 0.2912\hspace{1em}& 0.1346\\ {} 0.7703\hspace{1em}& 0.8154\hspace{1em}& 0.6484\hspace{1em}& 0.4091\\ {} 0.6032\hspace{1em}& 0.4999\hspace{1em}& 0.5330\hspace{1em}& 0.5758\\ {} 0.8980\hspace{1em}& 0.5758\hspace{1em}& 0.4589\hspace{1em}& 0.2859\\ {} 0.7255\hspace{1em}& 0.5061\hspace{1em}& 0.6362\hspace{1em}& 0.5330\end{array}\right|
for p=3;
{S_{D-F}}={\big[S{c_{F}}\big({D_{\text{p-ROFN}\hspace{2.5pt}}^{(ij)}}\big)\big]_{5\times 4}}=\left|\begin{array}{c@{\hskip4.0pt}c@{\hskip4.0pt}c@{\hskip4.0pt}c}0.6350\hspace{1em}& 0.6050\hspace{1em}& 0.3950\hspace{1em}& 0.3250\\ {} 0.7750\hspace{1em}& 0.8150\hspace{1em}& 0.6750\hspace{1em}& 0.4650\\ {} 0.6350\hspace{1em}& 0.5350\hspace{1em}& 0.5600\hspace{1em}& 0.6050\\ {} 0.8850\hspace{1em}& 0.6050\hspace{1em}& 0.4750\hspace{1em}& 0.3800\\ {} 0.7400\hspace{1em}& 0.5250\hspace{1em}& 0.6600\hspace{1em}& 0.5600\end{array}\right|
for p=2 (\lambda =0.5);
{S_{D-F}}={\big[S{c_{F}}\big({D_{\text{p-ROFN}\hspace{2.5pt}}^{(ij)}}\big)\big]_{5\times 4}}=\left|\begin{array}{c@{\hskip4.0pt}c@{\hskip4.0pt}c@{\hskip4.0pt}c}0.5945\hspace{1em}& 0.5585\hspace{1em}& 0.4415\hspace{1em}& 0.3925\\ {} 0.7425\hspace{1em}& 0.7555\hspace{1em}& 0.6075\hspace{1em}& 0.4815\\ {} 0.5945\hspace{1em}& 0.5185\hspace{1em}& 0.5280\hspace{1em}& 0.5585\\ {} 0.8605\hspace{1em}& 0.5585\hspace{1em}& 0.4905\hspace{1em}& 0.4380\\ {} 0.6710\hspace{1em}& 0.5095\hspace{1em}& 0.6040\hspace{1em}& 0.5280\end{array}\right|
for p=3 (\lambda =0.5).
In order to save more space for convenient storage, we do not state here the calculation of {S_{D-F}}={[S{c_{F}}({D_{\text{p-ROFN}\hspace{2.5pt}}^{(ij)}})]_{5\times 4}} for \lambda =0,1 (as samples of values \lambda \in [0,1]), and only the corresponding results will be reported in Step 5.
By the way, we obtain here:
(For p=2)
\begin{aligned}{}& {S_{D\text{-}\hspace{2.5pt}\mathit{YLW}}^{+}}={\Big[\underset{1\leqslant i\leqslant 5}{\max }\big\{S{c_{\mathit{YLW}}}\big({D_{\text{p-ROFN}\hspace{2.5pt}}^{(ij)}}\big)\big\}\Big]_{j=1}^{4}}=[0.7700,0.6300,0.3500,0.2100];\\ {} & {S_{D\text{-}\hspace{2.5pt}\mathit{YLW}}^{-}}={\Big[\underset{1\leqslant i\leqslant 5}{\min }\big\{S{c_{\mathit{YLW}}}\big({D_{\text{p-ROFN}\hspace{2.5pt}}^{(ij)}}\big)\big\}\Big]_{j=1}^{4}}=[0.2700,0.0500,-0.2100,-0.3500];\end{aligned}
(For p=3)
\begin{aligned}{}& {S_{D\text{-}\hspace{2.5pt}\mathit{YLW}}^{+}}={\Big[\underset{1\leqslant i\leqslant 5}{\max }\big\{S{c_{\mathit{YLW}}}\big({D_{\text{p-ROFN}\hspace{2.5pt}}^{(ij)}}\big)\big\}\Big]_{j=1}^{4}}=[0.7210,0.5110,0.2150,0.1170];\\ {} & {S_{D\text{-}\hspace{2.5pt}\mathit{YLW}}^{-}}={\Big[\underset{1\leqslant i\leqslant 5}{\min }\big\{S{c_{\mathit{YLW}}}\big({D_{\text{p-ROFN}\hspace{2.5pt}}^{(ij)}}\big)\big\}\Big]_{j=1}^{4}}=[0.1890,0.0190,-0.1170,-0.2150];\end{aligned}
(For p=2)
\begin{aligned}{}& {S_{D\text{-}\hspace{2.5pt}\mathit{PDG}}^{+}}={\Big[\underset{1\leqslant i\leqslant 5}{\max }\big\{S{c_{\mathit{PDG}}}\big({D_{\text{p-ROFN}\hspace{2.5pt}}^{(ij)}}\big)\big\}\Big]_{j=1}^{4}}=[0.8725,0.8584,0.7196,0.6021];\\ {} & {S_{D\text{-}\hspace{2.5pt}\mathit{PDG}}^{-}}={\Big[\underset{1\leqslant i\leqslant 5}{\min }\big\{S{c_{\mathit{PDG}}}\big({D_{\text{p-ROFN}\hspace{2.5pt}}^{(ij)}}\big)\big\}\Big]_{j=1}^{4}}=[0.5819,0.4581,0.1079,-0.0896];\end{aligned}
(For p=3)
\begin{aligned}{}& {S_{D\text{-}\hspace{2.5pt}\mathit{PDG}}^{+}}={\Big[\underset{1\leqslant i\leqslant 5}{\max }\big\{S{c_{\mathit{PDG}}}\big({D_{\text{p-ROFN}\hspace{2.5pt}}^{(ij)}}\big)\big\}\Big]_{j=1}^{4}}=[0.8980,0.8154,0.6484,0.5758];\\ {} & {S_{D\text{-}\hspace{2.5pt}\mathit{PDG}}^{-}}={\Big[\underset{1\leqslant i\leqslant 5}{\min }\big\{S{c_{\mathit{PDG}}}\big({D_{\text{p-ROFN}\hspace{2.5pt}}^{(ij)}}\big)\big\}\Big]_{j=1}^{4}}=[0.6032,0.4999,0.2912,0.1346];\end{aligned}
(For p=2 (\lambda =0.5))
\begin{aligned}{}& {S_{D-F}^{+}}={\Big[\underset{1\leqslant i\leqslant 5}{\max }\big\{S{c_{F}}\big({D_{\text{p-ROFN}\hspace{2.5pt}}^{(ij)}}\big)\big\}\Big]_{j=1}^{4}}=[0.8850,0.8150,0.6750,0.6050];\\ {} & {S_{D-F}^{-}}={\Big[\underset{1\leqslant i\leqslant 5}{\min }\big\{S{c_{F}}\big({D_{\text{p-ROFN}\hspace{2.5pt}}^{(ij)}}\big)\big\}\Big]_{j=1}^{4}}=[0.6350,0.5250,0.3950,0.3250];\end{aligned}
(For p=3 (\lambda =0.5))
\begin{aligned}{}& {S_{D-F}^{+}}={\Big[\underset{1\leqslant i\leqslant 5}{\max }\big\{S{c_{F}}\big({D_{\text{p-ROFN}\hspace{2.5pt}}^{(ij)}}\big)\big\}\Big]_{j=1}^{4}}=[0.8605,0.7555,0.6075,0.5585];\\ {} & {S_{D-F}^{-}}={\Big[\underset{1\leqslant i\leqslant 5}{\min }\big\{S{c_{F}}\big({D_{\text{p-ROFN}\hspace{2.5pt}}^{(ij)}}\big)\big\}\Big]_{j=1}^{4}}=[0.5945,0.5095,0.4415,0.3925].\end{aligned}
Hereafter, we do not give the details of computation of p-ROFNs for p=3, and only the corresponding results for p=2 are returned.
Step 3. We construct the normalized nearest-best and farthest-worst solution matrices as follows:
{S_{D\text{-}\hspace{2.5pt}\mathit{YLW}}^{\mathit{near}}}:={\big[{S_{D\text{-}\hspace{2.5pt}\mathit{YLW}}^{\mathit{near}}}(ij)\big]_{5\times 4}}=\left|\begin{array}{c@{\hskip4.0pt}c@{\hskip4.0pt}c@{\hskip4.0pt}c}1.0000\hspace{1em}& 0.7241\hspace{1em}& 1.0000\hspace{1em}& 1.0000\\ {} 0.4400\hspace{1em}& 0\hspace{1em}& 0\hspace{1em}& 0.5000\\ {} 1.0000\hspace{1em}& 0.9655\hspace{1em}& 0.4107\hspace{1em}& 0\\ {} 0\hspace{1em}& 0.7241\hspace{1em}& 0.7143\hspace{1em}& 0.8036\\ {} 0.5800\hspace{1em}& 1.0000\hspace{1em}& 0.0536\hspace{1em}& 0.1607\end{array}\right|,
for p=2,
{S_{D\text{-}\hspace{2.5pt}\mathit{PDG}}^{\mathit{near}}}:={\big[{S_{D\text{-}\hspace{2.5pt}\mathit{PDG}}^{\mathit{near}}}(ij)\big]_{5\times 4}}=\left|\begin{array}{c@{\hskip4.0pt}c@{\hskip4.0pt}c@{\hskip4.0pt}c}1.0000\hspace{1em}& 0.6402\hspace{1em}& 1.0000\hspace{1em}& 1.0000\\ {} 0.5206\hspace{1em}& 0\hspace{1em}& 0\hspace{1em}& 0.4485\\ {} 1.0000\hspace{1em}& 1.0000\hspace{1em}& 0.2871\hspace{1em}& 0\\ {} 0\hspace{1em}& 0.6402\hspace{1em}& 0.5647\hspace{1em}& 0.7465\\ {} 0.2878\hspace{1em}& 0.9057\hspace{1em}& 0.0850\hspace{1em}& 0.0841\end{array}\right|,
for p=2,
{S_{D-F}^{\mathit{near}}}:={\big[{S_{D-F}^{\mathit{near}}}(ij)\big]_{5\times 4}}=\left|\begin{array}{c@{\hskip4.0pt}c@{\hskip4.0pt}c@{\hskip4.0pt}c}1.0000\hspace{1em}& 0.7241\hspace{1em}& 1.0000\hspace{1em}& 1.0000\\ {} 0.4400\hspace{1em}& 0\hspace{1em}& 0\hspace{1em}& 0.5000\\ {} 1.0000\hspace{1em}& 0.9655\hspace{1em}& 0.4107\hspace{1em}& 0\\ {} 0\hspace{1em}& 0.7241\hspace{1em}& 0.7143\hspace{1em}& 0.8036\\ {} 0.5800\hspace{1em}& 1.0000\hspace{1em}& 0.0536\hspace{1em}& 0.1607\end{array}\right|,
for p=2 (\lambda =0.5), and
{S_{D\text{-}\hspace{2.5pt}\mathit{YLW}}^{\mathit{far}}}:={\big[{S_{D\text{-}\hspace{2.5pt}\mathit{YLW}}^{\mathit{far}}}(ij)\big]_{5\times 4}}=\left|\begin{array}{c@{\hskip4.0pt}c@{\hskip4.0pt}c@{\hskip4.0pt}c}0\hspace{1em}& 0.2759\hspace{1em}& 0\hspace{1em}& 0\\ {} 0.5600\hspace{1em}& 1.0000\hspace{1em}& 1.0000\hspace{1em}& 0.5000\\ {} 0\hspace{1em}& 0.0345\hspace{1em}& 0.5893\hspace{1em}& 1.0000\\ {} 1.0000\hspace{1em}& 0.2759\hspace{1em}& 0.2857\hspace{1em}& 0.1964\\ {} 0.4200\hspace{1em}& 0\hspace{1em}& 0.9464\hspace{1em}& 0.8393\end{array}\right|,
for p=2,
{S_{D\text{-}\hspace{2.5pt}\mathit{PDG}}^{\mathit{far}}}:={\big[{S_{D\text{-}\hspace{2.5pt}\mathit{PDG}}^{\mathit{far}}}(ij)\big]_{5\times 4}}=\left|\begin{array}{c@{\hskip4.0pt}c@{\hskip4.0pt}c@{\hskip4.0pt}c}0\hspace{1em}& 0.3598\hspace{1em}& 0\hspace{1em}& 0\\ {} 0.4794\hspace{1em}& 1.0000\hspace{1em}& 1.0000\hspace{1em}& 0.5515\\ {} 0\hspace{1em}& 0\hspace{1em}& 0.7129\hspace{1em}& 1.0000\\ {} 1.0000\hspace{1em}& 0.3598\hspace{1em}& 0.4353\hspace{1em}& 0.2535\\ {} 0.7122\hspace{1em}& 0.0943\hspace{1em}& 0.9150\hspace{1em}& 0.9159\end{array}\right|,
for p=2,
{S_{D-F}^{\mathit{far}}}:={\big[{S_{D-F}^{\mathit{far}}}(ij)\big]_{5\times 4}}=\left|\begin{array}{c@{\hskip4.0pt}c@{\hskip4.0pt}c@{\hskip4.0pt}c}0\hspace{1em}& 0.2759\hspace{1em}& 0\hspace{1em}& 0\\ {} 0.5600\hspace{1em}& 1.0000\hspace{1em}& 1.0000\hspace{1em}& 0.5000\\ {} 0\hspace{1em}& 0.0345\hspace{1em}& 0.5893\hspace{1em}& 1.0000\\ {} 1.0000\hspace{1em}& 0.2759\hspace{1em}& 0.2857\hspace{1em}& 0.1964\\ {} 0.4200\hspace{1em}& 0\hspace{1em}& 0.9464\hspace{1em}& 0.8393\end{array}\right|,
for p=2 (\lambda =0.5).
Step 4. If we keep the above normalized nearest-best and farthest-worst solution matrices together with the weighting vector w=({w_{1}}=0.25,{w_{2}}=0.40,{w_{3}}=20,{w_{4}}=0.15) in mind, then we will be able to calculate the group utility and the individual regret for each alternative {x_{i}} in both best and worst cases:
(Best case: for p=2)
\begin{aligned}{}& {S_{i}^{\mathit{best}}}:={\sum \limits_{j=1}^{4}}{w_{j}}\times {S_{D\text{-}\hspace{2.5pt}\mathit{YLW}}^{\mathit{near}}}(ij)={[0.8897,0.1850,0.7183,0.5530,0.5798]^{T}},\\ {} & {R_{i}^{\mathit{best}}}:=\underset{1\leqslant j\leqslant 4}{\max }\big\{{w_{j}}\times {S_{D\text{-}\hspace{2.5pt}\mathit{YLW}}^{\mathit{near}}}(ij)\big\}={[0.2897,0.1100,0.3862,0.2897,0.4000]^{T}},\\ {} & {S_{i}^{\mathit{best}}}:={\sum \limits_{j=1}^{n}}{w_{j}}\times {S_{D\text{-}\hspace{2.5pt}\mathit{PDG}}^{\mathit{near}}}(ij)={[0.8561,0.1974,0.7074,0.4810,0.4638]^{T}},\\ {} & {R_{i}^{\mathit{best}}}:=\underset{1\leqslant j\leqslant n}{\max }\big\{{w_{j}}\times {S_{D\text{-}\hspace{2.5pt}\mathit{PDG}}^{\mathit{near}}}(ij)\big\}={[0.2561,0.1302,0.4000,0.2561,0.3623]^{T}},\\ {} & {S_{i}^{\mathit{best}}}:={\sum \limits_{j=1}^{n}}{w_{j}}\times {S_{D-F}^{\mathit{near}}}(ij)={[0.8897,0.1850,0.7183,0.5530,0.5798]^{T}},\\ {} & (\lambda =0.5)\\ {} & {R_{i}^{\mathit{best}}}:=\underset{1\leqslant j\leqslant n}{\max }\big\{{w_{j}}\times {S_{D-F}^{\mathit{near}}}(ij)\big\}={[0.2897,0.1100,0.3862,0.2897,0.4000]^{T}},\\ {} & (\lambda =0.5).\end{aligned}
(Worst case: for p=2)
In this case, we omit the calculations of {S_{i}^{\mathit{worst}}} and {R_{i}^{\mathit{worst}}} because they are similar to those given above.
Step 5. We construct the normalized nearest-best group utility and nearest-best individual regret values, respectively, of alternative {x_{i}} as the following: (for p=2)
\begin{aligned}{}& {\overline{\overline{S}}_{i}}(YLW)={[1.0000,0,0.7569,0.5223,0.5603]^{T}},\\ {} & {\overline{\overline{R}}_{i}}(YLW)={[0.6195,0,0.9524,0.6195,1.0000]^{T}},\\ {} & {\overline{\overline{S}}_{i}}(PDG)={[1.0000,0,0.7743,0.4305,0.4045]^{T}},\\ {} & {\overline{\overline{R}}_{i}}(PDG)={[0.4666,0,1.0000,0.4666,0.8602]^{T}},\\ {} & {\overline{\overline{S}}_{i}}(F)={[1.0000,0,0.7569,0.5223,0.5603]^{T}},\hspace{1em}(\lambda =0.5),\\ {} & {\overline{\overline{R}}_{i}}(F)={[0.6195,0,0.9524,0.6195,1.0000]^{T}},\hspace{1em}(\lambda =0.5).\end{aligned}
The calculations of the normalized farthest-worst group utility values {\underline{\underline{S}}_{\hspace{0.1667em}i}} and farthest-worst individual regret values {\underline{\underline{R}}_{\hspace{0.1667em}i}} are omitted due to lack of space.
On the basis of Step 6 and Step 7, we can determine the relative closeness degree of each alternative {x_{i}} for both cases p=2,3:
(For p=2)
\begin{aligned}{}& C{C_{YLW}}=[1.0000,0,0.8755,0.5674,0.7802],\\ {} & C{C_{\mathit{PDG}}}=[1.0000,0,0.8871,0.4657,0.5460],\\ {} & C{C_{F}}=[1.0000,0,0.8735,0.7750,0.8189],\hspace{1em}(\lambda =0),\\ {} & C{C_{F}}=[1.0000,0,0.8755,0.5674,0.7802],\hspace{1em}(\lambda =0.5),\\ {} & C{C_{F}}=[1.0000,0,0.9155,0.9731,0.1313],\hspace{1em}(\lambda =1),\end{aligned}
(For p=3)
\begin{aligned}{}& C{C_{YLW}}=[1.0000,0,0.8688,0.5596,0.7902],\\ {} & C{C_{\mathit{PDG}}}=[1.0000,0,0.8720,0.5109,0.7329],\\ {} & C{C_{F}}=[1.0000,0,0.8832,0.7900,0.8149],\hspace{1em}(\lambda =0),\\ {} & C{C_{F}}=[1.0000,0,0.8688,0.5596,0.7902],\hspace{1em}(\lambda =0.5),\\ {} & C{C_{F}}=[1.0000,0,0.9444,0.9601,0.1027],\hspace{1em}(\lambda =1),\end{aligned}
where the smaller value of the relative closeness degree indicates the better preference order of alternative {x_{i}}. In this regard, the preference orders of the alternatives are given in Table 7.
Table 7
Rankings of alternatives for different score-based MCDM techniques under p-ROFN environment.
Score function p The final ranking
S{c_{\mathit{YLW}}} (given by Yager, 2017; Wei et al., 2018; Liu and Wang, 2018) p=2 {x_{2}}>{x_{4}}>{x_{5}}>{x_{3}}>{x_{1}}
p=3 {x_{2}}>{x_{4}}>{x_{5}}>{x_{3}}>{x_{1}}
S{c_{\mathit{PDG}}} (given by Peng et al.’s, 2018) p=2 {x_{2}}>{x_{4}}>{x_{5}}>{x_{3}}>{x_{1}}
p=3 {x_{2}}>{x_{4}}>{x_{5}}>{x_{3}}>{x_{1}}
Proposed S{c_{F}}\hspace{2.5pt}\text{for}\hspace{2.5pt}\lambda =0 p=2 {x_{2}}>{x_{4}}>{x_{5}}>{x_{3}}>{x_{1}}
p=3 {x_{2}}>{x_{4}}>{x_{5}}>{x_{3}}>{x_{1}}
Proposed S{c_{F}}\hspace{2.5pt}\text{for}\hspace{2.5pt}\lambda =0.5 p=2 {x_{2}}>{x_{4}}>{x_{5}}>{x_{3}}>{x_{1}}
p=3 {x_{2}}>{x_{4}}>{x_{5}}>{x_{3}}>{x_{1}}
Proposed S{c_{F}}\hspace{2.5pt}\text{for}\hspace{2.5pt}\lambda =1 p=2 {x_{2}}>{x_{5}}>{x_{3}}>{x_{4}}>{x_{1}}
p=3 {x_{2}}>{x_{5}}>{x_{3}}>{x_{4}}>{x_{1}}
From Table 7, we can observe that the results of ranking orders for suppliers based on the existing score functions of Yager (2017), Wei et al. (2018), Liu and Wang (2018), and Peng et al. (2018) compared to the proposed score function S{c_{F}} remain unchanged for the values \lambda =0,0.5, and more or less different for \lambda =1. However, a decision maker may select the diverse values of parameter λ in accordance with his/her diverse preferences and attitudes in real and actual decision making cases. Therefore, the application range of proposed non-algorithmic ranking technique of p-ROFNs is wider than the existing ones, and it can flexibly handle more general decision information compared to the algorithmic ranking techniques. Moreover, by taking the new transformation function MIN into account, we can prevent violence of division by zero which may occur in the traditional version of VIKOR techniques. These superiorities of the proposed score-based MCDM algorithm compared to the existing approaches indicate that it is more suitable for the actual situations.

5 Conclusions and Further Research Perspectives

The purpose of this paper was to present an innovative and non-algorithmic ranking score function for p-ROFSs. The comparison of innovative score function for p-ROFSs with the existing non-algorithmic ranking ones showed some inherent advantages of the former one over the latter ones. Eventually, the performance of innovative score function for p-ROFSs compared to that of other score functions was demonstrated in a MCDM problem. Although, it usually seems that an algorithmic ranking technique should be more reliable than the proposed non-algorithmic ranking technique, but the existing algorithmic technique of Liu and Wang (2018) does not work logically for the present problem.
By the way, there exist a lot of fruitful research perspectives that can be productively pursued through the application of p-ROFS concept in conjunction with decision making situations. Indeed, the future works can be further extended by applying the proposed MCDM technique to the other fields which may be classified as
  • • The scholars which may be considered for defining a class of reasonable comparative techniques, not only based on the score and the accuracy functions, but also based on more comparable rules of p-ROFSs;
  • • The contributions which are based on the integration theory of p-ROFSs, specifically, those that are focusing on the aggregation operators of p-ROFSs;
  • • The studies which deal with the information measures for p-ROFSs such as distance, similarity and entropy measures, and those studies that suggest a variety of systematic transformations of information measures;
  • • Those working on the preference relations of p-ROFSs, and subsequently on the group consensus measures which are mainly divided into iterative and interactive categories;
  • • The scholars which propose fruitful classes of decision making techniques under p-rung orthopair fuzzy environment.

References

 
Atanassov, K.T. ( 1986). Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 20, 87– 96.
 
Chen, S.M., Cheng, S.H., Lan, T.C. ( 2016). Multicriteria decision making based on the TOPSIS method and similarity measures between intuitionistic fuzzy values. Information Sciences: An International Journal, 367, 279– 295.
 
Cong, B. ( 2014). Picture fuzzy sets. Journal of Computer Science and Cybernetics, 30, 409– 420.
 
Du, W.S. ( 2018). Minkowski-type distance measures for generalized orthopair fuzzy sets. International Journal of Intelligent Systems, 33, 802– 817.
 
Farhadinia, B. ( 2014). A novel method of ranking hesitant fuzzy values for multiple attribute decision-making problems. International Journal of Intelligent Systems, 29, 184– 205.
 
Farhadinia, B. ( 2016a). Determination of entropy measures for the ordinal scale-based linguistic models. Information Sciences: An International Journal, 369, 63– 79.
 
Farhadinia, B. ( 2016b). Multiple criteria decision-making methods with completely unknown weights in hesitant fuzzy linguistic term setting. Knowledge-Based Systems, 93, 135– 144.
 
Farhadinia, B., Xu, Z.S. ( 2017). Distance and aggregation-based methodologies for hesitant fuzzy decision making. Cognitive Computation, 9, 81– 94.
 
Farhadinia, B., Herrera-Viedma, E. ( 2018). Entropy measures for extended hesitant fuzzy linguistic term sets using the concept of interval-transformed hesitant fuzzy elements. International Journal of Fuzzy Systems, 20, 2122– 2134.
 
Garg, H. ( 2016). A new generalized improved score function of interval-valued intuitionistic fuzzy sets and applications in expert systems. Applied Soft Computing, 38, 988– 999.
 
Lai, Y.J., Liu, T.Y., Hwang, C.L. ( 1994). TOPSIS for MODM. European Journal of Operational Research, 76, 486– 500.
 
Liou, J.J.H., Tsai, C.Y., Lin, R.H., Tzeng, G.H. ( 2011). A modified VIKOR multiple-criteria decision making for improving domestic airlines service quality. Journal of Air Transport Management, 17, 57– 61.
 
Liu, P., Liu, J. ( 2018). Some q-rung orthopai fuzzy Bonferroni mean operators and their application to multi-attribute group decision making. International Journal of Intelligent Systems, 33, 315– 347.
 
Liu, P., Wang, P. ( 2019). Multiple-attribute decision-making based on Archimedean Bonferroni operators of q-rung orthopair fuzzy numbers. IEEE Transactions on Fuzzy Systems, 27, 834– 848.
 
Liu, P.D., Wang, P. ( 2018). Some q-rung orthopair fuzzy aggregation operators and their applications to multiple-attribute decision making. International Journal of Intelligent Systems, 33, 259– 280.
 
Peng, X., Dai, J., Garg, H. ( 2018). Exponential operation and aggregation operator for q-rung orthopair fuzzy set and their decision making method with a new score function. International Journal of Intelligent Systems, 33( 11). https://doi.org/10.1002/int.22028.
 
Si, A., Das, S., Kar, S. ( 2019). An approach to rank picture fuzzy numbers for decision making problems. Decision Making: Applications in Management and Engineering, 2, 54– 64.
 
Wei, G., Gao, H., Wei, Y. ( 2018). Some q-rung orthopair fuzzy Heronian mean operators in multiple attribute decision making. International Journal of Intelligent Systems, 33, 1426– 1458.
 
Yager, R.R. ( 2013). Pythagorean fuzzy subsets. In: Proceedings of the Joint IFSAWorld Congress and NAFIPS Annual Meeting, pp. 57– 61.
 
Yager, R.R. ( 2017). Generalized orthopair fuzzy sets. IEEE Transactions on Fuzzy Systems, 25, 1222– 1230.
 
Zadeh, L.A. ( 1965). Fuzzy set. Information and Control, 8, 338– 353.
 
Zhang, X.L., Xu, Z.S. ( 2014). Extension of topsis to multiple criteria decision making with pythagorean fuzzy sets. International Journal of Intelligent Systems, 29, 1061– 1078.
 
Zhang, F., Chen, J., Zhu, Y., Zhuang, Z., Li, J. ( 2018). Generalized score functions on interval-valued intuitionistic fuzzy sets with preference parameters for different types of decision makers and their application. Applied Intelligence. https://doi.org/10.1007/s10489-018-1184-4.
 
Zhang, F., Wang, S., Sun, J., Ye, J., Liew, G.K. ( 2019). Novel parameterized score functions on interval-valued intuitionistic fuzzy sets with three fuzziness measure indexes and their application. IEEE Access, 7, 8172– 8180.
 
Zhang, C., Liao, H., Luo, L. ( 2019). Additive consistency-based priority-generating method of q-rung orthopair fuzzy preference relation. International Journal of Intelligent Systems, 34, 2151– 2176.
 
Zhang, C., Liao, H., Luo, L., Xu, Z.S. in press. Multiplicative consistency analysis for q-rung orthopair fuzzy preference relation. International Journal of Intelligent Systems. https://doi.org/10.1002/int.22197.

Biographies

Farhadinia Bahram
https://orcid.org/0000-0003-2580-8789
bfarhadinia@qiet.ac.ir

B. Farhadinia is an associate professor at Quchan University of Technology, Iran. He has published 2 monographs, 1 chapter, and more than 50 peer-reviewed papers, many in high-quality international journals including Cognitive Computation, Knowledge-Based Systems, Soft Computing, Iranian Journal of Fuzzy Systems, Information Sciences. He is an Iranian Highly Cited Researcher since 2019.

Liao Huchang
liaohuchang@scu.edu.cn

H. Liao is a research fellow at the Business School, Sichuan University, Chengdu, China. He has published 3 monographs, 1 chapter, and more than 200 peer-reviewed papers, many in high-quality international journals including European Journal of Operational Research, Omega, IEEE Transactions on Fuzzy Systems, IEEE Transaction on Cybernetics, Information Sciences. He is a Highly Cited Researcher since 2019 and the Senior Member of IEEE since 2017.


Reading mode PDF XML

Table of contents

Copyright
© 2021 Vilnius University

Keywords
p-rung orthopair fuzzy set multiple criteria decision making score function

Metrics
since January 2020
1786

Article info
views

792

Full article
views

988

PDF
downloads

288

XML
downloads


Share


RSS