Abstract
Very recently, side-channel attacks have threatened all traditional cryptographic schemes. Typically, in traditional cryptography, private/secret keys are assumed to be completely hidden to adversaries. However, by side-channel attacks, an adversary may extract fractional content of these private/secret keys. To resist side-channel attacks, leakage-resilient cryptography is a countermeasure. Identity-based public-key system (ID-PKS) is an attractive public-key setting. ID-PKS settings not only discard the certificate requirement, but also remove the construction of the public-key infrastructure. For solving the user revocation problem in ID-PKS settings, revocable ID-PKS (RID-PKS) setting has attracted significant attention. Numerous cryptographic schemes based on RID-PKS settings have been proposed. However, under RID-PKS settings, no leakage-resilient signature or encryption scheme is proposed. In this article, we present the first leakage-resilient revocable ID-based signature (LR-RIBS) scheme with cloud revocation authority (CRA) under the continual leakage model. Also, a new adversary model of LR-RIBS schemes with CRA is defined. Under this new adversary model, security analysis is made to demonstrate that our LR-RIBS scheme with CRA is provably secure in the generic bilinear group (GBG) model. Finally, performance analysis is made to demonstrate that our scheme is suitable for mobile devices.
1 Introduction
Identity-based public-key system (ID-PKS) (Shamir,
1984; Boneh and Franklin,
2001) not only discards the certificate requirement, but also removes the construction of the public-key infrastructure. In an ID-PKS setting, there are two roles, namely, users and a private key generator (PKG). A user’s identity information is regarded as the user’s public key. The PKG employs the user’s identity information to generate the user’s associated private key. For public-key settings, user revocation mechanisms are required to revoke the misbehaving or compromised users before the intended expiration date of their public keys. Typically, a conventional public-key setting adopts the certificate revocation list (CRL) (Housley
et al.,
2002) to manage the revoked users. In such a setting, each user has a public key and the associated certificate. Before employing a user’s public key, one must validate its associated certificate while looking up the CRL to ensure that the user’s certificate was not revoked. However, ID-PKS settings do not require the usage of certificates so that the CRL mechanism cannot be employed to the ID-PKS settings.
Recently, Tseng and Tsai (
2012) proposed a revocable ID-PKS (RID-PKS) setting with a public channel. In the RID-PKS setting, a user’s private key includes two parts, namely, a secret key and a time update key. Initially, the PKG employs a user’s identity information to generate and send the associated secret key to the user using a secure channel. Also, the PKG generates the time update key by time period and the user’s identity information. Namely, for all non-revoked users, the PKG periodically generates and sends the associated time update keys to these users using a public channel. Subsequently, numerous cryptographic primitives based on RID-PKS settings were presented, such as revocable ID-based encryption (RIBE) (Tsai
et al.,
2012,
2013a) and revocable ID-based signature (RIBS) schemes (Tsai
et al.,
2013b; Hung
et al.,
2017). Furthermore, several RIBE and RIBS schemes (Li
et al.,
2015; Tseng
et al.,
2018; Jia
et al.,
2017) have been proposed to outsource the periodical generations of time update keys to a cloud revocation authority (CRA).
Quite recently, side-channel attacks have threatened all traditional cryptographic schemes because private/secret keys are assumed to be completely hidden to adversaries in traditional cryptography. By various kinds of side-channel attacks (Boneh
et al.,
1997; Kocher
et al.,
1999; Brumley and Boneh,
2005; Biham
et al.,
2008), an adversary can extract fractional content of private/secret keys participated in computation rounds. To resist side-channel attacks, leakage-resilient cryptography is a countermeasure while the design of leakage-resilient cryptographic schemes has attracted significant attention from researchers. For leakage-resilient cryptographic schemes, adversaries are allowed to extract fractional content of private/secret keys while these schemes still retain secure. However, no leakage-resilient RIBS scheme based on RID-PKS settings is proposed. In the article, our goal is to propose the first leakage-resilient RIBS (LR-RIBS) scheme.
1.1 Related Work
Here, let us briefly review some leakage-resilient encryption and signature schemes based on conventional and ID-PKS settings.
According to the amount of leaked content of private/secret keys during the life time, the leakage model has two kinds, namely, bounded leakage model (Alwen
et al.,
2009) and continual leakage model (Brakerski
et al.,
2010). In a leakage-resilient cryptographic scheme under the bounded leakage model, the overall amount of leaked content has to be limited to a ratio or a fixed bit-length of private/secret keys. On the contrary, a leakage-resilient cryptographic scheme under the continual leakage model allows adversaries to continuously extract fractional content of private/secret keys so that its overall amount of leaked content is unlimited. For security robustness, a cryptographic scheme under the continual leakage model is stronger than that under the bounded leakage model. The properties of continual leakage model have four properties as below:
-
– Bounded leakage of single observation: A cryptographic scheme typically includes several computation rounds (i.e. observations). In each computation round, an adversary can extract fractional content of private/secret keys. Namely, adversaries can select a leakage function f for each computation round and then obtain the leakage information $f(SK)$, where $SK$ denotes the involved private/secret keys and the output information of $f(SK)$ is bounded to λ bits.
-
– Only computation leakage: Adversaries are only allowed to extract fractional content of private/secret keys involved in the current computation round.
-
– Independent leakage: Any two leaked fractional contents of private/secret keys in various computation rounds are mutually independent. For achieving this property, a private/secret key must be updated before (or after) running each computation round.
-
– Overall unbounded leakage: The total amount of leakage information is overall unbounded. Indeed, by the independent leakage property, the total leakage amount of private/secret keys is not strict.
Under the continual leakage model, there are several leakage-resilient encryption and signature schemes based on the conventional public-key settings. In the generic bilinear group (GBG) model (Boneh
et al.,
2005), Kiltz and Pietrzak (
2010) presented a leakage-resilient encryption scheme that allows adversaries to continually extract fractional content of secret/private keys. In Kiltz and Pietrzak’s scheme, each user’s secret key is divided into two components. After/before performing the decryption procedure, a receiver (user) must refresh two components of her/his secret key. The key idea of refreshing employs the multiplicative blinding technique which appeared in Kiltz and Pietrzak (
2010). Based on this key idea, Galindo
et al. (
2016) presented an efficient leakage-resilient ElGamal public-key encryption scheme. Also, Galindo and Virek (
2013) proposed the first leakage-resilient signature scheme under the continual leakage model. To improve the performance of their scheme, Tang
et al. (
2014) presented a modified leakage-resilient signature scheme by employing Boneh
et al.’s short signature (Boneh
et al.,
2001).
Based on an ID-PKS setting, Brakerski
et al. (
2010) presented the first leakage-resilient ID-based encryption (LR-IBE) scheme under the continual leakage model. Subsequently, Yuen
et al. (
2012) presented an improvement on Brakerski
et al.’s scheme in terms of computational costs. under the continual leakage model, Wu
et al. (
2016) proposed the first leakage-resilient ID-based signature (LR-IBS) scheme.
1.2 Contribution and Organization
Up to date, no work has been published on leakage-resilient revocable ID-based signature (LR-RIBS) scheme. In the article, we present a new adversary model of LR-RIBS schemes with a cloud revocation authority (CRA) under the continual leakage model. In the adversary model, there are two types of adversaries, namely, Type I adversary (a curious CRA or an outsider) and Type II adversary (a revoked user). As compared with the adversary models of RIBS schemes presented in Tsai
et al. (
2013b), Hung
et al. (
2017), Jia
et al. (
2017), three new key leakage queries, namely, the key extract leak query, time key update leak query and signing leak query are added to our new adversary model. These added leak queries allow an adversary to continuously extract fractional content of private/secret keys participated in the computation rounds.
The
first LR-RIBS scheme with CRA is proposed while the revocation functionality is outsourced to the CRA. By employing Kiltz and Pietrzak’s key refreshing idea (Kiltz and Pietrzak,
2010), the proposed LR-RIBS scheme with CRA allows adversaries to continuously gain fractional content of private/secret keys so that its overall amount of leaked content is unbounded and it possesses overall unbounded leakage property. Under the new adversary model and generic bilinear group (GBG) model (Boneh
et al.,
2005), security analysis is given to show that our LR-RIBS scheme is existential unforgeability against adaptive chosen-message (UF-LR-RIBS-ACMA) attacks of both Types I and II adversaries. Finally, performance analysis and comparisons are made to demonstrate that the proposed LR-RIBS scheme requires some additional computation costs than the previously proposed RIBS schemes. The point is that the proposed LR-RIBS scheme with CRA can resist side-channel attacks. By the simulation experiences (Lynn,
2015) on a smartphone, the proposed LR-RIBS scheme with CRA is still suitable for mobile devices.
The rest of the paper is organized as follows. In Section
2, preliminaries are given. In Section
3, we define the framework and adversary model of LR-RIBS schemes with CRA. In Section
4, we propose a secure LR-RIBS scheme with CRA under the continual leakage model. Section
5 demonstrates the security analysis of the proposed LR-RIBS scheme. In Section
6, we present the performance analysis and comparisons with the previously proposed RIBS schemes. Finally, conclusions are given in Section
7.
2 Preliminaries
Several preliminaries are introduced in this section.
2.1 Bilinear groups
Let G and ${G_{T}}$ be two multiplicative cyclic groups with (large) prime order p. Let g be a generator of G. An admissible bilinear map $\hat{e}:G\times G\to {G_{T}}$ possesses the following three properties:
-
1. Non-degeneracy: $\hat{e}(g,g)\ne $1.
-
2. Bilinearity: for all r, $s\in {Z_{p}^{\ast }}$, $\hat{e}({g^{r}},{g^{s}})=\hat{e}{(g,g)^{rs}}$.
-
3. Computability: $\hat{e}{(g,g)^{rs}}$ can be computed efficiently for any r, $s\in {Z_{p}^{\ast }}$.
For the detailed properties and settings with regard to bilinear groups, please refer to Boneh and Franklin (
2001), Tsai
et al. (
2013b), Lynn (
2015), Scott (
2011).
2.2 Generic Bilinear Group Model
By extending the generic group model presented by Shoup (
1997), Boneh
et al. (
2005) introduced the generic bilinear group (GBG) model. Their GBG model is an adversary model played by adversaries and a challenger. In the GBG model, to perform various kinds of group operations, adversaries have to request the associated group oracles/queries to the challenger. Also, the challenger uses bit strings to denote group elements of
G and
${G_{T}}$. More precisely, the challenger employs two random injective functions
$\varepsilon :{Z_{p}}\to \xi $ and
${\varepsilon _{T}}:{Z_{p}}\to {\xi _{T}}$, respectively, to transform the elements of
G and
${G_{T}}$ into bit strings in
ξ and
${\xi _{T}}$. In addition, both
ξ and
${\xi _{T}}$ have
p elements and are disjoint, namely
$|\xi |=|{\xi _{T}}|=p$ and
$\xi \cap {\xi _{T}}=\phi $. The discrete logarithm problem on
G or
${G_{T}}$ will be solved if the adversary discovers a collision encoding element of
G or
${G_{T}}$.
-
– Discrete logarithm problem: Let
G and
${G_{T}}$ be two multiplicative cyclic groups of a large prime order
p. Let
g and
$\hat{e}(g,g)$ denote the generators of
G and
${G_{T}}$, respectively. Given a group element
${g^{z}}\in G$ or
$\hat{e}(g,g)$ $\in {G_{T}}$ with unknown
$z\in {Z_{p}^{\ast }}$, the discrete logarithm problem in
G and
${G_{T}}$ is that no probabilistic polynomial time (PPT) algorithm
A may obtain
z with a non-negligible probability (Boneh
et al.,
2005).
In the GBG model, there are three group operations, namely, the multiplication
${Q_{G}}$ on
G, the multiplication
${Q_{T}}$ on
${G_{T}}$, and the bilinear map
${Q_{p}}:G\times G\to {G_{T}}$, which is denoted by
$\hat{e}$ above. For any
r,
$s\in {Z_{p}^{\ast }}$, we have the following properties:
-
– ${Q_{G}}(\varepsilon (r),\varepsilon (s))\to \varepsilon (r+s\operatorname{mod} p)$.
-
– ${Q_{T}}({\varepsilon _{T}}(r),{\varepsilon _{T}}(s))\to {\varepsilon _{T}}(r+s\operatorname{mod} p)$.
-
– ${Q_{P}}(\varepsilon (r),\varepsilon (s))\to {\varepsilon _{T}}(rs\operatorname{mod} p)$.
2.3 Entropy of Leakage Content
In information theory, entropy is usually employed to measure the uncertainty of unknown private/secret values. Assume that W is a discrete random variable (i.e. secret value) and Pr[$W=w$] denotes the probability of $W=w$. The min-entropy of W is the estimation of $W=w$ with the largest probability, namely, the worst-case predictability of W. Two types of min-entropies are defined as below:
-
-
• Average conditional min-entropy of W under the condition
$Z=z$:
To measure the entropy of a finite discrete random variable (secret value) with fractional leakage content, Dodis
et al. (
2008) derived the following consequence.
Lemma 1 (See Dodis et al., 2008).
Assume that a leakage function $f:W\to {\{0,1\}^{\lambda }}$ takes as input a discrete random variable W and the maximal output bit-length is λ. Under the event $f(W)$, the average conditional min-entropy of W is ${\widetilde{H}_{\infty }}(W|f(W))\geqq {H_{\infty }}(W)-\lambda $.
By Lemma
1, Galindo and Virek (
2013) derived the following consequence to measure the probability distribution of a polynomial with multiple random variables and leakage content.
Lemma 2 (See Galindo and Virek, 2013).
Let $F\in {Z_{p}}[{W_{1}},{W_{2}},\dots ,{W_{n}}]$ be a non-zero polynomial. Its maximal output bit-length of fraction leakage content and degree are λ $(0\leqq \lambda \leqq \log p)$. and at most d, respectively. Let ${P_{i}}$ be the associated probability distributions of ${W_{i}}={w_{i}}$, for $i=1,2,\dots ,n$, that satisfy ${H_{\infty }}({P_{i}})\geqq \log p-\lambda $. Thus, we have $\Pr [F({w_{1}},{w_{2}},\dots ,{w_{n}})=0]\leqq \frac{d}{p}{2^{\lambda }}$ if ${w_{i}}\stackrel{{P_{i}}}{\longleftarrow }{Z_{p}}$ (for $i=1,2,\dots ,n$) are mutually independent. Therefore, $\Pr [F({w_{1}},{w_{2}},\dots ,{w_{n}})=0]$ is negligible if $\lambda <\log p-\omega (\log \log p)$.
3 System Architecture, Framework and Adversary Model
Here, let us present the system architecture, framework and adversary model of LR-RIBS schemes with CRA. In an LR-RIBS scheme with CRA, there are three roles, namely, PKG, CRA and users. Several notations are defined as below:
-
• SPK: the PKG’s system public key.
-
• SSK: the PKG’s system secret key.
-
• TPK: the CRA’s time public key.
-
• TSK: the CRA’s time secret key.
-
• ID: a user’s identity, where $\mathit{ID}\in {\{0,1\}^{\ast }}$.
-
• ${T_{t}}$: a time period, for $t=1,2,\dots ,z$, where z represents the number of periods.
-
• ${\mathit{UTK}_{\mathit{ID},t}}$: the time update key of the user with identity ID at period ${T_{t}}$.
-
• ${\mathit{USK}_{\mathit{ID}}}$: the secret key of the user with identity ID.
-
• msg: a message.
-
• σ: a signature value.
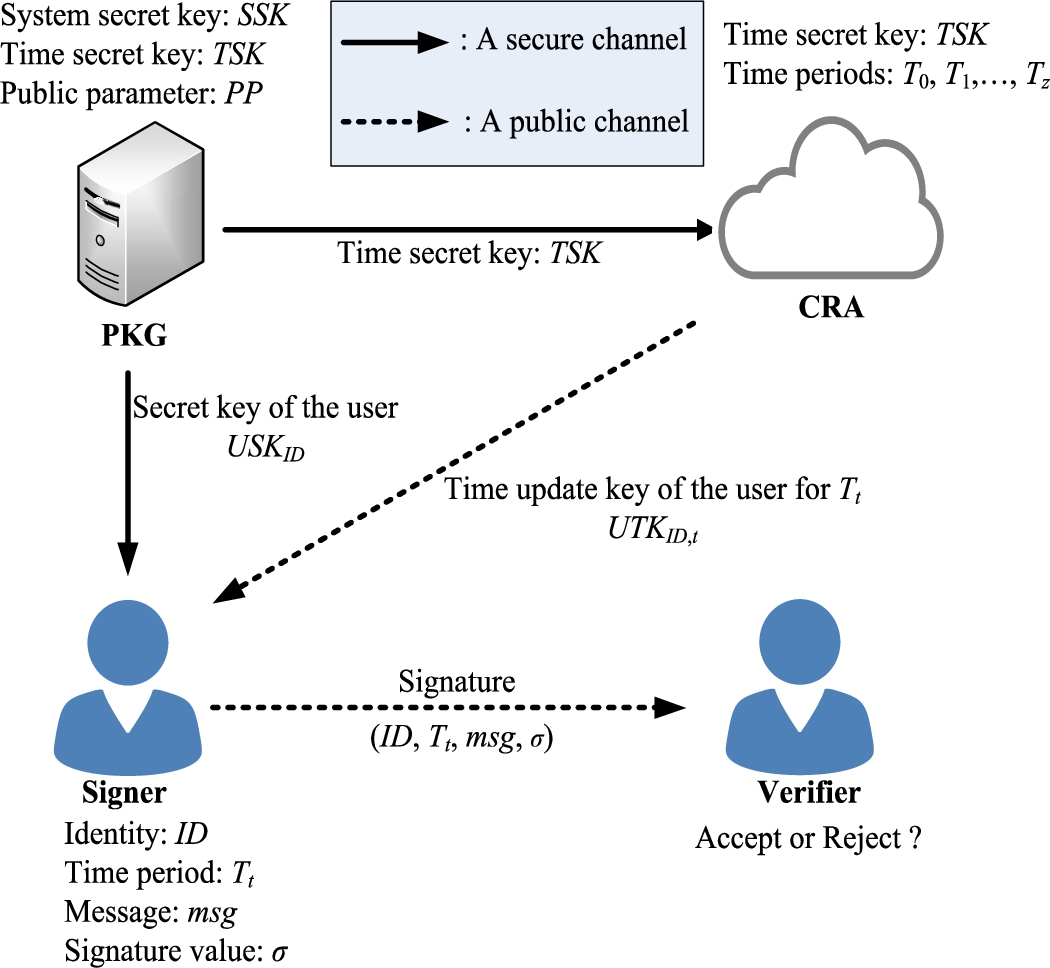
Fig. 1
The system architecture of LR-RIBS schemes with CRA.
3.1 System Architecture
The system architecture of LR-RIBS schemes with CRA is depicted in Fig.
1. Firstly, the PKG sets the system secret key
SSK, the time secret key
TSK and a total number
z of periods
${T_{0}},{T_{1}},\dots ,{T_{z}}$ while computing public parameters
PP and sending
TSK to the CRA. The PKG employs
SSK to generate the secret key
${\mathit{USK}_{\mathit{ID}}}$ of the user with identity
ID. By a secure channel, the PKG sends
${\mathit{USK}_{\mathit{ID}}}$ to the user. For non-revoked user
ID at time period
${T_{t}}$, the CRA employs
TSK to generate the time update key
${\mathit{UTK}_{\mathit{ID},t}}$. By a public channel (e.g. e-mail), the CRA sends
${\mathit{UTK}_{\mathit{ID},t}}$ to the user. Hence, a user’s private key consists of two parts, namely,
${\mathit{USK}_{\mathit{ID}}}$ and
${\mathit{UTK}_{\mathit{ID},t}}$. Suppose that the user (signer) with identity
ID at period
${T_{t}}$ would like to sign a message
msg, the signer employs
${\textit{USK}_{\mathit{ID}}}$ and
${\textit{UTK}_{\mathit{ID},t}}$ to generate a signature value
σ and sends it to a verifier.
3.2 Framework
To achieve overall unbounded leakage property (Galindo and Virek,
2013; Wu
et al.,
2016,
2018,
2019), a private/secret key must be split into two components. Additionally, each private/secret key participated in the associated algorithm is also refreshed before/after each algorithm invocation. In such a case, the PKG’s system secret key
SSK, the CRA’s time secret key
TSK and a user’s secret key
${\textit{USK}_{\mathit{ID}}}$ must, respectively, be split into two components. In the meantime, the PKG’s
SSK must be refreshed before/after performing the key extract algorithm. Also, the CRA’s
TSK and a user’s secret key
${\textit{USK}_{\mathit{ID}}}$ must be refreshed before/after performing the time key update and signing algorithms, respectively. In the following, we define the framework (syntax) of LR-RIBS schemes with CRA.
Definition 1.
An LR-RIBS scheme with CRA includes five algorithms as follows:
-
• System setup: The PKG first sets the system secret key $\mathit{SSK}=({\mathit{SSK}_{0,1}},{\mathit{SSK}_{0,2}})$, a time secret key $\mathit{TSK}=({\mathit{TSK}_{0,1}},{\mathit{TSK}_{0,2}})$ and z periods ${T_{0}},{T_{1}},\dots ,{T_{z}}$ while generating public parameters PP and sending TSK to the CRA using a secure channel. The PKG holds $\mathit{SSK}=({\mathit{SSK}_{0,1}}$, ${\mathit{SSK}_{0,2}}$) and publishes PP.
-
• Key extract: In the i-th invocation of the Key extract algorithm, the PKG refreshes $({\mathit{SSK}_{i-1,1}},{\mathit{SSK}_{i-1,2}})$ to set the current system secret key $({\mathit{SSK}_{i,1}},{\mathit{SSK}_{i,2}})$. The PKG takes as input a user’s identity ID and generates the user’s associated secret key ${\mathit{USK}_{\mathit{ID}}}$. The PKG returns ${\mathit{USK}_{\mathit{ID}}}$ to the user via a secure channel. Afterwards, the user sets her/his initial secret key ${\mathit{USK}_{\mathit{ID}}}=({\mathit{USK}_{\mathit{ID},0,1}},{\mathit{USK}_{\mathit{ID},0,2}})$.
-
• Time key update: In the j-th invocation of the Time key update algorithm, the CRA refreshes $({\mathit{TSK}_{j-1,1}},{\mathit{TSK}_{j-1,2}})$ to set the current time secret key $({\mathit{TSK}_{j,1}},{\mathit{TSK}_{j,2}})$. The CRA takes as input a user’s identity ID and a period ${T_{t}}$, and generates the user’s time update key ${\mathit{UTK}_{\mathit{ID},t}}$. The CRA sends ${\mathit{UTK}_{\mathit{ID},t}}$ to the user via a public channel.
-
• Signing: In the k-th invocation of the Signing algorithm, the user ID refreshes $({\mathit{USK}_{\mathit{ID},k-1,1}},{\mathit{USK}_{\mathit{ID},k-1,2}})$ to set her/his current secret key $({\mathit{USK}_{\mathit{ID},k,1}},{\mathit{USK}_{\mathit{ID},k,2}})$. At period ${T_{t}}$, the user ID employs her/his current secret key $({\mathit{USK}_{\mathit{ID},k,1}},{\mathit{USK}_{\mathit{ID},k,2}})$ and time update key ${\mathit{UTK}_{\mathit{ID},t}}$ to generate a signature value σ on a message msg. The user outputs a signature tuple $(\textit{ID},{T_{t}},\mathit{msg},\sigma )$.
-
• Verifying: Upon receiving $(\textit{ID},{T_{t}},\textit{msg},\sigma )$, the verifier returns either “accept” or “reject”.
3.3 Adversary Model (Security Notions)
By extending the adversary model (security notions) presented in the RIBS schemes (Tsai
et al.,
2013b; Hung
et al.,
2017; Jia
et al.,
2017), we present an adversary model of LR-RIBS schemes with CRA, which allows an adversary to extract fractional content of the private/secret keys. According to our framework, an adversary can extract fractional content of the PKG’s system secret key
$({\mathit{SSK}_{i,1}},{\mathit{SSK}_{i,2}})$ in the
i-th invocation of the
Key extract algorithm. Also, an adversary can extract fractional content of the CRA’s time secret key
$({\mathit{TSK}_{j,1}},{\mathit{TSK}_{j,2}})$ in the
j-th invocation of the
Time key update algorithm. In the
k-th invocation of the
Signing algorithm by the user
ID at period
${T_{t}}$, an adversary can extract fractional content of the user’s secret key
$({\mathit{USK}_{\mathit{ID},k,1}},{\mathit{USK}_{\mathit{ID},k,2}})$. Six leakage functions
${f_{\mathit{KE},i}}$,
${h_{\mathit{KE},i}}$,
${f_{\mathit{TKU},j}}$,
${h_{\mathit{TKU},j}}$,
${f_{S,k}}$,
${h_{S,k}}$ are employed to model the leakage abilities. More precisely, the output is in the form of three pairs (
${f_{\mathit{KE},i}}({\mathit{SSK}_{i,1}})$,
${h_{\mathit{KE},i}}({\mathit{SSK}_{i,2}})$), (
${f_{\mathit{TKU},j}}({\mathit{TSK}_{j,1}})$,
${h_{\mathit{TKU},j}}({\mathit{TSK}_{j,2}}))$ and (
${f_{S,k}}({\mathit{USK}_{\mathit{ID},k,1}})$,
${h_{S,k}}({\mathit{USK}_{\mathit{ID},k,2}})$) to indicate, respectively, the fractional content of (
${\mathit{SSK}_{i,1}}$,
${\mathit{SSK}_{i,2}}$), (
${\mathit{TSK}_{j,1}}$,
${\mathit{TSK}_{j,2}}$) and (
${\mathit{USK}_{\mathit{ID},k,1}}$,
${\mathit{USK}_{\mathit{ID},k,2}}$). Also, we require that the output bit-string lengths of the six leakage functions are at most
λ. For brevity, we introduce the following notation which will be used in the sequel:
-
– $\varLambda {f_{\mathit{KE},i}}={f_{\mathit{KE},i}}({\mathit{SSK}_{i,1}})$.
-
– $\varLambda {h_{\mathit{KE},i}}={h_{\mathit{KE},i}}({\mathit{SSK}_{i,2}})$.
-
– $\varLambda {f_{\mathit{TKU},j}}={f_{\mathit{TKU},j}}({\mathit{TSK}_{j,1}})$.
-
– $\varLambda {h_{\mathit{TKU},j}}={h_{\mathit{TKU},j}}({\mathit{TSK}_{j,2}})$.
-
– $\varLambda {f_{S,k}}={f_{S,k}}({\mathit{USK}_{\mathit{ID},k,1}})$.
-
– $\varLambda {h_{S,k}}={h_{S,k}}({\mathit{USK}_{\mathit{ID},k,2}})$.
In the adversary model of LR-RIBS schemes with CRA, there are two types of adversaries:
-
• Type I adversary ${A_{I}}$ (a curious CRA or an outsider): ${A_{I}}$ denotes a curious CRA or an outsider. ${A_{I}}$ is allowed to acquire the time update key ${\mathit{UTK}_{\mathit{ID},t}}$ for any user ID and period ${T_{t}}$. Meanwhile, ${A_{I}}$ can acquire the secret key ${\mathit{USK}_{\mathit{ID}}}$ for any ID, except for the target identity ${\mathit{ID}^{\ast }}$. In addition, ${A_{I}}$ can extract fractional content of the target user’s secret key ${\mathit{USK}_{{\mathit{ID}^{\ast }}}}$ in the $Signing$ algorithm and the PKG’s system secret key SSK in the Key extract algorithm.
-
• Type II adversary ${A_{\mathit{II}}}$ (a revoked user): ${A_{\mathit{II}}}$ denotes the adversary who was a legal user with identity ${\mathit{ID}^{\ast }}$ and has been revoked at period ${T_{t}^{\ast }}$. In such a case, ${A_{\mathit{II}}}$ is allowed to acquire the secret key ${\mathit{USK}_{\mathit{ID}}}$ and time update key ${\mathit{UTK}_{\mathit{ID},t}}$ for any ID and ${T_{t}}$. But, ${A_{\mathit{II}}}$ is disallowed to acquire the time update key ${\mathit{UTK}_{\mathit{ID},{t^{\ast }}}}$ for the target identity ${\mathit{ID}^{\ast }}$ at period ${T_{t}^{\ast }}$. In addition, ${A_{\mathit{II}}}$ can extract fractional content of the CRA’s time secret key TSK in the Time key update algorithm.
The following security game
${G_{\mathit{LR}\text{-}\mathit{RIBS}}}$ is used to model the adversary model (security notions) of LR-RIBS schemes with CRA.
Definition 2 (${G_{\mathit{LR}\textit{-}\mathit{RIBS}}}$).
For the LR-RIBS scheme with CRA, the game
${G_{\mathit{LR}\text{-}\mathit{RIBS}}}$ is used to model the interactions between an adversary
A (
${A_{I}}$ or
${A_{\mathit{II}}})$ and a challenger
C. It is said that the LR-RIBS scheme with CRA is existential unforgeability against adaptive chosen-message attacks (UF-LR-RIBS-ACMA) if no probabilistic polynomial-time (PPT) adversary may win
${G_{\mathit{LR}\text{-}\mathit{RIBS}}}$ with a non-negligible probability. Three phases of
${G_{\mathit{LR}\text{-}\mathit{RIBS}}}$ are presented as below:
-
– Setup phase. The challenger
C performs the
System setup algorithm in Definition
1 to set a system secret key
$\mathit{SSK}=({\mathit{SSK}_{0,1}},{\mathit{SSK}_{0,2}})$, a time secret key
$\mathit{TSK}=({\mathit{TSK}_{0,1}},{\mathit{TSK}_{0,2}})$ and a total number
z of periods
${T_{0}},{T_{1}},\dots ,{T_{z}}$. Meanwhile,
C sets and publishes public parameters
PP. In addition, by a secure channel,
C sends the time secret key
TSK to the CRA. Also, if
A is a Type I adversary, the time secret key
TSK is sent to
A.
-
– Query phase. The adversary A can request the following queries to C adaptively.
-
• Key extract query (ID): Upon receiving a user’s ID, C generates and sends the user’s corresponding secret key to A.
-
• Key extract leak query $(i,{f_{\mathit{KE},i}},{h_{\mathit{KE},i}})$: Upon receiving two leakage functions ${f_{\mathit{KE},i}}$ and ${h_{\mathit{KE},i}}$, C computes the fractional leakage content $\varLambda {f_{\mathit{KE},i}}$ and $\varLambda {h_{\mathit{KE},i}}$ of the PKG’s system secret key $({\mathit{SSK}_{i,1}},{\mathit{SSK}_{i,2}})$. Afterwards, C sends $\varLambda {f_{\mathit{KE},i}}$ and $\varLambda {h_{\mathit{KE},i}}$ to A. For the i-th Key extract query, A is allowed to request the Key extract leak query only once.
-
• Time key update query $(\mathit{ID},{T_{t}})$: Upon receiving a user’s ID and a period ${T_{t}}$, C generates and sends the user’s time update key ${\mathit{UTK}_{\mathit{ID},t}}$ to A.
-
• Time key update leak query $(j,{f_{\mathit{TKU},j}},{h_{\mathit{TKU},j}})$: Upon receiving two leakage functions ${f_{\mathit{TKU},j}}$ and ${h_{\mathit{TKU},j}}$, C computes the fractional leakage content $\varLambda {f_{\mathit{TKU},j}}$ and $\varLambda {h_{\mathit{TKU},j}}$ of the CRA’s time secret key (${\mathit{TSK}_{j,1}}$, ${\mathit{TSK}_{j,2}}$). Afterwards, C sends $\varLambda {f_{\mathit{TKU},j}}$ and $\varLambda {h_{\mathit{TKU},j}}$ to A. For the j-th Time key update query, A is allowed to request the Time key update leak query only once.
-
• Signing query $(\mathit{ID},{T_{t}},\mathit{msg})$: Upon receiving a message $\mathit{msg}$ and a user’s ID at period ${T_{t}}$, C generates a signature value σ and returns (ID, ${T_{t}}$, msg, σ) to A.
-
• Signing leak query (ID, k, ${f_{S,k}}$, ${h_{S,k}}$): Upon receiving two leakage functions ${f_{S,k}}$ and ${h_{S,k}}$, C computes the fraction leakage content $\varLambda {f_{S,k}}$ and $\varLambda {h_{S,k}}$ of the signer’s secret key (${\mathit{USK}_{\mathit{ID},k,1}}$, ${\mathit{USK}_{\mathit{ID},k,2}}$), and returns $\varLambda {f_{S,k}}$ and $\varLambda {h_{S,k}}$ to A. In the k-th Signing query requested by the user $\mathit{ID}$, A is allowed to issue the Signing leak query only once.
-
– Forgery phase. The adversary A outputs a signature tuple $({\mathit{ID}^{\ast }},{T_{t}^{\ast }},{\mathit{msg}^{\ast }},{\sigma ^{\ast }})$ and A wins ${G_{\mathit{LR}\text{-}\mathit{RIBS}}}$ if the following conditions hold.
-
(1) If A is a Type I adversary (a curious CRA or an outsider), the Key extract query on ${\mathit{ID}^{\ast }}$ cannot be requested.
-
(2) If A is a Type II adversary (a revoked user), the Time key update query on (${\mathit{ID}^{\ast }}$, ${T_{t}^{\ast }}$) cannot be requested.
-
(3) The Signing query on (${\mathit{ID}^{\ast }}$, ${T_{t}^{\ast }}$, ${\mathit{msg}^{\ast }}$) cannot be requested.
-
(4) The output of the Verifying algorithm on (${\mathit{ID}^{\ast }}$, ${T_{t}^{\ast }}$, ${\mathit{msg}^{\ast }}$, ${\sigma ^{\ast }}$) is “accept”.
4 The Proposed LR-RIBS Scheme with CRA
Here, let us present the first LR-RIBS scheme with CRA that consists of five algorithms as below:
-
– System setup: The PKG runs the System setup algorithm to choose two groups $G=\langle g\rangle $ and ${G_{T}}=\langle \hat{e}(g,g)\rangle $ of a large prime order p. The algorithm sets a total number z of periods ${T_{0}},{T_{1}},\dots ,{T_{z}}$. Moreover, the algorithm performs the following steps to compute the system secret key $\textit{SSK}=({\textit{SSK}_{0,1}},{\textit{SSK}_{0,2}})$, the time secret key $\textit{TSK}=({\textit{TSK}_{0,1}},{\textit{TSK}_{0,2}})$ and public parameters PP.
-
(1) Choose a random integer $\alpha \in {Z_{p}^{\ast }}$, and compute the system secret key SSK = ${g^{\alpha }}$ and the system public key $\textit{SPK}=\hat{e}(g,{g^{\alpha }})$. Also, choose an integer $\alpha \in {Z_{p}^{\ast }}$ at random, and compute the initial system secret key $({\textit{SSK}_{0,1}},{\textit{SSK}_{0,2}})=({g^{\alpha }},\mathit{SSK}\cdot {g^{-a}})$.
-
(2) Choose a random integer $\beta \in {Z_{p}^{\ast }}$, and set the time secret key TSK = ${g^{\beta }}$ and time public key TPK = $\hat{e}(g,{g^{\beta }})$.
-
(3) Choose six random integers u, v, w, x, y, $z\in {Z_{p}^{\ast }}$, and set $U={g^{u}}$, $V={g^{v}}$, $W={g^{w}}$, $X={g^{x}}$, $Y={g^{y}}$ and $Z={g^{z}}$.
-
(4) Set $\textit{PP}=(p,G,{G_{T}},\hat{e},g,\textit{SPK},\textit{TPK},U,V,W,X,Y,Z)$.
-
(5) Finally, the PKG holds $({\textit{SSK}_{0,1}},{\textit{SSK}_{0,2}})$ and publishes PP while sending TSK to the CRA via a secure channel. Afterwards, the CRA selects a random integer $b\in {Z_{p}^{\ast }}$, and uses TSK to set the initial time secret key $({\textit{TSK}_{0,1}},{\textit{TSK}_{0,2}})=({g^{b}},\mathit{TSK}\cdot {g^{-b}})$.
-
– Key extract: In the i-th invocation of the Key extract algorithm, the PKG sets the current system secret key $({\textit{SSK}_{i,1}},{\textit{SSK}_{i,2}})$ by refreshing $({\textit{SSK}_{i-1,1}},{\textit{SSK}_{i-1,2}})$. Afterwards, the PKG takes as input a user’s identity ID and carries out the following steps:
-
(1) Choose a random integer $a\in {Z_{p}^{\ast }}$, and update the PKG’s system secret key $({\textit{SSK}_{i,1}},{\textit{SSK}_{i,2}})=({\textit{SSK}_{i-1,1}}\cdot {g^{a}},{\textit{SSK}_{i-1,2}}\cdot {g^{-a}})$.
-
(2) Choose a random integer $\gamma \in {Z_{p}^{\ast }}$, and compute ${\textit{QK}_{\mathit{ID}}}={g^{\gamma }}$.
-
(3) Compute $\textit{TID}=\mathit{STID}\hspace{0.3em}(\operatorname{mod} \hspace{0.3em}p)$, where STID is the integer value of the bit string ${\mathit{IDQK}_{\mathit{ID}}}$. And compute the temporary information ${\mathit{TI}_{\mathit{KE}}}={\textit{SSK}_{i,1}}\cdot {(U\cdot {V^{\mathit{TID}}})^{\gamma }}$ and the user’s secret key USK $\textit{ID}={\textit{SSK}_{i,2}}\cdot {\mathit{TI}_{\mathit{KE}}}$.
-
(4) Finally, by a secure channel, the PKG sends ${\textit{USK}_{\mathit{ID}}}$ and ${\mathit{QK}_{\mathit{ID}}}$ to the user. Upon receiving ${\textit{USK}_{\mathit{ID}}}$ and ${\mathit{QK}_{\mathit{ID},1}}$, the user randomly selects an integer $c\in {Z_{p}^{\ast }}$, and sets the user’s initial secret key $({\textit{USK}_{\mathit{ID},0,1}},{\textit{USK}_{\mathit{ID},0,2}})=({g^{c}},{\textit{USK}_{\mathit{ID}}}\cdot {g^{-c}})$.
-
– Time key update: In the j-th invocation of the Time key update algorithm, the CRA sets the current time secret key $({\textit{TSK}_{j,1}},{\textit{TSK}_{j,2}})$ by refreshing (${\textit{TSK}_{j-1,1}}$, ${\textit{TSK}_{j-1,2}}$). Afterwards, the CRA takes as input a user’s identity ID and a period ${T_{t}}$, and carries out the following steps:
-
(1) Choose a random integer $b\in {Z_{p}^{\ast }}$, and update the CRA’s current time secret key $({\textit{TSK}_{i,1}},{\textit{TSK}_{i,2}})=({\textit{TSK}_{i-1,1}}\cdot {g^{b}},{\textit{TSK}_{i-1,2}}\cdot {g^{-b}})$.
-
(2) Randomly select an integer $\eta \in {Z_{p}^{\ast }}$, and compute ${\mathit{QTK}_{\mathit{ID},t}}={g^{\eta }}$.
-
(3) Compute $\mathit{TTD}=\mathit{STTD}\hspace{0.3em}(\operatorname{mod} \hspace{0.3em}p)$, where $\mathit{STTD}$ is the integer value of the bit string $\textit{ID}||{T_{t}}||{\mathit{QTK}_{\mathit{ID},t}}$. And compute the temporary information ${\mathit{TI}_{\mathit{TKU}}}={\textit{TSK}_{j,1}}\cdot {(W\cdot {X^{\mathit{TTD}}})^{\eta }}$ and the user’s time secret key ${\textit{UTK}_{\mathit{ID},t}}={\textit{TSK}_{j,2}}\cdot {\mathit{TI}_{\mathit{TKU}}}$.
-
(4) Finally, by a secure channel, the CRA sends ${\textit{UTK}_{\mathit{ID},t}}$ and ${\mathit{QTK}_{\mathit{ID},t}}$ to the user.
-
– Signing: For the k-th invocation of the Signing algorithm, the user ID sets her/his current secret key (${\textit{USK}_{\mathit{ID},k,1}}$, ${\textit{USK}_{\mathit{ID},k,2}}$) by refreshing (${\textit{USK}_{\mathit{ID},k-1,1}}$, ${\textit{USK}_{\mathit{ID},k-1,2}}$). At period ${T_{t}}$, the user employs her/his current secret key (${\textit{USK}_{\mathit{ID},k,1}}$, ${\textit{USK}_{\mathit{ID},k,2}}$) and time update key ${\textit{UTK}_{\mathit{ID},t}}$ to output a signature tuple $(\textit{ID},{T_{t}},\mathit{msg},\sigma )$ with $\sigma =({\sigma _{1}}={\mathit{QK}_{\mathit{ID}}},{\sigma _{2}}={\mathit{QTK}_{\mathit{ID},t}},{\sigma _{3}},{\sigma _{4}})$ by carrying out the following steps:
-
(1) Choose a random integer $c\in {Z_{p}^{\ast }}$, and update the signer’s secret key $({\textit{USK}_{\mathit{ID},k,1}},{\textit{USK}_{\mathit{ID},k,2}})=({\textit{USK}_{\mathit{ID},k-1,1}}\cdot {g^{c}},{\textit{USK}_{\mathit{ID},k,2}}\cdot {g^{-c}})$.
-
(2) Choose a random integer $\delta \in {Z_{p}^{\ast }}$, and compute ${\sigma _{3}}={g^{\delta }}$, the temporary information ${\mathit{TI}_{S}}={\textit{USK}_{\mathit{ID},k,1}}\cdot {\textit{UTK}_{\mathit{ID},t}}\cdot {(Y\cdot {Z^{\mathit{msg}}})^{\delta }}$ and ${\sigma _{4}}={\textit{USK}_{\mathit{ID},k,2}}\cdot {\mathit{TI}_{S}}$.
-
(3) Set the signature tuple ($\textit{ID},{T_{t}},\mathit{msg},\sigma $) with $\sigma =({\sigma _{1}}={\mathit{QK}_{\mathit{ID}}},{\sigma _{2}}={\mathit{QTK}_{\mathit{ID},t}},{\sigma _{3}},{\sigma _{4}})$.
-
– Verifying: For a signature tuple $(\textit{ID},{T_{t}},\mathit{msg},\sigma =({\sigma _{1}},{\sigma _{2}},{\sigma _{3}},{\sigma _{4}}))$, the verifier compute $\mathit{TID}=\mathit{STID}\hspace{0.3em}(\operatorname{mod} \hspace{0.3em}p)$ and $\textit{TTD}=\mathit{STTD}\hspace{0.3em}(\operatorname{mod} \hspace{0.3em}p)$, where STID and STTD are the integer values of the bit strings $\textit{ID}||{\sigma _{1}}$ and $\textit{ID}||{T_{t}}||{\sigma _{2}}$, respectively. The verifier outputs “accept” if the verifying equality $\hat{e}(g,{\sigma _{4}})=\textit{SPK}\cdot \textit{TPK}\cdot \hat{e}({\sigma _{1}},U\cdot {V^{\mathit{TID}}})\cdot \hat{e}({\sigma _{2}},W\cdot {X^{\mathit{TTD}}})\cdot \hat{e}({\sigma _{3}},Y\cdot {Z^{\mathit{msg}}})$ holds; otherwise outputs “reject”.
Here, let us discuss the correctness of the verifying equality. By the key refreshing procedures of those secret values employed in the proposed scheme, we have:
-
• $\textit{SSK}={\textit{SSK}_{0,1}}\cdot {\textit{SSK}_{0,2}}=\cdots ={\textit{SSK}_{i-1,1}}\cdot {\textit{SSK}_{i-1,2}}={\textit{SSK}_{i,1}}\cdot {\textit{SSK}_{i,2}}$.
-
• $\textit{TSK}={\textit{TSK}_{0,1}}\cdot {\textit{TSK}_{0,2}}=\cdots ={\textit{TSK}_{j-1,1}}\cdot {\textit{TSK}_{j-1,2}}={\textit{TSK}_{j,1}}\cdot {\textit{TSK}_{j,2}}$.
-
• ${\textit{USK}_{\mathit{ID}}}={\textit{USK}_{\mathit{ID},0,1}}\cdot {\textit{USK}_{\mathit{ID},0,2}}=\cdots ={\textit{USK}_{\mathit{ID},k-1,1}}\cdot {\textit{USK}_{\mathit{ID},k-1,2}}={\textit{USK}_{\mathit{ID},k,1}}\cdot {\textit{USK}_{\mathit{ID},k,2}}$.
Hence, the equality is verified by
5 Security Analysis
Let us analyse the security of our LR-RIBS scheme with CRA. By the adversary model (i.e. security game
${G_{\mathit{LR}\text{-}\mathit{RIBS}}}$) of LR-RIBS schemes with CRA, there are two types of adversaries. In the GBG model, Theorem
1 demonstrates that our scheme is provably secure against Type I adversary. In Theorem
2, we prove that our scheme is also provably secure against Type II adversary.
Theorem 1.
In the GBG model, our LR-RIBS scheme with CRA possesses existential unforgeability under the UF-LR-RIBS-ACMA attack of Type I adversary (a curious CRA or an outsider).
Proof.
Let
${A_{I}}$ denote a Type I adversary in the security game
${G_{\mathit{LR}\text{-}\mathit{RIBS}}}$ played with a challenger
C.
${A_{I}}$ is allowed to request all queries in the security game
${G_{\mathit{LR}\text{-}\mathit{RIBS}}}$ while the number of queries issued by
${A_{I}}$ is at most
q times. In the GBG model introduced in earlier section, there are three group queries (oracles)
${Q_{G}}$,
${Q_{T}}$ and
${Q_{p}}$. In such a case, the challenger
C also responses the queries
${Q_{G}}$,
${Q_{T}}$ and
${Q_{p}}$ issued by the adversary
${A_{I}}$, where these queries are provided in the
Query phase of
${G_{\mathit{LR}\text{-}\mathit{RIBS}}}$. For
${G_{\mathit{LR}\text{-}\mathit{RIBS}}}$ on the proposed LR-RIBS scheme with CRA, three phases (
Setup,
Query and
Forgery) are presented as below:
-
– Setup phase: The challenger
C carries out the
System Setup algorithm of our scheme to generate
SSK,
TSK, a total number
z of periods
${T_{0}},{T_{1}},\dots ,{T_{z}}$ and
$\textit{PP}=(p,G,{G_{T}},\hat{e},g,\textit{SPK},\textit{TPK},U,V,W,X,Y,Z)$. Additionally, C constructs four lists
${L_{G}}$,
${L_{T}}$,
${L_{K}}$ and
${L_{\mathit{TK}}}$ to record the related parameters and results of the queries issued by the adversary.
-
• ${L_{G}}$ and
${L_{T}}$ are, respectively, employed to record all group elements of
G and
${G_{T}}$.
-
(1) ${L_{G}}$ contains pairs of the form $(\varXi {G_{m,n,r}},\xi {G_{m,n,r}})$, where $\varXi {G_{m,n,r}}$ represents an element (multivariate polynomial) in G and $\xi {G_{m,n,r}}$ is the associated bit string. Here, m and n, respectively, denote the query type and the n-th query, and the index r represents the r-th element of G. Initially, nine pairs $(\varXi g,\xi {G_{I,1,1}})$, $(\varXi U,\xi {G_{I,1,2}})$, $(\varXi V,\xi {G_{I,1,3}})$, $(\varXi W,\xi {G_{I,1,4}})$, $(\varXi X,\xi {G_{I,1,5}})$, $(\varXi Y,\xi {G_{I,1,6}})$, $(\varXi Z,\xi {G_{I,1,7}})$, $(\varXi \mathit{SSK},\xi {G_{I,1,8}})$ and $(\varXi \mathit{TSK},\xi {G_{I,1,9}})$ are recorded in ${L_{G}}$.
-
(2) ${L_{T}}$ contains pairs of the form $(\varXi {T_{m,n,r}},\xi {T_{m,n,r}})$, where $(\varXi {T_{m,n,r}}$ represents an element (multivariate polynomial) in $G/{G_{T}}$ and $\xi {G_{m,n,r}}$ is the associated bit string. The meanings of the indices m, n and r are the same with those in ${L_{G}}$. Initially, two pairs $(\varXi \mathit{SPK},\xi {T_{I,1,1}})$ and $(\varXi \mathit{TPK},\xi {T_{I,1,2}})$ are recorded in ${L_{T}}$, where $\varXi \mathit{SPK}=\varXi g\cdot \varXi \mathit{SSK}$ and $\varXi \mathit{TPK}=\varXi g\cdot \varXi \mathit{TSK}$.
It is worth mentioning that
C employs two rules to respond the transformation request as below:
-
(1) When C receives $\varXi {G_{m,n,r}}/\varXi {T_{m,n,r}}$, C looks for $(\varXi {G_{m,n,r}},\xi {G_{m,n,r}})/(\varXi {T_{m,n,r}},\xi {T_{m,n,r}})$ in ${L_{G}}/{L_{T}}$. If so, C returns the associated bit string $\xi {G_{m,n,r}}/\xi {T_{m,n,r}}$. Otherwise, C randomly selects a distinct bit string $\xi {G_{m,n,r}}/\xi {T_{m,n,r}}$ and returns it. Finally, C adds $(\varXi {G_{m,n,r}},\xi {G_{m,n,r}})/(\varXi {T_{m,n,r}},\xi {T_{m,n,r}})$ in ${L_{G}}/{L_{T}}$.
-
(2) When C receives $\xi {G_{m,n,r}}/\xi {T_{m,n,r}}$ in ${L_{G}}/{L_{T}}$, C returns the associated multivariate polynomial $\varXi {G_{m,n,r}}/\varXi {T_{m,n,r}}$ if it is found. Otherwise, C terminates the game.
-
• ${L_{K}}$ contains tuples of the form $(\textit{ID}$, $\varXi {\textit{USK}_{\mathit{ID}}}$, $\varXi {\mathit{QK}_{\mathit{ID}}}$), where the multivariate polynomials $\varXi {\textit{USK}_{\mathit{ID}}}$ and $\varXi {\mathit{QK}_{\mathit{ID}}}$, respectively, denote the user’s ${\textit{USK}_{\mathit{ID}}}$ and ${\mathit{QK}_{\mathit{ID}}}$ in the Key extract phase.
-
• ${L_{\mathit{TK}}}$ contains tuples of the form (ID, ${T_{t}}$, $\varXi {\textit{UTK}_{\mathit{ID},t}}$, $\varXi {\mathit{QTK}_{\mathit{ID},t}}$), where the multivariate polynomials $\varXi {\textit{UTK}_{\mathit{ID},t}}$ and $\varXi {\mathit{QTK}_{\mathit{ID},t}}$, respectively, denote the user’s ${\textit{UTK}_{\mathit{ID},t}}$ and ${\mathit{QTK}_{\mathit{ID},t}}$ in the Time key update phase.
Finally,
C sends these public parameters
$\varXi g$,
$\varXi U$,
$\varXi V$,
$\varXi W$,
$\varXi X$,
$\varXi Y$,
$\varXi Z$,
$\varXi \mathit{SPK}$ and
$\varXi \mathit{TPK}$ to
${A_{I}}$.
-
– Query phase: ${A_{I}}$ can request the following queries to C adaptively.
-
• Group query ${Q_{G}}(\xi {G_{Q,i,1}},\xi {G_{Q,i,2}},OP)$: Upon receiving the i-th ${Q_{G}}$ with a pair of bit strings ($\xi {G_{Q,i,1}}$, $\xi {G_{Q,i,2}}$) and an $\mathit{OP}$ operation, C carries out the following steps:
-
(1) Transform $\xi {G_{Q,i,1}}$ and $\xi {G_{Q,i,2}}$, respectively, to gain the corresponding polynomials $\varXi {G_{Q,i,1}}$ and $\varXi {G_{Q,i,2}}$ in ${L_{G}}$.
-
(2) Compute the resulting polynomial $\varXi {G_{Q,i,3}}=\varXi {G_{Q,i,1}}+\varXi {G_{Q,i,2}}$ if $\mathit{OP}$ = “multiplication”, and $\varXi {G_{Q,i,3}}=\varXi {G_{Q,i,1}}-\varXi {G_{Q,i,2}}$ if $\mathit{OP}$ = “division”.
-
(3) Transform and return the bit string $\xi {G_{Q,i,3}}$ of $\varXi {G_{Q,i,3}}$.
-
• Group query ${Q_{T}}(\xi {T_{Q,i,1}},\xi {T_{Q,i,2}},\textit{OP})$: Upon receiving the i-th ${Q_{T}}$ with a pair of bit strings ($\xi {T_{Q,i,1}}$, $\xi {T_{Q,i,2}}$) and an $\mathit{OP}$ operation, C carries out the similar steps with ${Q_{G}}$ and returns the bit string $\xi {T_{Q,i,3}}$.
-
• Pairing query ${Q_{P}}(\xi {G_{P,i,1}},\xi {G_{P,i,2}})$: Upon receiving the i-th ${Q_{P}}$ with a pair of bit strings ($\xi {G_{P,i,1}}$, $\xi {G_{P,i,2}}$), C carries out the following steps:
-
(1) Transform $\xi {G_{P,i,1}}$ and $\xi {G_{P,i,2}}$, respectively, to gain the corresponding polynomials $\varXi {G_{P,i,1}}$ and $\varXi {G_{P,i,2}}$.
-
(2) Compute the resulting polynomial $\varXi {T_{P,i,1}}=\varXi {G_{P,i,1}}\cdot \varXi {G_{P,i,2}}$.
-
(3) Transform and return the bit string $\xi {T_{P,i,1}}$ of $\varXi {T_{P,i,1}}$.
-
• Key extract query (ID): Upon receiving the i-th Key extract query with a user’s ID, C looks for (ID, $\varXi {\textit{USK}_{\mathit{ID}}}$, $\varXi {\mathit{QK}_{\mathit{ID}}}$) in ${L_{K}}$. If so, C returns two corresponding bit strings $\xi {\textit{USK}_{\mathit{ID}}}$ of $\varXi {\textit{USK}_{\mathit{ID}}}$ and $\xi {\mathit{QK}_{\mathit{ID}}}$ of $\varXi {\mathit{QK}_{\mathit{ID}}}$ to ${A_{I}}$. Otherwise, C carries out the following steps:
-
(1) Choose a new variate $\varXi T{G_{\mathit{KE},i,1}}$ in G.
-
(2) Set the polynomial $\varXi {\mathit{QK}_{\mathit{ID}}}=\varXi T{G_{\mathit{KE},i,1}}$ and $\varXi \mathit{TID}=\textit{ID}||\varXi {\mathit{QK}_{\mathit{ID}}}$.
-
(3) Compute the user’s secret key $\varXi {\textit{USK}_{\mathit{ID}}}=\varXi \mathit{SSK}+\varXi {\mathit{TG}_{\mathit{KE},i,1}}\cdot (\varXi U+\varXi V\cdot \varXi \mathit{TID})$ while adding (ID, $\varXi {\textit{USK}_{\mathit{ID}}}$, $\varXi {\mathit{QK}_{\mathit{ID}}}$) in ${L_{K}}$.
-
(4) Transform and return two corresponding bit strings $\xi {\textit{USK}_{\mathit{ID}}}$ of $\varXi {\textit{USK}_{\mathit{ID}}}$ and $\xi {\mathit{QK}_{\mathit{ID}}}$ of $\varXi {\mathit{QK}_{\mathit{ID}}}$ to ${A_{I}}$.
-
• Key extract leak query $(i,{f_{\mathit{KE},i}},{h_{\mathit{KE},i}})$: Upon receiving the i-th Key extract leak query with two leakage functions ${f_{\mathit{KE},i}}$ and ${h_{\mathit{KE},i}}$, C returns the fraction leakage content $\varLambda {f_{\mathit{KE},i}}$ and $\varLambda {h_{\mathit{KE},i}}$ to ${A_{I}}$, where $\varLambda {f_{\mathit{KE},i}}={f_{\mathit{KE},i}}({\textit{SSK}_{i,1}},a,\gamma )$ and $\varLambda {h_{\mathit{KE},i}}={h_{\mathit{KE},i}}({\textit{SSK}_{i,2}},a,\gamma ,{\mathit{TI}_{\mathit{KE}}})$. Note that in the i-th Key extract query, ${A_{I}}$ is allowed to issue the Key extract leak query only once.
-
• Time key update query (
ID,
${T_{t}}$): In the
j-th
Time key update query with
ID and
${T_{t}}$,
C looks for (
ID,
${T_{t}}$,
$\varXi {\textit{UTK}_{\mathit{ID},t}}$,
$\varXi {\mathit{QTK}_{\mathit{ID},t}}$) in
${L_{\mathit{TK}}}$. If so,
C returns two corresponding bit strings
$\xi {\textit{UTK}_{\mathit{ID},t}}$ and
$\xi {\mathit{QTK}_{\mathit{ID},t}}$ to
${A_{I}}$. Otherwise,
C carries out the following steps:
-
(1) Choose a new variate $\varXi T{G_{\mathit{TKU},\textit{ID},t,1}}$ in G.
-
(2) Set the polynomial $\varXi {\mathit{QTK}_{\mathit{ID},t}}=\varXi T{G_{\mathit{TKU},\textit{ID},t,1}}$ and $\varXi \mathit{TTD}=\textit{ID}||{T_{t}}||\varXi {\mathit{QTK}_{\mathit{ID},t}}$.
-
(3) Set the user’s time update key $\varXi {\textit{UTK}_{\mathit{ID},t}}=\varXi \mathit{TSK}+\varXi T{G_{\mathit{TKU},\textit{ID},t,1}}\cdot (\varXi W+\varXi X\cdot \varXi TT{D_{\mathit{ID},t}})$ while adding $(\textit{ID},{T_{t}},\varXi {\textit{UTK}_{\mathit{ID},t}},\varXi {\mathit{QTK}_{\mathit{ID},t}})$ in ${L_{T}}K$.
-
(4) Transform and return two corresponding bit strings $\xi {\textit{UTK}_{\mathit{ID},t}}$ of $\varXi {\textit{UTK}_{\mathit{ID},t}}$ and $\xi {\mathit{QTK}_{\mathit{ID},t}}$ of $\varXi {\mathit{QTK}_{\mathit{ID},t}}$ to ${A_{I}}$.
Note that
${A_{I}}$ is a curious CRA or an outsider who can gain the user’s time update key by the
Time key update query. Hence
${A_{I}}$ has no need to request the
Time key update leak query.
-
• Singing query (ID, ${T_{t}}$, msg): Upon receiving the k-th Signing query of the user ID, by taking the period ${T_{t}}$ and the message msg as input, C carries out the following steps:
-
(1) By ID, look for $(\textit{ID},\varXi {\textit{USK}_{\mathit{ID}}},\varXi {\mathit{QK}_{\mathit{ID}}})$ in ${L_{K}}$.
-
(2) By ID and ${T_{t}}$, look for the time update key $(\textit{ID},{T_{t}},\varXi {\textit{UTK}_{\mathit{ID},t}},\varXi {\mathit{QTK}_{\mathit{ID},t}})$ in ${L_{\mathit{TK}}}$.
-
(3) Set $\varXi {\sigma _{1}}=\varXi {\mathit{QK}_{\mathit{ID}}}$ and $\varXi {\sigma _{2}}=\varXi {\mathit{QTK}_{\mathit{ID},t}}$.
-
(4) Choose a new variate $\varXi T{G_{S,k,1}}$ in G and set $\varXi {\sigma _{3}}=\varXi T{G_{S,k,1}}$.
-
(5) Set $\varXi {\sigma _{4}}=\varXi {\textit{USK}_{\mathit{ID}}}+\varXi {\textit{UTK}_{\mathit{ID},t}}+\varXi T{G_{S,i,1}}\cdot (\varXi Y+msg\cdot \varXi Z)$.
-
(6) Transform ($\varXi {\sigma _{1}}$, $\varXi {\sigma _{2}}$, $\varXi {\sigma _{3}}$, $\varXi {\sigma _{4}}$) to gain the corresponding bit strings ($\xi {\sigma _{1}}$, $\xi {\sigma _{2}}$, $\xi {\sigma _{3}}$, $\xi {\sigma _{4}}$) and return them to ${A_{I}}$.
-
• Signing leak query $(\textit{ID},k,{f_{S,k}},{h_{S,k}})$: Upon receiving the k-th $Signing$ $query$ of the user ID, by taking as input two leakage functions ${f_{S,k}}$ and ${h_{S,k}}$, C returns the fraction leakage content $\varLambda {f_{S,k}}$ and $\varLambda {h_{S,k}}$ to ${A_{I}}$, where $\varLambda {f_{S,k}}={f_{S,k}}({\textit{USK}_{\mathit{ID},k,1}},{\textit{UTK}_{\mathit{ID},t}},c,\delta )$ and $\varLambda {h_{S,k}}={h_{S,k}}({\textit{USK}_{\mathit{ID},k,2}},c,{\mathit{TI}_{S}})$. Note that for the k-th Signing query, ${A_{I}}$ is allowed to issue the Signing leak query only once.
-
– Forgery phase: ${A_{I}}$ outputs (${\textit{ID}^{\ast }}$, ${T_{t}^{\ast }}$, ${\mathit{msg}^{\ast }}$, ($\xi {\sigma _{1}^{\ast }}$, $\xi {\sigma _{2}^{\ast }}$, $\xi {\sigma _{3}^{\ast }}$, $\xi {\sigma _{4}^{\ast }}$)). ${A_{I}}$ is disallowed to request the Signing query $({\textit{ID}^{\ast }},{T_{t}^{\ast }},{\mathit{msg}^{\ast }})$. Since ${A_{I}}$ is a curious CRA or an outsider, ${A_{I}}$ may request the Time key update query $({\textit{ID}^{\ast }},{T_{t}^{\ast }})$, but does not request the Key extract query (${\textit{ID}^{\ast }}$). C transforms ($\xi {\sigma _{1}^{\ast }}$, $\xi {\sigma _{2}^{\ast }}$, $\xi {\sigma _{3}^{\ast }}$, $\xi {\sigma _{4}^{\ast }}$) to gain the corresponding polynomials $\varXi {\sigma _{1}^{\ast }}$, $\varXi {\sigma _{2}^{\ast }}$, $\varXi {\sigma _{3}^{\ast }}$, $\varXi {\sigma _{4}^{\ast }}$ while setting ${\mathit{TID}^{\ast }}={\textit{ID}^{\ast }}||\xi {\sigma _{1}^{\ast }}$ and ${\mathit{TTD}^{\ast }}={\textit{ID}^{\ast }}||{T_{t}^{\ast }}||\xi {\sigma _{2}^{\ast }}$. If the equality $\varXi g\cdot \varXi {\sigma _{4}^{\ast }}=\varXi \mathit{SPK}+\varXi k\mathit{TPK}+\varXi {\sigma _{1}^{\ast }}\cdot (\varXi U+{\mathit{TID}^{\ast }}\cdot \varXi V)+\varXi {\sigma _{2}^{\ast }}\cdot (\varXi W+{\mathit{TTD}^{\ast }}\cdot \varXi X)+\varXi {\sigma _{3}^{\ast }}\cdot (\varXi Y+{\mathit{msg}^{\ast }}\cdot \varXi Z)$ holds, we say that ${A_{I}}$ wins the game ${G_{\mathit{LR}\text{-}\mathit{RIBS}}}$.
For evaluating the probability that
${A_{I}}$ wins
${G_{\mathit{LR}\text{-}\mathit{RIBS}}}$, let us first compute the number of group elements and the maximal degrees of polynomials in
${L_{G}}/{L_{T}}$.
If one of the following two cases occurs, we say that
${A_{I}}$ wins
${G_{\mathit{LR}\text{-}\mathit{RIBS}}}$:
Case 1.
${A_{I}}$ discovers a collision of group elements in ${L_{G}}$ or ${L_{T}}$. Let n denote the total number of all variates in ${L_{G}}$ and ${L_{T}}$. Now, C selects n random values ${v_{i}}\in {Z_{p}^{\ast }}$ for $i=1,\dots ,n$. In this case, there exist two polynomials $\varXi {G_{i}}$ and $\varXi {G_{j}}$, both in ${L_{G}}$ or both in ${L_{T}}$, that satisfy $\varXi {G_{i}}({v_{1}},{v_{2}},\dots ,$ ${v_{n}}$) = $\varXi {G_{j}}({v_{1}},{v_{2}},\dots ,{v_{n}})$.
Case 2.
${A_{I}}$ outputs a correct signature (${\textit{ID}^{\ast }}$, ${T_{t}^{\ast }}$, ${\mathit{msg}^{\ast }}$, ($\xi {\sigma _{1}^{\ast }}$, $\xi {\sigma _{2}^{\ast }}$, $\xi {\sigma _{3}^{\ast }}$, $\xi {\sigma _{4}^{\ast }}$)) that satisfies $\varXi g\cdot \varXi {\sigma _{4}^{\ast }}=\varXi \mathit{SPK}+\varXi TPK+\varXi {\sigma _{1}^{\ast }}\cdot (\varXi U+{\mathit{TID}^{\ast }}\cdot \varXi V)+\varXi {\sigma _{2}^{\ast }}\cdot (\varXi W+{\mathit{TTD}^{\ast }}\cdot \varXi X)+\varXi {\sigma _{3}^{\ast }}\cdot (\varXi Y+{\mathit{msg}^{\ast }}\cdot \varXi Z)$, where ${\mathit{TID}^{\ast }}={\textit{ID}^{\ast }}||\xi {\sigma _{1}^{\ast }}$ and ${\mathit{TTD}^{\ast }}={\textit{ID}^{\ast }}||{T_{t}}||\xi {\sigma _{2}^{\ast }}$.
Let us evaluate ${A_{I}}$’s advantage of winning ${G_{\mathit{LR}\text{-}\mathit{RIBS}}}$ without requesting Key extract leak query and Signing leak query. Note that ${A_{I}}$ is a curious CRA or an outsider who can gain the user’s time update key ${\textit{UTK}_{\mathit{ID},t}}$ by the Time key update query. Hence, ${A_{I}}$ has no need to request the Time key update leak query. Subsequently, ${A_{I}}$’s advantage in ${G_{\mathit{LR}\text{-}\mathit{RIBS}}}$ with requesting two kinds of leak queries (Key extract leak query and Signing leak query) is evaluated.
∙
Without requesting two kinds of leak queries: Under this circumstance,
${A_{I}}$ may request all the queries in
${G_{\mathit{LR}\text{-}\mathit{RIBS}}}$ except for the
Key extract leak query and Signing leak query. In the following, let us discuss the probability that
${A_{I}}$ wins
${G_{\mathit{LR}\text{-}\mathit{RIBS}}}$ without requesting two kinds of leak queries.
Case 1.
The probability that
${A_{I}}$ discovers a collision of group elements in
${L_{G}}$ or
${L_{T}}$ is evaluated. Let
$\varXi {G_{i}}$ and
$\varXi {G_{j}}$ denote two distinct polynomials in
${L_{G}}$. The collision probability is the probability that
$\varXi {G_{C}}=\varXi {G_{i}}-\varXi {G_{j}}$ is a zero polynomial, namely,
$\varXi {G_{C}}({v_{1}},{v_{2}},\dots ,{v_{n}})=0$. By Lemma
2, the probability of
$\varXi {G_{C}}({v_{1}},{v_{2}},\dots ,{v_{n}})=0$ is at most
$3/p$ because there is no fraction leakage content
$(\lambda =0)$ and the maximal polynomial degree in
${L_{G}}$ is 3. We have that the probability of discovering a collision in
${L_{G}}$ is
$(3/p)\left(\genfrac{}{}{0pt}{}{|{L_{G}}|}{2}\right)$ since there are
$\left(\genfrac{}{}{0pt}{}{|{L_{G}}|}{2}\right)$ distinct pairs (
$\varXi {G_{i}}$,
$\varXi {G_{j}}$) in
${L_{G}}$. By similar arguments, the probability that
${A_{I}}$ discovers a collision in
${L_{T}}$ is (
$(6/p)\left(\genfrac{}{}{0pt}{}{|{L_{T}}|}{2}\right)$. Moreover, the total number of group elements in
${L_{G}}$ and
${L_{T}}$ is at most
$6q$, namely,
$|{L_{G}}|+|{L_{T}}|\leqq 6q$. Then the probability of Case
1, denoted by Pr[Case
1], satisfies the inequality
Case 2.
Let us evaluate the probability that ${A_{I}}$ outputs a signature (${\textit{ID}^{\ast }}$, ${T_{t}^{\ast }}$, ${\mathit{msg}^{\ast }}$, ($\xi {\sigma _{1}^{\ast }}$, $\xi {\sigma _{2}^{\ast }}$, $\xi {\sigma _{3}^{\ast }}$, $\xi {\sigma _{4}^{\ast }}$)) that satisfies $\varXi f=\varXi \mathit{SPK}+\varXi \mathit{TPK}+\varXi {\sigma _{1}^{\ast }}\cdot (\varXi U+{\mathit{TID}^{\ast }}\cdot \varXi V)+\varXi {\sigma _{2}^{\ast }}\cdot (\varXi W+TT{D^{\ast }}\cdot \varXi X)+\varXi {\sigma _{3}^{\ast }}\cdot (\varXi Y+{\mathit{msg}^{\ast }}\cdot \varXi Z)-\varXi g\cdot \varXi {\sigma ^{\ast }}4=0$. The probability of outputting a correct signature is $5/p$ because the degree of $\varXi f$ is at most 5.
Let
${\Pr _{A-I-W}}$ denote the advantage that
${A_{I}}$ wins
${G_{\mathit{LR}\text{-}\mathit{RIBS}}}$ without requesting two kinds of leak queries. By Cases
1 and
2, we have the inequality
∙
With requesting two kinds of leak queries: Under this circumstance,
${A_{I}}$ is allowed to issue all the leak queries in
${G_{\mathit{LR}\text{-}\mathit{RIBS}}}$. In the
i-th
key extract leak query with
$|{f_{\mathit{KE},i}}|\leqq \lambda $ and
$|{h_{\mathit{EK},i}}|\leqq \lambda $,
${A_{I}}$ gains the fraction leakage content
$\varLambda {f_{\mathit{KE},i}}={f_{\mathit{KE},i}}({\textit{SSK}_{i,1}},a,\gamma )$ and
$\varLambda {h_{\mathit{KE},i}}={h_{\mathit{KE},i}}({\textit{SSK}_{i,2}},a,\gamma ,{\mathit{TI}_{\mathit{KE}}})$ discussed as below.
-
■ a, γ: In each Key extract query, a and γ are random values. Therefore, the leakage of a or γ is of no help to learn the system secret key SSK.
-
■ (${\textit{SSK}_{i,1}}$, ${\textit{SSK}_{i,2}}$): We have SSK = ${\textit{SSK}_{i-1,1}}\cdot {\textit{SSK}_{i-1,1}}={\textit{SSK}_{i,1}}\cdot {\textit{SSK}_{i,2}}$. By the multiplicative blinding technique, the fraction leakage content of ${\textit{SSK}_{i-1,1}}/{\textit{SSK}_{i-1,2}}$ is independent of that of ${\textit{SSK}_{i,1}}/{\textit{SSK}_{i,2}}$. Hence, $AI$ gains at most λ bits of SSK.
-
■ ${\mathit{TI}_{\mathit{KE}}}$: The temporary value ${\mathit{TI}_{\mathit{KE}}}$ is employed to compute the user’s secret key ${\textit{USK}_{\mathit{ID}}}$. Since ${A_{I}}$ can obtain the entire ${\textit{USK}_{\mathit{ID}}}$ except for ${\textit{ID}^{\ast }}$, ${\mathit{TI}_{\mathit{KE}}}$ is helpless for ${A_{I}}$.
In the
k-th
Signing query of the user
ID, by taking as input two leakage functions
${f_{S,k}}$ and
${h_{S,k}}$ with
$|{f_{S,k}}|\leqq \lambda $ and
$|{h_{S,k}}|\leqq \lambda $,
${A_{I}}$ gains the fraction leakage content
$\varLambda {f_{S,k}}$ =
${f_{S,k}}({\textit{USK}_{\mathit{ID},k,1}},{\textit{UTK}_{\mathit{ID},t}},c,\delta )$ and
$\varLambda {h_{S,k}}={h_{S,k}}({\textit{USK}_{\mathit{ID},k,2}},c,{\mathit{TI}_{S}})$ discussed as below.
-
■ $c,\delta $: In each signing query, c and δ are random values. Therefore, the leakage about c and δ is of no help to learn the user’s secret key ${\textit{USK}_{\mathit{ID}}}$.
-
■ (${\textit{USK}_{\mathit{ID},k,1}}$, ${\textit{USK}_{\mathit{ID},k,2}}$): We have ${\textit{USK}_{\mathit{ID}}}={\textit{USK}_{\mathit{ID},k-1,1}}\cdot {\textit{USK}_{\mathit{ID},k-1,2}}={\textit{USK}_{\mathit{ID},k,1}}\cdot {\textit{USK}_{\mathit{ID},k,2}}$. By the multiplicative blinding technique, the fraction leakage content of ${\textit{USK}_{\mathit{ID},k-1,1}}/{\textit{USK}_{\mathit{ID},k-1,2}}$ is independent of that of ${\textit{USK}_{\mathit{ID},k,1}}/{\textit{USK}_{\mathit{ID},k,2}}$. Hence, ${A_{I}}$ gains at most λ bits of ${\textit{USK}_{\mathit{ID}}}$.
-
■ ${\mathit{TI}_{S}}$: The temporary value ${\mathit{TI}_{S}}$ is used to generate the signature ${\sigma _{4}}$. Since ${A_{I}}$ can obtain the entire ${\sigma _{4}}$ by the Sign query, ${\mathit{TI}_{S}}$ is helpless for ${A_{I}}$.
Let
${\mathit{Adv}_{A-I}}$ be the advantage that
${A_{I}}$ wins
${G_{\mathit{LR}\text{-}\mathit{RIBS}}}$ with requesting the
Key extract leak query and
Signing leak query. For forging a correct signature, let us discuss the useful leakage content of the target user’s secret
USK and the system secret key
SSK that consists of three events as below:
-
(1) $\mathit{ESSK}$ denotes the event that ${A_{I}}$ knows the whole SSK by $\varLambda {f_{\mathit{KE},i}}$ and $\varLambda {h_{\mathit{KE},i}}$, and its complement event is denoted by $\overline{\mathit{ESSK}}$.
-
(2) $\mathit{EUSK}$ denotes the event that ${A_{I}}$ knows the whole ${\textit{USK}_{\mathit{ID}}}$ by $\varLambda {f_{S,k}}$ and $\varLambda {h_{S,k}}$, and its complement event is denoted by $\overline{\mathit{EUSK}}$.
-
(3) $\mathit{ESF}$ denotes the event that ${A_{I}}$ forges a correct signature.
Hence, the advantage
${\mathit{Adv}_{A-I}}$ is Pr[
ESF] and satisfies the inequality
In our LR-RIBS scheme with CRA, the PKG employed SSK and a user’s information
$\textit{ID}||{\mathit{QK}_{\mathit{ID}}}$ to generate the user’s secret key
${\textit{USK}_{\mathit{ID}}}$ by using the signature scheme in Galindo and Virek (
2013). By Lemma 5 in Galindo and Virek (
2013), we have Pr[
$\mathit{ESSK}$] ≦
$O(({q^{2}}/p)\cdot {2^{2\lambda }})$. Next,
${A_{I}}$ may gain fractional content of
${\textit{USK}_{\mathit{ID}}}$ by the
Signing leak query. Hence, Pr[
$\mathit{ESF}\wedge \mathit{EUSK}$] is the probability that
${A_{I}}$ can get fractional content of
${\textit{USK}_{\mathit{ID}}}$ by
$\varLambda {f_{S,k}}$ and
$\varLambda {h_{S,k}}$. Thus, we can gain the probability Pr[
$\mathit{ESF}\wedge \mathit{EUSK}$] ≦
$O(({q^{2}}/p)\cdot {2^{2\lambda }})$. Finally, the event
$\overline{\mathit{ESSK}}\wedge \overline{\mathit{EUSK}}$ is that
${A_{I}}$ can gain fractional content of (
${\textit{USK}_{\mathit{ID},k,1}}$,
${\textit{USK}_{\mathit{ID},k,2}}$) by
$\varLambda {f_{S,k}}$ and
$\varLambda {h_{S,k}}$. In such a case,
${A_{I}}$ can gain at most
λ bits about
${\textit{USK}_{\mathit{ID}}}$, and so we have Pr[
$\mathit{ESF}\wedge \overline{\mathit{ESSK}}\wedge \overline{\mathit{EUSK}}$] ≦
$O(({q^{2}}/p)\cdot {2^{\lambda }})$. According to the events discussed above, we reach the inequality
Therefore,
${\mathit{Adv}_{A-I}}\leqq O({({q^{2}}/p)^{\ast }}{2^{2\lambda }})$. Finally, by Lemma
2,
${\mathit{Adv}_{A-I}}$ is negligible if
$\lambda <\log p-\omega (\log \log p)$. □
Theorem 2.
In the GBG model, our LR-RIBS scheme with CRA possesses existential unforgeability under the UF-LR-RIBS-ACMA attack of Type II adversary (a revoked user).
Proof.
Let
${A_{\mathit{II}}}$ denote a Type II adversary in the security game
${G_{\mathit{LR}\text{-}\mathit{RIBS}}}$ played with a challenger
C. Hence,
${A_{\mathit{II}}}$ may acquire the user’s secret key
${\textit{USK}_{\mathit{ID}}}$ and time update key
${\textit{UTK}_{\mathit{ID},t}}$ for any
ID at any period
${T_{t}}$, except for the target identity
${\textit{ID}^{\ast }}$ at period
${T_{t}^{\ast }}$. For
${G_{\mathit{LR}\text{-}\mathit{RIBS}}}$ on the proposed LR-RIBS scheme with CRA, three phases (
Setup,
Query and
Forgery) are described as below:
-
– Setup phase: The phase is the same with that of the proof in Theorem
1.
-
– Query phase: ${A_{\mathit{II}}}$ is allowed to issue the queries at most q times adaptively as below.
-
• ${Q_{G}}$,
${Q_{T}}$,
${Q_{P}}$,
Key extract query,
Time key update query,
Singing query and
Signing leak query are identical to these queries in Theorem
1. Note that
${A_{\mathit{II}}}$ is a revoked user who may acquire the user’s secret key
${\textit{USK}_{\mathit{ID}}}$ for any
ID. Hence,
${A_{\mathit{II}}}$ has no need to request the
Key extract leak query.
-
• Time key update leak query $(j,{f_{\mathit{TKU},j}},{h_{\mathit{TKU},j}})$: Upon receiving the j-th Key Time key update leak query with ${f_{\mathit{TKU},j}}$ and ${h_{\mathit{TKU},j}}$, C returns the fraction leakage content $\varLambda {f_{\mathit{TKU},j}}={f_{\mathit{TKU},j}}({\textit{TSK}_{j,1}},b,\eta )$ and $\varLambda {h_{\mathit{TKU},j}}={h_{\mathit{TKU},j}}({\textit{TSK}_{j,2}},b,\eta ,{\mathit{TI}_{\mathit{TKU}}})$ to ${A_{\mathit{II}}}$. Note that for the j-th Time key update query, ${A_{\mathit{II}}}$ is allowed to request the Time key update leak query only once.
-
– Forgery phase: ${A_{\mathit{II}}}$ outputs (${\textit{ID}^{\ast }}$, ${T_{t}^{\ast }}$, ${\mathit{msg}^{\ast }}$, ($\xi {\sigma _{1}^{\ast }}$, $\xi {\sigma _{2}^{\ast }}$, $\xi {\sigma _{3}^{\ast }}$, $\xi {\sigma _{4}^{\ast }}$)). ${A_{\mathit{II}}}$ is a revoked user who may request the Key extract query (${\textit{ID}^{\ast }}$) to obtain ${\textit{USK}_{{\mathit{ID}^{\ast }}}}$, but does not request the Time key update query (${\textit{ID}^{\ast }}$, ${T_{t}^{\ast }}$). C first transforms ($\xi {\sigma _{1}^{\ast }}$, $\xi {\sigma _{2}^{\ast }}$, $\xi {\sigma _{3}^{\ast }}$, $\xi {\sigma _{4}^{\ast }}$) to gain the corresponding polynomials $\varXi {\sigma _{1}^{\ast }}$, $\varXi {\sigma _{2}^{\ast }}$, $\varXi {\sigma _{3}^{\ast }}$ and $\varXi {\sigma _{4}^{\ast }}$. C sets $TI{D^{\ast }}={\textit{ID}^{\ast }}||\xi {\sigma _{1}^{\ast }}$ and $TT{D^{\ast }}={\textit{ID}^{\ast }}||{T_{t}^{\ast }}||\xi {\sigma _{2}^{\ast }}$. If the equality $\varXi g\cdot \varXi {\sigma _{4}^{\ast }}=\varXi \mathit{SPK}+\varXi \mathit{TPK}+\varXi {\sigma _{1}^{\ast }}\cdot (\varXi U+{\mathit{TID}^{\ast }}\cdot \varXi V)+\varXi {\sigma _{2}^{\ast }}\cdot (\varXi W+{\mathit{TTD}^{\ast }}\cdot \varXi X)+\varXi {\sigma _{3}^{\ast }}\cdot (\varXi Y+{\mathit{msg}^{\ast }}\cdot \varXi Z)$ holds, we say that ${A_{\mathit{II}}}$ wins ${G_{\mathit{LR}\text{-}\mathit{RIBS}}}$.
By the same arguments in Theorem
1, the total number of group elements in
${L_{G}}$ and
${L_{T}}$ is at most
$6q$, namely,
$|{L_{G}}|+|{L_{T}}|\leqq 6q$. The maximal polynomial degrees in
${L_{G}}$ and
${L_{T}}$ are 3 and 6, respectively. Let us evaluate
${A_{\mathit{II}}}$’s advantage winning
${G_{\mathit{LR}\text{-}\mathit{RIBS}}}$ without requesting
Time key update leak query and
Signing leak query. Subsequently,
${A_{\mathit{II}}}$’s advantage in
${G_{\mathit{LR}\text{-}\mathit{RIBS}}}$ with requesting two kinds of leak queries is evaluated.
∙
Without requesting two kinds of leak queries: Let
${\Pr _{A-II-W}}$ denote the advantage that
${A_{\mathit{II}}}$ wins
${G_{\mathit{LR}\text{-}\mathit{RIBS}}}$ without requesting two kinds of leak queries. By the similar discussions as Theorem
1, we have the inequality
Hence, ${\mathit{Adv}_{A-II-W}}$ is negligible if $q=poly(\log p)$.
∙
With requesting two kinds of leak queries: Under this circumstance,
${A_{\mathit{II}}}$ is allowed to request all queries in
${G_{\mathit{LR}\text{-}\mathit{RIBS}}}$. For the
j-th
time key update leak query with
${f_{\mathit{TKU},j}}$ and
${h_{\mathit{TKU},j}}$ that satisfy
$|{f_{\mathit{TKU},j}}|\leqq \lambda $ and
$|{h_{\mathit{TKU},j}}|\leqq \lambda $,
${A_{\mathit{II}}}$ can gain the fraction leakage content
$\varLambda {f_{\mathit{TKU},j}}={f_{\mathit{TKU},j}}({\textit{TSK}_{j,1}},b,\eta )$ and
$\varLambda {h_{\mathit{TKU},j}}={h_{\mathit{TKU},j}}({\textit{TSK}_{j,2}},b,\eta ,{\mathit{TI}_{\mathit{TKU}}})$ discussed below:
-
■ $b,\eta $: In each time key update query, b and η are random values. Therefore, the leakage about b and η is of no help to learn the time secret key TSK.
-
■ $({\textit{TSK}_{j,1}},{\textit{TSK}_{j,2}})$: For the time secret key TSK, we have $\textit{TSK}={\textit{TSK}_{j-1,1}}\cdot {\textit{TSK}_{j-1,1}}={\textit{TSK}_{j,1}}\cdot {\textit{TSK}_{j,2}}$. By the multiplicative blinding technique, the fraction leakage content of ${\textit{TSK}_{j-1,1}}/{\textit{TSK}_{j-1,2}}$ is independent of that of ${\textit{TSK}_{j,1}}/{\textit{TSK}_{j,2}}$. Thus, ${A_{\mathit{II}}}$ gains at most λ bits of TSK.
-
■ ${\mathit{TI}_{\mathit{TKU}}}$: The temporary value ${\mathit{TI}_{\mathit{TKU}}}$ is employed to generate user’s time key ${\textit{UTK}_{\mathit{ID},t}}$. Since ${A_{\mathit{II}}}$ can obtain the whole ${\textit{UTK}_{\mathit{ID},t}}$ by the time key update query, ${\mathit{TI}_{\mathit{TKU}}}$ is helpless for ${A_{\mathit{II}}}$.
For the
k-th
Signing leak query of the user
ID, by taking as input two leakage functions
${f_{S,k}}$ and
${h_{S,k}}$ such that
$|{f_{S,k}}|\leqq \lambda $ and
$|{h_{S,k}}|\leqq \lambda $,
${A_{\mathit{II}}}$ gains the fraction leakage content
$\varLambda {f_{S,k}}={f_{S,k}}({\textit{USK}_{\mathit{ID},k,1}},{\textit{UTK}_{\mathit{ID},t}},c,\delta $) and
$\varLambda {h_{S,k}}={h_{S,k}}({\textit{USK}_{\mathit{ID},k,2}},c,{\mathit{TI}_{S}})$. Indeed, a revoked user has possessed the user secret key
${\textit{USK}_{\mathit{ID}}}$. In particular, since the user’s time update key
${\textit{UTK}_{\mathit{ID},t}}$ is not generated, the
Signing leak query does not leak any content.
Let
${\mathit{Adv}_{A-II}}$ be the advantage that
${A_{\mathit{II}}}$ wins
${G_{\mathit{LR}\text{-}\mathit{RIBS}}}$ with requesting the
time key update query. Since
${A_{\mathit{II}}}$ simulates a revoked user, she/he can obtain the target user’s secret key
${\textit{USK}_{I}}D$. For forging a correct signature, let us discuss the helpful leakage content about the target user’s time key
${\textit{UTK}_{\mathit{ID},t}}$ that consists of two events as below:
-
(1) $\mathit{ETSK}$ denotes the event that ${A_{\mathit{II}}}$ gains the whole TSK by $\varLambda {f_{\mathit{TKU},j}}$ and $\varLambda {h_{\mathit{TKU},j}}$, and $\overline{\mathit{ETSK}}$ denotes the complement event of $\mathit{ETSK}$.
-
(2) $\mathit{ESF}$ denotes the event that ${A_{\mathit{II}}}$ forges a correct signature.
Hence, the advantage
${\mathit{Adv}_{A-II}}$ is Pr[
$\mathit{ESF}$] and satisfies the inequality
In the
Time key update phase of our scheme, the CRA employed the time secret key
TSK and a user’s content
$\mathit{TTD}=\textit{ID}||{T_{t}}||{\mathit{QTK}_{\mathit{ID},t}}$ to generate the user’s secret key
${\textit{UTK}_{\mathit{ID},t}}$ by using the signature scheme in Galindo and Virek (
2013). The probability Pr[
ETSK] is identical to Pr[
$\mathit{ESSK}$] in Theorem
1 so that we have
$\Pr [\mathit{ETSK}]\leqq O({({q^{2}}/p)^{\ast }}{2^{2\lambda }})$ Next, the event is that
${A_{\mathit{II}}}$ can gain at most
λ bits of (
${\textit{TSK}_{j,1}}$,
${\textit{TSK}_{j,2}}$), we have
$\text{Pr}[\mathit{ESF}\wedge \overline{ETSK}]\leqq O({({q^{2}}/p)^{\ast }}{2^{\lambda }})$. According to the events discussed above, we reach the inequality
Therefore,
${\mathit{Adv}_{A-II}}\leqq O({({q^{2}}/p)^{\ast }}{2^{2\lambda }})$. Finally, by Lemma
2,
${\mathit{Adv}_{A-II}}$ is negligible if
$\lambda <\log p-\omega (\log \log p)$. □
6 Performance Comparisons
Here, we compare the performance between previously proposed RIBS schemes (Tsai
et al.,
2013b; Jia
et al.,
2017) and our LR-RIBS scheme with CRA. In the following, four notations are defined respectively to represent four time-consuming operation costs of bilinear groups:
-
• ${T_{\mathit{bp}}}$: The executing cost of a bilinear map $\hat{e}:G\times G\to {G_{T}}$.
-
• ${T_{\mathit{me}}}$: The executing cost of a scalar multiplication on an additive cycle group G or an exponentiation operation on a multiplicative cycle group G.
-
• ${T_{\mathit{ex}}}$: The executing cost of an exponentiation operation on a multiplicative cycle group ${G_{T}}$.
-
• ${T_{\mathit{mh}}}$: The executing cost of a map-to-point hash function operation in G.
Table 1
Executing costs (in milliseconds) of several operations on a PC and a smartphone.
|
PC (2.4 GHz processor) |
Smartphone (1 GHz processor) |
| ${T_{\mathit{bp}}}$ |
7.5 |
260 |
| ${T_{\mathit{me}}}$ |
2.8 |
34 |
| ${T_{\mathit{ex}}}$ |
2.1 |
21 |
| ${T_{\mathit{mh}}}$ |
$\cong 2.8$ |
$\cong 34$ |
Table 2
Performance comparisons between our LR-RIBS scheme with CRA and the previously proposed RIBS schemes.
|
Tsai et al.’s RIBS scheme (Tsai et al., 2013b) |
Jia et al.’s RIBS scheme (Jia et al., 2017) |
Our LR-RIBS scheme (Tsai et al., 2013b) |
| Resisting side-channel attacks |
No |
No |
Yes |
| Overall unbounded leakage property |
No |
No |
Yes |
| Outsourced revocation authority |
No |
Yes |
Yes |
| Key extract |
$3{T_{\mathit{me}}}$ |
${T_{\mathit{me}}}+{T_{\mathit{mh}}}$ |
$7{T_{\mathit{me}}}$ |
| (Executing cost on PC) |
(8.4 ms) |
(5.6 ms) |
(19.6 ms) |
| Time key update |
$3{T_{\mathit{me}}}$ |
${T_{\mathit{me}}}+{T_{\mathit{mh}}}$ |
$5{T_{\mathit{me}}}$ |
| (Executing cost on PC) |
(8.4 ms) |
(5.6 ms) |
(14 ms) |
| Signing |
$2{T_{\mathit{me}}}$ |
$2{T_{\mathit{me}}}+{T_{\mathit{ex}}}$ |
$5{T_{\mathit{me}}}$ |
| (Executing cost on Smartphone) |
(68 ms) |
(89 ms) |
(170 ms) |
| Verifying |
$5{T_{\mathit{bp}}}$ |
$2{T_{\mathit{ex}}}+2{T_{\mathit{mh}}}+3{T_{\mathit{bp}}}$ |
$3{T_{\mathit{me}}}+4{T_{\mathit{bp}}}$ |
| (Executing cost on Smartphone) |
(1300 ms) |
(890 ms) |
(1142 ms) |
Indeed, the cost of the operation (additive/multiplicative) on an (additive/multiplicative) cyclic group
G is smaller than
${T_{\mathit{bp}}}$,
${T_{\mathit{me}}}$,
${T_{\mathit{ex}}}$ and
${T_{\mathit{mh}}}$ (Scott,
2011; Lynn,
2015), and so is negligible. The simulation experiences (Lynn,
2015) on a PC and a smartphone are employed as the benchmark costs of
${T_{pb}}$,
${T_{\mathit{me}}}$,
${T_{\mathit{ex}}}$ and
${T_{\mathit{mh}}}$. The simulation platform on both the PKG and CRA sides is an Intel Core-2 Quad Q6600 PC with 2.4 GHz processor and Ubuntu OS. Meanwhile, the simulation platform on the user side is a HTC Desire HD-A9191 smartphone with Qualcomm 1 GHz processor and Android 2.2 OS. Additionally, under the same security level with 1024-bit RSA system, an elliptic curve over a finite field
$E({F_{q}})$ are employed for bilinear pairing groups with a prime order
p, where
p and
q are 160 and is 512 bits, respectively. Table
1 lists the executing cost (in milliseconds) of
${T_{pb}}$,
${T_{\mathit{me}}}$,
${T_{\mathit{ex}}}$ and
${T_{\mathit{mh}}}$ on both a PC and a smartphone in Lynn (
2015).
Table
2 lists the performance comparisons between two previously proposed RIBS schemes (Tsai
et al.,
2013b; Jia
et al.,
2017) and our LR-RIBS scheme with CRA in terms of resisting side-channel attacks, overall unbounded leakage property, outsourced revocation authority and the computation costs of four phases. In Tsai
et al. (
2013b), the PKG is responsible to carry out both the
Key extract and
Time key update phases. On the other hand, the scheme in Jia
et al. (
2017) and our scheme employ a CRA to outsource the functionality of user revocation. Note that the executing costs of both the Key extract and Time key update phases are measured under a PC while the executing costs of both the
Signing and
Verifying phases are measured under a smartphone.
By Table
2, although performing worse than the other two schemes in the computation costs, our scheme is still well suited for a smartphone with limited computing capability. We should emphasize that our scheme can resist side-channel attacks with overall unbounded leakage property, but the other two cannot.
7 Conclusions
In the continual leakage model, we have defined a novel adversary model of LR-RIBS schemes with CRA. In the adversary model, Type I adversary (a curious CRA or an outsider) is allowed to extract fractional content of the target signer’s secret key and the PKG’s system secret key. Also, Type II adversary (a revoked user) is allowed to extract fractional content of the CRA’s time secret key. We have proposed the first LR-RIBS scheme with CRA and it possesses the overall unbounded leakage property. In the GBG model, security analysis demonstrated that the proposed LR-RIBS scheme with CRA is secure against Types I and II adversaries under the continual leakage model. Performance comparisons demonstrated that the proposed LR-RIBS scheme with CRA requires some additional computation costs than the previously proposed RIBS schemes. This point is that our scheme not only can resist side-channel attacks, but also is still suitable for mobile devices with limited computing capability.

