1 Introduction
The concept of fuzzy graph, introduced by Kauffman (
1973) initially, was interpreted by Rosenfeld (
1975). Samanta and Pal (
2015,
2013) introduced different types of fuzzy graphs. For further details about the fuzzy graphs, readers may see Mordeson and Nair (
2000), Samanta
et al. (
2016a), Sarkar and Samanta (
2017), Mahapatra
et al. (
2019a). Early in the literature, one of the useful problems, the traffic light problem, was solved using the crisp graph colouring technique. But, in traffic light problems, some routes are busier compared to the other routes. Also, sometimes, two routes are open simultaneously with some caution. Here “busy”, “caution” are fuzzy terms. So fuzzy/uncertainty could be included in the traffic light problem. Munoz
et al. (
2005) designed the traffic light problem by fuzzy graphs and introduced the method of colouring in fuzzy graphs. The edge colouring of fuzzy graphs could demonstrate the traffic light problem properly. The membership value of edges is calculated from the congestion of the route and the probability of accidents. If the signal lights are based on these membership values and used alongside the fuzzy colour, the density of the signal colours could indicate the flow of traffic in a particular region. In that paper, the fuzzy graphs were considered with crisp vertices and fuzzy edges. Then
α-cuts Mordeson and Nair (
2000) of these fuzzy graphs were coloured according to the method of the crisp graph colouring. Thus, for different values of
α, there are different crisp graphs, and these crisp graphs are coloured. Therefore, the chromatic index varies for the same fuzzy graphs for different values of
α. Also, Bershtein and Bozhenuk (
2001) proposed a different technique to colour fuzzy graphs. In this paper, a term separation degree of fuzzy graphs has been defined and based on the value of separation degree, the number of minimum colour is found. Vertex colouring on fuzzy graphs is applied for map colouring Samanta
et al. (
2016b). Recently, major developments on chromatic index on fuzzy graphs are obtained from the papers of Rosyida
et al. (
2016,
2015) and Chen
et al. (
2017). Kishore and Sunitha Kishore and Sunitha (
2014,
2016) introduced chromaticity and strong chromaticity of fuzzy graphs. Mahapatra
et al. (
2019b) advanced the colouring concept to radio fuzzy graphs and resolved radio frequency problems.
Sometimes, the relationship (edges) is more meaningful than the people (nodes). For example, the links in fuzzy social networks are more important than the nodes. Thus, it is essential to show the fuzzy links properly by colouring. Edge colouring, a related term, is important to the problems which are based on uncertainty. In Section
3 of this paper, edge colouring of fuzzy graphs is introduced. After that, in Section
4, chromatic index of fuzzy graphs, an associated term of graph colouring, is defined. Based on this technique, the number of basic colours is counted. In fuzzy graphs, edge colourings use colour density. Sometimes, deep/strong colours are to be used to emphasize the importance of the corresponding relation/edge. The definition of strong chromatic index is updated in Section
6. Here, a recruiting web site is represented from both companies’ and candidates’ point of view by edge colouring of fuzzy graphs in Section
6. Traffic light problems have been modified and solved in Section
7. At last, a conclusion is drawn in Section
8.
2 Preliminaries
A graph is defined as a pair ${G^{\ast }}=(V,E)$, where V is the set, and E is a relation on V. The elements of V are called vertices, and the elements of E are called edges of ${G^{\ast }}$.
A fuzzy set A on a universal set X is characterized by a mapping $m:X\to [0,1]$, which is called the membership function. A fuzzy set is denoted by $A=(X,m)$.
A
fuzzy graph Rosenfeld (
1975)
$\xi =(V,\sigma ,\mu )$ is a non-empty set
V together with a pair of functions
$\sigma :V\to [0,1]$ and
$\mu :V\times V\to [0,1]$, such that for all
$x,y\in V$,
$[\mu (x,y)\leqslant \min \{\sigma (x),\sigma (y)\}]$, where
$\sigma (x)$ and
$\mu (x,y)$ represent the membership values of the vertex
x and of the edge
$(x,y)$ in
ξ, respectively.
A path in a fuzzy graph is a sequence of distinct nodes ${x_{0}},{x_{1}},\dots ,{x_{n}}$, such that $\mu ({x_{i-1}},{x_{i}})>0,1\leqslant i\leqslant n$. The fuzzy path is said to be fuzzy cycle if ${x_{0}}$ and ${x_{n}}$ coincide.
The strength of a path is the minimum membership value of an edge in the path. The maximum of all strengths of paths between two vertices is the strength of connectivity between the vertices.
The underlying crisp graph of the fuzzy graph $\xi =(V,\sigma ,\mu )$ is denoted as $\xi =(V,\sigma ,{\mu ^{)}}$ where $\sigma =\{u\in V|\sigma (u)>0\}$ and $\mu =\{(u,v)\in V\times V|\mu (u,v)>0\}$. Thus, for underlying fuzzy graph, $\sigma =V$ is true.
A fuzzy graph $\xi =(V,\sigma ,\mu )$ is complete if $\mu (u,v)=\min \{\sigma (u),\sigma (v)\}$ for all $u,v\in V$, where $(u,v)$ denotes the edge between the vertices u and v.
A fuzzy graph $\xi =(V,\sigma ,\mu )$ is said to be bipartite if the vertex set V can be partitioned into two nonempty sets ${V_{1}}$ and ${V_{2}}$, such that $\mu ({v_{1}},{v_{2}})=0$ if ${v_{1}},{v_{2}}\in {V_{1}}$ or ${v_{1}},{v_{2}}\in {V_{2}}$. Furthermore, if $\mu ({v_{1}},{v_{2}})=\min \{\sigma ({v_{1}}),\sigma ({v_{2}})\}$ for all ${v_{1}}\in {V_{1}}$ and ${v_{2}}\in {V_{2}}$, then ξ is called a fuzzy complete bipartite graph.
3 Edge Colouring of Fuzzy Graphs
Samanta
et al. (
2016b) defined fuzzy colours as mixed colours. But when a colour is mixed with white, its intensity is reduced. Now, intensity is a fuzzy term. Suppose
β $(\leqslant 1)$ units of the colour
${c_{k}}$ are mixed with
$1-\beta $ units of white colour, then the mixture is called a standard mixture of the colour
${c_{k}}$. The resulted colour is called the fuzzy colour of the colour
${c_{k}}$ with membership value
β, whereas
${c_{k}}$ is called the basic colour. For example, red, black, green, etc. are basic colours. The definition of fuzzy colour is given as follows.
Definition 1.
Let $W=\{{w_{1}},{w_{2}},\dots ,{w_{\lambda }}\}$, $\lambda \geqslant 1$ be the set of basic colours. Then the fuzzy set $(W,h)$ where $h:W\to (0,1]$ is called the set of fuzzy colours such that $0<h({w_{i}})\leqslant 1$, the membership value of the colour ${w_{i}}$, is the amount of ${w_{i}}$ per unit of the mixture of ${w_{i}}$ with white colour.
Hence, the colour $({w_{i}},h({w_{i}}))$ is called the fuzzy colour corresponding to the basic colour ${w_{i}}$. Thus, $h({w_{i}})[\leqslant 1]$ amount of ${w_{i}}$ is mixed with $1-h({w_{i}})$ amount of white colour to form the fuzzy colour $({w_{i}},h({w_{i}}))$.
According to the above definition of fuzzy colour, different fuzzy colours are constructed from a basic colour. For example, red is a basic colour. A “fuzzy red” colour may be formed from red by mixing 0.9 units of red colour with 0.1 units of white colour. This “fuzzy red” colour is denoted by $(\mathit{red},0.9)$. Similarly, another fuzzy red colour $(\mathit{red},0.75)$ may be formed by mixing 0.75 units of red colour with 0.25 units of white colour, and so on. Now, these fuzzy colours are used for edge colouring of fuzzy graphs in the following ways.
3.1 Procedure of Edge Colouring of Fuzzy Graphs
In crisp graph colouring, two edges have different colours if they are adjacent. Otherwise, the colour may be the same. In fuzzy edge colouring, two edges have fuzzy colours whose basic colours are different, if they are adjacent. Otherwise, their fuzzy colours may be the same and from the same basic colour.
Let
$\xi =(V,\sigma ,\mu )$ be a connected fuzzy graph and
$C=({c_{1}},{c_{2}},\dots ,{c_{k}})$ be a set of basic colours. Now, only if two edges are adjacent, then the edges are given two fuzzy colours whose basic colours are different, otherwise, they may be given fuzzy colours whose basic colours may be the same. If the colour of any edge is
$({c_{i}},{f_{{e_{j}}}}({c_{i}}))$, then
${c_{i}}$ is the basic colour of the edge
${e_{j}}=(u,v)$ and
${f_{{e_{j}}}}({c_{i}})$ is its membership value which is calculated as
where
$\sigma (u)$ and
$\sigma (v)$ are the membership values of vertices
u and
v, respectively. Also,
$\mu (u,v)$ is the membership value of the edge
${e_{j}}$, i.e.
$(u,v)$ in the fuzzy graph
ξ.
3.2 Algorithm to Colour the Edges of a Fuzzy Graph
Input: A fuzzy graph $\xi =(V,\sigma ,\mu )$, $|V|=n$. Assume that the vertices are labelled as $1,2,\dots ,n$.
Output: Complete a edge coloured graph.
Step 1: Calculate ${f_{{e_{j}}}}({c_{i}})=\frac{\mu (u,v)}{\sigma (u)\wedge \sigma (v)}$ of all edges. Also, vertices are to be labelled as $1,2,\dots ,n$.
Step 2: First of all, the vertex “1” is focused to colour all its incident edges in such a way that no two incident edges are of the same colours. Here, depths of the colours depend on the $f-$ values which are calculated in Step 1.
Step 3: Proceed to direct neighbours of “1” except the previous one which is already focused and label them $11,12,\dots ,1m$, if there are m-such neighbours. Start with the vertex 11 and repeat Step 2 and so on for $12,13,\dots ,1m$.
Step 4: Repeat Step 3 until all edges of the graph have been coloured.
4 Chromatic Index of Fuzzy Graphs
The minimum number of basic colours needed to colour a fuzzy graph is called fuzzy chromatic index of a fuzzy graph. Suppose that such minimum number of basic colours is N. Now, this crisp chromatic index is not sufficient to mention the strengths of edges (i.e. the relationship among vertices). For example, chromatic indexes of two fuzzy graphs are the same. Then it is inconclusive when these graphs are being compared. Hence, the chromatic index is associated with some weight. The weight is denoted by W, and defined by $W={\textstyle\sum _{i=1}^{N}}\{{\max _{j}}{f_{{e_{j}}}}({c_{i}})\}$. Where the basic colour ${c_{i}}$ is used to colour the edge ${e_{j}}$ for some j, and depth of colour is ${f_{{e_{j}}}}({c_{i}})$. Thus, W is the sum of the maximum membership values of each basic colour. Now, the chromatic index of a fuzzy graph is denoted by $(N,W)$, where N is the minimum number of basic colours to colour a graph, and W is its weight. It is obvious that the weight of the chromatic index is to be determined by decision makers for a particular case.
4.1 Algorithm of Minimum Colouring of Edges of a Fuzzy Graph
Input: A fuzzy graph $\xi =(V,\sigma ,\mu )$, $|V|=n$. Assume that the vertices are labelled as $1,2,\dots ,n$.
Output: Complete a edge coloured graph.
Step 1: Now, f-value (${f_{{e_{j}}}}({c_{i}})=\frac{\mu (u,v)}{\sigma (u)\wedge \sigma (v)}$) of all edges are to be calculated.
Step 2: First of all, the vertex “1” is targeted to colour all its incident edges in such a way that the minimum number of colours would be used. Hence, if one colour is used, a different colour is to be used only if the edges are incident to the vertex.
Step 3: Proceed to direct neighbours of “1” except the previous one which is already focused and label them $11,12,\dots ,1m$, if there are m-such neighbours. Start with the vertex 11 and repeat Step 2 and so on for $12,13,\dots ,1m$.
Step 4: Repeat Step 3 until all edges of the graph have been coloured.
Formally, the definition of chromatic index for fuzzy graphs is given as follows. The concept of this chromatic index will allow to mention the weight of edge colouring.
Definition 2.
Let $G=(V,\sigma ,\mu )$ be a fuzzy graph. The order pair $(N,W)$ is said to be the chromatic index of G where N is the minimum number of colour needed to colour the graph G and $W={\textstyle\sum _{i=1}^{N}}\{ma{x_{j}}{f_{{e_{j}}}}({c_{i}})\}$, the basic colour ${c_{i}}$ is used to colour the edge ${e_{j}}$ for some j, and the depth of colour is ${f_{{e_{j}}}}({c_{i}})$.
The chromatic index on fuzzy graphs is a pair whose first element represents the crisp chromatic index, and the second element is its weight. The crisp number indicates only the number of different colours required to colour the edges of a graph while the weight represents the sum of strengths of the edges. This weight is meaningful only when it is of a very high or very low value, i.e. all edges are strong, or all edges are weak. Thus, the weight needs further restrictions.
Example 1.
An example is considered in Fig.
1. In this example, three basic colours (red, black and green) are used for the colouring of the fuzzy graph, i.e.
$N=3$. The depth of colouring is the strength of the corresponding edge. Here, red colour is given in the edges
$\mathit{CA}$ and
$\mathit{BD}$ with membership values 0.5 and 0.83 of the edge, respectively. The black colour is assigned to the edges
$\mathit{BC}$ and
$\mathit{AD}$ with membership value 1. The green colour is given to the edges
$CD$ and
$\mathit{AB}$ with membership values 1 and 0.71, respectively. So the weight
$W=0.83+1+1=2.83$. Thus, the chromatic index of this fuzzy graph is
$(3,2.83)$.
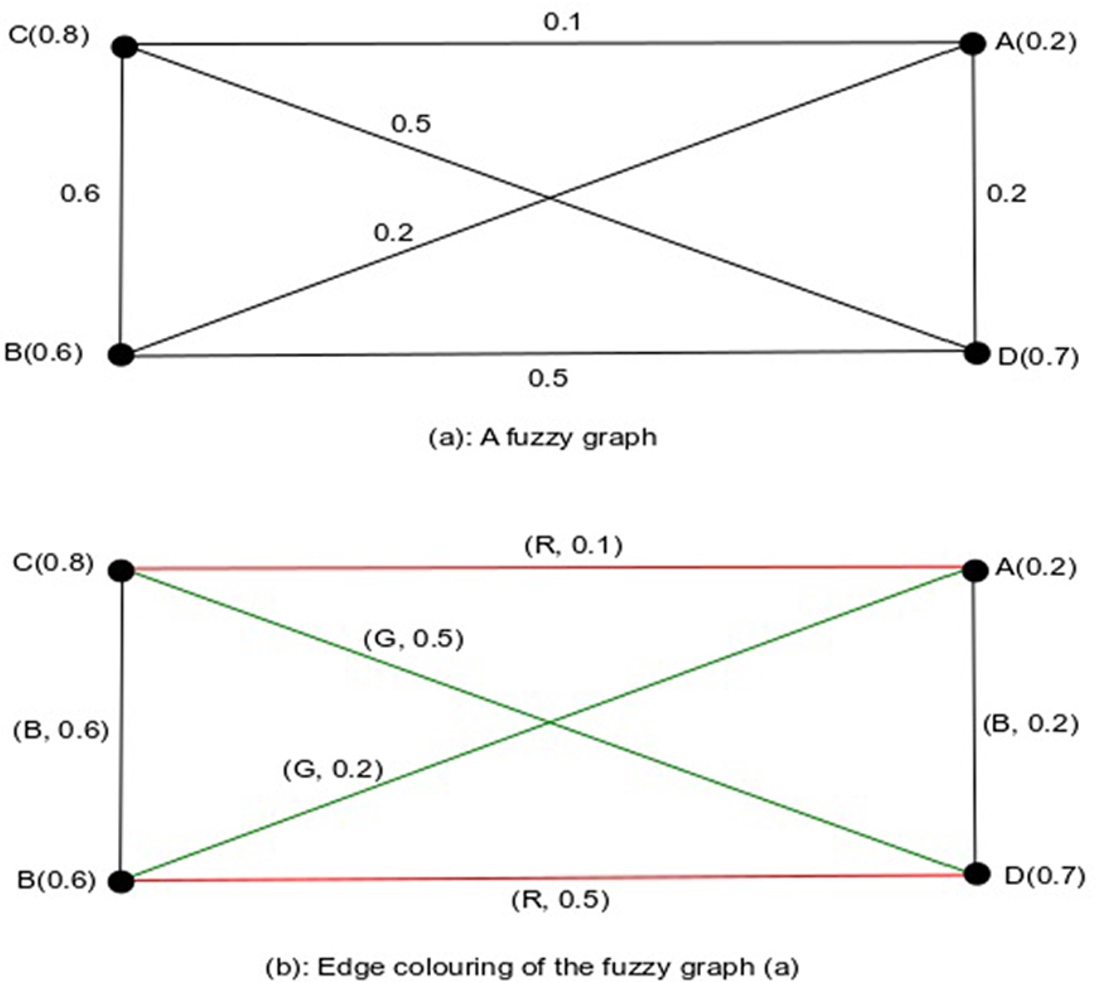
Fig. 1
Edge colouring of fuzzy graphs.
Lemma 1.
Chromatic index of a complete graph is $(N,N)$.
Proof.
Let $\xi =(V,\sigma ,\mu )$ be a complete fuzzy graph, then $\mu (x,y)=\sigma (x)\wedge \sigma (y)$. Thus, the membership value of each basic colour must be $\frac{\mu (x,y)}{\sigma (x)\wedge \sigma (y)}=1$. Since the graph is complete, N basic colour is required. Here, the membership value of each basic colour is 1. Then the weight of the chromatic index is $\{1+1+1+\cdots N\hspace{2.5pt}\text{times}\}=N$. So, the chromatic index of a complete graph is $(N,N)$. □
Lemma 2.
If the chromatic index of a fuzzy graph is $(N,W)$, then $0<W\leqslant N$.
Proof.
Let $\xi =(V,\sigma ,\mu )$ be a fuzzy graph with a chromatic index $(N,W)$. Also, $\mu (x,y)\leqslant \sigma (x)\wedge \sigma (y)$. It is obvious that the weight W is always positive, i.e. $W>0$. Also, $\mu (x,y)\leqslant \sigma (x)\wedge \sigma (y)$. Thus, $\frac{\mu (x,y)}{\sigma (x)\wedge \sigma (y)}$ ⩽ 1. So, the membership value of each colour is smaller or equal to 1. Now W is the sum of membership values of N basic colours. Hence, $W\leqslant N$, i.e. $0<W\leqslant N$. □
5 Strong Chromatic Index of Edge Colouring of Fuzzy Graphs
The weight of the chromatic number is significant only if the weight is very large or very small. Suppose that two fuzzy graphs have chromatic indexes which are
$(3,2.9)$ and
$(3,0.3)$. It can be said that the edges of the second graph are not strong. But any value which is near about half of its maximum value does not indicate any clear data. The strong chromatic index will be an improved concept of the chromatic index. Let
$\xi =(V,\sigma ,\mu )$ be a connected fuzzy graph. The edges, where
$\frac{\mu (x,y)}{\sigma (x)\wedge \sigma (y)}\geqslant 0.5$, are coloured with fuzzy colours whose membership values are greater than or equal to 0.5. These colours are called strong colours. Strong chromatic index is denoted by
${\gamma _{s}}(\xi )$ and defined by
${\gamma _{s}}(\xi )=({M_{s}},{W_{s}})$, where
${M_{s}}$ is the number of basic colours for colouring of
ξ and
${W_{s}}$ is the sum of the membership values of each basic colour. It is assumed that the maximum membership value is taken for the repeated, basic colours.
Example 2.
Let us consider a fuzzy graph shown in Fig.
2. Here, four basic colours (red, yellow, green and blue) are used for the colouring of the fuzzy graph. The membership values of the colours are 0.8, 0.25, 0.33, 1, respectively. Therefore,
${M_{s}}=2$ and
${W_{s}}=(0.8+1)=1.8$. So, the strong chromatic index of the fuzzy graph is
$(2,1.8)$.
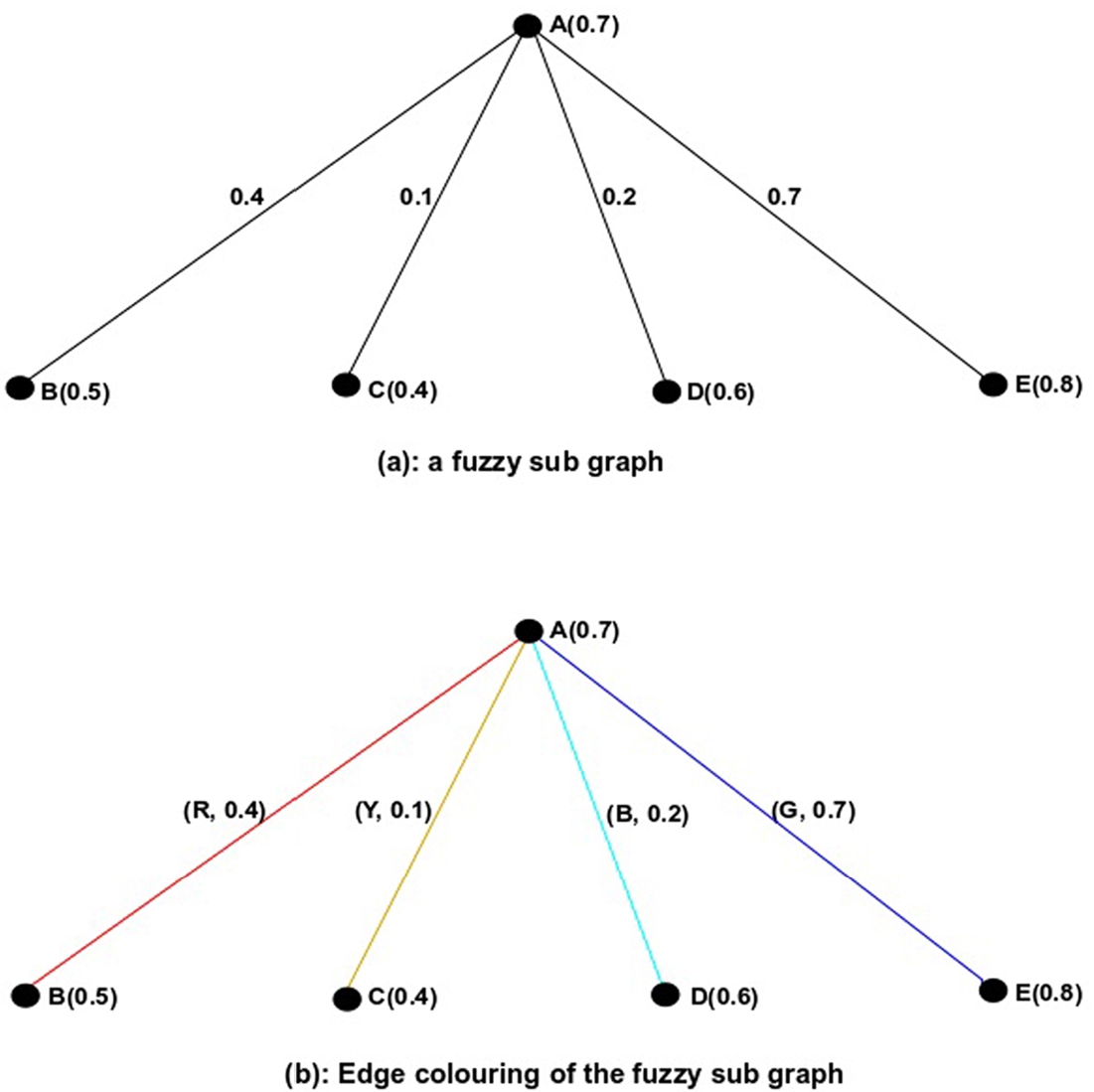
Fig. 2
Colouring of strong edge of fuzzy graphs.
Theorem 1.
Let ξ be a fuzzy graph, and the chromatic index of this fuzzy graph is $(N,W)$, and strong chromatic index is $({M_{s}},{W_{s}})$, then $N\geqslant {M_{s}}$ and $W\geqslant {W_{s}}$.
Proof.
Let $\xi =(V,\sigma ,\mu )$ be a fuzzy graph. The following three cases are considered. If all basic colours are strong, then the chromatic index of this fuzzy graph and the strong chromatic index are the same, i.e. $N={M_{s}}$ and $W={W_{s}}$.
Again, some of the basic colours are considered strong. However, there exist some basic colours which are not strong, i.e. $N>{M_{s}}$. Then W is the sum of the maximum membership value of each basic colour, and ${W_{s}}$ is the sum of all the maximum membership values of all strong basic colours. So, in this case, $W>{W_{s}}$.
Lastly, none of the basic colours is strong. In this case ${M_{s}}=0$ and $N>{M_{s}}$ are obvious. Also ${W_{s}}=0$ and $W>{W_{s}}$. Therefore, from these three cases it is concluded that $N\geqslant M$ and $W\geqslant {W_{s}}$. □
Lemma 3.
Let ξ be a fuzzy graph with a strong chromatic index $({M_{s}},{W_{s}})$. Then $2{W_{s}}-M$ is either zero or positive.
Proof.
Let $\xi =(V,\sigma ,\mu )$ be a fuzzy graph with a strong chromatic index $({M_{s}},{W_{s}})$. The fuzzy graph ξ is coloured by ${M_{s}}$ number of strong basic colours and the membership value of each of the strong basic colours is $\frac{\mu (x,y)}{\sigma (x)\wedge \sigma (y)}$ ($\geqslant 0.5$). Note that ${W_{s}}$ is the sum of membership values of each basic colour. It is assumed that the maximum membership value is taken for repeated basic colours. So, it is true that ${W_{s}}\geqslant 0.5\times {M_{s}}$, where ${M_{s}}$ is the number of basic colours. Hence, $2{W_{s}}-{M_{s}}\geqslant 0$. Then $2{W_{s}}-M$ is either zero or positive. □
Theorem 2.
Let ξ be a fuzzy graph with a strong chromatic index $({M_{s}},{W_{s}})$. Then $\frac{{M_{s}}}{2}\leqslant {W_{s}}\leqslant {M_{s}}$ is true.
Proof.
Let $\xi =(V,\sigma ,\mu )$ be a fuzzy graph and the strong chromatic index of this fuzzy graph ξ be $({M_{s}},{W_{s}})$. The fuzzy graph ξ coloured by ${M_{s}}$ number of strong basic colours and the membership values of all such strong basic colours are $\frac{\mu (x,y)}{\sigma (x)\wedge \sigma (y)}$ $(\geqslant 0.5)$. So, the minimum membership value of the strong colours is 0.5. If all of these ${M_{s}}$ strong basic colours have the minimum membership value, then ${W_{s}}=\{0.5+0.5+\dots {M_{s}}\langle \hspace{2.5pt}\text{times}\}=\frac{{M_{s}}}{2}$. So, the minimum value of the strong weight is $\frac{{M_{s}}}{2}$, i.e. $\frac{{M_{s}}}{2}\leqslant {W_{s}}$. Also, the maximum depth of colour is 1. Now, if each of all of these ${M_{s}}$ number of basic colours has the maximum depth, then ${W_{s}}=\{1+1+1+\dots M\hspace{2.5pt}\text{times}\}={M_{s}}$. So, the maximum value of the strong weight is ${M_{s}}$. Thus, ${W_{s}}\leqslant {M_{s}}$. So, $\frac{{M_{s}}}{2}\leqslant {W_{s}}\leqslant {M_{s}}$ is true. □
Lemma 4.
Let ξ be a fuzzy graph other than complete fuzzy graphs with a chromatic index $(N,W)$ and a strong chromatic index $({M_{s}},{W_{s}})$. Then $\frac{W-{W_{s}}}{N-{M_{s}}}\leqslant 0.5$.
Proof.
Let ξ be a fuzzy graph other than complete fuzzy graphs with a chromatic index $(N,W)$ and a strong chromatic index $({M_{s}},{W_{s}})$. So, $N\ne {M_{s}}$, i.e. $(N-{M_{s}})\geqslant 0$. Also, $(N-{M_{s}})$ is the number of coloured edges whose membership value is less than 0.5. And $(W-{W_{s}})$ is the weight of the $(N-{M_{s}})$ edges. Thus, $W-{W_{s}}$ = sum of membership values of $(N-{M_{s}})$ edges. So, $W-{W_{s}}\leqslant 0.5\times (N-{M_{s}})$.
Hence, $\frac{W-{W_{s}}}{N-{M_{s}}}\leqslant \frac{1}{2}$. □
Lemma 5.
Let ξ be a fuzzy cycle with a chromatic index $(N,W)$. If the fuzzy cycle has an even number of edges, then $N=2$ and $0<W\leqslant 2$. If the fuzzy cycle has an odd number of edges, then $N=3$, $0<W\leqslant 3$.
Proof.
If the fuzzy cycle has an even number of edges, then to colour this cycle, only two basic colours are needed. So,
$N=2$ and from Theorem
2, the range of
W is
$0<W\leqslant N$.
Hence, $0<W\leqslant 2$.
If the fuzzy graph has an odd number of edges, then for this cycle three basic colours are needed. So
$N=3$ and from Lemma
1,
$0<W\leqslant 3$. □
Note 1.
Let ξ be a bipartite fuzzy graph and Δ be the maximum degree of this fuzzy graph, then its chromatic index is $(\Delta ,W)$.
Theorem 3.
Let ξ be a fuzzy graph with vertex membership values 1 and $({M_{s}},{W_{s}})$ be its strong chromatic index. Then, ${M_{s}}$ lies between $[\frac{1}{2}{\Delta ^{\prime }}(\xi )]$ and $[{\Delta ^{\prime }}(\xi )+1]$. (${\Delta ^{\prime }}(x)=\max {\textstyle\sum _{y\in V,\mu (x,y)>0.5}}\mu (x,y)$ and $[x]$ represents greatest integer function).
Proof.
Suppose ξ is a fuzzy graph with vertex membership values 1 and $({M_{s}},{W_{s}})$ is its strong chromatic index. If ξ has a vertex u such that $d(u)={\textstyle\sum _{y\in V,\mu (u,y)>0.5}}\mu (u,y)$. Also, the vertex membership values are 1, thus strong edges refer to the edges with membership values more than 0.5. As the chromatic index of the graph is $({M_{s}},{W_{s}})$, $d\leqslant {W_{s}}$ and the number of strong edges incident to u must be smaller than or equal to ${M_{s}}$. Again, ${\Delta ^{\prime }}(x)={\max _{x\in V}}d(x)$. Thus, it is natural $N\geqslant [\frac{1}{2}{\Delta ^{\prime }}(\xi )]$.
In case of upper bound, the minimum number of colours required to colour a fuzzy cycle of 3 vertices is $2+1$, while the maximum degree is 2. This particular example can be generally taken for the odd cycle of degree n. The chromatic index for such cycle is $(n+1,W)$. Thus, the maximum value for chromatic index of such cycles is given as $(N,W)$ where $N=[{\Delta ^{\prime }}(x)+1]$. If edge membership values are maximum, then the chromatic index must have its maximum value $([{\Delta ^{\prime }}(x)+1],[{\Delta ^{\prime }}(x)+1])$. For other graphs, according to Vizing’s theorem, it is well known that the crisp graphs have its maximum chromatic index as ${\Delta ^{\prime }}(x)+1$. Hence, the result for fuzzy graphs that N lies between $[\frac{1}{2}{\Delta ^{\prime }}(\xi )]$ and $[{\Delta ^{\prime }}(\xi )+1]$ is true. □
6 Representation of Job Oriented Web Sites by Edge Colouring of Fuzzy Graphs
Fuzzy graph colouring problem has various practical applications. One of them is in job oriented web sites. Job oriented web sites are useful in recent years. A lot of recruiters and job seekers gather in these web sites. Fuzzy graphs represent each web site. The following example shows a step by step method of representation of web sites and edge colouring of fuzzy graphs. By looking at the colour of a fuzzy graph, an applicant could understand how many companies suit his/her expertise. Furthermore, on the other side, a company finds a suitable applicant. Thus, the representation of job oriented web sites can be prepared in an easier way using the edge colouring of fuzzy graphs.
Let us assume such a small web site, where
N number of candidates are registered for jobs with their Bio-Data, and
M number of companies (recruiters) have registered a certain number of vacancies and the brand value of the company for appropriate candidates (see Fig.
3).
If an applicant’s eligibility suits a company’s demand, it is obvious that there exists a relation between them. Here, the companies and candidates are represented as vertices and their links as edges. Now, the membership values of corresponding vertices of the company may depend on the following issues:
And the membership values of vertices to the corresponding applicant depend on following parameters.
The membership values of edges depend on matching the companies’ profiles with the applicants’ profiles. Then, the relationship between companies and applicants is shown as a fuzzy bipartite graph, shown in Fig.
5. If a company wants to find suitable candidates, firstly, it logins into this web site, then it will get a fuzzy subgraph like Fig.
3. The company may shortly find suitable candidates by using the concept of strong chromatic index.
Fig. 3
Representation of companies and applicants in a job oriented web site.
Suppose, in particular, 5 companies and 4 applicants are registered on this job oriented web site (see Fig.
5). Thus, a fuzzy bipartite graph is considered where the vertices are the companies
${C_{1}},{C_{2}},{C_{3}},{C_{4}},{C_{5}}$ and the applicants,
${P_{1}},{P_{2}},{P_{3}},{P_{4}}$. There is an edge if there exists a particular matching. So the edges are
$({C_{1}},{P_{1}})$,
$({C_{1}},{P_{2}})$,
$({C_{1}},{P_{3}})$,
$({C_{2}},{P_{1}})$,
$({C_{2}},{P_{2}})$,
$({C_{2}},{P_{4}})$,
$({C_{3}},{P_{1}})$,
$({C_{3}},{P_{3}}),({C_{3}},{P_{4}})$,
$({C_{4}},{P_{1}})$,
$({C_{4}},{P_{3}}),({C_{4}},{P_{4}})$,
$({C_{5}},{P_{1}})$,
$({C_{5}},{P_{2}})$,
$({C_{5}},{P_{3}})$,
$({C_{5}},{P_{4}})$. The membership value of vertices
${C_{1}},{C_{2}},{C_{3}},{C_{4}},{C_{5}}$ depend on the salary, company’s brand value, product value etc., as stated above. The membership values of the vertices
${P_{1}},{P_{2}},{P_{3}},{P_{4}}$ depend on qualification, experience, etc., as stated above. The membership values of edges depend on matching the companies with the applicants.
For example, in a particular case, the membership values of vertices ${C_{1}},{C_{2}},{C_{3}},{C_{4}},{C_{5}}$ are taken as $0.8,0.6,0.7,0.5,0.5$, respectively. The membership values of vertices ${P_{1}},{P_{2}},{P_{3}},{P_{4}}$ are considered as 0.9,0.8,0.5,0.7, respectively. Also the membership value of the edges $({C_{1}},{P_{1}})$, $({C_{1}},{P_{2}})$, $({C_{1}},{P_{3}})$, $({C_{2}},{P_{1}})$, $({C_{2}},{P_{2}})$, $({C_{2}},{P_{4}})$, $({C_{3}},{P_{1}})$, $({C_{3}},{P_{3}})$, $({C_{3}},{P_{4}})$, $({C_{4}},{P_{1}})$, $({C_{4}},{P_{3}})$, $({C_{4}},{P_{4}})$, $({C_{5}},{P_{1}})$, $({C_{5}},{P_{2}})$, $({C_{5}},{P_{3}})$, $({C_{5}},{P_{4}})$ are taken as 0.7, 0.6, 0.5, 0.6, 0.5, 0.4, 0.7, 0.4, 0.6, 0.4, 0.4, 0.5, 0.4, 0.3, 0.2, 0.3, 0.2, respectively.
When a company or an applicant logins into this web site, then they get a fuzzy subgraph like Fig.
5. Particularly, if an applicant
${P_{2}}$ logins into this web site, then he/she gets a fuzzy subgraph shown in Fig.
6(a). Also, if a company, in particular,
${C_{3}}$ logins into this web site, it gets another fuzzy subgraph shown in Fig.
6(b).
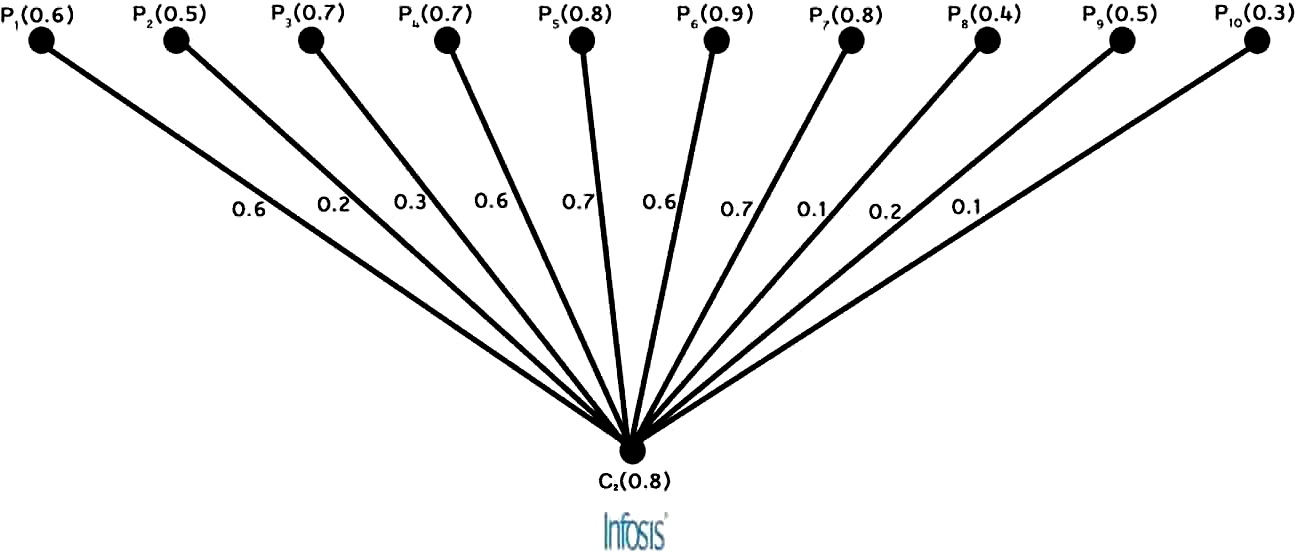
Fig. 4
Fuzzy sub graph for the vertex ${C_{2}}$.
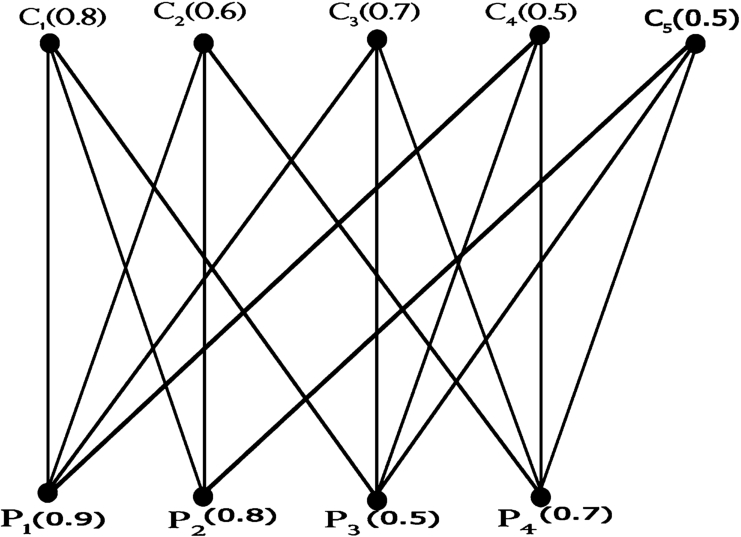
Fig. 5
Fuzzy graph of the job oriented web site.
If these two fuzzy subgraphs are coloured by fuzzy colours, then the applicant
${P_{2}}$ gets a coloured fuzzy subgraph shown in Fig.
7(a). Here three basic colours (red, green and brown) are used. The edge
$({P_{2}},{C_{1}})$ is coloured by
$(\textit{red},0.75)$. So 0.75 unit red colour is mixed with 0.25 unit white colour. Similarly, other two edges
$({P_{2}},{C_{2}})$ and
$({P_{2}},{C_{5}})$ are coloured by (green, 0.83) and (brown, 0.4), respectively. So the weight is
$(0.75+0.83+0.4)=1.98$ and the strong weight is
$(0.75+0.83)=1.58$. Hence, the chromatic index is
$(3,1.98)$ and the strong chromatic index is
$(2,1.58)$.
A company (say Infosis) wants to find suitable candidates. Then after login, it gets a fuzzy subgraph (Fig.
3). Suppose this company finds 10 applicants (see Fig.
4) and the number of vacancies is 2. If the company wants to call top suitable candidates for the test, then the company must use the strong chromatic index. The strong chromatic index is
$(5,4.357)$. So the company identifies the best 5 applicants.
From the chromatic index an applicant can realise how many companies are suitable for his/her recruitment and from the weight he/she can understand the chance of recruitment. And from the colour density of the fuzzy graph he understands which company is the best for him. Also, from the strong chromatic index it can be determined how many companies can select him.
Similarly, when a company logins, it gets a coloured fuzzy subgraph shown in Fig.
7(b). From the chromatic index and the strong chromatic index, it gets how many candidates are suitable for the company, and from the weight, it gets the deserved candidates.
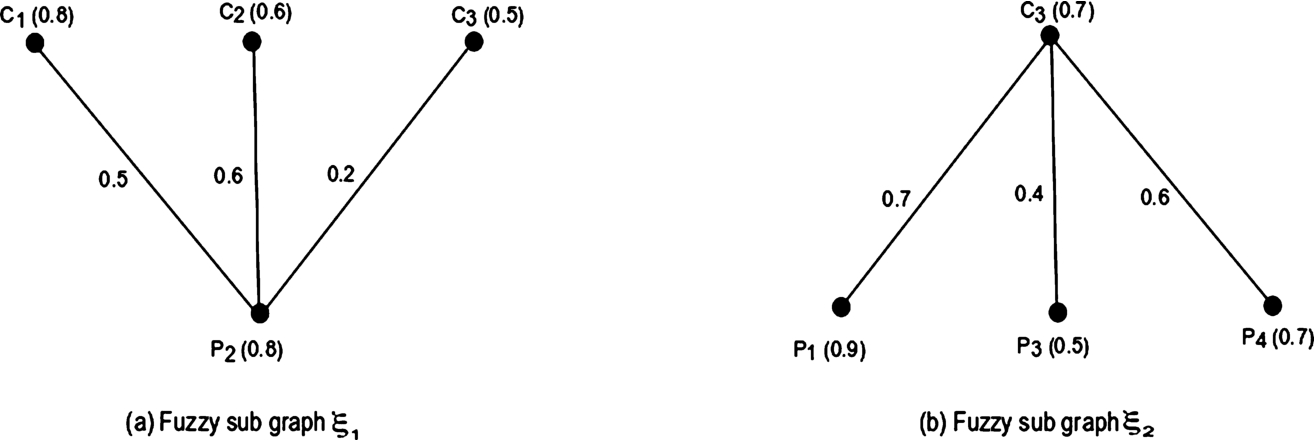
Fig. 6
Fuzzy sub graphs of the fuzzy graph of Fig.
5.
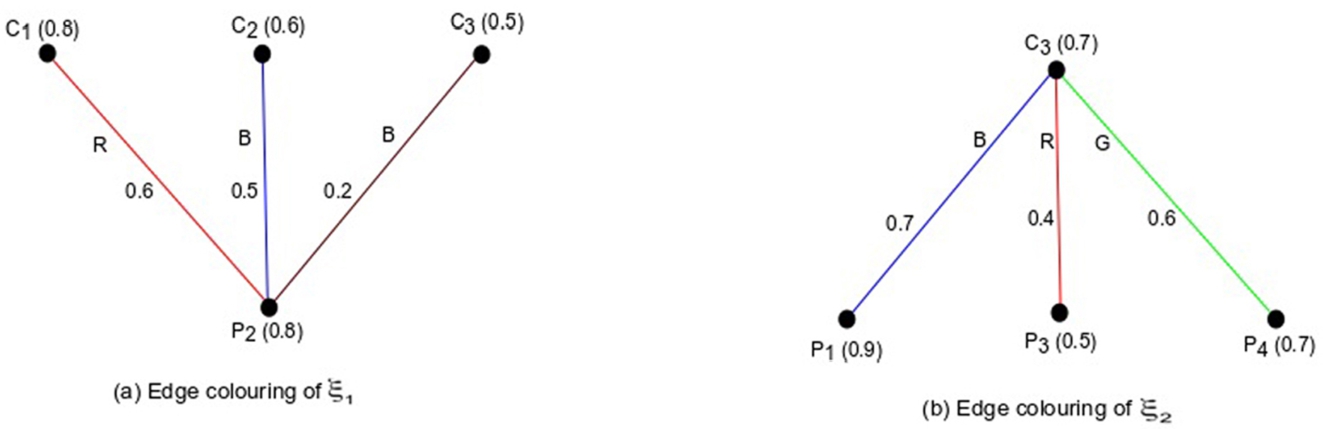
Fig. 7
Edge colouring of the fuzzy sub graphs.

Fig. 8
CCTV for collection of data.
7 Representation of Traffic Light Problem
One of the most useful real life applications of the edge colouring is in traffic light problems. Traffic light system uses three standard colours: red, amber (yellow), green, following the universal colour code. The green light allows traffic to proceed in the denoted direction. The amber (yellow) light warns that more precautions should be taken to cross the road. The red signal prohibits any traffic from proceeding. However, in the present traffic light system, a traveller does not know how much the traffic is congested. This limitation has to be removed here. Traffic light system will be modified by the edge colouring of fuzzy graphs.
It takes every route as a fuzzy vertex. An edge between two vertices is drawn if the routes have a junction. The edge membership values are calculated based on the congestion of routes and the road condition. The data is collected from real time CCTV (see Fig.
8).
Thus a fuzzy graph $\xi =(V,\sigma ,\mu )$ is formed. Let $C=({c_{1}},{c_{2}},\dots ,{c_{k}})$ be a set of basic colours. As traffic light system can not be used by more than three colors, the technique of the colouring is changed. In this particular traffic light system, if the colour of any edge is $({c_{i}},f({c_{i}}))$, then ${c_{i}}$ is a basic colour and $f({c_{i}})$ is its membership value which is calculated as $f({c_{i}})=\mu (u,v)$, where $\mu (u,v)$ is the membership value of the edge $(u,v)$.
Now, a seven point crossing (for example, Park circus seven point crossing, Kolkata, West Bengal, India, see Fig.
9) is taken as an example. The image is collected from Google Maps. This picture is converted into a fuzzy graph (see Fig.
10). Now, the membership value of the edges in the figure PA, PB, PC, PD, PE, PF, AB, AF, AE, AD, AC, BC, BD, BE, BF, CD, CE, CF, DE, DF, EF are calculated from real time CCTV showing the road conjunction and the road condition. A traveller from P road can visit any route of this crossing if all routes are open at that time. So a fuzzy subgraph can be constructed against the node P to represent the travellers possible visit, whose edges are PA, PB, PC, PD, PE, PF (see Fig.
11).
Fig. 9
Seven point crossing park circus, Kolkata (collected from Google Map).
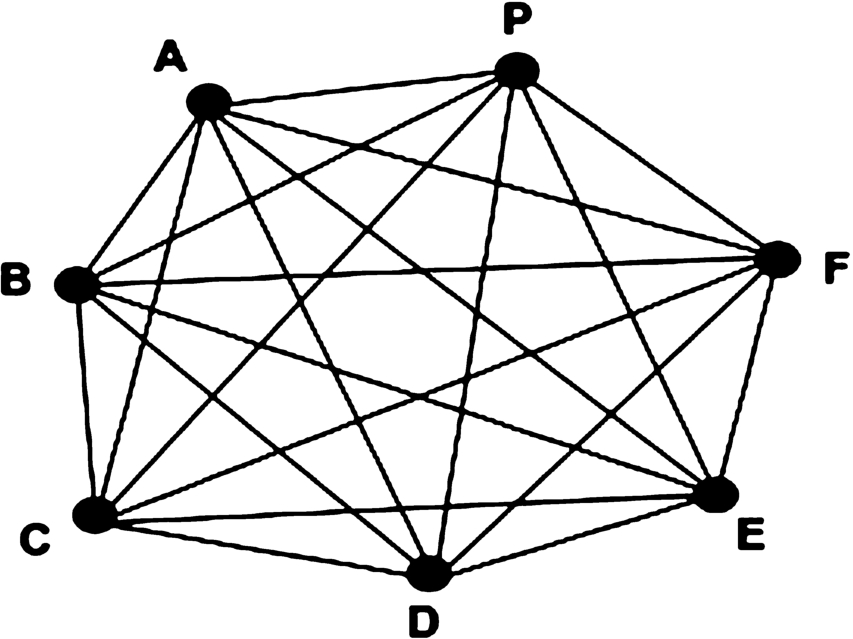
Fig. 10
Fuzzy graph of seven point crossing.
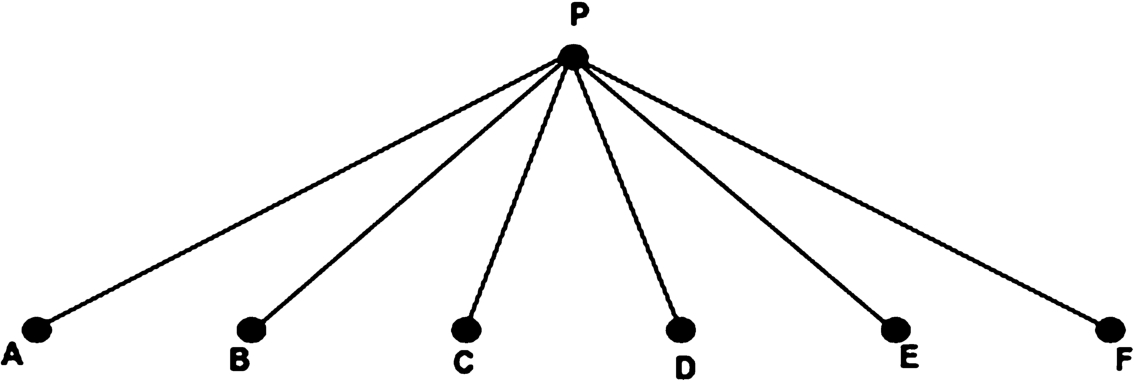
Fig. 11
Fuzzy subgraph of Fig.
10.
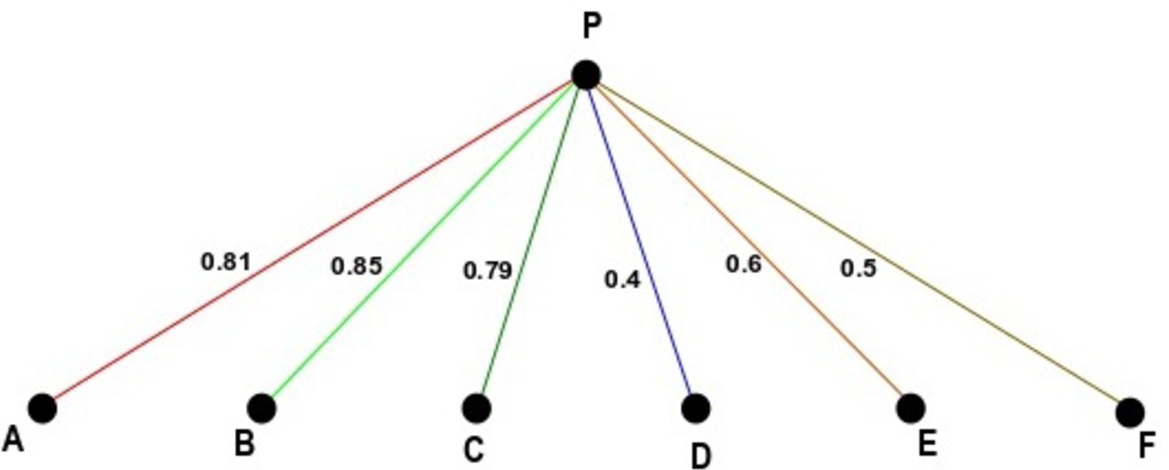
Fig. 12
Edge colouring of fuzzy graph.
Let us consider at a particular time the membership value of the edges PA, PB, PC, PD, PE, PF be
$0.81,0.85,0.79,0.4,0.6,0.5$, respectively. Next, this fuzzy subgraph is coloured using the edge colouring technique (see Fig.
12). In this subgraph, the chromatic index is 6 and the weight is
$(0.81+0.85+0.79+0.4+0.6+0.5)=3.95$.
When a traveller is travelling the P road, it would be helpful, if all the information about the next crossing was displayed in two or three display boards before the crossing. From the chromatic index the traveller can understand how many roads are open at the time of crossing, and from the weight, the total traffic condition. For this purpose, the congestion of the next crossing is to be represented in terms of percentage. Here, f-value, i.e. 0.81 indicates that the congestion is $81\% $. Displaying percentage is helpful in order to understand the congestion of a target road. So with the help of the colouring of the fuzzy subgraph, the traveller would get an idea before crossing about the present condition of the target road. With the help of the chromatic index, the traveller also understands the situation of the target road, i.e. whether the road will open or close.
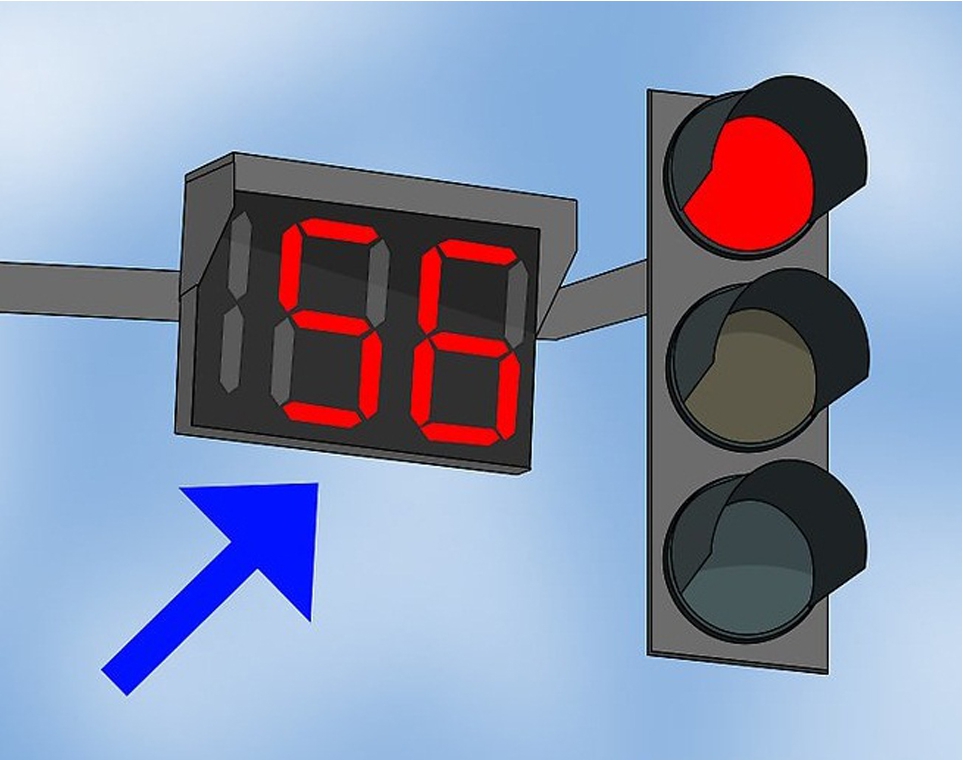
Fig. 13
Red signal with percentage of mixing of colours.
Also we can use this depth of colour in red (
$f({c_{i}})$) signal with percentage (see Fig.
13). If the membership value is increased, then the density of the red signal will be increased. On the other hand, the green signal can be used with the membership value
$1-{f^{1}}({c_{i}})$ which is the complement of the depth of red colour. The denser the green colour is, the less congested the route is. So the traveller can understand how much danger there is or how much time will be spent to cross.
The stopping time can be fixed with the help of the membership value of the red signal. If the membership value of the red colour is increased, then the stopping time will decrease.
8 Conclusion
In this study, a concept of edge colouring has been introduced. A related term, chromatic index, is also defined in a different way. A weight is associated with each of the chromatic indexes. This weight might be defined in different ways. But the proposed method mentions the depth of the colours to be used to colour a graph. At the end of this paper, the traffic light problem is updated. In that problem, if the subgraph is uploaded for online traffic condition, then the input graph will be compatible with Google Traffic indicating system. It is seen that Google Traffic system calculates the data from the flow of mobiles. But here, membership values are calculated from real-time CCTV. Google Traffic uses three or four colours to represent the condition of the traffic, but the proposed method uses the colour density with a percentage, which is much more helpful to the traveller. Thus, a user can easily understand the present condition of the traffic. There are many real field problems which can be solved using this technique of colouring, such as transportation problems, social networking problems, sport modelling. The proposed method may be implemented empirically in the existing traffic light systems. The theoretical approach of edge colouring will be beneficial to other graph colouring problems as well. In future studies, more uncertainty may be represented through generalized fuzzy graphs.

