1 Introduction
Though the presented here interpretation of free energy and entropy stems mainly from the thermodynamic principles, at the same time we imply that it has a strong relation with the information theory as well, which is crucial to understand the meaning of the thermodynamic free energy and entropy employment for modelling the brain state dynamics.
Despite the wealth of empirical data in neuroscience, there are relatively few global theories about how the brain works. A recently proposed free energy principle for adaptive systems tries to provide a unified account of action, perception and learning. Although this principle has been portrayed as a unified brain theory, its capacity to unify different perspectives on the brain function has yet to be established (Friston,
2010; Huang,
2008; Dayan,
1998).
Historically, Hinton realized first that some tough problems can be solved in machine learning by treating a prediction error of neural networks as free energy, and then minimizing it (Hinton and Terrence,
1999). His insight was that the constant updating of the brain’s states could also be expressed in terms of minimizing free energy. Around 2005 he proposed a “free energy principle” designed for one aspect of brain function – sensory perception (Huang,
2008). Later this principle has been generalized to other kinds of brain processes as well. According to the proposed “free energy principle” the brain is designed to minimize free energy or prediction error. Following this logic, everything that can change in the brain will change to suppress prediction errors, from the firing of neurons to the wiring between them, and from the movements of our eyes to the choices we make in daily life.
However, in more general terms, the free energy principle is essentially a mathematical formulation of how adaptive systems resist a natural tendency of disorderliness. We can see that although the motivation is quite straightforward, the implications are complicated and diverse. This diversity allows the principle to account for many aspects of brain structure and function and lends it the potential to unify different perspectives on how the brain works. Admittedly, the number of physiological and sensory states in which an organism can be is limited, and these states define the organism’s phenotype. Mathematically, this means that the probability of these sensory states must have low entropy. In other words, there is a high probability that a system will be in any of a small number of states, and a low probability that it will be in the remaining states. Biological agents must therefore minimize the long-term average of entropy to ensure that their sensory errors remain low. In other words, biological systems somehow manage to violate the fluctuation theorem, which generalizes the second law of thermodynamics (Friston,
2010).
Following Friston
et al. (
2006), we admit that the long-term imperative of maintaining states within physiological bounds translates into a short-term avoidance of entropy. The negative log-probability of the entropy outcome here relates not just to the current state, but also to movement from one state to another, which can change. This motion can be complicated and itinerant (wandering) provided that it probabilistically revisits a small set of states, i.e. global random attractors, which we denote as the basic brain states in this paper. It is this motion between states that puts at work the free energy optimization principle. The entropy and free energy constraints optimize the motion between brain states throughout the day period. We assume that an agent is constantly operating in the minimum free energy zone of attractor states (basic brain states). Hence, free energy level is maintained minimal and constant over time.
Before delving deeper into the proposed model details, let us recall that the research on the human brain state dynamics was basically concerned with impaired alertness and cognition, which was mathematically associated with the fundamental circadian sleep-wake cycle of restful and active brain states (Medeiros
et al.,
2001). Currently are dominating homeostatic and circadian drives for only two state (sleep-wake) modelling (Borbely,
1982; Borbély and Achermann,
1999; Buzsaki,
2011). While describing a two-state modelling approach and its recent advances an important paper of Borbely
et al. (
2016) presents the most recent review of this area. Following this review, the two-process model has strong functional implications, but it was formulated without specifying the function of sleep, except that sleep must subserve long-term maintenance of cerebral integrity. Tononi and Cirelli have proposed the synaptic homeostasis hypothesis of sleep regulation (Tononi and Cirelli,
2006,
2014). The main tenet is that synaptic and cellular processes that had been challenged during waking are re-established during sleep. Sleep is viewed as a price the brain pays for plasticity. In this regard.
However, such two-state approaches reduce the brain state space to the minimum. Admittedly, there are well known sleep states such as NREM (deep sleep) and REM (dreaming), which we think are imperative to employ for modelling too. In a similar way, there are quite a few “wake” states too. For instance, we have chosen active wakefulness and thinking states for transitions modelling. The former represents physical activity without mental concentration (dominated by alpha and beta EEG signals), whereas the latter represents a concentrated mental activity (dominated by beta and gamma EEG signals) (Kezys and Plikynas,
2014). Hence, this paper enlarges the traditional approach by splitting (i) the sleep state into deep sleep (NREM) and resting or dreaming (REM) states, and (ii) the wake state into physically active wakefulness and thinking states. In this way, we have gradually mapped brain activity states, starting from the least active NREM and ending with the most intensive thinking state (Plikynas,
2015). Hence, the traditional two-state model is increased into four-state model (NREM → REM → physically active wakefulness → thinking) in the proposed model.
Let us elucidate a bit more about the currently dominating two-state modelling approach. The field of brain states modelling has a strong history of using mathematical models to illustrate an understanding of sleep-wake cycling and circadian rhythms in general (Refinetti
et al.,
2007). These cyclic phenomena motivated the development of the classical mathematical models for sleep-wake regulation which include the two-process model for the timing of sleep based on the interaction of the homeostatic sleep drive and the circadian rhythm (Borbely,
1982; Daan
et al.
1984), coupled oscillator models for the same interactions (Strogatz,
1987; Kronauer
et al.,
1982) and the reciprocal interaction model for REM sleep cycling (McCarley and Hobson,
1975; McCarley and Massaquoi,
1986). Although generally phenomenological in nature, each of these mathematical models had a significant impact on the field by formalizing conceptual models to guide experimental investigations, and by providing a context for interpreting experimental data (Booth and Diniz Behn,
2014).
Recent advances in the clarification of the neural anatomy and physiology involved in the regulation of sleep and circadian rhythms have motivated the development of more detailed mathematical models that extend the approach introduced by the classical reciprocal-interaction model (Booth and Diniz Behn,
2014). Motivated by these recent results, mathematical models with a stronger conceptual basis are being developed to provide quantitative underpinnings for the classical physiological models.
The fact that a physiological rhythm could oscillate not only in the absence of periodic changes in the environment, but also at a period different from that of behavioural cyclicity, established the endogenous and physiologic nature of human circadian rhythms for the first time by Kleitman (
1963). Today it is already known that there exist endogenous sleep-regulating substances, build up in the body’s cerebrospinal fluid during our waking hours, which have the effect of increasing the pressure to sleep the more it accumulates. There are also theories, associated with the role of adenosine (core of ATP), that our regular desire for sleep comes from the periodic needs of the brain to replenish low stores of energy. However, we are a bit sceptical about such purely empirical findings as they do not provide fundamental reasons for understanding the cause of underlying intrinsic processes, which govern build-up of these substances during our waking hours. We have to look for answers to what causes such processes.
The endogenous factors are being investigated in various ways, mainly using neurophysiological data of neuronal activities, for instance, one can be referred to the sleep-wake studies (Borbely,
1982; Daan
et al.,
1984; McCarley and Hobson,
1975; McCarley and Massaquoi,
1986; Booth and Diniz Behn,
2014). However, due to the associated complexity and controversial results, researches assume existence of some sort of the homeostatic processes, which take the form of a relaxation oscillator that results in a monotonically increasing ‘sleep pressure’ during the time awake that is dissipated during sleep. Switching from wake to sleep and from sleep to wake occurs at the upper and lower threshold values of the sleep pressure respectively, when the thresholds are modulated by an approximately sinusoidal circadian oscillator (Skeldon
et al.,
2014; Booth and Diniz Behn,
2014).
Admittedly, both the ‘sleep pressure’ relaxation (homeostatic) oscillator and circadian oscillator are of intrinsic endogenous nature. The latter oscillations have been genetically encoded following daily natural rhythms of the sun’s activity during a day. However, despite recent discovery of above mentioned sleep-regulating cerebrospinal fluid substances or the role of adenosine, there is a lack of conceptual understanding of fundamental processes, which produce such endogenous homeostatic ‘sleep pressure’ regulators. Although there are some biological markers, the literature does not propose comprehensive explanations pertaining to the underlying fundamental mechanism.
In this regard, we were not so much concerned about finding a feasible empirically based physiological model for circadian or homeostatic rhythms modelling. Instead, we were concerned about finding a conceptual way for modelling and understanding of the fundamental principles of the so-called “homeostatic pressure” mechanism. The underlying fundamental reasoning of the homeostatic drive has yet to be understood.
Thus, the authors treat the brain as an organ with an intrinsic adaptive behaviour, constrained by fundamental physical and biological laws. It is assumed that self-organized oscillatory dynamics of free energy and entropy serves to keep brain homeostasis within certain confines. In this way, the brain as a complex biological organ, presumably maintains oscillatory self-organization that evokes brain states dynamics during a day.
In this regard, the main conceptual idea of this paper concerns deductive assumption, that the homeostatic relaxation oscillator can be nailed down to the fundamental free energy and entropy rhythmic processes taking place in the brain during a day period. Based on this assumption, we constructed a new way of modelling oscillations in the brain system that exhibit homeostatic adaptive behaviour. We argue that proposed fundamental endogenous model can simulate homeostatic rhythmic dynamics of brain states in a more meaningful way compared with the classical ‘sleep pressure’ modelling approach.
Terminology. Below we provide explanations of some basic terms used in the paper. In the proposed model, entropy (used instead of the ‘homeostatic sleep pressure’ term) and free energy terms are admitted as intrinsic and fundamental properties of the brain system. In the proposed approach, circadian daily rhythms occur endogenously, driven by marginal entropy values, which impose the homeostatic probabilistic transition processes between four basic brain states. In this fundamental research, we provide not only a theoretical model, but also some pilot simulation results of daily rhythms modelling. The proposed simulation model produces homeostatically driven self-organized circadian dynamics of brain states for two types of chronotypes. In this way, we investigate model’s validity depending on the chosen basic characteristics of the simulated agents. The term “agent”, explicitly used in the paper, refers to a human represented in terms of the basic brain states.
The free energy term, according to Helmholtz, is a quantity defined as the amount of useful work that is obtainable from a system while keeping its volume and temperature constant. Like the total internal energy, the free energy is a thermodynamic state function.
The term ‘stylized’, used for the free energy and entropy modelling, indicates that we are using only metaphoric estimates for the conceptual modelling purposes. We clearly admit that stylized estimates of free energy and entropy do not represent real physical values. However, stylized estimates represent similar mutual relations and constraints as real ones. Hence, they do fit for the conceptual modelling purposes.
The term ‘chronotype’ is used as the internal circadian rhythm or body clock of an individual that influences the cycle of sleep and activity in a 24-hour period. A nice overview of probing the mechanisms of chronotype using quantitative modelling can be found in Phillips
et al. (
2010). According to Skeldon
et al. (
2017) model, without artificial light humans wake up at dawn. Artificial light delays circadian rhythmicity and preferred sleep timing and compromises synchronization to the solar day when wake-times are not enforced. When wake-times are enforced by social constraints, such as work or school, artificial light induces a mismatch between sleep timing and circadian rhythmicity (‘social jet-lag’).
The term ‘open system’ is used as in thermodynamics and physics – a system where matter and energy can enter or leave, in contrast to a closed system where energy can enter or leave but matter cannot.
The term negentropy, according to Willard Gibbs, is the amount of entropy that may be increased without changing the internal energy or increasing its volume. In other words, it is the difference between the maximum possible entropy, under assumed conditions, and its actual entropy. Usually, negentropy is denoted as negative; therefore, we use the modulus. Negentropy for the dynamically ordered sub-system can be redefined as the specific entropy deficit relative to the surrounding chaos.
REM – Rapid Eye Movement during a dreaming state while sleeping. NREM – Non Rapid Eye Movement during a deep sleep state.
In the next section, the conceptual model is presented in terms of entropy and free energy. The third section describes the stochastic modelling of marginal and in-between transitions among BBS. The fourth section presents simulation results. The fifth section gives a brief discussion. The last section makes conclusions.
2 Modelling Brain States Using Stylized Free Energy and Entropy Terms
In this section, a specific purely conceptual research question is posed: whether there is a way to model the basic brain states (BBS), using free energy principles. After a discussion in terms of information theory below, this section describes how stylized Helmholtz free energy principles can be applied. Meanwhile, BBS characterization is presented in the third section, where each state is parameterized and a set of equations for the transition probabilities between states is set out. There we describe a discrete non-Markov stochastic process over four states, where transition probabilities depend basically on the (i) entropy and corresponding energy level of the current brain state, (ii) time of day and (iii) chronotype.
Hence, before delving deeper into the modelling subject, let us remind the context of this endeavour. In fact, the physiological mechanisms underlying interindividual differences in the chronotype are yet to be established, despite that both the circadian and homeostatic processes, proposed in the mainstream research, are involved. Admittedly, physiologically-based models are developed by combining the models of the sleep-wake switch and circadian pacemaker, providing a means for examining how interactions between these systems affect the chronotype (Phillips
et al.,
2010).
Following the traditional approach, some circadian (e.g. period and amplitude) or homeostatic (e.g. clearance and production rates) parameters should be adjusted in order to obtain different behaviour of chronotypes. However, in our model, different chronotypes are obtained not by substantial tailoring of circadian and homeostatic terms, but by introduction of chronotype dependent probabilities of transitions between brain states, which in turn are related to the specific dynamic patterns of entropy and energy change.
Coming back to the main issue, while searching for the most basic generalization of the neural metabolic processes, our attention was attracted to the universal thermodynamic laws. Admittedly, the brain as a complex biological system has to function according to these laws, where free energy as a primal energy source and entropy as a primal measure of order, play a key role. Following this line of thought, we admit that agent’s brain states are essentially dependent on the means of using available free energy, which can be exploited for every kind of cellular and consequently neural metabolic activities. It implies that neural metabolic activities, being specific for each BBS, can be recognized in terms of the specific dynamic patterns of entropy and energy change.
Admittedly, there are a few free energy interpretations. We adapted the Helmholtz free energy principle, which is commonly used for systems held at constant volume and temperature (as it is in the brain). For a system at constant temperature and volume, the Helmholtz energy is minimized at equilibrium. In fact, the equilibrium is a major condition. It applies to gases, liquids, solid matter and even living cells and organs. But how is this equilibrium achieved in the brain? Before delving into explanations, we do acknowledge that, strictly speaking, blood circulation makes the brain function as an open system. Blood stream, pressure and temperature are kept constant over time. The blood provides nutrients (energy source) and keeps away waste products while fuelling the whole brain system. In this sense, the brain can be understood as a biological engine, which keeps equilibrium (minimum of free energy), constant volume and temperature while performing a useful work, i.e. maintaining basic brain states, which are specific concerted neural processes involved in the consumption of comparatively large amounts of free energy (usually, even at rest, the brain consumes energy 10 times more than the rest of the body per gram of tissue, which indicates very intensive and dynamic neural processes).
Similarly, like inanimate matter in idealized conditions, the brain operates in highly idealistic and stable conditions regulated by the homeostatic physiological mechanisms. Homeostasis refers to stability, balance, or equilibrium within a cell, organ or the body. Hence, through the homeostasis it is the ability of an organism to keep a constant internal environment in the brain as an organ. In this sense, homeostasis is an important characteristic of equilibrium observed in the living forms. Keeping a stable internal environment requires constant adjustments as conditions change inside and outside the brain (e.g. osmoregulation, thermoregulation, chemical and endocrine metabolic regulation, etc.). In fact, all vertebrates have a blood-brain barrier that allows metabolism inside the brain to operate differently from metabolism in other parts of the body. Glial cells play a major role in brain metabolism by controlling the chemical composition of the fluid that surrounds neurons, including levels of ions and nutrients.
In our generalized model (see below), we take the above mentioned considerations, assuming that free energy is constantly minimized, i.e. is time constant. Hence, we do not solve here the problem of free energy minimization while doing some cognitive tasks. Instead, we are focusing on (i) the more general representation of basic brain states as entropy and energy processes, and (ii) modelling of stochastic transitions between basic brain states during a day period.
Now let us examine some basic principles of thermodynamic (Helmholtz) free energy
where the free energy term
A denotes the amount of work that a thermodynamic system (state function) can perform (like the total internal energy, the free energy is a thermodynamic state function);
U is the total internal energy of the brain system
$U>A$;
T is an intensive measure in thermodynamics called temperature, which in a more general sense, is sensitivity measured as the partial derivative of the internal energy
U with respect to the entropy
S
Instead of entropy for the biological systems, following Brillouin (
1953), Pitkänen (
2006), we can also use the term of negentropy,
N
Here,
${S_{\max }}$ denotes the maximum possible entropy in the brain system and
N denotes negentropy. For the sake of simplicity, we can interpret negentropy as order and entropy as disorder. As the entropy
$S\to {S_{\max }}$, the order (negentropy) in the system disappears, whereas, in the case of
$S\to 0$, the negentropy increases
$|N|\to {S_{\max }}$.
Hence, the product of
$\big(\frac{\partial U}{\partial S}\big)S$ plays an important role. The term
$\big(\frac{\partial U}{\partial S}\big)$ denotes the sensitivity of the change in total internal energy
$\partial U$ with respect to the change of entropy
$\partial S$, see Eq. (
2). Let us denote this sensitivity of the brain’s internal energy to the change in entropy by
η. This sensitivity parameter is individual and can vary for each agent, depending on the level of entropy
$\eta =f(S)$.
In our model, we also propose two fundamental ingredients for the total internal energy
U, i.e. stylized kinetic
${E_{k}}$ and stylized potential
${E_{p}}$ energy
where
${E_{k}}$ denotes all experimentally measurable corpuscular types of energy at the level of molecular movements. Whereas,
${E_{p}}$ denotes a form of the field-like “potential” energy, e.g. electromagnetic field energy emitted in the case of the EEG measurements, i.e. the spectral power of the measured fields of brainwaves - delta, theta, alpha, beta and gamma spectral bands (Plikynas
et al.,
2014a,
2014b).
Hence, according to the proposed approach free energy A is the source of useful energy (work), which expresses itself in the expendable energy forms of ${E_{k}}$ and ${E_{p}}$. As it was mentioned before, the nature of the source of free energy itself is beyond the current scope of our research.
Following Eq. (
2), the model also provides another important observation for the partial derivatives
Admittedly, for all known thermodynamic systems
$\textit{TS}>0$, as
$T>0$ and
$S>0$. That is, there are no biological systems with
$T\leqslant 0$ or
$S\leqslant 0$. Thus, the term
$T>0$ implies
$\delta {E_{k}}/\delta S\ne \delta {E_{p}}/\delta S$, see Eqs. (
2), and (
4). Next, we can deduce that
$\delta {E_{k}}/\delta S>0$ and
$\delta {E_{p}}/\delta S<0$, as the increase in entropy, certainly increases the thermal kinetic energy (heat)
${E_{k}}$, but decreases the negentropic potential energy
${E_{p}}$. Let us to remind that
${E_{p}}$ denotes field-based coherent EEG brain wave oscillations (delta, theta, alpha, beta, and gamma) or in other words ordered spectral patterns that stand out opposite to white noise spectra produced by heat oscillations (Plikynas,
2016).
In order to have
$T>0$ condition (see Eq. (
1)): if
$A>0$ and
$U>0$ then
$T>0$ and
$S>0$), the rate of change for
${E_{k}}$ and
${E_{p}}$ with respect to the change in
S has to be different (see Eq. (
5)), i.e.
In the proposed model, the potential energy refers to the mind-field type of energy, which can account for a minor portion of all the internal energy
U, where the thermal kinetic energy composes a major part. In this regard, one can say the other way round: slight reduction of the potential mind-field energy (brain wave coherence) can significantly increase entropy and the related thermal kinetic energy. Hence, in this model, we assume that the potential mind-field energy acts like a subtle brain power trigger (Plikynas,
2016).
For some people it might be better understood in terms of a field-effect transistor, where the terminals are labelled as gate, source, and drain, and a voltage at the gate (i.e. potential energy in our model) can control the current between the source and drain (i.e. kinetic energy in our model). For others, who are more theory-driven our approach might be better understood in terms of McFadden’s electromagnetic theory of consciousness, Pribram’s holonomic brain theory, Hameroff-Penrose Orchestrated Objective Reduction theory, etc. Such type of the research frontier has made room for field-theoretic modelling of consciousness (Libet,
2006; McFadden,
2002; Pessa and Vitiello,
2004; Pribram,
1999; Thaheld,
2005; Travis and Arenander,
2006; Travis and Orme-Johnson,
1989; Vitiello,
2001).
While looking for basic stylized mathematical functions suitable to represent the above-mentioned energy relationships, we employed a nonlinear logistic function, observed naturally in various biological systems. Admittedly, this function finds many applications throughout a vast range of fields, including biology, neural networks, ecology, biomathematics, chemistry, economics, geosciences, sociology, political sciences, etc.
Here we applied the classical logistic function, widely used for the versatile growth modelling inspired by nature. Hence, we assume that it is able to depict various nonlinear energy dependencies on S. To our knowledge, there are no plausible models with other functions employed in the similar simulation setting. In fact, for us it is most important that logistic functions are often used in neural networks and other artificial intelligence approaches to introduce nonlinearity in the models and to clamp signals within a specified range. Naturally logistic functions are a common choice for the activation or “squashing” functions, used to clip large magnitudes in order to keep the response bounded. Based on the above considerations, we employed it for the relation between energy dependencies on S.
The generalized logistic function has plenty of parameters that allow its flexibility and ability for adaptation in many applied cases.
where
${S_{0}}$ denotes the moment of maximum growth,
L denotes the curve’s maximum value and
k denotes the steepness of the curve. The values of these parameters were chosen to satisfy the below described
${E_{k}}(S)$ and
${E_{p}}(S)$ dependencies.
Hence, the logistic function is employed for the mathematical representation of the
${E_{k}}(S)$ and
${E_{p}}(S)$ dependencies. All other dependencies such as
$U(S)$,
$A(S)$,
TS were derived from these two, see Fig.
1, where we can see, the
${E_{k}}(S)$ and
${E_{p}}(S)$ dependencies so that to satisfy constant minimum energy level
$A=\text{const}=1$. In this way, we obey the main property of the free energy definition.
In order to plot the stylized
${E_{k}}$ and
${E_{p}}$ curves depicted in Fig.
1, we used the parameters of
${S_{\min }}=0$,
${S_{\max }}=1$,
$dS=0.01$,
${K_{s}}=15$,
${E_{k\min }}=0.5$,
${E_{k\max }}=0.9$,
${S_{0\hspace{0.1667em}{E_{k}}}}=0.45$,
${K_{k}}=15$,
${E_{p\min }}=0.4$,
${E_{p\max }}=0.5$,
${S_{0\hspace{0.1667em}{E_{p}}}}=0.55$, and
${K_{p}}=14$. The other curves
$U(S)$ and
$A(S)$ were obtained using the term provided below, see Eqs. (
1) and (
4).
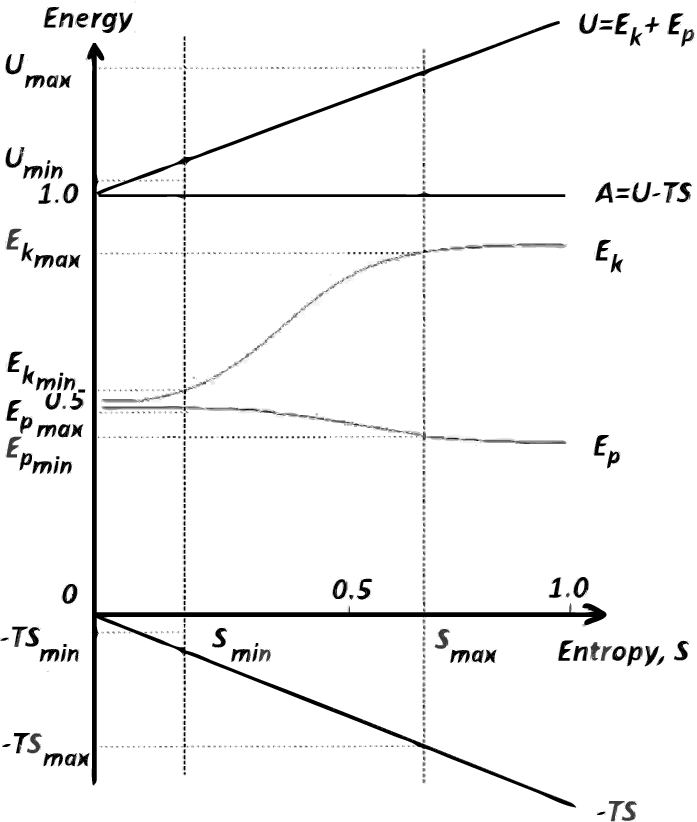
Fig. 1
Principal scheme of basic relationships between the entropy S and the dependant forms of energy ${E_{k}}(S)$, ${E_{p}}(S)$, $A(S)$, $U(S)$, and $-T(S)\cdot S$. Arbitrarily chosen entropy values ${S_{\min }}$ and ${S_{\max }}$ denote individual marginal conditions.
In Fig.
1, the assumption
$A=1$ comes from the description of the proposed model. In fact, the dependencies
${E_{k}}(S)$ and
${E_{p}}(S)$ were chosen so that to satisfy the constant minimum energy level
$A=\text{const}=1$. In this way, we obey the main property of the free energy definition. Let us explain it below.
First, we remind that just like the total internal energy, the free energy is a thermodynamic state function. According to Helmholtz, the free energy is a quantity defined as the amount of useful work obtainable from a system while keeping its volume and temperature constant. Second, the brain operates under highly idealistic and stable conditions regulated by the homeostatic physiological mechanisms. Homeostasis refers to stability, balance, or equilibrium within an organ (brain). It is the ability of an organism to keep a constant internal environment in the brain as an organ. In this sense, homeostasis is an important characteristic of equilibrium observed in the living forms, which keeps constant the free energy level at all costs.
When free energy starts to increase, self-organizing brain processes accelerate (transition to the active brain states takes place) in order to reduce the free energy level. The opposite happens when free energy starts to decrease. The brain processes start to slow down (transition to the passive brain states takes place) in order to maintain the free energy level within allotted bounds. Thus, the free energy level fluctuates within narrow bounds. However, we made simplification assuming that free energy is fixed and for modelling purposes equals 1. This chosen number can be different, but it does not make a big difference in terms of the scale-invariant features of the abstract model. Namely, we can use any multiplayer if needed.
In the proposed model, free energy as a constant factor was achieved using (i) aforementioned self-regulating dynamics of brain states, and (ii) interchange mechanism between potential
${E_{p}}(S)$ and kinetic
${E_{k}}(S)$ forms of free energy constituents. Both processes follow characteristic dynamical patterns (see Section
3).
Certainly, to know empirically and model exact values of the brain entropy and energy is not possible at the current state of neuroscience. Therefore, we have to emphasize again that the differential Helmholtz free energy equation should be interpreted as a means to model prevailing brain states in terms of stylized entropy and energy. Hence, we clearly admit that stylized estimates of free energy and entropy do not represent real physical values. However, the universal thermodynamic free energy equation revealed some important relations and constraints between entropy and energy dynamics, which most probably takes place in the brain.
In the next section, each basic brain state (BBS) as a dynamic process will be parameterized using above described stylized entropy and energy time dependent relations. Besides, we will introduce a stylized self-organizing mechanism of transitions between the basic brain states during a day period, where adaptive transitions between brain states lead to homeostatic rhythms and activity patterns of complex daily rhythmic brain states.
3 Analytical Modelling of Basic Brain States and Transition Dynamics
In this section, we first construct analytical representations of four basic brain states (BBS) as processes led by the specific entropy dynamics. The presented numerical modelling is not inductively derived from empirical data, although, inevitably it has been framed by some well-known empirical observations. The presented deductive approach utilizes modelling of brain states as stylized entropy processes, described in Section
2.
The second part of this section concerns analytical modelling of transitions between states as a discrete non-Markov stochastic process, based on the (i) entropy margins and transition probabilities, (ii) entropy and corresponding energy level of the state, (iii) time of day, and (iv) chronotype.
Hence, the presented model aims to simulate dynamics of BBS homeostatic-driven rhythms during a day. That is, we strive to create a self-regulating process of brain states dynamics using the above-described theoretical setup. In this section, we briefly present some practical ideas related to the simulation model design. It mainly concerns description of probabilistic marginal and in-between transitions between BBSs.
In the next section, numerical simulation results are presented, that indicate multiple probabilistically repeating occurrences of each state during a day. That corresponds to the experimental observations of the dynamics of real human states during a daytime and night-time, e.g. multiple repeating cycles of altering duration for the REM (BBSRE as dreaming), NREM (BBSDS – deep sleep) and wakeful (BBSAW) states during the night-time (Dijk,
1999; Möller-Levet
et al.,
2013; Nielsen
et al.,
2011) or similarly, during the daytime – multiple repeating cycles of altering duration for the BBSAW, BBSTH (thinking) and BBSRE states.
Before delving deeper into the analytical model details, let us remember that historically the mathematical two-process model was introduced by the well-known seminal work of Daan
et al. (
1984) and extended by Borbély and Achermann (
1999). As indicated by its title, the two-process model proposes that the sleep-wake cycle can be understood in terms of two processes, a homeostatic process and a circadian process. The homeostatic process takes the form of a relaxation oscillator that results in a monotonically increasing ‘sleep pressure’ during the time awake that is dissipated during sleep. Switching from wake to sleep and from sleep to wake occurs at the upper and lower threshold values of the sleep pressure respectively, when the thresholds are modulated by an approximately sinusoidal circadian oscillator.
Hence, traditional circadian models employ time dependent, exponential, two-process growth and decline functions, which are bounded by the circadian harmonic function. Hence, transitions occur when the exponents of the vaguely explained term “sleep pressure” approach the harmonic (circadian) function. In essence, it means that the marginal values for the two-process states are determined by the circadian harmonic function and vary during the day following the harmonic function.
In our model, entropy S is admitted as an intrinsic and fundamental driver of the brain states dynamics. Entropy defines more exactly the term “sleep pressure”, used in the classical two-process model. In the proposed approach, the homeostatic cycles occur naturally as a consequence of a) state dependent $S(t)$ dynamics and b) probabilistic (marginal and so-called in-between) transitions between states. In this regard, our model proposes a novel approach. It provides a stylized entropy and energy-based framework for the investigation of daily BBS rhythms.
It is important to remind that entropy
S in the proposed model has been constrained by lower
${S_{\min }}$ and upper
${S_{\max }}$ bounds, see Fig.
1. These marginal entropy values set constraints on the state entropy
$S(t)$ process. When the process
$S(t)$ reaches a lower or upper bound, the so-called marginal transition to another state occurs. The probability of transition to the particular another state depends on the current state, chronotype, and time of day.
According to the model setup, during activity (thinking and physically active states) entropy increases as brainwork processes increase the waste of free energy in the form of heat (entropy). Whereas, during resting (NREM and REM sleep) entropy decreases as brainwork processes are eliminating the excess of heat (entropy). Naturally, both processes have some bounds, that direct to the brain’s self-organizing mechanism to stop the current state process and switch to the opposite process (active vs. resting). Hence, entropy bounds act like a thermostat to keep system condition within certain homeostatic confines.
However, there is no fundamental difference between imposing a threshold that is oscillating and then adding some stochasticity to this, as was done for some of the earlier two-process model simulations, and introducing a probabilistic transition function that is oscillating in the presented model approach. In both cases, the rhythmicity is essentially imposed as part of the modelling assumptions. However, the main conceptual difference lies in the interpretation of the underlying oscillatory mechanisms. That is, the classical two-process model does not define a mechanism for occurrence of “sleep pressure” (a relaxation oscillator), although, it uses some biological markers intrinsic to this mechanism. Whereas, our model defines a possible fundamental mechanism for occurrence of a relaxation oscillator, which consequently eliminates the need to employ the “sleep pressure” term.
In our model, the underlying oscillatory mechanism is not solely based on the oscillating probabilistic transition function. It is important to note that the main novelty is in the simulation of the basic four brain states as self-organized energy and entropy processes, bounded by the daytime dependent entropy floor ${S_{\min }}(t)$ and ceiling ${S_{\max }}(t)$ values. To our knowledge, there are no other plausible models with similar simulating settings.
In the proposed model, transitions between BBS are visualized in the form of directed graphs, see Fig.
2. Directed graph approach stems from the transition (between states) assumptions constructed in the simulation model, which in turn is based on some empirical observations (Dijk,
1999; Möller-Levet
et al.,
2013; Nielsen
et al.,
2011) and also from the seminal work of Daan
et al. (
1984) and extended by Borbély and Achermann (
1999). It defines not only allowable transitions in the proposed model, but also their relative frequency.
Probabilistic transitions invoked by the marginal entropy limits are indicated using solid lines, and that, invoked by the in-between probabilities, are indicated using dashed lines. In this way, the basic brain state related processes (free energy and entropy) are governed by the thermodynamic processes (see Eqs. (
4), (
5) and (
8)) and transitions between states are governed by the probabilistic rules.
As can be inferred from Fig.
2, all the BBS participate in the daily dynamics. However, according to the model setup, some states naturally dominate. For instance, marginal transitions prevail between BBSAW and BBSRE. Whereas during the daytime, in-between transitions between BBSAW and BBSTH naturally prevail. At night-time, in-between transitions between BBSDS and BBSRE naturally dominate.
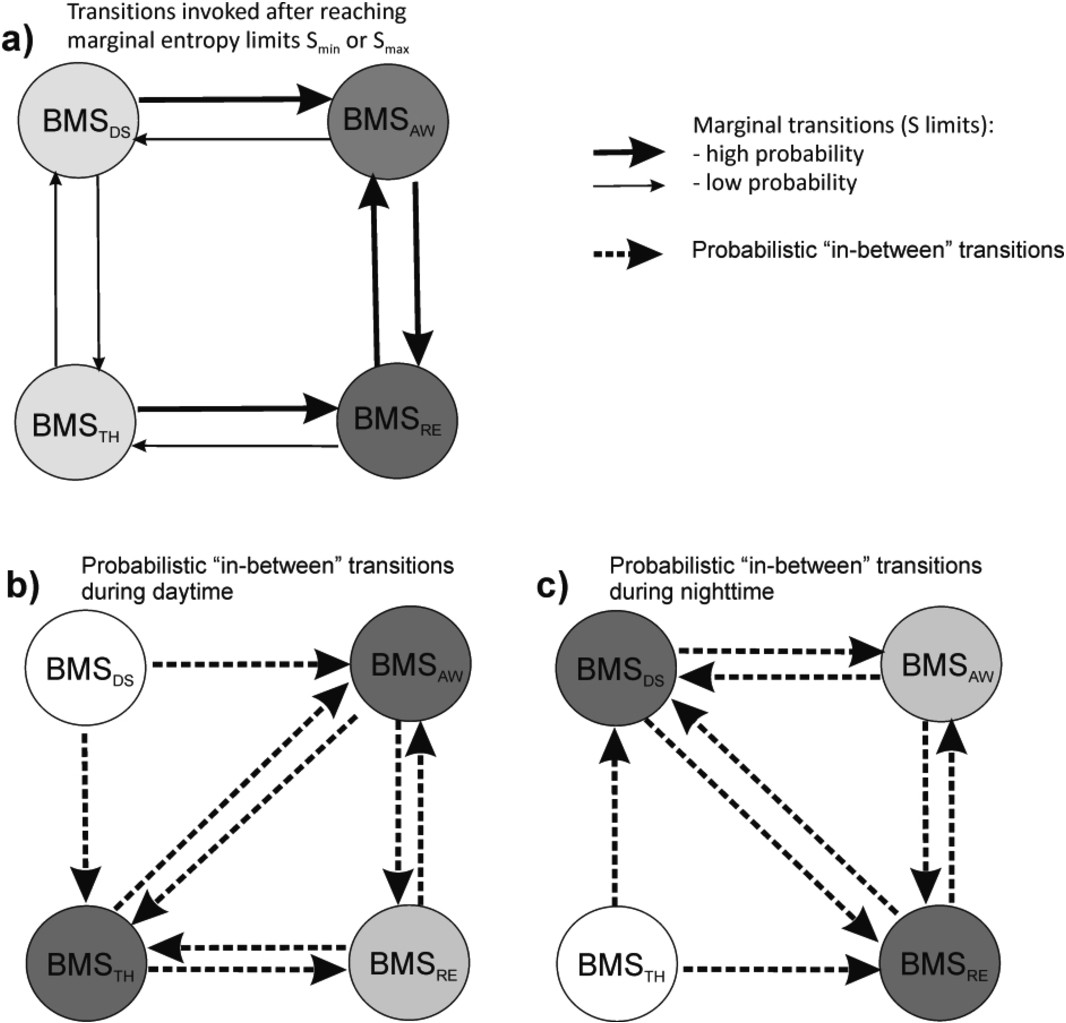
Fig. 2
Directed graphs for the depiction of nodes (BBS) and the transitions between them (directed lines). The more frequent states (shaded nodes) indicate the average time spent in the corresponding BBS and the thickness of the directed lines indicates the probability level of the transitions. Part (a) indicates marginal transitions when the ${S_{\min }}$ or ${S_{\max }}$ limit is reached. Parts (b) and (c) indicate probabilistic in-between transitions during daytime and night-time respectively.
It is important to emphasize that according to the model setup at each time moment an agent’s brain state is basically described by the entropy $S(t,n)$, where t denotes duration of the state ($t\leqslant 100$ minutes) and n denotes the number of a discrete period of the day $n=(1,72)$. In this way, the agent’s state dynamics is allowed to move in the network of predestined paths in the entropy space.
Thus, each 10 min time period during a day is represented by 4 specific
$S(t,n)$ curves. Each BBS has its own family of
$n=72$ specific day time period, dependent on entropy curves. These curves cover the daytime and night-time periods. That is, depending on the states, the daytime curves start from one end and the night-time curves from the other end of the same set of 72 entropy curves, see Fig.
3. In this way, the model is able to distinguish how 1) the BBS related entropy processes gradually change during a day, 2) the daytime and night-time related entropy curves shift in the opposite directions.
In order to obtain a set of entropy curves, a new homeostatic-circadian function ${c_{n}}(t)$ was employed, which generated a continuous and dense enough family of 72 curves $S(t,n)$ for each state depending on the period of the day (daytime and night-time separately). For each state, a corresponding family of 72 curves covers a daytime or night-time period separately. For instance, during a daytime period of $1440/2=720$ min, 72 curves, each covering a $720/72=10$ min interval of a daytime period are generated. A similar principle holds for the night-time period too.
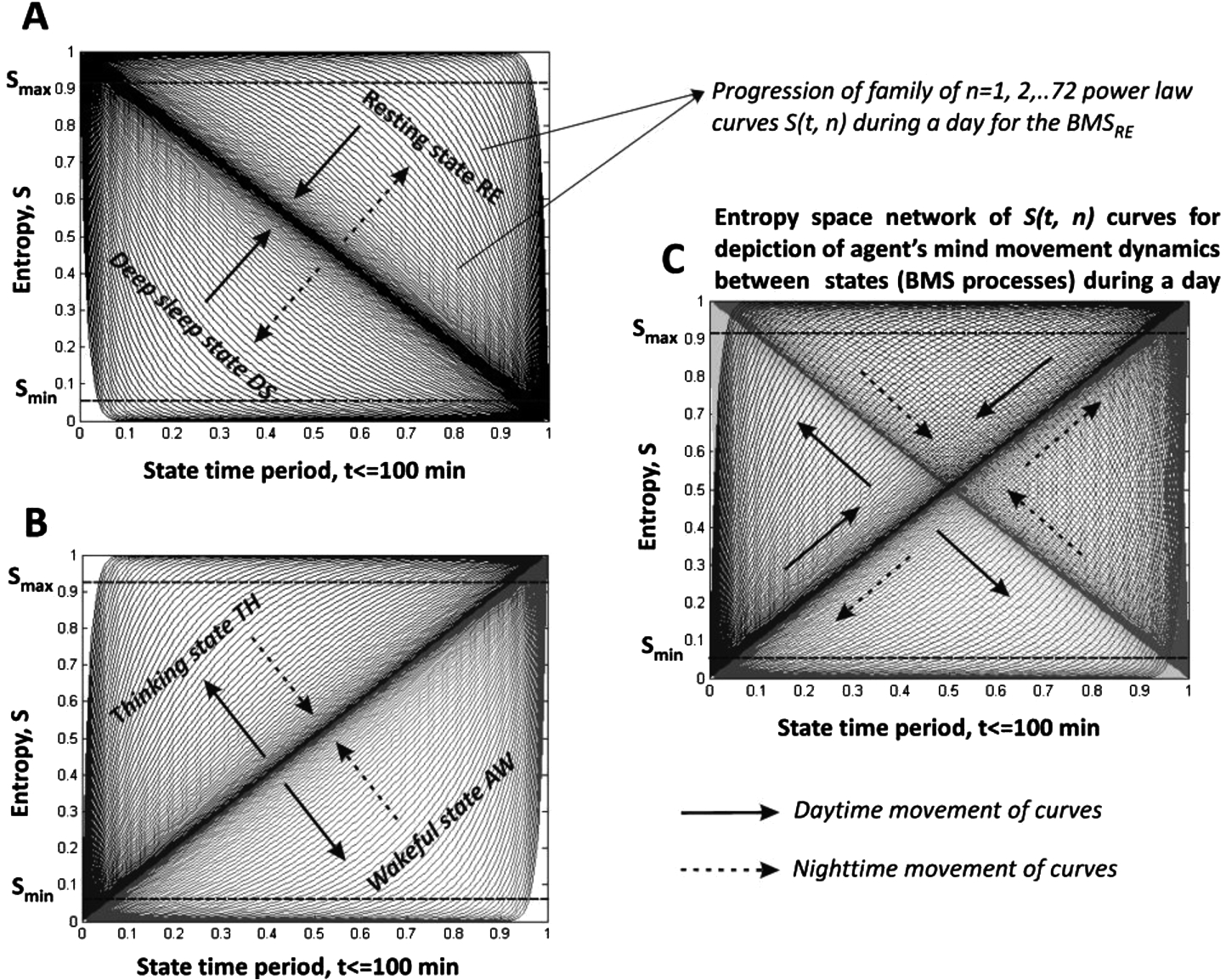
Fig. 3
Entropy space network $S(t,n)$ characterized by the corresponding families of the BBS related curves (72 curves for each state), which are used for the simulation of the S(t) dynamics for the daytime and night-time periods. Diagram A denotes the families of curves for the deep sleep (DS) and resting (RE) states. Diagram B denotes the families of curves for the wakeful (AW) and thinking (TH) states.
Hence, a new set of proposed mathematical
$S(t,n)$ formulas that generate the needed sets of entropy curves for each state, depending on the period of daytime or night-time, are depicted below
where rotation
R and shifting Φ operators are used to transform the
$S(t)$ function
here, the parameter
$\theta =\pi $ (in radians) denotes an angle for the rotation operator
R. The other variables, namely
t,
$\bar{t}$ and
n, contribute to the formation of the homeostatic and circadian rhythms during the day:
-
a) homeostatic individual curves $S(t)$ for each BBS, where t denotes the state related time period ($t<100$ min)
-
b) circadian movements of the homeostatic curves $S(n)$, depending on the period n of the day.
In fact, the variable
$\bar{t}$ denotes the inverse of
t, as after the use of rotation operator
R, the function is rotated by
π, rendering
$t=[1,0]$, and, consequently, the points of the corresponding curves are drawn in a reverse order, see Eqs. (
9), (
10) and Fig.
3. In order to restore the correct order, the time flow from 1 to 0 has to be corrected, using the inverse variable
$\bar{t}$.
Let us explain that the states as time varying entropy processes were defined analytically in Eqs. (
9) and (
10). Next to them variables and parameters are described for numerical estimates. We chose them in order to construct each state’s unique course in the entropy space, depending on the time of the day.
Thus, each state is progressing in the entropy space, see Fig.
3, but in a different way. Each state’s progression way has the corresponding mathematical function (see Eq. (
9)), which has to be parameterized (see Eq. (
10)). The functions and parameters were uniquely created and fitted in order to follow the proposed model’s assumptions. One of the main assumptions is that the shape of each state’s progression function is changing during the day. For instance, we propose a linear thinking state’s entropy progression function early in the morning (assuming that the brain had a good rest after the night sleep and involvement in the thinking process only slowly adds a fatigue, i.e. entropy), but gradually it becomes more and more hyperbolic during the course of the day (meaning that at the late evening time our mind gets tired and we get exhausted by the thinking process very fast), see the left lower diagram of a family of the corresponding thinking state entropy curves in Fig.
3.
We have arbitrary chosen a discrete set of corresponding curves (the same number of curves for a day and night $n=72$, corresponding to 10 min time interval between adjacent curves), meaning that one curve fits only for the 10 min time interval of the day. After this period another adjacent curve should be used and so on. In fact, one can choose as many curves as one pleases or even can use a non-discrete approach in another model. We have chosen a discrete family of curves for each state progression in the entropy space only in order to make a better visualization case of the model.
The proposed entropy space network of the
$S(t,n)$ curves restricts the entropy dynamics in certain pathways, described in Eqs. (
9) and (
10). The brain travels through these pathways during the day. At each time moment, the brain is involved in one entropy related process, which draws (actualizes) an associated curve’s section in the entropy space chart, see Fig.
3. In each simulation, the probabilistic nature of the transitions between brain states makes a unique pattern for the
$S(t,n)$ curves.
Admittedly, the law of entropy conservation should hold during transitions between states. Hence, there should be no gaps between the entropy levels when the transitions between states take place. That is, the continuity of entropy level holds during transitions and the next state proceeds from where the last state ends. The proposed entropy-based BBS modelling approach follows the conservation law in a mathematical sense; however, due to some programming approximations an attentive reader can notice slight shifts between S levels in the simulation results (see the next section). Notwithstanding such a drawback, which is stemming purely from the programming approximation, the mathematics of the model remains firmly in accordance with the law of succession of entropy.
Let us see an example for the BBSDS: during the night-time, the occasionally repeating deep sleep state gradually becomes shorter as the brain alternately shifts from the NREM to REM and awaking states (this is a well-known fact, well reported and documented in the mainstream literature (Booth and Diniz Behn,
2014; Borbély and Achermann,
1999; Daan
et al.,
1984; Fulcher
et al.,
2008; Phillips
et al.,
2011)); meanwhile, during the daytime, very occasional deep sleep periods become longer as the brain gets tired during the day and naturally tends to stay longer in the deep sleep state.
Depending on the obtained curves position (see Fig.
3), we can recognize a) the BBS process it represents and b) the time of the day. In this way, similarly like in the traditional phase space charts, we can observe the dynamics of states (attractors), and the main trends of the transitions between states. Admittedly, the phase space of a dynamic system depicts all the possible states of a system (represented in terms of the system’s main parameters) when the system’s evolving state over time traces a path (a phase space trajectory). Thus, the proposed entropy space network visualization approach serves as a useful tool for fast analyses of the simulation results. In the next section, the concrete simulation results of the proposed model are provided.
Let us discuss more about newly introduced in-between transitions, that were additionally incorporated into the model in order to add some stochasticity. According to the chosen model setup, they occasionally happen in all BBS processes before they reach the marginal entropy conditions (${S_{\min }}$ and ${S_{\max }}$). In each BBS, they occur probabilistically. A probability of the in-between transition is likely to increase during time an agent is in a particular BBS. According to the chosen programming setup, the probabilistic in-between transitions are periodically applied (by default, every 10 min) while the current brain state has not reached its marginal entropy conditions. It also depends on the period of the day, where daytime interval $t=[0;0.5]$, and the night-time interval $t=[0.5;1]$ have distinct functions for the in-between probabilities. According to the simulation setup, the daytime period lasts 12 hours [9AM–9PM], and correspondingly, the night-time period is [9PM–9AM].
In the proposed model, the general expression for the in-between probabilistic transitions, depending on whether it is daytime or night-time, is expressed using a simple harmonic function
where
${p^{\prime \max }_{\mathit{BBS}}}$ demonstrates the arbitrarily chosen maximum in-between probability value for each BBS (by default, it equals 0.05);
$2\pi {\nu ^{\prime }}$ denotes angular frequency
ω, where the frequency term
${\nu ^{\prime }}=1/2$ splits the day period (
$\nu =1$) into two parts, i.e. daytime and night-time periods;
t denotes the time of day;
φ denotes the phase shift of the sinusoidal function.
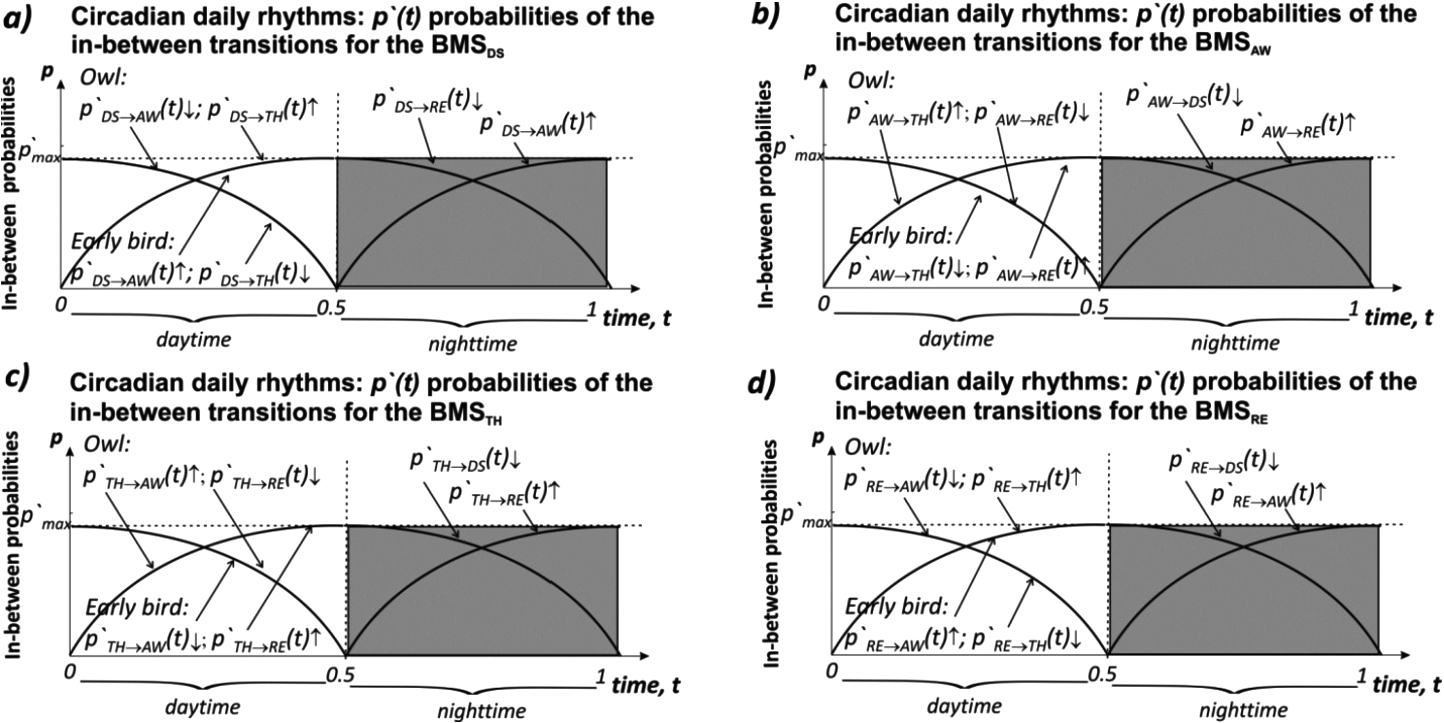
Fig. 4
Daytime and night-time functions of transition probabilities ${p^{\prime }}(t)$ of the in-between transitions for all BBS. The two chronotypes of people – night owls and early birds – are distinguished by their different daytime set of probabilistic transitions.
In the proposed model, we apply the sinusoidal function (see Eq. (
11)) with the corresponding phases and obtain continuous time varying in-between probabilistic transition functions
${p^{\prime }}(t)$ for both chronotypes, see Fig.
4. The chosen sinusoidal form of the transition function
${p^{\prime }}(t)$ curves gives gradual descend and rise of transition probabilities during the day. However, other continuous functions can be employed too. In fact, we have introduced the so called in-between transitions as a mean to overcome limitations of the marginal transitions (see Fig.
2a), as they omit a lot of transitions that take place in reality. In this regard, the presented scheme for the probabilistic in-between transitions helps to sort things out according to the real life observations, allowing for transitions between similar in kind states.
We do not assume that, for instance, evening types (owls) for some reason have a longer intrinsic period then morning types (early birds) (Phillips
et al.,
2010). Instead, based on the empirical observations, we assume that differences between chronotypes’ behaviour can arise because of different dynamics of probabilities of transitions between basic brain states BBS. In our model, probabilities of the in-between transitions were constructed in such a way as to make behavioural difference for both chronotypes. For instance, during daytime the probability of the in-between transitions from the inactive to the active state generally increases for the owls and decreases for the early birds, see Fig.
4. Night-time functions of the in-between transition probabilities
${p^{\prime }}(t)$ for both chronotypes do not differ in this experimental setup, see Fig.
4. However, in the prospective modelling they can be different for both chronotypes too. In this way, we made a difference between chronotypes behaviour, which corresponds with well-known empirical observations.
Hence, the model simulates the behavioural manifestation of the underlying circadian rhythms in terms of people’s chronotypes (night owl or early bird), see Fig.
4. The presented model admits the existence of two different types of people, i.e. “night owls” and “early birds” (Roenneberg
et al.,
2003; Vinne
et al.,
2015). Night owls tend to feel most energetic just before they go to sleep at night. Early birds (e.g. a lark) as opposed to night owls, feel more energetic early in the daytime and tend to feel sleepy at a time that is considered early. Researchers also use the terms “morningness” and “eveningness” for the two chronotypes (Horne and Ostberg,
1976). In this sense, for each chronotype, two different sets of circadian
p‘(t) graphs are depicted for each state, see Fig.
4. In this way, the proposed model is extended to simulate the circadian rhythms of two different types of people chronotypes (Plikynas,
2016).
4 Simulation Results
In this section, we aim to (i) show simulation results and (ii) examine the influence of some basic and optional model parameters. First, we explore a chronotype parameter, that defines the behavioural manifestation of a type of agent in terms of intrinsic circadian rhythms. That is, we model the night owl and the early bird behaviours (Plikynas,
2016). Next, we explore the max and min entropy value parameter that define the available entropy space, which influences the frequency of marginal transitions, i.e. a smaller entropy space makes marginal transitions occur more often. Other parameters define
${E_{p}}$ and
${E_{k}}$ energy margins, etc.
An example of the corresponding simulation results of the basic brain state (BBS) dynamics for the two chronotypes is provided in Fig.
5. All the basic and optional parameters used for obtaining the simulation results were discussed in terms of their meaning and feasible values earlier in this chapter and in the previous studies (Plikynas,
2016). In short, the interplay of these parameters generates simulation results.
Admittedly, night owl chronotype people tend to feel most energetic just before they go to sleep at night. Early bird chronotype people, as opposed to night owls, feel more energetic early in the daytime (Roenneberg
et al.,
2003; Vinne
et al.,
2015). Similar tendencies can be observed in the presented model. An example of the obtained BBS dynamics for both types of chronotypes can be found in Fig.
5a) and b). As we can observe from the BBS dynamics, at the beginning of the day, the night owl chronotype tends to stay longer in the resting state (RE) and deep sleep (DS) states and much less in the wakeful state (AW), whereas, at the end of the day, they stay longer in the active states (AW and TH). Meanwhile at the beginning of the day, the early bird chronotype tends to stay longer in the active states (AW and TH) and less in the passive states (DS and RE), whereas, at the end of the day, they stay longer in the passive states. In fact, such a simulation performance can be regulated using our model setup, see Fig.
2.
The simulation results show some behaviour, close to the real life, at night-time too. For instance, we observe an increase of DSRE(), REAW() and decrease of THDS(), REDS(), AWDS() of transitions at the end of the night period, see Fig.
5. It corresponds well with the setup of the in-between transitions (see Fig.
2) and real life observations.
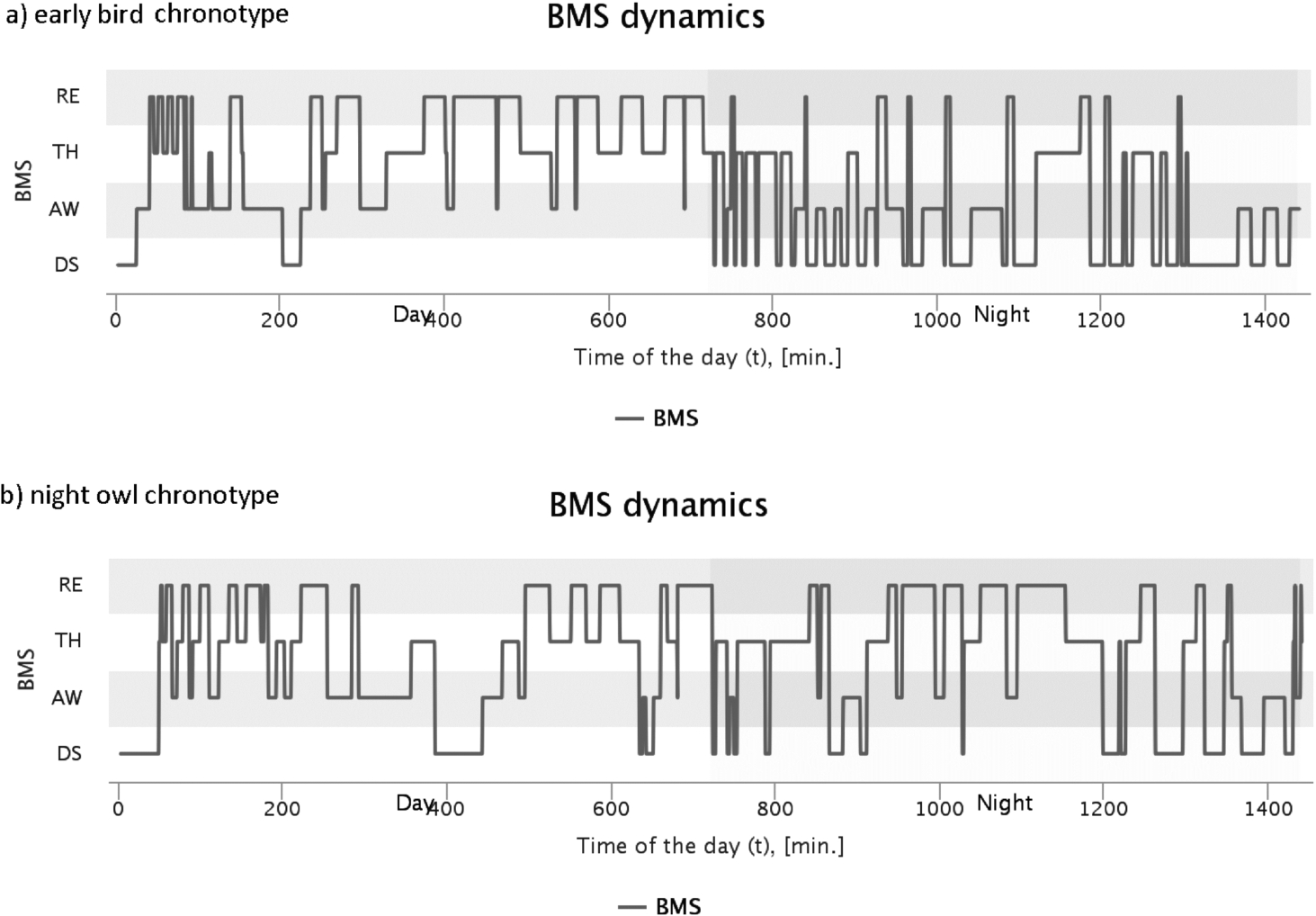
Fig. 5
BBS dynamics of two chronotypes: early bird and night owl. The graphs were obtained using default basic and optional parameters, except the checking time period ($\tau =2$ min) and probability (0.15) of the in-between transitions.
Statistical averages for the reiterated estimates of the number of BBS transitions during the daytime and night-time periods are provided in Table
1. It shows statistical averages for the marginal and in-between transitions. As we can see, the total number of marginal and in-between transitions for both chronotypes substantially change depending on the frequency of the applied probabilistic in-between transitions. That is, larger
τ values generate less frequent marginal and in-between transitions.
The analysis of transitions has revealed slight differences between chronotypes in terms of the total number of transitions during the daytime and night-time. That is, for the early birds more frequent transitions between states are during the night. An opposite tendency is observed for the night owls. It can be explained, keeping in mind that active states of brain have to be consciously controlled in order to prolong their duration. Otherwise, brain is controlled by involuntary (subconscious) transitions, which happen more often due to the intrinsic wandering nature of the mind. Therefore, early birds, being more consciously active in the daytime, tend to have less wandering transitions during the daytime, while night owls, being more consciously active at night-time, tend to have less wandering transitions during the night period.
In Table
2, we summarize simulation statistics of staying in each BBS for both chronotypes during the daytime and night-time periods, with different time periods
τ, which indicate the periodicity (in minutes) of the applied probabilistic in-between transitions.
Table 1
The number of transitions among BBSs. The results were averaged for 20 agents. Time period τ indicates the periodicity (in minutes) of the applied probabilistic in-between transitions.
| Number of transitions |
Early bird chronotype |
Night owl chronotype |
| $\tau =2$ |
$\tau =4$ |
$\tau =6$ |
$\tau =2$ |
$\tau =4$ |
$\tau =6$ |
| Total number of transitions |
102 |
89 |
45 |
121 |
79 |
45 |
| – daytime |
44 |
41 |
24 |
65 |
42 |
23 |
| – night-time |
58 |
48 |
21 |
56 |
37 |
22 |
| Total number of marginal transitions |
41 |
46 |
28 |
50 |
44 |
25 |
| – daytime |
19 |
19 |
16 |
27 |
23 |
12 |
| – night-time |
22 |
27 |
12 |
23 |
21 |
13 |
| Total number of in-between transitions |
61 |
43 |
17 |
71 |
35 |
20 |
| – daytime |
25 |
22 |
8 |
38 |
19 |
11 |
| – night-time |
36 |
21 |
9 |
33 |
16 |
9 |
Table 2
Duration of staying in BBSs (reiterated for 20 agents). The total time spent in each BBS is denoted as $\Sigma {t_{\mathit{DS}}}$, whereas, the average time as ${\bar{t}_{\mathit{BBS}}}$.
| Duration, t [min] |
Daytime/night-time |
Early bird chronotype |
Night owl chronotype |
| $\tau =2$ |
$\tau =4$ |
$\tau =6$ |
$\tau =2$ |
$\tau =4$ |
$\tau =6$ |
| $\Sigma {t_{\mathit{DS}}}$ |
|
358 |
295 |
228 |
225 |
235 |
352 |
| $\Sigma {t_{\mathit{AW}}}$ |
|
358 |
531 |
638 |
246 |
435 |
471 |
| $\Sigma {t_{\mathit{TH}}}$ |
|
358 |
138 |
127 |
429 |
162 |
155 |
| $\Sigma {t_{\mathit{RE}}}$ |
|
366 |
476 |
447 |
541 |
607 |
462 |
| ${\bar{t}_{DS}}$ |
Daytime |
44 (1 tr.) |
0 |
91 (1 tr.) |
16 (2 tr.) |
32 (2 tr.) |
62 (2 tr.) |
|
Night-time |
12 (27 tr.) |
15 |
20 (7 tr.) |
10 (19 tr.) |
19 (9 tr.) |
28 (8 tr.) |
| ${\bar{t}_{AW}}$ |
Daytime |
13 |
16 |
37 |
5 |
14 |
27 |
|
Night-time |
16 |
18 |
44 |
14 |
17 |
31 |
| ${\bar{t}_{TH}}$ |
Daytime |
15 |
14 |
14 |
10 |
14 |
25 |
|
Night-time |
16 |
14 |
86 |
14 |
11 |
30 |
| ${\bar{t}_{RE}}$ |
Daytime |
18 |
19 |
23 |
16 |
20 |
31 |
|
Night-time |
6 |
13 |
32 |
15 |
26 |
45 |
The standard deviation of the total time spent in BBS ($\Sigma {t_{\mathit{BBS}}}$) equals 84.5, whereas the standard deviation of the average time spent in the state (${\bar{t}_{\mathit{BBS}}}$) equals 2.9. This fact indicates a high variance of agent state dynamics, which is due to the heterogeneity of the agent population in terms of the brain state behavioural patterns.
Following the statistics in Table
2, some observations can be summarized in the following way. First, in the daytime agents spent most of the time in the active state (AW). Such a result corresponds well with the real life observations (Phillips and Robinson,
2007,
2008; Phillips
et al.,
2011,
2010). Next observation concerns the different total time spent in DS and AW states for both chronotypes while increasing
τ, i.e. for the early birds
$\Sigma {t_{DS}}(\downarrow )$,
$\Sigma {t_{\mathit{AW}}}(\uparrow )$ and
$\Sigma {t_{\mathit{TH}}}(\downarrow )$, whereas for the night owls
$\Sigma {t_{\mathit{DS}}}(\uparrow )$,
$\Sigma {t_{\mathit{AW}}}(\uparrow )$ and
$\Sigma {t_{\mathit{TH}}}(\downarrow )$. Thus, parameter
τ makes chronotypes behave in a slightly different way. Concerning dependencies
${\bar{t}_{\mathit{BMS}}}(\tau )$, as expected, we clearly notice the increasing average time spent in each state depending on the increment of
τ.
We also have to discuss those cases where the DS state occasionally occurs in the daytime. As we can see in Table
2, it happens a few times less frequently than during the night-time. In short, this is a consequence of the simulation of real life situations when the brain reaches the marginal entropy limit after intensive mental activity (e.g. concentrated thinking efforts) and completely “switches off” to recover in the DS state, see Fig.
5. The periods of complete recovery statistically are much longer during the daytime, as agents do not get so exhausted during the night-time recovery period.
Additionally, the concerted circadian model is also capable of simulating the empirically observed sleep-wake cycles during the night-time. Depending on the model parameters, we can obtain a different number of REM (i.e. RE state that can be associated with the dreaming state), NREM (DS state can be associated with the deep sleep state) and awakening states (in our model it can be associated with active wakefulness (AW) and thinking (TH) states) cycles during the night-time. The results obtained are relatively close to the numerous neurophysiological research results for sleeping stages during the night-time (Booth and Diniz Behn,
2014; Brown
et al.,
2012; Prerau
et al.,
2016).
Next, in Fig.
6, the simulation results of the number of in-between transitions and the average time spent in BBS are presented depending on the probabilities of the in-between transitions. The results confirm anticipated outcomes. That is, the number of in-between transitions is in direct ratio to probabilities of the in-between transitions. Accordingly, an average time spent in BBS is in inverse ratio with probabilities of the in-between transitions. As we can see, these dependencies are similar for both chronotypes.
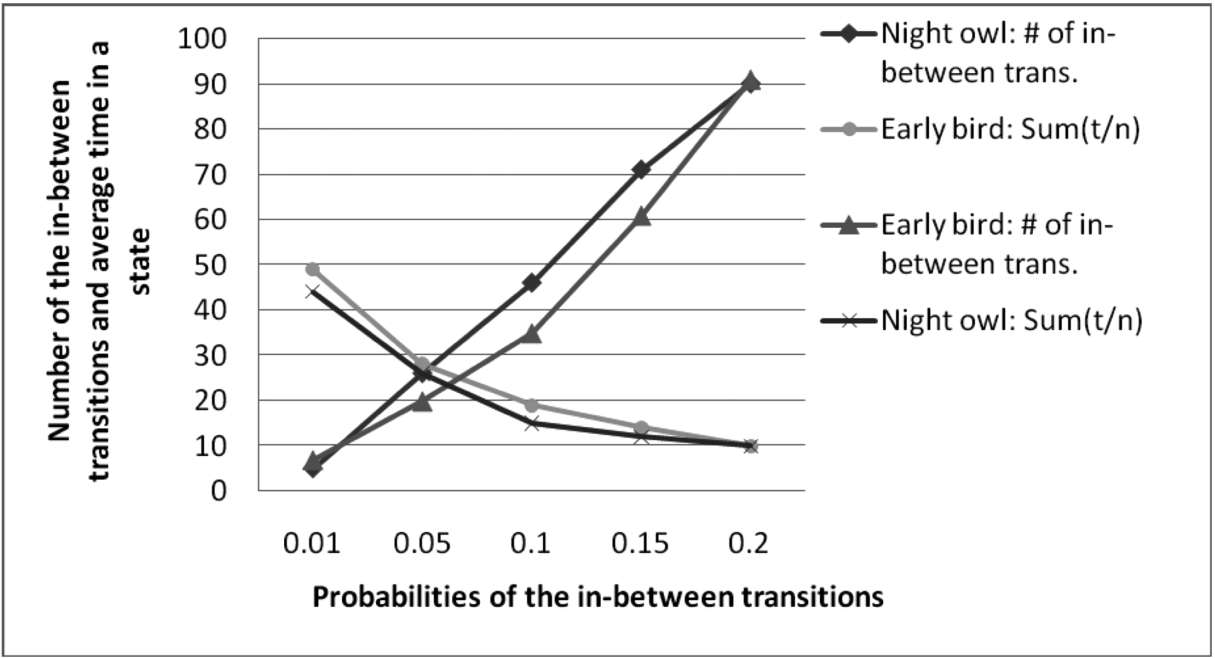
Fig. 6
The number of transitions and the average time ($\Sigma t/n$) spent in a BBS depending on the probabilities of the in-between transitions (probabilities of the in-between transitions are equally set for all states).
The authors argue that the model simulation, based on the conceptual framework, can be interpreted using entropy
S and stylized kinetic and potential energy. According to the proposed approach, free energy
A is the source of useful energy (work), which expresses itself in the terms of expendable energy:
${E_{k}}$ (kinetic) and
${E_{p}}$ (potential), see Eqs. (
4), (
5), and Fig.
1.
Hence, according to the model, the nature of underlying fundamental brain processes for each BBS can be directly revealed by the temporal dynamics of stylized entropy as well as stylized kinetic and potential energy patterns, see Fig.
7. Simply speaking, entropy
S, as a measure of disorder in the brain system, shows the level of internal informational noise (decoherence) and mental exhaustion.
According to thermodynamics and statistical mechanics, the most general interpretation of entropy results in a measure of uncertainty about a system or, in other words, disorder. In fact, such a measure has the opposite meaning to the order observed in the inner structures and the behaviour of living systems. This provides clear incentives for living systems to employ another measure, which is called negentropy. This term was first used by Schrödinger. He introduced the concept of negative entropy for a living system as entropy that it exports to keep its own entropy low. Negentropy for the dynamically ordered sub-system can be redefined as the specific entropy deficit relative to the surrounding chaos. In this way, negentropy can be understood as a measure of the distance
D of the entropy state
S to the white noise state
${S_{\max }}$
where
$S({r_{x}})$ – the entropy of the Gaussian white noise distribution
${r_{x}}$ with the same mean and variance as of the investigated systems distribution
${p_{x}}$;
$S({p_{x}})$ – the entropy of the investigated system. It is assumed that, if the signal is random, then the signal has a normal (Gaussian) distribution. When an investigated system state differs from the Gaussian white noise distribution, then negentropy
$d({p_{x}})>0$, and when it is equal to a random distribution, then negentropy
$d({p_{x}})=0$. In the first case, we have some degree of order, and in the second case, there is no order at all.
This makes perfect sense as a random variable with a Gaussian white noise distribution would need the maximum length of data to be accurately described. If
px is less random, then something about it is known beforehand, i.e. it contains less unknown information, and accordingly it needs a smaller length of data to be described. In other words, negentropy measures something which is known about a systems state. In this way, negentropy serves as a measure of order while entropy, as a measure of disorder. Hence, it is apparent that unlike engineering (where negentropy takes the form of digital information and is quantized in bits), social and biological systems are much more complex self-organizing processes and require a more sophisticated approach (Plikynas,
2016).
Similarly, we assume that another directly related variable, i.e. kinetic energy
${E_{k}}$, denotes a corpuscular type of energy at the level of molecular movements in the brain. According to the model assumptions,
${E_{k}}$ is in direct ratio to
S, whereas
${E_{p}}$ denotes a form of the field-like “potential” energy. According to the model assumptions, potential energy can be associated with the electromagnetic fields emitted in the case of the EEG (electroencephalography) measurements. In short, the potential energy is associated with negentropy, i.e. informational and biological self-organized order (coherence of the inner fields) in the brain (Plikynas,
2016).
It is important to note that the BBS dynamics (see Fig.
5) is generated via time dependent processes of entropy
S and stylized energy (see Eq. (
4)). In essence, each brain state is interpreted as a characteristic process entirely composed of the dynamics of these fundamental thermodynamic factors or, in other words, stylized entropy and energy directly reflect the inner activity of the brain system. For instance, from Fig.
7 we can clearly discern continuous ups and downs of the entropy
S and energy
E.
In fact, turning points in the diagram indicate transitions between BBS, which occur because the simulated brain system either reaches marginal limit
S (
${S_{\min }}$ or
${S_{\max }}$) or probabilistic in-between transitions. In the latter case, transitions (turning points) occur before the brain system reaches the marginal limits of
S, see Fig.
7. The intensity of transitions basically depends on the
S margins, probabilities of the in-between transitions (see Fig.
6) and time period
τ (in minutes) of the applicable probabilistic in-between transitions (see Table
2). Depending on the setup of chosen parameters, we can obtain various
S,
E and BBS patterns, which essentially characterize the brain states dynamics. In this way, after each simulation we get unique patterns of
S and
E curves and BBS dynamics respectively.
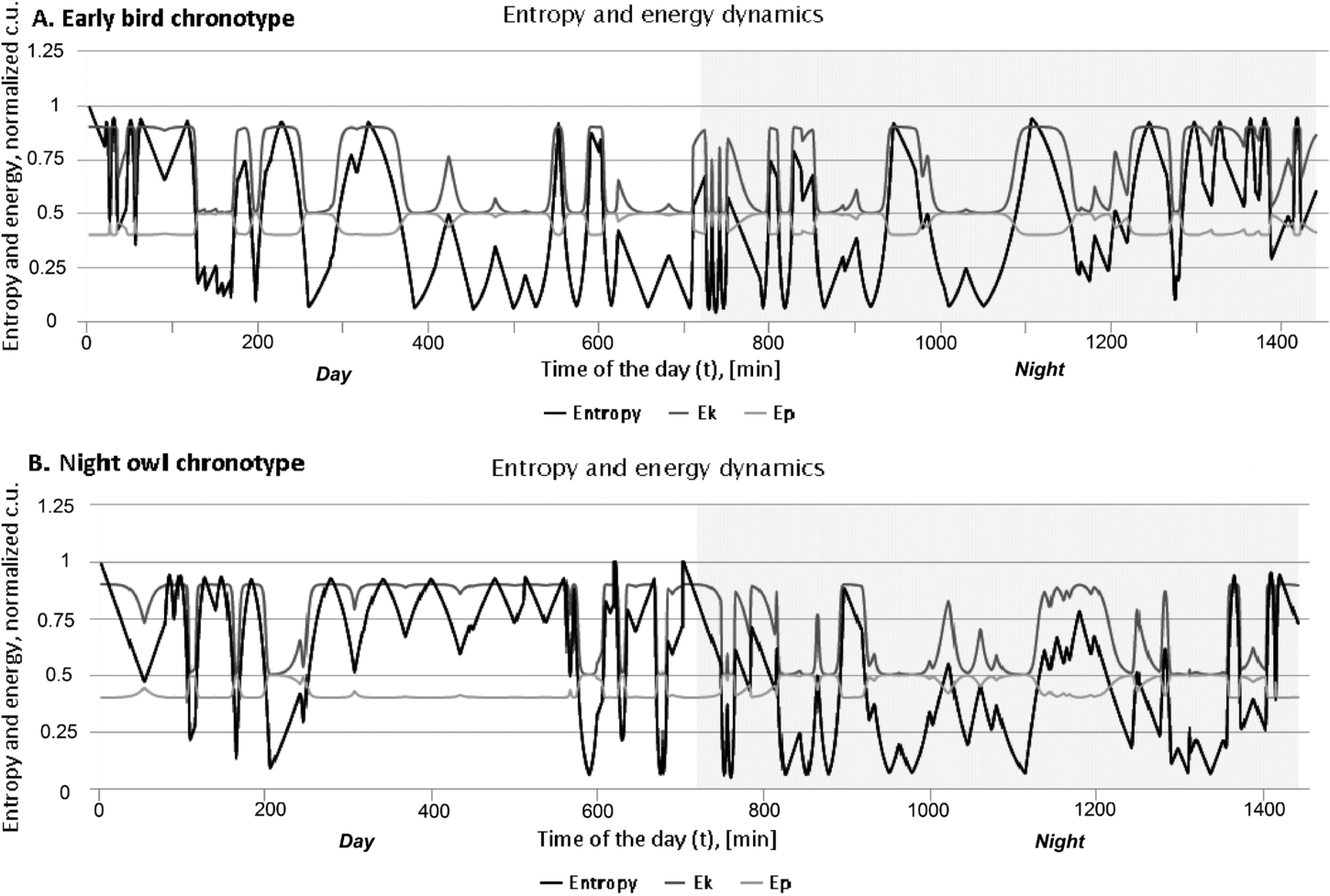
Fig. 7
Dynamics of entropy and stylized energy (kinetic and potential) for both chronotypes. Periodicity of the applied probabilistic in-between transitions $\tau =2$ min and probabilities of the in-between transitions are equal to 0.1.
Thus, entropy
S and both types of energy are cornerstone parameters. However, there are other secondary parameters like the chronotype of an agent, which, according to the model setup, implies a specific (chronotype dependent) behavioural pattern of the in-between transitions (see Fig.
4). Therefore, we can discern some differences in entropy and energy dynamics for both chronotypes in the simulations. For instance, in the daytime night owls tend to have a higher entropy, while at night-time, lower entropy
S levels, see Fig.
7. Let us recall again that entropy
S as a measure of disorder indicates the level of informational noise (decoherence) in the brain system and therefore can be associated with the mental exhaustion. Hence, following the presented simulation results, night owls naturally tend to be more exhausted during the daytime and less, during the night-time.
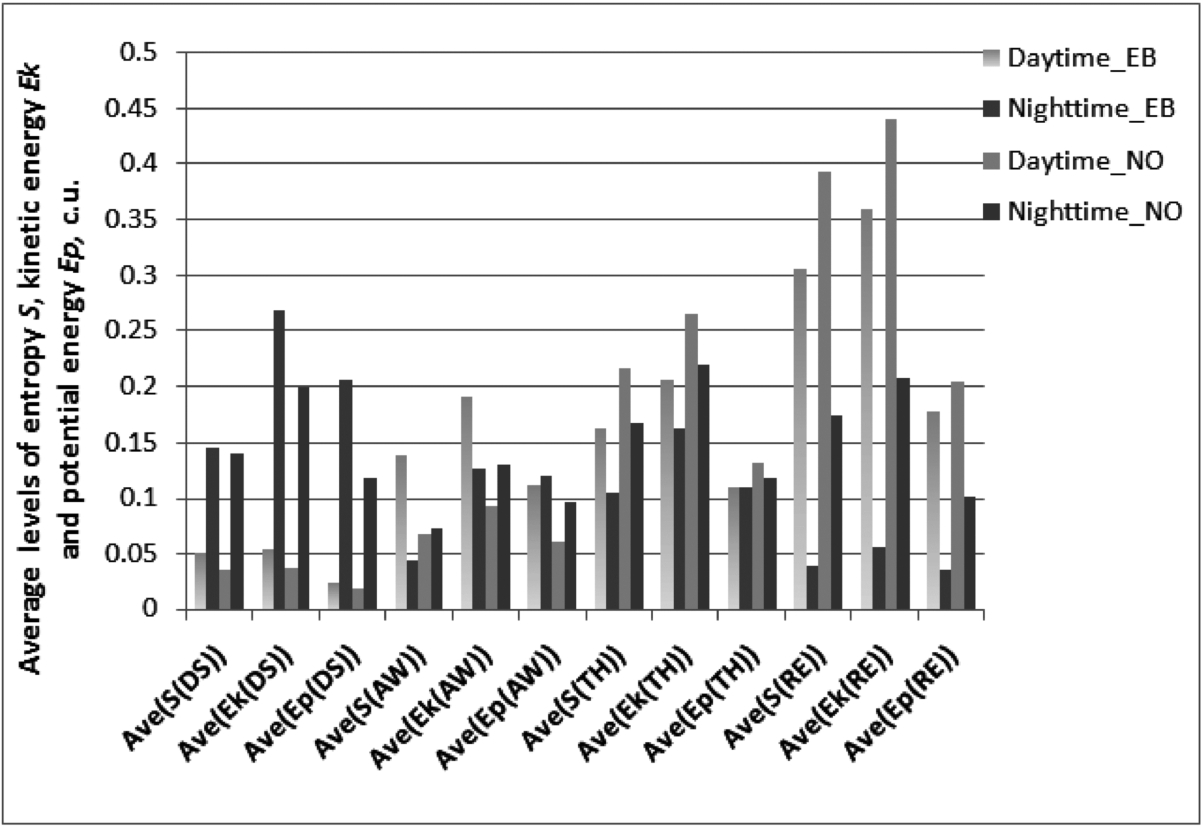
Fig. 8
Comparison of entropy S and stylized energy (${E_{k}}$ and ${E_{p}}$) for both chronotypes (EB – early birds, NO – night owls) in the daytime and night-time periods in each BBS.
Below we examine the average levels of fundamental factors, i.e. entropy
S and stylized energy (
${E_{k}}$ and
${E_{p}}$) for both chronotypes (EB – early birds, NO – night owls) during daytime and night-time periods in each BBS, see Fig.
8. Our primary goal is to see whether there are differences between the fundamental factors: (i) the states in the daytime and night-time periods and (ii) chronotypes. Hence, we can notice a few things:
-
1. In the deep relaxation DS (deep sleep) state, differently from all other states, for both chronotypes the average (i) entropy
S level and that of
${E_{k}}$ are smaller in the daytime compared to the night-time, and (ii) potential energy
${E_{p}}$ is comparatively much higher at night-time. The latter fact quite well corresponds to the model premises concerning the underlying process at night-time in the DS state: rapid increment of the potential energy and rapid reduction of entropy
S. The former observation can be interpreted, noting that the DP state happens quite rarely in the daytime (see Table
2) and it is mainly caused by probabilistic in-between transitions, whereas, at a night-time it is caused mostly by the marginal transitions, that occur as a consequence of reaching the condition
${S_{\max }}$. Therefore, deep sleep is “shallow” in the daytime and much deeper at night-time.
-
2. In the relaxation (RE) state, we observe a unique behaviour for both chronotypes: entropy S and ${E_{k}}$ respectively, are much larger in the daytime than at night-time. However, the difference is much more expressed for the early bird chronotype. It can be interpreted in a similar way as for the DS state. That is, the RE state happens in the daytime mostly because of the marginal transitions, when an agent needs rest after reaching the condition ${S_{\max }}$ (therefore the average S level remains high), whereas at night-time agents occur in the RE state (mostly dreaming) rather occasionally because of the probabilistic in-between transitions, when the entropy S level is usually low. Besides, entropy and energy levels are surprisingly higher for the night owls in the RE state.
-
3. Energy and entropy distribution in the active AW and TH states is more even.
Now let us examine entropy
S dynamics during the day in more detail. In the proposed simulation approach, entropy
S is the major underpinning factor, that governs all the BBS related processes. In this connection, during the day, the brain, in the sense of the brain state processes, probabilistically travels through an a priori set entropy map
$S(t,n)$, see Fig.
3. According to the proposed conceptual approach, we have introduced the entropy space to cover all the BBS processes and transitions between them in the sense of entropy dynamics, see Eqs. (
10) and (
11). In this way, at each moment of time, the brain is involved in one or another entropy-related BBS process, which is represented by the associated curve section in the entropy space chart, see Fig.
3.
Hence, in each simulation, the probabilistic nature of the marginal and in-between transitions between the BBS creates a unique
S pattern, see Fig.
9. Entropy patterns are unique in each simulation. However, they have characteristic traits depending on the main parameters, analysed in this paper. For instance, in Fig.
9, we have entropy space charts A, C and B, D with probabilities of in-between transitions 0.05 and 0.20, respectively. Both pairs of charts substantially differ in the sense of density and structure.
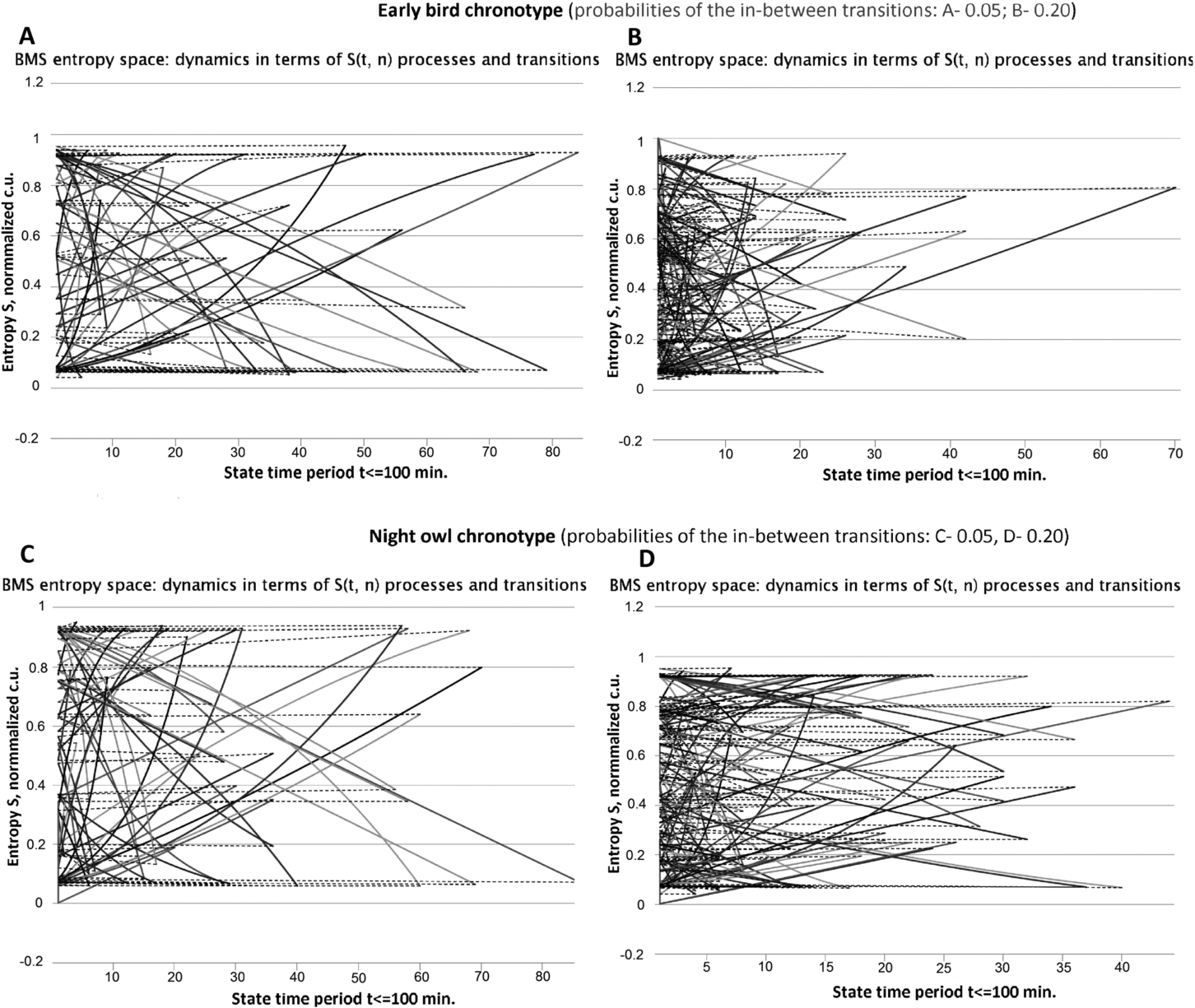
Fig. 9
Samples of the BBS entropy space charts depicted to illustrate the daily $S(t,n)$ dynamics for the early bird (upper charts) and night owl (lower charts) in terms of their characteristic entropy processes and probabilistic marginal and in-between transitions between the BBS.
In the charts, each curve represents a corresponding BBS process in terms of the entropy $S(t,n)$ dynamics. Here, entropy $S(t,n)$ curves are plotted in a line style. Meanwhile, transitions are marked in a dashed straight line (they return the state related time counter to zero). Each BBS process (curve) ends with a marginal or in-between probabilistic transition to another BBS process. In this way, a new BBS process begins again from $t=0$. Hence, in the BBS entropy space charts, time indicates the duration of a particular BBS process. Such an approach not only helps to visualize each BBS process, but it also helps to see the progression and overall picture of the BBS dynamics. For instance, in the dynamics of the BBS entropy space charts, we can observe 1) repeating BBS processes as dense curve areas, 2) marginal transitions occurring at the ${S_{\min }}$ and ${S_{\max }}$ margins, 3) in-between transitions occurring between the ${S_{\min }}$ and ${S_{\max }}$ margins, 4) DS and RE state processes as descending curves, 5) AW and TH state processes as ascending curves, 6) duration of each BBS, etc.
Hence, it is not clear whether the simulations give results that are different or better than previous models. However, we had a great difficulty to find any similar model and simulation results to compare. Sure, there are some related studies like (Borbely,
1982; Booth and Diniz Behn,
2014; Borbély and Achermann,
1999; Fulcher
et al.,
2008; Kronauer
et al.,
1982; McCarley and Massaquoi,
1986; Möller-Levet
et al.,
2013; Reilly and Bambaeichi,
2003; Skeldon
et al.,
2014); etc, but these models, their simulation setup and results are different too. Mostly they deal with the two-process sleep-wake rhythms and use EEG or other neurophysiologically-based modelling of brain states. In short, these are empirical and inductive in their natures of study. We, on the other hand, use a conceptually deductive approach, i.e. we construct
-
(i) the unique free energy and entropy model setup to describe the brain states as entropy and energy dependent processes,
-
(ii) four-process states (not two!),
-
(iii) entropy, chronotype and day time dependent stochastic transitions between states setup.
Hence, our model is different in kind. It models brain states dynamics in a different framework. Therefore, it is not an easy task to make a comparative analysis of our results with other approaches.
In sum, a thorough additional research needs to be done to examine, in detail, the issues and criteria that will help identify the validity of the proposed model by comparison with the established phenomenological two-process models, coupled oscillator models and the reciprocal interaction models (Booth and Diniz Behn,
2014). Hence, the proposed approach requires a more detailed and physiologically-based mathematical clarification and empirical validation in the prospective studies.
5 Discussion
Concerning further research directions, the presented model needs thorough parameter estimation, sensitivity analysis, and verification. Surely, it will be a main direction of the further research. In the prospective research, additional empirically-based investigations are needed to calibrate and validate the presented conceptual model as well.
Next, the presented model can also be expanded for simulating transitions between other types of mental states. Namely, it can be adapted for modelling dynamics of emotional states. Let us recall that psychologists map emotional states in two major axes – arousal (high to low) and valence (pleasure to displeasure). Such two-dimensional map has been theorized by Russell and Barrett (
1999) to capture one important component of emotion called core affect (Russell,
2003). Core affect gives emotional states attributes of felt energy – high, low, and intermediate levels of arousal – which we assume are directly correlated with the active and passive brain states measured in terms of free energy and entropy levels. Of course, such hypothesis has to be investigated from the point of view of neuroscience, cognitive science, and psychology. However, we suppose that all emotional (arousal) energy states can be interpreted and modelled as characteristic mental processes described in terms of entropy and free energy dynamics. We believe that it would give a novel way to model emotional arousal fluctuations during the day. In essence, it could be modelled as continuous, periodic, and stochastic process.
Due to the involved complexity of interstate transitions, such modelling could start from Paul Ekman’s six basic emotional states (happiness, hate, grief, hope, fear, desire) model (Ekman and Cordaro,
2011) and later it can be expanded to Plutchik (
2002) and Russell’s circumplex model of eight emotional states, and even more recent 12-Point Affect Circumplex (12-PAC) emotional model (Yik
et al.,
2011).
In future, we also foresee that this kind of research framework of brain states dynamics can also take a different application sphere. That is, it may be applied in the domain of cognitive agents and multi-agent systems research. It is an emerging multidisciplinary research trend in the domains of artificial intelligence and multi-agent systems. Simulation of agent state dynamics for a single agent leads to the simulation of collective state dynamics for groups or societies of agents. It concerns the simulation and prediction of individual and collective behavioural phenomena such as dynamics of emotional states, political moods, fashion trends, social capital distributions, cultural traits, etc. However, in order to get there, we first have to find a universal way to simulate human-like brain states and transitions between them in the most abstract and fundamental way for a single agent. We suppose that the intrinsic and universal nature of free energy and entropy terms serves well for this purpose.
6 Conclusions
In short, this paper provides a deductive conceptual framework, using universal free energy and entropy terms, that can provide a better understanding of brain states dynamics as self-organized energy and entropy processes. Based on the proposed modelling framework, we also presented a pilot simulation model to showcase dynamical transitions between the basic brain states during the day.
It is important to note that the presented conceptual model has been constructed on the deductive theoretical assumptions and does not directly stem from the empirical data modelling. The main purpose was to find out what inner fundamental processes in the brain can cause the main experimentally observable brain state dynamics.
According to the literature review, for the first time, stylized thermodynamic Helmholtz free energy and entropy terms were used to differentiate brain states and describe stochastic dynamics of transitions between states. We shared ideas how universal and intrinsic free energy and entropy principles can be employed for a better understanding and simulation of brain states as self-organized energy and entropy processes. Even a conceptual possibility to model such dynamics, using entropy terms, gives a very substantial new knowledge about the implicit self-organizing nature of entropy and energy processes taking place in the brain.
It is important to note that in our model, entropy constraints trigger motion (transitions between brain states). That is, marginal entropy constraints lead to the transition processes between attractor states so that brain functioning can be optimized during the day. In this way, the brain behaves as self-regulating and adaptive behavioural mechanism. Thus, we proposed each basic brain state to model as specific endogenous (entropy and energy) processes that, change over time following intrinsic patterns. Brain states are interpreted as specific entropy and energy-related thermodynamic processes, that follow characteristic pattern changes over time. Each process leads to the marginal entropy and energy boundaries, where stochastic transitions take place. Due to the complexity involved, we have approached such a process in a reductionist way, using stylized entropy and energy evaluations.
Our model is based on the deductive assumption that the homeostatic relaxation oscillator can be nailed down to the fundamental rhythmic processes of free energy and entropy, taking place in the brain during the day. Based on this assumption, we have constructed a new way of modelling the homeostatic relaxation oscillator. We argue that the proposed endogenous model can simulate homeostatic rhythmic dynamics of brain states in a more meaningful way as compared to the classical ‘sleep pressure’ approach.
The homeostasis simulation for two chronotypes was able meaningfully to differentiate the behaviour of both chronotypes. We obtained statistically significant differences of brain state dynamics for two chronotypes during the day. For instance, our simulations have revealed experimentally observed chronotype dependent features as follows: owls tend to feel most energetic just before sleep at night, while early birds feel more energetic early in the day.
The simulation setup has revealed how two major simulated chronotypes (early birds and night owls) behave with respect to the basic brain states, entropy and energy dynamics, depending on a few basic parameters such as the recalculation time period τ of probabilistic in-between transitions, the probability of in-between transitions, and the daytime/night-time periods. In essence, the simulation results were analysed in terms of (i) marginal and in-between transitions in the daytime and night-time periods, (ii) duration of staying in BBSs, and (iii) dynamics of entropy and stylized energy (kinetic and potential).
In sum, the simulation results show that after additional theoretical and empirical studies, the proposed conceptual research framework has a potential to (i) describe BBS using entropy and energy terms, (ii) generate homeostatic rhythms for different chronotypes, (iii) provide empirical predictions of brain state dynamics, (iv) be used for the studies of societies composed of such agents, and (v) be applied in the artificial intelligence domain, machine learning, and robotics while mimicking human-like robot state dynamics. In the prospective research, the chronotype behaviour modelling can be related with the social jetlag (misalignment of the biological and social time), cognitive abilities, depressive mood, insomnia, daytime sleepiness, etc.