1 Introduction
Biometrics studies the use of biological characteristics for automatic authentication. Fingerprints are one of the oldest and most used biometric traits, either in civilian or forensic applications. Depending on the fingerprints acquisition methodology, they can be classified into three types: plain (Fig. 1(a)), rolled (Fig. 1(b)) and latent (Fig. 1(c)) impressions. In order to obtain the entire fingerprint pattern, rolled impressions are acquired by rolling the finger nail to nail, while plain impressions are obtained by pressing down the finger on a flat surface, without rolling it. Rolled and plain fingerprints are expected to have high quality due to their supervised capture. This is different for latent impressions, which are normally partial fingerprints and present low quality, because they are lifted from surfaces of objects inadvertently touched by a person in a crime scene (Maltoni et al., 2009).
Automatic Fingerprint Identification Systems (AFIS) are used for solving crimes, for attendance system, for access control and so on. Fingerprint matching is an important stage in AFIS flow steps. Fingerprint features are separated in three levels depending on which scale was used to analyze the ridges pattern. Minutiae are the most used features (ridge endings and ridge bifurcations) for fingerprint recognition.
Although there are several advances in fingerprint matching, when the available fingerprint minutiae decrease, matching algorithms performance falls dramatically (Chen et al., 2013; Ahmed et al., 2016). There are many cases in which only a partial fingerprint image can be obtained, e.g. when compact silicon chip-based sensors are used, when latent fingerprints from crime scenes are processed, and others (Fang et al., 2007). In these cases, where the minutiae count is low, the use of other features extracted from the ridges pattern flow is needed (Sankaran et al., 2014).
In this work we propose a new fingerprint feature and representation for improving the partial fingerprint matching accuracy. Our main contributions are the following. (1) We introduce a new set of points describing ridges around minutiae alongside a triangular representation modified for taking advantage of the new features. This representation describes a more extensive area than the one obtained with only minutiae. (2) In addition, a set of triangle discriminative features for reducing false positives is defined. (3) Also, some improvements have been incorporated to a matching algorithm from literature, for comparing two proposed representations. With our proposal, we were able to achieve an accuracy similar to the best of the state of the art, while the amount of features is smaller.
The structure of this work is described below. A brief review of the existing partial fingerprint matching features is given in Section 2. The fingerprint features and the proposed representation are discussed in Section 3. In Section 4, the effectiveness of this approach is evaluated. Finally, conclusions and possible future works are presented.
2 Related Work
The main task of AFIS is the fingerprint matching process. There is a need for matching algorithms ready for dealing with partial fingerprint queries that present a small number of minutiae, especially for latent impression cases (Sankaran et al., 2014). In order to gain accuracy, some other features besides minutiae must be used. Some approaches have been proposed in partial fingerprint matching, for both cases, good and bad (latent) quality impressions.
2.1 Good Quality Partial Fingerprint Matching
For partial fingerprints of good quality, different features had been used along with minutiae. Secondary features (euclidean distance and orientation difference) calculated from each minutia and its two nearest neighbours have been proposed (Jea and Govindaraju, 2005).
Representative ridge points ($\mathit{RRPs}$) were proposed for describing ridges (Fang et al., 2007). These points are sampled one by one from each minutia and along the ridge associated to the minutia. These points are represented with their location, orientation and index. The idea is to use these $\mathit{RRPs}$ along with minutiae with the minutiae-based matching algorithms by modifying two constraints: minutiae can only match with minutiae, and, two $\mathit{RRPs}$ can only match if they have the same index. In cases where the minutiae count is very low, these points do not provide enough discriminative information. Besides, with these points only the ridges along minutiae are represented. Ridge shape features (RSFs) were used along minutiae for partial fingerprint matching (Lee et al., 2017). These features are extracted from convex and concave edges that appear in ridges. First, a minutiae matching stage is performed by comparing both minutiae and the RSFs in their local neighbourhood. Then, a second matching stage is performed using only the RSFs extracted in the overlapped area obtained by the previous stage. Finally, the global score is calculated by combining the two computed scores.
The minutiae types have been used in different approaches. A representation based on three Delaunay triangulations: i) for all minutiae, ii) for only minutiae endings and iii) for only minutiae bifurcations was proposed (Girgis et al., 2009). Also, it was proposed to partition each minutiae set into two sets: the terminations and the bifurcations, and then finding the two farthest bifurcation minutiae in the partial fingerprint, for matching them with two minutiae from the template (Asha and Chellappan, 2013). Due to the skin elasticity, when the pressure intensity varies, minutiae extraction algorithms can make mistakes in the minutiae type estimation process. This implies that an algorithm based on this feature is not a reliable option. The fingerprint area information combined with minutiae in a fusion scheme was proposed by Chen et al. (2013), based on a study of the influence of the fingerprint area in partial fingerprint recognition.
Deep neural networks have been used for extracting features in fingerprints. The combination of global and local deep features around minutiae was proposed (Zhang et al., 2017). GlobalNet, a CNN based on ResNet is proposed for extracting global features from the fingerprints and projecting them into the Euclidean space (Zhang and Feng, 2017). By using MinutiaNet, deep features around each minutia are extracted into the Euclidean space. First, the query is matched against each impression on the database by comparing the global features, then a minutiae-based matching is performed against the one with the highest global-based score. Finally, a fusion of both scores is calculated. In another work, first an alignment of the partial fingerprints based on phase-only correlation and polar Fourier transform is made (Qin et al., 2017). Then, a deep network is proposed for extracting a fixed-length feature vector from each overlapped region. The similarity score is calculated by comparing these two vectors.
Some features describing texture information have been proposed to be used in partial fingerprint recognition (Mathur et al., 2016; Aravindan and Anzar, 2017). For all these cases, the fingerprint impressions need to have a similar texture for obtaining a reliable correspondence. However, comparing impressions with different textures is commonly needed (impressions acquired from different scanners, or by using ink on different surfaces).
2.2 Latent Fingerprint Matching
In the case of bad quality partial fingerprints or latent fingerprints, there have been some improvements in the past few years (Sankaran et al., 2014; Ezhilmaran and Adhiyaman, 2017). The bad quality of these impressions restricts the universe of features to be used for latent fingerprint algorithms. Despite this fact, the little amount of minutiae found in this type of fingerprints has forced the researchers to look for other features.
The manually marked minutia (position and direction) is a feature utilized by every approach. In cases where minutiae are the only features used, accuracy is increased by adopting other strategies. The fusion of rolled and plain fingerprints at three different levels: feature, rank and score levels was tested, obtaining the best results for the score-level fusion (Feng et al., 2009). Also, a score-level fusion of manually marked minutiae and automatically extracted minutiae was proposed (Paulino et al., 2010). Additionally, a latent identification framework where multiple latent examiners and the AFIS can work in conjunction with each other was proposed (Arora et al., 2015). Furthermore, a Minutia Spherical Coordinate Code (MSCC) was presented by Zheng and Yang (2015). MSCC is a modified version of the Minutiae Cylinder Code (MCC) matching algorithm (Cappelli et al., 2010). This version allowed an improvement in feature size while the reached accuracy values were equal or better than the original MCC. Bezier ridge descriptors have been used for enhancing the latent fingerprint impressions. Then, by using minutiae as keys, a MapReduce process is proposed to recover the latent mate template from the database (Reddy, 2016). As it was already mentioned, due to the little amount of minutiae and their scattering, the matching accuracy of these proposals is still low. Recently, a clustering approach for obtaining the global minutiae pair matching was proposed (Medina-Pérez et al., 2016). The proposal does not depend on the minutiae descriptors used for obtaining the minutiae pairs similarity. First, a local matching is performed, then the matching pairs are clustered for decreasing the problems of global deformations. The obtained clusters are merged and a Thin-Plate Spline (TPS) model is generated for searching new matching minutiae pairs. Finally, the global similarity score is calculated.
The orientation map is a feature used for fingerprint matching, too. Paulino et al. (2013) proposed a descriptor-based Hough transform alignment algorithm for aligning and measuring fingerprints similarity using minutiae and orientation fields. Also, the full fingerprint minutiae set with respect to the query latent minutiae set was reduced with the latent orientation field information (Krish et al., 2014).
In another case, besides the orientation field, the frequency field is also used (Liu et al., 2013). The ridge orientation and ridge frequency of the latent fingerprints are improved by incorporating a “feedback from exemplar” and with the enhanced features, the candidates list is updated and resorted.
In addition to edited minutiae and the orientation map, Jain and Feng (2011) also used ridge wavelength maps, singularities, ridge quality maps and fingerprint skeletons, showing how far the accuracy can go when a large group of extended features are used. These features are regarded as extended features (CDEFFS, 2008). Their experiments showed that Level 1 (ridge quality map and ridge flow map) and Level 2 (ridge skeleton) features were the most effective for improving the accuracy.
Recently, other strategies have been proposed, like a descriptor formed by concatenating the resultant descriptors extracted with 14 trained ConvNets with multiple fingerprint local patches at different scales and regions around minutiae (Cao and Jain, 2017). Three minutiae templates are used, two minutiae templates extracted using different fingerprint preprocessing algorithms, and a texture template, all three providing complementary information. For latent fingerprints, the texture template is represented by extracting two virtual minutiae from each non-overlapped block of $16\times 16$. For reference prints, just one virtual minutia is extracted from each block. The descriptors are extracted from all three minutiae sets.
For both cases, partial fingerprint images of good and bad quality, there are proposals using some Level 3 extended features (e.g. pores) (Zhang et al., 2018). This level of features is highly dependent on the quality of the query and the enrolled fingerprints. Therefore, despite the fact that they can improve the accuracy of the matching algorithms, the quality of fingerprint images needs to be enhanced before these features can really play a more important role (Chen and Jain, 2007; Jain and Feng, 2011; Jain, 2011).
The merge of features beyond minutiae, that can be marked by experts or inferred from the interaction with them, has provided a new area for developing latent matching algorithms with betters results (Jain, 2011), and the new generation of AFIS needs to be prepared for it.
Considering the main difficulties still presented by the state of the art proposals regarding the latent fingerprint matching algorithms, in this article, we propose to use a group of distinctive ridge points in addition to the minutiae. At other occasions, points have been extracted from the minutiae, but on the minutia ridge. In this case, points are extracted both from the ridges along minutiae and from the neighbouring ridges. The main objective of these points is to describe in a compact manner the minutiae neighbouring ridges, and in this way incorporating new discriminative information to the representation. This is important, due to the low amount of minutiae present in latent fingerprints. The relationships between the points and the minutiae are represented by a state of the art representation, based on the well-known Delaunay Triangulation. Some new features, based specifically on the new points, are incorporated into these triangles.
3 Proposed Approach
Ridges are always present in a fingerprint impression, no matter how small the area could be. For manually comparing two impressions, experts use all ridges besides minutiae. Consequently, extracting features describing the ridges flow is a wise choice and this is the guide of what is presented below.
3.1 Distinctive Ridge Points Features
Throughout history it has been shown that minutiae are one of the most discriminative features extracted from fingerprints. Therefore, it is smart to think that minutiae should be integrated in every fingerprint representation, even if they are just a few. In addition, minutiae are very easy to manually mark by experts.
Ridges are always present in any fingerprint area, no matter how small it is. Furthermore, using them as a feature for the matching stage should increase the accuracy in comparison with the minutiae-based matching algorithms. One simple way for representing ridges is using points belonging to each ridge. Therefore, a high resolution image is not needed for obtaining a reliable set of points. By using ridge points, only a thin line of the ridges is needed. In this way, the interaction with experts is very easy, which is extremely needed for latent fingerprint matching (Arora et al., 2015).
Some approaches where the skeleton ridges are used have been proposed. In some cases each ridge is defined as a list of equidistant points, or many points from ridges are extracted as texture features (Feng et al., 2005; Jain and Feng, 2011; Aravindan and Anzar, 2017). Using all or many points of each ridge is a very computationally expensive option. In the other cases, a group of points is selected. One of the ways in where the points are selected needs a very good quality from the image (concave and convex edges from ridges) (Lee et al., 2017), and in the other one just a group of points from ridges along each minutiae are extracted (Fang et al., 2007), furthermore, the minutiae neighbourhood is not described entirely. In order to obtain a balance between accuracy and efficiency, a set of distinctive ridge points is proposed (${S_{\mathit{DRP}}}$) in this work.
As stated above, a group of distinctive points besides minutiae is extracted. These points, unlike other approaches, are extracted from neighbouring ridges of all minutiae, and also from ridges to which minutiae belong. These distinctive points are projections and extensions of minutiae. The projections are those points found by projecting the minutiae on the neighbouring ridges depending on their direction. The extensions are points extracted from each minutia in its own ridge or from the minutiae projections. The amount of projections or extensions is a pre-defined number. These points describe the whole fingerprint area presented in the image. At the same time, they have discriminative power. Finally, the ${S_{\mathit{DRP}}}$ is the set that results from the union of the minutiae, the projections and the extensions. Formally, our ${S_{\mathit{DRP}}}$ proposal is defined as follows.
Let $M=\{{m_{1}},{m_{2}},\dots ,{m_{mc}}\}$ be the set of minutiae extracted from a fingerprint image and $mc$ the amount of minutiae. Each minutia ${m_{i}}$ is a tuple ${m_{i}}=\langle {x_{i}},{y_{i}},{\theta _{i}}\rangle $, where ${x_{i}}$ and ${y_{i}}$ are the minutia coordinates and ${\theta _{i}}$ is the minutia direction.
Using M, two disjoint sets are defined: $\mathit{Pr}$ and $\mathit{Ex}$.
3.1.1 The $\mathit{Pr}$ Set
In order to describe the ridges around each minutia, a new set containing neighbouring ridges points is introduced.
Definition 1 (Neighbouring ridges).
Let ${m_{i}}\in M$ be a minutia. The neighbouring ridge ${r_{j}}$ of ${m_{i}}$ is the j-th intersected ridge with the tangent vector to the minutia direction ${\theta _{i}}$. Neighbouring ridges are enumerated from the minutia ridge in the positive and negative directions. The ridge along minutia is denoted as ${r_{0}}$.
An example of the ridge enumeration can be seen in Fig. 2. For both minutiae, two ridges in the two possible directions are selected.
Definition 2 (Projection point).
Let ${m_{i}}\in M$ be a minutia and let ${r_{j}}$ be a neighbouring ridge of ${m_{i}}$. The projection point ${p_{ij}}=\langle {x_{ij}},{y_{ij}},{\phi _{ij}}\rangle $ can be defined as the intersection point of the tangent line to the minutia direction ${\theta _{i}}$ and the j-th neighbouring ridge, where ${x_{ij}}$ and ${y_{ij}}$ are the projection point coordinates, ${\phi _{ij}}$ is the orientation at the point $({x_{ij}},{y_{ij}})$.
Definition 3 (Minutia projections set).
Let ${m_{i}}\in M$ be a minutia and let $rc$ be the maximum number of neighbouring ridges intersected for each direction. The set of projection points generated from the minutia ${m_{i}}$ can be denoted as ${P_{i}}=\{{p_{ij}}|-rc\leqslant j\leqslant rc\}$. The point ${p_{ij}}$ is incorporated to ${P_{i}}$ if no minutiae or projection points already exist in the j-th ridge at a distance less than a predefined threshold ${\delta _{Close}}$ to ${p_{ij}}$.
Definition 4 (Projection points set).
Let M be a minutiae set, let $rc$ be the maximum number of neighbouring ridges intersected for each direction and let ${P_{i}}$ be the projection points calculated from each minutia ${m_{i}}$. The projection points set produced from M can be defined as $\mathit{Pr}={P_{1}}\cup {P_{2}}\cup \cdots \cup {P_{mc}}$.
A visual example for illustrating these points is given in Fig. 2. Figures 2(a) and 2(b) show the projection points generated from minutia ${m_{i}}$ and ${m_{j}}$, respectively. Also, the ridges numbers are shown starting from ${r_{0}}$ (the minutia ridge) and passing through two neighbouring ridges crossing each tangent direction (red arrows) to the minutia direction (blue arrow).
3.1.2 The $\mathit{Ex}$ Set
In order to describe the ridge along each minutia, a set of points representing the minutia ridge is presented.
Definition 5 (Extension point).
Let ${m_{i}}\in M$ be a minutia. The extension point ${e_{ij}}=\langle {x_{ij}},{y_{ij}},{\phi _{ij}}\rangle $ can be defined as the j-th point multiple of s, found by following the minutia ridge starting from ${m_{i}}$, where s is a predefined step value. ${x_{ij}}$ and ${y_{ij}}$ are the point coordinates, ${\phi _{ij}}$ is the orientation at the point $({x_{ij}},{y_{ij}})$.
Definition 6 (Extensions set given a point ${mp_{i}}$).
Let $\mathit{MP}=M\cup \mathit{Pr}$ be the set of all minutiae and projection points. Let ${mp_{i}}\in \mathit{MP}$ be a minutia or a projection and let $ec$ be the maximum number of extension points located for each followed branch. The set of extension points for ${mp_{i}}$ can be denoted as ${E_{i}}=\{{e_{ij}}|-ec\leqslant j\leqslant ec\}$. The point ${e_{ij}}$ is added to ${E_{i}}$ if no minutiae, projection or extension points already exist in that ridge at a distance less than a predefined threshold ${\delta _{Close}}$ to ${e_{ij}}$.
Definition 7 (Extension points set).
Let $\mathit{MP}=M\cup \mathit{Pr}$ be the set of all minutiae and projection points, let $c=|\mathit{MP}|$ be the cardinality of $\mathit{MP}$, let $ec$ be the maximum number of extension points located for each followed branch, let ${E_{i}}$ be the extension points located for each point in $\mathit{MP}$. The entire extension points set can be defined as the union of all minutiae and projection extensions as follows $\mathit{Ex}={E_{1}}\cup {E_{2}}\cup \cdots \cup {E_{c}}$.
A visual example of this set is given in Fig. 3. In this case, Figs. 3(a) and 3(b) present the extension points originated from minutiae ${m_{i}}$ and ${m_{j}}$ respectively. The extension points are on the minutia ridge at a previously defined distance, and they can also be extracted from the projection points. They are numbered in appearing order. It can be noted that when errors in the preprocessing and minutiae extraction steps are produced, the extension points undergo modifications.
3.1.3 The ${S_{\mathit{DRP}}}$ Set
Finally, after selecting all the points that will describe the minutiae neighbouring ridges, the ${S_{\mathit{DRP}}}$ set can be computed.
Definition 8 (Distinctive ridge points set).
Let M, $\mathit{Pr}$ and $\mathit{Ex}$ be the minutiae set, the projection points set and the extension points set, respectively. The distinctive ridges points set can be defined as ${S_{\mathit{DRP}}}=M\cup \mathit{Pr}\cup \mathit{Ex}$.
Once defined the ${S_{\mathit{DRP}}}$, the general idea of the entire process is presented in Algorithm 1. First, the fingerprint image is preprocessed, the ridges skeleton image ($ske{l_{I}}$) and minutiae set (M) are obtained (line 2). Then, the minutiae projections ($\mathit{Pr}$) are generated (from line 3 to line 11), by ensuring that no two points whose distance is smaller than ${\delta _{Close}}$ threshold are generated (line 7). Depending on how much information about ridges is needed around each minutiae, extension points can be extracted or not from minutiae projections. So, the ${S_{\mathit{MP}}}$ set for locating extension points is created, with minutiae and minutiae projections (line 13) or only with minutiae (line 15). Extension points are selected using ${S_{\mathit{MP}}}$ set (from line 17 to line 25) and no two points whose distance is smaller than ${\delta _{Close}}$ threshold are generated (line 21). Finally, the resultant set ${S_{\mathit{DRP}}}$ is the union of all three sets (M, $\mathit{Pr}$, $\mathit{Ex}$).
3.2 Fingerprint Triangle-Based Representation
Triangle-based representations are used in many approaches for fingerprint matching and indexing (Muñoz-Brise no et al., 2013; Gago-Alonso et al., 2013; Jain and Prasad, 2015; Sandhya et al., 2016). Due to the relation between minutiae and the geometrical information that can be described with triangles, the results reached with this type of representation have been very effective.
Due to the small size of latent impressions, the use of local structures for describing the impressions is needed. By using local sub-structures for representing fingerprints, the same sub-structures should be generated for both the latent impression and its mate impression.
In the present work a new fingerprint representation based on the expanded triangle set defined by Gago-Alonso et al. (2013) is proposed.
The expanded triangle set (Gago-Alonso et al., 2013) represents accurately a fingerprint impression. When the amount of minutiae is low (latent impressions), the triangle set structure generated for these cases greatly differs from the triangle set structure constructed from a much bigger minutiae set (tenprint impressions), despite the fact that the latent minutiae set could be a subset of the minutiae extracted from the tenprint. This is the main motivation for introducing the new fingerprint representation.
For solving this problem, the new representation is build by the union of local triangle representations (one for each minutia) and the triangles for only minutiae. Each local representation, with its respective minutia as the centre, contains the triangles formed by all the points (minutiae, projections and extensions) in its neighbourhood. This technique provides a representation with a structure more robust to the changes in the amount of minutiae.
3.2.1 The Proposed Triangle Set
After the ${S_{\mathit{DRP}}}$ set is extracted, a neighbours set is defined from each minutia point.
Definition 9.
Let ${S_{\mathit{DRP}}}$ be the distinctive ridge points describing the fingerprint rides, let ${m_{i}}\in M$ be a minutia and let ϵ be a predefined threshold. The neighbours set for ${m_{i}}$ can be considered as ${N_{i}}=\{{n_{ij}}|{n_{ij}}\in {S_{\mathit{DRP}}}\hspace{2.5pt}\text{and}\hspace{2.5pt}\text{euclidean}\text{Distance}({m_{i}},{n_{ij}})\leqslant \epsilon \}$.
In order to increase the probability of obtaining a partial fingerprint representation with similar structure to its mate tenprint representation, and to also be able to describe the ridge patterns present on the impression, a more representative triangle set is finally defined.
Definition 10.
Let ${N_{i}}$ be the neighbours set for the minutia ${m_{i}}$, let ${T_{M}}$ be the expanded triangle set for the minutiae set M and let ${T_{i}}$ be the expanded triangle set for the neighbourhood ${N_{i}}$. The final ${S_{\mathit{DRP}}}$ triangle set can be defined as ${T_{\mathit{DRP}}}={T_{M}}\cup {T_{1}}\cup \cdots \cup {T_{mc}}$.
A visual example of this set can be seen in Fig. 4, where minutiae are the blue points and the points describing the ridges around minutiae are the red ones.
3.2.2 Triangle Features
For triangle matching algorithms usually a features vector is calculated from each triangle in order to perform the comparison. Features vectors must be invariant for all the impressions generated from the same finger, despite the differences between them.
Definition 11.
Let ${T_{\mathit{DRP}}}=\{{t_{1}},{t_{2}},\dots ,{t_{k}}\}$ be the entire triangle set proposed for representing the discriminative ridge points, where ${t_{i}}=({p_{1}},{p_{2}},{p_{3}})$, with ${p_{1}},{p_{2}},{p_{3}}$ being the points forming the triangle and ${p_{i}}\in {S_{\mathit{DRP}}}$. The points are ordered using their opposite triangle sides length. The triangle feature set for matching is denoted as ${F_{T}}=\{{f_{1}},{f_{2}},\dots ,{f_{k}}\}$, where ${f_{i}}=f({t_{i}})$ is the feature vector obtained from the triangle ${t_{i}}$ using a features function.
The function used for calculating the triangles features is denoted as:
where ${s_{t}}$ is the triangle sign, ${\beta _{i}}$ is the relative direction of ${p_{i}}$, ${d_{i}}$ is the length of the i-th segment, ${\rho _{i}}$ is a label representing the relative position of ${p_{i}}$ regarding a reference point, ${\tau _{i}}$ is the ${p_{i}}$ type, ${\sigma _{i}}$ represent whether the points of a segment belong to the same sub-ridge or not and depending on the point type ${\Phi _{i}}={\theta _{i}}$ when the point ${p_{i}}$ is a minutia and ${\Phi _{i}}={\phi _{i}}$ for the other cases, the features are ordered using the triangle sides length.
(1)
\[ f(t)=({s_{t}},{\beta _{1}},{\beta _{2}},{\beta _{3}},{d_{1}},{d_{2}},{d_{3}},{\rho _{1}},{\rho _{2}},{\rho _{3}},{\tau _{1}},{\tau _{2}},{\tau _{3}},{\sigma _{1}},{\sigma _{2}},{\sigma _{3}},{\Phi _{1}},{\Phi _{2}},{\Phi _{3}}),\]The triangle sign ${s_{t}}$ (Bhanu and Tan, 2003) is a feature invariant to rotation, and it is used to avoid the mirror effect (a left loop is mated with a right loop).
The relative direction ${\beta _{i}}$ (Gago-Alonso et al., 2013) is the angle intersecting the segment denoted by the direction/orientation of the point ${p_{i}}$ and the opposite side to this point.
The length ${d_{i}}$ (Germain et al., 1997) is the euclidean distance between the points describing the i-th segment. This feature is used for measuring the triangle similarity in the matching stage.
The label ${\rho _{i}}$ is a label describing the relative position of the point ${p_{i}}$ with respect to the reference point (Muñoz-Brise no et al., 2014). This should provide enough information to avoid false matches between features located in different places of the impressions.
The feature ${\tau _{i}}$ describes the point type, whether it is a minutia (value 0), a minutiae projection (value 1), a minutiae extension (value 2) or an extension of a minutia projection (value 3). This feature will ensure that minutiae can only mate with minutiae, projection points only with projection points, and so on.
A sub-ridge is a part of a ridge, where the ending points of a sub-ridge are minutiae or the ridge comes to an end. The feature ${\sigma _{i}}$ indicates if two points are found in the same sub-ridge. This feature can eliminate some false positive matches.
A model representation to be used by the matching algorithm in this work is defined as follows.
Definition 12.
Let ${S_{\mathit{DRP}}}$ be the points set describing the continuities and discontinuities of the fingerprint ridges pattern, let ${T_{\mathit{DRP}}}$ and ${F_{T}}$ be the triangle set proposed and the set of triangles features calculated respectively. The model representation of a given fingerprint impression can be defined as $M=\langle {S_{\mathit{DRP}}},{T_{\mathit{DRP}}},{F_{T}}\rangle $.
Once the representation of the fingerprint is defined, a general idea of the method is presented in Algorithm 2. First, the expanded triangles from minutiae set are calculated (line 2 and 3). Then, for each minutia the neighbouring points are located (line 5) and the expanded triangle set for those points is obtained (line 6). Each new triangle (adding distinctive information to the representation) is incorporated to the final set of triangles (from line 7 to line 11). Finally, the triangles features set is computed (from line 13 to line 17) and the model is returned.
3.3 Fingerprint Matching
The matching stage performs the comparison between two models. Let ${M_{q}}=\langle {S_{q}},{T_{q}},{F_{q}}\rangle $ and ${M_{t}}=\langle {S_{t}},{T_{t}},{F_{t}}\rangle $ be the query and template models, respectively. The matching algorithm proposed to be used is an enhanced version of the algorithm presented by Hernández-Palancar et al. (2014). This algorithm is modified according to the intrinsic properties of the introduced representation.
The algorithm’s general idea is to build a similarity graph from the local correspondences found by using the triangles set. From this similarity graph, the spanning tree of every connected component is selected. Then, the spanning trees with similar transformation are merged. Finally, a similarity score between the two models is calculated. The specific modifications and the algorithm idea are presented in this subsection.
3.3.1 Corresponding Triangles
Let ${f_{q}}\in {F_{q}}$ and ${f_{t}}\in {F_{t}}$ be the features vector of the triangles ${t_{q}}\in {T_{q}}$ and ${t_{t}}\in {T_{t}}$, respectively. The function $g({f_{q}},{f_{t}})$ is defined as follows:
where $i\in \{1,2,3\}$, ${\delta _{\beta }}$ and ${\delta _{\Phi }}$ are predefined thresholds. The function ${d_{\Phi }}$ calculates the difference between two directions when ${{\tau _{i}}_{q}}$ and ${{\tau _{i}}_{t}}$ indicate that the points are minutiae, and the difference between orientations (in the double angle space) for other cases (Maltoni et al., 2009).
(2)
\[ g({f_{q}},{f_{t}})=\left\{\begin{array}{l@{\hskip4.0pt}l}1,& \begin{array}[t]{l}\textbf{if}\hspace{2.5pt}{{s_{t}}_{q}}={{s_{t}}_{t}}\hspace{2.5pt}\textbf{and}\hspace{2.5pt}|{{\beta _{i}}_{q}}-{{\beta _{i}}_{t}}|\leqslant {\delta _{\beta }}\hspace{2.5pt}\textbf{and}\hspace{2.5pt}\\ {} \{\exists i|\hspace{2.5pt}{{\rho _{i}}_{q}}={{\rho _{i}}_{t}}\}\hspace{2.5pt}\textbf{and}\hspace{2.5pt}{{\tau _{i}}_{q}}={{\tau _{i}}_{t}}\hspace{2.5pt}\textbf{and}\hspace{2.5pt}\\ {} {{\sigma _{i}}_{q}}={{\sigma _{i}}_{t}}\hspace{2.5pt}\textbf{and}\hspace{2.5pt}{d_{\Phi }}({{\Phi _{i}}_{q}}-{{\Phi _{i}}_{t}})\leqslant {\delta _{\Phi }}\end{array}\\ {} 0,& \text{otherwise},\end{array}\right.\]The function $g({f_{q}},{f_{t}})=1$ (equation (2)) indicates that triangles ${t_{q}}\in {T_{q}}$ and ${t_{t}}\in {T_{t}}$ are corresponding.
The size of the proposed triangles set is higher than the previous version because of the amount of points and the minutiae neighbourhoods triangles included. Therefore, for eliminating false positive matches another constraint is incorporated to the algorithm. In order to reduce the set of corresponding triangles, a measure of the similarity between the triangles is used. For this, the ratio ${r_{i}}$ between the points of the i-th triangle side is calculated using the distance ${{d_{i}}_{q}}$ and ${{d_{i}}_{t}}$ from ${f_{q}}\in {F_{q}}$, and ${f_{t}}\in {F_{t}}$, respectively with the equation (3).
where $i\in \{1,2,3\}$.
All corresponding sides for similar triangles have the same proportion, so the difference between each pair of proportion values is obtained (equation (4)) for deciding if the triangles are similar or not.
where $i\in \{1,2,3\}$ and $j=1$ if $i=3$ and $j=i+1$, otherwise.
Let function $h({d{f_{1}}_{qt}},{d{f_{2}}_{qt}},{d{f_{3}}_{qt}})$ be defined as follows:
where ${\delta _{df}}$ is a predefined threshold.
(5)
\[ h({d{f_{1}}_{qt}},{d{f_{2}}_{qt}},{d{f_{3}}_{qt}})=\left\{\begin{array}{l@{\hskip4.0pt}l}1,\hspace{1em}& \textbf{if}\hspace{2.5pt}\max (\max ({d{f_{1}}_{qt}},{d{f_{2}}_{qt}}),{d{f_{3}}_{qt}})<{\delta _{df}},\\ {} 0,\hspace{1em}& \text{otherwise},\end{array}\right.\]Two triangles ${t_{q}}\in {T_{q}}$ and ${t_{t}}\in {T_{t}}$ are similar enough if $h({d{f_{1}}_{qt}},{d{f_{2}}_{qt}},{d{f_{3}}_{qt}})=1$.
Definition 13 (Corresponding triangles pair).
Let ${t_{qj}}\in {T_{q}}$ and ${t_{tl}}\in {T_{t}}$ be triangles in the query and the template, respectively, let ${d{f_{i}}_{qt}}$ be the ratios for these triangles. The pair $\langle {t_{qj}},{t_{tl}}\rangle $ represents two corresponding triangles if $g({f_{qj}},{f_{tl}})=1$ and $h({d{f_{1}}_{qt}},{d{f_{2}}_{qt}},{d{f_{3}}_{qt}})=1$.
Finally, all corresponding triangles between two impressions can be organized as follows.
Definition 14 (Corresponding triangles set).
The set of all corresponding triangles between two fingerprint models can be defined as ${T_{c}}=\{\langle {t_{q1}},{t_{t1}}\rangle ,\langle {t_{q2}},{t_{t2}}\rangle ,\dots ,\langle {t_{qn}},{t_{tm}}\rangle \}$, where ${t_{qj}}\in {T_{q}}$, ${t_{tl}}\in {T_{t}}$ and $\langle {t_{qj}},{t_{tl}}\rangle $ is a pair of corresponding triangles.
3.3.2 General Idea for the Fingerprint Matcher
The matching method used is a previous work (Hernández-Palancar et al., 2014) with the explained modifications added. The general idea of the algorithm is presented in Algorithm 3. The steps are roughly explained. More specific details of the algorithm are explained in the original article.
First, the corresponding triangles set is obtained (line 2). The correlation tuples set ${T_{c}}=\{{ct_{1}},{ct_{2}},\dots ,{ct_{e}}\}$ is created (line 3), where ${ct_{i}}=({\alpha _{i}},\overline{{{p_{j}}_{q}}{{p_{k}}_{q}}},\overline{{{p_{j}}_{t}}{{p_{k}}_{t}}})$ with $k=1$ if $j=3$ and $k=j+1$, otherwise, ${\alpha _{i}}$ is the normalized difference between the i-th interior angles of ${t_{q}}\in {T_{q}}$ and ${t_{t}}\in {T_{t}}$ and $\overline{{{p_{j}}_{q}}{{p_{k}}_{q}}}$, $\overline{{{p_{j}}_{t}}{{p_{k}}_{t}}}$ are the triangles sides. Then the set ${T_{c}}$ is reduced by keeping the tuples with the most probable value of relative rotation (line 4). The similarity graph ${G_{s}}$ is constructed using the correlation tuples, where each vertex from it represents a pair of corresponding points and the edges represent the corresponding triangles sides (line 5). A visual example can be seen in Fig. 5, where a similarity graph is constructed from a pair of corresponding triangles.
Kruskal algorithm is used for obtaining the spanning forest from the similarity graph (spanning tree of every connected component) (Cormen et al., 2009) (line 6). When the entire set of spanning trees is obtained and ordered in descending order using the amount of edges, a strategy for merging the trees with similar transformation is performed (line 7). Finally, a similarity score between the two compared models is calculated and returned using the final similarity graph (lines 8 and 9).
3.4 Proposed Matching Scheme
In latent scenario, experts are expected to be part of the feature extraction and matching processes. By using this as an advantage, a matching scheme that takes into account the expert judgement is proposed.
The proposed features improve the fingerprint representation in cases where minutiae are not discriminative enough. In other cases, they are redundant information. Due to the fact that minutiae matching algorithms obtain reliable results when minutiae number is high enough or when the extracted minutiae have a high discriminative value, $\mathit{DRP}$ features are intended to be used in a later stage than minutiae matcher step. They are used when the expected result can not be obtained using only minutiae.
In Fig. 6 a flow chart shows the proposed matching scheme, where experts decide whether a latent fingerprint mate found by the minutia matcher is the true positive or not. In cases where the minutiae matcher does not find the template fingerprint, the ${S_{\mathit{DRP}}}$ matcher is called for finding the mate fingerprint.
4 Experimental Results
In this section, two experiments using three well known databases were carried out. Both experiments showed the discriminative power incorporated to the fingerprint representation using the proposed approach. The results were measured by using the identification rate obtained for the search of suspects linked to crime scenes. Final results were also shown for each of the latent impressions quality levels specified in the database description (good, bad and ugly).
4.1 Database and Experimental Scenarios
Three experiments were designed for testing the proposal performance. Both experiments were conducted using the NIST27 database, for calculating the accuracy in a latent fingerprint identification scenario. The NIST27 database is integrated by 258 latent impressions and 258 tenprint impressions. Latent impressions were classified by experts in three quality levels: Good, Bad and Ugly. The dataset has one repeated tenprint impression (Mikaelyan and Bigün, 2012), so 257 tenprint impressions were used in this work. For both experiments, the background added was of 27000 and 2000 impressions taken from NIST14 and NIST4 databases, respectively.
The first experiment was performed using the ground true minutiae given in the NIST27 database for both latent and tenprint impressions. For latent impressions, minutiae were edited by experts without seeing their mated fingerprints, while for tenprint impressions, minutiae were automatically extracted and then they were fixed by the experts. After preprocessing steps, in the skeleton image obtained, ridge ending positions and ridge bifurcation positions are displaced with respect to the original fingerprint image. Therefore, edited minutiae were not located on the skeleton fingerprint ridges. Accordingly, a coordinates relocation was needed in order to extract the $\mathit{DRP}$ points. For this, a correspondence step between edited minutiae and the automatic extracted minutiae was performed. Preprocessing and minutiae extraction processes were carried out using Verifinger 4.2 (Neurotechnology, 2004). When a minutiae pair matched, the edited minutia $(x,y)$ coordinates were relocated. Minutiae from fingerprint images in NIST14 and NIST4 databases were extracted with Verifinger 4.2 (Neurotechnology, 2004).
The second experiment was conducted using the edited minutiae relocated for latent fingerprints and the automatic minutiae extracted with Verifinger 4.2 (Neurotechnology, 2004) for all tenprint impressions. Due to the extraction problems present in this algorithm, the region of interest ($\mathit{ROI}$) is detected before the features extraction step. The segmentation process was performed using an algorithm developed by our research group.
In the third experiment the rank-1 identification rate for the proposed approach is compared with the rank-1 accuracy reported for other approaches in the state of the art. The features and the database used in each case are also presented.
The proposed matching scheme is used in the experiments. Fingerprint impressions on top of the candidate list using only minutiae and reference point, in addition to those using the proposed features and representation, fall into rank-1 when this scheme is used. The rest of the candidate list is ordered by the similarity score computed by the proposed matching algorithm. Skeleton images for latent fingerprints were provided by the authors of a previous proposal (Jain and Feng, 2011). The minutiae for the relocation step were extracted using Verifinger 4.2 (Neurotechnology, 2004) for both latent and template impressions.
4.2 Matching Accuracy
Figures 7(a) and 7(b) show the performance for the current proposal using tenprint edited minutiae and tenprint automatic extracted minutiae, respectively. In both figures, three CMC curves are plotted for representing the identification rate on three different scenarios: i) the matching algorithm presented by Hernández-Palancar et al. (2014) using minutiae (Min) and reference point (RP), ii) the current proposal using minutiae (Min), reference point (RP), minutiae projections (Pr) and minutiae extensions (Em) and iii) the current proposal using minutiae (Min), reference point (RP), minutiae projections (Pr), minutiae extensions (Em) and extensions from projections (Ep).
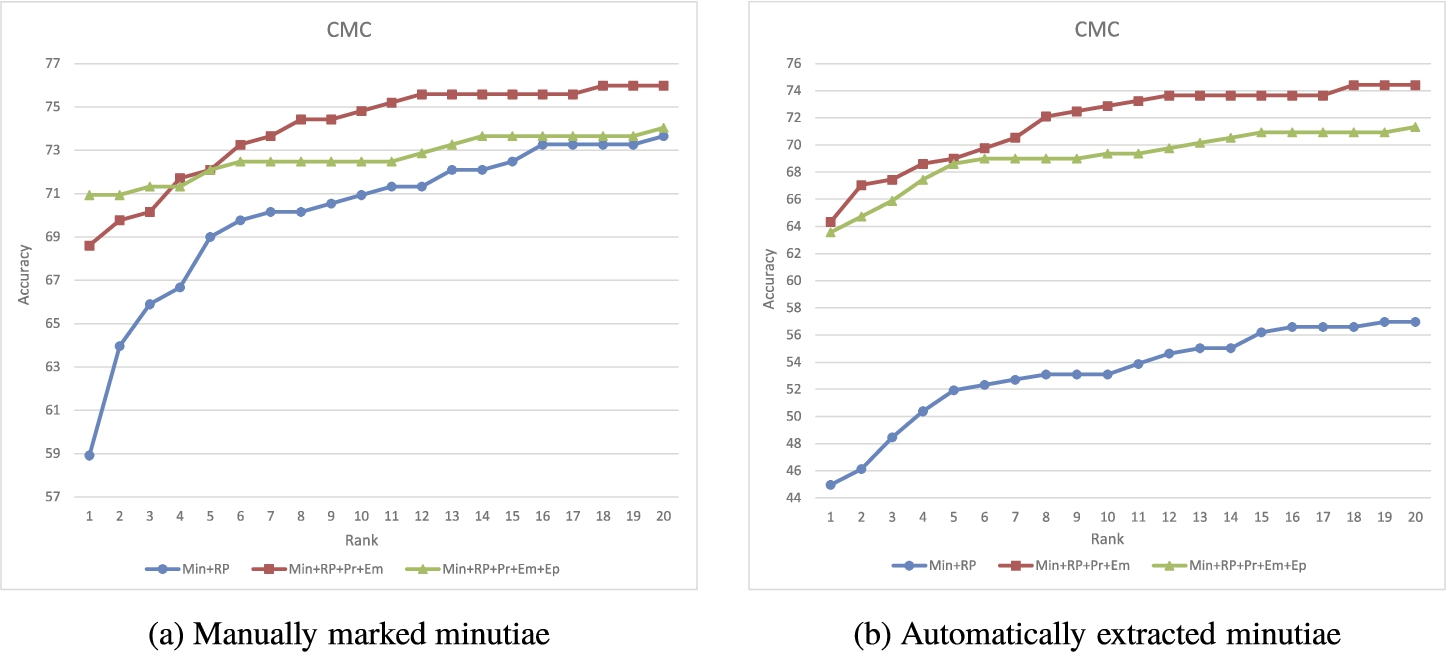
Fig. 7
CMC graphics for manually marked and automatically extracted minutiae from template impressions.
Both experiments showed that the use of $\mathit{DRP}$ points along with the proposed matching scheme outperforms the algorithm using only minutiae and reference points. In the graphics, it can be seen that the rank-1 accuracy is increased when the proposed representation is being used.
Also, it should be noted that the impact of the features and the representation proposed is considerably greater when minutiae are automatically extracted from tenprint impressions. When minutiae are automatically extracted there are more missed or spurious minutiae. This experiment indicates that in a scenario where more problems with the minutiae exist, the distinctive points extracted from ridges add reliable and exclusive information to the representation. This is an important behaviour because minutiae automatically extracted from database impressions is the most probable scenario, due to the large size of templates databases.
For the experimental results, the parameters values for extracting the features were $ec=1$, $pr=1$, $s=39$ and ${\delta _{\mathit{Close}}}=13$. For generating the representation, the parameters values were set as follows: $\epsilon =100$, ${\delta _{\beta }}=20$ and ${\delta _{df}}=0.25$. These were the optimal parameters found and they were experimentally found. The amount of points derived from each minutia is not high because of the small $\mathit{ROI}$ of latent impressions. Therefore, for obtaining neighbourhood representations with similar geometric relations from the same minutia in the query and the template impressions, the group of points in that neighbourhood should not be too large.
When extensions are extracted from both minutiae and projections, better results are reached at the top of the candidate list. However, when extensions are extracted only from minutiae, results become more consistent than in the previous case. This is related with the fact that the negative impact of non-linear distortions in latent impressions increases as the sub-structures size grows.
When edited minutiae for tenprints are used, the extensions of projections have a positive impact at the top of the candidate list, despite the minutiae coordinates relocation. This is because of the features information in this case is more reliable than the automatic process case. When the extraction process is automatic, the preprocessing step errors cause spurious minutiae. Finally, more false positives occur when more points are calculated from those false minutiae.
The accuracy reached using manually marked minutiae and reference point is considerably higher than the accuracy obtained using automatically extracted minutia and reference point. Despite this fact, the identification rate obtained until rank-20 for the candidate list in both cases using the proposed approach is quite similar. This proves the consistency of the proposed algorithm.
Figures 8(a), 8(b) and 8(c) show the identification rates for each of the quality levels separately (good, bad and ugly) for the case of automatically extracted minutiae. The proposed scheme outperforms the accuracy levels obtained by the minutiae and reference point matching algorithm as expected. In these cases, the impact of adding new information besides minutiae and reference point is more visible. This is due to the common errors that have the automatic minutiae extraction algorithms. For the three cases, when no extensions from the projections are used, the results are slightly better. This is caused because when the amount of points increases, more similar triangles between two different impressions are found which implies an increase in the false positive correspondences.
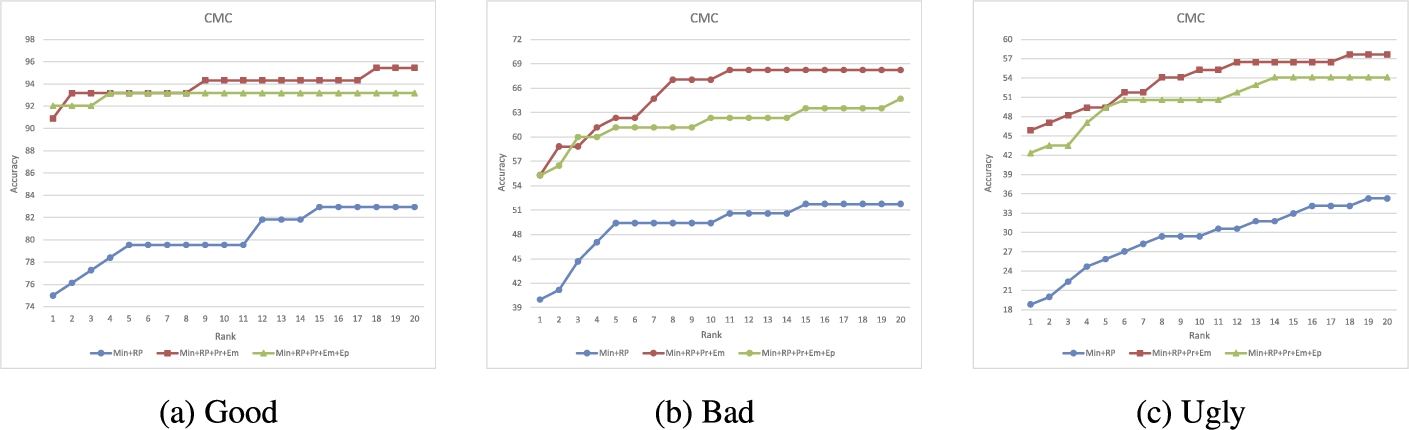
Fig. 8
CMC for latent impressions of good, bad and ugly qualities, with minutiae automatically extracted for tenprint impressions.
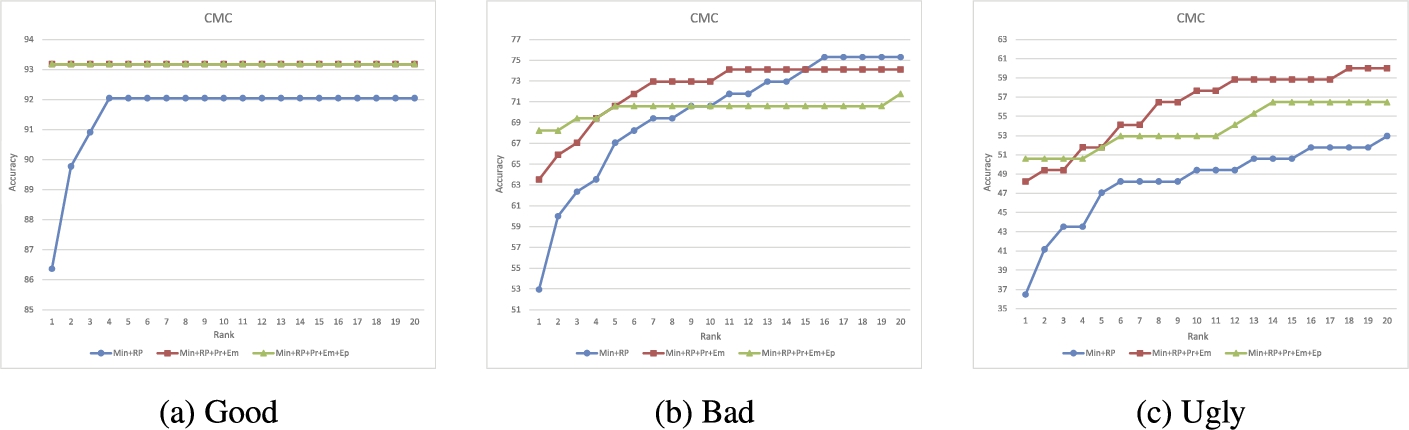
Fig. 9
CMC for latent impressions of good, bad and ugly qualities, with minutiae manually marked for tenprint impressions.
Figures 9(a), 9(b) and 9(c) show the identification rates for each of the quality levels for manually marked minutiae. In this case, also by using the ${S_{\mathit{DRP}}}$ the best results are reached. The biggest improvement in accuracy added by the proposed scheme is observed for ugly latent impressions, and the worst performance for minutiae and reference point only is obtained. For these cases, as the edited minutiae are used for tenprint impressions, less errors in minutiae are found. This is why, the accuracy of the algorithm only using minutiae and reference point is better. The performance of the algorithm using or not extensions in projections is similar at the one for the automatically extracted minutiae. But also in these cases, edited minutiae in tenprints have their position moved from ridges, due to the preprocessing steps. Therefore, the represented relationships between the new points and the minutiae in some cases are affected, as can be seen for bad quality latent impressions.
Figure 10 shows the scalability of the proposed algorithm when the background impressions amount increases to 313845. Besides the images from NIST27, NIST4 and NIST14 (29257), 284,588 rolled ink impressions from the Cuban AFIS database are added. In the figure, it can be seen how the proposed scheme outperforms the algorithm using minutiae and reference point. Also, a rank-1 comparison between the accuracy obtained for the proposed approach and the rank-1 recognition rate for some reported works is presented in Table 1. Furthermore, the features and the database size used in each case are presented.
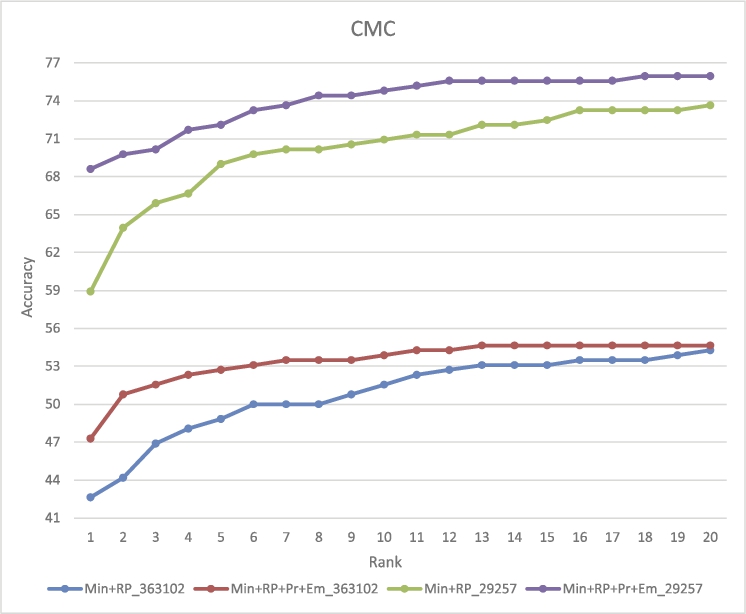
Fig. 10
CMC graphic for manually marked minutiae from template impressions, for 313845 impressions as background.
In the case of latent fingerprints, minutiae, due to the low amount presented, have a limit in terms of reliability and identifying value. This is the main reason why other features have to be selected. In this approach a set of features is proposed which can be easily inferred from the interaction with experts. Also, these features add to the representation a high discriminating value. Due to the used representation (linear growth), the matching algorithm still maintains its high efficiency and its ability to be used in real time applications. It can be seen that the accuracy achieved by Jain and Feng (2011) is higher than the accuracy reached by the proposed approach, but these values are quite close. Besides, the amount of features used by the proposed approach is smaller than (Jain and Feng, 2011) proposal.
Table 1
Rank-1 recognition rate for reported results in NIST27.
| Method used | Features size | Gallery | Rank-1 |
| (Jain and Feng, 2011) | Manually marked minutiae, singularities, ridge quality map, ridge flow map, ridge wavelength map and fingerprint skeleton | 29,257 | 74% |
| Proposed Approach | Manually marked minutiae, reference point and $\mathit{DRP}$ points | 29,257 | 70.9% |
| (Medina-Pérez et al., 2016) (Cylinder-Codes) | Manually marked minutiae | 29,257 | 68.6% |
| (Medina-Pérez et al., 2016) (m-triplets) | Manually marked minutiae | 29,257 | 68.2% |
| Proposed Approach | Manually marked minutiae for latent impressions and automatically extracted for templates, reference point and $\mathit{DRP}$ points | 29,257 | 64.34% |
| (Medina-Pérez et al., 2016) (NMD) | Manually marked minutiae | 29,257 | 64.0% |
| (Hernández-Palancar et al., 2014) | Manually marked minutiae and reference point | 29,257 | 59% |
| (Paulino et al., 2013) | Manually marked minutiae and orientation field | 31,998 | 53.5% |
| (Jain and Feng, 2011) | Manually marked minutiae and singularities | 29,257 | 50% |
| (Zheng and Yang, 2015) MSCC + MCC | Manually marked minutiae | 32,062 | 49.2% |
| (Zheng and Yang, 2015) MSCC | Manually marked minutiae | 32,062 | 42.2% |
| (Paulino et al., 2010) | Automatic & manually marked minutiae | 27,258 | 48% |
| (Jain and Feng, 2011) | Manually marked minutiae | 29,257 | 34.9% |
5 Conclusions and Future Work
In this work novel fingerprint features for partial to full fingerprint matching were proposed. A triangle-based representation from a new set of points was defined. The experiments were carried out using the NIST27 latent database. The present work was compared with another approach based on minutiae and reference point. Also, the rank-1 identification rate was compared with other rank-1 approaches from literature. Results showed the advantages obtained by using the approach introduced.
Experimental results proved that the presented approach is robust to the absence of minutiae and the coordinates distortions between the query and the template. The reached accuracy values for each of the three quality levels were increased with respect to the minutiae matching algorithm. The global accuracy is comparable with the best result of the state of the art. Moreover, while the proposal describes the discriminative areas from fingerprints, the amount of features used by the representation is lower than those proposed in other works. Besides, the defined features can be easily extracted from the interaction with experts.
Future works will be aimed at decreasing the ridge points dependence with minutiae. Besides, other research lines are directed to reduce the negative impact of non-linear distortion on the proposed algorithm. In this way, better accuracy values for latent fingerprint impressions of low quality are pursued. These researches are consistent with the objective of eliminating the existing differences between automatic matching algorithms and latent experts work.
