1 Introduction
In recent competitive industrial environment, a manufacturer should be able to produce qualitative products with on-time delivery to the customers. So, designing a manufacturing environment including production department, machines’ layout, etc. is an important issue to reach the goals like better quality and on-time delivery. An effective way to have such design is to establish and balance a production (assembly) line. An assembly line consists of some tasks to be performed in a given order for producing the final product. The order of tasks is determined according to their precedence graph which defines the relationships among the tasks. The line is balanced when the tasks are assigned to some stations in order to optimize a given criterion (or a set of criteria). The stations are usually connected with a conveyor and the parts and semi-products are moved among the stations on the conveyor to be completed at the end of the line. In a balanced line each station consists of one or more tasks to be operated by usually one (in some cases more than one) worker in a given common time for all stations called cycle time of the line. The cycle time forces the line to send out a product from its last station in each cycle time. The order of stations and assigning the tasks to them must be determined in a way that would respect the precedence relationships of the tasks (precedence graph). The usual criteria used in an optimization problem of an assembly line balancing can be cycle time minimization, number of stations minimization, equipment purchasing cost minimization, worker-related cost minimization, etc. As a line balancing problem, one or more than one of these criteria may be considered for an assembly line. As an instance given by Fig.
1, assuming an assembly line which contains 8 tasks, the precedence relationships among the tasks are shown by graph (a). In this figure, the graphs (b) and (c) represent two feasible solutions which assign the tasks to 4 and 3 stations, respectively.
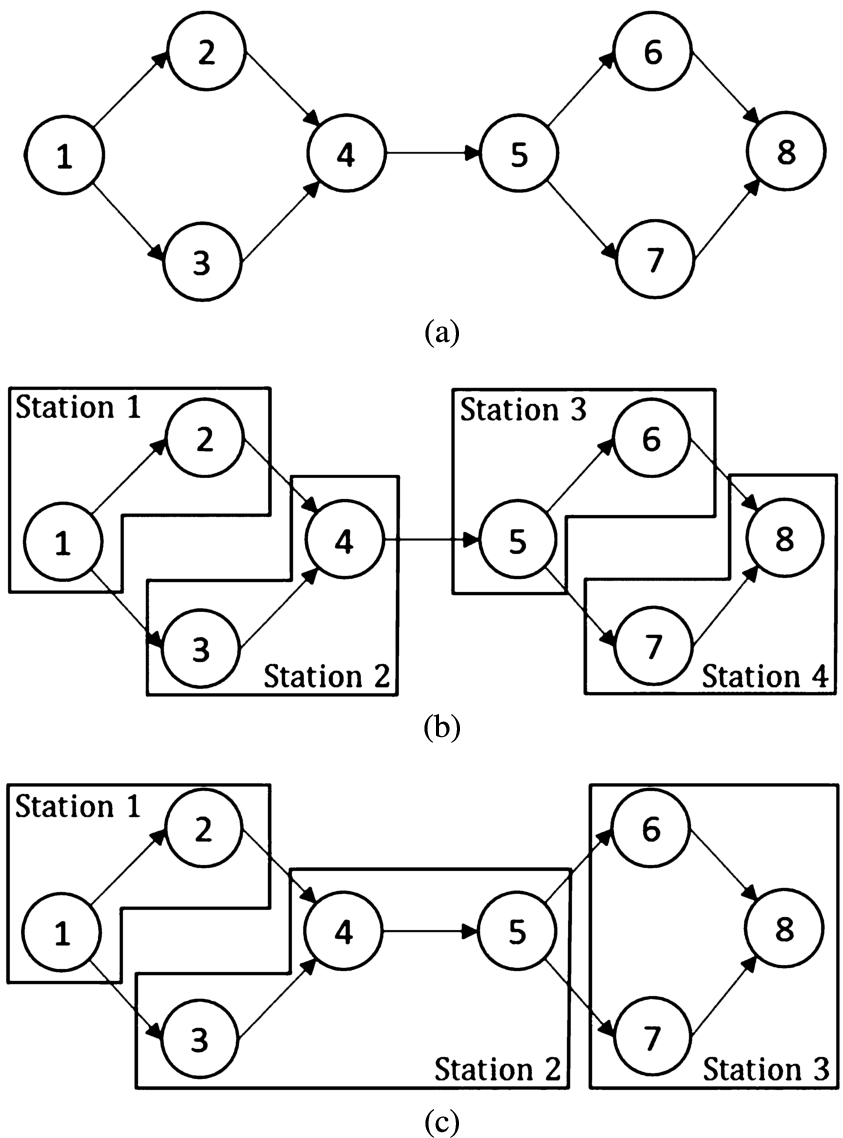
Fig. 1
A graphical illustration of input (a) and output (b and c) for a simple assembly line balancing problem.
Assembly lines are classified from different aspects. From a physical point of view, a line can have different shapes. A line can have a straight shape if there is enough straight available space. On the other hand, it can be a U-shaped line in case of small available spaces (Baybars,
1986). Moreover, the stations may be placed on one or both sides of any assembly line. As another physical issue, the use of parallel stations may be of interest for the cases when there is a task with operating time longer than the cycle time of the line. From product variety point of view, a line can be designed to produce one type product (single model) or to produce more than one type of products (mixed-model). As another classification, a line can be designed to employ one worker in each station or to employ more than one worker in each station.
Although the literature of assembly line balancing problem is full of interesting studies, only some of its most recent studies are reported here. Lea and Gub (
2016) studied a two-sided assembly line balancing problem for cycle time minimization purpose. Yuguang
et al. (
2016) applied a PSO meta-heuristic algorithm for a typical multi-objective hull assembly line balancing problem to minimize the goals like cycle time, static load balancing between workstations, dynamic load balancing in all workstations, and multi-station associated complexity. Sepahi and Jalali Naini (
2016) modelled a two-sided assembly line balancing problem considering parallel performance of tasks. A typical two-sided assembly line balancing problem (see also Tuncel and Aydin,
2014) with mixed-model products (see also Kucukkoc and Zhang,
2014; Ramezanian and Ezzatpanah,
2015; Yang and Gao,
2016) was studied by Kucukkoc and Zhang (
2016) where they used a flexible agent-based ant colony optimization solution approach. Buyukozkan
et al. (
2016) applied artificial bee colony and tabu search meta-heuristic approaches for a typical two-sided assembly line balancing problem. As an interesting field of assembly line balancing problems, the number of U-shaped line related studies has increased recently (see Ogan and Azizoglu,
2015; Fattahi and Turkay,
2015; Hazır and Dolgui,
2015; Alavidoost
et al.,
2016). Moreover, multi-objective assembly line balancing problems in certain and uncertain environments have been of interest by the studies such as Alavidoost
et al. (
2015), Alavidoost
et al. (
2016), Samouei
et al. (
2016), Zacharia and Th. Nearchou A. C (
2016), etc. In addition to these studies, Salehi
et al. (
2018) considered a multi-objective assembly line balancing problem with worker’s skill and qualification considerations in fuzzy environment. Mardani-Fard
et al. (
2018) considered a multi-objective straight assembly line balancing problem with stochastic parameters. As an interesting problem, ergonomic issues of workers was considered in assembly line balancing problems by Battini
et al. (
2015) while the robotic type assembly lines were considered by Pereira and Álvarez-Miranda (
2018), Borba
et al. (
2018), etc. For more applications of multi-objective optimization in engineering and non-engineering topics the studies of Kovács and Marian (
2002), Jablonsky (
2007), Tavana
et al. (
2014a), Hajipour
et al. (
2016), Zeng
et al. (
2016), etc. can be referred.
In this study, as a new assembly line balancing problem, an entropy-based objective function plus equipment purchasing cost and worker time-dependent wage are considered to be optimized simultaneously in an assembly line. The entropy-based non-linear objective function is linearized using a bounded variable technique which gives a good approximation of the non-linear function. As a multi-objective problem (Jablonsky,
2014; Tavana
et al.,
2014a; Zeng
et al.,
2015; Tavana
et al.,
2016), we propose a new hybrid fuzzy programming solution approach which has a superior performance comparing to the existing methods of the literature in the case of the problem of this study.
The rest of this paper is organized as follows. Section
2 proposes the new multi-objective assembly line balancing formulation. Section
3 describes the new solution approach proposed for the formulation of Section
2. A very detailed computational experiments are performed in Section
4. Finally, the paper ends with conclusion in Section
5.
3 Solution Approaches
In this section of the paper, an effective solution approach is proposed to tackle the multi-objective formulation (
24)–(
36) for finding a Pareto-optimal solution. Various approaches like goal programming,
ε-constraint approach (Keshavarz Ghorabaee
et al.,
2017), fuzzy programming approach, etc. have been applied in the literature of multi-objective optimization to solve such problems. Zimmermann (
1996) for the first time applied fuzzy programming approach (max-min operator) to solve a multi-objective model but this solution approach may not give efficient (Pareto-optimal) solutions in some cases (Alavidoost
et al.,
2016). This weakness of fuzzy programming approach later was focused in some studies by introducing some hybrid versions of fuzzy programming method. Therefore, the methods like SO (Selim and Ozkarahan,
2008), TH (Torabi and Hassini,
2008), DY (Demirli and Yimer,
2008), and ABS (Alavidoost
et al.,
2016) were proposed. In this section a new hybrid version of fuzzy programming approach is proposed to solve multi-objective problem (
24)–(
36). The method is explained in the next sub-section and after that its efficiency is proved in another sub-section.
3.1 The Proposed Solution Approach
The proposed solution approach of this study is a new hybrid version of fuzzy programming method to produce efficient solution to the multi-objective formulation (
24)–(
36). This approach is presented by the following steps.
Step 1. Solve the following sub-models to obtain the positive ideal solution (POS) and negative ideal solution (NIS) of each objective function individually.
Step 2. As each objective function can be related to a fuzzy membership function (MF), therefore, the MFs of the objective functions are calculated by the following relationships (see also Fig.
3),
where
${\mu _{r}}(x)$ for
$r\in \{1,2,\dots ,R\}$ (where
$R=3$) is the linear MF of the objective function
${f_{r}}$.
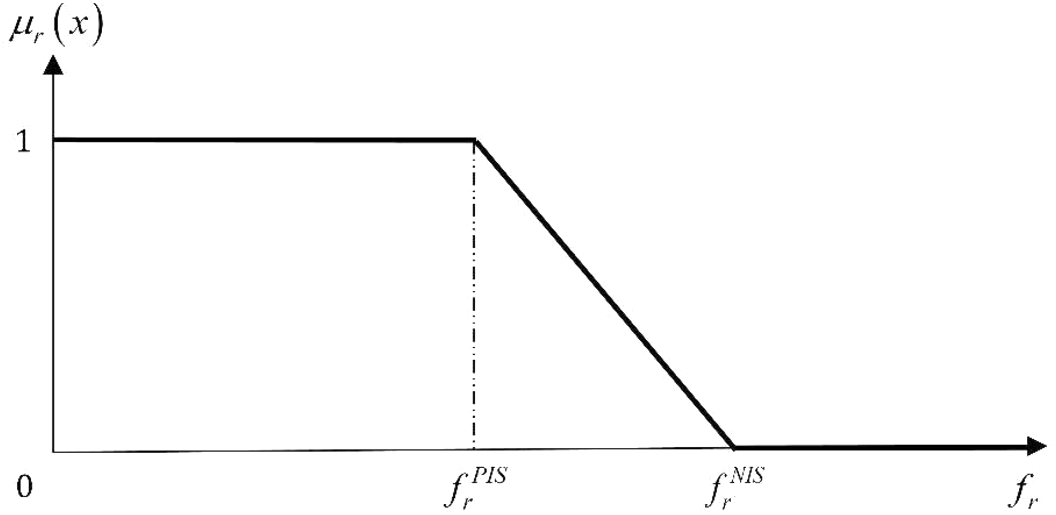
Fig. 3
Schematic representation of the fuzzy membership functions (Zimmermann,
1996).
Step 3 (Single-objective model step). Convert the multi-objective problem (
24)–(
36) to the following proposed single objective formulation.
In the formulation (
46), the positive value
${\theta _{r}}$ is the importance weight of
r-th objective function with the condition of
${\textstyle\sum _{r=1}^{R}}{\theta _{r}}=1$. The continuous and non-negative variables
${\lambda _{0}}$ and
${\lambda _{r}}$ (
$r\in \{1,2,\dots ,R\}$) are used to control the minimum satisfaction level of the objective functions as well as their compromise degrees.
Step 4. Solve the single-objective model (
46) with a given set of values for weights of the objective functions (
${\theta _{r}}$). If the obtained solution satisfies the decision maker, stop. Otherwise, do one of the following changes and repeat the steps 1 to 4 until a satisfactory solution is obtained.
-
• Increase the NIS value for maximization type objective functions,
-
• Decrease the PIS value for minimization type objective functions,
-
• Change the given set of values for weights of the objective functions (${\theta _{r}}$).
3.2 On the Single-Objective Model Step (Model (46)) of the Proposed Approach
As the most important step of any hybrid version of fuzzy programming approach is single-objective model phase, some advantages of single-objective model of the proposed approach of this study (formulation (
46)), are detailed here:
-
• The optimization procedure of the single-objective model is done in one phase.
-
• Obtaining unique or efficient solution is guaranteed.
-
• The varying weights of the objective functions are eliminated.
-
• Membership function values are not used in the objective function.
-
• The goals are partially prioritized in the objective function and constraints. The weight of membership functions in the objective function depends on the number of objective functions of the main problem.
Of course, some of these advantages can reflect the differences of the proposed single-objective model of this study with those of the literature. The last three advantages are actually the difference of the proposed single-objective model with those of the literature.
The feasibility and efficiency of the formulation (
46) is also detailed by Theorem
1.
Theorem 1.
Formulation (
46)
has a solution and its solution is efficient to the multi-objective problem (
24)–(
36)
.
Proof.
Let’s first define the following formulation which is a part of formulation (
46).
Clearly, considering sign of constraints and type of objective function, problem (
47) has an optimal solution (say,
${x^{0}}$). Now, considering
${\theta _{r}}$ values which are between zero and one,
${x^{0}}$ and
${\lambda _{r}}=0$ $(r\in \{1,2,\dots ,R\})$ together is a feasible solution to the problem (
46). Therefore, the feasible region of the problem (
46) is not empty.
The efficiency of the solution of model (
46) is proved by a contradiction. Suppose that
${x^{\ast }}$ is an optimal solution of model (
46) which is inefficient solution to the problem (
24)–(
36). Therefore, there should be an efficient solution like
${x^{\ast \ast }}$ to the problem (
24)–(
36) which is obtained by model (
46) satisfying the conditions
-
i. ${f_{r}}({x^{\ast \ast }})\leqslant {f_{r}}({x^{\ast }})$ ($\forall r\in \{1,2,\dots ,R\}$) and $\exists i\in [0,1]:{f_{i}}({x^{\ast \ast }})<{f_{i}}({x^{\ast }})$,
-
ii. ${\mu _{r}}({x^{\ast \ast }})\geqslant {\mu _{r}}({x^{\ast }})$ ($\forall r\in \{1,2,\dots ,R\}$) and $\exists \hspace{0.1667em}i\in [0,1]:{\mu _{i}}({x^{\ast \ast }})>{\mu _{i}}({x^{\ast }})$.
So, to respect the minimum satisfaction level of the objectives of
${x^{\ast }}$ and
${x^{\ast \ast }}$, the condition
${\lambda _{0}^{\ast \ast }}\geqslant {\lambda _{0}^{\ast }}$ should be true. Now, considering the objective functions of these two solutions in formulation (
46), the following inequality is obtained:
Therefore,
${x^{\ast }}$ is not an optimal solution of the problem (
46) which is contradictory to the initial assumption for
${x^{\ast }}$ and the theorem is proved. □
3.3 Comparison Metrics
In order to compare the performance of the proposed approach of this study to the other methods of the literature presented in the previous sub-section, the following distance measure is used (Alavidoost
et al.,
2016),
Some well-known distance measures obtained from formula (
49) are defined below.
Manhattan distance ($p=1$): This distance is actually the weighted sum of distance from goal which takes value of one here. The value of this distance has inverse relation with the value of MF as follows:
Euclidean distance ($p=2$): This distance plays the same role as Manhattan distance. In addition, the quality of membership function values are evaluated. Meaning that closer MF values give less distance in the case of equal solutions.
Tchebycheff distance ($p=\infty $): This is the shortest distance comparing to the above two distances. When this distance (also other distances with
$p>1$) is calculated, more penalty is given to the smaller MF values. Therefore, the solutions having close MFs will get less distance value when this distance is considered.
5 Concluding Remarks
A typical assembly line balancing problem with different scale objective functions was studied in this paper. An entropy function was used as an objective function in order to balance the work load of the stations of assembly line plus two more objective functions like equipment purchasing cost and worker time-dependent wage. The most important limitations of this problem were its non-linearity and its multi-objective nature. The non-linearity of the entropy-based objective function was approximated as a linear function using the bounded variable method of linear programming. A new hybrid fuzzy programming approach was developed to solve the proposed multi-objective formulation. In order to compare the efficient solutions of the problem, three distance metrics were used. The required computational experiments were performed by the proposed hybrid fuzzy programming approach and some other approaches of the literature on some test problems. According to the obtained results and using the distance metrics, the proposed solution approach performs either the same or better than the multi-objective solution approaches of the literature like ABD, DY, TH, and SO.
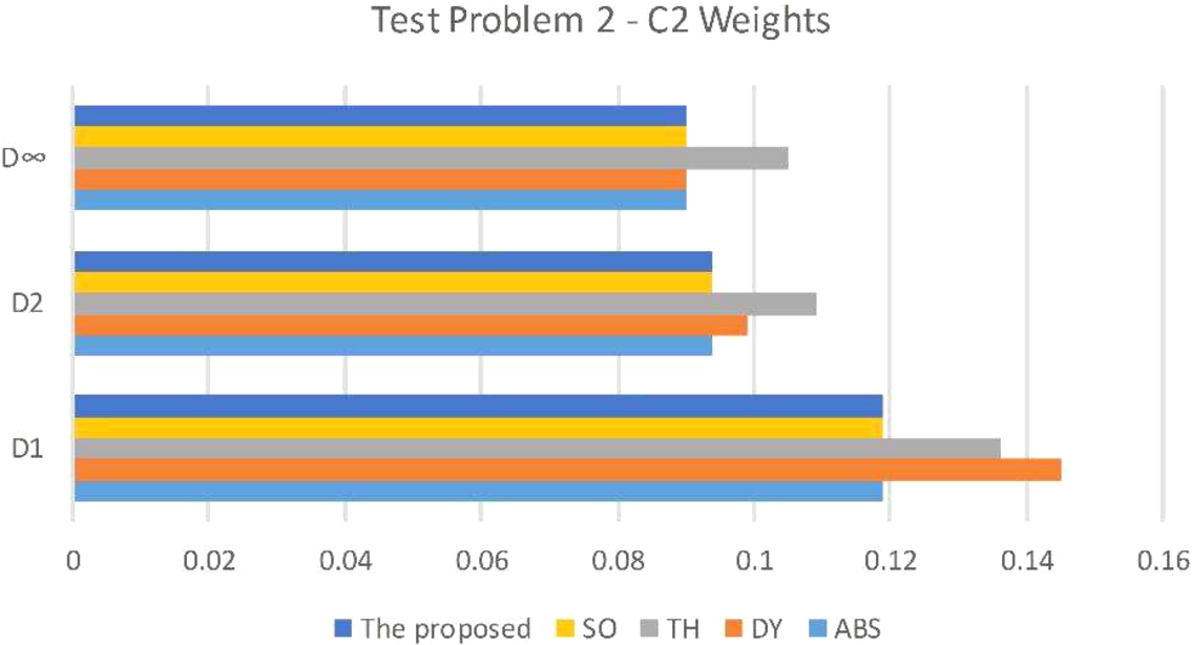
Fig. 13
Chart of the performance of the proposed and employed approaches for test problem 2 with weight combination C2.
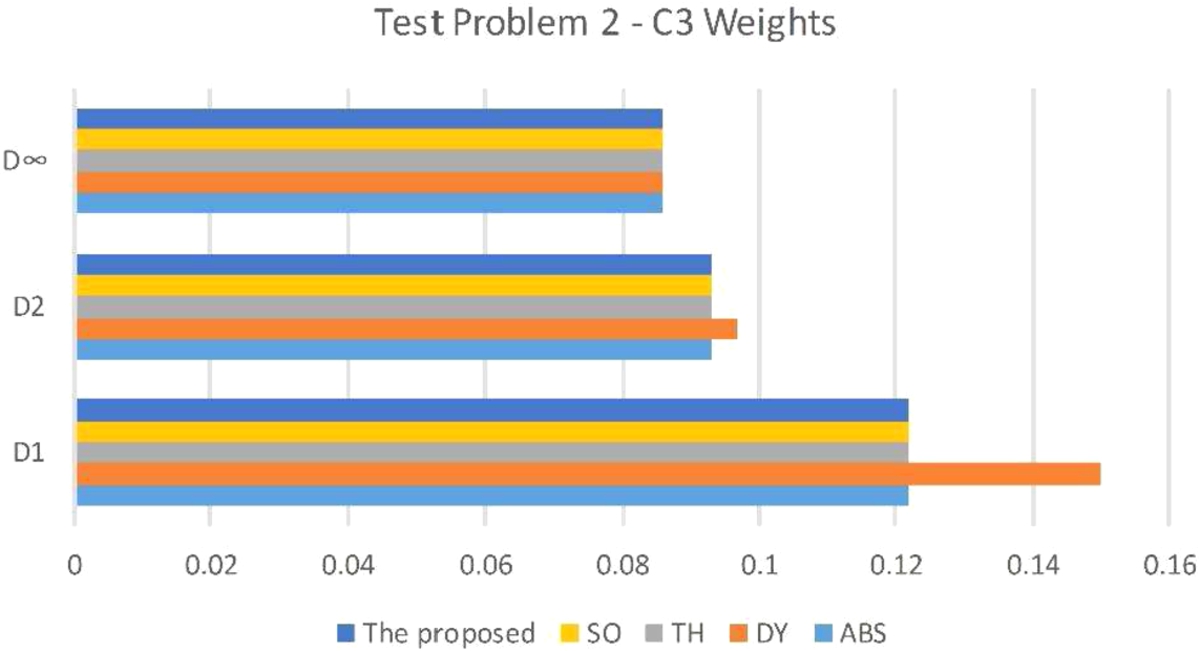
Fig. 14
Chart of the performance of the proposed and employed approaches for test problem 2 with weight combination C3.

Fig. 15
Chart of the performance of the proposed and employed approaches for test problem 2 with weight combination C4.
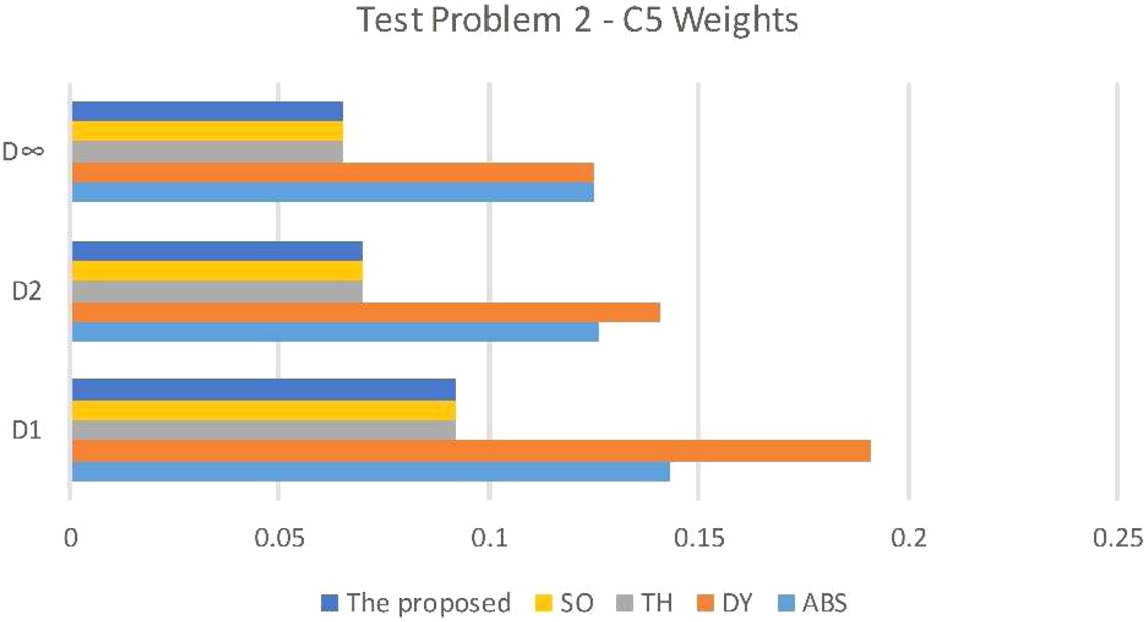
Fig. 16
Chart of the performance of the proposed and employed approaches for test problem 2 with weight combination C5.

