1 Introduction
Orthopair fuzzy sets are fuzzy sets in which the membership grades of an element
x are pairs of values in the unit interval,
$\langle \mu (x),\nu (x)\rangle $, one of which indicates support for membership in the fuzzy set and the other support against membership. Two examples of orthopair fuzzy sets are Atanassov’s classic intuitionistic fuzzy sets (IFSs) (Atanassov,
1986,
2012; Atanassov
et al.,
2013) and a second kind of intuitionistic fuzzy sets (Atanassov,
1983,
2016). This idea has been followed up in Parvathi (
2005), Parvathi
et al. (
2012), Vassilev
et al. (
2008), Vassilev (
2012;
2013). It is noted that for classic IFSs the sum of the support for and against is bounded by one, while for the second kind, Pythagorean fuzzy sets (PFSs), the sum of the squares of the support for and against is bounded by one. (Yager,
2017) introduced a general class of these sets called
q-rung orthopair fuzzy sets in which the sum of the
qth power of the support for and the
qth power of the support against is bounded by one. He noted that as
q increases, the space of acceptable orthopairs increases and thus gives the user more freedom in expressing their belief about membership grade. When
$q=3$, Senapati and Yager (
2019a) have considered
q-rung orthopair fuzzy sets as Fermatean fuzzy sets (FFSs).
PFSs have attracted the attention of many researchers within a short period of time. For example, Yager (
2014) built up a helpful decision technique in view of Pythagorean fuzzy aggregation operators to deal with Pythagorean fuzzy MCDM issues. Yager and Abbasov (
2013) explained the Pythagorean membership grades (PMGs) and the thoughts identified with PFSs and presented the connection between the PMGs and the complex numbers. Reformat and Yager (
2014) applied the PFNs in handling the collaborative-based recommender system. Gou
et al. (
2016) initiated a few Pythagorean fuzzy mappings and studied their basic properties like derivability, continuity, and differentiability in details. Zeng
et al. (
2018) established an aggregation procedure for the PFS and utilized its application in solving MADM problems. Zhang (
2016) introduced a MCDM approach in view of the idea of the similarity measure. PFSs have been effectively connected in different fields, for example, the investment decision (Garg,
2016; Peng and Yang,
2015), the candidate selection of Asian Infrastructure Investment Bank (Ren
et al.,
2016) and the service quality of domestic airline (Zhang and Xu,
2014).
Senapati and Yager (
2019a) have given an example to prove the reasonability of the FFS: When a person wants to give his preference for the degree of an alternative
${x_{i}}$ to a criterion
${C_{j}}$, he may allow the degree to which the alternative
${x_{i}}$ satisfies the criterion
${C_{j}}$ as 0.9, and similarly when the alternative
${x_{i}}$ dissatisfies the criterion
${C_{j}}$ as 0.6. We can definitely get
$0.9+0.6>1$, and, therefore, it does not follow the condition of IFSs. Also, we can get
${(0.9)^{2}}+{(0.6)^{2}}=0.81+0.36=1.17>1$, which does not obey constraint condition of PFS. However, we can get
${(0.9)^{3}}+{(0.6)^{3}}=0.729+0.216=0.945\leqslant 1$, which is appropriate to engage the FFS to capture it. This is to mention that the FFSs have more uncertainties than IFSs and PFSs, and are capable to handle higher levels of uncertainties.
Senapati and Yager (
2019a) defined basic operations over the FFSs and introduced new score functions and accuracy functions of FFSs. They extended the technique for order preference by similarity to ideal solution (TOPSIS) approach to handling the MCDM problem with Fermatean fuzzy information. Senapati and Yager (
2019b) introduced several Fermatean fuzzy aggregation operators, for example, the Fermatean fuzzy weighted average (FFWA) operator, Fermatean fuzzy weighted geometric (FFWG) operator, Fermatean fuzzy weighted power average (FFWPA) operator and Fermatean fuzzy weighted power geometric (FFWPG) operator.
The subtraction and division operations of IFS have been introduced by some authors (Atanassov,
2009; Atanassov and Riecan,
2006; Chen,
2007) and finally been established by Atanassov (
2012) in his recently published book. Since subtraction and division operations are also necessary for FFS, we are going to introduce those two new operations on FFS. The contributions of this paper are the following: Section
2 displays the preliminary information of the paper. Then, in Section
3, we concentrate on basic knowledge of FFS and their fundamental operations. Section
4 proposes the subtraction operation and the division operation over FFSs. Several operational laws of these two operations are given. In addition, the relationships between these two operations are also established in this paper. In Section
5, we discuss two theorems on Fermatean arithmetic mean operations over FFNs. Section
6 describes the concept of weighted product models (WPMs). In next Section, we utilize Fermatean fuzzy weighted product model to solve multi-criteria decision-making problems. Section
8 exhibits the reliability and sustainability of the proposed method in fruitful and flawless application by attaching it to an MCDM problem for choosing the most appropriate bridge construction method. Finally, in Section
9, the conclusion and scope of future research are outlined and discussed.
3 Fermatean Fuzzy Sets
In this section, Fermatean fuzzy sets are defined in detail and their corresponding properties are discussed. Score and accuracy functions of these sets have been defined and compared.
Definition 3.
(See Senapati and Yager,
2019a.) Let
X be a universe of discourse. A Fermatean fuzzy set
$\mathcal{F}$ in
X is an object having the form
where
${\alpha _{F}}(x):X\to [0,1]$ and
${\beta _{F}}(x):X\to [0,1]$, including the condition
for all
$x\in X$. The numbers
${\alpha _{F}}(x)$ and
${\beta _{F}}(x)$ denote, respectively, the degree of membership and the degree of non-membership of the element
x in the set
$\mathcal{F}$.
For any FFS $\mathcal{F}$ and $x\in X$, ${\pi _{F}}(x)=\sqrt[3]{1-{({\alpha _{F}}(x))^{3}}-{({\beta _{F}}(x))^{3}}}$ is identified as the degree of indeterminacy of x to $\mathcal{F}$.
For convenience, Senapati and Yager called $({\alpha _{F}}(x),{\beta _{F}}(x))$ a Fermatean fuzzy number (FFN) denoted by $\mathcal{F}=({\alpha _{F}},{\beta _{F}})$.
We shall point out the membership grades related to Fermatean fuzzy sets as Fermatean membership grades (FMGs).
Theorem 1.
(See Senapati and Yager,
2019a.) The set of FMGs is larger than the set of Pythagorean membership grades (PMGs) and intuitionistic membership grades (IMGs).
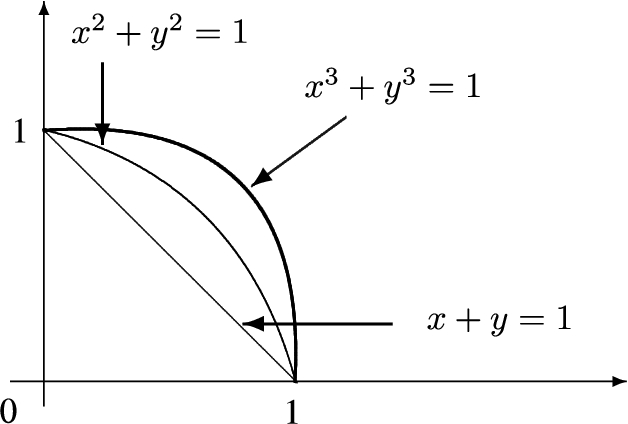
Fig. 1
Comparison of space of FMGs, PMGs and IMGs.
This development can be evidently recognized from Fig.
1. Here we notice that IMGs are all points beneath the line
$x+y\leqslant 1$, the PMGs are all points with
${x^{2}}+{y^{2}}\leqslant 1$ and the FMGs are all points with
${x^{3}}+{y^{3}}\leqslant 1$. We see then that the FMGs enable the presentation of a bigger body of nonstandard membership grades than IMGs and PMGs.
Definition 4.
(See Senapati and Yager,
2019a.) Let
$\mathcal{F}=({\alpha _{F}},{\beta _{F}})$,
${\mathcal{F}_{1}}=({\alpha _{{F_{1}}}},{\beta _{{F_{1}}}})$ and
${\mathcal{F}_{2}}=({\alpha _{{F_{2}}}},{\beta _{{F_{2}}}})$ be three FFNs, then their operations are defined as follows:
-
(i) ${\mathcal{F}_{1}}\cap {\mathcal{F}_{2}}=\big(\min \{{\alpha _{{F_{1}}}},{\alpha _{{F_{2}}}}\},\max \{{\beta _{{F_{1}}}},{\beta _{{F_{2}}}}\}\big)$;
-
(ii) ${\mathcal{F}_{1}}\cup {\mathcal{F}_{2}}=\big(\max \{{\alpha _{{F_{1}}}},{\alpha _{{F_{2}}}}\},\min \{{\beta _{{F_{1}}}},{\beta _{{F_{2}}}}\}\big)$;
-
(iii) ${\mathcal{F}^{c}}=({\beta _{F}},{\alpha _{F}})$.
Definition 5.
(See Senapati and Yager,
2019a.) Let
$\mathcal{F}=({\alpha _{F}},{\beta _{F}})$,
${\mathcal{F}_{1}}=({\alpha _{{F_{1}}}},{\beta _{{F_{1}}}})$ and
${\mathcal{F}_{2}}=({\alpha _{{F_{2}}}},{\beta _{{F_{2}}}})$ be three FFNs and
$\lambda >0$, then their operations are interpreted in this way:
-
(i) ${\mathcal{F}_{1}}\boxplus {\mathcal{F}_{2}}=\Big(\sqrt[3]{{\alpha _{{F_{1}}}^{3}}+{\alpha _{{F_{2}}}^{3}}-{\alpha _{{F_{1}}}^{3}}{\alpha _{{F_{2}}}^{3}}},{\beta _{{F_{1}}}}{\beta _{{F_{2}}}}\Big)$;
-
(ii) ${\mathcal{F}_{1}}\boxtimes {\mathcal{F}_{2}}=\Big({\alpha _{{F_{1}}}}{\alpha _{{F_{2}}}},\sqrt[3]{{\beta _{{F_{1}}}^{3}}+{\beta _{{F_{2}}}^{3}}-{\beta _{{F_{1}}}^{3}}{\beta _{{F_{2}}}^{3}}}\hspace{0.1667em}\Big)$;
-
(iii) $\lambda \mathcal{F}=\Big(\sqrt[3]{1-{(1-{\alpha _{F}^{3}})^{\lambda }}},{\beta _{F}^{\Lambda }}\Big)$;
-
(iv) ${\mathcal{F}^{\lambda }}=\Big({\alpha _{F}^{\lambda }},\sqrt[3]{1-{(1-{\beta _{F}^{3}})^{\lambda }}}\hspace{0.1667em}\Big)$.
Theorem 2.
(See Senapati and Yager,
2019a.) For three FFNs
$\mathcal{F}=({\alpha _{F}},{\beta _{F}})$,
${\mathcal{F}_{1}}=({\alpha _{{F_{1}}}},{\beta _{{F_{1}}}})$ and
${\mathcal{F}_{2}}=({\alpha _{{F_{2}}}},{\beta _{{F_{2}}}})$, the following ones are valid
:
-
(i) ${\mathcal{F}_{1}}\boxplus {\mathcal{F}_{2}}={\mathcal{F}_{2}}\boxplus {\mathcal{F}_{1}}$;
-
(ii) ${\mathcal{F}_{1}}\boxtimes {\mathcal{F}_{2}}={\mathcal{F}_{2}}\boxtimes {\mathcal{F}_{1}}$;
-
(iii) $\lambda ({\mathcal{F}_{1}}\boxplus {\mathcal{F}_{2}})=\lambda {\mathcal{F}_{1}}\boxplus \lambda {\mathcal{F}_{2}}$, $\lambda >0$;
-
(iv) $({\lambda _{1}}+{\lambda _{2}})\mathcal{F}={\lambda _{1}}\mathcal{F}\boxplus {\lambda _{2}}\mathcal{F}$, ${\lambda _{1}},{\lambda _{2}}>0$;
-
(v) ${({\mathcal{F}_{1}}\boxtimes {\mathcal{F}_{2}})^{\lambda }}={\mathcal{F}_{1}^{\lambda }}\boxtimes {\mathcal{F}_{2}^{\lambda }}$, $\lambda >0$;
-
(vi) ${\mathcal{F}^{{\lambda _{1}}}}\boxtimes {\mathcal{F}^{{\lambda _{2}}}}={\mathcal{F}^{({\lambda _{1}}+{\lambda _{2}})}}$, ${\lambda _{1}},{\lambda _{2}}>0$.
Theorem 3.
(See Senapati and Yager,
2019a.) For three FFNs
${\mathcal{F}_{1}}=({\alpha _{{F_{1}}}},{\beta _{{F_{1}}}})$,
${\mathcal{F}_{2}}=({\alpha _{{F_{2}}}},{\beta _{{F_{2}}}})$ and
${\mathcal{F}_{3}}=({\alpha _{{F_{3}}}},{\beta _{{F_{3}}}})$, the following ones are valid
:
-
(i) ${\mathcal{F}_{1}}\cap {\mathcal{F}_{2}}={\mathcal{F}_{2}}\cap {\mathcal{F}_{1}}$;
-
(ii) ${\mathcal{F}_{1}}\cup {\mathcal{F}_{2}}={\mathcal{F}_{2}}\cup {\mathcal{F}_{1}}$;
-
(iii) ${\mathcal{F}_{1}}\cap ({\mathcal{F}_{2}}\cap {\mathcal{F}_{3}})=({\mathcal{F}_{1}}\cap {\mathcal{F}_{2}})\cap {\mathcal{F}_{3}}$;
-
(iv) ${\mathcal{F}_{1}}\cup ({\mathcal{F}_{2}}\cup {\mathcal{F}_{3}})=({\mathcal{F}_{1}}\cup {\mathcal{F}_{2}})\cup {\mathcal{F}_{3}}$;
-
(v) $\lambda ({\mathcal{F}_{1}}\cup {\mathcal{F}_{2}})=\lambda {\mathcal{F}_{1}}\cup \lambda {\mathcal{F}_{2}}$;
-
(vi) ${({\mathcal{F}_{1}}\cup {\mathcal{F}_{2}})^{\lambda }}={\mathcal{F}_{1}^{\lambda }}\cup {\mathcal{F}_{2}^{\lambda }}$.
Theorem 4.
(See Senapati and Yager,
2019a.) Let
$\mathcal{F}=({\alpha _{F}},{\beta _{F}})$,
${\mathcal{F}_{1}}=({\alpha _{{F_{1}}}},{\beta _{{F_{1}}}})$ and
${\mathcal{F}_{2}}=({\alpha _{{F_{2}}}},{\beta _{{F_{2}}}})$ be three FFNs, then
-
(i) ${({\mathcal{F}_{1}}\cap {\mathcal{F}_{2}})^{c}}={\mathcal{F}_{1}^{c}}\cup {\mathcal{F}_{2}^{c}}$;
-
(ii) ${({\mathcal{F}_{1}}\cup {\mathcal{F}_{2}})^{c}}={\mathcal{F}_{1}^{c}}\cap {\mathcal{F}_{2}^{c}}$;
-
(iii) ${({\mathcal{F}_{1}}\boxplus {\mathcal{F}_{2}})^{c}}={\mathcal{F}_{1}^{c}}\boxtimes {\mathcal{F}_{2}^{c}}$;
-
(iv) ${({\mathcal{F}_{1}}\boxtimes {\mathcal{F}_{2}})^{c}}={\mathcal{F}_{1}^{c}}\boxplus {\mathcal{F}_{2}^{c}}$;
-
(v) ${({\mathcal{F}^{c}})^{\lambda }}={(\lambda \mathcal{F})^{c}}$;
-
(vi) $\lambda ({\mathcal{F}^{c}})={({\mathcal{F}^{\lambda }})^{c}}$.
Theorem 5.
(See Senapati and Yager,
2019a.) Let
${\mathcal{F}_{1}}=({\alpha _{{F_{1}}}},{\beta _{{F_{1}}}})$,
${\mathcal{F}_{2}}=({\alpha _{{F_{2}}}},{\beta _{{F_{2}}}})$ and
${\mathcal{F}_{3}}=({\alpha _{{F_{3}}}},{\beta _{{F_{3}}}})$ be three FFNs, then
-
(i) $({\mathcal{F}_{1}}\cap {\mathcal{F}_{2}})\boxplus {\mathcal{F}_{3}}=({\mathcal{F}_{1}}\boxplus {\mathcal{F}_{3}})\cap ({\mathcal{F}_{2}}\boxplus {\mathcal{F}_{3}})$;
-
(ii) $({\mathcal{F}_{1}}\cup {\mathcal{F}_{2}})\boxplus {\mathcal{F}_{3}}=({\mathcal{F}_{1}}\boxplus {\mathcal{F}_{3}})\cup ({\mathcal{F}_{2}}\boxplus {\mathcal{F}_{3}})$;
-
(iii) $({\mathcal{F}_{1}}\cap {\mathcal{F}_{2}})\boxtimes {\mathcal{F}_{3}}=({\mathcal{F}_{1}}\boxtimes {\mathcal{F}_{3}})\cap ({\mathcal{F}_{2}}\boxtimes {\mathcal{F}_{3}})$;
-
(iv) $({\mathcal{F}_{1}}\cup {\mathcal{F}_{2}})\boxtimes {\mathcal{F}_{3}}=({\mathcal{F}_{1}}\boxtimes {\mathcal{F}_{3}})\cup ({\mathcal{F}_{2}}\boxtimes {\mathcal{F}_{3}})$.
In order to rank FFNs, we define the score function of the FFN:
Definition 6.
For any FFN
$\mathcal{F}=({\alpha _{F}},{\beta _{F}})$, the score function of
$\mathcal{F}$ can be defined as follows:
where
$\mathit{score}(\mathcal{F})\in [-1,1]$. For any two FFNs
${\mathcal{F}_{1}}=({\alpha _{{F_{1}}}},{\beta _{{F_{1}}}})$ and
${\mathcal{F}_{2}}=({\alpha _{{F_{2}}}},{\beta _{{F_{2}}}})$, if
$\mathit{score}({\mathcal{F}_{1}})<\mathit{score}({\mathcal{F}_{2}})$, then
${\mathcal{F}_{1}}<{\mathcal{F}_{2}}$. If
$\mathit{score}({\mathcal{F}_{1}})>\mathit{score}({\mathcal{F}_{2}})$, then
${\mathcal{F}_{1}}>{\mathcal{F}_{2}}$. If
$\mathit{score}({\mathcal{F}_{1}})=\mathit{score}({\mathcal{F}_{2}})$, then
${\mathcal{F}_{1}}\sim {\mathcal{F}_{2}}$.
By Definition
6, we recognize that the score function is well organized to rank the FFNs. But, in some instances, this function is not suitable to suggest which FFN is superior, for example, if
${\mathcal{F}_{1}}=\big(\frac{\sqrt[3]{4}}{2},\frac{\sqrt[3]{4}}{2}\big)$ and
${\mathcal{F}_{2}}=(0.5,0.5)$, then
$\mathit{score}({\mathcal{F}_{1}})=\mathit{score}({\mathcal{F}_{2}})=0$. More generally, if any FFN satisfies
${\alpha _{F}}={\beta _{F}}$, then its score is 0. But we realize that these FFNs are not identical. So impelled by the definition of the score function, an accuracy function for FFN can be described as:
Definition 7.
Let
$\mathcal{F}=({\alpha _{F}},{\beta _{F}})$ be an FFN, then the accuracy function of
$\mathcal{F}$ may be described as follows:
Clearly, $\mathit{acc}(\mathcal{F})\in [0,1]$. In fact, $0\leqslant \mathit{acc}(\mathcal{F})={\alpha _{F}^{3}}+{\beta _{F}^{3}}\leqslant 1$. The larger the value of $\mathit{acc}(\mathcal{F})$ is, the higher is the degree of accuracy of the FFS $\mathcal{F}$.
From Definitions
3 and
7, we can get
${\pi _{F}^{3}}+\mathit{acc}(\mathcal{F})=1$. The lower degree of indeterminacy makes the higher accuracy of the FFN
$\mathcal{F}=({\alpha _{F}},{\beta _{F}})$.
Depending upon these score and accuracy functions of FFNs, the ranking technique for any two FFNs can be described as:
Definition 8.
Let
${\mathcal{F}_{1}}=({\alpha _{{F_{1}}}},{\beta _{{F_{1}}}})$ and
${\mathcal{F}_{2}}=({\alpha _{{F_{2}}}},{\beta _{{F_{2}}}})$ be two FFNs.
$\mathit{score}({\mathcal{F}_{i}})$ and
$\mathit{acc}({\mathcal{F}_{i}})$ $(i=1,2)$ are the score values and accuracy values of
${\mathcal{F}_{1}}$ and
${\mathcal{F}_{2}}$, respectively, then
-
1. If $\mathit{score}({\mathcal{F}_{1}})<\mathit{score}({\mathcal{F}_{2}})$, then ${\mathcal{F}_{1}}<{\mathcal{F}_{2}}$;
-
2. If $\mathit{score}({\mathcal{F}_{1}})>\mathit{score}({\mathcal{F}_{2}})$, then ${\mathcal{F}_{1}}>{\mathcal{F}_{2}}$;
-
3. If $\mathit{score}({\mathcal{F}_{1}})=\mathit{score}({\mathcal{F}_{2}})$, then
-
(i) If $\mathit{acc}({\mathcal{F}_{1}})<\mathit{acc}({\mathcal{F}_{2}})$, then ${\mathcal{F}_{1}}<{\mathcal{F}_{2}}$;
-
(ii) If $\mathit{acc}({\mathcal{F}_{1}})>\mathit{acc}({\mathcal{F}_{2}})$, then ${\mathcal{F}_{1}}>{\mathcal{F}_{2}}$;
-
(iii) If $\mathit{acc}({\mathcal{F}_{1}})=\mathit{acc}({\mathcal{F}_{2}})$, then ${\mathcal{F}_{1}}={\mathcal{F}_{2}}$.
6 Weighted Product Model
The weighted product model (WPM) is one of the best known and often applied MCDM methods for evaluating a number of alternatives in terms of a number of decision criteria. Each decision alternative is compared with the others by multiplying a number of ratios, one for each decision criterion. Each ratio is raised to the power equivalent to the relative weight of the corresponding criterion. Some of the first references to this method are due to Bridgman (
1922) and Miller and Starr (
1969). More details on this method are given in the MCDM book by Triantaphyllou (
2000).
Its application first requires development of a decision/evaluation matrix,
$X={[{x_{ij}}]_{m\ast n}}$ where
${x_{ij}}$ is the performance of
i-th alternative with respect to
j-th criterion,
m is the number of alternatives and
n is the number of criteria. To make the performance measures comparable and dimensionless, all the elements in the decision matrix are normalized using the following two equations:
where
${\overline{x}_{ij}}$ is the normalized value of
${x_{ij}}$.
According to WPM the total relative importance of alternative
i, denoted as
${Q_{i}}$, is defined as follows:
where
${w_{j}}$ denotes the weight (relative importance) of
j-th criterion.
7 WPM Approach to MCDM Problem with Fermatean Fuzzy Data
In this section, I am going to introduce the MCDM problem under Fermatean fuzzy environment. Then, an effective decision-making method is hereby indicated to handle such MCDM problems.
7.1 Description of the MCDM Problem with FFNs
The main work done in most of the MCDM problem is to rank one or more alternatives from a collection of possible alternatives regarding multiple criteria. For a stated MCDM problem under Fermatean fuzzy domain, presume that there are
m alternatives
${S_{i}}$ $(i=1,2,\dots ,m)$ and
n criterion
${C_{j}}$ $(j=1,2,\dots ,n)$ with the criteria weight vector
$w={({w_{1}},{w_{2}},\dots ,{w_{n}})^{T}}$ such that
$0\leqslant {w_{j}}\leqslant 1$,
$j=1,2,\dots ,n$, and
${\textstyle\sum _{j=1}^{n}}{w_{j}}=1$. We express the assessment values of the alternative
${S_{i}}$ with respect to the criterion
${C_{j}}$ by
${x_{ij}}=({u_{ij}},{v_{ij}})$, and
$R={({x_{ij}})_{m\times n}}$ is a Fermatean fuzzy decision matrix. Thus, the MCDM problem with FFNs can be considered as the subsequent matrix form:
where each of elements
${x_{ij}}=({u_{ij}},{v_{ij}})$ is an FFN, which implies that those degrees should the alternative
${S_{i}}$ fulfills the attributes
${C_{j}}$ will be the value
${u_{ij}}$ and the degree should the alternative
${S_{i}}$ disappoints the attributes
${C_{j}}$ may be the worth
${v_{ij}}$.
7.2 The Proposed Decision Method
For an effective solution of the MCDM problem, mentioned above, we suggest a Fermatean fuzzy WPM (FF-WPM) method.
The first step in FF-WPM is to normalize the
$R={({x_{ij}})_{m\times n}}$ matrix with a linear method. Let the criteria be classified to a subset of benefit criteria,
B, and a subset of cost criteria,
C. The linear normalization for any
$j\in B$ is defined as follows:
where
${\max _{i}}{x_{ij}}$ is determined as
${\max _{i}}{x_{ij}}=({\max _{i}}{u_{ij}},{\min _{i}}{v_{ij}})$.
And the linear normalization for any
$j\in C$ is defined as follows:
where
${\min _{i}}{x_{ij}}$ is determined as
${\min _{i}}{x_{ij}}=({\min _{i}}{u_{ij}},{\max _{i}}{v_{ij}})$.
By applying score functions, we can easily get the result that
${x_{ij}}\leqslant {\max _{i}}{x_{ij}}$ and
${\min _{i}}{x_{ij}}\leqslant {x_{ij}}$,
$\forall i,j:i=1,2,\dots ,m$,
$j\in C$. The division operations in Eq. (
5) and Eq. (
6) are done based on the Definition
9(ii). The decision matrix
R is transformed into the normalized matrix
$\overline{R}$:
According to WPM the total relative importance of alternative
i, denoted as
${\overline{Q}_{i}}$, is defined as
In Eq. (
8), the power operation
${({\overline{x}_{ij}})^{{w_{j}}}}$,
$j=1,2,\dots ,n$ is done based on Definition
5(iv), while the product operation of obtained values is performed based on Definition
5(i). It is notable that
${\overline{Q}_{i}}$ is a FFN.
In the last step, the score and accuracy functions are calculated for ${\overline{Q}_{i}}$, $i=1,2,\dots ,m$ and the final rankings of alternatives are determined based on the descending order of ${\overline{Q}_{i}}$, $i=1,2,\dots ,m$.
8 Applications to Bridge Construction Selection
In this section, we expand the implementation of the proposed WPM approach with a numerical example, which is discussed in Chen (
2012). There are four available bridge construction methods, including the advanced shoring method (
${S_{1}}$), the incremental launching method (
${S_{2}}$), the balanced cantilever method (
${S_{3}}$), and the precast segmental method (
${S_{4}}$). The set of all candidate methods is denoted by
$S=\{{S_{1}},{S_{2}},{S_{3}},{S_{4}}\}$. The criteria for evaluating bridge construction methods contain durability (
${C_{1}}$), damage cost (
${C_{2}}$), construction cost (
${C_{3}}$), traffic conflict (
${C_{4}}$), site condition (
${C_{5}}$), weather condition (
${C_{6}}$), landscape (
${C_{7}}$), and environmental effect (
${C_{8}}$). Among these criteria,
${C_{1}}$ and
${C_{5}}$ are the benefit criteria, whereas the others are cost criteria. The set of evaluative criteria is denoted by
$C=\{{C_{1}},{C_{2}},\dots ,{C_{8}}\}$ with
${C_{b}}=\{{C_{1}},{C_{5}}\}$ and
${C_{c}}=\{{C_{2}},{C_{3}},{C_{4}},{C_{6}},{C_{7}},{C_{8}}\}$. In order to avoid influencing each other, the decision makers are required to evaluate the four available bridge construction methods
${S_{i}}$ $(i=1,2,3,4)$ under the above eight criterions and the decision matrix
$R=({x_{ij}})$ is presented in the middle of Table
1, where
${x_{ij}}$ (
$i=1,2,3,4$,
$j=1,2,\dots ,8$) are in the form of FFNs. The weight vector of
${C_{j}}$ $j=1,2,\dots ,8$ is
$w={(0.142875,0.059524,0.214251,0.095238,0.142875,0.119048,0.059524,0.166665)^{T}}$.
Table 1
Fermatean fuzzy decision matrix.
| Criteria |
Optimization direction |
Weight ${S_{1}}$
|
${S_{2}}$ |
${S_{3}}$ |
${S_{4}}$ |
max/min ${x_{ij}}$
|
| ${C_{1}}$ |
max 0.142875 |
$(0.38,0.52)$ |
$(0.73,0.28)$ |
$(0.78,0.23)$ |
$(0.57,0.44)$ |
$(0.78,0.23)$ |
| ${C_{2}}$ |
min 0.059524 |
$(0.62,0.22)$ |
$(0.56,0.87)$ |
$(0.08,0.81)$ |
$(0.35,0.65)$ |
$(0.08,0.87)$ |
| ${C_{3}}$ |
min 0.214251 |
$(0.24,0.80)$ |
$(0.25,0.47)$ |
$(0.21,0.65)$ |
$(0.42,0.57)$ |
$(0.21,0.80)$ |
| ${C_{4}}$ |
min 0.095238 |
$(0.51,0.47)$ |
$(0.25,0.71)$ |
$(0.46,0.48)$ |
$(0.40,0.51)$ |
$(0.25,0.71)$ |
| ${C_{5}}$ |
max 0.142875 |
$(0.68,0.35)$ |
$(0.39,0.33)$ |
$(0.65,0.34)$ |
$(0.29,0.63)$ |
$(0.68,0.33)$ |
| ${C_{6}}$ |
min 0.119048 |
$(0.16,0.75)$ |
$(0.23,0.79)$ |
$(0.38,0.45)$ |
$(0.86,0.61)$ |
$(0.16,0.79)$ |
| ${C_{7}}$ |
min 0.059524 |
$(0.25,0.42)$ |
$(0.68,0.29)$ |
$(0.21,0.75)$ |
$(0.17,0.87)$ |
$(0.17,0.87)$ |
| ${C_{8}}$ |
min 0.166665 |
$(0.11,0.90)$ |
$(0.40,0.31)$ |
$(0.38,0.63)$ |
$(0.23,0.76)$ |
$(0.11,0.90)$ |
The normalized decision matrix will be obtained by applying Eq. (
5) and Eq. (
6) based on Definition
9(ii), as shown in Table
2.
Table 2
Normalized decision matrix.
| Criteria |
${S_{1}}$ |
${S_{2}}$ |
${S_{3}}$ |
${S_{4}}$ |
| ${C_{1}}$ |
$(0.38,0.52)$ |
$(0.73,0.28)$ |
$(0.78,0.23)$ |
$(0.57,0.44)$ |
| ${C_{2}}$ |
$(0.08,0.87)$ |
$(0.08,0.87)$ |
$(0.08,0.87)$ |
$(0.08,0.87)$ |
| ${C_{3}}$ |
$(0.21,0.80)$ |
$(0.21,0.80)$ |
$(0.21,0.80)$ |
$(0.21,0.80)$ |
| ${C_{4}}$ |
$(0.25,0.71)$ |
$(0.25,0.71)$ |
$(0.25,0.71)$ |
$(0.25,0.71)$ |
| ${C_{5}}$ |
$(0.68,0.35)$ |
$(0.39,0.33)$ |
$(0.65,0.34)$ |
$(0.29,0.63)$ |
| ${C_{6}}$ |
$(0.16,0.79)$ |
$(0.16,0.79)$ |
$(0.16,0.79)$ |
$(0.16,0.79)$ |
| ${C_{7}}$ |
$(0.17,0.87)$ |
$(0.17,0.87)$ |
$(0.17,0.87)$ |
$(0.17,0.87)$ |
| ${C_{8}}$ |
$(0.11,0.90)$ |
$(0.11,0.90)$ |
$(0.11,0.90)$ |
$(0.11,0.90)$ |
Finally, the FF-WPM is calculated for all of the alternatives. The results are shown in Table
3. The rankings of alternatives in Table
3 are obtained by calculating the score and accuracy functions of FF-WPM. It can be seen that the most preferred alternative is
${S_{1}}$ and then the alternatives
${S_{2}}$,
${S_{3}}$ and
${S_{4}}$ are in the 3rd, 2nd and 4th places, respectively. Therefore, the advanced shoring method will be preferred to other alternatives.
Table 3
Numerical results obtained by FF-WPM.
| Alternatives |
FF-WPM |
Score |
Rank |
| ${S_{1}}$ |
$(0.7088603,0.558145642)$ |
0.182312972 |
1 |
| ${S_{2}}$ |
$(0.5582420,0.693929450)$ |
$-0.16018621$ |
3 |
| ${S_{3}}$ |
$(0.6793039,0.693499322)$ |
$-0.02006513$ |
2 |
| ${S_{4}}$ |
$(0.4626257,0.691596519)$ |
$-0.23178229$ |
4 |

