1 Introduction
In surveillance-video scenes, the presence of crowds (Fig.
1) grows over time. The analysis of these scenes is important for detecting, preventing and predicting dangerous situations (i.e. riots, manifestations, terrorist actions, among others) through systematic observations. This analysis becomes a challenging task for humans because psychological studies indicate that their perception is affected when, in scenarios with crowds, two or more scenes are analysed simultaneously Li
et al. (
2015). In Pattern Recognition and Computer Vision, several works have been focused on automating of scene analysis based on some social Hall (
1966), biological Zhang
et al. (
2010) and psychological Levine and Moreland (
2004) studies. These works have also shown that scenes with crowds are structurally composed by small people groups and their behaviours are given by interactions with each other Moussaïd
et al. (
2010).
In crowded scene analysis, the detection of distinguishable people groups is an essential step. Also, it is a challenging task because there are different groups with distinctive shapes in scenes. Moreover, these groups can appear in crowded scenes with different densities (cf. Fig.
1 parts). Free standing conversational group (F-Formation) has emerged as a kind of group with a great interest in scientific community. It is a social group where people interact with social signal Vinciarelli
et al. (
2009) aside from proximity distances. In this work, we are focused on detecting F-Formation in crowded scenes.
An F-Formation is determined by spatial patterns and orientations between people Kendon (
2010). Their participants make a space between them, where they have equal and exclusive access. F-Formations represent groups of people almost stationary (e.g. some people playing chess, waiting in a queue or talking). Furthermore, they are composed by three spaces: O-space, P-space and R-space. The O-space is an empty space which is surrounded by the person set oriented towards it. This space is the most important one because most of the algorithms reported in the literature only detect it. The P-space involves the O-space where the people bodies are interacting, while the R-space is farther than the P-space. An example of these spaces is illustrated in Fig.
2(a), where an F-Formation can take different forms according to the amount of participants: L-form (Fig.
2(b)), Face-to-Face (Fig.
2(c)), Side-by-Side (Fig.
2(d)) and Circular (Fig.
2(e)). An F-Formation with more than two people commonly has a circular shape.

Fig. 1
Examples of crowded scenes with different densities.
The F-Formation detection methods (Zhang and Hung (
2016); Cristani
et al. (
2011); Vascon
et al. (
2014),
2016; Hung and Kröse (
2011)) use the people positions on the ground floor and orientations of part of people’s body as initial features. Moreover, they have been split into two approaches according to the detection place: (1) still image, and (2) image sequences (i.e. video). Furthermore, F-Formation detection methods are generally composed by two steps (i.e. social representation and clustering step) for detection on a still image, and one additional step (i.e. fusion step) for detection in video. In social representation step, the social relationship value between each people is computed; whereas, the fusion step deletes redundant information of social representation in a sequence of images.
In still image approach, the first reported methods are based on Hough transform Mukhopadhyay and Chaudhuri (
2015), where a vote strategy is performed, for creating an accumulator space and finding a local maximum. The local maximum represents the centre of each O-space Cristani
et al. (
2011); Setti
et al. (
2013). Other methods are based on graph theory, where the people and their relations are represented by vertices and edges, respectively. In this way, the F-Formation detection is reduced to the maximal clique detection (i.e. dominant set) problem Zhang and Hung (
2016); Hung and Kröse (
2011). However, for F-Formation detection over video, according to our knowledge, only methods based on evolutionary game-theory clustering are reported (Vascon
et al. (
2014),
2016). In these methods, fusion and clustering steps are performed over an evolutionary environment, where the social representation is codified on an affinity matrix. Although good results have been obtained, they have a high computational complexity, because social representation modelling is
$O(k{p^{2}})$; where
p is the amount of people and
k is the amount of points in the cloud. This complexity is due to each person being represented with a cloud of points, and each social relation being represented by interceptions between the selected cloud of points. This social representation generates false positives in F-Formation detection. On the other hand, in the fusion step, the affinity matrix sets are integrated in exponential time, in terms of
$O({2^{i}})$ where
i is the number of pivots Somasundaram and Baras (
2009) (e.g. they use simplex method), the clustering step is
$O(pce)$ Bulò and Pelillo (
2009), where
c is the average number of iteration required for converging and
e is the amount of social relations. Thus, the complexity of the method proposed in Vascon
et al. (
2016) is
$O(k{p^{2}}+{2^{i}}+pce)$. For this reason, in this paper we propose a more efficient method for F-Formation detection.
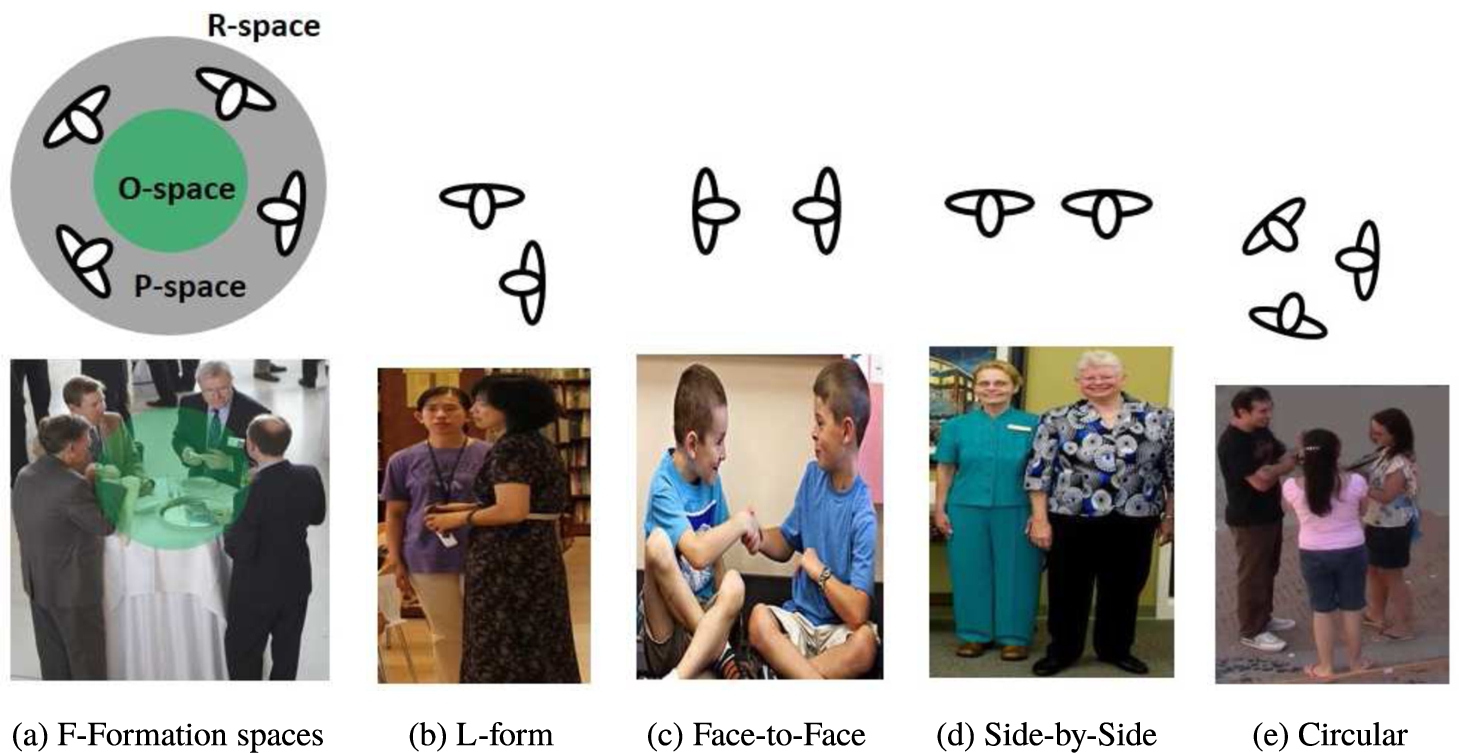
Fig. 2
Examples of F-Formation spaces (a) and forms (b)–(e).
The main contributions of this paper are follows:
-
1. A method for F-Formation detection in video based on fuzzy relations.
-
2. A social representation that is codified on fuzzy matrix.
-
3. A membership function for computing social relations between people.
-
4. A fusion strategy over several fuzzy matrices with a fuzzy operator.
-
5. A clustering for partitioning a fuzzy matrix.
The basic outline of this paper is the following. In Section
2, some basic concepts are provided. Section
3 contains the description of the proposed method. The experimental results are discussed in Section
4. Finally, conclusions and some ideas about future directions are exposed in Section
5.
2 Basic Concepts
In this section, we show a set of concepts, which are required for understanding our proposal.
Definition 1.
A fuzzy relation from a set X to a set Y is a membership function $\rho :X\times Y\to [0,1]$. If $X=Y$, then ρ is named a fuzzy relation on X.
Definition 2.
The fuzzy relation
ρ on
X is a similarity relation Zadeh (
1971) if for all
$x,y\in X$ the followed properties are fulfilled:
-
• Reflexivity: $\rho (x,x)=1$;
-
• Symmetry: $\rho (x,y)=\rho (y,x)$;
-
• Transitivity: $\rho (x,y)\geqslant \underset{z\in X}{\max }\left\{\min \left\{\rho (x,z),\rho (z,y)\right\}\right\}$.
A fuzzy relation
ρ on
X can be represented by a square fuzzy matrix
M, where each cell value
$M(x,y)=\rho (x,y)$. Notice that
$x,y\in X$ and are index (i.e. rows and cols) of
M. In this paper, we perform the fusion by using the
S-norm operator.
Definition 3.
An
S-norm is a function
$S:[0,1]\times [0,1]\to [0,1]$ that fulfills the following properties for all
$a,b$ and
c, which are in a fuzzy relation:
-
• Commutativity: $S(a,b)=S(b,a)$;
-
• Monotony: $S(a,b)\leqslant S(c,d)$ if $a\leqslant c$ and $b\leqslant d$;
-
• Associativity: $S(a,S(b,c))=S(S(a,b),c)$;
-
• Identity: $S(a,0)=a$.
3 The Proposed Method
In this section, we introduce a new method for detecting F-Formations in video based on fuzzy relations. It is important to highlight that, unlike Takagi and Sugeno (
1985), our proposal is not a fuzzy inference system. For this reason, we do not mention aspects as fuzzy inference system such as the number of fuzzy input and output variables.
Our method is composed by three consecutive steps (Fig.
3): (1) social representation, (2) fusion and (3) clustering. We slide a window of length
K on video, and apply the previous steps for each
K selected video frame.
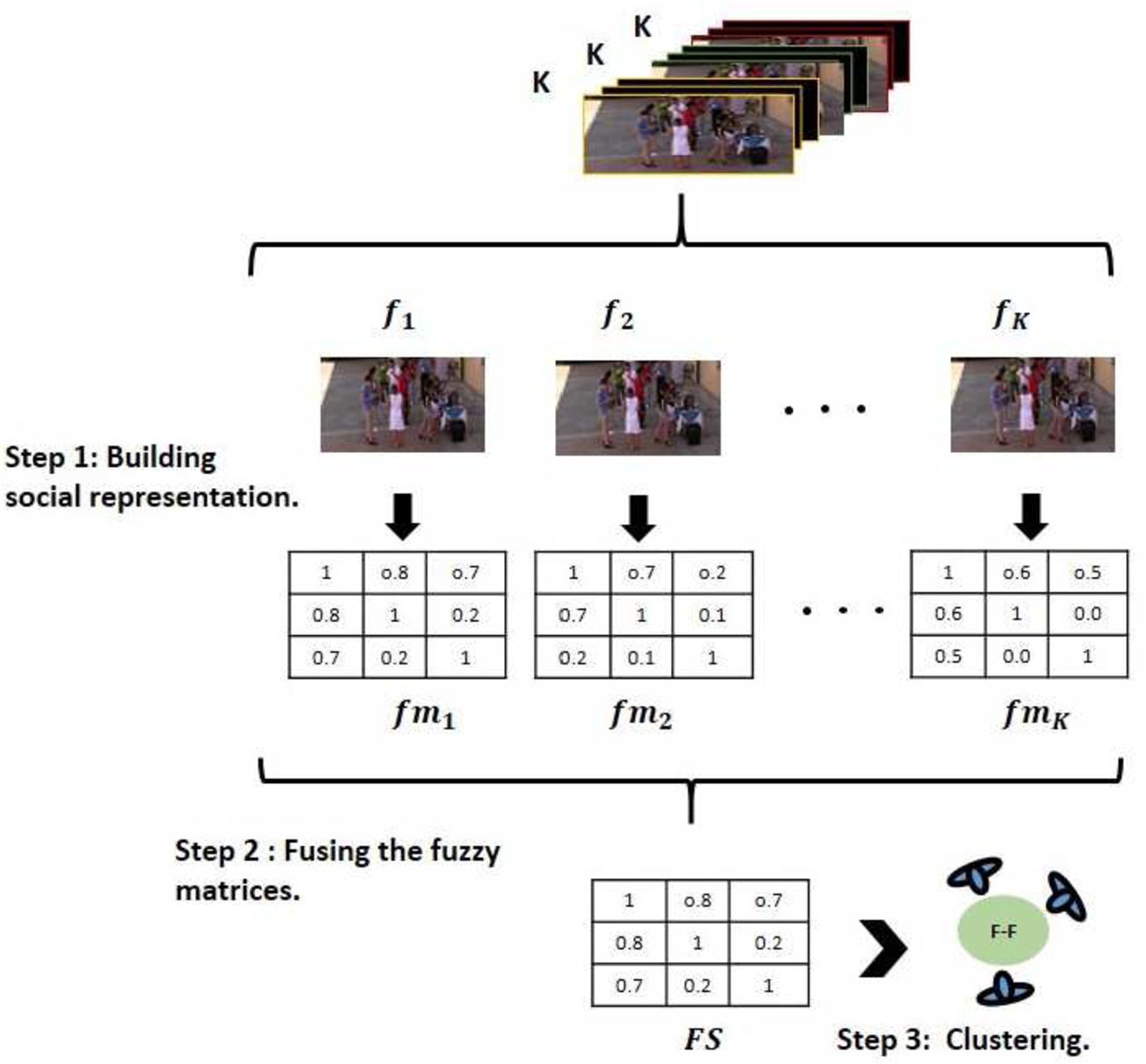
Fig. 3
Workflow of our method for detecting F-Formation in video.
Our proposal uses extracted features (i.e. position on ground plane and head orientation of people) of each video frame. These features are used in social representation step (Section
3.1), which generates a fuzzy matrix by each frame, too. After wards the fuzzy matrices are integrated by fusion (Section
3.2), and a new fuzzy matrix is generated. Finally, a clustering (Section
3.3) is accomplished over new fuzzy matrix.
3.1 Social Representation
A frustum is a biological area where interactions between people often occur. It is also the place where people show more interest through their interactions. In Vascon
et al. (
2016), the social representation is based on frustum concept. The relational degree between people are computed with the interception of their frustum. Each person-frustum is represented by a cloud of points, which is generated by a normal distribution. However, this way of computing the relational degree between people in sequences image has two weaknesses. First, it is expensive over time because a frustum for each person in each time is generated. Second, its accuracy depends on the number of points assigned to each frustum, assuming that the cloud of points has a normal distribution.
We propose an efficient social representation which is
$O(p\log p)$, where
p is the amount of people. Notice that in our representation a frustum is represented with only one point (Fig.
4(b)). In this way, our social representation is more efficient than the proposed in Vascon
et al. (
2016), because we avoid to generate the cloud of points (Fig.
4(a)), deleting the assumption of the data distribution. Furthermore, we propose a membership function for computing the interception between person-frustum, too. Thereby, the membership function value is coded on a symmetric fuzzy matrix.
In Fig.
4(b), an example of relations between two people
${p_{1}}$ and
${p_{2}}$ is shown. These people are placed over the positions
$({x_{1}},{y_{1}})$ and
$({x_{2}},{y_{2}})$ in the ground plane. The distance between them is
${d_{1}}$ and their orientations are
${\sigma _{1}}$ and
${\sigma _{2}}$, respectively. Besides, each person
${p_{k}}$ $(k=1,2)$ votes for a position
${v_{k}}=({x_{k}}+r\cdot \cos {\sigma _{k}},{y_{k}}+r\cdot \sin {\sigma _{k}})$ where the distance between
${v_{1}}$ and
${v_{2}}$ is
${d_{2}}$ and
r is the vote length. The membership function defined in
and represented by Fig.
4(c) computes the interception between frustums. A valid interception between person-frustum is based on the following rules: first, the distance between people votes
${d_{2}}$ is smaller than the distances between people, which are interacting (
${d_{2}}\leqslant {d_{1}}$). Second, the people votes share the side of the line formed with their positions (e.g. the line labelled as
${d_{1}}$ in Fig.
4(b)). Furthermore, if the value of
${\mu _{\widetilde{p}}}$ is near to 1, there is a strong relation between two people, and if it is near to 0, it means that there is a weak relation between them.
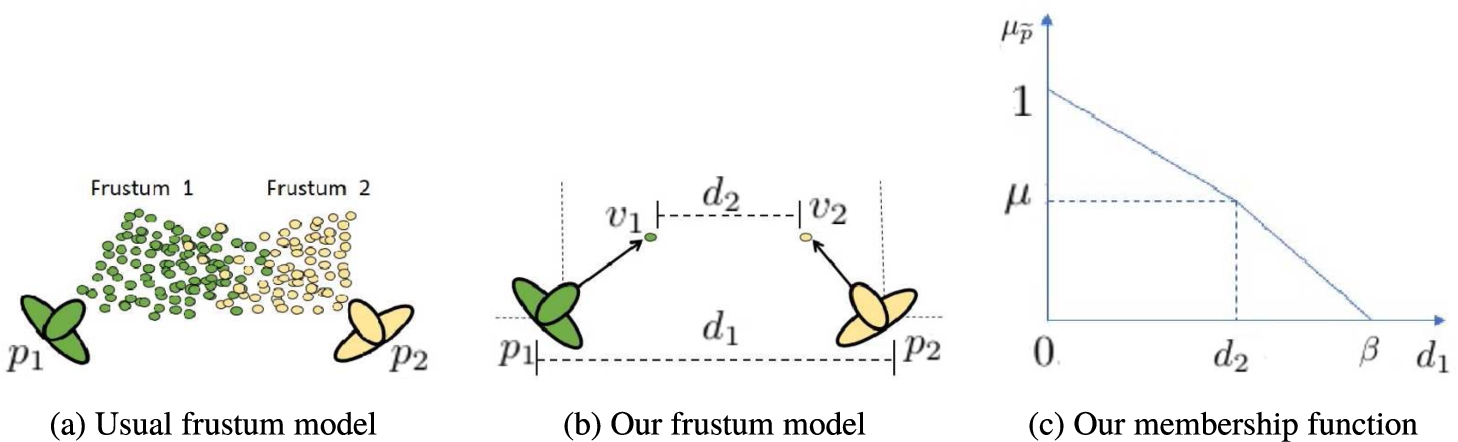
Fig. 4
Social representation model for F-Formation detection in video.
The parameter
μ in (
1) is the value obtained by the membership function when the people are looking to the same place, and their orientations are of
${90^{\circ }}$. In the previous situation, it is non-trivial to decide if the people-frustum is intercepted, where two rough viewpoints can be emitted (i.e. when frustums are intercepted or not). For this reason, we relax the viewpoint setting values in the range
$[0,1]$ for
μ.
On the other hand,
β is the smooth parameter that indicates weak relations between people, and
δ takes value 1 if the people votes share the same side in the plane, otherwise it is 0. Moreover, the value range of
${d_{1}}$ is taken from Hall theory Hall (
1966). This theory characterizes physical distances when the people have social interactions.
3.2 Fusion
In the fusion step (see the Step 2 of Fig.
3), we select a window with length
K, to indicate the number of frames which will be processed. The fuzzy matrix of each frame
${f_{i}}$ (
$i\in [1,K]$) is built through the membership function proposed in Section
3.1. At this point, all
${f_{i}}$ are associated to a fuzzy matrix
$f\hspace{-0.1667em}{m_{i}}$, then, we perform a fusion
$F\hspace{-0.1667em}S=S(\cdots S(S(f\hspace{-0.1667em}{m_{1}},f\hspace{-0.1667em}{m_{2}}),f\hspace{-0.1667em}{m_{3}}),\dots ,f\hspace{-0.1667em}{m_{k}})$ over
$f\hspace{-0.1667em}{m_{i}}$, where
S is an
S-norm and
$F\hspace{-0.1667em}S$ is the fuzzy matrix obtained by applying
S operator. In Gupta and Qi (
1991) there are several examples of
S-norm operator that can be used in our proposal.
We base on the idea proposed by Vascon (2016), where smoothness is considered between consecutive frames (i.e. the movement of people between consecutive frame has small variation). They integrate affinity matrices for searching a consensus and obtain a new affinity matrix without redundant information. However, the value in a new affinity matrix is quite different of integrated affinity matrices. This gives erroneous data for the clustering process.
In our case, we integrate with an
S-norm operator as mentioned above, because we use fuzzy relations represented by fuzzy matrices. Our objective is to search an
S-norm which returns an
$F\hspace{-0.1667em}S$, where their values correspond with the values of
$f\hspace{-0.1667em}{m_{1}},f\hspace{-0.1667em}{m_{2}},f\hspace{-0.1667em}{m_{3}},\dots ,f\hspace{-0.1667em}{m_{k}}$. Thus, our fusion step is
$O(Kp\log p)$, where
K is the window length and
$p\log p$ is the cost of iterating a symmetric fuzzy matrix
$f\hspace{-0.1667em}{m_{k}}$. Notice that the complexity of our proposal, unlike the proposed in Vascon
et al. (
2016), is not exponential.

Algorithm 1
ClusteringRF(M, α)
3.3 Clustering
For clustering, we introduce the Algorithm 1, which receives a fuzzy matrix and a threshold, and returns clustering of fuzzy relation with membership value equal or bigger than the threshold. However, our membership function represented by the input fuzzy matrix has to fulfill with reflexivity, symmetry and transitivity properties Zadeh (
1971). It is easy to verify that our membership function fulfills the reflexivity and symmetry properties, but it is not transitive. To solve this situation, the Tamura
n-step procedure Tamura
et al. (
1971) is applied for computing the transitive closure of input fuzzy matrix. The results of the procedure is a new fuzzy matrix which represents a similarity relation.
The indices
$i,j$ of a new fuzzy matrix are in the same group if
$M(i,j)\geqslant \alpha $. Notice that in Algorithm 1 we search the neighbours of each index in
M. However, we visit only once the neighbours because
M is symmetric (i.e.
$M(i,j)=M(j,i)$). Furthermore, the out of algorithm is a partition of index set
$LI$. Thus, our clustering step is
$O({p^{5}})$, where
p is the amount of people, because computing the transitive closure is expensive in time Zadeh (
1965). However, a more practical solution can be adopted Lee (
2001) where the complexity could be
$O({p^{2}})$.
4 Experimental Results
In this section, we present the experimental evaluation of our proposed method; comparing its results with the best scores reported in the literature.
The proposed method is evaluated over the Coffee Break database Cristani
et al. (
2011), which was obtained from a real-world environment. Coffee Break is composed by social events of people which are interacting and enjoying a cup of coffee. This database comprises two image sequences: (1) the sequence one with 11 people and (2) the sequence two with 14 people. The head orientations were estimated considering four directions: front, back, left and right. Besides, the sequences were annotated by psychologists using several questionnaires; resulting 45 and 75 labelled images for the sequence one and two, respectively.
To evaluate our proposal we use the validation protocol proposed by Vascon (2016), where a group is correctly detected if at least
$\lceil T\cdot |G|\rceil $ of its members are found and not more than
$\lceil (1-T)\cdot |G|\rceil $ are detected as not members. The value
$|G|$ is the cardinality of the labelled group and
$T=2/3$. For each sequence, the precision
p, sensitivity
s and
$F1$ are computed as follows:
Our experiments were carried out with MATLAB, on the Windows 8 over a personal computer Intel Core
$i5\text{-}3470$ CPU with 3.20 GHz and 8 GB RAM.
Figure
5 shows the results obtained by different methods reported in the literature and our proposal over image sequence (1) and image sequence (2) of Coffee Break database. The corresponding subfigures are labelled in vertical axis with
$F1$ score of each method, and by the number of selected frame (
K) in horizontal axis.
We compare our method regarding the strategies (a, b, c, d) reported in Vascon
et al. (
2016), which have achieved the best results on the analysed database. These methods are validated until a maximum number of frame of
$K=9$, because they turn inconsistent for a greater number. However, we use 12 frames, and our proposal keeps stable with good results. Notice that our method (cf. Fig.
5 parts) achieves the best results for
$K>4$. Besides, its efficacy increases accordingly as the frame number increases unlike in other methods. This is due to the fact that we consider temporal information, taking into account the most frequent and strong relations over time. In this way, we search the real relations between conversational groups in scenes with crowds. Thus, as we expected, in most of the cases, our proposal has better results than the methods reported by Vascon (2016). Moreover, our results over sequence one (Fig.
5(a)) are better than sequence two (Fig.
5(b)) of Coffee Break. This is due to crowds in the sequence one being not as dense as in the sequence two (i.e. 11 people for sequence one and 14 people for sequence two). Besides, the frequent concurrence rate of the groups in sequence one is also smaller than in sequence two.
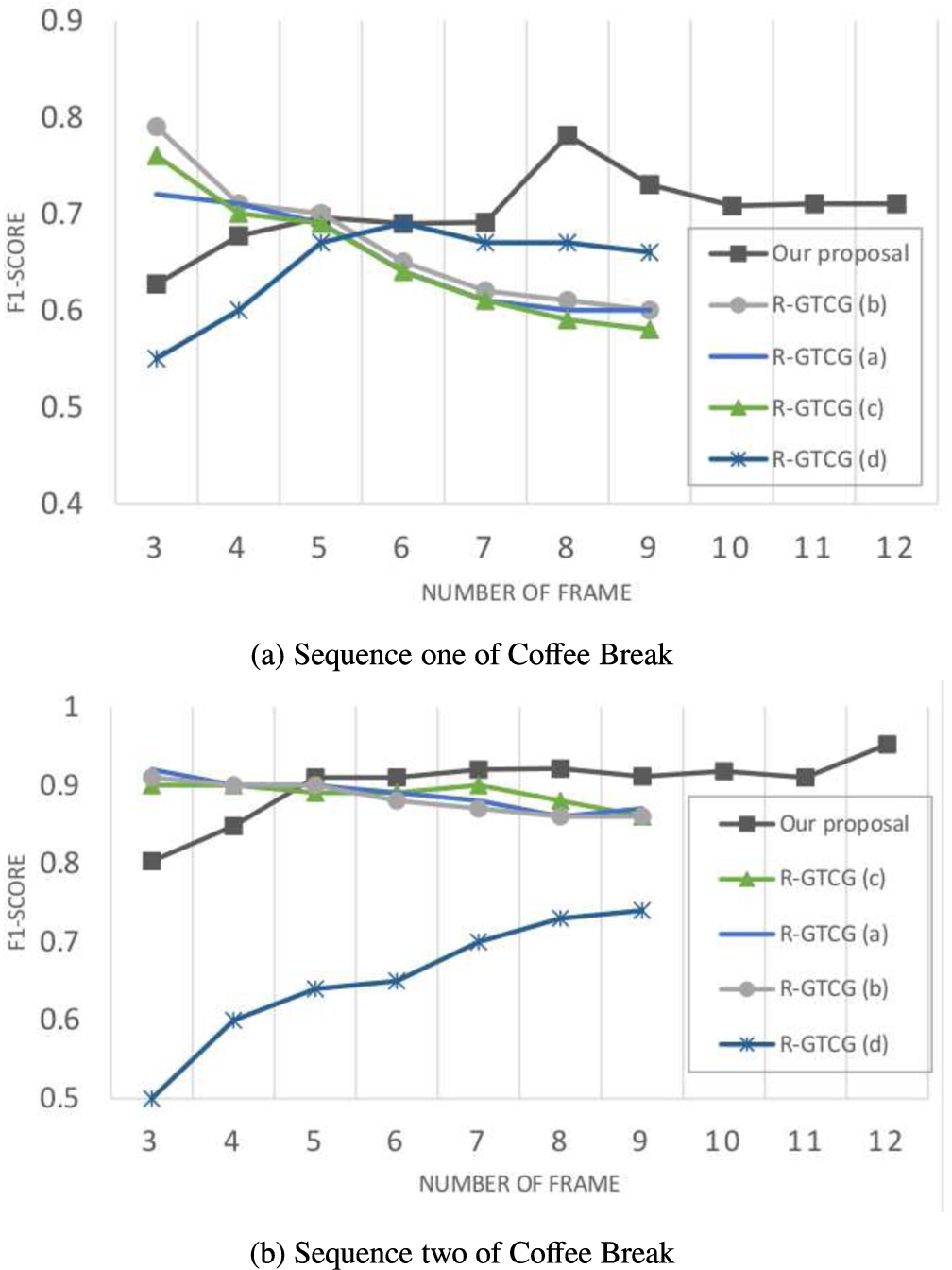
Fig. 5
Results achieved over Coffee Break database.
In our experiments we establish that interactions between two people happen in a diameter of 120 cm. This physical distance is proposed in Hall theory Hall (
1966) as social space where social relations occur. Moreover, we test several
S-norm operators Gupta and Qi (
1991) and parameters values (
$r,\mu ,\beta $) in the fusion step and get the better result with a Zadeh’s max operator and with radius
$r=60$,
$\mu =0.5$ and
$\beta =80$. Also, in the clustering step, we tested several
α-cut from 0.5 to 1 with increments of 0.1. Then, we obtained the best results in the sequence one and the sequence two of the Coffee Break database with
α-cut
$=0.8$ and 0.6, respectively. Notice that our best results for both sequences were achieved with the same values for
r,
μ and
β, because these sequences are quite similar (e.g. distance between people). However, these sequences have different densities, which require different
α-cut (i.e. 0.8 and 0.6).
Our proposal is sensible to the type of crowded scene. The above results suggest that our proposal should set parameter $r=60$, $\mu =0.5$ and $\beta =80$ in Coffee Break database to detect an F-Formation; however, the α-cut should decrease according to the scene density increment.
5 Conclusions
In this paper, we propose a new method for detecting free steading conversational group (F-Formation) in surveillance-video crowded scene. We introduce a new representation for social interactions between people in multiple frame and clustering. Our solution is based on fuzzy relations theory where we proposed a membership function for computing strength of people relations.
Our experiments help us to show that our representation is useful to represent social interactions between people in multiple frames. Moreover, in this representation, only one point vote of each person is enough to compute the frustum. We can conclude that our proposal is an efficient, effective and straightforward solution, too.
In the future, we are going to analyse other possibility of membership function to decrease the parameter number. Moreover, we are going to analyse the common crowd density to automatically obtain an α-cut in the clustering step.

