1. Home
  2. Issues
  3. Volume 29, Issue 1 (2018)
  4. Fuzzy Logic Models for Non-Programmed De ...

Fuzzy Logic Models for Non-Programmed Decision-Making in Personnel Selection Processes Based on Gamification
Volume 29, Issue 1 (2018), pp. 1–20
Pub. online: 1 January 2018      Type: Research Article      Open accessOpen Access
Received
1 March 2017
Accepted
1 November 2017
Published
1 January 2018

Abstract

Non-programmed decision-making is an activity that requires a number of methods to try to capture the rational behaviour of an aspirant in situations of uncertainty. Thus, there is a varied list of attributes, methods, and mechanisms that are intended to describe the way in which aspirants can be profiled. However, this modelling proves to be complex if it is approached in scenarios based on game mechanics from gamification. For this reason, the following article aims to contribute to the processes of selection of personnel delimited only to the making of non-programmed decisions, through the implementation of game mechanics. In order to model this selection, the purpose of the following study is to carry out the formulation of inference rules based on fuzzy logic in order to capture the tacit transfer of certain types of information in personnel selection processes and to determine aspects that allow the shaping of aspirants. Finally, the results and conclusions obtained are presented.

1 Introduction

The staff selection process is considered “a critical process in the integrated management of human resources in organizations given it strongly influences the effectiveness of management processes that occur after the selection” as it is presented by Salgado and Moscoso (2008). The authors highlight that the activities that are usually carried out in the selection processes deserve reconsideration. This is because doubts have been identified about the effectiveness of applying a written test that makes clear the pretensions of what it’s been investigating, in addition to the fact that they take long application times.
For his part, Highhouse (2008) mentions that the traditional unstructured interview is more effective than other procedures involving resolutions using paper and pencil. However, most companies perform these procedures more frequently (handmade, usually multiple-choice). This is complemented by the fact that human resources professionals are aware of the limitations of the informal interview, which is mentioned by Rynes et al. (2002) and Vakkayil et al. (2017). Similarly, authors such as He and Gong (2010) agree with these positions, as they support the following limitations in some methods of recruitment: false or incorrect information can be obtained during the background investigation; interviews need to be applied by experts trained to not be carried away by a certain bias; and there is a high probability of false positives with polygraphs. In addition, the procedure is long and arduous, and in some countries, it is not legal to administer polygraphs or they have no regulation.
Gamification is an unexplored area in issues related to selection of personnel. Authors like Burke (2012) and Kim (2015), in addition to mentioning the topic of employee performance, summarize gamification as the trend of using gaming mechanics in other non-entertainment environments such as innovation, marketing, training, health, and social change.
In the literature we can find different decision making approaches based on fuzzy tools, see Capuano et al. (2017), Liu et al. (2017), Zhang et al. (2017), Pérez et al. (2010), Cabrerizo et al. (2013, 2014). One of the motivations of the following article is to raise, from the point of view of fuzzy logic, a series of rules of inference that can be linked to the management of the profiles of the aspirants to top management positions (players) through a test based on gamification. The characters that support the profiling of aspiring players within the game were defined from two conceptual notions: the first notion, related to an organizational theory about leadership in which employees are classified as eagles or ducks, and the second notion, which describes human behaviour from five global dimensions: anxiety, independence, tenacity, extraversion, and self-control. All these features of the game model developed are specified in Albadán Romero et al. (2016), with emphasis on the gamification details. Finally, it is intended to propose a series of guidelines that facilitate the modelling of profiles in function of the non-programmed decision-making supported in the gamification.
The paper is organized as follows: Section 2 presents the background, where the rules that define mathematical modelling for non-programmed decision-making are discussed, and the characteristics about gamification are also presented. Section 3 defines the method of work based on the methodology used in our study. Section 4 presents the analysis of the results obtained from a case study defined in a test based on gamification. Section 5 presents the discussions, and, finally, Section 6 presents the conclusions and recommendations for future work.

2 Background

2.1 Decision-Making

The upper cognitive layer of the brain contains almost four dozen fundamental cognitive processes, as established in Wang et al. (2003), which are categorized into two large groups: subconscious processes and conscious processes, each group with two layers as modelled in Albadán Romero and Gaona-García (2015). There are several proposals of benefits of decision-making in cognitive tasks and psychiatric process: Grant et al. (2011), Deegan and Drake (2006), and Duncan et al. (2010). For non-programming decision-making for the personal selection process, the following sources have proposals: Nicolas (2004), McKenzie et al. (2011), and Kao et al. (2012). Still there are no literature reviews supported by gamification. By making an analysis based on decision-making, it is necessary to detail that the conscious processes are characterized by being acquired and moulded and can be controlled deliberately by will, aspirations, and motivations. Within conscious processes, decision-making is part of higher cognitive processes. The authors refer to other functions of the brain that are classified in the upper layer, among which are reasoning, analysis, and quantification, among others.

2.2 Mathematical Models of Decision-Making

There is a variety of strategies developed from the traditional perspective, as well as from game theory, cognitive science, management sciences, and economics, that lead to different mathematical models about decision-making. Under these approaches, authors like Wang et al. (2004) present a taxonomy of models and decision-making criteria with four categories. Table 1 shows the taxonomy mentioned.
Table 1
Taxonomy of decision-making strategies and criteria Wang et al. (2004).
Strategy Criteria
1. Intuitive
 a. Arbitrary Based on the easiest or familiar selection
 b. Preferential Based on propensity, hobby, tendency, expectation
 c. Common sense Based on axioms and judgements
2. Empirical
 a. Trial and error Based on exhaustive tests
 b. Experimental Based on the results of experiments
 c. Experience Based on existing knowledge
 d. Consultor Based on professional consultation
 e. Estimate Based on an approximate assessment
3. Heuristic
 a. Principles Based on scientific theories
 b. Ethics Based on philosophical criteria and beliefs
 c. Representative Based on common thumb rules
 d. Availability Based on limited information or local maxima
 e. Anchor Based on a presumption or bias and its justification
4. Rational
4.1 Static
 a. Minimum cost Based on the minimization of energy, time and money
 b. Maximum benefit Based on the maximization of functionality, reliability, quality, usability
 c. Maximum utility Based on cost-benefit ratio
 d. Certainty Based on maximum chance, statistical data
 e. Risks Based on minimal loss or regret
 f. Uncertainty
 g. Pessimistic Based on minimax
 h. Optimistic Based on maximax
4.2 Dynamic
 a. Interactive Events Based on automatons
 b. Games Based on conflicts
 c. Zero Summation Based on the summation (gain + loss) = 0
 d. Not Zero Summation Based on the summation (gain + loss) = 0
The first two categories (intuitive and empirical) are in the path of human intuitive cognitive psychology and therefore do not have a rational model to explain such selection criteria. Therefore, the mathematical modelling is not detailed in this category of strategies; however, the model proposed here to characterize non-programmed decision-making processes involves capturing actions that determine whether the player (who makes the decisions) appealed to one of the strategies mentioned. The following is a preliminary mathematical model followed by an illustration of some of the main mathematical models of decision-making, which are implemented mainly in decision support systems.

2.3 Preliminary Mathematical Model

In this section, we will work on the fundamental and general mathematical models of decision-making addressed in Wang et al. (2004). In a first approximation, the selection axiom states that there exists a function of selection for some non-empty collection of sets of non-empty disjoint alternatives indicated in (1):
(1)
\[ {A_{i}}|{A_{i}},\hspace{1em}i\in I,\hspace{1em}{A_{i}}\subseteq U,\hspace{1em}y,{A_{i}}\ne \varnothing .\]
Therefore, we have a function as shown below in (2):
(2)
\[ f:\{{A_{i}}\}\to {A_{i}},\hspace{1em}i\in I.\]
That function is considered a selection function if we obtain as a result an element, which would represent a selected alternative, which belongs to a set of alternatives ${A_{i}}$, as reflected in (3):
(3)
\[ f({A_{i}})={a_{i}},\hspace{1em}{a_{i}}\in {A_{i}}.\]
The set of alternatives, which is characterized because each of the alternatives is different from the others but all belong to a set of possible alternatives, is expressed in (4):
(4)
\[ {A_{i}},{A_{i}}\cap {A_{{i^{\prime }}}}=\varnothing ,\hspace{1em}i\ne {i^{\prime }},\hspace{1em}i\in I,\hspace{1em}{i^{\prime }}\in I,\hspace{1em}{A_{i}}\subseteq U.\]
From (3), we can obtain the formal specification of a decision (d), which is a selected alternative (${a_{i}}$) from a non-empty set of alternatives (${A_{i}}$) and which is obtained when a set of criteria is added for the selection of alternatives (C), which is expressed in (5):
(5)
\[ d=f({A_{i}},C).\]
Finally, the cognitive decision-making process is modelled as a Cartesian product between the selection alternatives (${A_{i}}$) and established criteria (C) to achieve a given decision goal, as expressed in (6):
(6)
\[ d=f:{A_{i}}\times C\to {A_{i}},\hspace{1em}i\in I,\hspace{2em}{A_{i}}\subseteq U,\hspace{1em}{A_{i}}\ne \varnothing .\]
The possible number of decisions (n) can be determined from the sizes of ${A_{i}}$ and C.
(7)
\[ n=\mathrm{\# }({A_{i}})\cdot \mathrm{\# }(C)\]
where # is a cardinal calculation on the sets. If any of the two sets, selection alternatives, or criteria is equal to zero, the decision cannot be derived.

2.4 General Mathematical Models

Decision theory covers diverse models and formal methods to carry out an analytical and systematic approach to studying the optimization of selection processes. An already well-known approach is the operations research with its different strategies and problem-solving models, as evidenced by Hillier et al. (2005), who approach this discipline as an application to “conducting and coordinating activities in an organization” and authors Al-Azab and Ayu (2010), who explain some of the models that are most commonly implemented to make a correct decision in environments of certainty, risk, uncertainty, with experimental information, and so on.
To easily understand each of the criteria presented below, one must start from the premise that in order to make a decision, you must have several alternatives (for example: $X,Y,Z$). These alternatives that will solve the problem will have different values or results, which can be influenced by the characteristics of the environment where the decision will be made (for example: ${X_{1}},{X_{2}},{X_{3}},{Y_{1}},{Y_{2}},{Y_{3}},{Z_{1}},{Z_{2}},{Z_{3}}$).

2.4.1 Wald Criterion (Minimax)

The Wald criterion is a decision-oriented criterion to maintain a “prudent” position. It basically consists of taking each alternative solution, assigning it the worst possible result, and choosing the best one from among them.
Initially, we will have a set of alternatives ${A_{i}}$, from which we must choose the one with the lesser weight, as evidenced in (8), where ${r_{ij}}$ implies having a set of weights by a single alternative. For its part, ${m_{i}}$ is the set with the lowest weights obtained by each alternative.
(8)
\[ {A_{i}}=\operatorname{Min}{r_{ij}}={m_{i}}.\]
Subsequently, we take the set of the lower weights, or worse results, of each alternative to select the largest of them, as described in (9):
(9)
\[ d=\operatorname{Max}(\operatorname{Min}{r_{ij}})=\operatorname{Max}({m_{i}}).\]
It is considered a convenient method when the decision-maker expects the worst condition for himself and tries to find the solution to facing the opposition, according to Xiaogang and Qijie (2011), who keep in mind that research in these decision situations is also called game theory. In Radner (2015), it is mentioned that the Wald criterion, also known as the minimax rule, is the most promising candidate method for rational behaviour in situations that consider uncertainties.

2.4.2 Maximax Criterion

The maximax criterion is the counterpart of the Wald criterion and characterizes an “optimistic” or “risky” orientation towards decision-making. Radzian et al. (2010) synthesize it as the strategy that is intended to maximize the gain. Basically, each alternative will be taken and assigned the maximum possible value, and from these maximum values, the best is selected again.
This starts from an initial set of alternatives ${A_{i}}$, which can contain several weights, and from them, the best one must be chosen, the greatest one being presented in (10) ${r_{ij}}$ implies having a set of weights by a single alternative. For its part, ${m_{i}}$ is the set with the highest weights obtained by each alternative.
(10)
\[ {A_{i}}=\operatorname{Max}{r_{ij}}={M_{i}}.\]
From the set of the best weights, or better results, of each alternative ${m_{i}}$, the greater of them is selected, as expressed in (11):
(11)
\[ d=\operatorname{Max}(\operatorname{Max}{r_{ij}})=\operatorname{Max}({M_{i}}).\]
The following criteria present mathematical processes that involve tabulating, graphing, or making use of decision support systems. Therefore, it is pertinent to clarify that the present work will not be detailed about that, as it is being assumed that the study of non-programmed decision-making refers to a decision-maker who would not carry out extensive processes or rely on applications or software in general.

2.4.3 Hurwicz Criterion

The Hurwicz criterion is a decision-making criterion that is found in the middle of the Wald and maximax criteria. The decision-maker evaluates the degree of pessimism with a coefficient called α.
With the coefficient, a convex linear combination between the best and worst results for each alternative is determined, and the best one is chosen. (12) includes the coefficient α of the degree of pessimism in each term of the expression.
(12)
\[ {A_{i}}\to {C_{i}}=\alpha {m_{i}}+(1-\alpha ){M_{i}}.\]
Then, the decision is obtained from the highest value after the combinations, as evidenced in (13):
(13)
\[ d\to \operatorname{Max}{C_{i}}=\operatorname{Max}\big\{\alpha {m_{i}}+(1-\alpha ){M_{i}}\big\}.\]
In this criterion, the coefficient of the degree of pessimism becomes an indispensable element. In the research of Van Nam et al. (2009), the authors demonstrate that if there is no information on the probability of distribution for α, it is reasonable to assume that these values are evenly distributed in the interval $[0,1]$. For their part, in Al-Azab and Ayu (2010), the authors illustrate the development of the combinations by means of a table where they develop each of the expressions expressed in (12) and later graphically.

2.4.4 Savage Criterion

This criterion measures the opportunity cost of an erroneous decision using the minimax criterion. It requires the elaboration of an array of regrets, which is characterized as the difference between the best results for each alternative solution with each of its corresponding results. After obtaining the matrix, it makes use of the criterion of Wald, but takes into account that the matrix is of unfavourable results.

2.4.5 Laplace Criterion

The Laplace criterion transforms the uncertainty problem into a risk one by assigning an equiprobability to the solution alternatives and rests on the criterion of the mean value to solve it. (14) expresses the Laplace criterion, where, if there are four possibilities, the probability P will be $\frac{1}{4}$.
(14)
\[ \sum P({A_{i}})=\sum \frac{1}{m}({A_{i}}),\hspace{1em}\text{for each}\hspace{2.5pt}i=1,2,3,\dots ,m.\]
If the above equation is related to the Wald and Maximax criteria, the difference is that the two previous ones extract the highest or lowest value for each solution alternative. On the other hand, in Laplace’s criterion, the probability for each possible result is multiplied, and a summation is performed for each alternative. That is, if a solution alternative has four possible values or results, you will get four terms, which will be added together. Subsequently, since we have summations for each alternative solution, we choose the maximum value of that set, as it is shown in (15). If we have three alternatives, the set will be conformed to those values.
(15)
\[ d\to \operatorname{Max}A({M_{i}}).\]

2.4.6 Linear Programming

Authors like Anderson et al. (2015) mentioned that the problems for which the method of linear programming was developed correspond to real situations in which it is intended to maximize or minimize a linear function to linear constraints that limit the degree to which the target can be reached. As becomes evident in the development of Al-Azab and Ayu (2010), this method involves the establishment of inequalities, graphic representation, and selection of the preferred value.

2.4.7 Multi-Criteria Decisions (Multi-Objective Analysis)

A multi-criteria approach is used when decision problems are presented with specific objectives. This criterion is also known as vector optimization and is based on explicit criteria to evaluate different alternatives.
In general terms, decision variables are established, the model is presented with its constraints (inequalities), graphically represented, and it is possible to use linear programming applications to find the value of the objective function.

2.4.8 Sequential Decisions

Sequential decision-making consists of a situation in which decision-making is carried out from successive observations of a process, as discussed in Diederich (2015). The procedure to determine when to stop taking observations and at what point to continue determines the optimal stop rule and depends on the specific assumptions about the situation: knowledge of the distribution of observations, the distribution properties of observations, if the number of possible observations is delimited or unlimited, the sampling procedure, and the cost function for each observation.

2.4.9 Game Theory

Game theory is a set of techniques for making decisions in conflict situations based on the elaboration of a formal matrix that makes it possible to understand the conflict and its solution alternatives.
What is interesting when approaching this perspective is that strategies are highlighted to study the ideal choice when the decisions depend on the others involved, making use of arguments of rationality and present restrictions. It is considered appropriate to apply this strategy when you do not have full control of the factors that influence a result. The in-depth study of this area of knowledge would make developing a whole collection of academic products possible, so it is not the intention of this work to delve into this area.

2.5 Gamification

The term gamification represents the extrapolation of game mechanics in non-entertainment contexts to engage the user and solve problems as explained in Burke (2012) and Zichermann and Cunningham (2011). As said in Domínguez et al. (2013), an accurate definition of gamification is a “challenge” because it is an emerging concept, and this is because it has grown rapidly in recent years, as detailed in Seaborn and Fels (2015). However, as is evident in Kapp (2012), the elements that constitute and define gamification are nothing new, originating from game mechanics. In order to go into detail, a definition that is considered important for obtaining several components of gamification is that “gamification is the use of game-based mechanics, aesthetics and game thinking to engage people, motivate action, promote learning and solve problems” which is proposed in Kapp (2012).
For their part, authors like Bruzzone et al. (2014) detail the importance and potential of serious games for the identification, development, and learning of soft skills. In interaction with a game, soft skills correspond to the ability to catch sight of the details of a scenario or the identification of the missing elements in a set of information. Riedel and Hauge (2011) illustrate a classification of skills that are measured by serious games, which differs from what Bruzzone et al. (2014) expose, because not only are soft skills measured, but hard skills are as well. The study was conducted in the top 100 organizations on a list drawn up by a UK-recognized journal. Table 2 presents a classification of the abilities that are measured by the serious company games made by Riedel and Hauge (2011), and then the methodological elements related to the investigation are presented.
Table 2
Classification of skills measured by serious games in companies. Source Riedel and Hauge (2011).
Soft skills Hard skills
Teamwork Products/Knowledge Services
Communication Sales and Customer Service
 Interpersonal skills Discipline-Based Training, e.g. Finance, Purchasing, Stock Control
Negotiation Skills Project Management
Creativity Decision-Making Skills
Collaborative Skills Innovation and Risk Management
Learning Health and Security
Legal Compliance/Regulation

3 Methodology

In order to define a systematic method for our study as provided in the introduction section, we used an experimental research method. First, we defined an experimental research method based on mathematical modelling in order to measure and define rules for a fuzzy logic system. Then, we applied a quasi-experimental research method in order to define the profiles of the participants, based on Teddlie and Tashakkori (2006). Next, we made these rules apply to the game to validate the results found in the exploration process for our study case. Finally, derived from the participation results, we made an experimental research method to validate the results according to the profiles and roles defined.
In particular, four phases were proposed in the work methodology, covering the basic aspects of research: analysis, exploration, application, and validation. The details of each of these phases are illustrated below in Fig. 1.
info1166_g001.jpg
Fig. 1
Methodology used in research.
The analytical phase focused on the mathematical models discussed in the background section. It was hoped, therefore, to have enough basis to set up the inference rules of fuzzy logic, which are exposed in the next phase, the exploratory phase, inasmuch as it is intended to discuss a conceptual connection between the inference rules and profile management in personnel selection processes, topics with great detail for work in future research.
Subsequently, an applied phase was projected, through the definition of a case study, that contains the design of several interactions, covered by gamification concepts that are detailed in earlier studies, as mentioned before. In this way, metrics and indicators are thrown in to confirm, in the last phase, how close the model was to the inference rules in order to get profiles during selection processes.

4 Proposed Model from Fuzzy Logic

There are several proposed models based on the fuzzy logic system for studies in the field of decision-making like those in Zeng et al. (2016) and Shouzhen (2016); however, there is no research or literature review available related to the use of the gamification model. Using the Matlab Fuzzy Logic Toolbox, a Mandami fuzzy logic system was created to perform the process illustrated in Fig. 2. First, criteria were established to evaluate the results obtained by the players in each of the 10 attributes: adaptability, self-control, conviction, dynamism, initiative, integrity, leadership, perseverance, persuasion, and planning. The range was classified with values between 0 and 100, such that the values between 0 and 50 were classified as bad, the values between 50 and 80 were classified as average, and 80 to 100 were high.
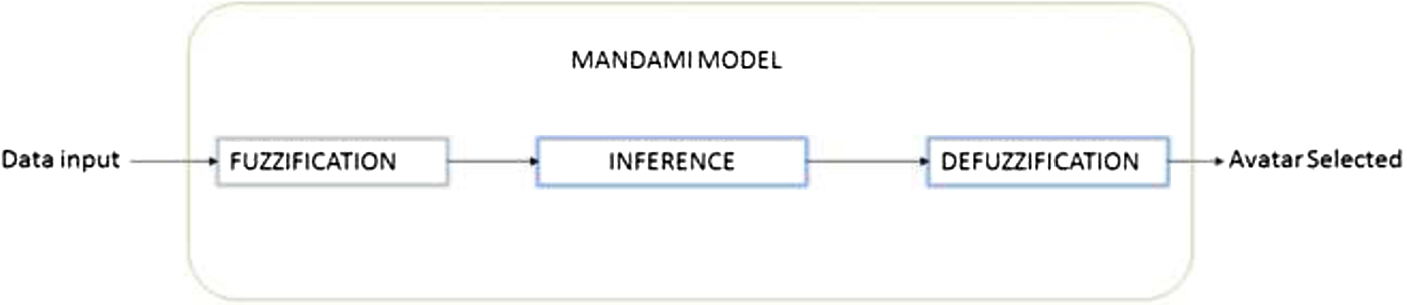
info1166_g002.jpg
Fig. 2
Fuzzy logic model to determine the avatar according to the obtained scores.

4.1 Proposed Rules for the Avatar

To classify the results into avatars, five rules of inference were used, as shown in Table 3, one for each possible avatar (monkey, eagle, owl, duck, and jaguar). This was done so that when entering the results obtained during the tests by each player, the model evaluates the results with fuzzy logic, allowing it to determine to which avatar the skills shown by the player correspond.
Table 3
Inference rules for avatars.
Eagle Jaguar Owl Duck Monkey
Adaptability HIGH AVERAGE AVERAGE HIGH AVERAGE
Self-control LOW LOW HIGH HIGH AVERAGE
Conviction HIGH AVERAGE AVERAGE LOW AVERAGE
Dynamism AVERAGE AVERAGE LOW AVERAGE HIGH
Initiative HIGH HIGH LOW AVERAGE HIGH
Integrity LOW LOW HIGH AVERAGE AVERAGE
Leadership AVERAGE HIGH AVERAGE AVERAGE AVERAGE
Perseverance AVERAGE AVERAGE HIGH HIGH AVERAGE
So, using the minimum criterion in the ‘and’ method in the model, the rules are described as follows:
  • • If (Adaptability is High) and (Self-Control is Low) and (Conviction is High) and (Dynamism is Average) and (Initiative is High) and (Integrity is Low) and (Leadership is Average) and (Perseverance is Average) and (Persuasion is Low) and (Planning is High) → Avatar is Eagle.
  • • If (Adaptability is Average) and (Self-Control is Low) and (Conviction is Average) and (Dynamism is Average) and (Initiative is High) and (Integrity is Low) and (Leadership is High) and (Perseverance is Average) and (Persuasion is High) and (Planning is Average) → Avatar is Jaguar.
  • • If (Adaptability is Average) and (Self-Control is High) and (Conviction is Average) and (Dynamism is Low) and (Initiative is Low) and (Integrity is High) and (Leadership is Average) and (Perseverance is High) and (Persuasion is Average) and (Planning is Average) → Avatar is Owl.
  • • If (Adaptability is High) and (Self-Control is High) and (Conviction is Low) and (Dynamism is Average) and (Initiative is Average) and (Integrity is Average) and (Leadership is Average) and (Perseverance is High) and (Persuasion is Average) and (Planning is Low) → Avatar is Duck.
  • • If (Adaptability is Average) and (Self-Control is Average) and (Conviction is Average) and (Dynamism is High) and (Initiative is High) and (Integrity is Average) and (Leadership is Average) and (Perseverance is Average) and (Persuasion is High) and (Planning is Low) → Avatar is Monkey.

4.2 Definition of Rules for Strategies for Non-Programmed Decision-Making Activities

The proposal elaborated in this study is based on the decision-making strategies presented in Wang et al. (2004) as presented in Table 4 and the mathematical models discussed in Al-Azab and Ayu (2010) to propose a model of the activities of non-programmed decision-making. The mathematical criteria must allow for the measurements of or give indicators of the abilities to be demonstrated by the player who will make the respective decisions. The result of this analysis is shown in Table 4.
Table 4
Relationship between non-programmed decision-making activities and strategies.
MD strategy: mathematical model
Certainty (probabilities): $\textstyle\sum P({A_{i}})=\textstyle\sum \frac{1}{m}({A_{i}})$, for each $i=1,2,3,\dots ,m$
Pessimistic: $d=\operatorname{Max}(\operatorname{Min}\hspace{2.5pt}{r_{ij}})=\operatorname{Max}({m_{i}})$
Optimistic: $d=\operatorname{Max}(\operatorname{Max}\hspace{2.5pt}{r_{ij}})=\operatorname{Max}({M_{i}})$
Minimum Cost, Maximum Benefit
Arbitrary, Preferential, Common Sense
These eight strategies were the most registered in the developed web application. Their relationship to the graphs of the results is given, in which these strategies determined the decisions made by the candidates in the selection process, while they played a game directing a herd of animals with certain goals. In the future, greater potential can be obtained from this determination, because for now, it only delimits them of all the strategies presented in Table 1, according to the characteristics of gamification addressed in the investigation.
Strategies that are not described by some mathematical criteria imply a parameterization based on the user interaction in the gamified environment; for example, the “test and error” or “experimental” strategy can be captured from the number of choices repeated by a user or the number of times a particular action is repeated. Meanwhile, “Minimum cost” and “Maximum benefit” will depend on how the information is delivered to the user.

4.3 Key Metrics Applied to the Game

The following are the indicators or metrics under which the psychological competencies associated with non-programmed decision-making are modelled:
  • • Dynamism: given by the progress curve of the click/min ratio in terms of reviewing indicators of preservation of attention to and action in the game, as it becomes a repetitive activity in which the player goes in search of food and simultaneously responds to the eventualities that appear. So, we apply the (16) equation to get the click variation, minute by minute, from which we obtain averages. In addition, a three-stage discrimination of the whole game is performed, with the same logic, to verify more precise details that are thrown in the profile of the player:
    (16)
    \[ D=\frac{{\textstyle\textstyle\sum _{i=0}^{m-1}}P{c_{i+1}}-P{c_{i}}}{m-1}\]
    where D is the value of the dynamism obtained, Pc is the sum of partial clicks that were recorded for each minute, m is the number of minutes played, in this case 15, and i, is the iteration for each minute.
  • • Planning: given by the relation between order of execution and control of the members of the herd in terms of checking to see if one executes the actions in a specific order, waiting for a parallel completion of all the elements, or executes actions at random times, without maintaining a specific order. (17) details the procedure for obtaining the planning metrics, obtaining an average of the variations of the order in which the members are sent for food. In this case, the absolute value is used because it is required to determine the variation regardless of whether the slope from one point to another is positive or negative.
    (17)
    \[ P=\frac{{\textstyle\textstyle\sum _{i=0}^{E-1}}|{N_{i+1}}-{N_{i}}|}{S-1}\]
    where P is the value obtained from planning, N is the number of members sent for food, E is the length of the vector containing the totality of the records of membership sends, and i, is the iteration for each minute. On the other hand, this planning metric is affected by the request for information before executing an action, which was described in the Challenges section and specified in (18).
    (18)
    \[ S=\frac{TR}{TE}\]
    where S is the average requests for information to support decision-making, obtained from operating total requests, TR, on the total random events that were generated, TE.
  • • Self-control: given by the average of the times an action took to be taken, after the eventuality was generated, as detailed in (19). Also described by the factor of requesting information before acting, as described above.
    (19)
    \[ ATa={\sum \limits_{i=1}^{a}}\frac{a{t_{i}}}{a}\]
    where ATa is the average of the duration of the actions, obtained from adding each of the times of actions, at, to the number of actions, a.
  • • Conviction: due to the number of combats versus withdrawals of a member at the moment of presenting an eventuality that was randomly generated, which is represented in (20). This metric is demarcated with more relevance in the moment of responding to major challenges proposed with greater weight to collect, but more probability to lose the member.
    (20)
    \[ \mathit{AF}=\frac{\mathit{TF}}{\mathit{TE}}\]
    where PC is the average of fights, obtained from operating the total of fights, TF, on the total of events, TE.
  • • Perseverance: given by the percentage of reaching the final objective in relation to certain periods of time. (21) presents the modelling to see if its intention to reach the goal was maintained in a similar way to the measurement of dynamism. Additionally, at the end of the game, as it is unlikely that you have reached the requested amount of food, a message will appear if you wish to continue until the indicated amount is reached, under the persuasive message described in the previous section. So, the decision to persist and continue to reach the goal or to give up and stop playing contributes to determining the perseverance of the player.
    (21)
    \[ P={\sum \limits_{i=0}^{m-1}}\frac{Tw-Cw}{m-1}\]
    where P is the value of the perseverance obtained, Tw is the total weight to be reached, as the target of the scenario, Cw is the amount of current weight the player has achieved, m is the number of minutes played, and i, is the iteration by each minute.

5 Results Analysis

In the game, the initial scenario is an environment where the player must parameterize basic skills as a moment of self-evaluation. Subsequently, in the main scenario of the game, the capture of several events that are generated during the interaction of the player is highlighted. These events allow the characterization of the decision-making processes according to the approach made in Albadán Romero et al. (2016, in press), where a small group of psychological capacities was chosen starting from the base, resulting in the following ones being chosen: 1) dynamism, 2) planning, 3) self-control, 4) conviction, and 5) perseverance.
During a trip back and forth, random events are generated in which the player must make decisions, which are then stored. The decision might be to escape and return to the lair, or you can fight against the opponent. That combat is solved by probabilities (Math.random) and under comparison against a threshold, the outcome of the combat (win or loss) is determined. In the first outcome, the tour continues to the lair and food is added to the total. If the combat is lost, the member’s health decreases and the trip is lost. The capture of information from the events given in the interaction in the game is in relation of determining indicators of the psychological competences described above, which will allow for the consolidation of the characterization of the processes of non-programmed decision-making.
Approximately 50 tests were carried out, with people of different academic characteristics (30 professionals and 20 university students), to test the interaction in the game and to corroborate how the reports are obtained, contributing to the establishment of the candidate profile. Each test generates a small description of the profile of the player/applicant, and linked to the textual description is a statistical report of the psychological skills already mentioned. Initially, the report of self-evaluation of psychological skills, with the traits that the person pretends to show as the most outstanding in his personality, were created. As an example, Fig. 3 shows a comparison in relation to the psychological competence of dynamism. This is observed in the upper part, where the player maintains, in general terms, an ascending level of attention. On the other hand, in the lower part of the figure, a descending level of attention is observed. These opposing cases are textually described in the candidate’s profile and supported by the corresponding graphs.
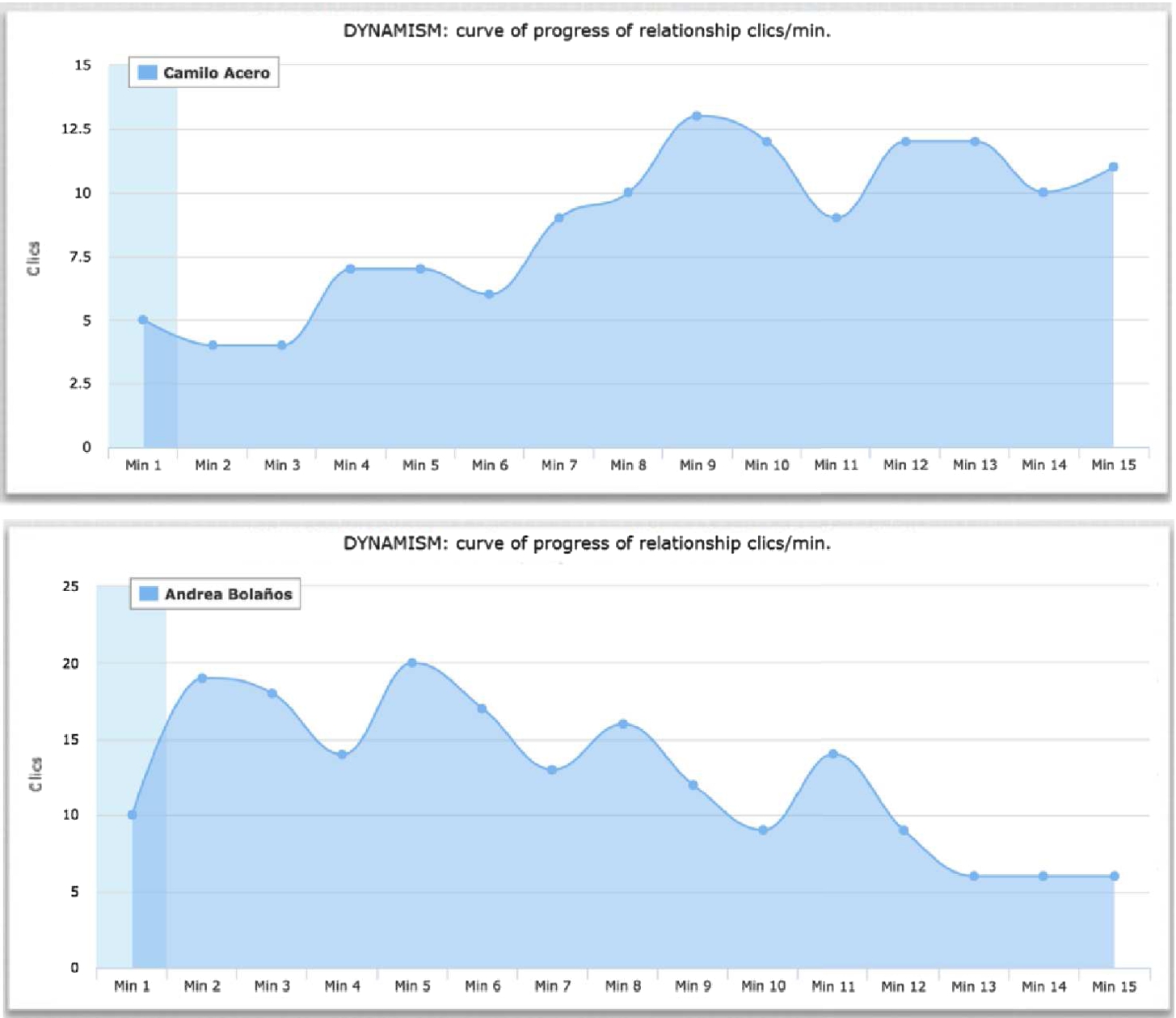
info1166_g003.jpg
Fig. 3
Curve of dynamism arranged in the profile report of the aspirant.
In terms of planning, the following is the curve with the sequence of points that identify the profile of a methodical person who carries out actions in a sequential way and waits for the complete conclusion of all actions in progress to start again. However, if a player executes actions without any order, it denotes a person who, in the face of unexpected events, manages to deal with them as they arise without performing sequential actions. These two opposite situations are evident in the planning curve in Fig. 4.
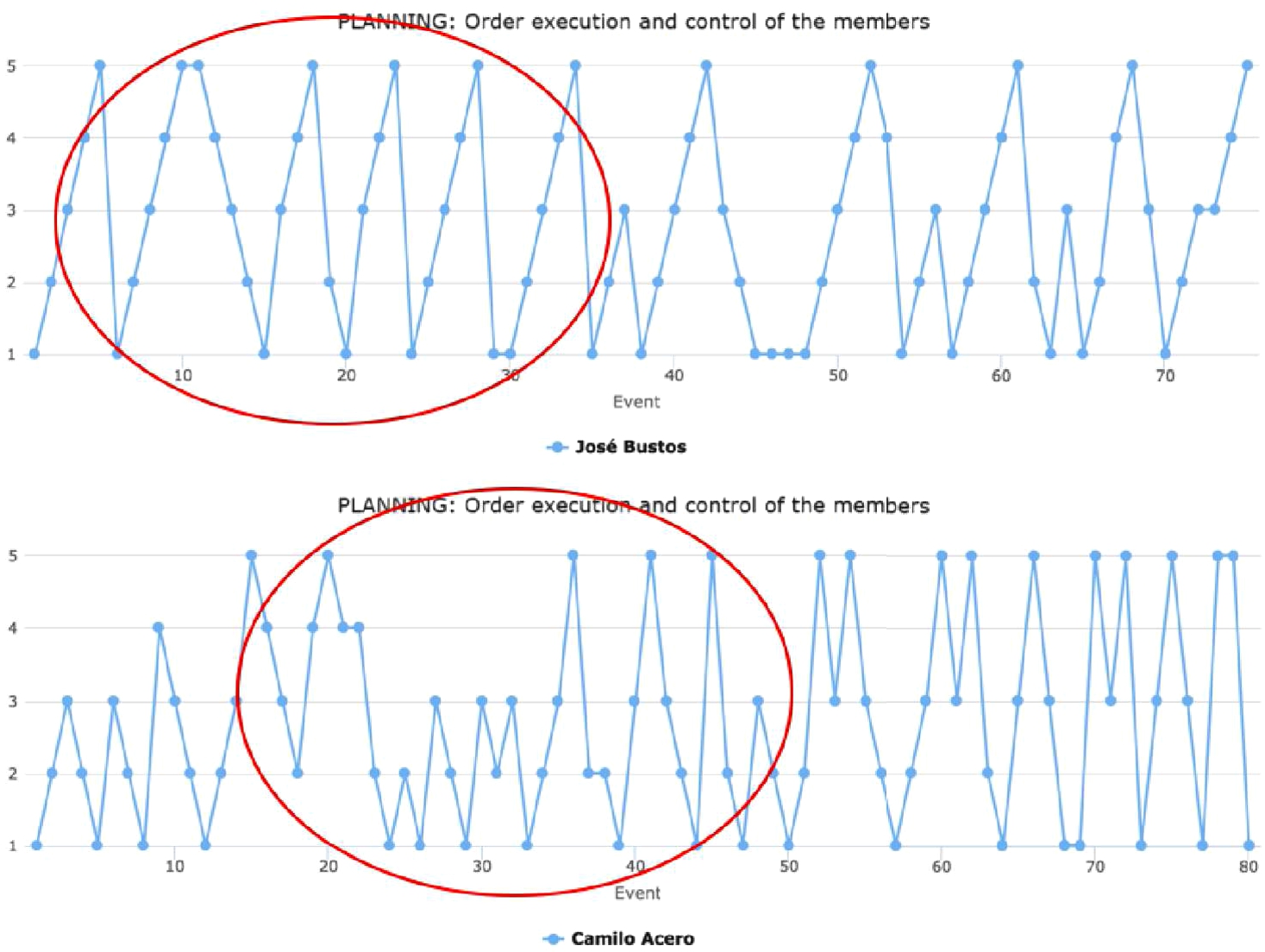
info1166_g004.jpg
Fig. 4
Points sequence curve denoting an applicant’s planning competence.

6 Discussions

The gamification of the tests proves to be a very attractive proposal and offers great support for the processes of personnel selection. Nevertheless, to carry out the capture of events for non-programmed decision-making, it is necessary to model more psychological competences that allow for a real estimate for tests that are given to applicants in real time. There are few proposals in this area of human resources, despite proposals such as those presented in Guenaga et al. (2014) and Supendi and Prihatmanto (2015), so the determination of which psychological aspects that are evaluated in a selection process can be carried out within a scenario based on game mechanics is still open for discussion.
The most relevant aspects on which deep reflection can be carried out are related to the presentation of the test in a selection process, and in that order of ideas, the time factor of the application of the test stands out. It is presented as an advantage with this game model while reducing, between 40% and 70%, the time records. These data have as a reference Albadán Romero et al. (2016), where it is argued that a psychological test, within a selection process, takes about an hour. This comparison is made considering the duration records of the proposed game. The advantage affects the two parties involved in the selection process: the applicants and the organization.
Based on the results obtained, models based on rules of inference can be applied to consolidate the profile of an applicant. However, there are variables associated with psychological competencies that require a more detailed analysis from strategies that allow for the analysis of the behaviours of an aspirant when making certain decisions. To this end, it is suggested to apply tests by implementing methodologies based on eye tracking, as supported by Bobić and Graovac (2016), with which it is possible to capture subjective aspects such as facial expressions or vision, from more specific tests, as detailed in Ujbanyi et al. (2016) and Zhang and Chen (2016).

7 Conclusions

The design of a test model based on gamification was carried out with the inclusion of different organizational and psychological theories. These characteristics allow one to obtain the characteristics of the behaviour of the aspirant while playing and even use them to complement the scenario of self-evaluation, facilitating the processing of those aspects without the player even being aware that it is being analysed.
In that order of ideas, there is a great advantage to obtaining such data, in terms of consolidating the profile information in the background. So, we have grounds to affirm that the data capture works in an optimal way when implementing game mechanics, while allowing the implicit transfer of information.
Although certain decision-making strategies have been linked directly to the connotation of non-programmed decision-making, it is evident that the large amount of data generated after interaction in the game does not make it easier to determine if the applicant made a decision using a pessimistic approach, an optimistic approach, or other criteria, considering that in many cases, this can be a product of rapid actions within the dynamics of the same game, beyond reaching to contemplate and analyse all the possibilities of choice to make use of the criterion.
Considering that we designed randomly generated events, which appear unexpectedly, and that it is not possible to know how many times and at what moment something specific happens, or if a fight is won or lost, it is considered that there was adequate work done to delimit the characteristic of non-programmed to the decision-making. On the other hand, the psychological competencies consolidated in the reports were chosen from a list of psychological abilities associated with the decision-making processes, with which considerable statistical details about the profile of the aspirant are considered.

References

 
Al-Azab, F.G.M., Ayu, M.A. (2010). Web based multi-criteria decision making using AHP method. In: 2010 International Conference on the Information and Communication Technology for the Muslim World (ICT4M).
 
Albadán Romero, J., Gaona-García, P.A. (2015). Modelo de actividades para la caracterización de procesos de toma de decisiones no programadas enmarcadas en escenarios de negociación. Research in Computing Science, 108, 107–115.
 
Albadán Romero, J., Gaona-García, P.A., Montenegro Marin, C. (2016). Assessment model in a selection process based in gamification. IEEE Latin America Transactions, 14(6), 2789–2794. https://doi.org/10.1109/TLA.2016.7555256.
 
Albadán Romero, J., Gaona-García, P.A., Montenegro Marin, C. Gamification applied to aspirant selection process model. (in press). Universidad Distrital Francisco José de Caldas Editorial, Bogotá (in Spanish).
 
Anderson, D., Sweeney, D., Williams, T., Camm, J., Cochran, J. (2015). An Introduction to Management Science: Quantitative Approaches to Decision Making. Cengage Learning, Boston.
 
Bobić, V., Graovac, S. (2016). Development, implementation and evaluation of new eye tracking methodology. In: 24th the 2016 Telecommunications Forum (TELFOR) 2016. IEEE, pp. 1–4.
 
Bruzzone, A.G., Massei, M., Tremori, A., Poggi, S., Nicoletti, L., Baisini, C. (2014). Simulation as enabling technologies for agile thinking: Training and education aids for decision makers. International Journal of Simulation and Process Modelling, 9(1–2), 113–127.
 
Burke, B. (2012). Gamification 2020: What is the Future of Gamification? Gartner. Retrieved from http://dotgroup.com.br/wp-content/uploads/2014/04/Gartner-2020-Trends.pdf.
 
Cabrerizo, F.J., Herrera-Viedma, E., Pedrycz, W. (2013). A method based on PSO and granular computing of linguistic information to solve group decision making problems defined in heterogeneous contexts. European Journal of Operational Research, 230(3), 624–633.
 
Cabrerizo, F.J., Ureńa, R., Pedrycz, W., Herrera-Viedma, E. (2014). Building consensus in group decision making with an allocation of information granularity. Fuzzy Sets and Systems, 255((supplement C)), 115–127. Theme: Decision and Optimisation.
 
Capuano, N., Chiclana, F., Fujita, H., Herrera-Viedma, E., Loia, V. (2017). Fuzzy group decision making with incomplete information guided by social influence. IEEE Transactions on Fuzzy Systems, PP(99), 1.
 
Deegan, P.E., Drake, R.E. (2006). Shared decision making and medication management in the recovery process. Psychiatric Services, 57(11), 1636–1639.
 
Diederich, A. (2015). Decision and choice: sequential decision making. In: Wright, J.D. (Ed.), International Encyclopedia of the Social & Behavioral Sciences, 2nd ed. Elsevier, Oxford, pp. 906–910.
 
Domínguez, A., Saenz-de-Navarrete, J., De-Marcos, L., Fernández-Sanz, L., Pagés, C., Martínez-Herraiz, J.-J. (2013). Gamifying learning experiences: practical implications and outcomes. Computers & Education, 63, 380–392.
 
Duncan, E., Best, C., Hagen, S. (2010). Shared decision making interventions for people with mental health conditions. Cochrane Database of Systematic Reviews, 1, CD007297. https://doi.org/10.1002/14651858.CD007297.pub2.
 
Grant, J.E., Chamberlain, S.R., Schreiber, L.R.N., Odlaug, B.L., Kim, S.W. (2011). Selective decision-making deficits in at-risk gamblers. Psychiatry Research, 189(1), 115–120.
 
Guenaga, M., Eguḳluz, A., Rayón, A., Nśńez, A., Quevedo, E. (2014). A serious game to develop and assess teamwork competency. In: International Symposium on Computers in Education (SIIE). IEEE, pp. 183–188.
 
He, Y., Gong, R. (2010). A review of integrity tests in personnel selection. In: The 2010 International Conference on E-Product E-Service and E-Entertainment, ICEEE. IEEE, pp. 1–6.
 
Highhouse, S. (2008). Stubborn reliance on intuition and subjectivity in employee selection. Industrial and Organizational Psychology, 1(3), 333–342. https://doi.org/10.1111/j.1754-9434.2008.00058.x.
 
Hillier, F.S., Lieberman, G.J., Osuna, M.G. (2005). Investigación de Operaciones, 8th ed. McGraw-Hill.
 
Kao, H., Kao, S.P.-H., Chen, S.-C., Chiu, K.K.-S. (2012). Decision making models and knowledge management preferences: Taiwanese expatriates in China. Australian Journal of Business and Management Research, 2(4), 1.
 
Kapp, K.M. (2012). The Gamification of Learning and Instruction: Game-Based Methods and Strategies for Training and Education. John Wiley & Sons, San Francisco.
 
Kim, S. (2015). An observational research on the limitations and side effects of gamification in educating human resources. Journal of Korea Game Society, 15(3), 87–96.
 
Liu, W., Dong, Y., Chiclana, F., Cabrerizo, F.J., Herrera-Viedma, E. (2017). Group decision-making based on heterogeneous preference relations with self-confidence. Fuzzy Optimization and Decision Making, 16(4), 429–447.
 
McKenzie, J., van Winkelen, C., Grewal, S. (2011). Developing organisational decision-making capability: a knowledge manager’s guide. Journal of Knowledge Management, 15(3), 403–421.
 
Nicolas, R. (2004). Knowledge management impacts on decision making process. Journal of Knowledge Management, 8(1), 20–31.
 
Pérez, I.J., Cabrerizo, F.J., Herrera-Viedma, E. (2010). A mobile decision support system for dynamic group decision-making problems. IEEE Transactions on Systems, Man, and Cybernetics – Part A: Systems and Humans, 40(6), 1244–1256.
 
Radner, R. (2015). Decision and choice: bounded rationality. In: Wright, J.D. (Ed.), International Encyclopedia of the Social & Behavioral Sciences. 2nd ed. Elsevier, Oxford, pp. 879–885.
 
Radzian, A.M., Itoh, M., Inagaki, T. (2010). Power transformer diagnosis decision-making based on unified combination rule and maximax-maximin criterion. In: TENCON 2010. IEEE, pp. 106–111.
 
Riedel, J.C.K.H., Hauge, J.B. (2011). State of the art of serious games for business and industry. In: ICE ’11: 2011 17th International Conference on Concurrent Enterprising (ICE). IEEE, pp. 1–8.
 
Rynes, S.L., Colbert, A.E., Brown, K.G. (2002). HR professionals’ beliefs about effective human resource practices: correspondence between research and practice. Human Resource Management, 41(2), 149–174.
 
Salgado, J.F., Moscoso, S. (2008). Selección de personal en la empresa y las AAPP: de la visión tradicional a la visión estratégica. Papeles del Psicólogo, 29(1), 16–24.
 
Seaborn, K., Fels, D.I. (2015). Gamification in theory and action: a survey. International Journal of Human-Computer Studies, 74, 14–31.
 
Shouzhen, Z. (2016). An extension of OWAD operator and its application to uncertain multiple-attribute group decision-making. Cybernetics and Systems, 47(5), 363–375.
 
Supendi, K., Prihatmanto, A.S. (2015). Design and implementation of the assesment of publik officers web base with gamification method. In: ICIDM ’15: 2015 4th International Conference on Interactive Digital Media. IEEE, pp. 1–6.
 
Teddlie, C., Tashakkori, A. (2006). A general typology of research designs featuring mixed methods. Research in the Schools, 13(1), 12–28.
 
Ujbanyi, T., Katona, J., Sziladi, G., Kovari, A. (2016). Eye-tracking analysis of computer networks exam question besides different skilled groups. In: CogInfoCom ’16: 2016 7th IEEE International Conference on Cognitive Infocommunications. IEEE, pp. 277–282.
 
Vakkayil, J., Della Torre, E., Giangreco, A. (2017). It’s not how it looks! Exploring managerial perspectives on employee wellbeing. European Management Journal, 35(4), 548–562. https://doi.org/10.1016/j.emj.2016.12.002.
 
Van Nam, H., Nakamori, Y., Chenyi, H., Kreinovich, V. (2009). On decision making under interval uncertainty: a new justification of Hurwicz optimism-pessimism approach and its use in group decision making. In: ISMVL ’09: 2009 39th International Symposium on Multiple-Valued Logic. IEEE, pp. 214–220.
 
Wang, Y., Dong, L., Ruhe, G. (2004). Formal description of the cognitive process of decision making. In: The Third IEEE International Conference on Cognitive Informatics. IEEE, pp. 124–130.
 
Wang, Y., Patel, S., Patel, D., Ying, W. (2003). A layered reference model of the brain. In: The 2003 Second IEEE International Conference on Cognitive Informatics. IEEE, pp. 7–17.
 
Xiaogang, W., Qijie, W. (2011). Study on the Wald-W method of uncertain decision-making. Procedia Engineering, 15, 4527–4531. https://doi.org/10.1016/j.proeng.2011.08.850.
 
Zeng, S., Palacios-Marques, D., Zhu, F. (2016). A new model for interactive group decision making with intuitionistic fuzzy preference relations. Informatica, 27(4), 911–928.
 
Zhang, Y., Chen, Z. (2016). Revisiting visual attention identification based on eye tracking data analytics. The VCIP ’16: Visual Communications and Image Processing.
 
Zhang, H., Dong, Y., Herrera-Viedma, E. (2017). Consensus building for the heterogeneous large-scale gdm with the individual concerns and satisfactions. IEEE Transactions on Fuzzy Systems, PP(99), 1.
 
Zichermann, G., Cunningham, C. (2011). Gamification by Design: Implementing Game Mechanics in Web and Mobile Apps. O’Reilly Media, Inc.

Biographies

Albadán Javier
jalbadanr@udistrital.edu.co

J. Albadán received his master’s degree in information and communication sciences from the Francisco José de Caldas District University, in Bogotá, Colombia. He has a degree in technological design from the National Pedagogical University. He is a member of the GIIRA research group. He has more than 6 years of experience as a teacher in higher education institutions and for more than 3 years he has focused on studying web design and graphic user interfaces. These being the main areas of study of their research.

Gaona Paulo
pagaonag@udistrital.edu.co

P. Gaona is a titular professor at Engineering Faculty of Universidad Distrital Francisco José de Caldas, Bogotá, Colombia, and active member of GIIRA research group since 2008. He is a director of multimedia research group at Universidad Distrital Francisco José de Caldas. He earned a PhD in information and knowledge engineering from University of Alcalá in 2014 and is working as a collaborator researcher in the information engineering research unit at University of Alcalá since 2012. He has a master in information science and communication from Distrital University (Bogotá Colombia). His research interest includes web science, semantic web, network and communications, e-learning, information visualization and visual analytics.

Montenegro Carlos
cemonenegrom@udistrital.edu.co

C. Montenegro is an associate professor at Engineering Faculty of Universidad Distrital Francisco José de Caldas, Bogotá, Colombia. He has a PhD in systems and informatics services for internet, University of Oviedo, Spain, and is the director of GIIRA research group of Universidad Distrital Francisco José de Caldas. He has a master in information science and communication from Distrital University (Bogotá, Colombia). His research interest includes internet of things, cloud computing, programing language and e-learning.

González-Crespo Rubén
ruben.gonzalez@unir.net

R. González has a PhD in computer science engineering. Currently he is the dean of Higher School of Engineering from UNIR and director of the AENOR (Spanish Association for Standardization and Certification) chair in certification, quality and technology standards. He is an advisory board member for the Ministry of Education at Colombia and evaluator from the National Agency for Quality Evaluation and Accreditation of Spain (ANECA). He is a member from different committees at ISO organization. He has published more than 150 research papers and he is also the editor in chief of the International Journal of Interactive Multimedia and Artificial Intelligence (www.ijimai.org). He has managed several projects funded by European Commission and Ministry of Industry at Spain. Currently his main research areas are soft computing and accessibility development.

Herrera-Viedma Enrique
viedma@decsai.ugr.es

E. Herrera was born in Jódar, Spain, in 1969. He received the MSc and PhD degrees in computer science from the University of Granada, Granada, Spain, in 1993 and 1996, respectively. He is currently a professor of computer science with the Department of Computer Science and Artificial Intelligence, University of Granada, and also the new vice-president for research.

Around 27 of his papers are classed as highly cited in the Thomson Reuters database as well as being in the top 1% of the most cited papers in its field (computer science and engineering). His h-index is 52 according to the web of science with more than 10.000 citations received and 63 according to Google Scholar with more than 18.000 citations received and he is ranked in the top 1% of the most cited scientists in engineering according to the Essential Science Indicators of Thomson.

He has recently published in Science [339:6126, p. 1382, 2013] on the new role of the public libraries and he has been identified in the list of Highly Cited Researchers published in 2014 and 2015 by Shangai Center and Thomson Reuters in the categories of Engineering and Computer Science, therefore, being considered one of the world’s most influential scientific researchers. His current research interests include group decision making, consensus models, linguistic modelling, aggregation of information, information retrieval, bibliometric, digital libraries, web quality evaluation, recommender systems, and social media.

Dr. Herrera-Viedma is an associate editor of seven core ISI journals such as the IEEE Transactions on Systems, Man, and Cybernetics: Systems, Knowledge Based Systems, Soft Computing, Fuzzy Optimization and Decision Making, Applied Soft Computing, Journal of Intelligent and Fuzzy Systems, Information Fusion and Information Sciences; and a member of the editorial boards of three core ISI journals: Fuzzy Sets and Systems, International Journal of Information Technology and Decision Making, and International Journal of Computational Intelligence. From 2014 he is a member of the government of the IEEE SMC Society.


Exit Reading PDF XML


Table of contents


Share


RSS