Abstract
A novel approach to pricing on data marketplaces is proposed, which is based on the Name Your Own Price (NYOP) principle: customers suggest their own price for a (relational) data product and in return receive a custom-tailored one. The result is a fair pricing scheme where sellers can achieve a higher revenue, while buyers receive a product which matches both their preferences and budget. NYOP is contrasted with previous research on view-based pricing on data marketplaces as well as on discount schemes to increase revenue.
1 Introduction
Information is one of the key elements of the Internet and has been described as the fuel of an information economy (Hui and Chau,
2002). Consequently, data – as the basic unit of information – and data-related products are now being traded on
data marketplaces, which act as intermediaries between providers and users (customers) of data. In this paper, a pricing scheme is introduced that is fair to both buyers and sellers.
Even though there is undoubtedly a market for data and data-related services as well as the recognition that data has a price (Miller,
2012; Bodenbenner
et al.,
2011; Tempich
et al.,
2011), there is little understanding so far of where this price stems from Balazinska
et al. (
2011), Miller (
2012). Similar to the observation that data quality can best be gauged by an eventual consumer, it can be argued that its value is different to distinct people (Shapiro and Varian,
1999). From an interview study (Muschalle
et al.,
2012) and the relevant economic literature, e.g. (Shapiro and Varian,
1999), it is obvious that the value of data is highly domain-specific, owing to the fact that data has no inherent meaning (Davenport and Prusak,
2000). The combination of both subjective
quality attribution and subjective
value attribution makes the matter even more complicated. Thus, it can be stated that pricing on data marketplaces in general is still a vastly unsolved issue. In particular the fact that it is difficult for providers to gauge the willingness to pay of customers, as they do not know the purpose the data is being bought for. Furthermore, no pricing model exists that considers two providers offering similar information goods (Balazinska
et al.,
2013). In this paper, which extends (Stahl and Vossen,
2016a) and is based on Stahl (
2015), we present a novel framework addressing these issues.
As an illustrative example, consider two providers of weather forecast data. Weather data has a number of characteristics that makes it particularly interesting. For instance, it is relevant that weather forecast data is a consumable information good which allows for considering timeliness when pricing because most of the time weather data is only relevant for future dates. To create this data, the weather is constantly observed and different data are collected using a number of weather stations. These raw weather data are then used to forecast the weather for several days to come. More precisely, particular attributes of the weather, such as temperature, are forecast. Thus, it is supposed that weather data providers A and B both provide past, current, and forecast weather data, i.e. providers constantly fill their database with new data as well as update forecast data which becomes more precise the closer the forecast date comes. It is further supposed that the data is not complete, as some data may get lost due to equipment malfunction.
In the remainder of this paper, we first review previous work on pricing of data on data marketplaces and define the exact research gap from that, namely a pricing mechanism that considers heterogeneous willingness to pay and is able to provide custom-tailored data products even when competing data sources are available. Based on this, we look at the most important factor when buying data products, which is data quality; we do this in pricing-focused fashion. Then, data marketplaces will be formally defined in Section
3. Subsequently, Section
4 will extensively discuss data quality and its dimensions, in order to establish which dimensions can be used when pricing data products. After that, Section
5 develops a quality-based pricing model for data marketplaces using the
MCKP. Eventually, this paper is concluded in Section
6 by summarizing the main points and outlining possible future work.
2 Related Work and Problem Outline
In 2011, Balazinska
et al. (
2011) put the topics of data marketplaces and data pricing on the research agenda of the database community, identifying an understanding of how the price of data is determined and modified on data marketplaces as one of the main problems. In general, work on data pricing can be categorized into two groups: (1)
query-based pricing and (2)
quality-based pricing. In the first context, Koutris
et al. (
2012a) present a framework that allows data providers to set prices for some (sets of) views and then computes prices for queries automatically. Furthermore, it is ensured that the resulting price function is arbitrage-free as well as discount-free. A prototype has been described in Koutris
et al. (
2012b). It provides guidance to sellers in that it highlights if the set prices violate the arbitrage-free criterion. In a next step, presented in Koutris
et al. (
2013), the group introduced
QueryMarket, a middle-layer software that can be run atop of any database management system that supports the
SQL. Besides the arbitrage-free criterion it allows multiple sellers and shares revenue fairly between them. While this system has an advanced capability to calculate prices for individual queries based on an overall price, it does not address the problem of how much data is actually worth. Also, it does not take into account that the same query may have a different value to different people, which can be exploited to maximize profits.
Balazinska
et al. (
2013) present a discussion of pricing on relational data, arguing that views can essentially be interpreted as versions of data, a suggestion that will also be applied in this paper. Furthermore, they identify three open problems. Firstly, they name pricing of data updates, i.e. what price to charge if a consumer has purchased a data set that has been updated in the meantime and the consumer only wants to pay for the new data. Secondly, they mention the pricing of integrated data and present a complex value chain in which provider
A generates data, provider
B conducts data mining, and provider C integrates the mining result with other data sets. Finally, they discuss the pricing of competing data sources that provide essentially the same data, but in a different quality.
The first challenge can be addressed by calculating the difference between the full price of the new and the old data product. This is similar to the approach suggested by Tang
et al. (
2014) for buying samples of
XML data. The second problem can be addressed by introducing intermediary pricing for all providers refining the raw data. This means the raw data vendor operates using established means. Furthermore, all vendors following in the value chain have to deal with the output price of the lower level vendor as cost and build their prices accordingly. The last challenge will be addressed in this paper.
Another group that investigates data pricing and that focuses on
quality-based pricing is formed around Tang. They argue that using views to attach prices is too coarse and adopt the idea of attaching prices to tuples and use a pricing model that is based on minimal provenance (Tang
et al.,
2013a). However, computing prices in this model is
$\mathcal{NP}$-hard. Therefore, they also present and evaluate heuristics to approximate the prices. In Tang
et al. (
2013b), the authors introduce the concept of trading data quality for a discount, with cheaper data being less accurate. This is in contrast to all other work looked at so far, in which buying data is a “take-it-or-leave-it-decision” – a customer may buy the data at the advertised price or not buy it at all. The authors propose to offer buyers the option of naming their own price in order to address customers with a willingness to pay below the full price.
Tang
et al. (
2013b) present a framework in which – if less than the full price is offered – values are randomly drawn from a probability distribution, where the distance between the probability distribution and the real distribution correlates to the discount. This approach is similar to Li
et al. (
2013) in that both approaches offer data with lower quality at cheaper prices. While Tang
et al. (
2013b) allow customers to name a price and decrease the quality accordingly, Li
et al. (
2013) use the standard deviation to calculate prices.
Tang
et al. (
2014) present a framework to price
XML data, keeping the idea of allowing users to trade quality for a discount. In this work, the authors focus on completeness as a quality criterion, i.e. users can decide to get an incomplete sample by proposing a price lower than that advertised by the vendor. To this end, an algorithm collocates a sub-tree of the overall
XML tree at random that matches the price offered by the customer. They suppose two application scenarios for this framework. Users might be on a restricted budget and hence satisfied with a subset of the data, or users might want to get a sample to explore the data set. While the latter is a reasonable argument, bearing in mind that data is an experience information good, the first case has a minor weakness: customers with limited funds are usually particularly price-sensitive; therefore, it is questionable whether they are willing to buy random data as they would not know what they get for their little budget. That said, the idea of asking customers to reveal their preferences by naming a price is further explored here.
From an economic point of view, this can be seen as a form of Pay What You Want (PWYW) or Name Your Own Price (NYOP) pricing. In this case, the speciality is that the threshold value is known and that for prices below it quality is adjusted. Furthermore, the provider receives exactly the reservation price of the customer who in turn receives a personalized (i.e. quality degraded) offer, as long as a customer’s willingness to pay is below the ask price. If it is above the ask price, the demander receives some surplus. From this, it can be concluded that the profit with NYOP is greater, as it reaches additional customers. However, this only holds true if customers do not change from the high-end product to a cheaper version.
Commonly, it is suggested that online retailers can employ much more fine-grained pricing models compared to offline alternatives (Hinz
et al.,
2011). However, there is little guidance for firms (Hinz
et al.,
2011; Balazinska
et al.,
2011). Despite initial attempts (Balazinska
et al.,
2011; Koutris
et al.,
2012a,
2012b; Tang
et al.,
2013a,
2013b,
2014), the challenge of lacking guidance remains, particularly if multiple data providers are concerned (Balazinska
et al.,
2013). Furthermore, to date, there is no understanding for value of data (Miller,
2012). Both research groups, while providing technical means to model prices, do not address the more pressing issue of pricing data based on perceived customer value. Our work will particularly focus on a pricing scheme that supports data providers in setting appropriate prices which will also incorporate the idea that data sets are not of equal value to different people, which can be exploited to maximize profits. In this way, we follow the view-based approach of Balazinska
et al. (
2013) as well as the idea of quality-based pricing suggested by Tang
et al. (
2013b) and we are able to provide a value-based pricing scheme that even allows for pricing competing sources.
Precisely, we introduce an approach that does not require sellers to have an idea of the value of their goods. This will be done by adopting the NYOP idea implicitly used by Tang
et al. (
2013b) and combining it with a hidden threshold and
Goldilocks Pricing as described by Shapiro and Varian (
1999). This means data sets – actually views – will initially be offered at a rather high price. Then customers can name the price they are willing to pay. If it is greater than a possibly undisclosed threshold price, customers get the full quality product at their suggested price. If it is smaller, however, the view – or version for that matter – is transparently adjusted extemporaneously to meet the customer’s price. To this end, customers will have a say in how the data product is modified by stating preferences. Hence buying a data product could be compared to buying a car: for the full price one receives the full-fledged car with all possible features, such as powerful engine, expensive interior and entertainment system. However, it is also possible to buy the same car for a cheaper price if one waives one or more of the expensive features and chooses a mediocre engine and/or a less expensive interior. This mode of pricing is particularly promising if customers have very heterogeneous will (or possibilities) to pay. While basically similar to previous studies by Tang
et al. (
2013b,
2014) here more than one quality dimension will be looked at.
In order to make use of versioning of products, which has been established to be beneficial (Shapiro and Varian,
1999), some assumptions are made to satisfy the prerequisites for versioning identified in Reinartz (
2002), Narahari
et al. (
2005):
-
1. Customers are heterogeneous in their willingness to pay.
-
2. Customers are identifiable (e.g. student id’s for student discounts).
-
3. Customers are not allowed to resell products.
Given that quality is also data-inherent it builds a perfect starting point for versioning. Furthermore, it also allows for an objective value comparison – if supposing that quality is the value-bearing factor for customers – of two data sets that have similar content. To this end, a reversed pricing mechanism is proposed that builds upon the idea of NYOP pricing incorporating quality as a versioning factor as well as a possibility for users to express their preferences for certain quality criteria, in order to receive a custom-tailored data product. To this end, a framework will be presented that is capable of deriving a data quality score for data traded on a data marketplace adjusted with users’ preferences. Given that data quality is inherent to all data, the method can be used domain-independently and data quality criteria have only to be adjusted with domain-specific weights.
3 A Relational View on Data Marketplaces
In this work, we focus on structured data, which will be provided through an infrastructure where a data marketplace will be an electronic platform that allows for the exchange of data. It is further assumed that this data marketplace is an independent one fitting the framework presented in Stahl
et al. (
2016) in order to exclude any potential bias. While the pricing of services provided through such a platform is also interesting, the focus here will be on the pricing of the good
data. More precisely, data marketplaces host data for a number of providers who sell tabular, i.e. relational, data.
Providers sell data in a tabular format with given column names or attributes. This data can be described as a relation r with k unique attributes ${A_{i}}$ with domain $\mathit{dom}({A_{i}})$, $1\leqslant i\leqslant k$. The set of attributes is $X=\{{A_{1}},\dots ,{A_{k}}\}$. Consequently, the data (relation) may be described as an instance r of the relational schema R, which for simplicity is identified with X. Most of the time, data providers will not only sell one relation but many of them. Let a provider sell $s>1$ relation instances, then one provider can be considered providing a database instance d of size s with the corresponding schema D comprising s relation schemas.
While, in some cases, it might be appropriate to view an entire data marketplace as a database, in this work every provider is supposed to provide an individual database instance. This is a practical presumption based on the assumption that it would be difficult to enforce a common schema across providers. Furthermore, this would require data vendors to adapt their data to the schema of any data marketplace they are selling on.
Even viewing data offerings as databases can be complicated, as customers will often require data from different relations, which then have to be joined upon request. To simplify this and to add clarity, in this work data providers’ offerings will be treated as a
universal relation u, a tool which has a long history in database theory, e.g. Maier
et al. (
1984). For our purposes, a universal relation is created by joining all
${r_{j}}\in d$ in such a way that no data is lost, using a full outer join. It can be argued that joining could be done only when necessary – an approach that might be followed in an implementation; however, using only a universal relation has the advantage that no further joins are necessary during subsequent formal elaborations, which improves understandability. Furthermore, any original relation
${r_{j}}$ may be arrived at by appropriate selections and projections over
u. Formally, the universal relation
u over a database instance
d can be defined as the full outer join of relations
${r_{1}},\dots ,{r_{l}}$.
It should be noted that this approach requires attribute names to be unique within each single database. However, this is a minor technicality and can be achieved by renaming when necessary.
Returning to the weather data example, in the following provider A uses very reliable weather sensors but fewer, which results in more complete but less extensive data. Nevertheless, because of the better sensors, provider A can forecast three days, which provider B cannot. In contrast, provider B collects more data (more attributes) using less reliable sensors and has more weather stations. Moreover, both providers collect similar but not identical data. Provider A offers data for AirPresure in hPa, Humidity in percent, and Temperature in degree centigrade. Provider B offers the same as provider A and additionally WindSpeed in km/h, Cloudage in percent, and Precipitation (rainfall) in mm. The data sets of both providers also include the date and station for which the weather is forecast (or has been recorded), as well as when the data were last updated.
Table 1
Relation ${u_{A}}$ for provider A.
| Station |
AirPressure |
Humidity |
Temperature |
Date |
LastUpdated |
| FRA |
1021 |
52 |
17 |
2017-05-08 |
14:00 |
| FRA |
1020 |
43 |
19 |
2017-05-09 |
15:00 |
| FRA |
1005 |
40 |
15 |
2017-05-10 |
16:00 |
| LHR |
1025 |
69 |
16 |
2017-05-08 |
14:00 |
| LHR |
1008 |
65 |
14 |
2017-05-09 |
15:00 |
| LHR |
1003 |
70 |
12 |
2017-05-10 |
16:00 |
In this sample scenario, a customer such as an airline wants to buy weather forecast data at 5 pm (17:00) on 7th May 2017 for the next three days from three different airports (
FRA, LHR, AMS). The relevant data sets of providers
A and
B are depicted in Table
1 and Table
2, respectively. For reasons of clarity and comprehensibility, only the relevant view on
u is depicted.
Table 2
Relation ${u_{B}}$ for provider B.
| Station |
AirPressure |
Humidity |
Temperature |
WindSpeed |
Cloudage |
Precipitation |
Date |
Last update |
| FRA |
1022 |
⊥ |
18 |
8 |
70 |
0 |
2017-05-08 |
14:00 |
| FRA |
⊥ |
50 |
20 |
⊥ |
25 |
0 |
2017-05-09 |
15:00 |
| LHR |
1015 |
⊥ |
⊥ |
23 |
⊥ |
41 |
2017-05-08 |
15:00 |
| LHR |
1004 |
79 |
13 |
⊥ |
93 |
17 |
2017-05-09 |
16:00 |
| AMS |
1021 |
59 |
13 |
16 |
⊥ |
⊥ |
2017-05-08 |
14:00 |
| AMS |
1002 |
82 |
12 |
23 |
97 |
70 |
2017-05-09 |
16:00 |
4 Data Quality
Data has a price that is highly dependent on the context as well as on what it can do for potential buyers, and it is therefore sensible to create different versions in order to tap the willingness to pay of heterogeneous customers. Data quality can be considered as a promising aspect for differentiating data products. Given that there is a number of data quality criteria that are relevant for customers and consequently allow for price discrimination, the approaches described in Tang
et al. (
2013b), Tang
et al. (
2014) can be considered somewhat limited. Furthermore, data quality, if expressed in a meaningful score, allows the comparison of two offers from different providers.
Much work regarding data quality and how to measure it has been published over the last decades. Focusing on data quality in a Web context – precisely the context of most data marketplaces and data providers –, Naumann (
2002) aggregated several works on data quality, namely (Basch,
1990; Redman,
1996; Wang and Strong,
1996; Jarke and Vassiliou,
1997; Chen
et al.,
1998; Weikum,
1999). Therefore, we build our argument on Naumann (
2002), rather than on the individual works. In Stahl and Vossen (
2016b), Stahl (
2015) we reviewed the quality criteria and discussed how a data quality score that helps judging the value for money or quality for money of relation data products can be developed. This helps when evaluating which source to buy data from. Here, we will again review the quality criteria of Naumann (
2002) with a particular focus on how well they are usable in the context of versioning.
Naumann’s criteria sets are: a) content-related, i.e. directly rooted in the data; b) technical, i.e. related to the organization and delivery of the data; c) intellectual, i.e. related to the knowledge of eventual users; and d) instantiation-related, i.e. related to the presentation of the data. In the following a brief description of each measure is given along with an elaboration of how it is relevant in the context of data marketplaces, i.e. whether it can be used for versioning.
4.1 Content-Related Quality Criteria
The following content-related criteria are mentioned in Naumann (
2002):
-
• Accuracy, the percentage of correct values in the data set;
-
• Completeness, the percentage of non-null values in the data set;
-
• Customer support, the amount and usefulness of available human help;
-
• Documentation, the extent of available meta data regarding the data sets;
-
• Interpretability, the match between a user’s technical understanding and the data;
-
• Relevancy, the degree to which the data satisfies a user’s information needs;
-
• Value-added, the value the use of the data provides to its users.
As previously argued, the value of data is highly customer-dependent. The same is true for the value-added. We want to approximate this through the other quality dimensions. Hence, it will not be further analysed to avoid recursion. Most other criteria cannot be calculated fully automatically, the exemption being completeness. All others require knowledge going beyond the actual data.
Regarding
customer support and
documentation, the existence and the extent can be evaluated. While this is a first step that allows for versioning, it does not say anything about the actual quality. Moreover, some criteria remain that cannot be automatically examined, namely
interpretability and
relevancy, as both require an in-depth understanding of users, which cannot be achieved in an automated way. Consequently, they cannot be used for versioning. For
accuracy, it can be said that it cannot be (fully) automatically computed without external knowledge, it allows for the creation of numerous versions by lowering the accuracy. In this work – similar to Tang
et al. (
2013b), who suppose that the available
accuracy is worth the full price – we assume that the accuracy is data inherent.
For
completeness, differently complete versions can be created easily. At this point, it should be mentioned we suppose that all information about the data necessary for pricing is already contained within the data. In other words, we follow a Closed World Assumption (CWA) (Batini and Scannapieca,
2006). While this potentially restricts the model, for the purpose of this work, it is not particularly relevant why a value is missing. The fact is, it cannot be delivered to the customer.
Completeness, as defined in Stahl (
2015), Stahl and Vossen (
2016a), will serve as an example later on. It is calculated as the number of non-null value cells divided by the overall number of cells:
4.2 Technical Quality Criteria
Naumann (
2002) mentions the following technical criteria:
-
• Availability, the probability that a query is answered within a given time period;
-
• Latency, the time between issuing a query and receiving its first response;
-
• Price, the amount of money a user has to pay for the data;
-
• Quality of service, the error rate when transmitting (mainly relevant in streaming);
-
• Response time, the time between issuing a query and receiving its full response;
-
• Security, the degree of protection through encryption and anonymization;
-
• Timeliness, the freshness of the data.
Following the argument of value-added, price will be excluded. The remaining criteria can all be influenced by providers in the same way
accuracy or
completeness can, i.e. while there is a (technical) upper limit, they can be lowered. Thus, they all can be used for versioning. The exemption is
quality of service for which it has to be defined what quality specifically means. Thus, it is overall not very precise and has, therefore, been excluded from further examination. Moreover,
availability requires multiple measurements over time in order to be properly evaluated. As a second example, we will consider
timeliness which we defined (Stahl,
2015; Stahl and Vossen,
2016a) as the average freshness of a tuple based on the delivery time, the last update timestamp and the usual volatility
v for this type of data.
4.3 Intellectual Quality Criteria
Next, the intellectual criteria shall be outlined:
-
• Believability, the expected accuracy;
-
• Objectivity, the degree to which the data is free of any bias;
-
• Reputation, the degree of high standing of the source perceived by customers.
All of these criteria are value drivers; however, regarding versioning, none of them can be used as it is difficult to influence them in the short run because they are perceived by the user rather than actively created.
4.4 Instantiation-Related Quality Criteria
Finally, the group of instantiation-related criteria will be discussed:
-
• Amount of data, the number of bytes returned as a query result;
-
• Representational conciseness, how well the representation matches the data;
-
• Representational consistency, how well the representation matches previous representations of the same data;
-
• Understandability, the degree to which a data set can be understood by a user;
-
• Verifiability, the degree to which a data set can be checked and verified.
While the amount of data and the representational consistency can be assessed automatically, the other three cannot. Representational conciseness and understandability cannot be assessed automatically because only humans can judge whether the data format matches the data or whether they understand the data. Verifiability depends very much on the actual use-case and is hard to generalize. Thus, it has been categorized as not automatically assessable.
The
amount of data and the
representational consistency can be used for versioning. For
representational consistency it is technically possible to change the representation (access
API or data format); however, it seems inappropriate to do so just to adjust the quality of the product. Nevertheless, different versions could have different guarantee levels that the representation does not change over certain time intervals. Thus, it has been categorized as applicable to versioning. The
representational conciseness can be used for versioning, in that there could be a low quality version that simply stores all data in one
binary large object and a high-quality version in which the data is organized in an appropriate relational structure. As a further example, we will consider
amount of data. More precisely, we will look at the amount of attributes or columns –
$AoC$ – which we defined as Stahl (
2015), where
Y denotes chosen (or available) columns:
$\mathit{AoC}(u):=\frac{|Y|}{|{X_{u}}|}$.
Having described the most relevant data quality criteria as well as having evaluated them with regards to versioning, they shall now be grouped into different sets for easy future reference. Regarding pricing and versioning, all criteria that allow for the dynamic creation of a large number of versions build the set $V=\{$Accuracy, Amount of Data, Availability, Completeness, Latency, Response Time, Timeliness}. Furthermore, there are criteria that generally allow for versioning but where the number of versions is strongly limited. For instance, it is not sensible to create a large number of customer support tiers. Sticking with the Goldilocks principle, it seems reasonable to provide three categories for all attributes in this set, which will be referred to as $G=\{$Customer Support, Documentation, Representational Conciseness, Representational Consistency, Security}. All of the criteria in this set but representational consistency and security are limited in their applicability as comparison criterion. As these are the only relevant quality criteria regarding versioning, they are combined in ${Q_{v}}=V\cup G$.
In our running example, the
completeness, as an example for a criterion in
V, can be calculated as follows: for provider
A the maximum completeness is
and for provider
B it is
$c(u)=0.6\bar{7}$; possible tiers for
customer support, as an example for a criterion in
G, are:
-
1. E-mail support with a 48 hour response guarantee;
-
2. Telephone support 9 to 5 and 24 hours response time e-mail support;
-
3. Telephone and e-mail support 24/7.
5 Quality-Based Pricing
Building on the data quality criteria review, this section proposes an approach of data pricing in which not only one quality dimension of a relational data product is adjusted according to a user’s willingness to pay but all dimensions are, taking user preferences into account. So let providers advertise a price P. If P exceeds a user’s willingness to pay, they may suggest a price W of their own and reveal their preferences for certain quality criteria. If customers want to pay less, i.e. $W<P$, then a data product will be tailored to their needs and willingness to pay is created and delivered.
A physical good with a similar procedure of a quality reduction for different use cases is ethanol. If it is sold for drinking, it is commonly expensive and highly taxed. However, if it is used as a fuel or as a solvent, it is comparatively cheap. In order to prevent abuse, i.e. drinking the cheaper alcohol, additives are used that make it bitter or toxic. Transferring this idea to data, it can be offered cheaper if it is of lesser quality as it provides less utility to consumers.
We now assume that users know their preferences and can express them in the form
${q_{i}}\geqslant {q_{j}}$ f.a.
${q_{i}},{q_{j}}\in {Q_{v}}$. Furthermore, preferences enjoy two properties (Pindyck and Rubinfeld,
2013): a) completeness, i.e. preferences exist for all combinations
${q_{i}}$ and
${q_{j}}$; b) transitivity, i.e. preferences are totally ordered, formally: if
${q_{1}}\geqslant {q_{2}}\wedge {q_{2}}\geqslant {q_{3}}$ then
${q_{1}}\geqslant {q_{3}}$. In order to express these preferences users are asked to provide their appreciation of each quality measure.
Seven quality criteria were identified that allow for continuous versioning (tailoring). This means that for these criteria an arbitrarily large number of versions can be created. They were assembled in the set $V=\{$Accuracy, Amount of Data, Availability, Completeness, Latency, Response Time, Timeliness}. Furthermore, five criteria have been established for which a limited number of versions can be created, i.e. which allow for discrete versioning, collocated in $G=\{$Customer Support, Documentation, Security, Representational Conciseness, Representational Consistency}. To handle all alike, all criteria will be treated in a way to create discrete versions. In the following the differentiation is subordinated and it will be referred to all quality criteria as: $Q=V\cup G$. However, the order will be of importance, hence, from now on, a list of quality criteria q will be used: $q=({q_{1}},\dots ,{q_{n}})$ with $n=|Q|$ elements.
5.1 Introducing Utility
A common assumption is that goods provide utility. Commonly, micro economists investigate utility functions for a set of
g goods, which will be referred to as benefit function
$b=f({x_{1}},\dots ,{x_{g}})$ (Pindyck and Rubinfeld,
2013) to not confuse utility and the universal relation. We here do not consider sets of goods, but focus on one relational data good and its quality attributes, the utility of which may be formalized as
$b=f({q_{1}},\dots ,{q_{n}})$, where
${q_{i}}$ represents the quality scores for quality criterion
${q_{i}}$.
We consider quality criteria to be independent, i.e. the consumption of one quality criterion does not have an effect on the utility of another. While this is not the case for extremes, e.g. an incomplete data set is less likely to be accurate than a complete one, this is a necessary simplification to handle all dimensions in the following model. Furthermore, it can be argued that when looking at one item only, and keeping the others constant, it is a valid assumption.
Two well-known classes of functions can be used as utility functions, logarithm functions – for which the natural logarithm has been chosen as representative – as well as any root function $\sqrt[a]{x}$, $a\in {\mathbf{N}_{\geqslant 2}}$. Given that the quantity of a good cannot be negative, the relevant domain for both functions is ${\mathbf{R}_{0}^{+}}$.
Since we propose to create versions based on the expected utility, the utility function is used to create ${m_{l}}$ utility-based versions or levels so that ${b_{j}}-{b_{j-1}}=\mathrm{const}$, $1\leqslant j\leqslant {m_{l}}$. To this end, the quality scores which have been standardized to fit the domain $[0,1]$ will be scaled to match a sector of the utility function’s domain $[{x_{\min }},{x_{\max }}]$, e.g. $[0,100]$ for the square root. Note that data with some quality scores beneath a certain threshold ${t_{q}}$ are useless. To address this, it is also possible to transform only the interval $[{t_{q}},1]$, $0\leqslant {t_{q}}\leqslant 1$ from the original score to the representative sector of the utility function, i.e. at quality score ${t_{q}}$ the utility level of that quality score is 0. To arrive at the necessary minimum quality score for each utility level, the inverted utility function is used, e.g. ${x^{2}}$ for $\sqrt{x}$.
While for the square root model the utility-based levels increase linearly with x because the difference of two levels can be calculated as ${x^{2}}-{(x-1)^{2}}=2x-1$, for the natural logarithm they increase exponentially in x because the difference of two levels is ${\mathrm{e}^{x}}-1-({\mathrm{e}^{x-1}}-1)={\mathrm{e}^{x}}-\frac{{\mathrm{e}^{x}}}{\mathrm{e}}={\mathrm{e}^{x}}(1-\frac{1}{\mathrm{e}})$. Thus, in the following, the square root function will be used as it produces more illustrative utility levels. The case can be made that other root functions $\sqrt[a]{x}$, which scale polynomially with the degree $a-1$, could be used as well. However, this is a matter of implementation as the model is – as will be seen – independent of the function.
The utility-based quality level vector
l contains the concrete values of the utility level
${l_{j}}$ in order. In the example manifestation presented here, it is supposed that
${l_{j}}=j$,
$0\leqslant j\leqslant {m_{l}}$. While this applies for those quality criteria that allow for continuous versioning (i.e.
$q\in V$), for those that only allow for discrete versioning (i.e.
$q\in G$) a smaller number has to be chosen, here four utility levels
${l_{0}},{l_{3}},{l_{6}},{l_{9}}$ are chosen from the utility function for
$q\in G$ – according to Goldilocks principle, proposed in Shapiro and Varian (
1999). To differentiate between the utility level vectors of both sets, they have an according superscript, resulting in the two vectors
${l^{V}}$ and
${l^{G}}$. Since quality levels in
${l^{G}}$ do not correspond to concrete quality scores, determining a value for them is meaningless. It is rather advisable to manually determine the amount of service for each level. Sample figures for both variants are presented in Table
3, where levels for the second type have been marked with an X. The used utility function and according versions are depicted in Fig.
1.
Table 3
Used utility levels mapped to versions; showing required quality score (QS).
| Utility level (${l_{j}}$) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| QS required to reach version ($q\in V$) |
0 |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
100 |
| QS required to reach version ($q\in G$) |
0 |
⊥ |
⊥ |
X |
⊥ |
⊥ |
X |
⊥ |
⊥ |
X |
⊥ |
While in reality utility does differ between customers, the general trend is the same, and will here be approximated by the same function. Furthermore, it is acknowledged that not all quality criteria have the same importance for customers. For example, completeness may be more important for a customer than timeliness because they want to do some time-independent analysis, while for another customer timeliness might be more important because they base time-critical decisions on the data. To represent this in the model, the utility gained from each ${q_{i}}$’s quality score is weighted with a user-provided ${\omega _{i}}$ that represents the importance of all quality criteria relative to each other.
To receive
${\omega _{i}}$, users are asked to express their preferences. This results in a stack of utility functions in which different aspects have a different influence on the overall utility for any individual customer. This is illustrated in Fig.
2. Moreover, this results in a weight vector
ω such that:
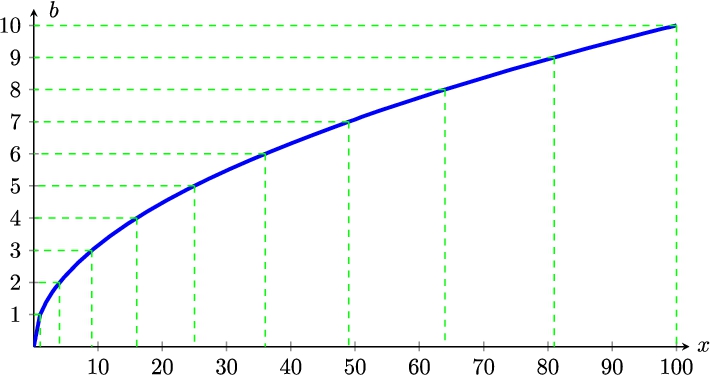
Fig. 1
Exemplary used utility functions with ten utility levels.
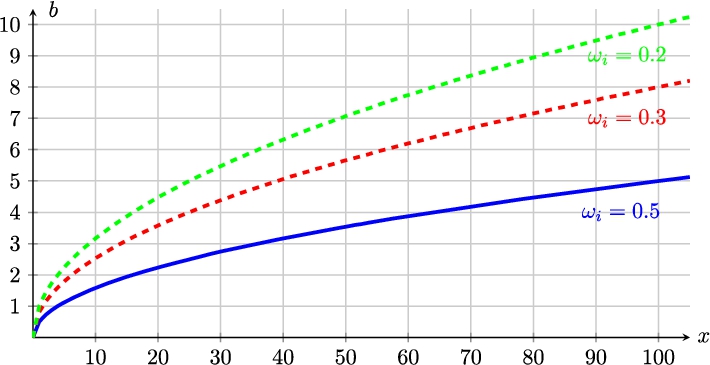
Fig. 2
Example utility function as stack of: $\omega \sqrt{x}$ for ${\omega _{1}}=0.5$, ${\omega _{2}}=0.3$, and ${\omega _{3}}=0.2$.
Based on all this, a benefit matrix
b can be calculated for each user. This matrix shows for which quality criterion
${q_{i}}$ with an according weight
${\omega _{i}}$ what actual utility
${b_{ij}}$ can be reached for the different utility levels
${l_{j}^{V}}$ and
${l_{j}^{G}}$. It is calculated as follows:
For future reference, the subscript i refers to elements in Q and j to elements in ${L_{V}}$ or ${L_{G}}$, respectively.
5.2 Price Attribution
Having extensively discussed for each quality criterion how a utility level is arrived at, we now elaborate on how prices can be attached to the different levels. Besides the overall ask price
P providers want to achieve, they have to specify the importance of different quality criteria from their point of view. This may either be done based on the cost the different quality criteria caused when being created or based on the perceived utility of the different criteria. As argued before, the utility-based approach is preferable; however, the cost-based approach can serve as point of reference if no further information is available. Additionally, it is also an option to attribute an equal weight to all quality criteria. Whatever method is chosen, the weights may be adapted in the course of time when providers learn about their customers. Similar to the user weighting vector
ω, providers define a weight vector
κ such that:
For the actual distribution of the overall ask price P to the different quality levels and quality criteria two fundamentally different approaches can be implemented. Prices can either be attributed to the different quality levels using the utility levels or using the relative satisfaction of each quality criterion. In any case the overall price would be distributed to the different quality criteria using κ. The first will lead to linear prices corresponding to the benefit, which is arguably a fair way of pricing a data product. In this case, the price ${w_{ij}}$ for each quality criterion ${q_{i}}$ at each quality level ${l_{j}}$ is calculated using a formula of the form ${w_{ij}}({b_{ij}})$, in detail: ${w_{ij}}=P\times {\kappa _{i}}\times \frac{{b_{ij}}}{{b_{i,{n_{q}}}}}$.
The alternative is to model prices linearly to the actual quality scores required to reach this level. This will result in increasing prices for the utility levels. However, looking at it from the discount perspective, this means that the biggest discount is granted for the sacrifice of the first utility level and then it decreases. Put differently, in this way customers will receive a product of comparably high quality at a very reasonable price. The calculation of
${w_{ij}}$ in this case is conducted based on the inverted utility function
${w_{ij}}(x)=P\times {\kappa _{i}}\times {b^{-1}}(x)$, in this case
${b^{-1}}(x)={x^{2}}$ and the overall utility levels in
l:
It cannot be decided per se which of the two alternatives is the better one. There are some quality scores, such as the amount of data, for which it is sensible to grant a good discount if less data is to be delivered. In other cases, such as accuracy, it might make more sense to scale prices according to the utility levels. That being said, what model to choose is a business decision that has to be made for each individual criterion depending on the attributes of the criterion as well as on the intended fairness of the pricing model. Given the stronger decrease when using the inverted utility function, the average price across all levels is smaller than in the linear case; this speaks in favour of the latter model from a customer’s perspective. After all, it is not important what product is actually delivered as the cost of creating it is marginal. What is more important is that customers get a fair discount for their sacrifice of quality. This is achieved by either of the two.
5.3 Fair Knapsack Pricing
Having shown how to attribute utility as well as a price to different quality criteria for relational data products, we now demonstrate that the pricing problem can be perceived as a Multiple-Choise Knapsack Problem (MCKP).
The objective of the knapsack problem, which we describe according to Kellerer
et al. (
2004), is to fit items (numbered from 1 to
${m_{l}}$) with a benefit
${b_{i}}$ and a weight
${w_{i}}$ into a knapsack, in a way that maximizes the utility given a maximum weight
W. This standard knapsack problem has been extended in several ways. One of the most flexible knapsack models is the herein-applied MCKP (Kellerer
et al.,
2004). In a MCKP, items are chosen from
${n_{q}}$ sets of available items rather than from just one set of available items, an additional restriction being that from each set exactly one item has to be chosen. Using the variables from the previous sections and extending the vector
a, which stores for each available item whether or not it has been put in the knapsack as
${a_{i}}\in \{0,1\}$, to a matrix, pricing can be formalized using the MCKP as presented in Kellerer
et al. (
2004). In the following, Eq. (
3) extends the original knapsack problem to multiple sets to choose from. Equation (
4) restricts the choice to one item per set and determines that items are indivisible.
5.4 Solving the Multiple-Choice Knapsack Pricing Problem
In order to create a custom-tailored relational data product, the Multiple-Choice Knapsack Pricing Problem (MCKPP) has to be solved. Despite the fact that MCKP is
$\mathcal{NP}$-complete, it can be solved in pseudo-polynomial time using, for instance, dynamic programming; several algorithms have been presented to achieve this (Pisinger,
1995). Most algorithms start by solving the linear MCKP to obtain an upper bound. For the linear MCKP the restriction
${a_{ij}}\in \{0;1\}$ has been relaxed to
${a_{ij}}\in [0,1]$, which means it allows the choosing of a fraction of an item (Pisinger,
1995).
Algorithm
5.1 presents a general greedy algorithm to solve the MCKPP. It has been adapted from the one outlined in Kellerer
et al. (
2004). The main difference is that the original algorithm contains a preparation step which is not necessary for the MCKPP. The algorithm eventually results in a matrix
a indicating which items to choose, a value
$W-\bar{c}$, which represents the total cost of these items, and a score
z, indicating the total utility achieved.
The greedy algorithm, presented in a pricing-tailored form in Algorithm
5.1, has a runtime of
$\mathcal{O}({n_{t}}\log {n_{t}})$ – with
${n_{t}}$ being the total number of items over all quality criteria
${n_{t}}={\textstyle\sum _{i=1}^{{n_{q}}}}{{m_{l}}_{i}}{n_{t}}={\textstyle\sum _{i=1}^{{n_{q}}}}{{m_{l}}_{i}}$ – owing to the sorting in Line 13. This form of a greedy-type algorithm is often used as a starting point for further procedures such as branch and bound (Kellerer
et al.,
2004). Furthermore, the split solution is generally a good heuristic solution; however, it has to be pointed out that as a solution algorithm – despite being illustrative – it is unsuited. The reason for this is that its performance is arbitrarily bad, i.e. while performing quickly, the solution is not guaranteed to be the optimal solution (Kellerer
et al.,
2004).
Further approximation algorithms exist that do have certain performance guarantees. Gens and Levner (
1998) have presented a binary search approximation algorithm running in time
$\mathcal{O}({n_{t}}\log {n_{q}})$, where
${n_{q}}$ is the number of quality criteria. At this point, it should be mentioned that
${{m_{l}}_{i}}$ is used here to indicate that depending on whether
${q_{i}}\in V$ or
${q_{i}}\in G$,
${{m_{l}}^{G}}$ or
${{m_{l}}^{V}}$ has to be substituted. However, the guarantee is
$\epsilon =0.8$, which is still a considerably bad result – 0 being the perfect solution – even though the authors argue that the actual performance may be much better than that. Using dynamic programming, a fully polynomial time approximation scheme can be developed (Kellerer
et al.,
2004). Lawler (
1977) presents an
ϵ-approximation that runs in
$\mathcal{O}({n_{t}}\log {n_{t}}+\frac{{n_{t}}{n_{q}}}{\epsilon })$, the first term being due to sorting which might be omitted here. A similar approach is also presented in Kellerer
et al. (
2004).

Algorithm 5.1
Greedy algorithm to solve MCKPP adapted from Kellerer
et al. (
2004).
Approaches to solve the MCKP to optimality include branch and bound (Dyer
et al.,
1984), dynamic programming (Dudzinski and Walukiewicz,
1987) (which is often used to solve dynamic pricing challenges (Narahari
et al.,
2005)), hybrid algorithms of the former (Dyer
et al.,
1995), and expanding core algorithms (Pisinger,
1995). Pisinger (
1995) presents a minimal expanding core algorithm solving the MCKP to optimality. It is based on the idea that the problem is first solved for a core set of classes, i.e. quality criteria,
$C\subseteq {Q_{v}}$ based on the split item. Then, gradually more classes are added. This results in a runtime of
$\mathcal{O}({n_{t}}+W{\textstyle\sum _{{q_{i}}\in C}}{{m_{l}}_{i}})$, where
W denotes the weight limit. This results in a linear solution time for a minimal core and pseudo-polynomial time for larger cores (Pisinger,
1995).
Notwithstanding this, the MCKP can commonly be solved quickly in practise (Dyer
et al.,
1995). Given that in the MCKPP the weights correlate with the benefits per definition, this results in strongly correlated data instances, which are particularly hard for knapsack algorithms, as no dominated items exist (Pisinger,
1995; Kellerer
et al.,
2004).
Pisinger (
1995) presented computational experiments on commodity hardware for his algorithm. Nearly a decade later, in
2004, results for the same algorithm on more recent commodity hardware were presented in Kellerer
et al. (
2004). Table
4 shows the results relevant for strongly correlated data instances in the problem scope of MCKPP. Two realistic cases will be presented for each year:
Case 1 considers 100 quality dimensions and 10 quality levels and
Case 2 considers 100 quality dimensions and 100 quality levels. Furthermore, two different maximum bid prices are considered
Max Bid 1 which is set to
$1,000$ and
Max Bid 2 which is set to
$10,000$. The time is reported in seconds.
Table 4
Experimental results for MCKP calculations using Pisinger (
1995) algorithm.
|
1995 (Pisinger, 1995) |
2004 (Kellerer et al., 2004) |
|
Max Bid 1 |
Max Bid 2 |
Max Bid 1 |
Max Bid 2 |
| Case 1 |
0.37 |
5.16 |
0.061 |
0.561 |
| Case 2 |
0.33 |
6.93 |
0.52 |
0.828 |
5.5 Application to the Running Example
Returning to our weather example, suppose that the customer has opted to buy data from provider
A presented in Table
1 before it is modified, i.e.
u. The advertised price
P is $ 1200.00 for both providers; however, the customer is only willing to pay
$W=1000.00$. For reasons of clarity and comprehensibility this section investigates only three quality attributes, namely:
For
customer service, the provider offers the three service levels described previously:
-
1. E-mail support with a 48 hour response guarantee;
-
2. Telephone support 9 to 5 and 24 hours response time e-mail support;
-
3. Telephone and e-mail support 24/7.
Furthermore, at quality level 0 no support is provided. The customer-provided preferences for the different quality criteria are:
$\omega =(0.35,0.5,0.15)$ and the provider specifies
$\kappa =(0.5,0.3,0.2)$. In the following, the index
i (rows) refers to quality criteria and the index
j (columns) refers to utility levels. Based on this the utility matrix
b, the weight matrix
w as well as the incremental utility matrix
$\tilde{b}$ and the incremental weight matrix
$\tilde{w}$ can be calculated. Eventually, this can be used to arrive at the incremental efficiency
$\tilde{e}$:
This results in the following ordered list of
${\tilde{e}_{ij}}$.
Nota bene,
${\tilde{e}_{1,1}},{\tilde{e}_{21}}$, and
${\tilde{e}_{31}}$ are missing because they are used to initialize the knapsack.
The knapsack is initialized as follows:
Then, the MCKPP is solved using Algorithm
5.1. The sequence of
$\bar{c}$, and the selected
${\tilde{e}_{ij}}$ in each step is shown in Table
5. Again, it has to be pointed out that this is just for illustrative purposes as better but less easy to comprehend algorithms exist to solve this.
Table 5
Development of $\bar{c}$ after each processing step.
| Iteration |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| Selected ${\tilde{e}_{ij}}$
|
${\tilde{e}_{2,2}}$ |
${\tilde{e}_{2,3}}$ |
${\tilde{e}_{2,4}}$ |
${\tilde{e}_{1,2}}$ |
${\tilde{e}_{2,5}}$ |
${\tilde{e}_{2,6}}$ |
${\tilde{e}_{1,3}}$ |
${\tilde{e}_{2,7}}$ |
${\tilde{e}_{2,8}}$ |
${\tilde{e}_{1,4}}$ |
| $\bar{c}$ |
952,93 |
934,93 |
909,73 |
891,73 |
859,33 |
819,73 |
789,73 |
742,93 |
688,93 |
646,93 |
| Iteration |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
| Selected ${\tilde{e}_{ij}}$
|
${\tilde{e}_{2,9}}$ |
${\tilde{e}_{2,10}}$ |
${\tilde{e}_{1,5}}$ |
${\tilde{e}_{3,2}}$ |
${\tilde{e}_{1,6}}$ |
${\tilde{e}_{1,7}}$ |
${\tilde{e}_{1,8}}$ |
${\tilde{e}_{1,9}}$ |
${\tilde{e}_{3,3}}$ |
${\tilde{e}_{1,10}}$ |
| $\bar{c}$ |
585,73 |
517,33 |
463,33 |
383,33 |
317,33 |
239,33 |
149,33 |
47,33 |
−86,00 |
−200,00 |
As can be seen in Table
5, the items that do not fit in the knapsack are
${\tilde{e}_{3,3}}$ and
${\tilde{e}_{1,10}}$. By implication, this means that items
${x_{1,9}}$,
${x_{2,10}}$ and
${x_{3,2}}$ are chosen, i.e.
timeliness at level 9,
amount of data at full level and
customer support at level 2. Thus,
customer support is served as 9 to 5 telephone support and 24 hours response time e-mail support.
Note that MCKPP can be applied to multiple vendors as well. In this case not the scores of one provider have to be mapped to the quality levels but only the best scores of all providers. This results in a problem scenario, where some providers might not be able to deliver all quality criteria to the highest level. To this end, consider one customer who is unsure which provider to buy from. Given that the average timeliness of both providers is the same, we now look at:
Again, customer service does not need to be calculated and the three levels stated above are considered here, too. For the other two criteria, the maximum scores for each provider have to be calculated. For provider A completeness was = 1 and amount of columns is $0.6\bar{7}$; provider B offers a maximum completeness of 0.8125 and an AoC of 1. Both provide the service levels as stated above. From this it can be concluded that the relevant mapping overall again is 0 to 1. However, it has to be stated that no provider can satisfy the highest level of all categories.
As with the previous example, the customer-provided preferences for the different quality criteria are:
$\omega =(0.35,0.5,0.15)$ and the provider specifies
$\kappa =(0.5,0.3,0.2)$. Therefore, the above calculus can be reused. As a result, the items that do not fit in the knapsack are
${\tilde{e}_{3,3}}$ and
${\tilde{e}_{1,10}}$; in this case
customer support at level 3 and
completeness at level 10. Consequently, the customer should chose/will be served by provider
B because they can provide the data that has been found to be optimal. In contrast, provider can provide
AoC only up to level 8, this is illustrated in Table
6.
Table 6
Utility levels offered by providers.
| Utility Level (${l_{j}}$) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| QS required to reach |
0.0 |
0.01 |
0.04 |
0.09 |
0.16 |
0.25 |
0.36 |
0.49 |
0.64 |
0.81 |
1.00 |
| version ($q\in V$) |
| Completeness |
$A/B$ |
$A/B$ |
$A/B$ |
X |
$A/B$ |
$A/B$ |
$A/B$ |
$A/B$ |
$A/B$ |
$A/B$ |
A |
| Amount of columns |
$A/B$ |
$A/B$ |
$A/B$ |
X |
$A/B$ |
$A/B$ |
$A/B$ |
$A/B$ |
$A/B$ |
B |
B |
However, if the customer favoured completeness over AoC, and supposing the same weights, the result would be different. In this case, provider A while being able to provide full completeness, still lacks the ability to provide AoC greater than level 8. Making up for this the algorithm would also suggest customer support at level 3 leaving a weight of 16 unused. Provider B in the same scenario is not able to offer completeness at level 10 but at level 9. Furthermore, provider B will in this case also offer AoC at level 9 and customer support at level 2. Given the customer’s preferences provider B is not a good choice despite leaving a residuum of less than 2. All this shows that while solving the MCKPP for all providers given a customer’s query and preference, it can also be determined which provider offers the best product for a customer.
5.6 Modifying Quality
For any of the quality measures presented previously an algorithm can easily be stated that creates a quality-adjusted relational data product according to a proposed discount. For accuracy, this has extensively been described in Tang
et al. (
2013b). Largely, modifications to the quality can be grouped into three categories:
-
1. The modification of accompanying services, e.g. delivery conditions and comprehensiveness of support;
-
2. The modification of the data itself, e.g. decreasing the accuracy;
-
3. The modification of the view on the data, e.g. a limited amount of data.
As examples this section will present algorithms to modify the completeness as representation of the second as well as timeliness and amount of data as representation of the third. No representation for the first will be given as this is a rather trivial contractual task and does not affect the data as such. Nevertheless, an example will be provided in the next subsection.
Obviously, the order in which the quality is decreased plays an important role. For instance, if null values are inserted first and then the accuracy is reduced, the accuracy reduction might build on a wrong distribution. Here, it is suggested to apply criteria first that reduce the size, i.e. criteria of the third type and also accuracy, before the rest of the quality is lowered.
The first quality measure to be looked at in more detail is
completeness as presented in Eq. (
1). This implies that in order to reduce the completeness further, null values have to be inserted at random. In the following
u is the universal relation to be sold before any modification and
${u^{\ast }}$ afterwards. The same applies to all other relevant variables,
${n_{v}}$ is the number of null values before and
${{n_{v}}_{t}}$ after the quality modification. The suffix
t indicates a target value. Furthermore,
${x_{\max }}$ denotes the maximum of the domain of the utility function and
x the utility score at the chosen level. To lower the completeness the actual value for completeness has to be determined and the target value for completeness has to be calculated based on the selected quality level:
Based on this the target number of null values
${{n_{v}}_{t}}$ can be calculated:
Resulting in:
Note that the ceiling function has to be used in Eq. (
7) to ensure
${n_{t}}$ is an integer as no half null values exist. Alternatively, the floor function could be used, this is at the provider’s discretion but would result in a slightly different product version. Based on this target value for null values
${n_{t}}$ Algorithm
5.3 presents an exemplary method to achieve the modified data set
u.
Given
${\mathit{AoC}_{t}}=\frac{{y_{t}}}{{x_{\max }}}$,
${y_{t}}=|Y|$ can be calculated. Similar to
completeness, the ceiling function is used to ensure that
${y_{t}}$ is an integer.

Algorithm 5.2
Adapting the relation to the amount of columns score.

Algorithm 5.3
Adapting the relation to the completeness score.
Furthermore, it is supposed that the customer provides a list of attributes
$Z\subseteq {X_{u}}$ in decreasing order of their liking, such that the first attribute is the most important and the last is the least important. If
Z is not provided, it is at the provider’s discretion which attributes actually to deliver. While this could also be the standard, giving customers the choice seems more fair. Algorithm
5.2 presents a sample method to achieve
$Y\subseteq {X_{u}}$ provided
${y_{t}},u,Z$.
Timeliness does not require an algorithm as it is concerned with delayed delivery. However, it requires some calculus, presented in the following building on Eq. (
2). For better readability
$\mu [\text{LastUpdated}]$ will be denoted as
LU and DeliveryTime will be denoted as
DT. Furthermore, the max function can be omitted supposing that the target score
${t_{\mathrm{target}}}=\frac{x}{{x_{\max }}}$ is positive. Additionally
$|u|$ will be represented by
n. Thus:
Plugging in a target value
${t_{\mathrm{target}}}$ yields
Given that only
LU is variable:
Eq. (
12) shows what the average timeliness depending on the target value
${t_{\mathrm{target}}}$ should be and could also be written as:
The delivery time will always be the current time. Thus, it will be represented by the variable
now, which will be replaced by the current timestamp upon query time. This allows for further modification to result in:
Introducing a delay function:
At first sight one might require each data set to have an average timeliness not greater than
$L{U_{\mathrm{target}}}$. However, using the overall average of a data set is slightly problematic, as this allows the selection of data that is very old together with very fresh data and then only use the fresh data. To avoid this, the timeliness of any record is required to be not greater than
${\mathit{LU}_{\mathrm{target}}}$. In this way it is ensured that records with a timeliness worse than or equal to what has been paid for is delivered. In practical terms customers do query a view
${u^{\ast }}$ on
u such that:
In this model it is important that when records are updated, the original record is kept so that customers can still access the older record rather than receiving an empty result set.
Continuing our example, remember that
timeliness was to be provided at level 9,
amount of data at full level and
customer support at level 2. The last dimension counts as a contractual category that does not influence the data. Since
amount of data is served at full level it also does not influence the data. Therefore,
$u={u^{\ast }}$ holds as no modifications to the data have to be made. However, given that time restrictions apply, in that the data cannot be queried as soon as it is entered into the system, a view has to be derived at. Here, the assumption is made that the volatility of weather forecast data is 24 hours. Given that the target quality score of
${t_{t}}=\frac{81}{100}=0.81$ is a result of the optimization process, based on the quality level 9, now the delay may be calculated using Eq. (
13):
Having identified a delay of 4.45 hours and supposing that constant
now is expressed in hours, too, the final delivery view can be expressed as:
6 Conclusions and Future Work
In this paper, we have demonstrated how data quality measures can be applied when pricing relational data goods. Concretely, we have presented a model that allows providers to apply an NYOP scheme for data. This paper also shows how this model can be used when competitive data sources exist. Thus, the model enables data providers to tap the willingness to pay of customers, who would otherwise not buy their relational data product; in turn customers receive a highly custom-tailored data product. By adjusting the quality, it can be ensured that customers get exactly what they pay for. In fact, using this model providers do not have to specify a price publicly at all. They also could use an internal price P and still apply the same pricing model. While this would require users to bid exactly the price they are willing to pay it lacks transparency. An alternative would be advertising a price ${P^{p}}$ greater than P publicly. This would result in additional profits from customers paying a price W for which $P\leqslant W\leqslant {P^{p}}$ holds.
This paper has excluded the issue of potential cannibalization, i.e. that customers who would have bought expensive products switch to a cheaper version if it becomes available. This is an organisational aspect subject to future research. Furthermore, it should be evaluated whether this pricing model is perceived as fair as this is an important issue when pricing (Reinartz,
2002; Narahari
et al.,
2005). To this end, it could be experimented with an alternative pricing model, in which not all prices are calculated automatically but users are provided with feedback regarding the actual quality levels while entering their prices and preferences. This might also increase the perceived fairness. Furthermore, using statistical analyses on the bid prices, data providers can learn what value customers attribute to their offerings. In this context, truth revelation might be an issue (Narahari
et al.,
2005); the question remains if customers can actually cheat the system by not mentioning their true preference. At this point, no formal proof can be provided but the argument is made that if the used algorithm indeed delivers optimal results, then customers cannot cheat the system as it delivers a custom-tailored product for exactly the suggested price. Depending on the number and size of the quality-based utility levels, there might be little room to minimize the residual capacity
$\bar{c}$ which might still occur; however, this is ineluctable.
Developing a quality-based pricing model, it has been shown that pricing on a data marketplace can be expressed as an MCKP. An implementation is important future work in order to evaluate the algorithm presented in Section
5.4 in the context of pricing. In this regard, it is particularly interesting from which number of quality levels and quality scores the algorithms become inefficient – if at all. Conducting such experiments, it can be verified if the assumption that using the proposed solution to the MCKPP the quality level can be determined in fractions of seconds can be held. Furthermore, some work has to be invested into the question of how to actually create the required relational data products on the spot as this might take a considerable amount of time.
To summarize, MCKPP is influenced by Quality Criteria, Customer Info comprising the preference vector ω and a bid price W, Provider Info comprising a weighting vector κ and an ask price P, a versioning function b, a weighting function $w(x)$ or $w(b)$, and a Quality Adaptation Algorithm for each Quality Criterion. It is a distinct feature of this model that all components can be adjusted to match the needs of data marketplace providers as well as the needs of data providers.