Abstract
Quantum computing has come to stay in our lives. Companies are investing billions of dollars in it because of the potential benefits that it can achieve, providing promising applications in almost every business sector. Although quantum computing is evolving at an exponential rate, the development of tools, techniques, or frameworks for the evolution of current information systems towards quantum software systems is still proving to be a challenge. This research contributes to the evolution of current information systems towards hybrid information systems (combining the classical and quantum computing paradigm). We propose a software modernization process, by following model-driven engineering principles, adapted to the quantum paradigm, based on modified versions of standards for reverse engineering of classical, quantum software assets, and for the design of the target system. In particular, this paper focuses on the restructuring transformation from KDM to UML models, where KDM models have been generated from Q# code. This proposal has been validated through a case study involving 17 programmes. The results obtained show optimistic values regarding the complexity of the UML models generated, their expressiveness and scalability. The main implication of this research is that UML models can indeed help the software evolution of/toward hybrid information systems.
1 Introduction
The current state of quantum computing is the result of years of research by private companies and public organizations. The interest in this new technology lies in its potential to perform processing and computations at speeds that would otherwise take years to achieve, even with today’s supercomputers (Courtland,
2017). This is mainly because quantum computers are able to exploit some of the principles of quantum mechanics. This allows them to employ unique new features, such as superposition and quantum entanglement (Rieffel and Polak,
2011), that are applied to the quantum bits (“qubits”).
It has been predicted that “services and software related to quantum computing will be worth $1.9 billion in 2023 and this amount is estimated to have risen to $8 billion by 2027” (Vernacchia,
2019). Perhaps in a few years or even months these values will have grown or accelerated over time, but what is certain is that, at some point in the not-too-distant future, most companies will adapt their classical information systems to accommodate the quantum paradigm in order to remain competitive. This adaptation does not imply a total discarding of their current “classical” systems, but rather an evolution of them. What is certain is that quantum computing has the potential to help us solve problems at speeds unattainable for today’s computers. Nevertheless, the problems that current quantum computing can solve are still concrete and with very specific characteristics, which means that not everything we run on a quantum computer is going to represent a gain in performance compared to conventional computers (Aaronson,
2008). This implies that information systems will evolve instead towards hybrid information systems (Piattini
et al.,
2021; Jiménez-Navajas
et al.,
2020), i.e. combining current information systems with quantum software.
The challenge of the evolution of information systems has already been faced before and solved thanks to software modernization. However, software modernization must be adapted to meet the underlying challenges of the evolution of/towards hybrid information systems. This adaptation must be able to solve at least two problems. First, quantum algorithms must be capable of being integrated into the information systems. Also, the replacement of its counterparts (developed by following classical algorithmic) must take place in an integrated way. Second, once the classical information has evolved, they must permit the introduction in the target hybrid information system of new functionalities inspired and based on the quantum paradigm.
Although the field of quantum computing is still developing, the necessity for integrating quantum applications into classical information systems is already pressing (Kshetri,
2024; Kim
et al.,
2023), especially during the NISQ (Noisy Intermediate-Scale Quantum) era (Preskill,
2018). Many quantum applications depend on dynamic interactions with classical systems, where classical software not only generates quantum circuits based on real-time data but also interprets and processes the output of quantum computations for end-users (Zhao
et al.,
2024). This integration is essential for enabling hybrid information systems that combine quantum and classical paradigms to address specific business needs effectively (Pérez-Castillo
et al.,
2021b). For instance, optimizing complex operations, such as logistics or financial modelling, often requires seamless communication between the classical and quantum components, highlighting the urgency for robust software modernization approaches tailored to this emerging hybrid paradigm.
There exists a great diversity of programming languages and several quantum software development platforms (Heim
et al.,
2020; Hevia
et al.,
2021), but practically none are focused on quantum software modernization. An exception to this is a tool developed (Pérez-Castillo
et al.,
2022a) on the pillars of Architecture-Driven Modernization (ADM) (Pérez-Castillo
et al.,
2011a), which involves the evolution of traditional reengineering by applying the principles of Model-Driven Engineering (MDE). The tool constitutes the second phase of reengineering, i.e. restructuring. Within this phase, a transformation has been accomplished of models compliant with the Knowledge Discovery Metamodel (KDM) to Unified Modelling Language (UML) models, as well as a generation of graphical activity diagrams. The notation of activity diagrams has been chosen since the representation of quantum programmes is similar to the representation of quantum circuits. Although this representation of activity diagrams is not an abstraction with respect to a graphical representation of a quantum circuit, it is an abstraction with regard to a quantum programme. It should be noted that a quantum circuit cannot always represent all the elements of a quantum programme, but a quantum programme can always implement a quantum circuit. In addition, using this notation can be convenient both for professionals outside software modelling (such as physicists and mathematicians) since it lies in an equivalent representation to quantum circuits, and for professionals who do have experience in software modelling, since UML is a well-known modelling language.
A preliminary study (Jiménez-Navajas
et al.,
2021) presented the automatic transformation of the representations (models) generated from quantum programmes to UML models, thus partially addressing the second challenge. Consequently, managing UML models addresses both challenges at the same time, since UML is already widely used in the industry (e.g. there are many software engineers working with UML in software developments projects). Thus, UML will allow them to incorporate, modify or adapt quantum functionalities in their current systems.
This paper proposes a model transformation from KDM models to UML models, extended for quantum computing. The primary research question focuses on determining, through empirical validation, whether this transformation is effective and efficient for use in hybrid software modernization processes.
The novel contribution of this work is twofold:
The structure of this paper will be as follows: Section
2 shows the current state of the art of the core elements of this research, which belong to quantum computing and software modernization. Section
3 explains the extensions accomplished in KDM and UML in order to be able to represent all the different quantum entities in those metamodels. Section
4 describes how the quantum model transformation of KDM towards UML works. Section
5 outlines the case study we conducted with the application of the model transformation and activity diagram generation to various quantum algorithms. Finally, Section
6 describes the implications of this research for practitioners and Section
7 depicts the conclusions obtained and outlines possible future work.
2 State of the Art
This section is divided into four subsections. Section
2.1 gives a brief explanation of the fundamentals of quantum computing. Section
2.2 relates how quantum software technology has emerged and evolved until its current state. Section
2.3 describes software modernization, focusing mainly on UML, and how it can help solve the problems that the evolution of hybrid information systems may entail. Section
2.4 covers how different organizations will have to manage their legacy information systems and their evolution.
2.1 Quantum Computing Fundamentals
The field of quantum computing got a boost in 1982 when Richard Feynman proposed developing a computer capable of simulating nature. At that time, it was already known that nature at the subatomic level is subject to the laws of quantum mechanics. Therefore, to best simulate nature, a computer that takes advantage of these laws is needed. These new computers are quantum computers (Feynman,
2018).
Quantum computing represents a paradigm shift in how computations are performed by leveraging the principles of quantum mechanics. Unlike classical computing, which relies on bits representing binary states (0 or 1), quantum computing uses quantum bits (qubits) that exist in superpositions of states. A qubit state is described as:
where
α and
β are complex probability amplitudes satisfying
$|\alpha {|^{2}}+|\beta {|^{2}}=1$. This enables qubits to simultaneously represent multiple states, allowing quantum computers to explore a vast solution space in parallel.
Qubits can be represented with different physics systems. For example, among other, the spin of the electron in which the two states can be taken as spin up and spin down; or the polarization of a single photon in which the two states can be taken to be the vertical polarization and the horizontal polarization (Wojcieszyn,
2022).
A practical example to understand the power of quantum computing could be the problem to search for the shortest path between two points, which could have millions of possible routes $(N)$. While a classical computer would need to go one by one analysing all the paths until finding the desired one (this means $N/2$ steps or iterations), a quantum computer takes advantage of quantum parallelism to consider several paths simultaneously (i.e. in $\sqrt{N}$ operations).
Another principle of quantum mechanics used by these computers is quantum entanglement. This principle causes that when two qubits are in this state, they will always be correlated to the measurement on the other qubit. This implies that the quantum state of each qubit cannot be described independently of the quantum state of the other (Horodecki
et al.,
2009). This is a key element of quantum communications.
Other important characteristic derived from superposition and entanglement is how the result is measured for a particular qubit. When something is measured at the quantum level, the quantum object that have been measured is no longer in a superposition of states, rather it collapses to a single classical state (Yanofsky and Mannucci,
2008). This means that once the spin of the electron or photon is measured (i.e. its value is observed), the possible values for the qubit are 0 or 1, and this value is unmodifiable afterwards. Thus, quantum computing initializes and uses qubits that work in the probability space until these values are measured becoming actual values.
There are currently different ways of working with quantum computing, including gate-based, adiabatic, and topological quantum computing among others, with the most frequently used is gate-based quantum computing. Gate-based quantum computing works in a similar way to the assembly language of conventional computers, where commands act directly on the hardware. However, in this type of quantum computing such commands are quantum gates which affect qubits by altering their properties (such as applying superposition, entanglement, modifying their amplitude, etc.).
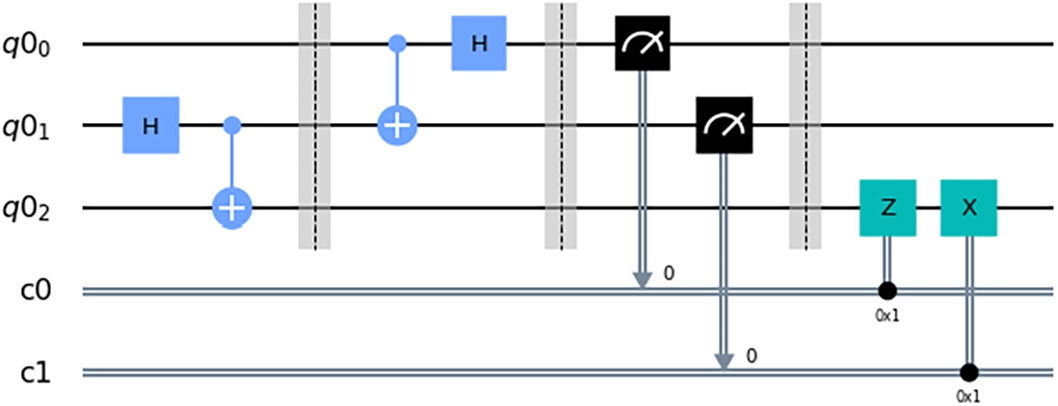
Fig. 1
Quantum teleportation algorithm.
2.2 Quantum Software Technologies
Developing quantum programmes in the gate-base quantum computing paradigm is usually done through quantum circuits. In these quantum circuits, qubits are represented by horizontal lines and, in order to alter their state (i.e. develop algorithms), quantum gates are placed on top of the qubits. Depending on the type of gate that is applied on the qubit, the qubit’s state will be altered in one way or another (e.g. with the Hadamard quantum gate the qubit goes into a superposition state). Figure
1 shows an example of a quantum circuit that represents the quantum teleportation algorithm where the lines labelled
q00,
q01 and
q02 represent the qubits, and the squares over those lines represent the quantum gates. The squares with an “H” represent the
Hadamard gate, and their function is to set the qubits in a superposition state. The gates with a cross in the middle and connected to another qubit are
Controlled Not gates, whose function is to change the state of a qubit (in this case,
q02) if the value of the state of the other qubit (
q01) is equal to 1. The black gates with a semicircle and a line represent the
measurement gate, which reveals the qubit’s state. The green gate with an “X” is a
Not gate and negates the state of the qubit. Finally, the gate with a “Z” flips the phase of the qubit.
There is a great range of programming languages and frameworks that allow us to work with this type of gate-based quantum programming languages, e.g. OpenQASM, Q#, Qiskit (IBM), Cirq (Google), pyQuil (Rigetti), etc. (Heim
et al.,
2020; Garhwal
et al.,
2021; Jimenez-Navajas
et al.,
2024b); as well as multiple development platforms, e.g. IBM Q Experience, Quantum Programming Studio, QPath, DWave Leap, Amazon Bracket, Orquestra, Strangeworks Quantum Computing, Classiq, or Quantum Inspire (Hevia
et al.,
2021).
Unfortunately, the radical differences between quantum and classical software have led mathematicians and scientists to follow non-systematic ways for developing quantum software (Piattini
et al.,
2021). Nevertheless, with the advent of “industrial” quantum software and its increasing use in many different business domains, a demand is growing for quantum software to be produced in a more systematic way (Dwivedi
et al.,
2024; Pérez-Castillo
et al.,
2024). This much was stated in “The Talavera Manifesto for Quantum Software Engineering and Programming” (Piattini
et al.,
2020) where it said that “given the recent rapid advances in quantum hardware, it is urgent that we step up our efforts in quantum software” (QuSoft,
2022). Similarly, the European Quantum Flagshipś Strategic Research Agenda (Flagship,
2020) proposes to investigate the “development of software stacks to integrate quantum computing into current computing environments”.
2.3 Software Modernization
Just like all technology, software is also affected by the course of time and, as a result, it must be constantly updated (Ulrich,
2002). In the case of seeking to maintain the business knowledge of such an information system, the use of reengineering might be useful. “Reengineering allows the preservation of business knowledge, by carrying out the evolutionary maintenance of the legacy information systems with low risks and low costs in comparison with (re)development from scratch” (De Lucia
et al.,
2008). The reengineering process, usually represented as a horseshoe model (cf. Fig.
2), is a process divided into three phases:
-
• Reverse engineering: all the different components which build the system, including its interrelationships, are represented through abstract representations of the system.
-
• Restructuring: at the same relative abstraction level, a transformation of the representations of the system is carried out. Furthermore, the system’s internal structure can be upgraded while the external behaviour of the system is preserved.
-
• Forward engineering: through means of the automatic generation of tools, the new source and software artefacts are built at a lower abstraction level.
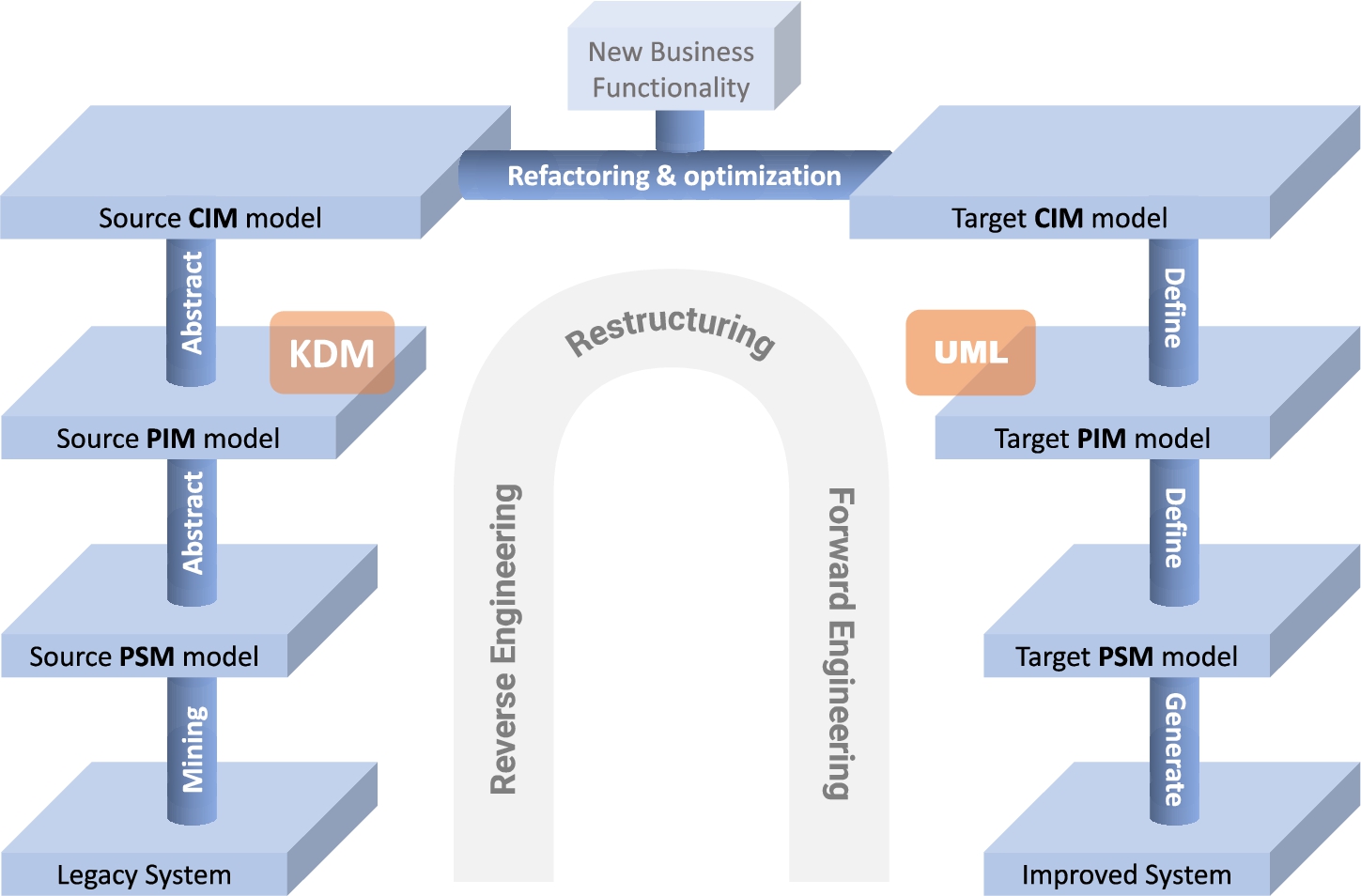
Fig. 2
The horseshoe model of the reengineering process (adapted from Pérez-Castillo
et al.,
2011a).
Furthermore, the code cannot be the only software asset that the standardization covers, since “the code does not contain all the information that is needed” (Müller
et al.,
2000). As a way to ensure that the source code and business rules (i.e. the knowledge of the systems) are properly integrated, the reengineering process must be formalized. Additionally, any possible failure in complex legacy systems must be avoided through a reengineering process which is sufficiently mature and repeatable (Canfora and Di Penta,
2007), and to minimize the maintenance costs automated tools should be provided for this reengineering process (Sneed,
2005). The evolution of software reengineering towards Architecture-Driven Modernization (ADM) has addressed the aforementioned problems (Ulrich and Newcomb,
2010). ADM applies the principles of Model-Driven Engineering (MDE) [33] in order to facilitate the modernization of tasks like analysis, refactoring and transformation of an existing system in order to support new requirements, together with the migration of systems or even their interoperability. The automatic transformation of abstract models accomplishes the different stages of software reengineering. The computation-independent model (CIM), the platform-independent model (PIM), and the platform-specific model (PSM) (see Fig.
2) are the most frequently employed models. ADM introduces the KDM standard to provide a metamodel to represent all the knowledge extracted by analysing software artefacts during reverse engineering, i.e. at PIM level. Similarly, UML could be used as PIM during forward engineering.
The KDM specification has several perspectives and to facilitate its management, 4 layers were defined. Each layer uses outputs from the previous layer and, within each layer, contains several packages representing different concerns related to legacy information systems. Depending on the particular artefact to be analysed, one or another layer (with its corresponding packages) will be used. As KDM has been used in this study to analyse source code, the “Programme Elements” layer and its packages “Code” and “Action” have therefore been used.
In order to address the need for the modernization of information systems that have suffered from the passage of time and the possible obsolescence of the technology with which they were developed, in 2009 the OMG presented the Knowledge Discovery Metamodel-ISO/IEC 19506 (KDM) standard (Pérez-Castillo
et al.,
2011b).
KDM models all the software artifacts involved in a legacy information system, which includes the source code of the information system itself, among other software artefacts. The high abstraction KDM models means that they are able to represent, in a technology-agnostic way, the different components as well as their interrelationships.
2.4 Software Modernization of Hybrid Information Systems
Once companies have access to quantum service providers to integrate some of their functionalities into the new paradigm, they will then need to evaluate which components of their information systems must be replaced or modernized. There are several reasons to believe that companies will not completely replace their information systems, but will rather opt for modernizing those systems (Pérez-Castillo
et al.,
2021b). Among other reasons, it is only on certain problems that quantum computing can achieve performances that are unattainable for classical computing. In short, not everything that we execute in this new paradigm will necessarily imply an improvement in performance. Another reason to think that this evolution will be partial only is that those “classical systems may embed a vast amount of critical-mission knowledge that probably is not located elsewhere and their replacement is highly risky” (Pérez-Castillo
et al.,
2022a). This raises the possibility that in the future, classical and quantum information systems will be used together to form hybrid information systems.
These hybrid information systems will be composed of two main parts, a classical computing section that will implement all those functions that do not make sense to “quantumfy”, and which will perform a transformation of the output of the quantum functions into legible information, and a quantum computing part that will implement such functions, either in the cloud or through simulations.
To carry out the modernization of the information systems of those organizations that will need to embrace the quantum paradigm in order to remain competitive, it is necessary to introduce quantum computing into the field of software engineering and, more specifically, into the field of software modernization.
An adaptation of software modernization has already been proposed in Jiménez-Navajas
et al. (
2020). In that solution, “quantum software reengineering” was presented, and it was stated that it could help software modernization in three different scenarios (see Fig.
3):
-
• To integrate existing quantum algorithms into the new hybrid information systems.
-
• To evolve the actual/classical legacy information systems toward hybrid information systems.
-
• To implement new business operations supported by quantum software into the target hybrid information systems.

Fig. 3
Quantum software modernization approach.
Figure
3 shows the overall process of quantum software modernization. In this process, it is intended to employ already existing standards such as KDM or UML. The first phase, which can be seen on the left-hand side of Fig.
3, consists of reverse engineering, where a model represents the different components of a system in a technology-agnostic way. This model is built through the analysis of the artifacts of the classical system (scenario 1) and quantum elements – if they exist (scenario 2). The second phase, which is at the top centre of Fig.
3, is the restructuring and is the main scope of this study. In this second phase the extended KDM models that were previously generated are transformed into high-abstraction level models. The meta-model chosen was UML since it is a widely known modelling language that has been widely embraced in the industry and which follows the technology-agnostic philosophy of the reverse engineering phase. Finally, on the right-hand side of Fig.
3 the forward engineering phase is depicted. In this final step of the quantum software modernization approach various tools could be used to automatically generate code fragments of the hybrid system which was designed employing the extended UML models.
The Quantum Software Modernization process can be used for any case that aims to the evolution of a classical information system towards a hybrid one. A possible case would be the modernization of a shipping routing system belonging to a logistics company, where it is intended to implement a quantum algorithm that, taking advantage of quantum parallelism, calculates the optimal route (cf. Section
2.1). Firstly, the company could explore the development of a quantum algorithm that calculates optimal routes (programmes for similar problems already exist, at least for quantum annealing devices, Weinberg
et al.,
2023). Secondly, once the quantum algorithm is developed, the company could have a quantum programme, that needs to be operated almost manually. Finally, the company will need to integrate with other parts of the existing classical software systems. This is crucial since the input parameters for the quantum algorithms come from those classical systems. The output of the quantum algorithms is essential for the classical counterparts, so users can make decisions based on them. In this scenario, the proposed software modernization process consists of:
-
• Reverse engineering to get the KDM model representing both the classical information system and the quantum programme. This quantum programme could be an implementation of a quantum circuit in a quantum programming language, but not the graphical quantum circuit. This is where the change of the abstraction level lies, as to model a quantum programme in KDM, one necessarily must change the abstraction level.
-
• Based on a model transformation, the target hybrid information system is restructured. In this phase, the UML representations of the quantum programme are integrated with the classical system representations, resulting in the design of the target hybrid information system.
-
• To cover all aspects of the model transformation, expert-based model refactoring would be employed. In our example, the integration of classical software parameters, and quantum response integration could be modelled.
-
• Finally, in the forward engineering phase, the source code backbone for the target hybrid information system is generated, at least the backbone that can be then completed by engineers.
As mentioned above, the notation of activity diagrams has been chosen since the representation of quantum programmes is similar to the representation of quantum circuits. However, it should be noted that the KDM models used in this proposal are not quantum circuits, but quantum programmes. Quantum circuits are already an abstraction of quantum code, as well as our representation based on UML. However, having quantum programmes represented in UML is an advantage when dealing with the modernization of information systems, as these UML quantum models can be integrated together with the UML models of the classical information system.
3 Metamodel Extensions for Quantum Software
This section depicts the two extensions developed in KDM and UML that are needed to represent the different quantum software elements. Section
3.1 presents how the KDM standard was used to represent quantum entities employing its default extension mechanism, i.e. the extension family. Then, Section
3.2 presents, among all the possible ways to extend the UML standard, the Quantum UML Profile.
3.1 Quantum KDM Extension
Despite all the efforts of OMG and the Architecture-Driven Modernization Task Force (ADMTF) to build a robust standard with the potential to represent all the components of an information system that are needed to be modernized, they never considered the quantum paradigm since quantum computing was not relevant in 2003 when the ADMTF was formed. Therefore, it was necessary to “extend the KDM metamodel through its built-in extension mechanism to support the representation of the different quantum entities” (Jiménez-Navajas
et al.,
2020). The KDM’s default extension mechanism is the extension family, Fig.
4 depicts the different components within this mechanism that can be found in a quantum programming language. The KDM extension is referred hereinafter as “Q-KDM”.

Fig. 4
Q-KDM extracted from Jiménez-Navajas
et al. (
2020).
Table 1
Matching KDM elements with the defined ones of the extension family.
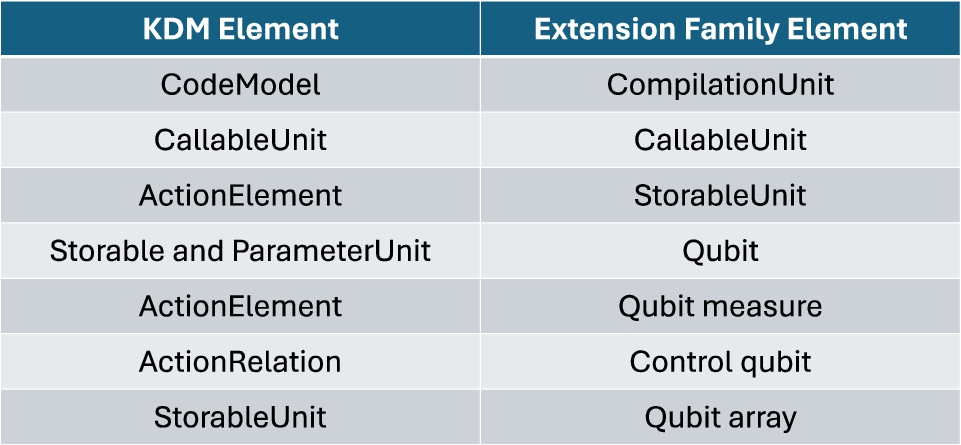
Whenever quantum programmes are reverse engineered, the Q-KDM appears in the KDM model of the quantum programme. In addition, each quantum component (i.e. a quantum gate or a qubit) is also defined in the KDM metamodel according to its operation. Table
1 shows which elements defined in KDM correspond to those in the Q-KDM. For example, if a qubit appears in a quantum algorithm, this qubit will be represented in KDM as a StorableUnit or ParameterUnit and will also point to the extension family stereotype “Qubit”. Associating quantum elements with their corresponding extension family stereotypes allows us to extend the semantics of KDM, since stereotypes may be used to indicate a difference in meaning or usage between two elements with identical structures (Pérez-Castillo
et al.,
2011b). This is necessary since the elements of quantum software are radically different from the elements that appear in classical software, which forces us to extend the metamodel to preserve as much information as possible. In addition, it is preferred to use standards already embraced by the industry as these have greater tool support and dominance by industry experts.
The CodeModel element is assigned to the root element of every KDM model, as this element has the aim of collecting the facts of the same programme, so the stereotype “Quantum Programme” was assigned. In Q#, the classical methods bear the name of the operation (i.e. quantum operations), so as they can be called between them, and the stereotype “Quantum Operation” was assigned to the CallableUnit element. Finally, the ActionElement elements are those which describe a basic unit of behaviour. This definition is suitable for quantum gates, so the “Quantum Gate” and “Qubit measure” stereotypes were assigned to the ActionElements.
3.2 Quantum UML profile
For the restructuring phase of the Quantum Software Reengineering process (explained in Section
2.4), the well-known UML standard was selected. The reengineering phase consists of the generation of high-level models where the relevant redesigns for the subsequent generation of the target hybrid information system are carried out. To perform this task, UML (Group,
2017) was chosen as the modelling language given that it is such a popular metamodel in the industry (it is a OMG and ISO/IEC standard), with a wide variety of tools available and a large community of software engineers who are proficient in this metamodel. It is worth highlighting the good results obtained when using UML for the analysis and design of information systems.
During the design of hybrid information systems, may occur problems concerning the representation of the new semantics and building blocks that quantum software can bring. However, like KDM, UML is not designed to represent these certain elements that may appear in a quantum algorithm, such as quantum gates or qubits. This is the reason why it was necessary to create an extension of the metamodel. UML offers three extension mechanisms (Ribo and Franch Gutiérrez,
2002):
-
• A new instance of the MOF model. This approach consists of creating a completely new metamodel based on MOF. The result of this heavyweight approach is a new Domain-Specific Modelling Language (DSML).
-
• Derivation of a new UML metamodel. This approach adds new metamodel elements to the existing one. As occurs with the first approach, it creates a different metamodel, but it at least considers the original UML metamodel as it is.
-
• UML Profile. This is a lightweight extension approach that is based on the UML built-in extension mechanism, UML Profiling. UML profiles are created as a set of stereotypes, tagged values, and constraints defined for some of the existing UML elements.
Of these three options, the last one was finally chosen – i.e. to extend UML through the creation of a UML Profile. There were two reasons for implementing it in this way: all models generated using such a profile will be fully compliant with the UML standard; and, in addition, it is easier to maintain extensions that have been defined as UML profiles, since the associated modelling tools do not need to be adjusted after each change. Furthermore, there is already an UML quantum profile that represents quantum elements through class and sequence diagrams (Pérez-Delgado and Perez-Gonzalez,
2020).
The Quantum UML Profile previously proposed in Pérez-Castillo
et al. (
2021a) allows the representation of quantum programmes through activity diagrams (see Fig.
5). On the right-hand side of Fig.
5, the different stereotypes added to the metamodel to represent the quantum components that might appear in a quantum programme can be seen: quantum circuit, qubit, quantum gate, controlled qubit, measure, and reset. Then, on the left-hand side of Fig.
5, an excerpt of the UML metamodel for representing Activity Diagrams is shown. Finally, the arrows which point from the stereotypes to the different metaclass elements indicate that the stereotype extends the properties of the metaclass elements. The UML extension is referred hereinafter as “Q-UML”.
The root element of a model which represents a quantum circuit will be a metaclass of type Activity with the «QuantumCircuit» stereotype. Inside this Activity, the qubits are typified as ActivityPartition with the «Qubit» stereotype because it is intended that the qubits are seen as horizontal lines where the quantum gates can be placed (as is done by IBM Quantum Experience (IBM,
2024) or any circuit composer). The quantum gates are represented by the metaclass Action but with the «QuantumGate» stereotype – but depending on what action they perform on the qubits, different metaclasses and stereotypes can be assigned. Further details of Q-UML can be seen in Pérez-Castillo
et al. (
2021a).
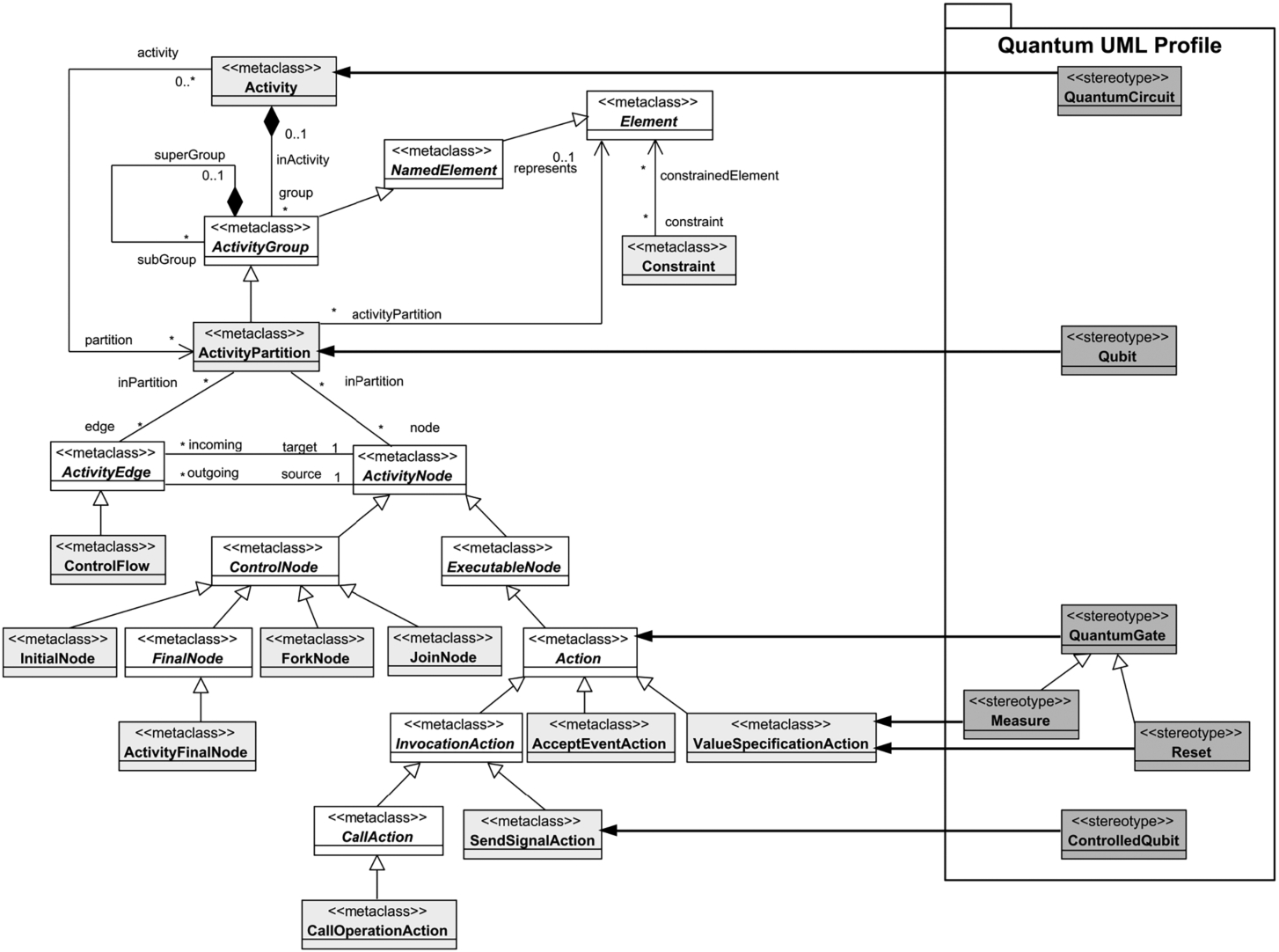
Fig. 5
Quantum UML Profile extracted from Pérez-Castillo
et al. (
2021a).
4 KDM to UML Model Transformation
This section presents the technical details for the proposed model transformation that is then empirically validated in Section
5. The general view of the proposal is shown in Fig.
6.
The left-hand side of Fig.
6 shows the ATL-based model transformation (explained in Section
2.4), where extended KDM models are transformed into extended UML models. Employing KDM models helps us to represent in a completely technology-agnostic way the different components and interrelationships of information systems and, thanks to the quantum extension family (explained in Section
3.1), it is now also possible to represent the different components of quantum algorithms independently in technology and programming languages. For this reason, the same technology-agnostic approach has been followed for the later stages of the Quantum Software Reengineering process. The UML models thus generated can be used for the later stages of analysis and design of the hybrid information systems in restructuring and forward engineering stages. Represented on the right-hand side of Fig.
6 is the activity diagram generation (explained in Section
3.2). This second step in the study consists of the generation of concrete syntax from the abstract one (the UML models built from the ATL model transformation) to generate graphical activity diagrams.

Fig. 6
Graphical representation of this study.
4.1 ATL Model Transformation
The designed KDM-to-UML transformation was accomplished employing the
ATLAS Transformation Language (ATL) (Eclipse Foundation,
2024). ATL is “a model transformation language as a combination of declarative and imperative language that provides mechanisms to produce a set of target models compliant with the specified metamodel, from a set of source models” (Jouault
et al.,
2008). A programme developed in ATL is composed of rules which define the transformation of the elements of the input metamodel.
The first step of the model transformation is to decide which metamodel will correspond to the input and which one will be the output. In this model transformation we have employed as the input the Q-KDM (i.e. the KDM extension already presented as input, as explained in Section 3.1), and the ECORE metamodel for UML version 2.5.1, which defines the abstract syntax of UML, as the output. This ECORE metamodel can be seen in the Github repository of this technique and contains the UML model description compliant with the Essential Meta Object Facility (EMOF) metamodel. The EMOF “provides a straightforward framework for mapping MOF models to implementations such as JMI and XMI for simple metamodels” (Group,
2019). The UML metamodel is used as is, although a quantum UML profile as depicted in Pérez-Castillo
et al. (
2021a) is used for modelling quantum circuits as UML activity diagrams (cf. Section
3.2).
Once the input and output metamodels have been established, the ATL transformation rules are designed. These rules identify the quantum entities and define their transformation into the previously assigned elements of the UML metamodel. The equivalences and definitions of the Quantum UML Profile have been previously explained in Section
3.2. This identification of the elements with the metamodel is essential for the transformation.
During the definition of the different rules for the transformation, a descending order was followed, i.e. the rules for transforming those elements that group the rest were defined first (e.g. the definition of a method groups a set of atomic operations and, at the same time, the definition of a class can group several methods). In the case of KDM, the root element is the Segment and the more atomic element is the actionRelation, which specifies on which qubit a quantum gate has acted and its flow control.
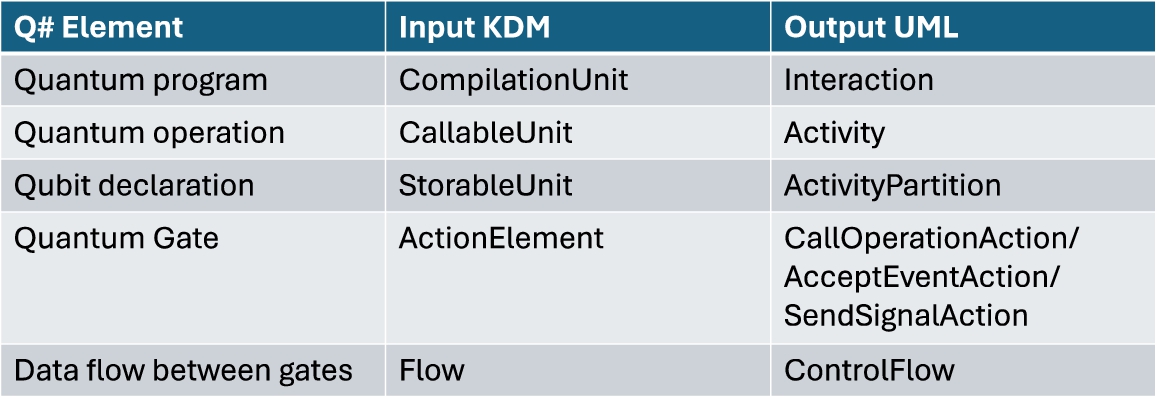
Table
2 shows a short summary of the transformations that have been carried out, where the Q# element that has been analysed is on the left-hand side, its KDM modelling is in the central column, and its UML transformation is on the right-hand side.
Table 2
Summary of the transformation accomplished.
4.1.1 Quantum Programme Rules
The CompilationUnit element is employed in KDM to represent the full quantum programme. This is due to the fact that the CompilationUnit defines a container of all the programme elements. This element has therefore been transformed into Interaction since this last element groups all the elements or actions that share a common objective.
A simplified and graphic example of this transformation can be seen in Fig.
7. On the left-hand side of the image, the input model defined in KDM is located that contains a
CompilationUnit and a qubit nested inside (with the attribute “name”) and a
CallableUnit (which has the attribute “name” that defines the name of such operation). In the middle of the image there is the transformation programme with the
CompUnit2Interaction rule, where it is defined that the name of the output Interaction will be the same as the
CompilationUnit found in the input. Furthermore, in the same rule it is defined through OCL that every
codeElement in the input which has the type of
CallableUnit will be transformed into
ownedBehavior with the same name.
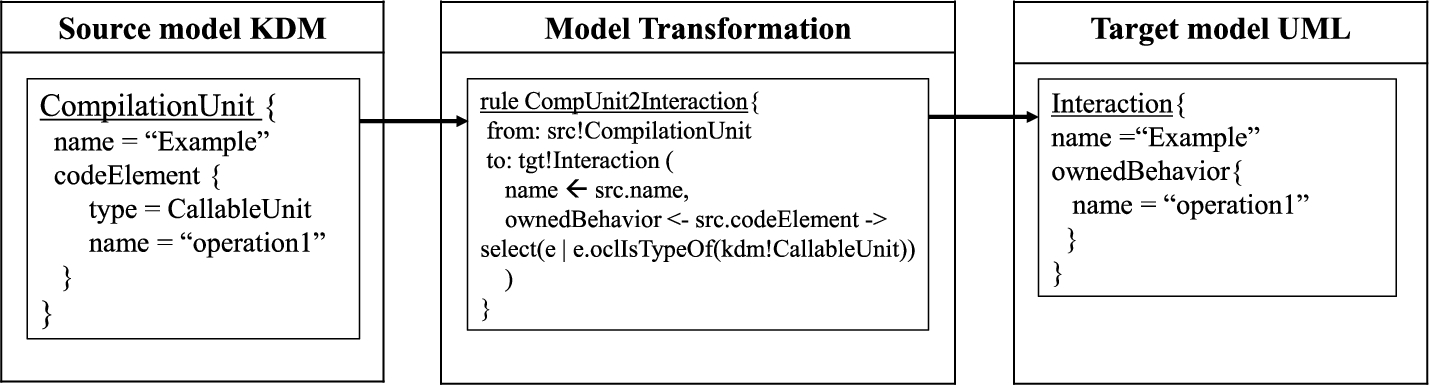
Fig. 7
Quantum programme rule transformation.
4.1.2 Qubit Declaration Rules
The
StorableUnit type was employed for defining the qubits in the Q-KDM model. This is because, looking at it from another perspective, a qubit is nothing more than a variable which stores a value. However, for the Q-UML model, those
StorableUnits, as mentioned before, have been transformed to
ActivityPartition because the qubits in the final model will be represented as horizontal lines on which the quantum gates (such as IBM Q Experience (IBM,
2024) or Quirk (Gidney,
2019)) can be placed, thus representing that a certain quantum gate acts on a certain qubit.
The rule used to transform the
StorableUnit into
ActivityPartition can be seen in Fig.
8, where the
ActivityPartition simply has the same “name” attribute as the
StorableUnit.

Fig. 8
StorableUnit to ActivityPartition.
4.1.3 Quantum Gates and Execution Flow
All the quantum gates have been identified as ActionElement in Q-KDM since this kind of element can be used whenever an element performs any action on other element (like qubits under those gates are applied). Nevertheless, UML is provided with several elements in a way that allows for a more precise definition of the actions, i.e. depending on the quantum gate employed in the algorithm, one or another element will be used.
The whole
Hadamard’s gate transformation to Q-UML can be seen in Fig.
9. As it affects only the state of a qubit, it has been defined as
CallOperationAction in UML. This is because
CallOperationAction transmits an operation call request to a target object. On the left-hand side of the image one can see the gate represented in Q-KDM with two attributes (“
name” and “
id”) and three children (one “
source” and two “
actionRelation”). The
actionRelation element of type
Addresses points the “
to” attribute to the qubit on which the quantum gate is applied and to the gate that acts (i.e. itself). The
actionRelation element of type
Flow specifies the flow that the information follows, where the “
to” attribute points to the quantum entity that precedes it.
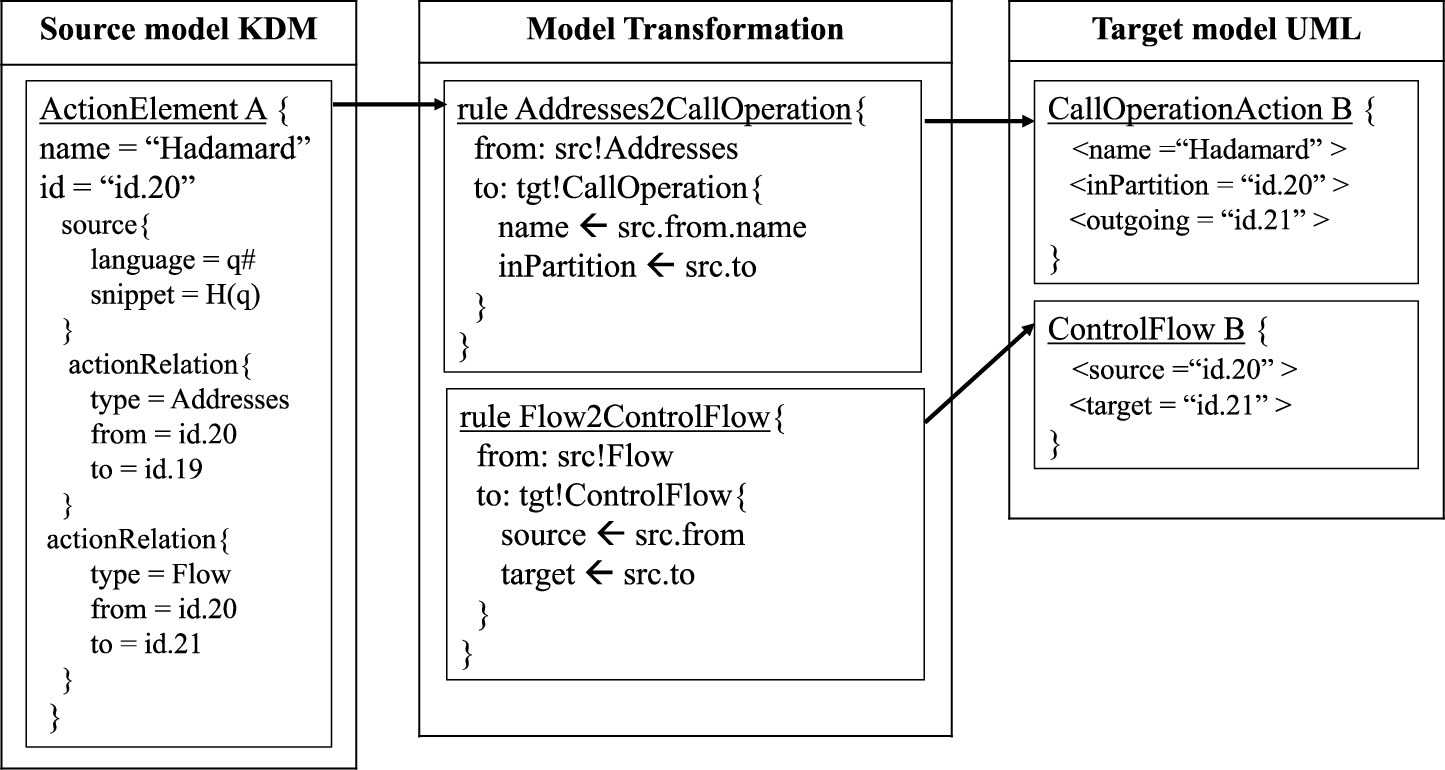
Fig. 9
StorableUnit to ActivityPartition.
In the middle of Fig.
9 one can see the two rules necessary for the transformation. The upper part shows the rule for the transformation of Address to
CallOperationAction (to make it simpler, the methods that check whether such quantum gate is
Hadamard or not have been omitted), where the attributes of the output model defined in that rule are “
name” and “
inPartition”. The “
name” attribute specifies the name of the gate and is taken from the element pointed to by its “
from” attribute, and the “
inPartition” attribute defines on which qubit the quantum gate is acting, which, as mentioned before, explains why the “
to” attribute is used. In the lower middle part of the image, one can see the rule to transform the
actionRelation from
Flow to
ControlFlow type. The standard mechanism of UML for specifying the flow of the information is by means of
ControlFlow, therefore this transformation is one of the most important. As a result, in order to define the target and source of the flow of the information, the “
to” and “
from” attributes of
Flow were employed.
Finally, on the right-hand side of Fig.
9 one can see how the transformation ends with
CallOperationAction and
ControlFlow – each one with its corresponding attributes. Thanks to the bidirectionality of the transformation, the outgoing attribute is set automatically in
CallOperationAction due to the target attribute in
ControlFlow. The real Q-UML representation of the
Hadamard’s gate can be seen in Fig.
10.

Fig. 10
StorableUnit to ActivityPartition transformation.
4.2 Activity Diagram Generation
As explained previously, the UML standard is defined as a metamodel compliant with MOF (Meta-Object Facility). Every metamodel has two separate but related syntax: “i) an abstract syntax that describes the concepts in the language, their characteristics and interrelationships; and ii) a concrete syntax that defines the specific textual or graphical notations required for the abstract elements” (Pérez-Castillo
et al.,
2021a). Although the ATL model transformation can generate UML models from KDM, these UML models are the abstract syntax representation. Whilst a second transformation from the abstract to the concrete syntax representation allow to visualize the UML diagrams in a graphical way.
To carry out the graphical representation, several tools that perform the same process of drawing an activity diagram based on a model were studied. Among the possible tools, this work considered Visual Paradigm (Paradigm,
2024) and
jsUML2 (Romero,
2011).
jsUML2 was chosen because it is an open-source library and it also has support for designing use case, classes, and activity diagrams, among others, and has support for JavaScript-based web applications. This entails the advantage of a better integration into a REST API solution.
Although the quantum algorithms modelled with the Quantum UML Profile were valid according to the standard, in order to represent them graphically with jsUML2, it was necessary to modify the models so that the library would generate activity diagrams. Among the different types of diagrams that jsUML2 allows to design, activity diagrams were chosen for modelling quantum programmes according to the UML extension. This is because the UML models built with the UML Profile belong to the abstract syntax specification of UML activity diagrams.
Activity diagrams work can be seen in a similar way to the quantum circuits developed with platforms such as IBM Quantum Experience or Quirk. The results of the definition of a quantum programme named “TeleportationSample.qs” can be seen in Fig.
11.

Fig. 11
Quantum programme UML definition.
Figure
12 shows the adaptation carried out, where the modification can be seen. There are no more headers (from line 1 to line 5 in Fig.
11), and attributes such as “x”, “y”, “width” or “height” appear, which define the visual attributes of the components of the diagrams.

Fig. 12
Activity programme adaptation.
Afterwards, the definition of the operations (whose analogues are the traditional methods) and the qubits in the metamodel are carried out, as shown in Fig.
13. In line 1, we can see the operation is declared with the type “
uml:Activity”, and in line 2, the qubit is declared with the type “
uml:ActivityPartition”. The latter type will cause each qubit to be represented by horizontal lines.
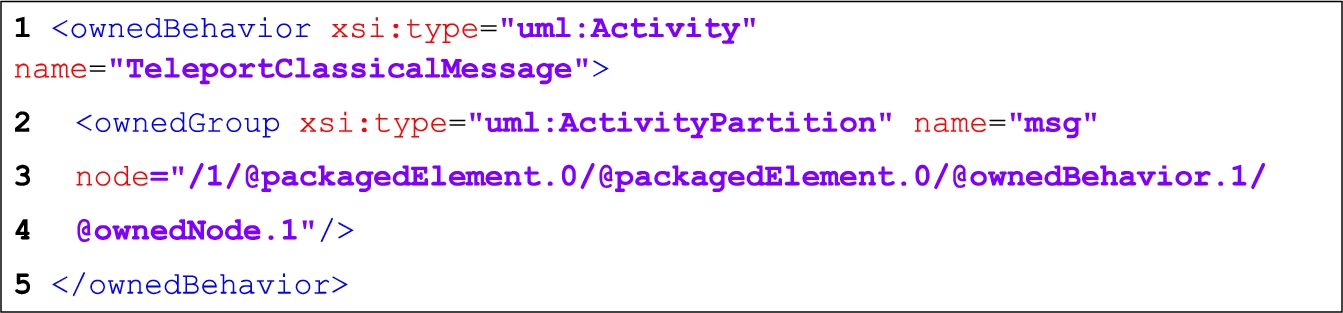
Fig. 13
Programme operation and qubit declaration.
If we go back to Fig.
1, we can get an idea of how we want to visualize the qubits, where each qubit used in the algorithm corresponds to a line and the quantum gates placed above it indicate the operation that has been performed on each one. Each operation will be represented by an “
UMLActivity” (line 1 in Fig.
14) where the different elements of the circuit, including the qubits (from line 5 to 16 in Fig.
14), will be placed inside. The representation of the qubits with the
jsUML2 library is done with two components, with line 5 of Fig.
14 showing the main component and each line (i.e. each qubit declared in the operation) being specified by the type “
Swimlane” (line 9), inside of which there will be all the quantum gates that will operate on the qubit in question.
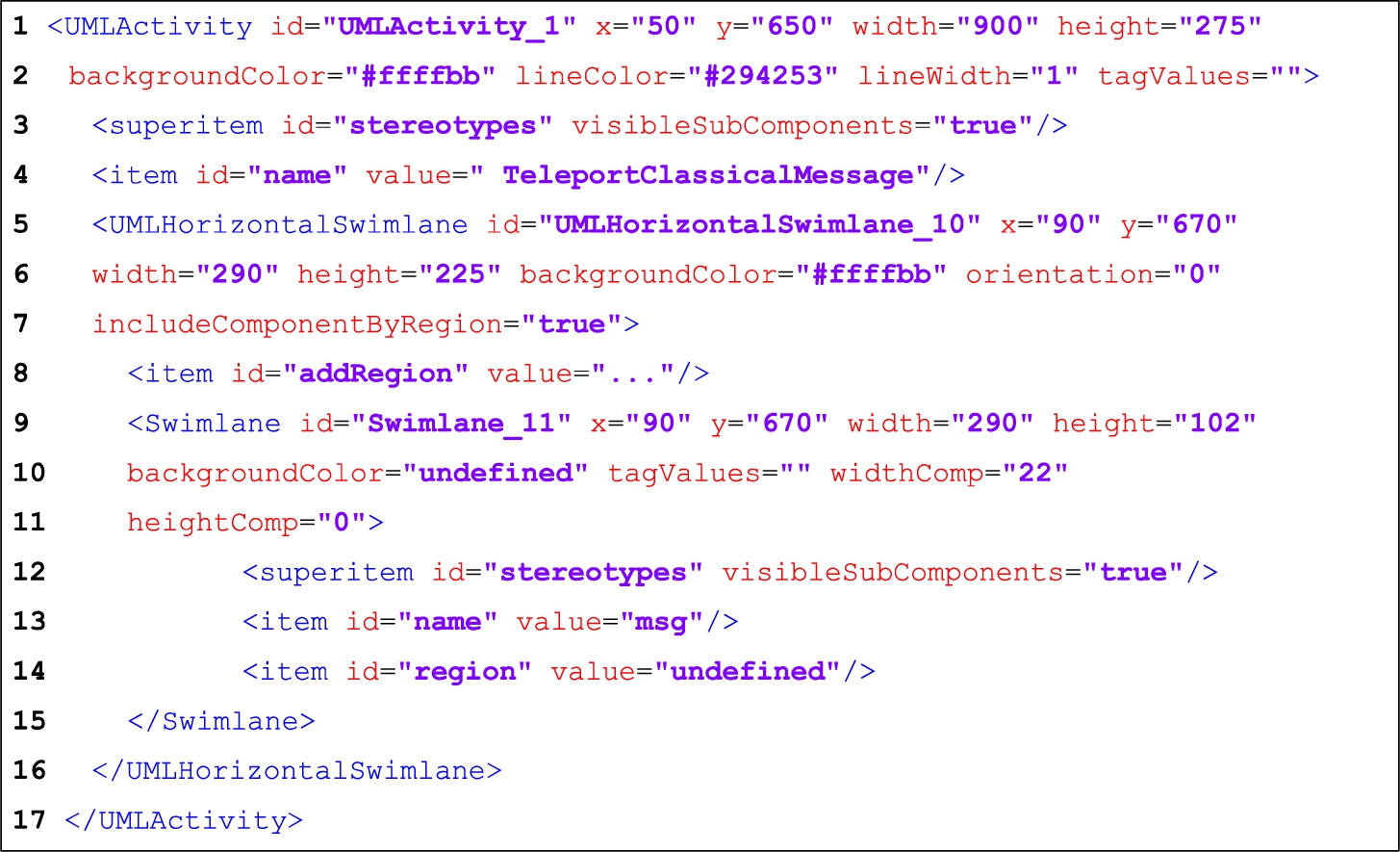
Fig. 14
Complete representation of an operation and two qubits declaration.
Next, a graphical representation of an activity diagram will be presented. For this, the teleportation algorithm will be used. The Q-KDM model generated from QRev, as well as the The Q-UML obtained from the transformation, can be seen in Jimenez-Navajas (
2023). The resulting image of the circuit can be seen in Fig.
15, where the three operations can be found (Teleport, TeleportClassicalMessage and TeleportRandomMessage) and each of the gates are located on the “
Swimlane” which corresponds to the relevant qubit, including their corresponding stereotypes as defined in the Quantum UML Profile.
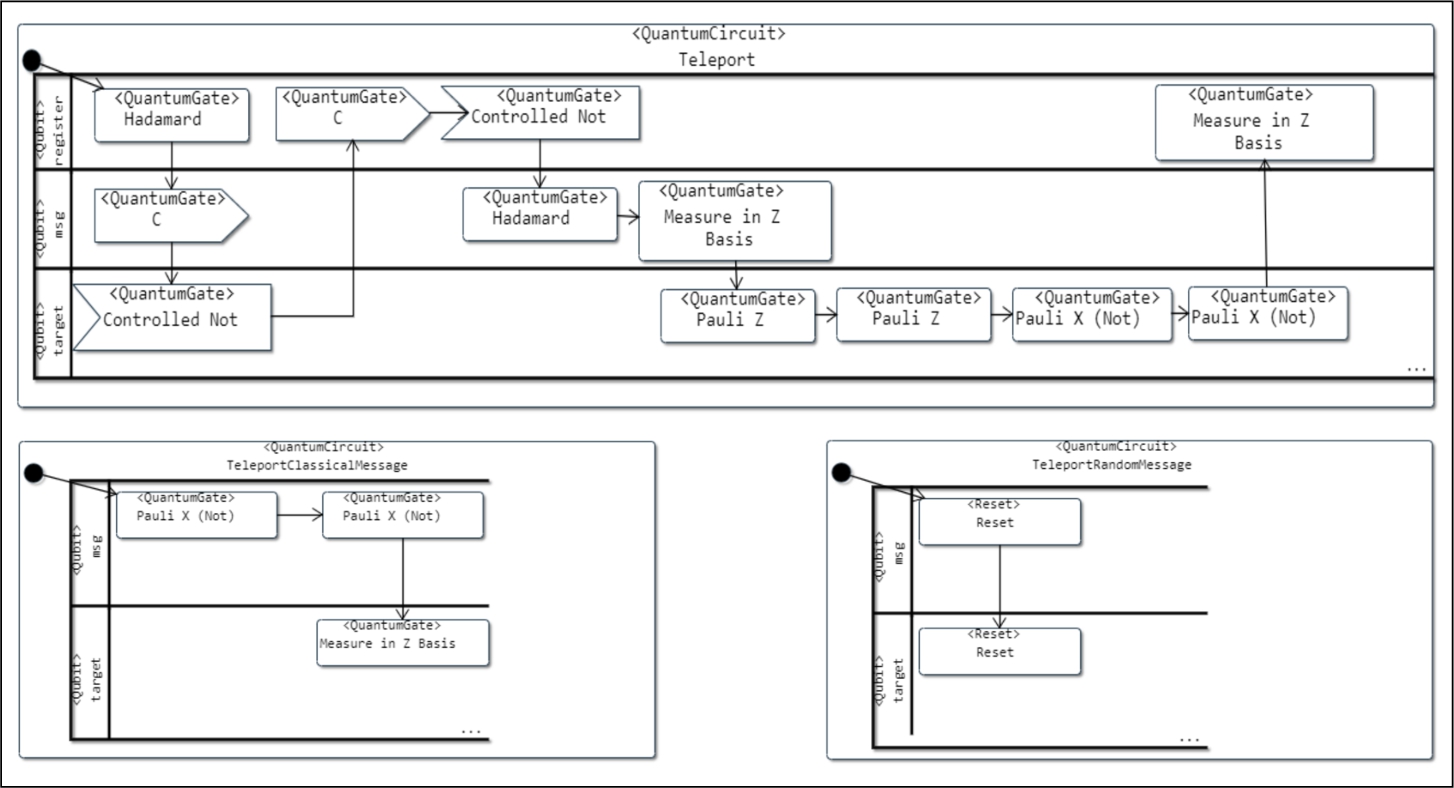
Fig. 15
Quantum Teleportation Algorithm.
5 Case Study
This section will present a multi-case study to validate the KDM-to-UML transformation proposed in the previous section and support the research question of this paper. Section
5.1 depicts how the case study has been designed. Section
5.2 shows the answers obtained from the research questions. Finally, Section
5.3 describes the evaluation of the validity of the results obtained in order to answer the research questions.
5.1 Case Study Design
This case study has been designed and conducted following the protocol proposed by Runeson and Höst (
2009). Therefore, the following subsections have been divided in accordance with this protocol.
5.1.1 Rationale and Objectives
As explained previously, companies that could benefit from quantum computing will eventually have to evolve their information systems towards hybrid information systems. The literature in this field suggests that software reengineering can help in this endeavour, and, for this reason, an adaptation called “Quantum Software Reengineering” was created. In this context, the restructuring phase is of great importance as organizations will be able to design their information systems using UML diagrams generated from classical information systems together with UML diagrams generated from quantum programmes.
The specific objectives of this case study are to determine whether it is possible to generate (i) non-complex UML models, i.e. which are easy to understand and modify, (ii) with enough expressiveness, and (iii) to check whether it is possible to transform KDM into UML in a linear time. The main research hypothesis is that if those three conditions are achieved, then the proposed model transformation can be used for the automation of software modernization of hybrid information systems.
5.1.2 Research Questions
This study defines three research questions. Firstly, RQ1 is related to the complexity of the UML models. Several studies have demonstrated that complexity is related to understandability and modifiability of outgoing models (Iacob
et al.,
2018; Cruz-Lemus
et al.,
2010). This fact is important since UML models, obtained through a model transformation, might have to be modified to refine them and complete them with missing elements. Also, a low complexity contributes to a better understanding, which is important in this context of modernization of hybrid information systems since it might be not only addressed by software engineers, but also by professionals outside software modelling (such as physicists and mathematicians experts in quantum computing). Secondly, RQ2 is related to the expressiveness of the output model and is introduced in this research as the ratio of input models that are eventually transformed into output elements. Finally, RQ3 is related to the efficiency of the model transformation. This focuses on scalability as regards the size of the input models to thus demonstrate its applicability even to larger systems. This is because we do not have benchmarks of similar model transformations to compare the transformation time:
-
• RQ1. How is the complexity of the UML models generated by the model transformation?
-
• RQ2. How expressive are the UML models generated by the model transformation?
-
• RQ3. How scalable is the model transformation for larger models?
5.1.3 Concepts and Measures
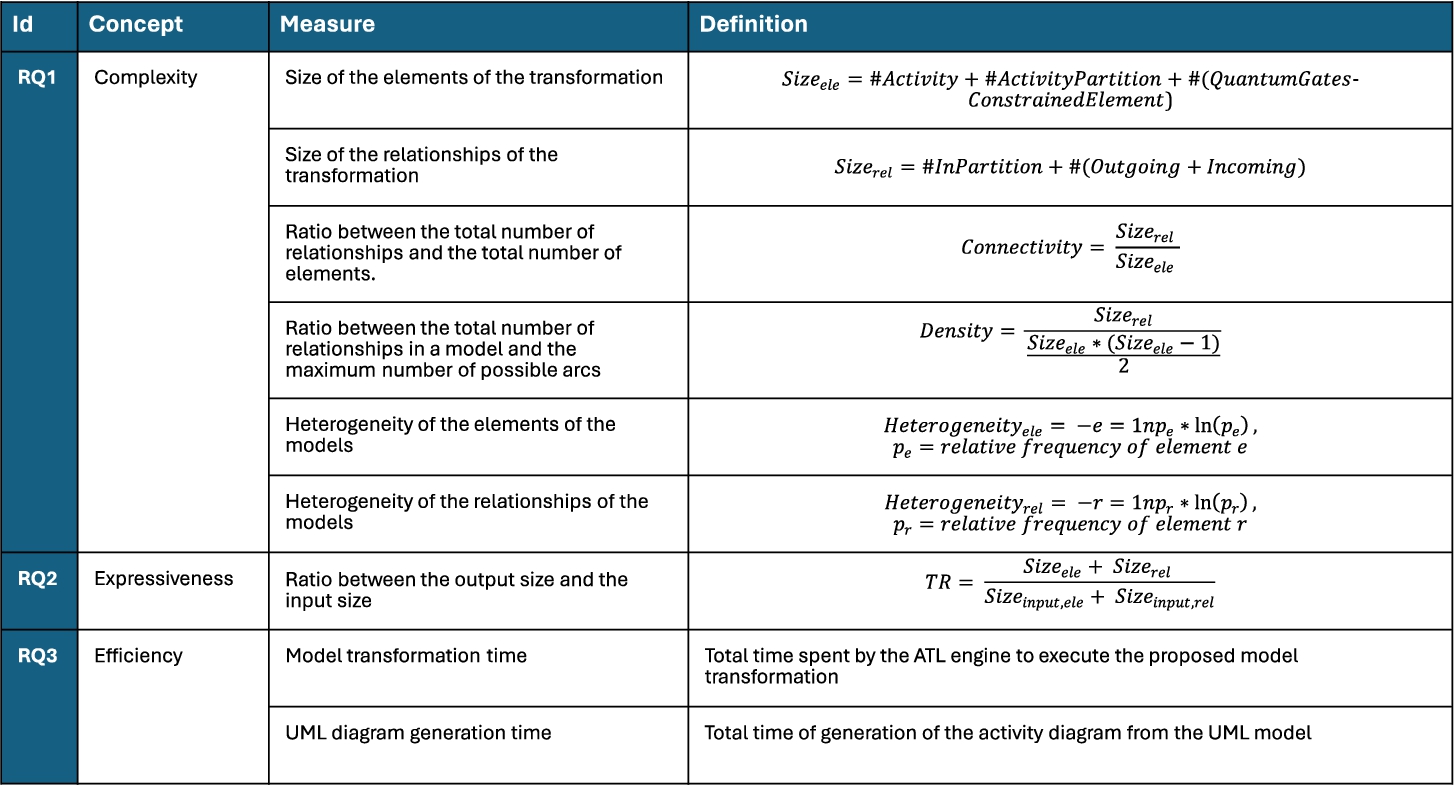
In this case study, several measures have been employed to answer the research questions previously contemplated and to obtain the correct conclusions. Table
3 provides a summary of the study variables, indicating for each one: (i) the research question that it will help to answer, (ii) the concept that will be measured, (iii) a short definition (or formula) of the variable involved, (iv) the scale type, and (v) the range definition for all the possible values.
The independent variable of the case under study is the output UML model generated from each selected system, which is the unit of analysis. Regarding RQ1, the case study considers various variables that are directly related to complexity. As Genero
et al. (
2004) stated, there is a lack in the literature for validating metrics for UML activity diagrams. The only paper which proposes some metrics for activity diagrams is Muñoz
et al. (
2010) but this is related to the modelling of processes related to data warehouses. So, for evaluating the output models we have had to consider measures used in similar output models for assessing complexity (Iacob
et al.,
2018; Schütz
et al.,
2013; Caivano
et al.,
2018; Pérez-Castillo
et al.,
2022b), as well as those measures proposed by Cruz-Lemus
et al. (
2021) for measuring the understandability of quantum circuits, which is in fact what the UML activity diagram represents.
-
• Size. This is defined as the set of elements or relationships in the output UML model. It is distinguished as between elements (
${\textit{Size}_{\textit{ele}}}$) and relationships (
${\textit{Size}_{\textit{rel}}}$). Size is an instrumental measure, but it is still associated with complexity (Iacob
et al.,
2018).
-
• Connectivity. This is the ratio between the total number of relationships and the total number of elements.
-
• Density. This represents the ratio between the total number of relationships in a model and the maximum number of possible arcs (considering UML models as directed graphs). Both connectivity and density affect the complexity (and therefore the understandability and maintainability) in a negative manner (Caivano
et al.,
2018). This means that lower connectivity and density values lead to UML models which are more understandable and modifiable, thanks to a lower level of intricacy.
-
• Heterogeneity (entropy). This concept is related to the measure of relationships in the UML model. It measures the diversity of the kind of elements or relationships used in a certain UML model. Heterogeneity is directly related to complexity (Caivano
et al.,
2018; Schütz
et al.,
2013).
where
${p_{e}}$ corresponds to the relative frequency of element
e, and
${p_{r}}$ corresponds to the relative frequency of relation
r.
With regard to RQ2, this evaluates the expressiveness that relates the output and input model. For this purpose, the measurable concept is the amount of class elements in the input model that are eventually transformed into one of the possible elements in the UML model. This seeks to provide a numeric value for the number of elements in the input models that were useful, and which were therefore transformed into some elements in the output model. In summary, having this research question in mind, it is expected to evaluate the amount of embedded knowledge that can be brought from the input model to the output model. So, the input elements that the model transformation is able to identify and transform into the target model.
-
• Transformation ratio. This is defined as the ratio between the output size and the input size for both elements and relationships. So, for the transformation ratio of elements it is evaluated how many elements from the input are transformed in the output. This is the same for the transformation ratio of relationships, calculated based on the number of relationships in the input and the output.
-
– ${\textit{Size}_{\textit{input},\textit{ele}}}$ is the sum of the number of CallableUnit which represents a unit that can be called, such as procedures or functions (in this case, Q#’s operations), the number of ParameterUnit (the qubits sent through a parameter of the operation), the number of StorableUnits which depicts the qubits declared in the CallableUnit, and the number of ActionElements, which are the number of quantum gates.
-
– ${\textit{Size}_{\textit{input},\textit{rel}}}$ is the sum of the number of Reads, which represent the number of times that a “NOT” gate is applied onto another quantum gate, the number of Addresses, which depict the number of times a quantum gate is applied to a qubit (that can be a
ParameterUnit or a
StorableUnit), and the number of Flow, which represents the flow of the information.
Finally, to assess RQ3, related to the study of the scalability, we consider the model transformation time to be analysed in comparison with
${\textit{Size}_{\textit{input}}}$.
-
• Model transformation time is the total time spent by the ATL engine to execute the proposed model transformation and generate the UML model.
-
• UML diagram generation time is the total time of generation of the activity diagram from the UML model.
Table 3
Summary of the variables.
5.1.4 Case Selection
To evaluate the performance of the transformation of KDM models to UML and the generation of activity diagrams from the previously generated models, it is necessary to define criteria for choosing the quantum programmes that will be used for the evaluation of this project. Table
4 shows the criteria chosen to select the cases.
Table 4
Criteria for case selection.

Criterion C1 is chosen due to the fact that this paper can be considered a continuation of QRev (Pérez-Castillo
et al.,
2022a). Since the tool presented was initially designed for analysing Q# programmes, the programmes employed for this case study were developed in Q#. In addition, together with OpenQASM3 and OpenQASM2, Q# is the language with the largest number of quantum algorithms available in an open-source manner. Finally, the last reason for selecting this criterion is that the University of Castilla-La Mancha is a Curriculum Partner in the Microsoft Quantum Network, being as such the first Spanish university to belong to it (Microsoft,
2018). Criterion C2 was established because normally in Q# projects there are at least two Q# files, where the first file usually has no quantum components and acts as an entry point with C# files (or any other language but developed in the classical paradigm), and the second file has all the necessary quantum functions implemented. This criterion is used to sieve the first files mentioned above so as not to generate empty activity diagrams (as they do not have quantum components, but their generation is correct) and so that their statistics can affect the metrics obtained. Finally, criterion C3 was chosen because, as mentioned above, this paper is a continuation of QRev and to generate a model transformation in this case it was necessary to have KDM models as input.
After applying the selection of cases based on the criteria mentioned in the previous section, 17 programmes from the Microsoft Quantum Repository in Github were selected. Table
5 shows the names of the chosen algorithms, the lines of code, and their link in the Github repository.
5.1.5 Case Study Protocol, Data Storage and Analysis
The study protocol defines how the selected cases were analysed and how the derived data was collected and eventually analysed.
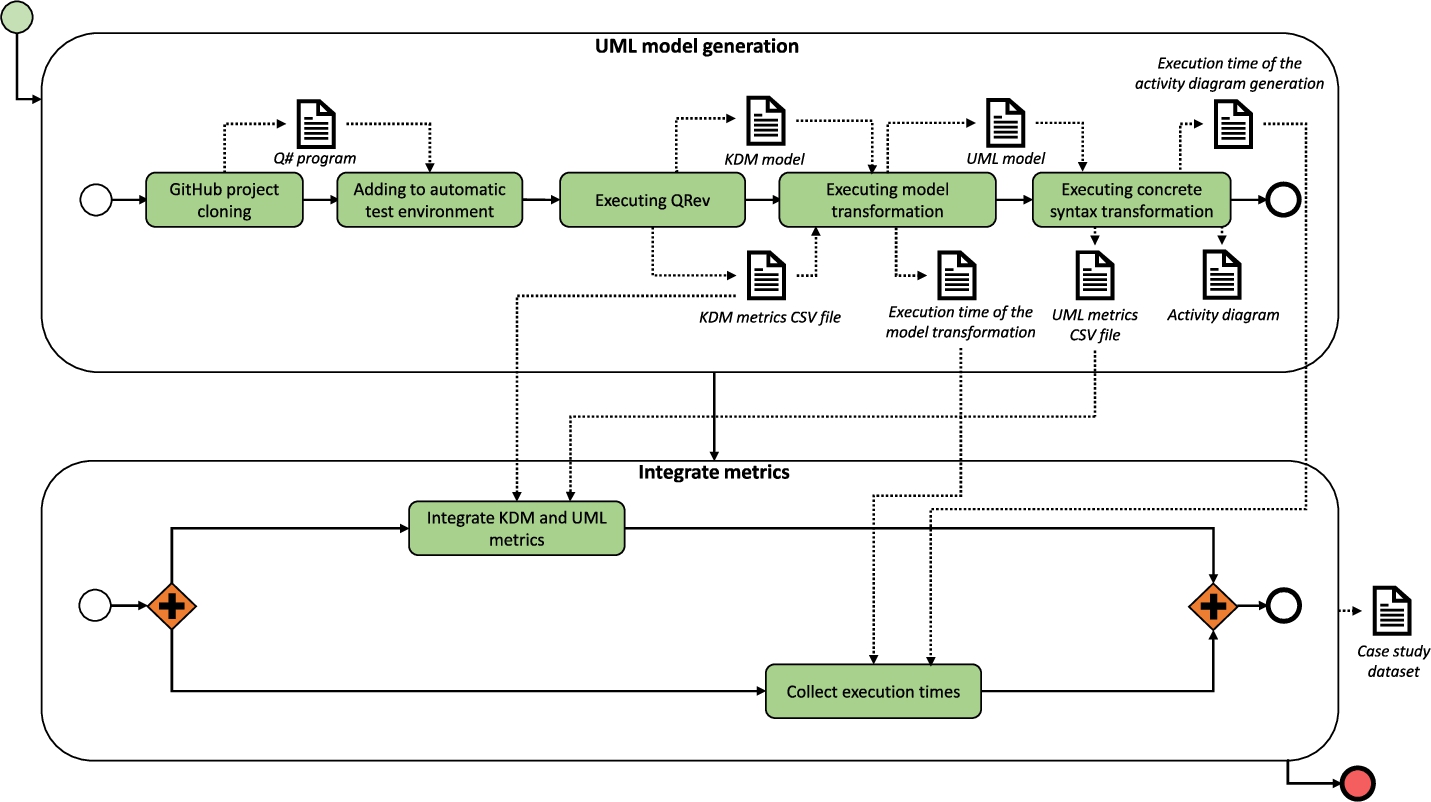
Fig. 16
Case study protocol.
Figure
16 shows the case study protocol which mainly consists in two phases with various steps. The first phase (the topside of Fig.
16) compromises the UML model transformation and the activity diagram generation. Within this phase the steps are: (i) cloning/downloading the Q# programmes from Microsoft’s GitHub repository (check final repository in Jimenez-Navajas (
2023)); (ii) adding them to the automatic test environment; (iii) executing QRev in order to have the most up-to-date KDM models possible; (iv) generating the UML model from the KDM model by means of the model transformation, and (v) transforming the UML model into activity diagrams based on the concrete syntax of the jsUML2-based tool. This phase generates the following outputs:
-
• The KDM model generated from reverse engineering the Q# programme extracted from the Microsoft’s GitHub repository.
-
• A file containing metrics from the KDM model. For this case study, a Java script was developed to generate metrics, such as the number of certain KDM elements, which will later help us for the comparison between the KDM and the UML model. The metrics generated for each programme are then integrated into the global case study dataset.
-
• The UML model generated from the model transformation of the KDM model accomplished with ATL.
-
• The execution time for the model transformation.
-
• A file containing metrics from the UML model. As well as with the metrics extracted from the KDM model, this file was obtained from a Java script. The metrics generated for each programme are then integrated into the global case study dataset.
-
• The activity diagram generated based on the concrete syntax of the jsUML2.
-
• The execution time for the generation of the activity diagram.
The second phase of the case study protocol (the bottom side of Fig.
16) concerns the collection of the information and its integration in the whole dataset from the metrics obtained in the previous phase. This last phase consists in two tasks:
-
• The integration into the common case study dataset and the comparison of the metrics obtained from the KDM and UML models.
-
• The collection of execution times from the model transformation and the activity diagram generation.
The main dataset containing the raw data of the case study and different models generated, as well as the script for the model transformation can be checked in Jimenez-Navajas (
2023). The Github’s repository of the technique can be seen in Jiménez-Navajas
et al. (
2024a).
Table 6
Dataset collected for the case study.

To complete the whole dataset, the application of the tool was done on a laptop with an i7 10510U with 2.30 GHz, 16 GB of RAM and running on an SSD with Windows
$11\times 64$ bits. Table
6 shows the whole dataset completed after the model transformation and the visual activity diagram generation employing the 17 cases selected. The first rows of Table
6 provide information about the input KDM models that were generated from QRev from the Q# quantum code. Then, the model transformation time in seconds is provided. The following set of rows provides a number of elements and relationships in the outgoing UML quantum model. Finally, the bottom rows provide the three variables to be analysed: complexity, expressiveness, and scalability. Furthermore, Table
6 also provides aggregated values for every row with minimum, maximum, mean, and standard deviation.
To achieve the most accurate conclusions from the analysis of the data thus obtained, two main methods of analysis were used for each research question:
-
• Descriptive statistics: these were used to analyse the numerical data obtained.
-
– RQ1 and RQ2: Descriptive statistics were employed for checking that the expected results of measured values after the application of the tool were acceptable.
-
– RQ3: The descriptive statistics were used in this research question mainly for evaluating the scalability through the variables related with size and time.
-
• Regression model: with this analysis the relationship between two variables is evaluated, where one variable is considered the dependent variable and the other as the independent variable. Then, the correlation coefficient is computed with the Pearson’s rank correlation test.
5.2 Analysis and Interpretation
This section presents the results of the analysis carried out for each research question, along with the main insights derived. The following subsections attempt to answer each research question.
5.2.1 RQ1. Complexity of the Output UML Models
In order to evaluate the complexity of the generated UML models, we first evaluated the size of the output models. These models’ size varies from 6 to 65 elements, and from 3 to 81 relationships (see Table
6). It can be noticed that the size of the output models does not provide valuable information to understand the complexity of the models since it depends on the size of the input model. Thus, these values are aligned with the input size.
Subsequently, the values obtained from the heterogeneity of the output models were assessed. These are, on average, 1.03 and 1.09 for elements and relationships, respectively (see Table
6). These values being close to 1.0 means that the design entropy is under control, which suggests that the complexity of the output UML models is appropriate. Figure
17 summarizes results for connectivity and density of the generated UML models. Connectivity is on average 1.17, while density is only 0.17. Low density values are correct since we can consider the output model with limited complexity, while a greater connectivity is desirable. Anyways, in some cases connectivity is lower than expected, which suggests that some relationships were missing during the model transformation.
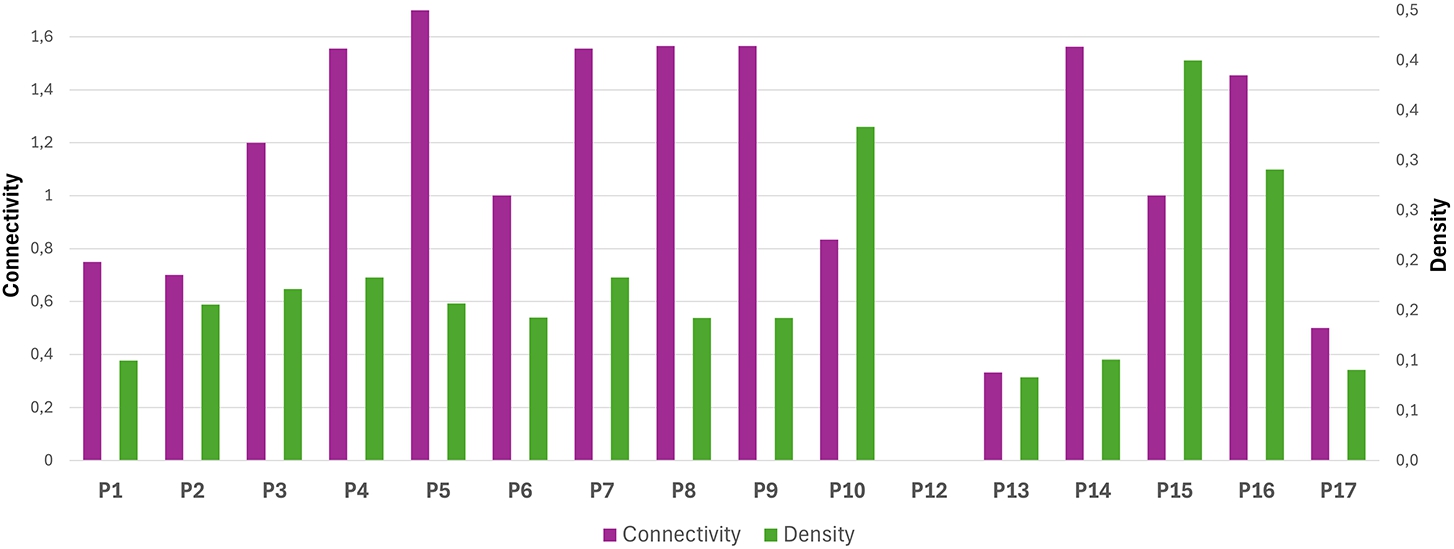
Fig. 17
Bar plot of the connectivity and density of the models.
Cases P10 and P15 are peculiar, since they have a very high density but a lower connectivity. This may be due to the fact that the elements generated from the transformation are independent of each other. For example, for P10 we can see that it has the same number of CallableUnit (methods) as ActionElement (quantum gates), but the methods do not call each other, but are called from an external programme. Other cases like P5 present a higher connectivity, which implies that the representation of the number of relations of the KDM model is in accordance with the number of quantum gates represented. So, a lower value could tell us that the transformation does not correctly follow the information flow.
Applying a more qualitative analysis, a complexity that depends on the size of a model and an appropriate level of modularity mean that the target UML models are suitable for modernizing hybrid information systems. Highly modularized and structured models, first, contribute to get a faster and better comprehension of the high-level design of the software and, second, it facilitates the improvement and addition of new functionalities during the restructuring phase. These qualitative insights can be noted analysing P1, a highly modularized case. P1 is the one with the most heterogeneity of elements since it can be observed that the number of
Activity,
ActivityPartition, and
OwnedNodes is very similar. The same happens for case P9, where the number of
InPartition,
Outgoing, and
Incoming relationships is very close. Having heterogeneity close to 1 implies that there is no big difference between the number of elements, which may mean that the code is well modularized (in the case of heterogeneity of elements) and structured. Figure
18 shows the representation of P1, one of the quantum programme with the highest degree of heterogeneity of elements (1.07 over 1.10). A total of 7 functions can be seen in this programme, demonstrating that this programme has a high level of modularization and comprehensibility. However, P12 is the case with less heterogeneity of elements (0.85). In this programme it can be seen how in the same method a large number of quantum operations on different qubits are condensed into a few functions. This could imply, among other things, difficulties in the maintenance and scalability of the software. This gives us to understand that obtaining an average element heterogeneity degree of 1.03 is optimal.
Fig. 18
Bar plot of the connectivity and density of the models.
In summary, answering to RQ1 with regards to the complexity of the output UML models, these results suggest that the complexity of the generated models is affordable, as the lower connectivity and density values lead to UML models which are more understandable and modifiable, thanks to a lower level of intricacy.
5.2.2 RQ2. Expresiveness of the Output UML Models
To assess the expressiveness of the generated UML models, the transformation ratio measure has been used. This will help us to answer whether the UML and KDM models express the same thing. Figure
19 shows a bar chart where the transformation ratio of the elements and relationships for each of the cases.
With respect to the transformation ratio of elements (blue bars in Fig.
19), it can be observed that values very close to 1 have been obtained (being the P14 case the one with the lowest transformation ratio with a value of 0.90). This indicates that most of the elements (functions, quantum gates and qubits) that were represented in KDM have been represented successfully in UML. However, if we look at the values obtained from the ratio transformation ratio (orange bars in Fig.
19), most elements exceed the ratio of 1.5. It might seem strange that the transformation ratio exceeds 1% in all cases. However, to answer RQ2, this is nevertheless a reliable indication as UML generally needs more metamodel elements to express the same information as KDM.
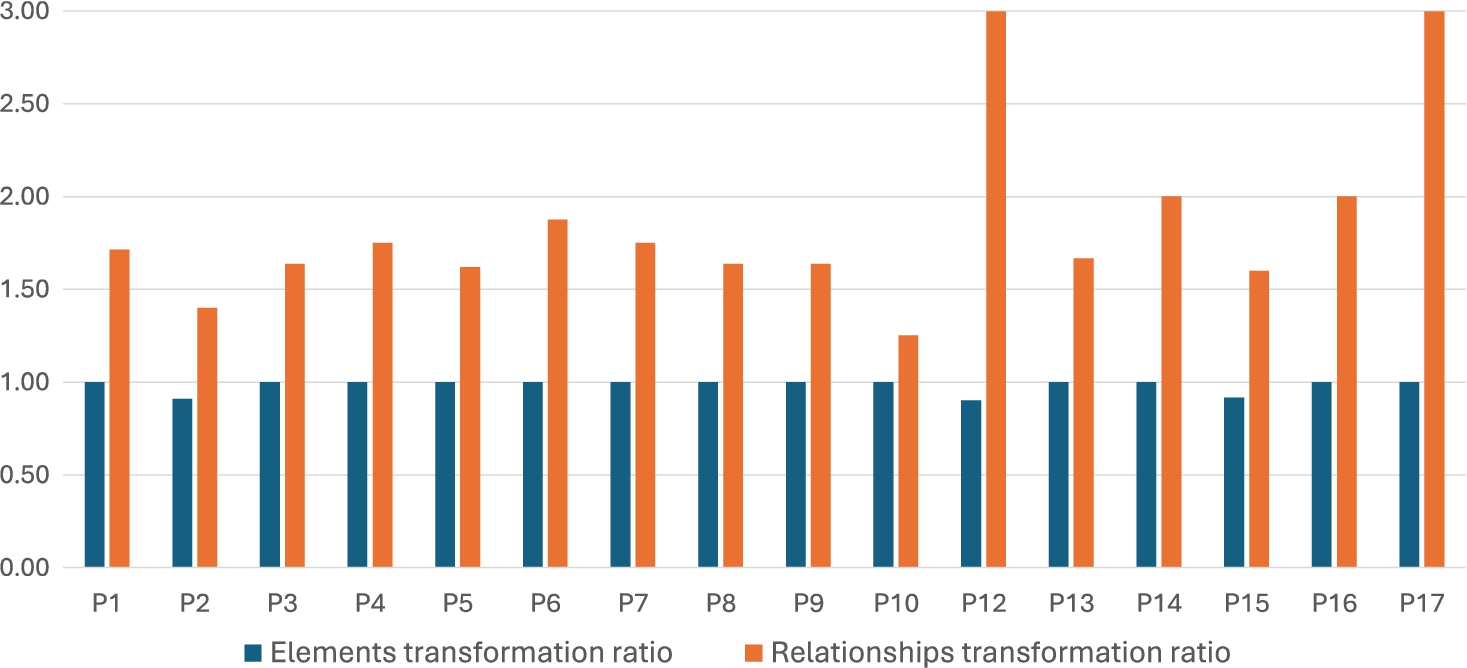
Fig. 19
Bar chart of the transformation ratio.
One reason why the transformation ratio is so high is due to the transformation of the
Controlled Not quantum gates. Figure
20 shows the declaration of a
Controlled Not quantum gate in KDM. This gate has two qubits as input and its function is to negate the state of the second qubit, depending on the state of the first qubit. Line 4 of Fig.
20 is used to represent which qubit is to be acted upon, and line 5 is used to determine which qubit is to be read. In addition, line 7 is used to indicate which is the flow of information, i.e. which is the next gate or component.

Fig. 20
CNOT gate representation in KDM.
Figure
21 illustrates how the same quantum gate would be represented in UML. First, we would need to declare the part that contains the attribute that reads the state of the qubit (line 6 to 11). Then, the part of the quantum gate that changes the state of the qubit is declared (line 1 to 5). As can be seen, both representations have the same
ownedNode label, which means that, in view of the numbers, one quantum gate is transformed into two quantum gates. There are several other similar examples.

Fig. 21
CNOT gate representation in UML.
Case P12 is a clear example of this. Figure
19 shows that P12 is the case with the highest transformation ratio of relationships. As explained before, to represent quantum gates in UML almost twice as many elements are needed than in KDM, so the number of relationships of the data flow also increases. Figure
22 shows a comparison between the method
applyOracleFromFunctionOnCleanTarget of the P12 case in KDM and UML through the Eclipse model viewer. In Fig.
22 A) there are represented in KDM a total of 4 quantum gates (one HY gate, two
Controlled Not and one
Hadamard gate). In Fig.
22 B) the same quantum gates are found, but with their respective transformation. As explained above, the
Controlled Not gate is represented by two elements in UML, where the first one indicates the reading of the qubit and the second one the action on the second qubit. Focusing only on the representations of quantum gates in the different metamodels of Fig.
22, in KDM there are 4 quantum gates while in UML there are 6. So the relationships needed to represent the new gates, in addition to the relationship which indicates the starting point of the data flow. All these factors lead to a higher level of relationships than the ones in the KDM model. Therefore, having a transformation ratio of elements higher than 1 is desirable to deduce that the expressivity of the output models with respect to the input is appropriate.
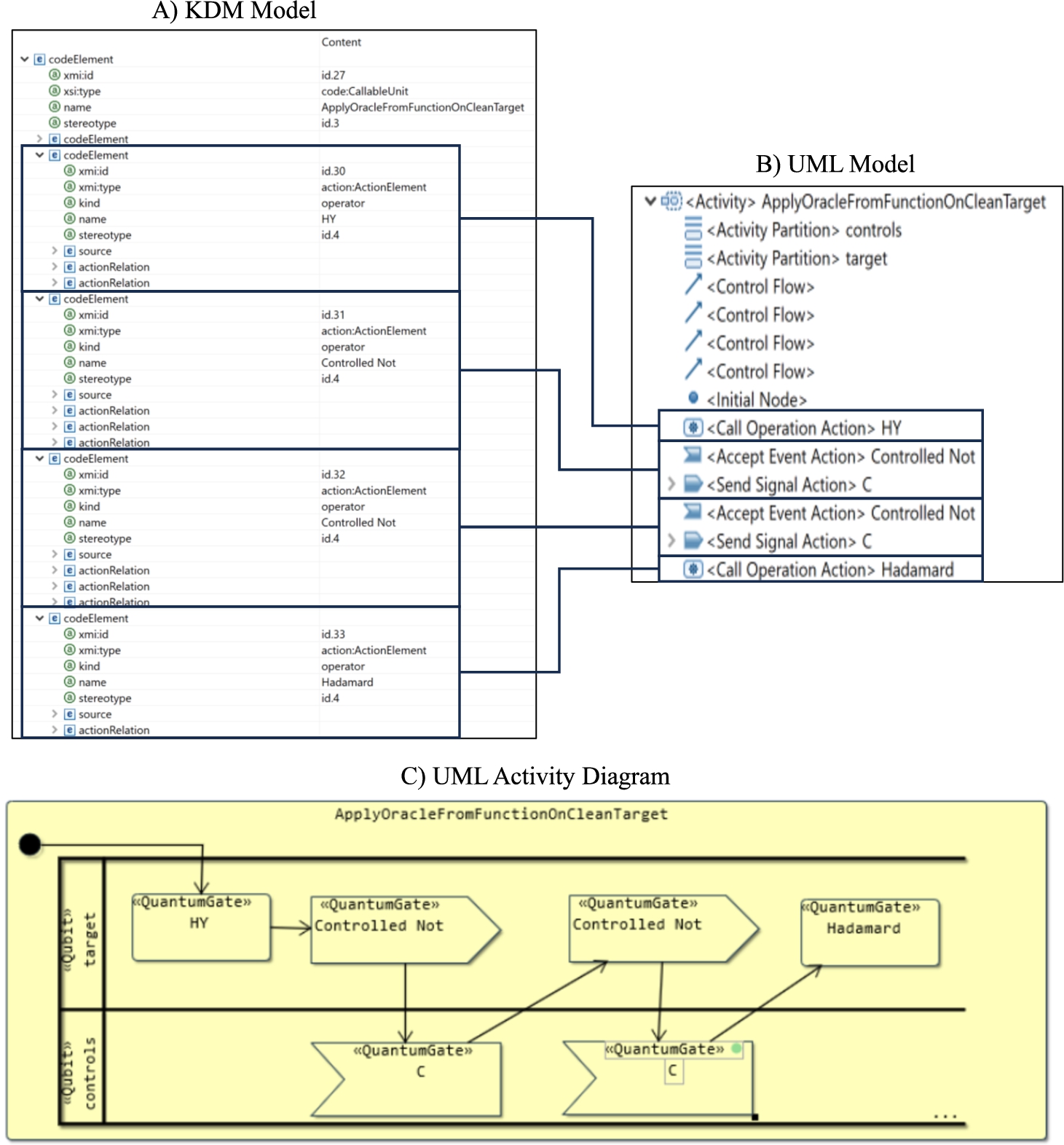
Fig. 22
Comparison between the method applyOracleFromFunctionOnCleanTarget in KDM and UML.
Figure
19 C) shows the activity diagram of the
applyOracleFromFunctionOnCleanTarget function. As explained previously, Controlled gates change the state of a qubit (in this case, target) if the value of the state of the other qubit (control) is equal to 1. In UML, it was decided to represent this gate with two elements:
AcceptEventAction and
SendSignalAction. This represents an extension in the semantics of the quantum circuit itself, since the UML element of type
SendSignalAction represents the evaluation of the state of the first qubit and the
AcceptEventAction element represents the change in the state of the second qubit according to the previous evaluation. This contribution of semantic value to the representation of quantum programmes affects the number of elements that are generated in the transformation.
Coming back to RQ2, the average transformation ratio of the elements is 0.93, if we include the case (P11) that could not be generated in UML, or 0.98, if we do not include it. Regarding the transformation ratio of the relationships, it is an average of 1.85. This is an acceptable value since, as explained above, the transformations of certain elements can be duplicated in UML, so the number of relationships increases, thus reaching a rate of 200%. In conclusion, answering to RQ2 which concerns how is the expressiveness of the UML models generated by the model transformation, it can be considered that, with about an average transformation ratio close to 2, the models can be considered with a reasonable expressiveness.
5.2.3 RQ3. Efficiency of the Tool
Finally, to answer what is the efficiency of the tool, several measures of the generation were taken. In absolute terms, the transformation spent between 0.8 and 1.49 seconds with an average time of 1.11 seconds for models that range between 12 and 92 elements in the KDM models. The input models are small. Hence, as we stated in the introduction, efficiency is primarily assessed in this study as the scalability of the model transformation, i.e. its capability to be applied to larger models without increasing the time exponentially. Therefore, Fig.
23 shows the scatter plot of the transformation time in seconds and the total size of both the input and the output model. Together with the scatter plot, the linear regression lines are visualized with the correlation coefficient. Both correlation values are high (close to 1), especially when considering the size of the UML model. This makes plausible the existence of a linear correlation between the size of the models and the transformation time. As a result, the answer for RQ3 is that the proposal is scalable for larger models, as the tool might have a good performance regarding the generation time for larger models.
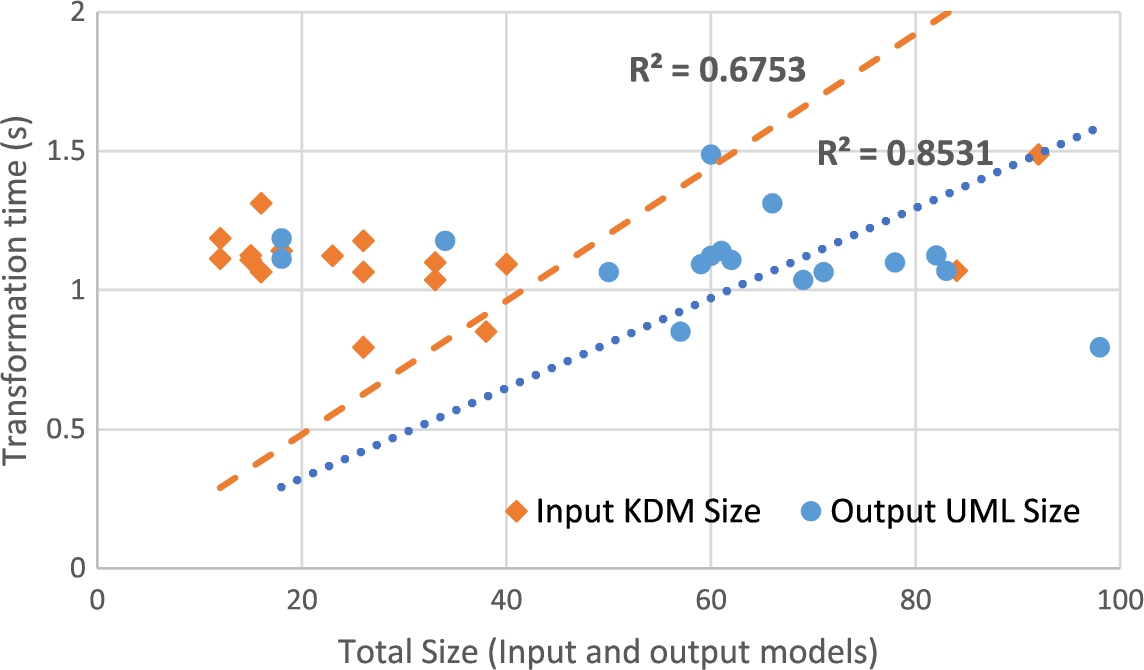
Fig. 23
Scalability of the tool.
Figure
23 shows that there are some outlier points regarding the hypothesized correlation. Regarding the input KDM size (diamond points), there are mainly two outlier points below the line, corresponding to cases P11 and P17. P11 is the only case that has not performed the model transformation because it fails at some point (see Table
6), while P17 is the one with the largest size of elements and relationships in both input and output models. Additionally, there are some outlier points above the line (left hand side). This is due to the fact that there is a common, constant time period spent in every model transformation, for example, due to the ATL transformation engine.
5.3 Evaluation of Validity
This section discusses threats to the validity of the case study and possible actions to mitigate them.
5.3.1 Construct Validity
The construct validity tries to ensure that the measures used in the case study are appropriate in order to draw conclusions that are useful to answer research questions. Measures previously used to evaluate the complexity of models similar to UML (e.g. ArchiMate models for Enterprise Architecture) have been used in this study. However, the lack of alternative measures in the literature to carry out an evaluation of the complexity of Q-UML may have affected certain results in this study. This also applies to the threat of validity with respect to the expressiveness of the generated models, as there are no measures that assess the expressivity of quantum models.
We can find two main threats related to the model transformation process. The first concerns its effectiveness, as there are no established metrics for validating the effectiveness of a model transformation. This forced us to follow a strategy based on assessing the model’s complexity and expressiveness, which may be considered a threat. The second threat concerns efficiency, as there are no benchmarks with which to compare the different times obtained in this study.
Finally, it should be noticed that the correlation and scatter plots used to evaluate the hypothesized linear relationship (between the size/complexity of programmes and the execution time) has been calculated with a limited number of measures. Hence, further replications by considering additional programmes will improve the insights of this study.
5.3.2 Internal Validity
Internal validity defines the degree to which conclusions can be drawn on the cause-effect relationship (independent-dependent variables). One such fact that threatens internal validity is that all cases have been extracted from the same repository (Microsoft) and using the same programming language (Q#). Possibly, if this same case study was replicated with different programmes (for example Qiskit programmes), the result of the metrics and their evaluation would be different. This thread was assumed due to the fact that the available tool for generating KDM models from quantum software only supports the analysis of Q# code. Therefore, in the future, alternative tools or an evolution of this tool could instead be used to generate alternative KDM models that may then be used as other input in a replication of this study.
The reduced LOC of the quantum programmes selected in the study can be considered as a threat, since it prevents generalizing results for larger programmes. Therefore, it would be necessary to achieve more evidence for larger quantum programmes. However, this is complicated since there is a lack of available open repositories of quantum software projects. In addition, the quantum programmes, that are currently available, are not very extensive and of course not comparable to classical software regarding the expected LOC.
5.3.3 External Validity
External validity helps us to define the degree to which the results achieved can be generalized when taking into account the population used and the other research parameters. A total of 17 cases were used to evaluate the tool, which, as mentioned above, necessarily had to be extracted from the Microsoft repository as this technique has been designed for Q#. This can be considered a thread to the generalizability of the results. However, this could be mitigated in the future by means of a replication of the study with programmes developed in programming languages different from Q#. To do this, the tool will be extended by incorporating KDM and UML analysis and model generation capabilities from quantum software developed in other quantum programming languages.
In addition, another fact that may threaten external validity is that more quantum algorithms are developed in Q# but cannot be generated in KDM. Of course, further experimentation might reveal more generalizable insights. Also, the type of programme can affect the external validity of the case study, i.e. programmes which are purely quantum algorithms have been analysed, while the entry points (which might be important in some cases) have not.
5.3.4 Reliability
When we talk about construct reliability, we want to know how far the conclusions can be regarded as statistically valid, i.e. whether the analysis and the results obtained are independent of the researchers who conducted the study.
To ensure that the reliability of the study is not compromised, the possibility of using the tool of this study to replicate the different tests is offered, as well as the data set accomplished in this case study (Jiménez-Navajas
et al.,
2024a). In addition, another measure to mitigate the aforementioned threat was the selection of quantum programmes from reputable and publicly available sources (such as the Microsoft repository) instead of using Q# examples freely created by the community.
6 Discussions and Implications for Practitioners
This research has demonstrated that it is possible to generate quantum UML models from quantum software previously reversed into KDM models. This can be seen as a major step forward for software engineering as it brings model-driven engineering closer to quantum computing and facilitates the evolution of today’s information systems towards hybrid information systems combining classical and quantum software.
As mentioned above, during the history of the evolution of legacy systems, two main problems have been encountered: lack of standardization and lack of automation. Both problems have been addressed in this research. First, the transformation is carried out between compliant models with well-known and industry-accepted standards, i.e. UML and KDM. This implies that the models can be used in a wide variety of tools that facilitate the analysis of hybrid information systems. Secondly, this research presents a tool for performing the model transformation, ensuring the repeatability of the transformations.
Thanks to the case study carried out, several insights have been obtained from the model transformation. Firstly, it has been found that the complexity and, so, its level of modularity, of the UML models generated from the model transformation is affordable. This means that the target UML models are suitable for modernizing hybrid information systems, as they have a better comprehension of the high-level design of the software and, second, it facilitates the improvement and addition of new functionalities during the restructuring phase. Secondly, the metrics indicate that the expressiveness of the output models is reasonable. So, this implies that the models generated do not suffer from a loss of knowledge, which is a common issue in reengineering processes.
Quantum software engineers have presented some efforts to adapt the MDE approach to the field of quantum computing. Currently, there are already several adaptations of metamodels to represent quantum programmes, such as UML (Pérez-Castillo
et al.,
2021a) or BPMN (Weder
et al.,
2020), among others. However, quantum software model transformations are not yet found in the literature, although it is a key aspect of MDE. Automatic model transformation reduces the burden of other activities, such as reverse engineering, view generation, application of patterns, or refactoring (Sendall and Kozaczynski,
2003), which is essential when dealing with several perspectives of the system. Model transformation is a fundamental part of MDE and in this research the first model transformation representing quantum elements has been carried out (which, hopefully, will be the first transformation of many more for the sake of MDE).
In this proposal, there are two main limitations. The first is related to the fact that this proposal only generates activity diagrams using programmes developed in Q#. This is a limitation for practitioners who develop quantum programmes in any other language. Another limitation of the proposal is that only activity diagrams are generated. In the case of looking for embedding quantum circuit (not quantum programmes) into hybrid information systems, it may not be appropriate to just have representations of such circuits in activity diagrams. Among other reasons, because these activity diagrams would not facilitate the understanding or maintenance of these quantum circuits.
This research leads to several implications for academia and industry. Both must collaborate for the further development of MDE applied to the field of quantum computing, either by developing new techniques or by giving feedback on how quantum software development is performed. The use of models in industrial software development is commonplace, and the utilization of these models is a must for quantum software to be developed in an industrial and controlled manner (Piattini
et al.,
2020).
7 Conclusions
The interest in software modernization within the context of quantum software arises from the pressing need to bridge the gap between classical and quantum paradigms, particularly in the era of hybrid information systems. As quantum computing matures, its integration into existing classical infrastructures becomes essential to leverage its potential while maintaining the critical knowledge embedded in legacy systems. This work contributes to this objective by proposing and validating a model transformation approach that facilitates the seamless incorporation of quantum functionalities into classical systems, ensuring scalability, compatibility, and maintainability. The growing adoption of quantum technologies across diverse industries underscores the importance of this endeavour, as organizations strive to remain competitive and future-ready in an increasingly quantum-enhanced landscape.
This first contribution of this research is a proposal to automatically transform KDM models to UML in the context of quantum software modernization. The model transformation can generate UML activity diagrams that represent quantum circuits according to an UML profile. The second main contribution was the empirical validation of the model transformation. In order to validate the proposal, 17 KDM models (generated from programmes developed in Q#) were used to apply the model transformation. During the validation, the complexity of the models generated, their expressiveness (i.e. whether the models generated in UML express the same as the input models), and the scalability of the transformation were evaluated.
The main benefit of generating quantum UML models is the fact that there is now a widely accepted industry standard with a vast variety of applications and software engineers working with it daily, and it therefore provides the ability for modelling quantum algorithms. In the near future, when it is time to proceed with the design of hybrid information systems, software engineers may not need to know the details of how certain quantum gates act with qubits, but this does not mean that they should not handle certain models of quantum algorithms designed by other roles (closer to physics and mathematics) to incorporate them into the final design of the system.
Regarding our future work, there are two main pathways to follow on the roadmap, which are precisely related to the mentioned limitations. The first one is to generate more types of diagrams apart from the activity ones, e.g. class diagrams for modelling designs of hybrid systems. For accomplishing this, it will be studied which other possible diagrams might be able to represent all the semantics of hybrid software. Additionally, the tool can be seen as limited since it just analyses Q# code – even though the metrics obtained do suggest a great performance. In this path of refining the tool we also include the addition of more quantum programming languages, such as OpenQASM3 or Qiskit (Python). Additionally, the greatest challenge we need to confront is how to transfer the ideas and techniques supported by QRev into a real environment, such as QPath (Peterssen
et al.,
2022), which is a Quantum Software Development and Lifecycle Application Platform.
The second path on the roadmap is to continue with the Quantum Software Modernization process explained before. Although only the forward engineering phase is yet to be completed, other lines of research have already been opened, such as the generation of new quantum UML diagrams or the enabling of the tool to model and transform quantum annealing software (e.g. D-Wave code).
Acknowledgements
This work is part of the QU-ASAP project (PID2019-104791RB-I00) funded by MICIU/AEI/10.13039/501100011033 and by the “European Union NextGenerationEU/PRTR”; the SMOOTH project (PID2022-137944NB-I00) funded by MICIU/AEI/10.13039/501100011033/PRTR,EU.
Footnotes
References
Aaronson, S. (2008). The limits of quantum. Scientific American, 298(3), 62–69.
Caivano, D., Fernández-Ropero, M., Pérez-Castillo, R., Piattini, M., Scalera, M. (2018). Artifact-based vs. human-perceived understandability and modifiability of refactored business processes: an experiment. Journal of Systems and Software, 144, 143–164.
Canfora, G., Di Penta, M. (2007). New frontiers of reverse engineering. In: Future of Software Engineering (FOSE’07), pp. 326–341. IEEE.
Cruz-Lemus, J.A., Maes, A., Genero, M., Poels, G., Piattini, M. (2010). The impact of structural complexity on the understandability of UML statechart diagrams. Information Sciences, 180(11), 2209–2220.
Cruz-Lemus, J.A., Marcelo, L.A., Piattini, M. (2021). Towards a set of metrics for quantum circuits understandability. In: International Conference on the Quality of Information and Communications Technology. Springer, Cham, pp. 239–249.
De Lucia, A., Ferrucci, F., Tortora, G., Tucci, M. (2008). Emerging Methods, Technologies, and Process Management in Software Engineering. John Wiley & Sons.
Dwivedi, K., Haghparast, M., Mikkonen, T. (2024). Quantum software engineering and quantum software development lifecycle: a survey. Cluster Computing, 27(6), 7127–7145.
https://doi.org/10.1007/s10586-024-04362-1.
Feynman, R.P. (2018). Simulating physics with computers. In: Feynman and Computation. CRC Press, pp. 133–153.
Flagship, E.Q. (2020).
The Quantum Flagship officially presents the Strategic Research Agenda to the European Commission.
https://shorturl.at/dzNX5.
Garhwal, S., Ghorani, M., Ahmad, A. (2021). Quantum programming language: a systematic review of research topic and top cited languages. Archives of Computational Methods in Engineering, 28, 289–310.
Genero, M., Piattini-Velthuis, M., Cruz-Lemus, J.-A., Reynoso, L. (2004). Metrics for UML models. UPGRADE-The European Journal for the Informatics Professional, 5, 43–48.
Heim, B., Soeken, M., Marshall, S., Granade, C., Roetteler, M., Geller, A., Troyer, M., Svore, K. (2020). Quantum programming languages. Nature Reviews Physics, 2(12), 709–722.
Hevia, J.L., Peterssen, G., Ebert, C., Piattini, M. (2021). Quantum computing. IEEE Software, 38(5), 7–15.
Horodecki, R., Horodecki, P., Horodecki, M., Horodecki, K. (2009). Quantum entanglement. Reviews of Modern Physics, 81(2), 865.
Iacob, M.E., Monteban, J., Van Sinderen, M., Hegeman, E., Bitaraf, K. (2018). Measuring enterprise architecture complexity. In: 2018 IEEE 22nd International Enterprise Distributed Object Computing Workshop (EDOCW), pp. 115–124.
Jiménez-Navajas, L., Pérez-Castillo, R., Piattini, M. (2020). Reverse engineering of quantum programs toward KDM models. In: International Conference on the Quality of Information and Communications Technology. Springer, Cham, pp. 249–262.
Jiménez-Navajas, L., Pérez-Castillo, R., Piattini, M. (2021). KDM to UML model transformation for quantum software modernization. In: International Conference on the Quality of Information and Communications Technology. Springer, Cham, pp. 211–224.
Jimenez-Navajas, L., Buhler, F., Leymann, F., Perez-Castillo, R., Piattini, M., Vietz, D. (2024b). Quantum software development: a survey. Quantum Information and Computation, 24(7 and 8), 0609–0642.
https://www.rintonpress.com/journals/doi/QIC24.7-8-4.html.
Jouault, F., Allilaire, F., Bézivin, J., Kurtev, I. (2008). ATL: a model transformation tool. Science of Computer Programming, 72(1–2), 31–39.
Kim, Y., Eddins, A., Anand, S., Wei, K.X., van den Berg, E., Rosenblatt, S., Nayfeh, H., Wu, Y., Zaletel, M., Temme, K., Kandala, A. (2023). Evidence for the utility of quantum computing before fault tolerance. Nature, 618(7965), 500–505.
https://doi.org/10.1038/s41586-023-06096-3.
Müller, H.A., Jahnke, J.H., Smith, D.B., Storey, M.-A., Tilley, S.R., Wong, K. (2000). Reverse engineering: a roadmap. In: Proceedings of the Conference on the Future of Software Engineering, pp. 47–60.
Muñoz, L., Mazón, J.-N., Trujillo, J. (2010). A family of experiments to validate measures for UML activity diagrams of ETL processes in data warehouses. Information and Software Technology, 52(11), 1188–1203.
Pérez-Castillo, R., de Guzmán, I.G.R., Piattini, M. (2011a). Architecture-driven modernization. In: Modern Software Engineering Concepts and Practices: Advanced Approaches. IGI Global, pp. 75–103.
Pérez-Castillo, R., De Guzman, I.G.-R., Piattini, M. (2011b). Knowledge discovery metamodel-ISO/IEC 19506: a standard to modernize legacy systems. Computer Standards & Interfaces, 33(6), 519–532.
Pérez-Castillo, R., Jiménez-Navajas, L., Piattini, M. (2021a). Modelling quantum circuits with UML. In: 2021 IEEE/ACM 2nd International Workshop on Quantum Software Engineering (Q-SE), pp. 7–12.
Pérez-Castillo, R., Serrano, M.A., Piattini, M. (2021b). Software modernization to embrace quantum technology. Advances in Engineering Software, 151, 102933.
Pérez-Castillo, R., Jiménez-Navajas, L., Piattini, M. (2022a). QRev: migrating quantum code towards hybrid information systems. Software Quality Journal, 30(2), 551–580.
Pérez-Castillo, R., Delgado, A., Ruiz, F., Bacigalupe, V., Piattini, M. (2022b). A method for transforming knowledge discovery metamodel to ArchiMate models. Software And Systems Modeling, 21, 311–336.
Pérez-Delgado, C.A., Perez-Gonzalez, H.G. (2020). Towards a quantum software modeling language. In: Proceedings of the IEEE/ACM 42nd International Conference on Software Engineering Workshops, pp. 442–444.
Peterssen, G., Hevia, J.L., Piattini, M. (2022). Quantum software development with QuantumPath®. In: Quantum Software Engineering. Springer, Cham, pp. 251–268.
Piattini, M., Peterssen, G., Pérez-Castillo, R., Hevia, J.L., Serrano, M.A., Hernández, G., de Guzmán, I.G.R., Paradela, C.A., Polo, M., Murina, E., Jiménez, L., Marqueño, J.C., Gallego, R., Tura, J., Phillipson, F., Murillo, J.M., Niño, A., Rodríguez, M. (2020). The talavera manifesto for quantum software engineering and programming. In: QANSWER, pp. 1–5.
Piattini, M., Serrano, M., Perez-Castillo, R., Petersen, G., Hevia, J.L. (2021). Toward a quantum software engineering. IT Professional, 23(1), 62–66.
Ribo, J.M., Franch Gutiérrez, J. (2002). A two-tiered methodology to extend the UML metamodel. ORKG Ask.
Rieffel, E.G., Polak, W.H. (2011). Quantum Computing: A Gentle Introduction. MIT Press.
Romero, J. (2011).
jsUML2-A lightweight HTML5/javascript library for UML 2 diagramming. Technical Report, Universidad de Córdoba.
http://code.google.com/p/jsuml2.
Runeson, P., Höst, M. (2009). Guidelines for conducting and reporting case study research in software engineering. Empirical Software Engineering, 14, 131–164.
Schütz, A., Widjaja, T., Kaiser, J. (2013). Complexity in enterprise architectures-conceptualization and introduction of a measure from a system theoretic perspective. In:
European Conference on Information Systems (ECIS).
Sendall, S., Kozaczynski, W. (2003). Model transformation: the heart and soul of model-driven software development. IEEE Software, 20(5), 42–45.
Sneed, H.M. (2005). Estimating the costs of a reengineering project. In: 12th Working Conference on Reverse Engineering (WCRE’05), p. 9.
Ulrich, W.M. (2002). Legacy Systems: Transformation Strategies. Prentice Hall PTR.
Ulrich, W.M., Newcomb, P. (2010). Information Systems Transformation: Architecture-Driven Modernization Case Studies. Morgan Kaufmann.
Vernacchia, S. (2019). Quantum leap: advancing a strategy for quantum computing that will inspire, support and safeguard economic growth in the Middle East. In:
World Government Summit.
Weder, B., Breitenbücher, U., Leymann, F., Wild, K. (2020). Integrating quantum computing into workflow modeling and execution. In: 2020 IEEE/ACM 13th International Conference on Utility and Cloud Computing (UCC), pp. 279–291.
Weinberg, S.J., Sanches, F., Ide, T., Kamiya, K., Correll, R. (2023). Supply chain logistics with quantum and classical annealing algorithms. Scientific Reports, 13(1), 4770.
Wojcieszyn, F. (2022). Introduction to Quantum Computing with Q# and QDK. Springer Nature.
Yanofsky, N.S., Mannucci, M.A. (2008). Quantum Computing for Computer Scientists. Cambridge University Press.
Zhao, X., Xu, X., Qi, L., Xia, X., Bilal, M., Gong, W., Kou, H. (2024). Unraveling quantum computing system architectures: an extensive survey of cutting-edge paradigms. Information and Software Technology, 167, 107380.
https://doi.org/10.1016/j.infsof.2023.107380.
https://www.sciencedirect.com/science/article/pii/S0950584923002355.