1 Introduction
The rapid growth in multimedia applications has led to the vast spread of multimedia information across public networks. As a consequence, such information has become vulnerable to eavesdropping. Therefore, the need for safeguarding algorithms has become of major concern. Digital images are amongst the most popular digital media, they are found in a number of applications including military, medical and geographical applications. Due to this wide range of applications, research for developing efficient safeguarding algorithms has grasped the attention of scientists and engineers more than ever.
Cryptography is a field of mathematics and computer science that provide many security services including encryption and data hiding. Data hiding is a process that intends to hide secret information within cover media in such a way that an eavesdropper is incapable to detect the presence of such information within the carrier. On the contrary, encryption is a process that transforms secret information into scrambled data which is totally meaningless to an eavesdropper (Katz
et al.,
1996; Rijmen and Daemen,
2001; Rivest
et al.,
1978). Both techniques require a secret key that entitles the recipient to recover back the secret information. One disadvantage of data hiding techniques is that most schemes hide the raw data within the cover media (Cheddad
et al.,
2010; Mao and Qin,
2013; Ghebleh and Kanso,
2014; Tang
et al.,
2014). Furthermore, secret images of large sizes require quite large carriers. Due to some inherent characteristics of digital images such as bulk data capacity, high redundancy and correlation between adjacent pixels, conventional encryption schemes such as the Data Encryption Standard (DES) (Katz
et al.,
1996), the Advanced Encryption Standard (AES) (Rijmen and Daemen,
2001), the Rivest, Shamir and Adleman’s scheme (RSA) (Rivest
et al.,
1978) are unsuitable for the encryption of digital images.
Chaotic systems have a number of important characteristics such as high sensitive dependence on initial conditions and control parameters, large keyspace, unpredictability, ergodicity, and mixing property. Furthermore, with suitable control parameters and initial conditions, they can generate random looking sequences indistinguishable from random sequences. Confusion and diffusion are two important properties of any suitable encryption scheme (Shannon,
1949). In image encryption, confusion makes the relationship between the cipher-image and the secret key as complex as possible. That is, the impact of a tiny change to the secret key results in a major change in the cipher-image. On the other hand, diffusion makes the statistical relationship between the plain-image and the cipher-image as complex as possible. That is, the impact of a tiny change in the plain-image results in a major change in the cipher-image. This complexity can be obtained by a number of permutations and substitutions. Owing to the strong relationship between the properties of chaotic systems and Shannon’s principles of confusion and diffusion (Shannon,
1949), which are ideal properties in the design of a strong image encryption scheme, chaotic systems have become promising building blocks in the construction of such schemes. In 1998, Fridrich (
1998) presented an elegant chaos-based image encryption scheme that consists of two phases: a shuffling phase to confuse the relationship between the cipher-image and the plain-image, and a masking phase to spread a small change in the plain-image throughout the whole cipher-image. Despite the fact that Fridrich’s scheme is shown to suffer from security issues under chosen cipher-image scenario (Solak
et al.,
2010; Xie
et al.,
2017), Fridrich’s approach has been adopted in the designs of most proposed chaos-based image encryption schemes. Throughout the last two decades, a number of chaos-based image encryption schemes have been developed (Chen
et al.,
2004; Guan
et al.,
2005; Behnia
et al.,
2008; Zhang
et al.,
2010; Liu Y.
et al.,
2016; Hua
et al.,
2015; Kanso and Ghebleh,
2012,
2015a; Khan
et al.,
2017; Fu
et al.,
2018; Khan and Shah,
2015). Chen
et al. (
2004) proposed an image encryption scheme that employs a 3-dimensional (3D) cat map. However, Chen et al.’s scheme (Chen
et al.,
2004) is shown to be vulnerable to differential attacks (Li and Chen,
2008; Wang
et al.,
2005). Guan
et al. (
2005) proposed an image encryption scheme based on Arnold cat map and Chen’s chaotic system. Cokal and Solak (
2009) proved that this scheme suffers from security weaknesses under chosen plain-image and known plain-image scenarios. Behnia
et al. (
2008) proposed a new kind of image encryption scheme based on composition of trigonometric chaotic maps. However, this scheme is shown to suffer from security issues under chosen plain-image scenario and differential attacks (Li
et al.,
2010). Zhang
et al. (
2010) proposed an image encryption scheme based on DNA addition in conjunction with two chaotic logistic maps. Hermassi
et al. (
2014) revealed a number of flaws including non-invertibility of Zhang et al.’s scheme (Zhang
et al.,
2010). In Zhu (
2012), Zhu proposed an image encryption scheme based on improved hyper-chaotic sequences. Li
et al. (
2013) showed that Zhu’s scheme can be broken with only one known plain-image. In Liu Y.
et al. (
2016), a hyper-chaos-based image encryption algorithm with linear feedback shift registers is proposed. Zhang
et al. (
2017) showed that this scheme has some flaws due to weak security of the diffusion process and it is vulnerable to differential attacks. Hua
et al. (
2015) introduced a new 2D sine logistic modulation map and proposed a chaotic magic transform image encryption scheme. Kanso and Ghebleh (
2012) proposed an image encryption scheme based on 3D cat map. In Kanso and Ghebleh (
2015a), a new family of 4D cat maps is proposed together with an image encryption scheme for medical applications. Khan
et al. (
2017) proposed a chaos-based image encryption scheme that utilizes a non-linear chaotic algorithm for destroying correlation and diffusion in plain-image. In Fu
et al. (
2018), Fu et al. proposed an algorithm based on a 4D hyper-chaotic system in conjunction with the hash function SHA-224. In addition to the aforementioned schemes, the research committee has proposed a number of schemes such as those presented in Wang
et al. (
2015), Zhou
et al. (
2014), Xu
et al. (
2016), Liu
et al. (
2016), Hua and Zhou (
2017), Zhou
et al. (
2013), Wu
et al. (
2014), Cao
et al. (
2018), Hua
et al. (
2019), Khan
et al. (
2017), Fu
et al. (
2018), Liu
et al. (
2019), Sun
et al. (
2020), Hemdan
et al. (
2019) and references therein.
Among the large number of image encryption schemes that have appeared in the literature, security flaws in some of these schemes have been revealed by the cryptographic community. Furthermore, the rapid advancement of digital media technology demands the attention of researchers to develop fast and efficient image encryption schemes. Arnold’s cat map (Arnol’d and Avez,
1968) is one of the most studied 2D chaotic maps. Due to its characteristics, it has been widely used in a number of cryptographic applications (Guan
et al.,
2005; Xiao
et al.,
2009; Fu
et al.,
2011; Ghebleh
et al.,
2014b; Soleymani
et al.,
2014; Kanso and Ghebleh,
2015a,b). Furthermore, a number of generalizations of the 2D cat map have appeared in the literature (Chen
et al.,
2004; Kanso and Ghebleh,
2013). In this paper, we propose a new family of 4D chaotic cat maps that is an extension of the generalization suggested in Kanso and Ghebleh (
2013) for use in cryptographic applications. The objective of this proposal is to increase the number of control parameters in the coefficient matrix defining the 4D cat map which in turn increases the size of the keyspace of any cryptographic scheme adopting the generalization. We then propose an image encryption scheme based on members of this family. The proposed scheme follows Fridrich’s approach. It is composed of a light shuffling phase and a masking phase, which operate on image-blocks. The shuffling phase preforms a circular shift on the rows and columns of the image at hand in conjunction with a zigzag ordering algorithm. The masking phase uses pseudorandom sequences generated by the proposed 4D cat map for diffusion of the resulting shuffle-image. Furthermore, the masking phase applies measures of central tendency to enhance security against a number of cryptanalytic attacks such as differential attacks. The mixing is designed so that while encryption is highly sensitive to the secret key and the input image, decryption is robust against noise and cropping of the cipher-image. Simulation results are presented to demonstrate the high performance of the proposed scheme and its high security level.
The main contributions of this work are as follows:
-
• The method is simple and efficient.
-
• The encryption scheme is highly sensitive to its key and input image, while the decryption scheme is robust against various alternations such as noise and cropping of cipher-image.
-
• The method is block-based. Based on the block size, there is a tradeoff between the security and the speed of the proposed scheme. However, simulations show that the chosen block size makes the scheme robust to existing attacks, insensitive to cipher-image attacks, and faster than existing schemes.
The paper is organized as follows: Section
2 presents the proposed family of 4D cat maps. In Section
3, we give a detailed description of the proposed image encryption scheme. We also demonstrate the randomness of matrices generated by successive iterations of the proposed 4D cat map. Section
4 showcases the efficiency of the proposed scheme. It also presents simulation results that demonstrate the robustness of the proposed scheme against statistical attacks. In Section
5, we further analyse the security of the proposed scheme. In Section
6, we showcase the superiority of the proposed scheme over some of the existing schemes. Finally, we end the paper with some concluding remarks.
2 The 4-Dimensional Cat Map
Arnold’s cat map (Arnol’d and Avez,
1968) is a chaotic map defined on the torus
${\mathbb{R}^{2}}/{\mathbb{Z}^{2}}$ by
The discrete cat map can be defined accordingly by
which starting from any initial state
$({x_{0}},{y_{0}})$ defines an infinite sequence of 2-vectors. This map can be generalized (Chen
et al.,
2004) using two positive integer parameters
a and
b as
Further generalizations of this map to higher dimensions are also known (Chen
et al.,
2004; Kanso and Ghebleh,
2013). Chen
et al. (
2004) proposed a generalization of the 2D cat map into a 3D cat map, where the coefficient matrix consists of six control parameters. Kanso and Ghebleh (
2013) extended the generalization of the 2D cat map into a 4D cat map, where the coefficient matrix consists of four control parameters. Despite existing generalizations, in this paper we extend the generalization of the 4D cat map suggested in Kanso and Ghebleh (
2013) so that the number of control parameters of the coefficient matrix increases to twelve positive integers. The increase in the number of control parameters is very beneficial to cryptographic applications since it leads to a larger keyspace of the cryptographic scheme.
We consider the following path to define a new
$4\times 4$ coefficient matrix for a 4D cat map. The building blocks for this definition are maps which fix two coordinates and apply Eq. (
1) to the other two coordinates. More specifically, we use the six matrices
where
${a_{1}},\dots ,{a_{6}},{b_{1}},\dots ,{b_{6}}$ are constant positive integers. Note that each
${M_{ij}}$ is obtained from the identity matrix
${I_{4}}$ via replacing a
$2\times 2$ principal minor by the coefficient matrix of Eq. (
1) using parameters
$a={a_{k}}$ and
$b={b_{k}}$. The
$4\times 4$ coefficient matrix is now defined to be
In turn, this matrix can be used in defining the 4D cat map
It is easy to see that each matrix
${M_{ij}}$ has determinant 1, thus
$\det (A)=1$. On the other hand, since this construction involves no subtraction, and since all its parameters are positive integers, each entry of the matrix
A of Eq. (
2) is greater than or equal to its corresponding entry in the matrix
${A_{0}}$ obtained with all parameters set to 1:
In particular,
$\mathrm{tr}(A)\geqslant \mathrm{tr}({A_{0}})=20$. Now if
${\lambda _{1}},{\lambda _{2}},{\lambda _{3}},{\lambda _{4}}$ denote the (possibly complex) eigenvalues of
A, then
Thus at least one eigenvalue of
A has modulus greater than 1, which justifies chaotic behaviour of the map of Eq. (
3). See Ott (
2002), Hua
et al. (
2017), Wang
et al. (
2018) for more information.
For all the experimental results presented in this work, we use the values
for the control parameters of the 4D cat map, while yield the coefficients matrix
whose eigenvalues are
Since
A has more than one eigenvalue greater than 1, the 4D cat map of Eq. (
3) exhibits hyper-chaotic behaviour (Hua
et al.,
2017).
6 Comparison with Existing Work
In this section, we compare the performance of the proposed scheme Pr-IES with existing ones. Figure
12 presents NPCR and UACI measures for cipher-images corresponding to 25 test images in Test-images (
2019) for a number of existing schemes. There are 7 test images of size
$256\times 256$ (top), 15 of size
$512\times 512$ (middle) and 3 of size
$1024\times 1024$ (bottom). Figure
12 shows that the pass rate for the proposed scheme is
$25/25$ with
$\alpha =0.05$ significance level for the NPCR and UACI measures. Table
11 reports the schemes under comparison and the pass rate of each scheme.
Table 11
The NPCR and UACI pass rates of the proposed scheme and some existing schemes. The pass rates for the schemes under comparison are quoted from Hua
et al. (
2019).
| Scheme |
Pass rate |
| NPCR |
UACI |
| WWZ (Wang et al., 2015) |
$23/25$ |
$22/25$ |
| ZBC1 (Zhou et al., 2014) |
$15/25$ |
$6/25$ |
| XLLH (Xu et al., 2016) |
$23/25$ |
$23/25$ |
| LSZ (Liu et al., 2016) |
$23/25$ |
$23/25$ |
| HZ (Hua and Zhou, 2017) |
$24/25$ |
$24/25$ |
| ZBC2 (Zhou et al., 2013) |
$23/25$ |
$7/25$ |
| WZNA (Wu et al., 2014) |
$23/25$ |
$22/25$ |
| CSL (Cao et al., 2018) |
$24/25$ |
$25/25$ |
| HZH (Hua et al., 2019) |
$25/25$ |
$25/25$ |
| Pr-IES |
$25/25$ |
$25/25$ |
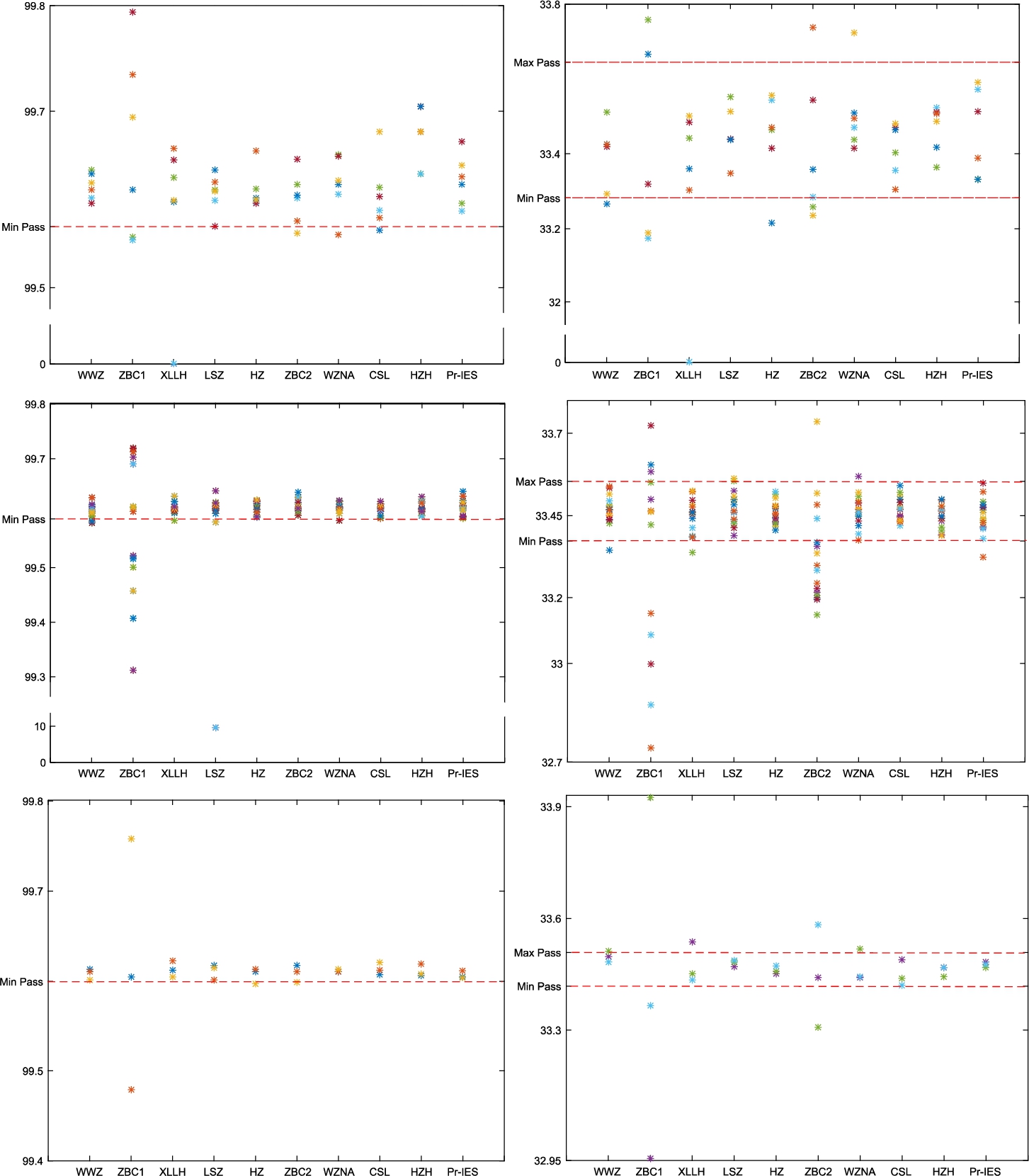
Fig. 12
NPCR (left) and UACI (right) measures for cipher-images generated by existing image encryption schemes and the proposed scheme. The measures for existing schemes are obtained from Hua
et al. (
2019).
We further compare the correlation coefficients between adjacent pixels of the proposed scheme and existing ones. Figure
13 depicts the correlation coefficients between adjacent intensity values in the horizontal, vertical and diagonal directions for the test image Lena and its corresponding cipher-images generated by the proposed scheme and existing schemes. Note the schemes proposed in Fu
et al. (
2011) and Liao
et al. (
2010) are referred to by FLMLC and LLZ, respectively.
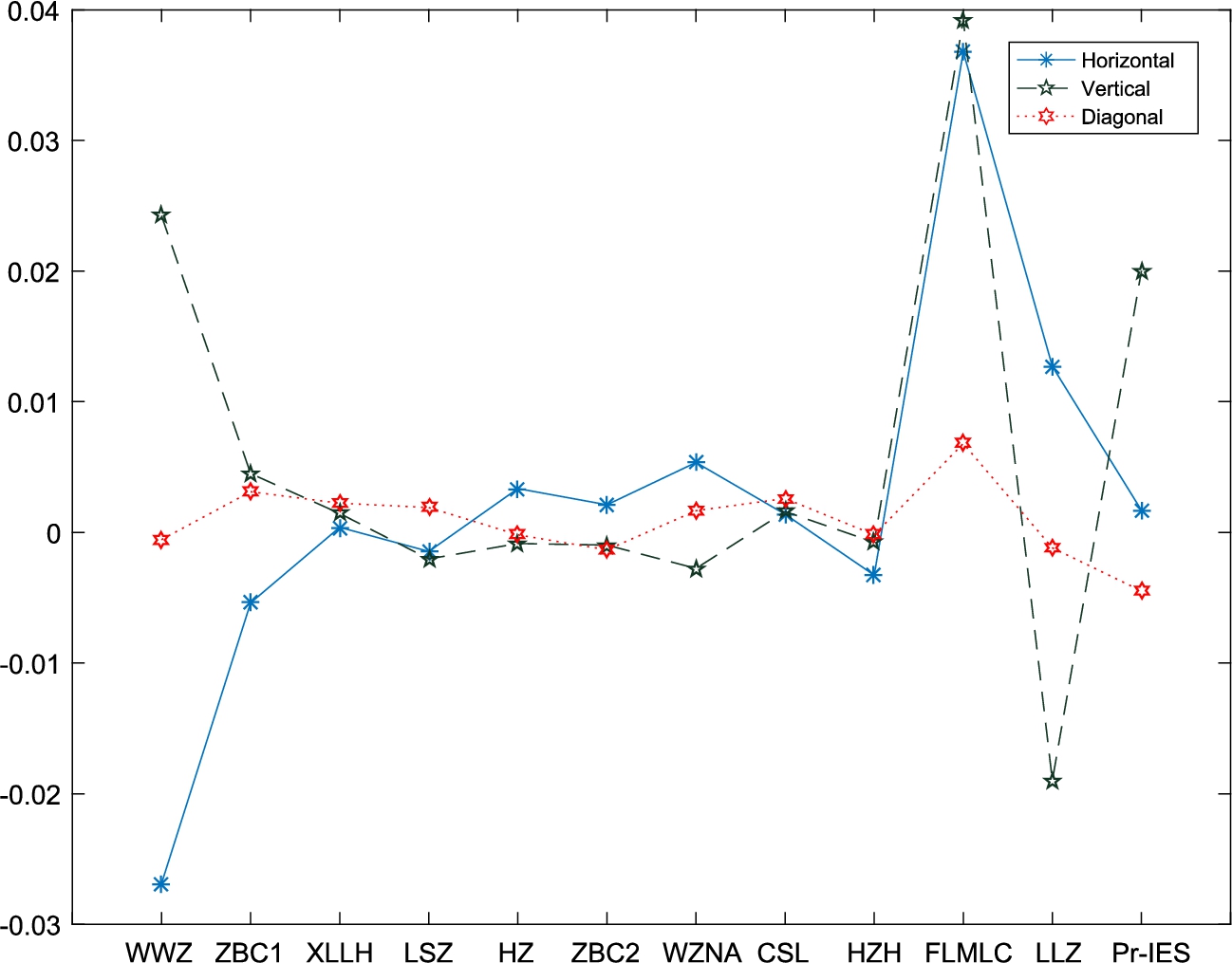
Fig. 13
Adjacent intensity values correlation coefficients for the test image Lena and corresponding cipher-images generated by existing schemes and the proposed scheme. The values for existing schemes are obtained from Hua
et al. (
2019).
Table
12 reports the running time in seconds for encrypting a single image with some existing schemes and the proposed scheme. The reported running times for the schemes under comparison are quoted from Hua
et al. (
2019). According to Hua
et al. (
2019), the reported running times for existing schemes are obtained on a computer under the following environments: Intel® Core™ i7-7700 CPU @3.60 GHz and 8 GB of memory, running Windows 10 operating system. While the reported running times for the proposed scheme Pr-IES are obtained on a desktop machine with an Intel® Core™ i7-4770 processor @3.40 GHz and 8GB of memory, running Windows 10 operating system.
Table 12
Running time in seconds for encrypting a single image by existing schemes and the proposed encryption scheme Pr-IES. The running times for the schemes under comparison are quoted from Hua
et al. (
2019) used under license CC BY-NC-ND 4.0 (License,
2020).
| Image size |
$128\times 128$ |
$256\times 256$ |
$512\times 512$ |
$1024\times 1024$ |
| (Diaconu, 2016) |
0.0579 |
0.2224 |
0.9731 |
3.8377 |
| (Ping et al., 2018) |
0.0902 |
0.3440 |
1.3357 |
5.3223 |
| (Chai et al., 2017) |
0.2757 |
0.9810 |
3.8539 |
15.4565 |
| (Hua and Zhou, 2017) |
0.1531 |
0.6347 |
2.4913 |
9.9185 |
| (Xu et al., 2016) |
0.0247 |
0.1164 |
0.4924 |
20.144 |
| (Zhou et al., 2014) |
0.0933 |
0.3843 |
1.4824 |
5.8175 |
| (Liao et al., 2010) |
0.0323 |
0.1440 |
0.5510 |
2.0864 |
| (Hua et al., 2019) |
0.0244 |
0.0949 |
0.4010 |
1.9857 |
| Pr-IES |
0.0217 |
0.0645 |
0.2422 |
1.0021 |
It is evident from the obtained results that the proposed scheme has superiority over existing schemes and competitive with others.