1 Introduction
The constant increase in the size of the databases used in Drug Discovery requires efficient techniques and methods that can be used to select the compounds most similarly to a query molecule and at the lowest possible cost. One of these techniques is Virtual Screening (VS). VS is an in-silico technique that allows large libraries with millions of compounds to be processed in order to find new compounds related to a pharmacological query based on one or more features (Hamza et al., 2012; Boström et al., 2013; Kumar and Zhang, 2016; Wang et al., 2009). This represents a great advantage over experimental methods such as High-Throughput Screening (HTS) in terms of efficiency, budget, time and development cost (Kar and Roy, 2013). The resulting compounds from VS are subsequently acquired and empirically tested in the laboratory. In addition, VS techniques are often used as a pre-filter for HTS (López-Ramos et al., 2009). All these advantages have increased the popularity of these techniques, which have experienced great advances over the last two decades. The interested reader is referred to previous works (Lešnik et al., 2015; Kalászi et al., 2014; Liu et al., 2011; Dou et al., 2018; Schmidt et al., 2018) for a description of different methods and tools currently used on VS.
However, there is still room for improvement regarding the accuracy of VS predictions so as not to discard promising compounds, or to reduce the time and error of calculations that compute the different features of the studied compounds (Böhm and Stahl, 2003). VS applied to the electrostatic similarity of compounds is a clear example of this. Contrary to what happens when VS is applied to select the most similar compounds in shape or pharmacophore properties, where the tools base their predictions on scoring functions that measure these particular features (Lešnik et al., 2015; Puertas-Martín et al., 2019; Yan et al., 2013), the predictions in this field are not exclusively based on this descriptor, but on both the similarity of the three dimensional shape and electrostatic similarity (Tresadern et al., 2009; Chu and Gochin, 2013; Kim et al., 2015; Kossmann et al., 2016; Woodring et al., 2017; Maccari et al., 2011; Kim et al., 2016; López-Ramos and Perruccio, 2010; Hevener et al., 2012; Kaoud et al., 2012; Tiikkainen et al., 2009; Massarotti et al., 2014; Oyarzabal et al., 2009).
Broadly speaking, all the previous works follow the same methodology, called LBVS-Shape throughout this paper, although they may differ in the selection procedure used to determine the compounds proposed as best predictions. Essentially, they initially optimize the compounds in the database against the query in terms of shape by using ROCS (OpenEye Scientific Software, 2019a). After that they select a number N of compounds with the highest shape similarity values and then finally evaluate them in terms of electrostatic similarity.
The value of N is not fixed, as it depends on the particular study. Usually, N is less than $10\% $ of the total compounds in the database (Kossmann et al., 2016; Hevener et al., 2012; Kaoud et al., 2012). A search for the best compounds basing on shape pre-filtering may be counterproductive, since the selection of a low value of N can rule many promising compounds out, which may have a significant impact on the final results.
Additionally, we also believe that using a more realistic description of compound bioactivity during the optimization procedure may help to obtain better predictions. As such, we propose a new approach as part of this work, named LBVS-Electrostatic, which involves the direct optimization of the electrostatic similarity. To do so, a new version of the algorithm OptiPharm, called OptiPharm_ES, has been implemented. OptiPharm (Puertas-Martín et al., 2019) was initially designed to optimize the shape similarity between two given molecules, but now it has been adapted to maximize the electrostatic similarity. As results will show, the new LBVS-Electrostatic methodology is able to obtain better solutions than the ones obtained with the classical LBVS-Shape approach.
The rest of the paper is organized as follows. Section 2 gives a brief description about the mathematical formulation of the scoring functions. Sections 3 and 4 describe the two methods used for virtual screening based on electrostatic similarity, both the literature approach and the novel proposal. The former is currently the method most frequently used in the literature. In short, it computes a sublist of molecules with the highest three-dimensional shape similarity. Usually, such a sublist is only composed of less than $10\% $ of the total number of compounds in the database. From the reduced list, the compound(s) with the greatest electrostatic similarity is/are selected. The second one involves the resolution of an optimization problem guided by a electrostatic similarity function. Section 5 describes the framework where the experiments have been carried out and the main results obtained. Finally, the conclusions and lines for future research are summarized in the last section.
2 Scoring Functions to Measure Similarity Between Compounds
This section is devoted to defining the mathematical functions used to guide the searching processes. The figures in which the values of these objective functions are graphically represented have been created with VIDA v4.4.0 (OpenEye Scientific Software, 2019b) using the default configuration.
2.1 Shape Similarity
The shape similarity of two compounds is calculated as follows:
where ${p_{i}}$ and ${p_{j}}$ are set to 2.7, ${\alpha _{i}}$ and ${\alpha _{j}}$ obtain the van der Waals value for each atom and
where ${R_{ij}}$ is the distance between atoms i and j.
(1)
\[ {V_{AB}^{g}}=\sum \limits_{i\in A,j\in B}{V_{ij}^{g}}=\sum \limits_{i\in A,j\in B}{p_{i}}{p_{j}}{K_{ij}}{\bigg(\frac{\pi }{{\alpha _{i}}+{\alpha _{j}}}\bigg)^{\frac{3}{2}}},\](2)
\[ {K_{ij}}=\exp \bigg(-\frac{{\alpha _{i}}{\alpha _{j}}{R_{ij}^{2}}}{{\alpha _{i}}+{\alpha _{j}}}\bigg),\]Notice that the accuracy obtained from (1) depends on the number of atoms in the two compared molecules, i.e. the higher this number, the longer the value of ${V_{AB}}$ as an absolute value. To be able to measure the level of similarity between compounds, regardless of the number of atoms that they are composed of and the descriptor used, the Tanimoto Similarity (Jaccard, 1901) value is computed as follows:
where ${V_{AB}}$ is the A molecule overlaid onto B molecule. ${V_{AA}}$ and ${V_{BB}}$ is the overlap of the molecules A and B, respectively. (3) has a value in the range $[0,1]$, where 0 means there is no overlapping and 1 means the shape of both molecules is the same.
2.2 Electrostatic Similarity
The electrostatic similarities are obtained by numerical solution of the Poisson equation (Böttcher et al., 1974), viz:
where $\phi (r)$ is the electrostatic potential, $\epsilon (r)$ is the dielectric constant, and ${\rho _{mol}}(r)$ is the molecular charge distribution. Electrostatic similarity between two compounds is compared by determining ${E_{AB}}$:
where Θ is a masking function to ensure potentials interior to the compound are not considered part of the comparison. The integral appearing in (5) is a volume integral, computed using a grid-spacing parameter, h.
(5)
\[ {E_{AB}}=\int {\phi ^{A}}(r){\phi ^{B}}(r){\Theta ^{A}}(r){\Theta ^{B}}(r)\mathbf{dr}\approx {h^{3}}\sum \limits_{ijk}{\phi _{ijk}^{A}}{\phi _{ijk}^{B}}{\Theta _{ijk}^{A}}{\Theta _{ijk}^{B}},\]Again the accuracy obtained by (5) depends on the number of atoms in the compared molecules. As such, similarly to what was done previously, the Tanimoto Similarity (Jaccard, 1901) value has been computed as follows:
where ${E_{AB}}$ is the A molecule overlaid onto B molecule. ${E_{AA}}$ and ${E_{BB}}$ is the overlap of the molecules A and B, respectively. In this case, (6) has a value in the range $[-0.33,1]$, where $-0.33$ means the charges of both compounds have the same value but opposite loads, 0 means there is no overlapping, and 1 means the charges of both molecules are the same.
3 The Previous Approach: The LBVS Method Guided by Molecular Shape (LBVS-Shape)
This method bases its predictions on a previous pre-filtering process consisting of identifying the N candidate compounds from the database with the highest shape similarity. After that, for each selected compound, the electrostatic similarity is calculated at the optimum superimposition obtained in the previous stage. Finally, the molecule with the highest electrostatic similarity value is selected as the one for the solution.
In this work, we have used the tool ROCS (OpenEye Scientific Software, 2019a) to optimize the shape similarity between two molecules. ROCS is a parametrized piece of software used to maximize volume overlapping similarity and utilizes the previously described (3) to represent molecules by means of Gaussian functions (Grant and Pickup, 1995; Grant et al., 1996). Electrostatic similarity has been calculated using the ZAP Toolkit (see (6)). This software has been downloaded without modification from the original website (OpenEye Scientific Software, 2019c). It is worth mentioning that ROCS and ZAP are, by far, the most widely used tools in the literature for VS based on shape and electrostatic similarity (Ellingson et al., 2010; Thomas et al., 2013; Hawkins and Stahl, 2018; Connelly et al., 2015; Gowthaman et al., 2015). For this reason they have been selected as part of this study; i.e. a fair and complete study must be carried out by making a comparison with the state-of-the-art methods.
4 The New Approach: A LBVS Method Guided by Electrostatic Similarity (LBVS-Electrostatic)
Our main aim when using this approach is to obtain the compound(s) with the highest electrostatic similarity values. Thus, an optimization problem must be defined with this aim in mind. Broadly speaking, any tool, method or algorithm used will be better guided towards the optima if the objective function is a numerical model representing the real objective. Until now, most methods focus on prioritizing the search of compounds with the same global shape, while they place electrostatic similarities at much lower priority. Consequently, they solve a shape similarity optimization problem instead of focusing on the electrostatic similarity, which may be more useful from the drug discovery point of view.
The new approach being presented here is based on the idea that the scoring function used to guide the optimization method must be mainly based on electrostatic similarity, since it is very likely that compounds with very high electrostatic similarity will share very similar chemical properties. The same can not be said while just focusing on shape similarity. In the latter, the search may converge to a sub-optimal solution (Ivorra et al., 2018; Fernández et al., 2017, 2019). OptiPharm (Puertas-Martín et al., 2019), a recent algorithm proposed for working on LBVS problems, is used to prove our hypothesis. The interested reader is referred to as Puertas-Martín et al. (2019) for an in-depth description of this algorithm. For the sake of completeness, some of its main strengths and important features are briefly described in the following.
OptiPharm is a global evolutionary optimizer that can solve any optimization problem that concerns the computation of the similarity of two compounds, named query and target. It implements procedures to increasingly adjust the query molecule to the target, which remains fixed throughout the optimization method. A solution s represents the rotation and translation of the query with respect to the target. The parameters associated with s are dynamically bounded for each particular instance to reduce as much as possible the feasible region.
OptiPharm analyses the entire search space looking for likely areas where the local and global optima can be. To do so, it runs on a set of M solutions, called population, on which it applies a sequence of reproduction, selection and improvement procedures during several iterations.
Each solution in the population has a radius value that delimits a multidimensional subarea of the search space where the reproduction and improvement methods are applied. The radius corresponding to a solution depends on the iteration i where it was created. The real strength of the radius is that it allows us to focus the search on different subareas since many solutions with different radii can coexist simultaneously during the optimization procedure. Therefore, at the same stage of the optimization procedure, new promising regions are systematically analysed, while others are examined thoroughly. Besides, the maximum number of initial solutions M, the number of iterations ${t_{max}}$ and the smallest radius value ${R_{{t_{max}}}}$ OptiPharm has, as input parameter, a maximum number N of function evaluations.
Figure 1 shows the main stages of the algorithm and a brief description of the procedures implemented.
During this work, the scope of its functionalities has been extended to include the electrostatic potential as the scoring function. The new version has been called OptiPharm_ES. The electrostatic similarity between two compounds has been computed by using the source code of the ZAP Toolkit, also downloaded from https://docs.eyesopen.com/toolkits/cpp/zaptk/thewayofzap.html (OpenEye Scientific Software, 2019c). This approach ensures that the comparisons between methodologies are made under the same conditions. Additionally, OptiPharm_ES have been made available at https://hpca.ual.es/optipharm/ES.
4.1 Hardware Setup
All the experiments in this work have been executed using a Bullx R424-E3, which consists of 2 Intel Xeon E5 2650v2 (16 cores), 128 GB of RAM memory and 1 TB HDD (http://hpca.ual.es/en/infraestructure) along with the cluster Eagle https://wiki.man.poznan.pl/hpc/index.php?title=Eagle.
4.2 Benchmarks
In this work, a database provided by The Food and Drug Administration has been used (FDA). The Food and Drug Administration is a federal agency of the United States Department of Health and Human Services responsible for protecting and promoting public health by controlling, among other things, prescription and over-the-counter pharmaceutical drugs (medications). This agency provides a data set containing 1751 compounds, which represents approved medicines that can be safely used on humans in the USA. This database is useful since in the high similarity cases it would directly contribute to drug re-purposing. This is of relevant utility given the clear trend regarding re-purposing drugs observed over the last 5 years (Dakshanamurthy et al., 2012; Kumar and Zhang, 2018; Yuan et al., 2017).
The version of the database used in this work was obtained from DrugBank v5.0.1 (Wishart et al., 2018) and necessary mol2 files for the VS calculations were set up by using AmberTools (Case et al., 2017) by removing salts and neutralizing their protonation state, computing partial charges by MMFF94 force field, adding hydrogen atoms and minimizing energies (default parameters) (Halgren, 1995).
A comprehensive computational analysis may cover a representative sample of the database. The compounds included in the FDA database have different attributes, one of the most relevant for the study at hand being the number of atoms. In this work, a selection of 50 compounds has been made in the following way: the compounds in the database have been sorted by the number of atoms, including hydrogen, and then divided into 24 intervals (see Fig. 2). From each sector, at least one compound was chosen at random and proportional to the number of compounds in the sector.
Finally, these comparisons between compounds have been run using OptiPharm_ES with the following input parameter configuration: $N=200000$ function evaluations, $M=5$ starting poses, ${t_{max}}=5$ iterations and ${R_{{t_{max}}}}=1$ as the smallest possible radius.
5 Results
5.1 Influence of the Size List of Top-Ranked Compounds in the LBVS-Shape Method
As previously mentioned, the LBVS-Shape bases its predictions on a pre-selection of the first best compounds in terms of superimposition score (N). In this subsection, a study has been conducted to know how the value of N affects the final results from the point of view of electrostatic similarity. In particular, the LBVS-Shape has been performed on the selected 50 queries and for five different values of N, i.e. N has been set to 175, 438, 876, 1313 and 1751 compounds. It means that for each query, we have selected either $10\% $, $25\% $, $50\% $, $75\% $ or $100\% $ of the ranked compounds during the pre-selection phase.
Figure 3 illustrates a toy example of the main steps of the LBVS-Shape method for the $\mathit{Query}$ DB01213 and $N=1751$, i.e. the total number of compounds in the FDA set. Initially, the $\mathit{Query}$ is compared to each compound ${\mathit{Target}_{S}}$ from the database to obtain their optimum position and corresponding shape similarity value $T{c_{S}}$. As previously mentioned, this stage is carried out by using ROCS. Afterwards, compounds are sorted ($R{k_{S}}$) in decreasing order by $T{c_{S}}$. The N best compounds are selected and evaluated to measure the corresponding electrostatic similarity value $T{c_{E}^{\mathit{Eval}}}$. Notice that the evaluation of the electrostatic similarity considers the pose obtained with the shape similarity optimization. The compound with the highest $T{c_{E}^{\mathit{Eval}}}$, called BestComp throughout this paper, is selected as the best prediction. Finally, as an additional and unconsidered stage in the LBVS-Shape method, we have computed the optimized superposition between the BestComp and the $\mathit{Query}$ by using OptiPharm_ES. The corresponding $T{c_{E}}$ value is then provided.
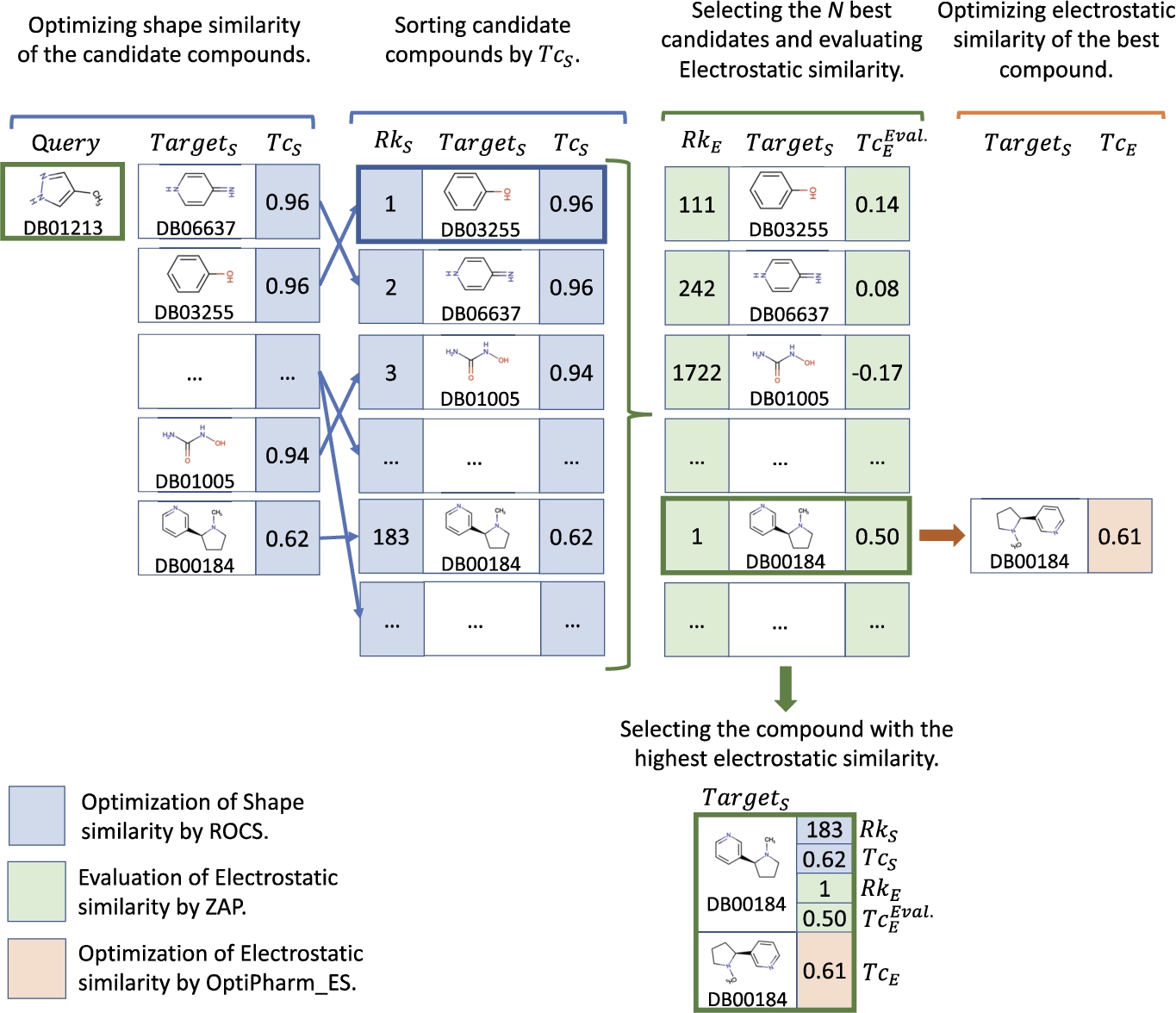
Fig. 3
Toy example of the performance of the LBVS-Shape method for a particular case where $\textit{Query}=DB01213$ and $N=1751$ using the FDA database.
To get an overview of the results, average values of the BestComp found for the 50 queries and each value for N have been computed, and shown in Table 1. In particular, the average position $Av(R{k_{S}})$ in the sorted list where the BestComp were located have been computed, together with the following: their mean number of atoms $Av({N_{S}})$, their average shape similarity value $Av(T{c_{S}})$, their corresponding electrostatic similarity value $Av(T{c_{E}^{\mathit{Eval}}})$ when they are evaluated, and finally, their mean electrostatic similarity when they are optimized $Av(T{c_{E}})$.
As it can be seen, the predictions seem to improve in term of electrostatic similarity as the number N of selected molecules in the sorted list increases (see columns $Av(T{c_{E}^{\mathit{Eval}}})$ and $Av(T{c_{E}})$). In accordance with these results, the posterior comparison between LBVS-Shape and LBVS-Electrostatic methods has been carried out by setting $N=1751$.
Table 1
Influence of the parameter N in the results obtained by the LBVS-Shape method. For each value of N, the following average values from the 50 queries, are shown: position in the shape ranking ($Av(R{k_{S}})$), number of atoms ($Av({N_{S}})$), shape similarity score ($Av(T{c_{S}})$), electrostatic similarity evaluation score ($Av(T{c_{E}^{\mathit{Eval}}})$) and electrostatic optimized similarity value ($T{c_{E}}$).
| N | $Av(R{k_{S}})$ | $Av({N_{S}})$ | $Av(T{c_{S}})$ | $Av(T{c_{E}^{\mathit{Eval}}})$ | $Av(T{c_{E}})$ |
| 175 | 73 | 53 | 0.627 | 0.451 | 0.559 |
| 438 | 162 | 50 | 0.587 | 0.486 | 0.568 |
| 876 | 287 | 51 | 0.564 | 0.495 | 0.569 |
| 1313 | 324 | 50 | 0.559 | 0.497 | 0.570 |
| 1751 | 362 | 49 | 0.554 | 0.497 | 0.569 |
5.2 Performance Comparison Between LBVS-Shape and LBVS-Electrostatic Methods
To analyse the performance of both methods, we have conducted a study in which the selected 50 molecular queries are processed with reference to the FDA database. Notice that comparing a query with itself always reaches the maximum similarity value, both for electrostatic potential as well as for shape. Subsequently, these results were removed when ranking the compounds. In other words, the compounds given as a result are not the most similar ones, but the second compounds in the ranked list. Additionally, as previously mentioned, the traditional method has been carried out considering the total number of compounds in the database $N=1751$, so as to increase the probability of finding better predictions.
To illustrate how we generate the later summarizing tables, a sample of the results obtained by both methods when comparing a query to the molecules in the dataset is studied. In particular, the instance $\textit{Query}=DB01213$ is analysed. Notice that this is the example used to illustrate the stages of the LBVS-Shape method in Fig. 3. After that, the same instance is considered to exemplify the performance of the LBVS-Electrostatic method (see Fig. 4). Notice that this $\textit{Query}$ has been selected because it is small and it helps to see the main ideas of the paper very easily by using figures. However, the conclusions inferred from the associated results can be extrapolated to any other $\mathit{Query}$. As can be observed, the LBVS-Electrostatic technique solves an optimization problem to determine the electrostatic similarity, $T{c_{E}}$, between the pharmaceutical $\mathit{Query}$ and every ${\mathit{Target}_{E}}$ in the database. Afterwards, the list of compounds is sorted by the $T{c_{E}}$ value and the one located in first position, $R{k_{E}}=1$, is selected as the best prediction. Finally, to complete the study, optimization is carried out to calculate the shape similarity $T{c_{S}}$ between the chosen compound and the $\mathit{Query}$.
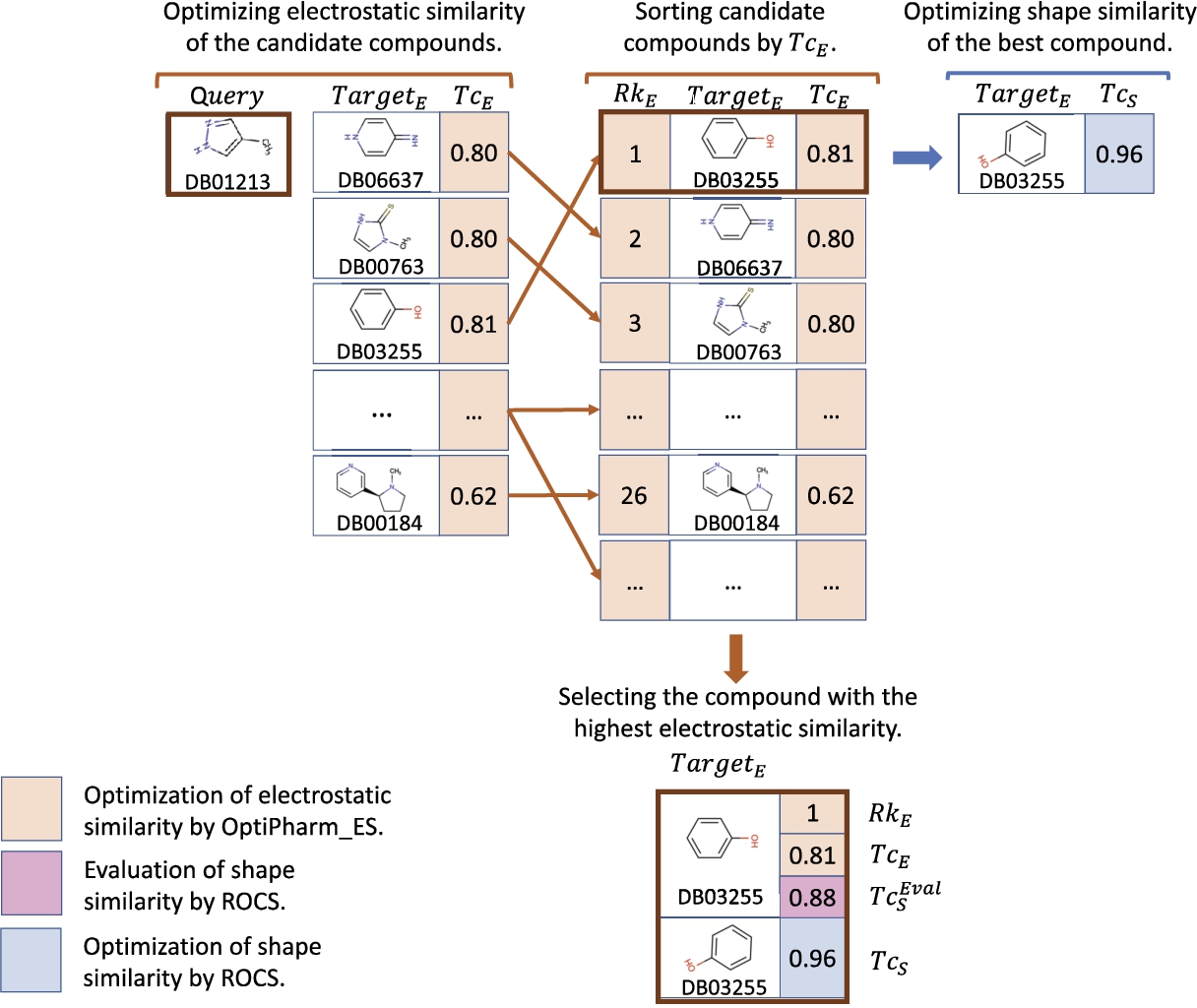
Fig. 4
An example of the performance of the LBVS-Electrostatic method for a particular case where $\mathit{Query}=DB01213$ is compared to the FDA database.
For the sake of clarity and comparison, the results shown in Figs. 3 and 4 are summarized in Table 2. The meaning of the columns as well as the particular values in the tables, are the ones previously explained and shown in each figure. The last row corresponds to the values associated with the best predictions. As can be observed, each method obtains a different compound as a top solution. LBVS-Shape provides the DB00184 molecule with a $T{c_{S}}=0.621$ and a $T{c_{E}^{\mathit{Eval}}}=0.500$. At the same time, LBVS-Electrostatic proposes the DB03255 compound as being the most similar to the query with $T{c_{E}}=0.810$ and $T{c_{S}^{\mathit{Eval}}}=0.880$. As such, the LBVS-Electrostatic method has not only obtained a more similar compound in terms of electrostatic potential, but also in shape. In Fig. 5, the final position for each case is shown.
Table 2
Summary of the results obtained for both LBVS-Shape and LBVS-Electrostatic methods for the query compound DB01213. The column notation, the colours included and the corresponding results come from Figs. 3 and 4, i.e. they maintain the same meaning as shown previously for those pictures. The last row indicates the results associated with the top solution selected for each method.
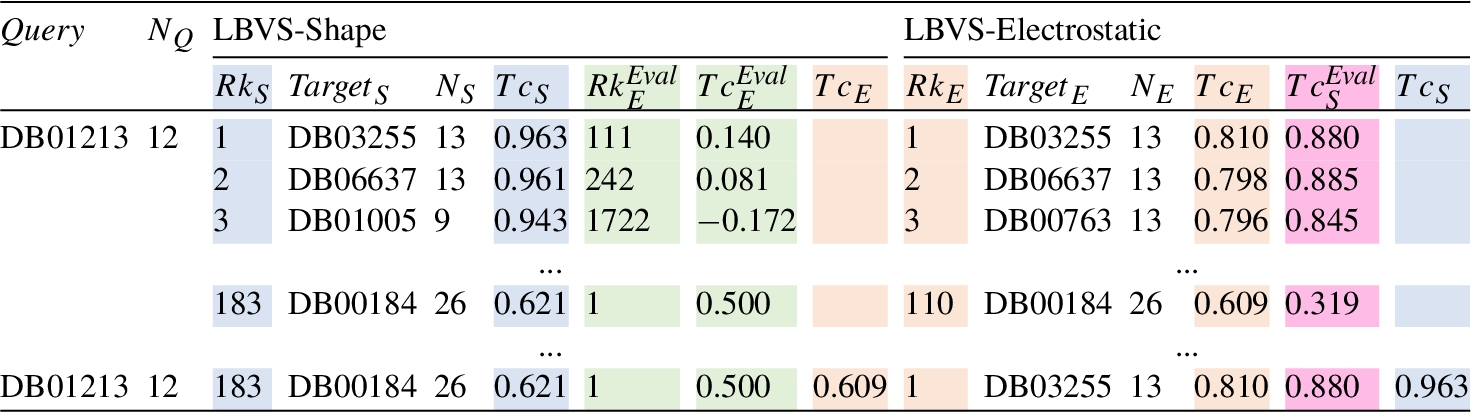
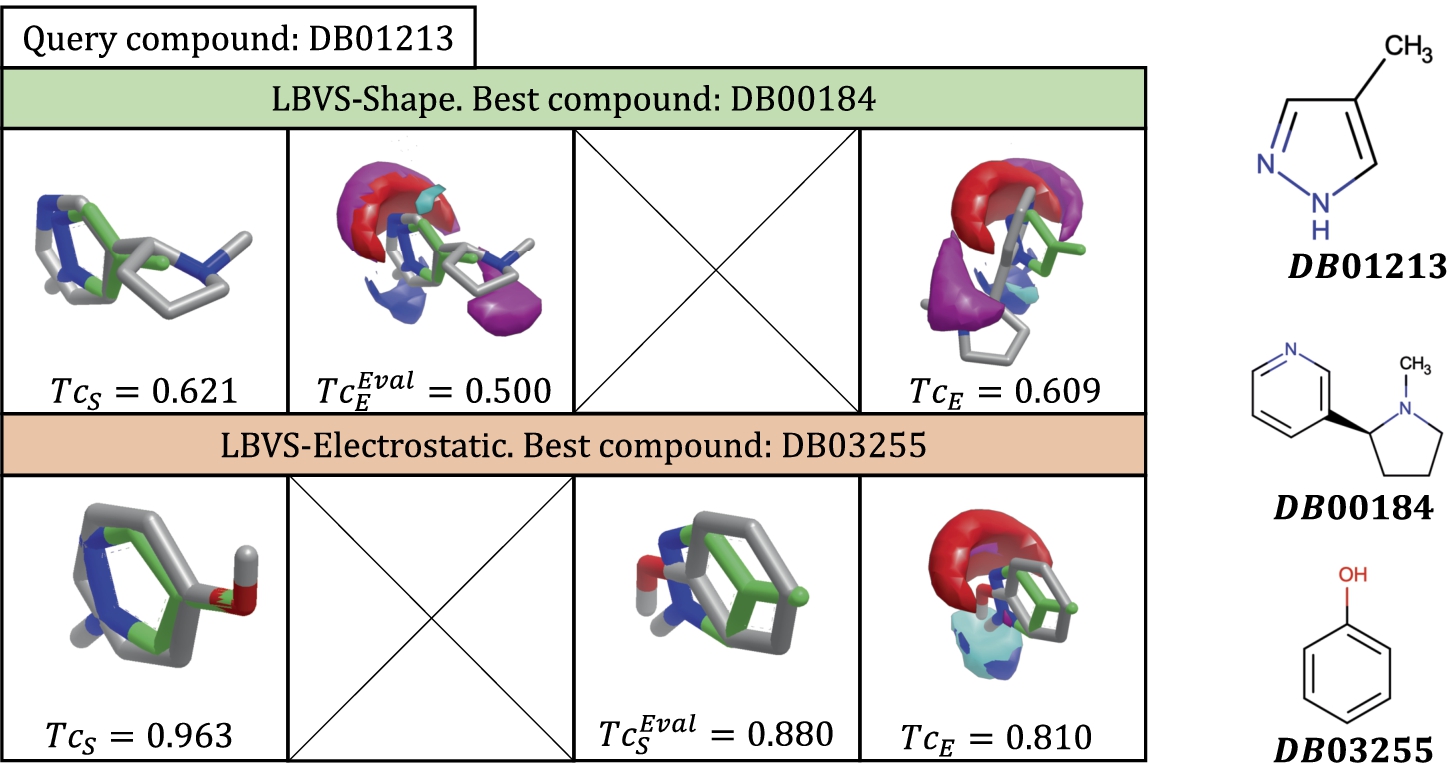
Fig. 5
Summary of results of LBVS-Shape and LBVS-Electrostatic where $\mathit{Query}=DB01213$. The Query compound is coloured green. Query electrostatic fields are coloured deep blue and red. Best compounds are shown in grey and their electrostatic potential fields, in light blue and pink.
Table 3
Rows are sorted by the number of atoms of queries. For each query, the same procedure explained in Table 2 is followed. The last row summarizes the average values for each column.
| $\mathit{Query}$ | ${N_{Q}}$ | LBVS-Shape | LBVS-Electrostatic | |||||||||
| $R{k_{S}}$ | ${\mathit{Target}_{S}}$ | ${N_{S}}$ | $T{c_{S}}$ | $T{c_{E}^{\mathit{Eval}}}$ | $T{c_{E}}$ | ${\mathit{Target}_{E}}$ | ${N_{E}}$ | $T{c_{E}}$ | $T{c_{S}^{\mathit{Eval}}}$ | $T{c_{S}}$ | ||
| DB00529 | 10 | 316 | DB05266 | 35 | 0.496 | 0.437 | 0.593 | DB00818 | 31 | 0.720 | 0.468 | 0.614 |
| DB01213 | 12 | 182 | DB00184 | 26 | 0.621 | 0.500 | 0.609 | DB03255 | 13 | 0.810 | 0.880 | 0.963 |
| DB00173 | 15 | 102 | DB00851 | 23 | 0.792 | 0.546 | 0.536 | DB01119 | 21 | 0.834 | 0.777 | 0.830 |
| DB00172 | 17 | 24 | DB00128 | 16 | 0.881 | 0.469 | 0.561 | DB00677 | 25 | 0.699 | 0.690 | 0.769 |
| DB00331 | 20 | 380 | DB00961 | 40 | 0.598 | 0.599 | 0.697 | DB01018 | 24 | 0.790 | 0.559 | 0.649 |
| DB01119 | 21 | 513 | DB00828 | 15 | 0.655 | 0.519 | 0.613 | DB00173 | 15 | 0.832 | 0.779 | 0.829 |
| DB02513 | 25 | 27 | DB01275 | 20 | 0.872 | 0.526 | 0.569 | DB06637 | 13 | 0.915 | 0.745 | 0.805 |
| DB00915 | 28 | 125 | DB00160 | 13 | 0.684 | 0.404 | 0.543 | DB00478 | 34 | 0.946 | 0.673 | 0.924 |
| DB01352 | 29 | 1 | DB00306 | 32 | 0.926 | 0.947 | 0.983 | DB00306 | 32 | 0.983 | 0.901 | 0.926 |
| DB01365 | 30 | 180 | DB01191 | 33 | 0.738 | 0.902 | 0.960 | DB01626 | 26 | 0.964 | 0.628 | 0.824 |
| DB00657 | 33 | 47 | DB06770 | 16 | 0.788 | 0.396 | 0.517 | DB01043 | 34 | 0.979 | 0.609 | 0.861 |
| DB00478 | 34 | 30 | DB00752 | 21 | 0.787 | 0.508 | 0.637 | DB01043 | 34 | 0.957 | 0.615 | 0.879 |
| DB01043 | 34 | 27 | DB00945 | 21 | 0.765 | 0.400 | 0.478 | DB00657 | 33 | 0.973 | 0.711 | 0.861 |
| DB00380 | 35 | 601 | DB00731 | 50 | 0.620 | 0.380 | 0.407 | DB08971 | 56 | 0.505 | 0.435 | 0.655 |
| DB00693 | 37 | 1034 | DB04575 | 59 | 0.525 | 0.362 | 0.429 | DB00692 | 40 | 0.454 | 0.391 | 0.783 |
| DB09185 | 37 | 243 | DB01233 | 43 | 0.722 | 0.839 | 0.506 | DB09021 | 39 | 0.916 | 0.429 | 0.650 |
| DB07615 | 40 | 71 | DB04552 | 28 | 0.704 | 0.861 | 0.866 | DB09218 | 28 | 0.892 | 0.610 | 0.574 |
| DB09219 | 40 | 123 | DB00321 | 44 | 0.698 | 0.347 | 0.329 | DB00316 | 20 | 0.450 | 0.249 | 0.462 |
| DB00674 | 42 | 279 | DB00575 | 23 | 0.688 | 0.505 | 0.653 | DB00514 | 45 | 0.662 | 0.415 | 0.695 |
| DB00887 | 45 | 209 | DB00232 | 31 | 0.642 | 0.401 | 0.454 | DB01127 | 39 | 0.662 | 0.378 | 0.576 |
| DB01198 | 45 | 273 | DB00209 | 59 | 0.648 | 0.748 | 0.768 | DB00123 | 25 | 0.894 | 0.334 | 0.491 |
| DB01155 | 48 | 1 | DB01165 | 46 | 0.858 | 0.671 | 0.818 | DB01208 | 50 | 0.899 | 0.385 | 0.835 |
| DB00246 | 50 | 467 | DB00268 | 44 | 0.542 | 0.843 | 0.852 | DB05271 | 48 | 0.877 | 0.391 | 0.604 |
| DB00381 | 53 | 525 | DB00573 | 32 | 0.577 | 0.285 | 0.278 | DB00630 | 27 | 0.377 | 0.397 | 0.524 |
| DB00876 | 54 | 576 | DB01002 | 49 | 0.516 | 0.395 | 0.505 | DB00774 | 28 | 0.532 | 0.276 | 0.524 |
| DB09237 | 54 | 380 | DB09092 | 44 | 0.580 | 0.759 | 0.824 | DB08998 | 40 | 0.902 | 0.447 | 0.596 |
| DB00254 | 55 | 1100 | DB00271 | 28 | 0.521 | 0.626 | 0.836 | DB00271 | 28 | 0.836 | 0.219 | 0.521 |
| DB01268 | 57 | 902 | DB09014 | 54 | 0.518 | 0.792 | 0.765 | DB01409 | 48 | 0.883 | 0.421 | 0.564 |
| DB01196 | 60 | 7 | DB00783 | 44 | 0.741 | 0.397 | 0.385 | DB08797 | 17 | 0.527 | 0.195 | 0.385 |
| DB01621 | 66 | 274 | DB00268 | 44 | 0.552 | 0.821 | 0.845 | DB04861 | 55 | 0.867 | 0.330 | 0.454 |
| DB09236 | 66 | 459 | DB00607 | 51 | 0.509 | 0.406 | 0.438 | DB00449 | 54 | 0.664 | 0.439 | 0.551 |
| DB00632 | 69 | 537 | DB00511 | 123 | 0.348 | 0.067 | 0.246 | DB00898 | 9 | 0.997 | 0.126 | 0.137 |
| DB08903 | 69 | 6 | DB01433 | 58 | 0.621 | 0.840 | 0.867 | DB01359 | 51 | 0.888 | 0.307 | 0.464 |
| DB01419 | 70 | 380 | DB09209 | 61 | 0.431 | 0.854 | 0.879 | DB01611 | 51 | 0.933 | 0.291 | 0.423 |
| DB00320 | 80 | 204 | DB00438 | 59 | 0.515 | 0.367 | 0.396 | DB00120 | 23 | 0.563 | 0.245 | 0.278 |
| DB00728 | 91 | 1383 | DB06204 | 40 | 0.399 | 0.688 | 0.761 | DB09131 | 3 | 0.874 | 0.068 | 0.101 |
| DB00503 | 98 | 655 | DB00206 | 84 | 0.371 | 0.256 | 0.243 | DB01144 | 22 | 0.401 | 0.180 | 0.280 |
| DB01232 | 100 | 639 | DB06480 | 52 | 0.389 | 0.691 | 0.741 | DB09089 | 58 | 0.791 | 0.290 | 0.387 |
| DB00309 | 110 | 385 | DB01603 | 45 | 0.455 | 0.241 | 0.297 | DB00319 | 63 | 0.467 | 0.267 | 0.534 |
| DB04786 | 120 | 4 | DB09158 | 82 | 0.377 | 0.424 | 0.708 | DB09159 | 18 | 0.910 | 0.108 | 0.120 |
| DB09114 | 130 | 117 | DB00595 | 57 | 0.376 | 0.273 | 0.506 | DB00583 | 26 | 0.876 | 0.183 | 0.190 |
| DB06439 | 137 | 657 | DB01628 | 39 | 0.383 | 0.336 | 0.425 | DB00878 | 64 | 0.488 | 0.274 | 0.423 |
| DB01078 | 140 | 34 | DB00204 | 56 | 0.424 | 0.201 | 0.259 | DB01085 | 31 | 0.540 | 0.169 | 0.211 |
| DB01590 | 151 | 1037 | DB01193 | 53 | 0.265 | 0.248 | 0.358 | DB00653 | 6 | 0.529 | 0.070 | 0.100 |
| DB04894 | 152 | 82 | DB01199 | 87 | 0.361 | 0.348 | 0.484 | DB09131 | 3 | 0.662 | 0.006 | 0.040 |
| DB00403 | 167 | 325 | DB04855 | 84 | 0.261 | 0.325 | 0.395 | DB06335 | 49 | 0.575 | 0.120 | 0.198 |
| DB00732 | 169 | 640 | DB08967 | 52 | 0.222 | 0.236 | 0.353 | DB00653 | 6 | 0.508 | 0.051 | 0.069 |
| DB00050 | 194 | 7 | DB01369 | 141 | 0.349 | 0.238 | 0.383 | DB00516 | 19 | 0.385 | 0.059 | 0.080 |
| DB06699 | 221 | 1465 | DB01245 | 56 | 0.119 | 0.365 | 0.513 | DB09131 | 3 | 0.642 | 0.013 | 0.029 |
| DB06219 | 229 | 69 | DB01369 | 141 | 0.293 | 0.277 | 0.394 | DB09131 | 3 | 0.670 | 0.009 | 0.021 |
| Mean | 74 | 362 | – | 49 | 0.554 | 0.497 | 0.569 | – | 31 | 0.738 | 0.372 | 0.505 |
Once the specific case of DB01213 has been explained in detail, the results of the 50 queries have been summarized in Table 3. Columns $R{k_{E}^{\mathit{Eval}}}$ and $R{k_{E}}$ have been removed in this table because their values are always 1. The last row summarizes the average of the results.
As evidenced, LBVS-Electrostatic obtains on average $T{c_{E}}=0.738$, which is higher than that given by LBVS-Shape, $T{c_{E}^{\mathit{Eval}}}=0.497$. Similar conclusions can be inferred when comparing the $T{c_{E}}$ average values for both methods. Additionally, when the results are analysed individually, we can see that LBVS-Electrostatic provides solutions with higher $T{c_{E}}$ values than those achieved by LBVS-Shape. In fact, in 48 out of 50 cases, LBVS-Electrostatic obtains a different compound than that reached by LBVS-Shape.
Regarding shape similarity, it is possible to infer that, on average, the methods are equivalent in terms of accuracy of the predictions, i.e. LBVS-Shape obtains an average value of $T{c_{s}}=0.554$ while LBVS-Electrostatic reaches a mean value of $T{c_{s}}=0.505$. Furthermore, analysing the obtained results individually, we can see that in 2 out of 50 cases, LBVS-Electrostatic offers better or equivalent predictions than that achieved by LBVS-Shape in terms of shape (see columns $T{c_{s}}$ in LBVS-Shape and $T{C_{s}^{\mathit{Eval}}}$ in LBVS-Electrostatic). It means that cases exist where two compounds can be very similar in terms of electrostatic potential, although they can be very different in terms of three-dimensional shape. It means that those solutions could not be obtained by using the methodology followed by the traditional LBVS-Shape method, since it only focuses on the compounds with the highest similarity in shape.
Making a somewhat more detailed approach for compounds smaller than 50 atoms, which means the first 23 query compounds in the table, there are 5 cases where the difference is less than 0.05 (DB00529, DB00173, DB00331, DB00915 and DB01352) and in another 3 cases the difference is 0.1 (DB01043, DB07615 and DB01268). Considering the values of these 7 cases in which the shape LBVS-Electrostatic is smaller than that of LBVS-Shape, the average difference is 0.048, while the mean gain in electrostatic similarity for those 7 compounds is 0.271. In large compounds, which includes 27 queries, there are only two cases with similar characteristics, which are compounds DB09236 with a difference of 0.07 and DB06699 with a difference of 0.013, both of them for shape similarity. In view of these results, the LBVS-Electrostatic method seems to be justified when proposing new solutions for small compounds.
However, not all the improvements are related to electrostatic fields. The optimization of electrostatic potential using OptiPharm_ES might allow a better solution to be found in terms of shape too. Compounds DB01119 and DB1213 in Table 3 are some outstanding examples. For example, in the case of $\mathit{Query}=DB01119$, the best compound found by LBVS-Shape is DB00828 with $T{c_{S}}=0.655$ and $T{c_{E}^{\mathit{Eval}}}=0.519$. Moreover, LBVS-Electrostatic’s best compound is DB00173. It has a better $T{c_{E}}$, i.e. 0.829, but also the position of those compounds after the electrostatic optimization is improved, $T{c_{S}^{\mathit{Eval}}}=0.779$.
5.3 ZAP Toolkit Accuracy Problem
The ZAP Toolkit has been widely used in the literature to calculate the electrostatic similarity score for two compounds (Boström et al., 2013; Tresadern et al., 2009; Chu and Gochin, 2013; Kim et al., 2015; Kossmann et al., 2016; Woodring et al., 2017; Maccari et al., 2011; Kim et al., 2016; López-Ramos and Perruccio, 2010; Hevener et al., 2012; Kaoud et al., 2012; Tiikkainen et al., 2009; Massarotti et al., 2014; Oyarzabal et al., 2009; Haque and Pande).
In this subsection we would like to remark that the ZAP Toolkit can return an erroneous value, which was discovered when using OptiPharm_ES. During the optimization procedure, OptiPharm_ES can progressively separate two input compounds aimed to escape from local optima and explore the searching space in depth. In fact, it is possible to analyse cases where no overlap exists between the input molecules. During the analysis of the results, we discovered that cases exist where the ZAP Toolkit can overflow, mainly when situations such as the previously mentioned happen. See Fig. 6 to see a particular example. Herein, compound DB01365 remains fixed on the left while compound DB00459 occupies three positions (red, blue and pink). The red compound obtains an electrostatic similarity value of 1. The light blue compound is displaced half a unit to the left, i.e. closer to the reference compound and its similarity value is 0.38. The pink compound is shifted 0.5 units to the right, that is, away from the reference compound. Its similarity value is 0. Calculations can be made using the ZAP Python script available at https://docs.eyesopen.com/toolkits/python/zaptk/thewayofzap.html in the Electrostatic Similarity section.
This problem has been solved in OptiPharm_ES by considering the poses with the previously mentioned problem unfeasible. It means that they are no longer considered during the optimization process.
6 Conclusions
In this work, a new approach to solve the LBVS problem based on the electrostatic similarity has been put forward. It has been called LBVS-Electrostatic. This methodology is based on the direct optimization of electrostatic similarity. For this purpose, a new version of OptiPharm has been used. Conversely, the method proposed in the literature, which has been named LBVS-Shape throughout the paper, looks for a sublist of the top compounds with the highest shape similarity by using ROCS, to later evaluate their electrostatic similarity with ZAP. In this work, a study to analyse the influence of the number of compounds in such a sublist has been carried out. As the results have shown, the larger the number of molecules considered, the better the prediction obtained in terms of electrostatic similarity. From this conclusion, a computational study has been carried out to compare the new method LBVS-Electrostatic with the one in the literature LBVS-Shape. To increase the probability of finding good predictions, LBVS-Shape has been executed taking into account the whole database prior to the electrostatic similarity evaluation. Even so, LBVS-Electrostatic performs better than LBVS-Shape, achieving better predictions in electrostatic potential for the 50 queries included in the study. Regarding the shape similarity, both methods behave in a similar fashion, on average obtaining compounds with similar shape similarity values. It is important to mention that the new methodology proposed in this paper is novel, which means that the predictions proposed have not been analysed previously.
Finally, we have shown that ZAP can return erroneous values. This is an important discovery, since it is the most commonly used software in the literature to measure the electrostatic similarity.
In the future, we have plans to implement this objective function from scratch, but for the study at hand, we considered that it was more important to compare it with the state-of-the-art software. Additionally, other functions measuring the pharmacophore similarity will be implemented. Finally, we will analyse the problem from a multi-objective perspective, where shape an electrostatic similarity are optimized simultaneously.