Abstract
Crossover operators play a very important role by creation of genetic algorithms (GAs) which are applied in various areas of computer science, including combinatorial optimization. In this paper, fifteen genetic crossover procedures are designed and implemented using a modern C# programming language. The computational experiments have been conducted with these operators by solving the famous combinatorial optimization problem – the quadratic assignment problem (QAP). The results of the conducted experiments on the characteristic benchmark instances from the QAP instances library QAPLIB illustrate the relative performance of the examined crossover operations.
All crossover procedures are publicly available with the intention that the GA researchers will choose a procedure which suits the individual demand at the highest degree.
1 Introduction
Many optimization problems belong to the class of NP-hard problems (Garey and Johnson,
1979). These problems pose a real challenge for the researchers who develop algorithms for solving such problems. A considerable progress is achieved by using, in particular, genetic algorithms, which are based on imitation of evolution occurring in live nature (Holland,
1975; Goldberg,
1989; Sivanandam and Deepa,
2008; Simon,
2013; Heaton,
2014).
The GA developers are constantly seeking to enhance the performance of GAs. The goal is to create the genetic algorithms that are in competitive advantage with respect to other types of (meta)heuristic optimization algorithms. To achieve this goal, there is a high need in developing and investigating the essential “building components” of the genetic algorithms, among others, the crossover (recombination) operators (Herrera
et al.,
2003). Despite the significant progress in the design of crossover operators during the last decades, there still is a room for further improvement of this kind of operators (Deep and Thakur,
2007; Maenhout and Vanhoucke,
2008; Abdoun and Abouchabaka,
2011; Kaya,
2011; Magalhães-Mendes,
2013).
The crossover operators (along with mutation operators) constitute the basis for successful functioning of GAs (Misevičius
et al.,
2005). Here, the key idea is that a new genetic information is created by reordering the genetic code which is present in two (or more) predecessors. In this way, the inheritance of the existing traits and the acquirement of completely new features well fit each other. In the course of the crossover procedure, the successor inherits what the best is accumulated in the predecessors; at the same time, a novel combination of the genetic code – which is absent in the parents – comes into being. Thus, the optimization process gets diversified by exploring new and promising areas in the search space. This synergy of creativeness and exploration is probably the most significant reason why the genetic algorithms are so successful (Goldberg,
2002).
In this paper, we consider, in particular, the genetic crossover operators of different kind and expose the results obtained from the numerical experiments with these operators. Although the principles of functioning of the majority of the considered operators are not new, the crossover implementations in modern C# programming language appear quite original. We also propose three innovative crossover operations.
-
• First, we offer an enhancement of the so-called swap-path crossover – swap-path descent crossover – which benefits from taking into account the problem-specific information.
-
• Second, the so-called universal crossover operator is proposed, where the goal is to provide more flexibility and versatility in the crossover process.
-
• Third, a gene translocation procedure is introduced, which is non-traditional in the sense that it is based on “many-parents-many-children” approach, rather than a usual “two-parents-one-child” scheme.
All these crossover operators are publicly available for the researchers who want to contribute to the further progress of genetic and evolutionary computation.
The paper is structured as follows. Firstly, some definitions are given and basic features of the crossover operations are described. Then, the crossover operator details are provided. The newly proposed crossover operators are marked with the symbol ‘⋆’. Finally, the results of experimental comparison of the considered crossover procedures are presented. The paper is completed with concluding remarks.
2 Preliminary Remarks
In the most general case, the crossover process enables to transmit the genetic code of two or more agents (called parents) to one or more successors (called children) in a specified deterministic-like way. Ideally, in the crossover operation, the chromosomes of two parents are recombined in such a way that the child’s chromosome contains only the parents’ genes. This is the main distinguishing feature of crossover process and, thus, crossover operation is quite opposite to mutation, which is of pure stochastic nature. However, it should be noted that the crossover process can involve indirect randomness due to explicit and implicit mutations (Misevičius,
2006).
Let us consider (without a significant loss of generality) the crossover operators intended for the permutation-based combinatorial optimization problems. Remember that the permutation
p is formally defined as a collection
$p=(p(1),p(2),\dots ,p(i),\dots ,p(n))$;
$p(i)\in \{1,2,\dots ,n\}$,
$i=1,2,\dots ,n$;
$p(i)\ne p(j)$, i,
$j=1,2,\dots ,n$,
$i\ne j$. Indeed, it is not very difficult to modify the permutation-based crossovers so that they become suitable also for the classical genetic algorithms, which commonly use the bit string-based crossovers. Mathematically, a two-parents-one-child crossover can be described using a binary operator
ψ:
${\Pi _{n}}\times {\Pi _{n}}\to {\Pi _{n}}$ such that:
where
${\Pi _{n}}$ denotes a set consisting of all possible permutations of size
n;
${p^{\prime }}$,
${p^{\prime\prime }}$,
${p^{\circ }}$ are permutations (here,
${p^{\prime }}$,
${p^{\prime\prime }}$ denote the parents,
${p^{\circ }}$ denotes the offspring). It appears that the offspring may sometimes be identical to one of the parents, especially in the cases where the parents tend to be very similar. The permutation is usually associated with the individual’s chromosome; then, the permutation element
$p(i)$ corresponds to a gene occupying the
ith locus of the current chromosome (consequently,
n is the length of the chromosome).
Formally, the crossover operator must ensure that the offspring’s chromosome necessary inherits the genes which are common for both parents, i.e.:
here, again,
${p^{\prime }}$,
${p^{\prime\prime }}$,
${p^{\circ }}$ denote parents and an offspring, respectively.
Every element in the permutation is unique and the crossover operation should address this aspect. It doesn’t concern the bit strings. Meanwhile, in the case of permutations, some discrepancies are possible, i.e. the so-called “foreign” (random) genes may occur. This does not mean that the crossover is incorrect – simply, this is caused by specific properties of permutations.
A plenty of variants of various computer realizations of crossover operators exist, depending on the details and peculiarities of implementation. There is a lot of freedom here for both the implementers and end-users of the crossover operators: the implementers offer new operator variations and the end-users choose them according to their special needs.
3 Genetic Crossover Operators Used in the Study
3.1 Representative Examples of Known Crossover Operators and Their Variants
3.1.1 Point-Based Crossovers
3.1.1.1 One-Point Crossover.
This is very likely the most commonly used crossover operator for the genetic algorithms (Goldberg,
1989). It is not difficult to implement, but still quite efficient. Roughly, the basic idea is as follows. A single crossover point is chosen in one of the two chromosomes. The point position
x can be determined by generating a (pseudo-)random number within the interval
$[1,n-1]$ (
n is the chromosome length). The offspring is obtained by copying
x genes from one parent, the rest of the genes are copied from the second parent. The feasibility of the offspring must be preserved (see Fig.
1).
3.1.1.2 Modified One-Point Crossover.
A slight disadvantage of the straightforward one-point crossover lies in tendency of having certain genes more “ordered” than others (compare, for example, the gene sequences “82396” and “1475” in Fig.
1). In the modified crossover, either the genes from 1 to
x, or the genes from
x to
n are copied with probability
$\frac{1}{2}$ from one of the parents, the rest are copied from the opposite parent.
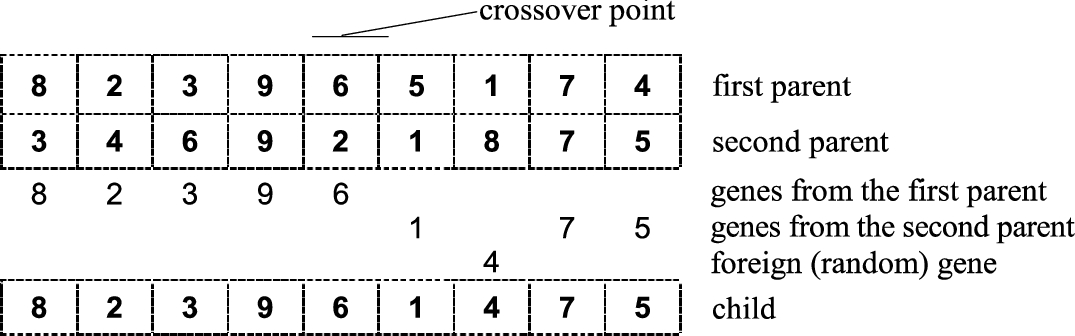
Fig. 1
Graphical illustration of one-point crossover.
3.1.1.3 Two-point crossover.
The two-point crossover works similarly to the one-point crossover, except that two crossover points
${x_{1}}$ and
${x_{2}}$ $(1\leqslant x1<{x_{2}}\leqslant n)$ are used. In a similar fashion, one can construct a three-point crossover, and so on (De Jong and Spears,
1992).
3.1.2 Uniform Crossovers
3.1.2.1 Uniform Crossover – I.
The principle of the uniform crossover is also simple (Syswerda,
1989). At first, the common genes are copied to the offspring’s chromosome. Then, the unoccupied loci (positions) in the offspring’s chromosome are scanned from left to right and the empty loci are assigned the genes – one at a time – from one of the parents with probability
$\frac{1}{2}$, i.e.
${p^{\circ }}(i)=\left\{\begin{array}{l@{\hskip4.0pt}l}{p^{\prime }}(i),\hspace{1em}& \varsigma <\frac{1}{2}\\ {} {p^{\prime\prime }}(i),\hspace{1em}& \text{otherwise};\end{array}\right.$ here,
ζ is a uniformly distributed (pseudo-)random number from the interval
$[0,1]$. The assigned gene must be unique. In case there are still empty loci, they are filled in with random genes (see Fig.
2).
3.1.2.2 Uniform Crossover −II (Quasi-Uniform Crossover).
The uniform crossover can be modified in such a way that the probability of the assignment of genes is no longer equal to $\frac{1}{2}$, but is greater or less than $\frac{1}{2}$. In this way, we can prefer one of the parents (for example, the better parent).
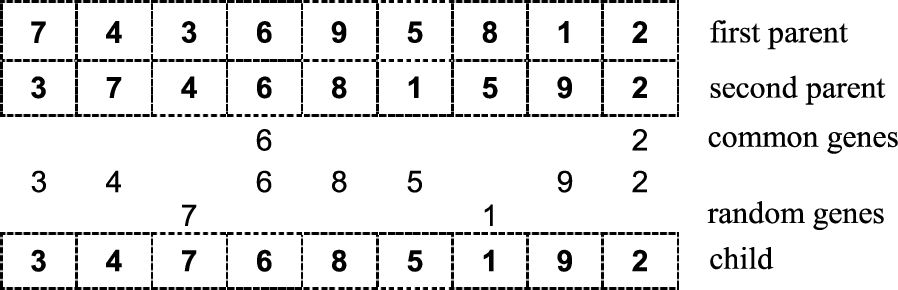
Fig. 2
Graphical illustration of uniform crossover.
3.1.2.3 Shuffle Crossover.
The shuffle crossover is obtained by randomly reordering the parents’ genes before applying the uniform crossover (Caruana
et al.,
1989). The same rearrangement rule must be used for both parents. After the uniform crossover is finished, the same (initial) rearrangement rule is again applied (see Fig.
3).
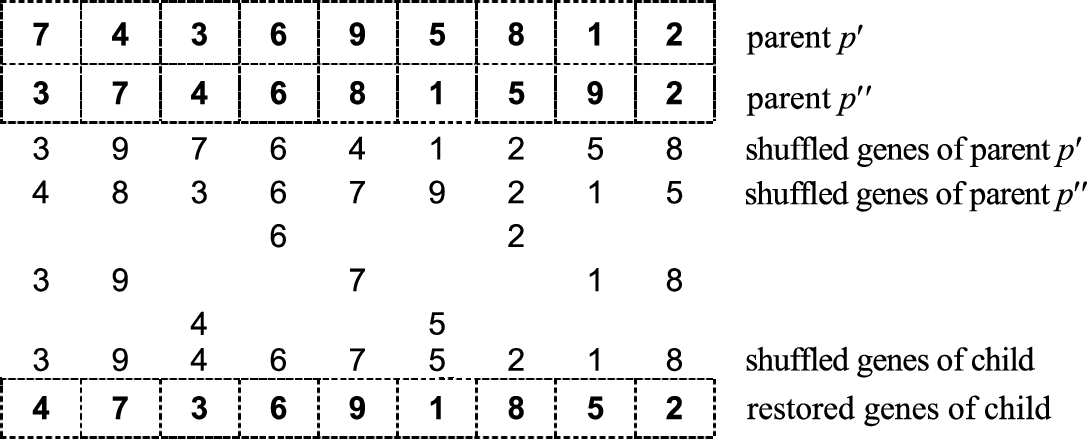
Fig. 3
Graphical illustration of shuffle crossover.
3.1.3 Partially-Mapped Crossover
Partially-mapped crossover (PMX) can be seen as a modified variant of the
k-point (multi-point) crossover. The initial version of PMX was designed for the travelling salesman problem (Goldberg and Lingle,
1985), but it may be adapted also for other optimization problems. The basic principle relies on the so-called mapping sections (the chromosome segments between mapping points). So, at first, the segments of the chromosome of the chosen parent are moved to the offspring’s chromosome. The same is done for the other parent. At last, the empty loci (if any) are filled in in a random way (see Fig.
4). Note that if
$k=n$, then PMX becomes very similar to the uniform crossover.
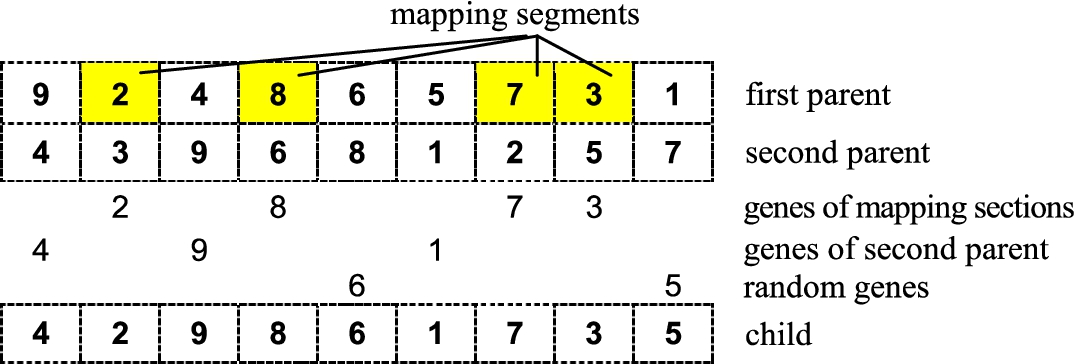
Fig. 4
Graphical illustration of partially-mapped crossover.
3.1.4 Swap-Path Crossovers
3.1.4.1 Swap-Path Crossover – I.
Swap-path crossover (SPX) (Glover,
1994) differs from the above crossover operators in that it is oriented basically to the permutation-based problems. The main distinguishing feature of SPX is that instead of transferring genes from parents to a child, the genes are, so to speak, rearranged in the chromosomes of the parents. Let
$({p^{\prime }},{p^{\prime\prime }})$ be a pair of parents. Then, the process starts from some chosen position and the loci are scanned from left to right. The process continues until a predefined number of swaps,
s,
$(s<n)$ are performed. If, in the current position, the genes are the same for both parents, then one moves to the next locus; otherwise, a pairwise interchange of genes of the parents’ chromosomes is accomplished. The interchange is performed in both parents. For example, if the current locus index is equal to
i and
$a={p^{\prime }}(i)$,
$b={p^{\prime\prime }}(i)$, then there exists a locus
j such that
$b={p^{\prime }}(j)$,
$a={p^{\prime\prime }}(j)$; then, after a swap,
${p^{\prime }}(i)=b$,
${p^{\prime\prime }}(i)=a$, in addition,
${p^{\prime }}(j)=a$,
${p^{\prime\prime }}(j)=b$. Consequently, the new chromosomes
${p^{\prime\prime\prime }}$,
${p^{\prime \prime \prime \prime }}$ are produced. Thus, in the next generation, a pair
$({p^{\prime\prime\prime }},{p^{\prime \prime \prime \prime }})$ is considered, and so on. The graphical example of SPX is shown in Fig.
5.
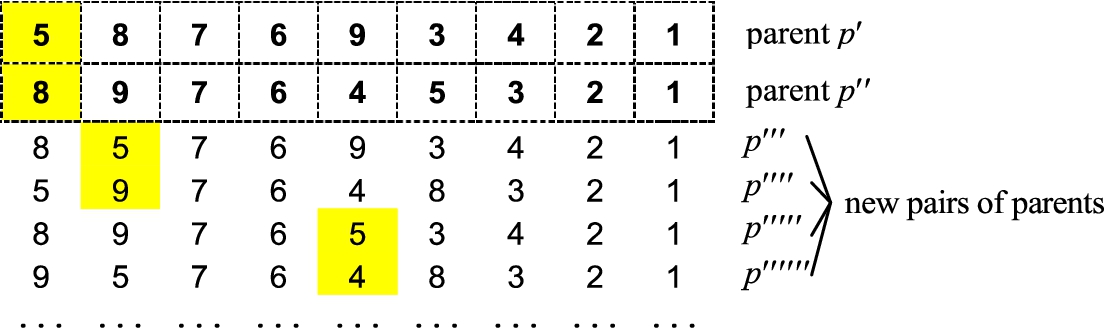
Fig. 5
Graphical illustration of fragment of swap-path crossover.
3.1.4.2 Swap-Path Crossover – II (Heuristic Swap-Path Crossover).
A modification to the standard SPX can be achieved when the best offspring (with respect to the fitness of the offspring) is retained in the course of gene interchanges (Ahuja
et al.,
2000). In this way, we get a heuristic swap-path crossover, where the quality of the offspring is taken into account.
3.1.5 Cycle Crossover
The cycle crossover (CX) (Oliver
et al.,
1987) slightly resembles the swap-path crossover and is based on the pairwise gene interchanges. The principal property of CX is the ability to produce the offspring without distortion of the genetic code; in other words, CX enables to create the chromosome with no foreign genes. The negative aspect of CX is that the offspring may genetically be very close to their predecessors or even identical to them. (For example, if in the given illustration (see Fig.
6) the second chromosome is a bit changed to “254169783”, then, after the cycle crossover, the offspring’s chromosome becomes duplicate to the chromosome of the first parent.)
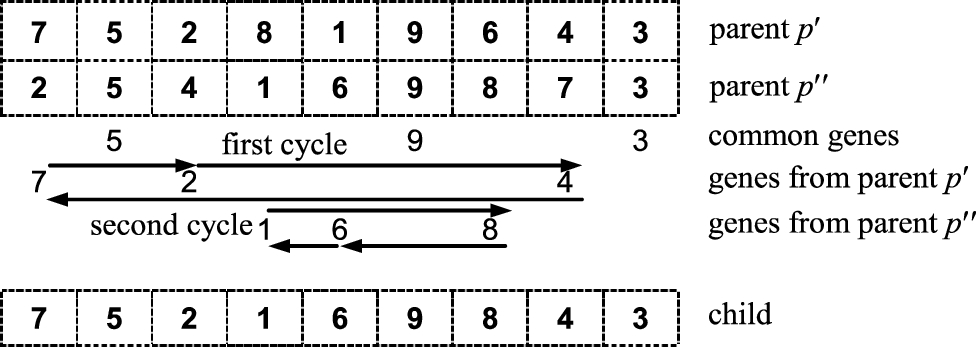
Fig. 6
Graphical illustration of cycle crossover.
3.1.6 Cohesive Crossover
The cohesive crossover was proposed by Z. Drezner to efficiently recombine individuals’ genes by solving the quadratic assignment problem. In this case, the appropriateness of the genes – which is calculated according to the problem data – is taken into consideration. From the several recombinations of genes, the recombination is selected that minimizes the objective function. The details of implementation of the cohesive crossover are described in Drezner (
2003).
3.1.7 Multi-Parent Crossover
In the multi-parent crossover, several (or all) members of a population participate in creation of the offspring (Eiben
et al.,
1994). More precisely, the
ith locus of the offspring’s chromosome
${p^{\circ }}$ is assigned the value
j with the probability
$\text{P}({p^{\circ }}(i)=j)$ (under condition that the value
j has not been utilized before).
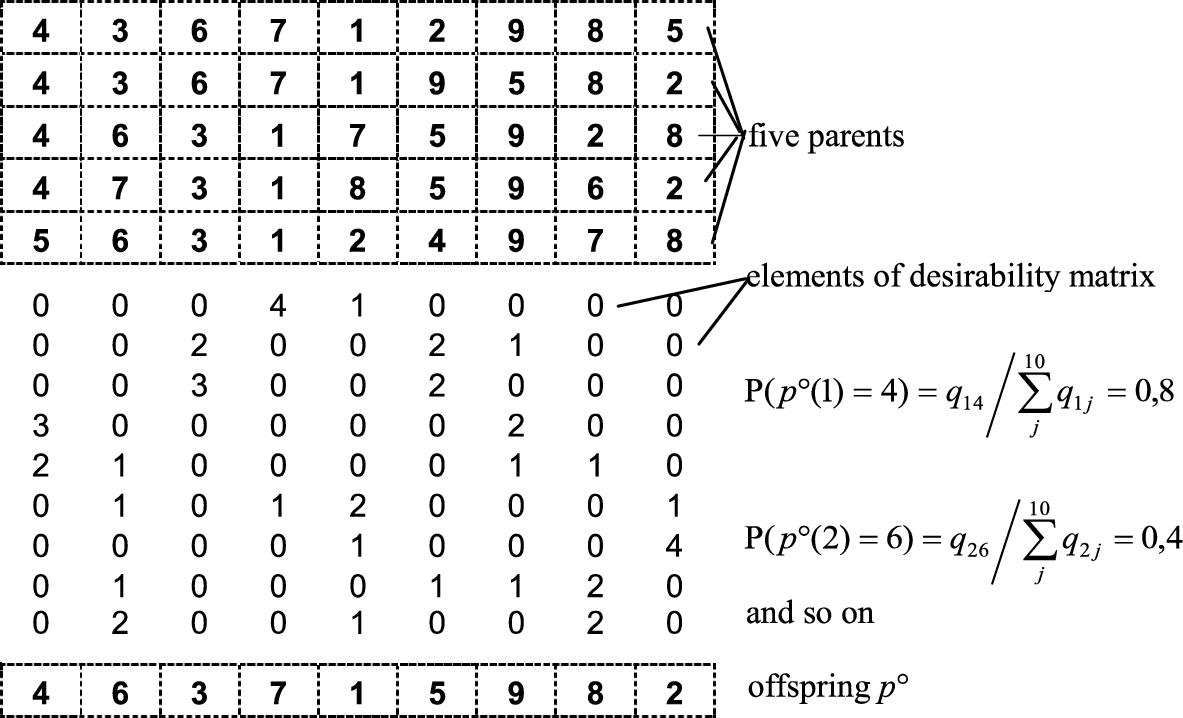
Fig. 7
Graphical illustration of multi-parent crossover.
The probability
$\mathrm{P}({p^{\circ }}(i)=j)$ is calculated according to the formula:
where
$\mathrm{P}({p^{\circ }}(i)=j)$ denotes the probability that
${p^{\circ }}(i)=j$;
${q_{ij}}$ is an element of a desirability matrix
$\textbf{Q}={({q_{ij}})_{n\times n}}$; here,
${q_{ij}}$ denotes the number of times that the
ith locus takes the value
j in the parental chromosomes. Of course,
${q_{ij}}\leqslant t$ (
t is the number of parents). If there exist several values
$({j_{1}},{j_{2}},\dots \hspace{0.1667em})$ with the same probability, then one of them is chosen randomly. The above rule applies to all genes of the offspring (see Fig.
7).
3.2 Newly Proposed Crossover Operators
3.2.1 Swap-Path Descent Crossover${^{\mathrm{\star }}}$
The swap-path descent crossover (SPDX) is similar to the heuristic swap-path crossover in that it takes into consideration the values of the objective function. The SPDX operator resembles the descent local search (hill-climbing) procedure in some sense. The advantage of this operator is in the dynamic evaluation of the offspring fitness: only the gene interchanges that improve the value of the objective function and lead to a better fitness of the offspring are accepted.
3.2.2 Universal Crossover${^{\mathrm{\star }}}$
The universal crossover (UNIVX) distinguishes for its versatility and the possibility of flexible usage. It is somewhat similar to what is known in the literature as a simulated binary crossover (Deb and Agrawal,
1995).
Our operator is based on the use of a random mask. There are four controlling parameters: α, β, γ, χ. The mask length is equal to α, where α is a (pseudo-)random number within the interval $[{\varepsilon _{1}},n]$, n is the chromosome length, ${\varepsilon _{1}}=\lfloor h\cdot n\rfloor $, h – the user’s parameter close to 1, for example, 0.9. The mask contains binary digits 0 and 1, where 1 means that the corresponding gene of the first parent needs to be cloned and 0 means that the gene of the second parent is cloned. The main goal is to create the mask as versatile as possible. The randomness of the mask can be controlled by parameters β, γ. The parameter β ($\beta \in [{\varepsilon _{2}},{\varepsilon _{3}}]$, $0<{\varepsilon _{2}}\hspace{2.5pt}\leqslant {\varepsilon _{3}}<1$) enables to regulate how many 0’s and 1’s there are in the mask: the more value of β, the bigger total number of 1’s is in the mask, and vice versa. The arrangement of bits is dictated by the parameter γ. The bit generation itself can be accomplished by using an (indeterministic) sorting algorithm, which may be viewed as a kind of “anytime” algorithm. If the sorting algorithm is interrupted at some random moment, one gets the randomized sequence of bits. The moment of interruption is defined by the number z, where $z=\gamma \cdot w$, here γ is a (pseudo-)random real number from the interval $[0,1]$, w – maximum number of iterations of the sorting algorithm. (For example, if the bits of the mask “000001111” are sorted in descending order and the algorithm is stopped when $\gamma =0.9$, then the random mask “101100010” is generated.) Having the mask generated, the decision is made as to about what genes have to be transmitted to the offspring’s chromosome. The starting position of the transferred genes, χ, is generated randomly so that $\chi \in [1,n]$. At last, the empty loci (if any) are filled in randomly.
The illustrative example of the universal crossover with the parameters
$\alpha =9$,
$\beta =\frac{4}{9}$,
$\gamma =0.9$,
$\chi =1$ is presented in Fig.
8.
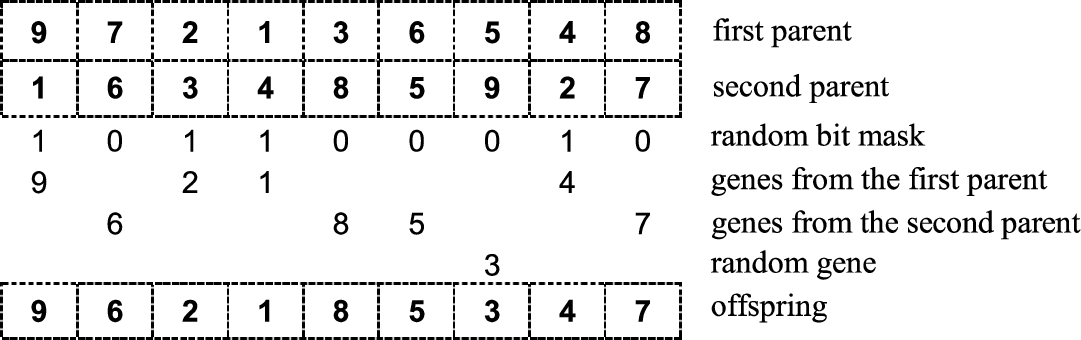
Fig. 8
Graphical illustration of universal crossover.
3.2.3 Gene Translocation${^{\mathrm{\star }}}$
So far, a single child is created from two or more parents. In the gene translocation (GT) procedure, many children are produced from many parents. The GT procedure is performed in an iterative way. The total number of iterations is equal to m, $m=\max \{1;0,01\cdot c\cdot d(n-1)\}$, where c denotes a translocation coefficient (in percent) $(0<c\leqslant 100)$, d is the population size and n denotes the chromosome length. At each iteration of the GT procedure, three random integers ${\zeta _{1}},{\zeta _{2}},{\zeta _{3}}$ are generated. The first two integers (${\zeta _{1}},{\zeta _{2}}$) are from the interval $[1,d]$, ${\zeta _{1}}\ne {\zeta _{2}}$. The integer ${\zeta _{3}}$ is within the interval $[1,n]$. Let (${p_{{\zeta _{1}}}},{p_{{\zeta _{2}}}}$) be a pair of parents such that ${p_{{\zeta _{1}}}}$ is the ${\zeta _{1}}$th member of the current population, meanwhile ${p_{{\zeta _{2}}}}$ is the ${\zeta _{2}}$th member of the population. Then, if the genes at the ${\zeta _{3}}$th locus are the same for both parents, one continues with the next iteration; otherwise, the pairwise gene interchange is performed (similarly to the swap-path crossover). That is, if the current locus index is equal to ${\zeta _{3}}$ and ${a_{{\zeta _{1}}}}={p_{{\zeta _{1}}}}({\zeta _{3}})$, ${a_{{\zeta _{2}}}}={p_{{\zeta _{2}}}}({\zeta _{3}})$, then, after the interchange, either ${p_{{\zeta _{1}}}}({\zeta _{3}})$ becomes equal to ${a_{{\zeta _{2}}}}$, or ${p_{{\zeta _{2}}}}({\zeta _{3}})$ equal to ${a_{{\zeta _{1}}}}$. The iterations of gene translocations are continued until the maximum number of iterations has been reached. As a result, the new population is produced in which there are c percent new genes.
An illustrative example of the GT procedure with the parameters
$n=9$,
$d=4$,
$c=20\% $,
$m=6$ is shown in Fig.
9.
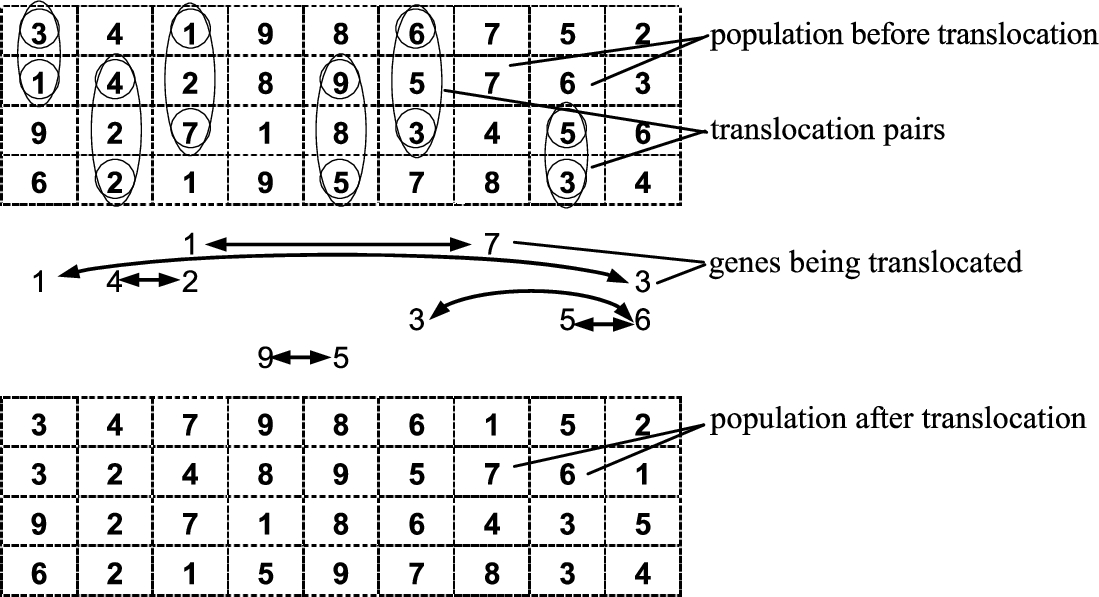
Fig. 9
Graphical illustration of gene translocation.
4 Computational Experiments
We have conducted the computational experiments in order to compare the efficiency of the considered crossover operators. The experiments have been carried out on the basis of the difficult combinatorial optimization problem – the quadratic assignment problem (Çela,
1998). This problem can be concisely formulated as follows. Given two integer matrices
$\textbf{A}={({a_{ij}})_{n\times n}}$,
$\textbf{B}={({b_{kl}})_{n\times n}}$ and a set
${\Pi _{n}}$ of permutations of the integers from 1 to
n, find a permutation
$p=(p(1),p(2),\dots ,p(n))\in {\Pi _{n}}$ that minimizes
In the experiments, we have used the benchmark instances from the electronic public library of the QAP instances – QAPLIB (Burkard
et al.,
1997). We experimented with the following fifteen crossover operators:
1) one-point crossover – 1PX;
2) modified one-point crossover – M1PX;
3) two-point crossover – 2PX;
4) uniform crossover – UX;
5) quasi-uniform crossover – QUX;
6) shuffle crossover – SX;
7) partially-mapped crossover – PMX;
8) swap-path crossover – SPX;
9) heuristic swap-path crossover – HSPX;
10) swap-path descent crossover – SPDX;
11) cycle crossover – CX;
12) cohesive crossover – COHX;
13) multi-parent crossover – MPX;
14) universal crossover – UNIVX;
15) gene translocation – GT.
All the above crossover operators have been tested using the genetic algorithm, which was implemented in C# programming language by A. Misevičius and D. Kuznecovaitė. In this algorithm, the number of generations is equal to 100 and the population size is equal to 10. The crossover operators were run 10 times with the different chromosome pairs during each generation of GA (thus, each crossover procedure was run 1000 times on every benchmark instance). (The exception was gene translocation, which was run 100 times.) The experiments were performed on a 3.1 GHz personal computer.
In the experiments, we used the following criteria for the evaluation of the efficiency of the crossover operators: 1) the minimum deviation (
${\delta _{\min }}$) of the best found solution from the best known (pseudo-optimal) solution (BKS) (BKSs are from QAPLIB); 2) the average deviation (
$\bar{\delta }$) from BKS; 3) the decrement of minimum deviation (
${\Delta _{\min }}$) during the execution of GA; 4) the decrement of average deviation (
$\bar{\Delta }$). The following are the formula for calculation of the above criteria:
The notations are as follows:
${f_{\min }}$ – the best found value of the objective function (see formula (
4));
${f^{\ast }}$ – the best known (pseudo-optimal) value of the objective function;
$\bar{f}$ – the objective function value averaged over all members of the final obtained population;
${\delta _{\min }^{0}}$ – the minimum deviation calculated for the best individual of the initial population;
${\bar{\delta }^{0}}$ – the average deviation calculated for all the individuals of the initial population (note that the initial population is generated randomly before the execution of GA).
We have utilized two different types of benchmark instances: tai10a (
$n=10$), tai30a
$(n=30)$, tai50a
$(n=50)$ and tai10b
$(n=10)$, tai30b
$(n=30)$, tai50b
$(n=50)$. The instances tai10a, tai30a, tai50a are generated in a random way (Taillard,
1991); whereas the instances tai10b, tai30b, tai50b are generated pseudo-randomly in such a way that the data resemble a distribution of real-world problems (Taillard,
1995).
For the sake of more fairness, the following three different variants of the genetic algorithm were examined: 1) the standard genetic algorithm without mutation; 2) the standard genetic algorithm with a mutation procedure; 3) the hybrid genetic algorithm with an integrated local search procedure. Mutation is operationalized by the use of random pairwise gene interchanges, meanwhile the local search uses deterministic gene exchanges which improve the fitness of an individual.
Table 1
Results of the comparison of crossover operators for the instances tai10a, tai10b (GA variant 1).
|
tai10a |
tai10b |
|
${\delta _{\min }}$ |
$\bar{\delta }$ |
${\Delta _{\min }}$ |
$\bar{\Delta }$ |
${\delta _{\min }}$ |
$\bar{\delta }$ |
${\Delta _{\min }}$ |
$\bar{\Delta }$ |
| 1PX |
11,01 |
20,80 |
25,69 |
17,28 |
24,29 |
30,20 |
62,58 |
49,54 |
| M1PX |
12,11 |
21,66 |
24,51 |
16,45 |
24,29 |
30,20 |
62,58 |
49,54 |
| 2PX |
19,99 |
24,50 |
16,67 |
13,80 |
41,98 |
46,44 |
38,18 |
32,95 |
| UX |
17,46 |
20,33 |
19,07 |
17,74 |
38,65 |
42,57 |
40,78 |
36,56 |
| QUX |
21,57 |
26,17 |
15,21 |
12,29 |
47,02 |
52,74 |
34,48 |
27,47 |
| SX |
20,07 |
23,60 |
26,58 |
14,62 |
15,84 |
33,64 |
62,60 |
45,68 |
| PMX |
15,50 |
18,09 |
21,00 |
19,98 |
30,37 |
35,31 |
47,82 |
43,88 |
| SPX |
12,65 |
16,73 |
23,93 |
21,37 |
26,20 |
31,40 |
51,71 |
48,17 |
| HSPX |
18,28 |
22,63 |
31,27 |
15,53 |
21,33 |
30,25 |
56,60 |
49,48 |
| SPDX |
5,34 |
9,46 |
34,87 |
33,34 |
7,67 |
9,44 |
70,82 |
72,03 |
| CX |
20,00 |
30,74 |
16,66 |
8,36 |
47,98 |
67,23 |
33,80 |
16,42 |
| COHX |
0,59 |
4,09 |
38,19 |
36,11 |
20,86 |
22,50 |
57,09 |
58,93 |
| MPX |
15,44 |
17,72 |
21,07 |
20,35 |
15,49 |
27,63 |
63,00 |
52,54 |
| UNIVX |
21,37 |
24,44 |
15,39 |
13,85 |
52,82 |
54,88 |
30,51 |
25,70 |
| GT |
12,61 |
13,31 |
23,98 |
25,03 |
1,54 |
3,40 |
84,27 |
88,29 |
Table 2
Results of the comparison of crossover operators for the instances tai10a, tai10b (GA variant 2).
|
tai10a |
tai10b |
|
${\delta _{\min }}$ |
$\bar{\delta }$ |
${\Delta _{\min }}$ |
$\bar{\Delta }$ |
${\delta _{\min }}$ |
$\bar{\delta }$ |
${\Delta _{\min }}$ |
$\bar{\Delta }$ |
| 1PX |
0,00 |
1,47 |
100,00 |
69,61 |
0,00 |
1,03 |
100,00 |
90,70 |
| M1PX |
0,43 |
1,94 |
73,42 |
68,97 |
0,00 |
1,08 |
100,00 |
90,62 |
| 2PX |
2,30 |
3,45 |
70,97 |
66,95 |
0,28 |
1,65 |
93,17 |
89,53 |
| UX |
0,00 |
1,38 |
100,00 |
69,75 |
0,00 |
0,96 |
100,00 |
90,84 |
| QUX |
0,45 |
1,81 |
73,38 |
69,16 |
0,00 |
0,94 |
100,00 |
90,88 |
| SX |
2,30 |
3,66 |
70,97 |
66,68 |
0,00 |
0,91 |
100,00 |
90,93 |
| PMX |
2,43 |
3,88 |
70,81 |
66,38 |
0,00 |
0,96 |
100,00 |
90,84 |
| SPX |
0,64 |
2,07 |
73,13 |
68,81 |
1.65 |
2,58 |
91,11 |
88,80 |
| HSPX |
0,59 |
2,11 |
73,19 |
68,74 |
0,00 |
0,96 |
100,00 |
90,84 |
| SPDX |
0,43 |
1,70 |
74,95 |
72,06 |
0,00 |
0,95 |
100,00 |
90,86 |
| CX |
0,00 |
3,44 |
100,00 |
66,96 |
0,28 |
2,11 |
93,17 |
88,66 |
| COHX |
3,33 |
5,24 |
69,67 |
64,62 |
0,00 |
1,05 |
100,00 |
90,68 |
| MPX |
2,43 |
5,40 |
70,81 |
64,42 |
0,00 |
0,92 |
100,00 |
90,92 |
| UNIVX |
2,43 |
4,18 |
70,81 |
65,99 |
0,00 |
0,96 |
100,00 |
90,84 |
| GT |
0,92 |
2,94 |
72,76 |
67,63 |
0,00 |
1,13 |
100,00 |
90,52 |
The obtained results of all performed experiments are presented in Tables
1–
7. The best achieved values of the crossover operators are in bold. Note that the CPU times differ unimportantly and are omitted.
After analysis of the experimental results, the most essential observations are as follows.
-
• The obtained results are very influenced by the size and nature of test data. The large instances are more difficult to solve when comparing to smaller instances. Also, it seems that the random medium- and large-scale instances are harder than their real life counterparts. This is true for all the crossover operators.
Table 3
Results of the comparison of crossover operators for the instances tai30a, tai30b (GA variant 2).
|
tai30a |
tai30b |
|
${\delta _{\min }}$ |
$\bar{\delta }$ |
${\Delta _{\min }}$ |
$\bar{\Delta }$ |
${\delta _{\min }}$ |
$\bar{\delta }$ |
${\Delta _{\min }}$ |
$\bar{\Delta }$ |
| 1PX |
5,82 |
6,68 |
16,40 |
13,28 |
4,18 |
4,63 |
93,32 |
91,85 |
| M1PX |
6,73 |
7,22 |
15,44 |
12,71 |
7,56 |
7,67 |
98,49 |
86,32 |
| 2PX |
5,49 |
6,93 |
16,75 |
13,01 |
12,42 |
12,89 |
82,07 |
77,53 |
| UX |
6,39 |
7,28 |
15,80 |
12,65 |
4,17 |
5,01 |
93,33 |
91,14 |
| QUX |
6,83 |
7,59 |
15,33 |
12,32 |
3,68 |
3,94 |
94,05 |
93,16 |
| SX |
6,51 |
7,55 |
15,67 |
12,37 |
1,67 |
1,85 |
97,10 |
97,21 |
| PMX |
5,48 |
6,31 |
16,76 |
13,67 |
5,35 |
5,60 |
91,62 |
89,94 |
| SPX |
7,15 |
7,57 |
15,00 |
12,35 |
6,74 |
7,04 |
89,64 |
87,45 |
| HSPX |
4,37 |
5,68 |
17,96 |
14,35 |
7,94 |
8,28 |
87,98 |
85,25 |
| SPDX |
4,51 |
5,73 |
17,00 |
13,97 |
7,65 |
7,81 |
98,44 |
88,78 |
| CX |
6,30 |
6,76 |
15,89 |
13,20 |
9,49 |
10,77 |
95,88 |
88,00 |
| COHX |
4,56 |
5,33 |
17,75 |
14,73 |
9,11 |
9,26 |
96,38 |
83,55 |
| MPX |
6,68 |
7,88 |
15,50 |
12,02 |
7,77 |
7,85 |
98,21 |
86,01 |
| UNIVX |
6,84 |
7,76 |
15,33 |
12,14 |
12,72 |
12,83 |
81,70 |
77,62 |
| GT |
7,60 |
8,21 |
14,54 |
11,68 |
9,13 |
9,41 |
96,36 |
84,30 |
Table 4
Results of the comparison of crossover operators for the instances tai50a, tai50b (GA variant 2).
|
tai50a |
tai50b |
|
${\delta _{\min }}$ |
$\bar{\delta }$ |
${\Delta _{\min }}$ |
$\bar{\Delta }$ |
${\delta _{\min }}$ |
$\bar{\delta }$ |
${\Delta _{\min }}$ |
$\bar{\Delta }$ |
| 1PX |
8,70 |
8,98 |
13,32 |
10,35 |
8,13 |
9,15 |
65,02 |
55,71 |
| M1PX |
7,16 |
7,92 |
14,90 |
11,42 |
8,84 |
9,67 |
64,08 |
54,97 |
| 2PX |
8,13 |
8,67 |
13,90 |
10,66 |
7,31 |
7,96 |
66,13 |
57,43 |
| UX |
8,41 |
8,89 |
13,62 |
10,43 |
9,78 |
10,74 |
62,84 |
53,48 |
| QUX |
8,68 |
9,03 |
13,35 |
10,29 |
6,12 |
7,92 |
67,77 |
57,49 |
| SX |
6,65 |
7,32 |
15,42 |
12,06 |
11,78 |
13,33 |
60,28 |
49,97 |
| PMX |
7,91 |
8,59 |
14,13 |
10,74 |
6,33 |
6,40 |
67,48 |
59,75 |
| SPX |
5,31 |
5,96 |
16,85 |
13,49 |
5,47 |
6,16 |
68,68 |
60,10 |
| HSPX |
6,88 |
7,59 |
14,18 |
11,77 |
8,07 |
8,62 |
65,10 |
56,47 |
| SPDX |
4,93 |
5,07 |
17,13 |
14,52 |
6,08 |
6,45 |
67,09 |
59,81 |
| CX |
7,76 |
8,65 |
14,28 |
10,68 |
8,93 |
10,04 |
63,96 |
54,46 |
| COHX |
5,71 |
5,98 |
16,42 |
13,46 |
12,45 |
12,79 |
59,45 |
50,69 |
| MPX |
9,17 |
9,58 |
12,85 |
9,74 |
5,57 |
5,77 |
68,54 |
60,70 |
| UNIVX |
7,15 |
7,73 |
14,91 |
11,62 |
7,32 |
7,63 |
66,12 |
57,91 |
| GT |
9,26 |
9,61 |
12,77 |
9,71 |
10,69 |
12,25 |
61,67 |
51,42 |
-
• The main differentiation in the results is due to distinct configurations of the inner structure of the genetic algorithm, rather than due to the crossover operations themselves. Presumably, not only the crossover operator, but also mutation is important. The crossover enables to diversify the search process, it is explorative and can discover new regions in the search space. Meanwhile, the mutation allows to intensify the search process, it is rather exploitative and creates random, but small diversions staying near (in the neighbourhood of) the parent. Both have their role. They complement each other; there exists a mutual interaction between them, which increases the overall performance of the genetic algorithm.
Table 5
Results of the comparison of crossover operators for the instances tai10a, tai10b (GA variant 3).
|
tai10a |
tai10b |
|
${\delta _{\min }}$ |
$\bar{\delta }$ |
${\Delta _{\min }}$ |
$\bar{\Delta }$ |
${\delta _{\min }}$ |
$\bar{\delta }$ |
${\Delta _{\min }}$ |
$\bar{\Delta }$ |
| 1PX |
0,00 |
1,01 |
100,00 |
97,57 |
0,00 |
1,12 |
100,00 |
98,82 |
| M1PX |
0,00 |
1,06 |
100,00 |
97,45 |
0,00 |
1,05 |
100,00 |
98,90 |
| 2PX |
0,00 |
1,04 |
100,00 |
97,50 |
0,00 |
1,26 |
100,00 |
98,67 |
| UX |
0,00 |
1,01 |
100,00 |
97,57 |
0,00 |
1,28 |
100,00 |
98,65 |
| QUX |
0,00 |
0,54 |
100,00 |
98,71 |
0,00 |
0,81 |
100,00 |
99,15 |
| SX |
0,00 |
0,92 |
100,00 |
97,80 |
0,00 |
0,91 |
100,00 |
99,04 |
| PMX |
0,00 |
0,87 |
100,00 |
97,91 |
0,00 |
0,97 |
100,00 |
98,98 |
| SPX |
0,00 |
0,87 |
100,00 |
97,91 |
0,00 |
1,43 |
100,00 |
98,49 |
| HSPX |
0,00 |
1,38 |
100,00 |
96,70 |
0,00 |
1,10 |
100,00 |
98,84 |
| SPDX |
0,00 |
0,46 |
100,00 |
99,13 |
0,00 |
0,98 |
100,00 |
99,02 |
| CX |
0,00 |
1,46 |
100,00 |
96,51 |
0,00 |
1,17 |
100,00 |
98,76 |
| COHX |
0,00 |
1,04 |
100,00 |
97,49 |
0,00 |
0,72 |
100,00 |
99,24 |
| MPX |
0,00 |
0,75 |
100,00 |
98,20 |
0,00 |
0,94 |
100,00 |
99,01 |
| UNIVX |
0,00 |
0,59 |
100,00 |
98,57 |
0,00 |
0,99 |
100,00 |
98,95 |
| GT |
0,00 |
0,75 |
100,00 |
98,20 |
0,00 |
1,24 |
100,00 |
98,69 |
Table 6
Results of the comparison of crossover operators for the instances tai30a, tai30b (GA variant 3).
|
textbftai30a |
tai30b |
|
${\delta _{\min }}$ |
$\bar{\delta }$ |
${\Delta _{\min }}$ |
$\bar{\Delta }$ |
${\delta _{\min }}$ |
$\bar{\delta }$ |
${\Delta _{\min }}$ |
$\bar{\Delta }$ |
| 1PX |
2,12 |
2,26 |
88,83 |
89,18 |
0,19 |
0,26 |
99,68 |
99,75 |
| M1PX |
1,55 |
1,96 |
91,83 |
90,60 |
0,17 |
0,30 |
99,71 |
99,71 |
| 2PX |
0,72 |
0,98 |
96,19 |
95,29 |
1,40 |
1,51 |
97,66 |
98,56 |
| UX |
1,28 |
1,70 |
93,23 |
91,84 |
0,00 |
0,03 |
100,00 |
99,97 |
| QUX |
2,04 |
2,65 |
89,21 |
87,31 |
1,40 |
1,62 |
97,65 |
98,45 |
| SX |
1,43 |
1,53 |
92,47 |
92,66 |
0,00 |
0,04 |
100,00 |
99,96 |
| PMX |
0,74 |
1,03 |
96,10 |
95,06 |
0,00 |
0,05 |
100,00 |
99,95 |
| SPX |
1,45 |
1,84 |
92,35 |
91,17 |
1,40 |
1,46 |
97,66 |
98,61 |
| HSPX |
3,00 |
3,84 |
84,14 |
81,56 |
1,70 |
2,79 |
97,16 |
97,34 |
| SPDX |
0,87 |
1,05 |
95,56 |
94,45 |
0,00 |
0,08 |
100,00 |
99,92 |
| CX |
2,24 |
2,75 |
88,15 |
86,80 |
1,40 |
2,07 |
97,65 |
98,03 |
| COHX |
0,94 |
1,27 |
95,05 |
93,91 |
2,22 |
2,54 |
96,29 |
97,58 |
| MPX |
1,00 |
1,42 |
94,72 |
93,18 |
0,00 |
0,04 |
100,00 |
99,96 |
| UNIVX |
1,59 |
1,94 |
91,62 |
90,69 |
0,00 |
0,03 |
100,00 |
99,97 |
| GT |
1,39 |
1,86 |
92,66 |
91,07 |
0,11 |
0,20 |
99,82 |
99,81 |
-
• The results clearly demonstrate that the hybrid genetic-local search algorithm outperforms the standard variant of the genetic algorithm with respect to all examined criteria. Thus, the deterministic intensification, i.e. local search, is evidently more helpful than the stochastic intensification, i.e. mutation.
-
• The differences in the effectiveness of particular crossover operators are not statistically very significant. These differences are even more minimized if crossovers are tested in the “hybrid environment”. Still, it can be observed that the multi-parent crossover and especially the swap-path descent crossover – which uses the heuristic information – seem, on average, to be superior to other operators. Further experiments could be recommended in order to corroborate this observation.
Despite the limited extent of our experiments, the scope of applications of the considered crossover operators is not constricted to the permutation-based problems as long as bit-string genetic algorithms are utilized. Regardless of the differences of implementation, the principles of functioning of these crossovers (possibly with the exception of heuristic crossovers) are rather general and invariant. This is especially true for our proposed universal crossover that is straightforwardly replicable to bit-string GAs, which, in turn, are applicable to both combinatorial and continuous optimization problems.
Table 7
Results of the comparison of crossover operators for the instances tai50a, tai50b (GA variant 3).
|
tai50a |
tai50b |
|
${\delta _{\min }}$ |
$\bar{\delta }$ |
${\Delta _{\min }}$ |
$\bar{\Delta }$ |
${\delta _{\min }}$ |
$\bar{\delta }$ |
${\Delta _{\min }}$ |
$\bar{\Delta }$ |
| 1PX |
2,47 |
2,67 |
86,91 |
86,82 |
0,41 |
0,44 |
99,28 |
99,37 |
| M1PX |
1,46 |
1,59 |
92,23 |
92,15 |
0,25 |
0,32 |
99,56 |
99,55 |
| 2PX |
2,06 |
2,23 |
89,04 |
88,99 |
1,01 |
1,03 |
98,22 |
98,53 |
| UX |
2,60 |
2,76 |
86,17 |
86,38 |
0,30 |
0,34 |
99,48 |
99,51 |
| QUX |
1,56 |
1,70 |
91,73 |
91,62 |
1,19 |
1,24 |
97,91 |
98,23 |
| SX |
1,97 |
2,10 |
89,56 |
89,65 |
1,24 |
1,27 |
97,82 |
98,19 |
| PMX |
2,00 |
2,20 |
89,38 |
89,14 |
1,49 |
1,52 |
97,38 |
97,83 |
| SPX |
1,78 |
2,23 |
90,53 |
89,01 |
0,78 |
0,81 |
98,63 |
98,84 |
| HSPX |
3,53 |
4,05 |
81,25 |
80,00 |
1,84 |
3,96 |
96,77 |
94,34 |
| SPDX |
1,37 |
1,46 |
93,27 |
93,18 |
0,21 |
0,29 |
99,61 |
99,58 |
| CX |
2,55 |
2,85 |
86,45 |
85,93 |
0,60 |
0,68 |
98,94 |
99,03 |
| COHX |
2,13 |
2,41 |
88,68 |
88,11 |
0,67 |
0,70 |
98,82 |
98,99 |
| MPX |
2,44 |
2,52 |
87,06 |
87,57 |
0,63 |
0,64 |
98,90 |
99,08 |
| UNIVX |
1,58 |
2,08 |
91,60 |
89,71 |
1,46 |
1,51 |
97,44 |
97,85 |
| GT |
1,83 |
2,10 |
90,26 |
89,63 |
0,46 |
0,48 |
99,20 |
99,31 |
5 Concluding Remarks
In this paper, fifteen crossover operators for genetic algorithms were investigated. The investigation has been carried out on the quadratic assignment problem, which is a representative example of the challenging permutation-based combinatorial optimization problems.
We experimented with the point-based crossovers, uniform crossovers, shuffle crossover, partially-mapped crossover, swap-path crossovers, cycle crossover, cohesive crossover, multi-parent crossover, among others. In addition, we have introduced the enhanced swap-based crossover (swap-path descent crossover), in which the improvements of the values of the objective function are taken into consideration. Also, we propose the so-called universal crossover, which can be flexibly adapted to meet the requirements/requests of the algorithm’s user. Additionally, the gene translocation procedure is presented, in which many parents produce many children during each generation of the genetic algorithm.
We expect that the considered crossover procedures, along with the proposed new ones, will be beneficial for the solution of a wide class of optimization problems. Problem-oriented, heuristic crossover procedures seem to be a good alternative to canonical, general-purpose crossover operators. It also seems that the attention should be focused on the deterministic local search procedures, thereby capitalizing on the synergy of recombination (diversification) and intensification in genetic algorithms.