Abstract
Strategic management is a process of determining a business long-term objectives and the way to achieve these goals. Considering importance of strategic planning in long-term competitive power of organizations, different frameworks are proposed to formulate strategies. How to choose the best strategy is a challenging activity due to its multi criteria nature and lack of information. In this paper, a method comprised of grey DEMATEL – grey analytic network process is proposed to deal with this challenge. The proposed method considered interrelationship among factors using DEMATEL and then these relations are applied in strategy ranking by ANP. The uncertainty and lack of information is handled using grey numbers. Application of the proposed method is illustrated in an ecotourism company.
1 Introduction
Strategic management is a set of decisions and actions that determines the long-term performance of a company. By a review, the importance of the concept of strategic management can be realized. According to the environmental changes that have already taken a lot of momentum, and the complexity of organizational decisions, the need to implement a comprehensive program to deal with these issues is more tangible than ever before. Strategic management is based on dynamic mentality, perspective and contingency holistic solutions to many problems of today’s organizations.
David (
2013) believed that strategic management includes three phases of planning, deployment, and evaluation. The concept of SWOT established the foundation of strategic planning. It expresses that formulating a good strategy relies on monitoring and evaluation of external opportunities and threats, along with internal strengths and weaknesses (Wheelen and Hunger,
2008).
Since the strategies of an organization, called strategic alternatives, are formulated, e.g. by using SWOT framework, the more challenging problem is how to select the best strategies among proposed ones. Many qualitative and quantitative approaches are suggested for solving the strategy selection problem. Multi-criteria decision making (MCDM) is one of the applicable methods for dealing with this problem. MCDM is broad field of operations research including two distinct fields of (1) multi-attribute decision making (MADM) for selection problems, and (2) multi-objective decision making (MODM) for designing problems (Triantaphyllou,
2000). MCDM plays a vital role in different levels of decision making; from strategic to operational decisions (Aliakbari Nouri
et al.,
2015; Karabasevic
et al.,
2016; Hosseini-Nasab
et al.,
2016; Xu
et al.,
2016). The strategy selection problems lie in the field of MADM. A comprehensive review on MADM can be found in Hwang and Yoon (
1982) and Figueira
et al. (
2006).
MADM methods have had wide usages in prioritizing and choosing the strategies. In recent years Analytical Hierarchy Process (AHP) and Analytical Network Process (ANP), both proposed by Saaty (
1980,
1996) respectively, have been applied in the problem of evaluating and choosing strategies. The enhanced SWOT-AHP method is used to determine the strategic planning of natural resource management (Pesonen
et al.,
2001), analyse the global competitiveness of manufacturers of machine tools (Shinno
et al.,
2006), determine the business strategy in textile firm (Yüksel and Akin,
2006), shipping registry selection in maritime transportation industry (Kandakoglu
et al.,
2009), determine the outsourcing decisions for sport marketing (Lee
et al.,
2011), and strategic implementation of integrated water resources management in Mozambique (Gallego-Ayala and Juízo,
2011). The AHP method doesn’t check the existing interdependency and dependency among all components of SWOT analysis; owing to this limitation, the researchers use ANP method. It can check relations between strategies, factors and sub-factors. Dağdeviren and Yüksel (
2007) used SWOT analysis and ANP integrated model to select an alternative strategy for a textile firm. Wang
et al. (
2011) applied the ANP embedding into SWOT to analyse the cumulative effect of pollution in the atmospheric environment management. Azimi
et al. (
2011) proposed an integrated model for prioritizing the strategies of Iranian mining sector. They used ANP to obtain the weight of SWOT factors. Ostrega
et al. (
2011) structured ANP based SWOT approach to minimize environmental impacts on mining activities. Fouladgar
et al. (
2011) purposed integrated model with ANP to obtain the weight of SWOT factors. Babaesmailli
et al. (
2012) for identification of the best strategies of a tile manufacturing firm used the SWOT analysis and fuzzy ANP Method to prioritize strategies. Kabak (
2013) applied fuzzy decision-making trial and evaluation laboratory (DEMATEL)-ANP model to select snipers. Sadeghi
et al. (
2013) used grey TOPSIS method to evaluate action plans of balanced scorecard (BSC). Grošlej and Stirn (
2015) employed SWOT-ANP framework to solve the environmental management problem of Pohorje in Slovenia. Mardani
et al. (
2015) applied a systematic review of MCDM techniques and approaches (AHP and F-AHP, ANP and VIKOR, TOPSIS and F-TOPSIS, PROMETHEE, integrated method and other methods) in sustainable and renewable energy systems problems. Dimic
et al. (
2016) used SWOT analysis and DEMATEL-ANP to survey sustainable transport management in Serbian Oil Industry (NIS). Also Shen and Tzeng (
2016) combined RSA decision-rules with FCA-based DANP evaluation for identifying performance gaps to improve financial performance.
Considering the problem of strategy selection, a forthcoming issue is that many of the formulated and selected strategies cannot be implemented successfully due to insufficient budget assignment. Therefore, it seems necessary that budget constraint is considered when choosing strategies. This feature is not considered in the above mentioned works on strategy selection. On the other hand, considering the futuristic approach of strategic planning, evaluation of strategies based on internal and external factors is an uncertain problem. Different frameworks are proposed for dealing with uncertainty. Liu and Lin (
2006) introduced three main approaches of (1) probability and statistics, (2) fuzzy set theory, and (3) grey systems theory as the main approach of dealing with uncertainty.
There has been a wide range of researches in the application of multi-criteria decision making methods for selecting the right strategies. However, the current research presents a three-stage approach to prioritize and select strategies, while considering the uncertainty of the decision makers in the form of grey numbers and also consider the budget limitations in choosing strategies. These three stages include (1) formulating strategies using SWOT analysis, (2) evaluating formulated strategies using grey DEMATEL-ANP, (3) choosing the final strategies by considering budget constraint using a 0–1 programming problem. Thus, the main contributions of the current work can be stated as proposing a 0–1 programming model for choosing the best strategies by considering the budget limitation.
The paper is organized as follows. The literature about using MCDM method in strategy selection problem is reviewed in the next section. Then, a brief review about grey numbers, DEMATEL and ANP is presented as the preliminaries of the proposed method. At the next step, the hybrid grey DEMATEL-ANP methodology is explained and its application in a real world case of selecting a tourism company is illustrated. Finally, the paper is concluded in the last section.
2 Preliminaries
In the current paper, a combination of different tools is used as the fundamental elements of the proposed approach. A brief overview on these tools is given in this section.
2.1 SWOT Analysis
The influencing internal and external factors for a company’s future are referred to as strategic factors. In SWOT analysis, these factors are grouped into four parts called SWOT groups: strengths, weaknesses, opportunities, and threats. By applying SWOT in strategic decisions, the purpose is to select or constitute and implement a strategy resulting in a good fit between the internal and external factors (Kangas
et al.,
2003). Moreover, the chosen strategy has also to be in line with the current and future purposes of the decision makers (Pesonen
et al.,
2001). SWOT involves systematic thinking and comprehensive diagnosis of factors relating to a new product, technology, management, or planning. SWOT matrix is a commonly used tool for analysing external and internal environments concurrently in order to support for a decision situation (Kurttila
et al.,
2000; Kangas
et al.,
2003; Dağdeviren and Yüksel,
2007).
2.2 Grey System Theory
Grey system theory can be used to deal with uncertainty of information (Deng,
1989). The major advantage is that it can generate satisfactory outcomes using a relatively small amount of data or with great variability in factors (Li
et al.,
1997). Grey system theory provides an approach for analysing and modelling the systems with limited and incomplete information.
Let
x denote a closed and bounded set of real numbers. A grey number
$\textstyle\bigotimes x$, is defined as an interval with known upper and lower bounds but unknown distribution information for
x (Deng,
1989). That is,
$\textstyle\bigotimes x=[\underline{x},\overline{x}]=[{x^{,}}\in x\mid \underline{x}\leqslant {x^{,}}\leqslant \overline{x}]$ where
$\underline{x}$ and
$\overline{x}$ are the lower and upper bounds of
$\textstyle\bigotimes x$, respectively.
Some basic grey number mathematical operations are represented by the following relationships (expressions (
1)–(
4)) (Liu and Lin,
2006):
Different methods are proposed to transfer a grey number into crisp equivalent. A variation of the CFCS (Converting Fuzzy data into Crisp Scores) method is applied in this paper. This approach has been deemed to be more effective by researchers for arriving at crisp values (e.g. when compared with the Centroid method) (Opricovic and Tzeng,
2003; Wu and Lee,
2007).
Consider an $m\times n$ grey matrix ${X^{p}}=[\textstyle\bigotimes {x_{ij}^{p}}]$, corresponding to a given decision maker p, whose elements $\textstyle\bigotimes {x_{ij}^{p}}=[{\underline{x}_{ij}^{p}},{\overline{x}_{ij}^{p}}]$ are grey numbers.
The modified-CFCS method includes three-step procedure described as follows:
-
-
2) Compute total normalized crisp value:
-
2.3 DEMATEL
Decision-making trial and evaluation laboratory (DEMATEL) method was originally developed between 1972 to 1979 by the Science and Human Affairs Program of the Battelle Memorial Institute of Geneva, with the purpose of studying the complex and intertwined problematic group. It has been widely accepted as one of the best tools to solve the cause and effect relationships among the evaluation criteria (Chiu
et al.,
2006; Liou
et al.,
2007; Tzeng
et al.,
2007; Wu and Lee,
2007; Lin and Tzeng,
2009). This method is applied to analyse and form the relationship of cause and effects among evaluation criteria (Yang
et al.,
2008) or to derive interrelationship among factors (Lin and Tzeng,
2009). DEMATEL incorporates four generic stages:
Step 1. Calculating the direct-influence matrix by scores. Based on experts’ opinions, evaluations are made of the relationships among elements (or variables/attributes) of mutual influence. Using a scale ranging from 0 to 4, with scores representing ‘no influence (0)’, ‘low influence (1)’, ‘medium influence (2)’, ‘high influence (3)’, and ‘very high influence (4)’, respectively.
Step 2. Normalizing the direct-influence matrix. Based on the direct-influence of matrix
$\boldsymbol{A}$, the normalized direct-relation matrix
$\boldsymbol{D}$ is acquired by using formulas (
10) and (
11)
where
Step 3. Attaining the total-influence matrix T. Once the normalized direct influence matrix
$\boldsymbol{D}$ is obtained, the total-influence matrix
$\boldsymbol{T}$ of NRM can be obtained through formula (
12), in which
$\boldsymbol{I}$ denotes the identity matrix
Step 4. Analysing the results: in this stage, the sum of rows and the sum of columns are separately expressed as vector
r and vector
c by using formulas (
13), (
14), and (
15). Then, the horizontal axis vector
$(r+c)$ is made by adding
r to
c, which exhibits importance of the criterion. Similarly, the vertical axis
$(r-c)$ is made by deducting
r from
$\boldsymbol{c}$, which may separate criteria into a cause group and an affected group. In general, when
$(r-c)$ is positive, the criterion will be part of the cause group. On the contrary, if the
$(r-c)$ is negative, the criterion is part of the affected group. Therefore, the causal graph can be achieved by mapping the dataset of the
$(r+c,r-c)$.
2.4 Analytic Network Process (ANP)
The ANP can be used as an MCDM method to systematically select the most suitable alternatives. The ANP is a relatively simple and systematic approach that can be used by decision makers. The ANP is an extension of AHP by Saaty (
1996) that helps to overcome the problem of interdependence and feedback among criteria and alternatives.
The Analytic Network Process is a generalization of the Analytic Hierarchy Process. Many decision problems cannot be structured hierarchically because they involve the interaction and dependence of higher level elements in a hierarchy on lower level elements (Saaty and Özdemir,
2005). While the AHP represents a framework with a unidirectional hierarchical relationship, the ANP allows for complex interrelationships among decision levels and attributes (Dağdeviren and Yüksel,
2007).
ANP approach comprises four steps (Saaty,
1996; Chung
et al.,
2005; Dağdeviren and Yüksel,
2007):
Step 1. Model construction and problem structuring: the problem should be stated clearly and decomposed into a rational system like a network.
Step 2. Pairwise comparisons and priority vectors: in ANP, like AHP, pairs of decision elements at each cluster are compared with respect to their importance towards their control criteria. In addition, interdependencies among criteria of a cluster must also be examined pairwise; the influence of each element on other elements can be represented by an eigenvector. The relative importance values are determined with Saaty’s scale.
Step 3. Super matrix formation: the super matrix concept is similar to the Markov chain process. To obtain global priorities in a system with interdependent influences, the local priority vectors are entered in the appropriate columns of a matrix. As a result, a super matrix is actually a partitioned matrix, where each matrix segment represents a relationship between two clusters in a system.
Step 4. Synthesis of the criteria and alternatives: priorities and selection of the best alternatives. The priority weights of the criteria and alternatives can be found in the normalized super matrix. To achieve these weights, the limiting power of the super matrix should be computed. This concept is parallel to the Markov chain process (Meade and Sarkis,
1998). The limiting power of the super matrix has an equilibrium distribution, as in the Markov chain process. Alternatives in the model can be ordered using limiting priorities obtained from the equilibrium distribution of the super matrix.
According to this research, pairwise comparisons are done based on grey data in pairwise comparison matrix, thus this research needs a method for grey pairwise comparison matrix analysis.
Consider grey pairwise comparison matrix of
$\textstyle\bigotimes P=[\textstyle\bigotimes {a_{ij}}],\textstyle\bigotimes {a_{ij}}=[{l_{ij}},{u_{ij}}]$. The weight vector is donated as
$W=({w_{1}},{w_{2}},\dots ,{w_{n}})$. Yu
et al. (
2011) proposed a goal programming based approach for obtaining the weight vector
W from grey pairwise matrix
$\textstyle\bigotimes P$. Their model is constructed based on multiplicative normalization condition, i.e.
${\textstyle\prod _{j=1}^{n}}{w_{j}}=1$,
$i=1,2,\dots ,n-1$,
$j=i+1,i+2,\dots ,n$,
$j>i$. Their proposed goal programming model based on upper triangular judgement (above main diagonal) is formulated as:
where,
${x_{j}}=\ln ({w_{j}})$, and
${p_{ij}}$ and
${q_{ij}}$ are defined as nonnegative deviation variables. Solving the above model and determining the optimal value of variables
${x_{j}}$,
$j=1,2,\dots ,n$, using converse logarithmic transformation the weights,
${w_{j}}$,
$j=1,2,\dots ,n$, are figured out. Then, the weights are normalized and final weights are calculated. Interested readers can refer to Yu
et al. (
2011) paper for details of formulating the above model.
3 Research Methodology
The purpose of this research is to provide a framework for choosing the best strategies by considering their utilities and budgetary constraints. The suggested framework composed three different stages of strategy planning, strategy evaluation, and strategy selection. Figure
1 presents the proposed approach.
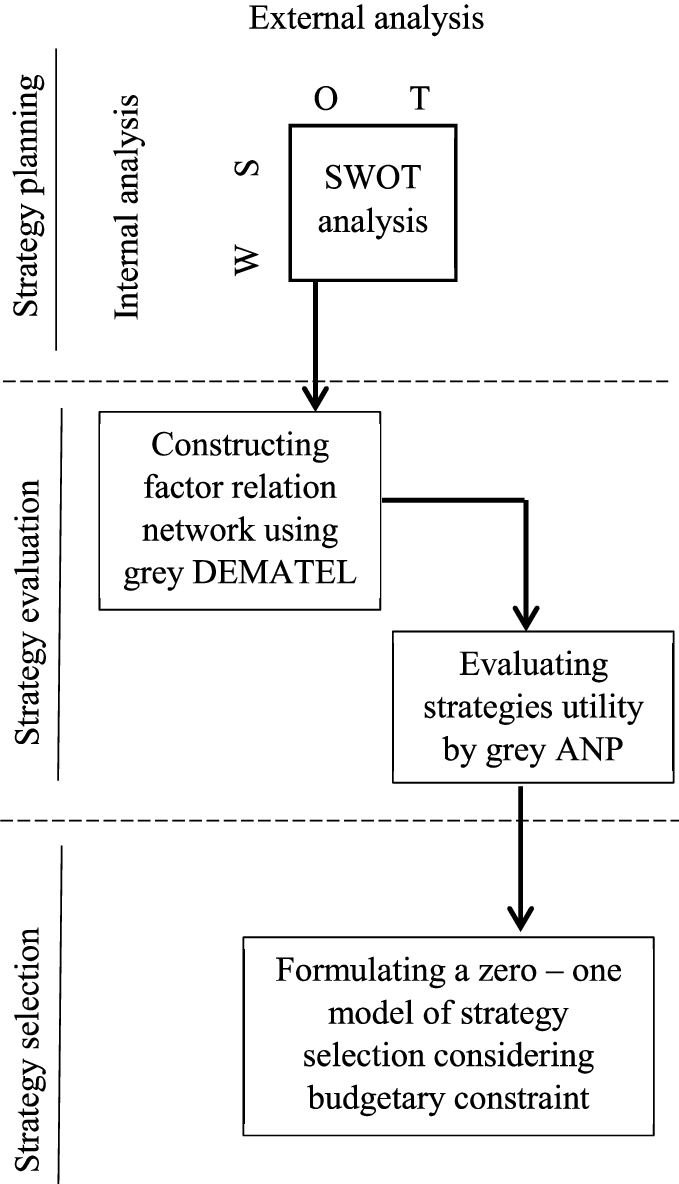
Fig. 1
Strategy planning, evaluation and selection approach.
The first step is trying to identify strengths, weaknesses, opportunities and threats based on the internal and external analysis of the environment. Then, by forming the SWOT matrix, organization’s strategic alternatives are codified. These internal and external factors along with proposed strategies are entered to the second phase of strategy evaluation. In this step, Grey DEMATEL method is used to determine the interrelation network among the clusters, including strengths, weaknesses, opportunities, threats, and strategies. By forming the network between clusters, the pairwise comparisons begin. In this step, in order to calculate the weight of the result of the grey pairwise comparisons, the goal programming method is used, as illustrated in previous section. By calculating vector of weights, super matrix of problem is formed and finally the last weights of the indicators (SWOT factors) and the alternatives (strategies) are calculated. At the last stage of strategy selection, a zero one model is formulated by considering the budget constraints.
Suppose that there are
k different strategic alternatives
${S_{1}},{S_{2}},\dots ,{S_{k}}$ that are evaluated using grey ANP and their final weights are calculated as
${u_{1}},{u_{2}},\dots ,{u_{k}}$. Let assume that there is totally a budget of amount
B to perform these strategies and each strategy is evaluated at least a budget of amount
${b_{1}},{b_{2}},\dots ,{b_{k}}$ to be performed. If
${x_{i}}=1$ when strategy
i is selected and
${x_{i}}=0$ when this strategy is not selected, then the strategy selection problem is formulated as the following knapsack based problem:
The proposed approach can be summarized as the following steps:
-
1. Internal analysis to identify strengths and weaknesses;
-
2. External analysis to identify opportunities and threats;
-
3. Create SWOT matrix to formulate strategic options;
-
4. Design interrelation network among internal factors, external factors and strategies using Grey DEMATEL;
-
5. Pairwise comparisons based on constructed network in step 4;
-
6. Calculate weights of grey pairwise comparison matrices (solving the model (
16) for each grey pairwise matrix) and creating super matrix;
-
7. Calculate super matrix limiting power for determining the weights of factors and strategies;
-
8. Formulate the knapsack based problem of Eq. (
17) to select the final strategies considering budget constraint.
An application of the proposed method is illustrated at the next section.
4 Application
To clarify the application of proposed methodology, in this section the strategic planning and selecting in an Iranian tourism agency, named ABC, is illustrated. Considering great competition in tourism industry and its growing market size in recent years, it seems that companies must adopt a set of suitable strategies to benefit from the upcoming market situations. As mentioned in the methodology, for identifying decision making factors, an SWOT analysis is conducted. The SWOT analysis was conducted by participation of five experts from the company, including its CEO, two deputy managers and two chief tour-leaders. The experts were chosen because they have specific experiences dealing with tourism in terms of implementation and they understand both the benefits and risks of tourism industry.
4.1 Strategy Formulation
| Strengths (S) |
Weaknesses (W) |
| S1: Advisory and participation system |
W1: Lack of design in different products for different customers |
| S2: Staff are committed to their tasks |
W2: Sellers’ unprofessional treatment with customers |
| S3: Utilize the appropriate software at the company |
W3: Inappropriate communication with suppliers of transport and hotels |
| S4: Having complete database about their customers |
W4: Local tour leaders are not qualified |
| S5: Suitable working capital |
W5: The communicative ways of the customers are limited (bounded) |
| S6: Well-known brand in the field of ecotourism |
W6: Lack of diversity in field of foreign trips |
| S7: They can explore the causes of customer’s dissatisfaction and manage the customer’s satisfaction |
W7: Incomplete site and unable to produce the contents |
| Opportunities (O) |
Threats (T) |
| O1: Sanction reduction |
T1: Tax and insurance costs |
| O2: Competitors’ weakness in the field of ecotourism |
T2: The possibility of suspension of agency |
| O3: There are opportunities to develop cooperation with small companies |
T3: The possibility of presence of smart competitors and owners of capital |
| O4: Internet and social networks availability is easier than past time |
T4: There are limitation in existence of strong suppliers |
| O5: The new government has a long-term program about tourism developing |
T5: Non-observance of the copyright law in this field |
| O6: People have become more sensitive about environmental issues, culture and traditions |
T6: In this organization, the senior managers have weakness in their decision making |
Table 2
Strategies of the company.
| Strategies |
| 1. |
Establishing human resource management (recruitment, training, promotion and retention) |
| 2. |
Designing the product portfolio in order to utilize the market opportunities |
| 3. |
Identifying, documenting and improving company business processes |
| 4. |
Designing and implementing suitable and attractive programs about company’s marketing for current and future services |
| 5. |
Establishing a thinking room for decision making about all of the activities in company in order to increase employee participation |
| 6. |
Planning in order to penetrate into tourism market and attract customers |
| 7. |
Holding the training courses in order to enhance the ability of employees |
Following the guidelines of David (
2013) and based on a PESTEL analysis, the main internal factors (including strengths and weaknesses) and external factors (including opportunities and threats) are determined. These SWOT factors are summarized in Table
1.
Using the framework of SWOT analysis (David,
2013), seven strategic alternatives are developed for this study as presented in Table
2.
4.2 Determining Interrelationship of Factors by Grey DEMATEL
This study considers 4 experts of company for completing the matrixes. Each expert expresses his/her opinion about the relation among strengths, weakness, opportunities, threats, and strategies, using a grey scale. According to Eqs. (
5) to (
9), the average matrix of DEMATEL is computed as follows:
Normalizing the matrix,
A, initial direct impact matrix,
D, is constructed.
Then, using Eq. (
12), the completed direct/ indirect matrix,
T, is computed.
Using maximum mean de-entropy method of Li and Tzeng (
2009), the threshold value is determined equal to 0.8857. Therefore, the network of interrelation among factors is constructed according to Fig.
2.
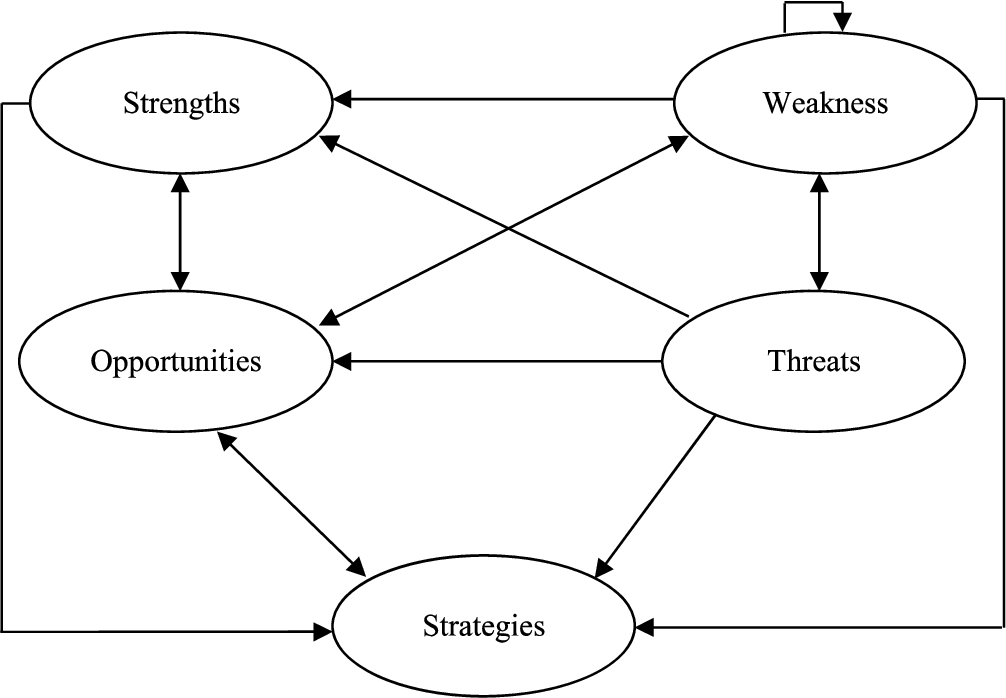
Fig. 2
Network of relation among factors.
4.3 Determining Strategies Utility by Grey ANP
In the next stage, according to decision network, Fig.
2, the pairwise comparisons are done. In this regard, all the elements of an impacted cluster are pair-wisely compared in regards to the elements of an affecting cluster. Then, the weight vector of each pairwise decision matrix is obtained and the super matrix is constructed by combining these weight vectors.
To normalize the obtained super matrix, the clusters are compared in regards to each other and based on the relationships in the network. For example, since “strengths” cluster has an impact on “opportunities” and “strategies” cluster, the latter two clusters are compared with the first one. Again, the pairwise matrices are distributed among experts and their judgements are combined via geometric mean. The aggregated pairwise matrix is shown as:
| Strengths |
Opportunities |
Strategies |
| Opportunities |
$[1,1]$ |
$[1.34,1.73]$ |
| Strategies |
|
$[1,1]$ |
To obtain the weight vector of above grey-pairwise matrix, the model in Eq. (
16) is formulated as:
Solving the above model, the result obtained is
${x_{o}^{\ast }}=0$,
${x_{st}^{\ast }}=0.2939$, since
${w_{i}}=exp({x_{i}})$, then
${w_{o}^{\ast }}=1$, and
${w_{st}^{\ast }}=1.34$. Normalizing these values, the final weight vector will be
${w_{o}^{\ast }}=0.427$, and
${w_{st}^{\ast }}=0.573$. Similarly, other weights are calculated. Table
3 summarizes the weights of cluster in regards to each other.
Table 3
The weight of clusters of strategy ranking problem.
|
Strengths |
Weaknesses |
Opportunities |
Threats |
Strategies |
| Strengths |
0.000 |
0.401 |
0.661 |
0.227 |
0.000 |
| Weaknesses |
0.000 |
0.278 |
0.148 |
0.415 |
0.000 |
| Opportunities |
0.427 |
0.080 |
0.000 |
0.227 |
1.000 |
| Threats |
0.000 |
0.160 |
0.000 |
0.000 |
0.000 |
| Strategies |
0.573 |
0.080 |
0.191 |
0.131 |
0.000 |
Then to obtain the weighted super matrix or stochastic super matrix, the entries of initial super matrix are multiplied by the elements of their corresponding cluster weight in Table
3. This weighted super matrix then rose to limiting powers. After 19th iteration (19th power), the limited super matrix is obtained as is shown in Table
4.
Each column of Table
4 determines the final ratio scale priority of elements in network. In this table, the cluster’s ratio scale priority is equal to sum of its elements’ ratio scale priority. The ratio scale priorities of the elements within their clusters (last column) are calculated by normalizing their ratio scale priority in the related cluster.
Table 4
The relative importance of clusters and elements.
| Clusters |
Elements |
(1) |
(2) |
(3) = (1)/(2) |
| Ratio scale priority in the network |
Ratio scale priority of clusters |
Ratio scale priority of elements in their cluster |
| Strengths |
S1 |
0.0536 |
0.2845 |
0.1884 |
|
S2 |
0.0442 |
|
0.1554 |
|
S3 |
0.0459 |
|
0.1613 |
|
S4 |
0.0435 |
|
0.1529 |
|
S5 |
0.0480 |
|
0.1687 |
|
S6 |
0.0493 |
|
0.1884 |
| Weaknesses |
W1 |
0.0123 |
0.0844 |
0.1457 |
|
W2 |
0.0111 |
|
0.1315 |
|
W3 |
0.0099 |
|
0.1173 |
|
W4 |
0.0107 |
|
0.1268 |
|
W5 |
0.0144 |
|
0.1706 |
|
W6 |
0.0260 |
|
0.1457 |
| Opportunities |
O1 |
0.0440 |
0.3745 |
0.1175 |
|
O2 |
0.0446 |
|
0.1191 |
|
O3 |
0.0475 |
|
0.1268 |
|
O4 |
0.0365 |
|
0.0975 |
|
O5 |
0.0710 |
|
0.1896 |
|
O6 |
0.1309 |
|
0.1175 |
| Threats |
T1 |
0.0008 |
0.0135 |
0.0593 |
|
T2 |
0.0020 |
|
0.1481 |
|
T3 |
0.0019 |
|
0.1407 |
|
T4 |
0.0011 |
|
0.0815 |
|
T5 |
0.0019 |
|
0.1407 |
|
T6 |
0.0058 |
|
0.0593 |
| Strategies |
ST1 |
0.0365 |
0.2431 |
0.1501 |
|
ST2 |
0.0284 |
|
0.1168 |
|
ST3 |
0.0300 |
|
0.1234 |
|
ST4 |
0.0261 |
|
0.1074 |
|
ST5 |
0.0285 |
|
0.1172 |
|
ST6 |
0.0254 |
|
0.1045 |
|
ST7 |
0.0682 |
|
0.2805 |
Table
4 indicates that among SWOT clusters, the most important one is “opportunities”, and then strengths, weaknesses, and threats are in the second to fourth rank of importance. Also, in each cluster all factors are ranked. The most important strategy is “Holding the training courses in order to enhance the ability of employees”. The 2nd and 3rd strategies are “Establishing human resource management (recruitment, training, promotion and retention)”, and “Identifying, documenting and improving company business processes”, respectively. Therefore, if the considered organization has a limited budget for performing its strategic plan, it must allocate this budget according to the obtained ranking of strategies.
4.4 Choosing Strategies by 0–1 Programming
In ANP method, priority of the strategies is determined by using different criteria of SWOT. On the basis of these criteria, organization has a list of prioritized strategies for implementing. In this organization, there are not huge amount of financial resources and budget for performing the strategies. According to the past studies, one of the main reasons in failure of strategies is lack of budgeting and lack of financial resource allocation. Therefore, considering the financial aspect to select strategies is very important.
For solving this problem, a zero/one model is formulated by considering the budget constraints. This model is formulated as:
The objective function of above model is seeking to maximize the utility of selected strategies. The first limitation shows that total needed budget for implementing the strategies couldn’t be more than total budget. The second limitation indicates the establishment of the organization’s limitations to select strategies. Finally, the last limitation shows the nature zero/one of variable of model.
Zero/one Integer Programming can be solved with lots of methods like direct counting method, implicit counting method and branch and bound methods. In this research, Lingo software is used to solve the model.
According to the surveys, researcher predicts some projects for implementing each of the strategies. Each project has an estimated budget. Table
5 shows anticipated budget for each strategy, their utilities and corresponding decision variables.
Table 5
Model parameters.
| Row |
Strategy |
Marginal utility |
Suggested budget (million rials) |
Decision variable |
| 1 |
Establishing human resource management (recruitment, training, promotion and retention) |
0.1501 |
200 |
${x_{1}}$ |
| 2 |
Designing the product portfolio in order to utilize the market opportunities |
0.1168 |
150 |
${x_{2}}$ |
| 3 |
Identifying, documenting and improving company business processes |
0.1234 |
350 |
${x_{3}}$ |
| 4 |
Designing and implementing suitable and attractive programs about company’s marketing for current and future services |
0.1074 |
200 |
${x_{4}}$ |
| 5 |
Establishing a thinking room for decision making about all of the activities in company in order to increase employee participation |
0.1172 |
150 |
${x_{5}}$ |
| 6 |
Planning in order to penetrate into tourism market and attract customers |
0.1045 |
300 |
${x_{6}}$ |
| 7 |
Holding the training courses in order to enhance the ability of employees |
0.2805 |
200 |
${x_{7}}$ |
| Total budget |
1000 |
Also company defined some restrictions about selecting the strategies as below:
-
• Second strategy must be selected in the first year;
-
• While selecting the first strategy, the third strategy must not be done in the same year and vice versa;
-
• If the second strategy is selected, the fourth strategy also should be selected;
-
• Selection of the fourth and sixth strategy should be done concurrently;
-
• While selecting the fourth strategy, the seventh strategy must not be selected in the same year and vice versa;
-
• If the fourth strategy is chosen, the seventh strategy shouldn’t be selected in the same year and vice versa;
-
• According to the respective projects for the strategies, the company shouldn’t select more than three strategies per year.
According to the above information, strategy selection model based on budget constraints is formulated as follows:
Lingo Software is used to solve the above model. After solving the model, the optimal solution is determined as follows:
These outputs indicate that the second, fourth and sixth strategies should be done for the first year.
After implementing the above strategies, the model must specify other strategies for the other year. Therefore, other strategies will be remodelled after removing the accomplished strategies and updating the budget parameters and inserting them in the model. Table
6 illustrates priority of strategies for different years.
Table 6
Priority of strategies for different years.
| Year |
Selected strategies |
| First |
Designing the product portfolio in order to utilize the market opportunities |
|
Designing and implementing suitable and attractive programs about company’s marketing for current and future services |
|
Planning in order to penetrate into tourism market and attract customers |
| Second |
Establishing human resource management (recruitment, training, promotion and retention) |
|
Establishing a thinking room for decision making about all of the activities in company in order to increase employee participation |
|
Holding the training courses in order to enhance the ability of employees |
| Third |
Identifying, documenting and improving company business processes |
5 Conclusion
Strategy planning is a crucial managerial role that determines the orientation and main activities of an organization to reach its long term goals. This activity also plays a major role in determining the effective ways of resources allocation. Considering its importance, different frameworks are developed to formulate strategies. However, how to choose right strategies is a challenging question. This difficulty is magnified considering the uncertainty of managers dealing with strategic aspects of an organization.
Considering these difficulties, in this paper a method is developed for considering the problem of strategy formulation and selection. Considering the internal strengths and weaknesses along with external opportunities and threats as the main aspects of strategic planning, the proposed method comprises a grey DEMATEL – grey ANP methodology. Since the internal/external factors of an organization are determined and its strategies are developed, the grey DEMATEL is used to identify the interrelationship among SWOT factors and strategies. Then, using the determined interrelationships, the grey ANP is employed to rank and select the best strategies. Therefore, beyond using grey DEMATEL – grey ANP methodology in ranking strategies, the main contribution of the proposed method is to develop a binary programming method of strategy selection by considering the required budget for strategy implementation. This method can prevent the failure of strategies due to lack of budget assignment in selection phase. Application of the proposed method is shown in a company competing in tourism industry. Further researchers can develop the proposed methodology in a fuzzy environment. Application of the proposed method in other fields is also interesting.
It is recommended to researcher to use Interpretative structural modelling in order to identify the network among strategic factors.
It is also suggested considering the common resources and strategy related resources in modelling the future papers.