Abstract
To provide better overall performance, identity (ID)-based signcryption (IBSC) has been constructed by combining ID-based signature (IBS) and ID-based encryption (IBE) in a secure manner. Undoubtedly, the IBSC fulfills the authentication and the confidentiality by signature and encryption, respectively. All the previously proposed IBSC schemes are inseparable in the sense that the two-layer sign-then-encrypt procedure must be performed only by the same entity. However, the entities, such as wireless sensors and smart cards, are resource-constrained and become time consuming in executing the two-layer sign-then-encrypt procedure. Nowadays, the usage of mobile cloud computing is gaining expanding interest which provides scalable and virtualized services over the Internet or wireless networks while users with resource-constrained devices can enjoy the advantages of mobile cloud computing environments. Hence, we aim to reduce the computational cost for resource-constrained devices by employing a third party. In this article, we present the first separable ID-based signcryption (SIBSC) scheme in which the signing and encrypting layers are performed by the device and a third party, respectively. Under the computation Diffie–Hellman (CDH) and bilinear Diffie–Hellman (BDH) assumptions, we demonstrate that the proposed SIBSC scheme offers the provable security of authentication and confidentiality while retaining communication performance.
1 Introduction
In conventional public key systems, encryption and signature are respectively used to offer the confidentiality and the authentication which are two of the most important security issues. In addition, for both encryption and signature schemes in conventional public key systems, certificates are needed to provide an unforgeable and trusted link between identities and public keys. In 1984, Shamir (
1984) introduced the concept of identity (ID)-based cryptography to eliminate the need of certificates by which Shamir replaced the public keys of users with their identity information. Hence, ID-based cryptography provides a convenient alternative equipped with no public key infrastructure (PKI). A practical ID-based construction was not constructed until 2001 when Boneh and Franklin (
2001) presented the very first one based on bilinear pairings. Boneh and Franklin’s construction was an important breakthrough and offered a pathway to build other ID-based cryptographic mechanisms such as ID-based key agreement protocols (Chen
et al.,
2007; Wu and Tseng,
2010; Tseng
et al.,
2016), ID-based encryption (IBE) schemes (Boneh and Boyen,
2004; Waters,
2005; Boyen and Waters,
2006; Libert and Vergnaud,
2009; Tsai
et al.,
2012) and ID-based signature (IBS) schemes (Cha and Cheon,
2003; Paterson and Schuldt,
2006; Boneh
et al.,
2006; Narayan and Parampalli,
2008; Tsai
et al.,
2013,
2014).
A signcryption scheme provides an efficient solution to fulfill both the functions of signature and encryption simultaneously. The performance of a signcryption scheme is better than that of performing a signature and a public-key encryption schemes apart. Hence, signcryption is useful in many applications, such as mobile communications and smart cards. The first ID-based signcryption (IBSC) scheme was constructed by Malone-Lee (
2002). Further research on IBSC (Libert and Quisquater,
2003; Boyen,
2003; Chow
et al.,
2004; Chen and Malone-Lee,
2005) has been done to improve both the security and performance. The environment of IBSC includes three roles, namely, a trusted private key generator (PKG), senders and receivers. The PKG is responsible to generate the private keys of both senders and receivers by using their identities. A sender, by using her/his private key and a designated receiver’s identity, performs a two-layer sign-then-encrypt procedure on a message to generate a ciphertext. Upon receiving the ciphertext, the designated receiver is able to decrypt it to obtain the signature and message, while verifying the signature using the sender’s identity.
1.1 Related Work
Zheng (
1997) presented the notion of public key signcryption by which signature and encryption are performed simultaneously to reduce computational cost or communication size, compared with those performing signature and encryption separately. Zheng presented two signcryption schemes based on the discrete logarithm problem. Indeed, a signcryption scheme fulfills the authentication and the confidentiality offered by signature and encryption, respectively.
Following Boneh and Franklin (
2001), Malone-Lee (
2002) proposed the first ID-based signcryption (IBSC) scheme by combining IBS and IBE schemes. Later, Libert and Quisquater (
2003) pointed out a security drawback on Malone-Lee’s scheme, namely, semantically insecure. Libert and Quisquater also presented three improved IBSC schemes, but these schemes lack public verifiability and forward security. In 2004, Chow
et al. (
2004) proposed an IBSC scheme to resolve the weakness in Libert and Quisquater (
2003). In order to provide ciphertext unlinkability and anonymity, Boyen (
2003) proposed a multi-purpose IBSC scheme. A couple of years later, Chen and Malone-Lee (
2005) modified Boyen’s scheme to improve efficiency. All the IBSC schemes mentioned above are proved to be secure in the random oracle model (Bellare and Rogaway,
1993; Canetti
et al.,
2004). In order to provide more robust security, several researchers (Jin
et al.,
2010; Zhang,
2010; Li
et al.,
2011; Li and Takagi,
2013) eliminated the use of random oracles to create several IBSC schemes in the standard models. Indeed, these schemes enhance the security, but degrade the performance.
1.2 Motivation and Contribution
Nowadays, the usage of cloud computing is gaining expanding interest. Cloud computing environment, defined by the National Institute of Standards and Technology (NIST) (Mell and Grance,
2009), provides scalable and virtualized services over the Internet or wireless networks. To enjoy the advantages of cloud computing environments, encryption and signature schemes (Fahl
et al.,
2012) are generally demanded to achieve authentication and confidentiality, respectively. With the popularity of Internet and wireless networks, many clients employ mobile devices (e.g. smart phone or pad) or computers (notebook or PC) to access cloud computing services through open channels (Suo
et al.,
2013; Tysowski and Hasan,
2013; Ma
et al.,
2015). If clients use mobile devices or computers to store the private keys (credentials) while performing some operations, it is dangerous and not secure because the stored private keys (credentials) could be stolen by embedding virus or hacker software on these mobile devices or computers. Therefore, it is the most accredited way to store the private keys in smart cards while some cryptographic computations using the private keys are also performed by smart cards. However, smart cards are resource-constrained and possess limited computing capability, so the heaviest computations of applications must be executed by mobile devices or computers instead, except some cryptographic computations such as encryption and signature because of security consideration.
When smart cards are involved in ID-based cryptography, they become time consuming in executing cryptographic computations such as pairing operations in Boneh and Franklin’s IBE scheme (
2001). Undoubtedly, based on Boneh and Franklin’s ID-based public-key setting, the existing IBE, IBS, and IBSC schemes still require pairing operations, which are heavy computation load for resource-constrained devices. For achieving both authentication and confidentiality simultaneously, as mentioned earlier, the performance of an IBSC scheme is better than that of performing an IBS scheme and an IBE scheme separately.
In an IBSC scheme, the same ephemeral secrets, parameters and keys are used in the two-layer sign-then-encrypt procedure, which includes a signing layer and an encryption layer. We observe that all the previously proposed IBSC schemes are
inseparable in the sense that the two-layer sign-then-encrypt procedure must be performed only by the same entity. The reason is that if the encryption layer were performed by a third party, the private key of the sender could be revealed by the third party because the same ephemeral secrets are involved in both the signing and encryption layers. In this article, to reduce the computational cost of resource-constrained devices (e.g. smart cards) in IBSC schemes, we will employ a third party to assist with expensive pairing computations without endangering the private keys of senders. Indeed, we will propose a novel
separable ID-based signcryption (SIBSC) scheme in which the signing and encryption layers are performed by a resource-constrained device and a third party, respectively. Under the computation Diffie–Hellman (CDH) and bilinear Diffie–Hellman (BDH) assumptions (Boneh and Franklin,
2001; Cha and Cheon,
2003), we demonstrate that our proposed SIBSC scheme offers the provable security of authentication and confidentiality in the random oracle model (Bellare and Rogaway,
1993; Canetti
et al.,
2004).
Here, we present a usage scenario of the proposed SIBSC scheme which is depicted in Fig.
1. In a client-server environment, a client with smart card would like to have access to multiple (
m) remote service servers via open channels (e.g. Internet). The client may use a third party (smart phone or PC with a card reader) to perform the proposed SIBSC scheme to achieve authentication and confidentiality for remote service servers. In which, the client’s private key is involved in the signing layer which is performed by the smart card. Meanwhile, the public-key encryption layer is performed by a smart phone or a PC with a card reader due to it does not require the client’s private key to involve in the computation. It is notable that the smartcard directly connects to a smart phone with a transmission-line-connected card reader or a PC with an embedded card reader. If the smart card connects to the third party using wireless communication, it will incur extra communication cost.
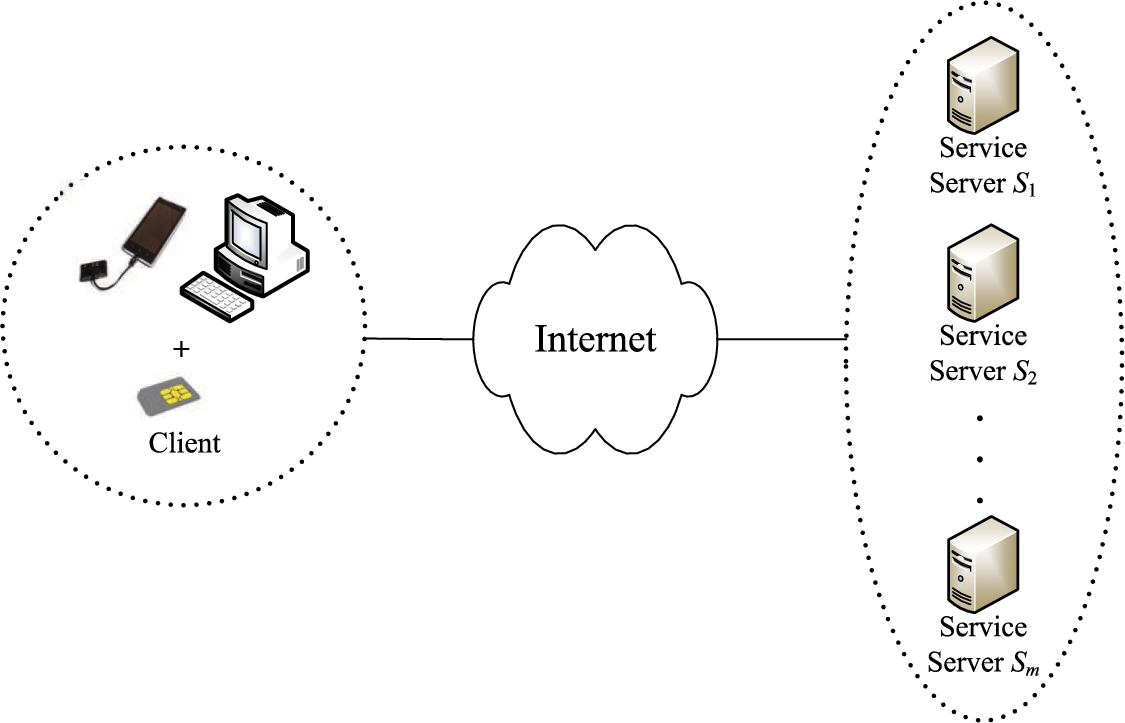
Fig. 1
The usage scenario of the SIBSC scheme.
1.3 Merits of Our SIBSC Scheme
Here, we demonstrate the merits of our SIBSC scheme which is suitable to provide both authentication and confidentiality for many applications with resource-constrained devices. For example, a smart card with limited computing capability could not efficiently execute heavy computations (such as pairing operations) and, in such a case, it needs to rely on a third party to perform these heavy computations. In order to achieve both authentication and confidentiality, we observe four solutions (combinations) according to running entities (smart card and third party) and the employed schemes (IBS + IBE, IBSC and SIBSC) as follows.
-
• Solution 1: an intuitive solution is that the smart card performs both IBS and IBE schemes as depicted in Fig.
2(a). In this case, the smart card takes all computational loads.
-
• Solution 2: the IBS scheme is performed by the smart card, while the IBE scheme is executed by a third party as shown in Fig.
2(b). This solution aims at reducing the computational cost of the smart card. Note that running an IBE scheme does not need the sender’s private key.
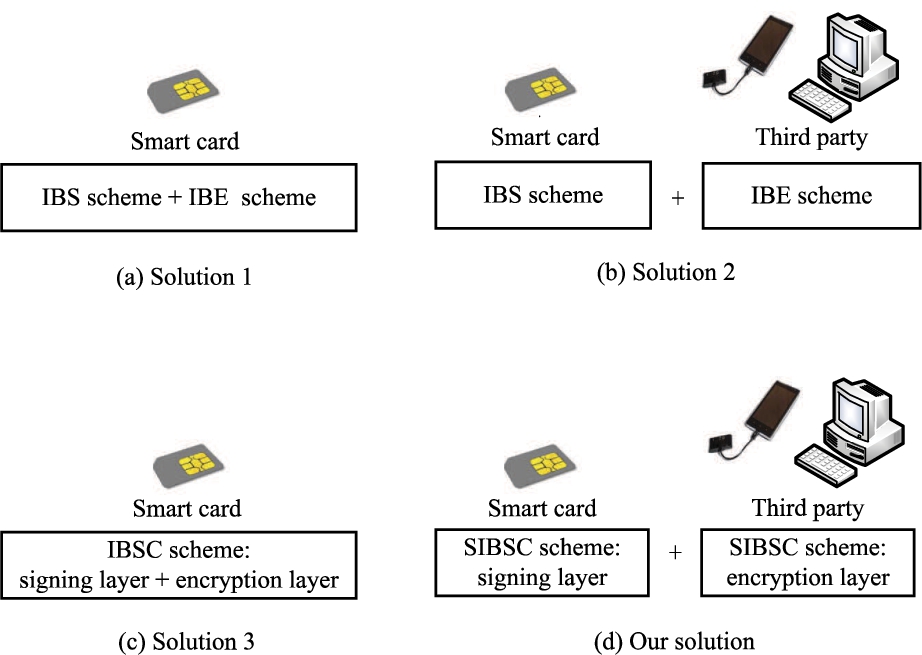
Fig. 2
Four solutions to achieve authentication and confidentiality.
Table 1
Comparisons between the SIBSC scheme and other schemes.
|
Solution 1 |
Solution 2 |
Solution 3 |
Our solution |
| Hired scheme |
CC’s IBS |
CC’s IBS |
CM’s IBSC |
Our SIBSC |
|
(2003) |
(2003) |
(2005) |
|
|
+ BF’s IBE |
+ BF’s IBE |
|
|
|
(2001) |
(2001) |
|
|
| Computational cost of |
Signing + Encryption |
Signing |
Signcryption |
Signing layer |
| smart card |
(High) |
(Low) |
(High) |
(Low) |
| Computational cost for |
– |
Encryption |
– |
Encryption layer |
| third party |
|
(Low) |
|
(Low) |
| Communication size |
High |
High |
Low |
Low |
-
• Solution 3: the smart card performs the two-layer sign-then-encrypt procedure in the IBSC scheme as shown in Fig.
2(c). This solution is more efficient than Solutions 1 and 2, in particular, in communication size.
-
• Our solution: By our SIBSC scheme, the signing and encryption layers are performed by the smart card and a third party, respectively, as shown in Fig.
2(d). Our solution aims at reducing not only the computational cost of the smart card but also the communication size.
Table
1 lists the comparisons between the proposed SIBSC scheme (our solution) and the other three solutions in terms of computational costs of smart card and third party, and communication size. Here, we adopt, respectively, the Cha and Cheon’s IBS (for short, CC’s IBS) and Boneh and Franklin’s IBE (for short, BF’s IBE) schemes in Cha and Cheon (
2003) and Boneh and Franklin (
2001). In the meantime, we employ the most efficient IBSC (CM’s IBSC) scheme constructed by Chen and Malone-Lee (
2005). By Table
1, it is clear that our solution possesses the merits of both Solutions 2 and 3. The detailed comparisons regarding communication and computational costs will be discussed in Section
6.
1.4 Outline of the Paper
The rest of this paper is organized as follows. Preliminaries are given in Section
2. Then, in Section
3, we give framework and security notions. In Section
4, a concrete SIBSC scheme is proposed. Section
5 gives the security analysis of the proposed scheme. Finally, we demonstrate performance analysis in Section
6 before making conclusions in Section
7.
2 Preliminaries
Before presenting our construction, we briefly review the concept of bilinear pairings and two mathematical assumptions on which our construction is based. We first define the following notations.
-
• q is a large prime.
-
• ${\mathbb{G}_{1}}$ is an additive cyclic group of order q.
-
• ${\mathbb{G}_{2}}$ is a multiplicative cyclic group of order q.
-
• P is a generator of ${\mathbb{G}_{1}}$.
2.1 Bilinear Map
We say that
$\hat{e}:{\mathbb{G}_{1}}\times {\mathbb{G}_{1}}\to {\mathbb{G}_{2}}$ is an admissible bilinear map if it satisfies three properties as follows.
-
(1) Non-degeneracy: $\hat{e}(P,P)\ne 1$.
-
(2) Bilinearity: for all $Q,R\in {\mathbb{G}_{1}}$ and $a,b\in {\mathbb{Z}_{q}^{\ast }}$, $\hat{e}(aQ,bR)=\hat{e}{(Q,R)^{ab}}$.
-
(3) Computability: for $Q,R\in {\mathbb{G}_{1}}$, there exists an efficient algorithm to compute $\hat{e}(Q,R)$.
For full descriptions of groups, maps and other parameters, the reader can refer to Boneh and Franklin (
2001).
2.2 Related Mathematical Assumptions
The computational Diffie–Hellman (CDH) and the bilinear Diffie–Hellman (BDH) assumptions in
${\mathbb{G}_{1}}$ and
${\mathbb{G}_{2}}$, respectively, are defined as below.
Definition 1 (CDH assumption).
Given
$P,aP,bP\in {\mathbb{G}_{1}}$ with unknown
$a,b\in {\mathbb{Z}_{q}^{\ast }}$, we assume that there exists no probabilistic polynomial-time (PPT) adversary
$\mathcal{A}$ with non-negligible probability who can compute
$abP$. The successful probability (advantage) of the adversary
$\mathcal{A}$ is presented as
Definition 2 (BDH assumption).
Given
$P,aP,bP,cP\in {\mathbb{G}_{1}}$ with unknown
$a,b,c\in {\mathbb{Z}_{q}^{\ast }}$, we assume that there exists no PPT adversary
$\mathcal{A}$ with non-negligible probability who can compute
$\hat{e}{(P,P)^{abc}}$. The successful probability of the adversary
$\mathcal{A}$ is presented as
3 Framework and Security Notions
Here, we informally describe our separable ID-based signcryption (SIBSC). The proposed SIBSC consists of four roles, namely, a trusted private key generator (PKG), a semi-trusted third party (e.g. smart phone), senders (with resourced-constrained devices) and receivers. The work of the PKG is to generate the secret key and public parameters of the system, and produce private keys of users (senders and receivers). A sender (signer) A with identity ${\mathit{ID}_{A}}$ first chooses an ephemeral secret value ${r_{A}}$, and generates a signature ${\sigma _{A}}$ on a message M by using her/his private key ${\mathit{SID}_{A}}$. For a designated receiver B with identity ${\mathit{ID}_{B}}$, the sender A first transmits $({\sigma _{A}},M,{\mathit{ID}_{A}},{r_{A}},{\mathit{ID}_{B}})$ to the third party via a secure channel. Then, the third party is responsible to generate a ciphertext ${\mathit{CT}_{B}}$ using $({\sigma _{A}},M,{\mathit{ID}_{A}},{r_{A}},{\mathit{ID}_{B}})$, and transmit ${\mathit{CT}_{B}}$ to the receiver B. Finally, the ciphertext ${\mathit{CT}_{B}}$ can be decrypted and verified by B. Here, we emphasize that the semi-trusted third party is unable to reveal the private key of the sender A by appealing to the message $({\sigma _{A}},M,{\mathit{ID}_{A}},{r_{A}},{\mathit{ID}_{B}})$.
3.1 Framework
In IBSC schemes of Boyen (
2003), Chen and Malone-Lee (
2005), the framework consists of six algorithms, namely, the
system setup, the
key extract, the
signing, the
encryption, the
decryption and the
verification. Here, our framework for SIBSC schemes is identical to that of the above IBSC schemes, except that our
encryption algorithm does not require the input of the sender’s secret key. The details of six algorithms are described below.
-
• System setup: on input of a security parameter l, this algorithm produces a secret key $\mathit{SK}$ and public parameters $\mathit{PK}$ of the system. $\mathit{PK}$ is publicly known and available for all other algorithms.
-
• Key extract: on input of $\mathit{SK}$ and the identity ${\mathit{ID}_{U}}$ of a user U, this algorithm computes the corresponding secret key ${\mathit{SID}_{U}}$ and then returns it to U via a secure channel.
-
• Signing: on input of the identity ${\mathit{ID}_{A}}$, the secret key ${\mathit{SID}_{A}}$ of a user A, and a message M, this algorithm produces a pair $({\sigma _{A}},{r_{A}})$, where ${\sigma _{A}}$ is a signature and ${r_{A}}$ is an ephemeral data.
-
• Encryption: on input of the identity ${\mathit{ID}_{B}}$ of a user B, a message M and a pair $({\sigma _{A}},{r_{A}})$, this algorithm produces a ciphertext ${\mathit{CT}_{B}}$.
-
• Decryption: on input of the secret key ${\mathit{SID}_{B}}$ of a user B and the ciphertext ${\mathit{CT}_{B}}$, this algorithm produces the message M and the signature ${\sigma _{A}}$.
-
• Verification: on input of the identity ${\mathit{ID}_{A}}$ of a user A, the message M and the signature ${\sigma _{A}}$, the algorithm outputs either “accept” or “reject”.
3.2 Security Notions
In a SIBSC scheme, both security properties of authentication (unforgeability) and confidentiality must be fulfilled. It is obvious that the attacking ability of the semi-trusted third party is stronger than that of any outsider because it possesses more information (i.e. ephemeral secret and signature) sent by a sender. Hence, for unforgeability, it suffices to demonstrate that the third party cannot violate the authentication of the proposed SIBSC scheme, which will be done in Section
5. In the following, we introduce two kinds of adversaries to address the two security properties.
-
• Type I adversary: this adversary is the semi-trusted third party, which assists the sender with heavy computation and attempts to forge a signature on behalf of the sender.
-
• Type II adversary: upon capturing a ciphertext, a Type II adversary attempts to decrypt it to obtain the plaintext message. This adversary excludes the designated receiver.
Definition 3 (Unforgeability for Type I adversary).
We say that a SIBSC scheme is existential unforgeability against adaptive chosen message attack (SIBSC-UF-ACMA) if no Type I adversary
$\mathcal{A}$ has a non-negligible advantage in the following SIBSC-UF-ACMA game played between a challenger
$\mathcal{C}$ and the adversary
$\mathcal{A}$.
-
• Initial: the challenger $\mathcal{C}$ runs the system setup algorithm to generate a secret key $\mathit{SK}$ and public parameters $\mathit{PK}$ of the system. $\mathcal{C}$ then gives $\mathit{PK}$ to the adversary $\mathcal{A}$ while keeping $\mathit{SK}$ secret.
-
• Phase 1: the adversary $\mathcal{A}$ may make a number of different queries to the challenger $\mathcal{C}$ in an adaptive manner as follows:
-
– Key extract query: the adversary $\mathcal{A}$ submits this query along with identity ${\mathit{ID}_{U}}$. The challenger $\mathcal{C}$ runs the key extract algorithm to generate the private key ${\mathit{SID}_{U}}$ of ${\mathit{ID}_{U}}$ and returns it to $\mathcal{A}$.
-
– Signing query: the adversary $\mathcal{A}$ submits this query along with a message M and an identity ${\mathit{ID}_{U}}$. The challenger $\mathcal{C}$ runs the signing algorithm to generate a signature ${\sigma _{U}}$ and then returns it to $\mathcal{A}$.
-
• Forge: the adversary $\mathcal{A}$ returns a tuple $({M^{\ast }},$ ${\sigma _{U}^{\ast }},$ ${\mathit{ID}_{U}^{\ast }})$, and we say that $\mathcal{A}$ wins this game if the following conditions are satisfied:
-
(1) The response of verification algorithm on $({M^{\ast }},{\sigma _{U}^{\ast }},{\mathit{ID}_{U}^{\ast }})$ is “accept”.
-
(2) ${\sigma _{U}^{\ast }}$ has not been returned during signing queries on the input $({M^{\ast }},{\mathit{ID}_{U}^{\ast }})$.
-
(3) ${\mathit{ID}_{U}^{\ast }}$ did not appear in key extract queries.
Definition 4 (Confidentiality for Type II adversary).
We say that a SIBSC scheme is semantically secure against an adaptive chosen plaintext attack (IND-SIBSC-CPA) if no Type II adversary
$\mathcal{A}$ has a non-negligible advantage in the following IND-SIBSC-CPA game played between a challenger
$\mathcal{C}$ and the adversary
$\mathcal{A}$.
-
• Initial: same as the
Initial in
Definition 3.
-
• Phase 1: the adversary
$\mathcal{A}$ may make a number of
key extract queries, as described in
Phase 1 of
Definition 3, to the challenger
$\mathcal{C}$ in an adaptive manner.
-
• Challenge: the adversary $\mathcal{A}$ outputs an identity ${\mathit{ID}_{U}^{\ast }}$ and a target plaintext pair $({M_{0}},{M_{1}})$. After receiving them, $\mathcal{C}$ randomly selects a value $\mathfrak{b}\in \{0,1\}$ and runs the encryption algorithm on ${M_{\mathfrak{b}}}$ to generate a ciphertext ${\mathit{CT}_{U}^{\ast }}$ encrypted under the identity ${\mathit{ID}_{U}^{\ast }}$. Then $\mathcal{C}$ returns the ciphertext ${\mathit{CT}_{U}^{\ast }}$ to $\mathcal{A}$. Here, we impose the restriction that ${\mathit{ID}_{U}^{\ast }}$ has not appeared in the key extract queries.
-
• Phase 2: the adversary $\mathcal{A}$ may make further queries as in Phase 1. The restriction is that ${\mathit{ID}_{U}^{\ast }}$ has not appeared in the key extract queries.
-
• Guess: the adversary $\mathcal{A}$ returns its guess ${\mathfrak{b}^{\prime }}\in \{0,1\}$. We say that $\mathcal{A}$ wins the IND-SIBSC-CPA game if ${\mathfrak{b}^{\prime }}=\mathfrak{b}$.
Remark 1.
A separable ID-based signcryption scheme against an adaptive chosen plaintext attack (IND-SIBSC-CPA) is weaker than that against an adaptive chosen ciphertext attack (IND-SIBSC-CCA). The IND-SIBSC-CCA game is identical to the IND-SIBSC-CPA game except by adding the decryption queries in Phases 1 and 2. Indeed, Kitagawa
et al. (
2006) have proposed a simple conversion from a weak scheme (IND-ID-CPA) to a strong one (IND-ID-CCA) in the random oracle model (Bellare and Rogaway,
1993; Canetti
et al.,
2004). The only restriction is that the hash functions used in the weak scheme must be random oracles (Kitagawa
et al.,
2006). Hence, following this conversion, one can also construct a strong ID-based signcryption scheme from our proposed scheme in the random oracle model.
4 Our SIBSC Scheme
Our SIBSC scheme consists of six algorithms: the system setup, the key extract, the signing, the encryption, the decryption and the verification.
-
• System setup: given a security parameter
l, a trusted private key generator (PKG) chooses two groups
${\mathbb{G}_{1}}$ and
${\mathbb{G}_{2}}$ of prime order
$q>{2^{l}}$ such that an admissible bilinear map
$\hat{e}:{\mathbb{G}_{1}}\times {\mathbb{G}_{1}}\to {\mathbb{G}_{2}}$ can be constructed. Let
P be a generator of
${\mathbb{G}_{1}}$. The PKG randomly selects a value
$s\in {\mathbb{Z}_{q}^{\ast }}$ as the system secret key, computes
${P_{\mathit{pub}}}=s\cdot P$ and picks five hash functions
${f_{1}},{f_{2}}:{\{0,1\}^{\ast }}\times {\mathbb{G}_{1}}\to {\mathbb{Z}_{q}^{\ast }}$,
${H_{1}}:{\{0,1\}^{\ast }}\times {\mathbb{G}_{1}}\to {\mathbb{G}_{1}}$,
${H_{2}}:{\{0,1\}^{\ast }}\to {\mathbb{G}_{1}}$ and
${H_{3}}:{\mathbb{G}_{2}}\to {\{0,1\}^{k}}$, where
k denotes the output length of
${H_{3}}$. Finally, the secret key
$\mathit{SK}$ and public parameters
$\mathit{PK}$ of the system are set, respectively, as
and
-
• Key extract: to generate the private key of a user (sender or receiver)
U with identity
${\mathit{ID}_{U}}$, the PKG selects a random value
${l_{U}}\in {\mathbb{Z}_{q}^{\ast }}$, sets
${\mathit{QID}_{U}^{(1)}}={l_{U}}\cdot P$ and computes
${\mathit{DID}_{U}^{(1)}}={l_{U}}+{h_{U}^{(1)}}\cdot s$, where
${h_{U}^{(1)}}={f_{1}}({\mathit{ID}_{U}},{\mathit{QID}_{U}^{(1)}})$. Finally, the PKG sets
${\mathit{QID}_{U}^{(2)}}={H_{2}}({\mathit{ID}_{U}})$ and computes
${\mathit{DID}_{U}^{(2)}}=s\cdot {\mathit{QID}_{U}^{(2)}}=s\cdot {H_{2}}({\mathit{ID}_{U}})$. The private key
${\mathit{SID}_{U}}$ of the user
U with identity
${\mathit{ID}_{U}}$ is
Note that
${\mathit{QID}_{U}^{(1)}}$ will be a component of each signature signed by the user
U with identity
${\mathit{ID}_{U}}$, so it can be viewed as a part of the user’s public key.
-
• Signing: the sender A with identity ${\mathit{ID}_{A}}$ generates a signature ${\sigma _{A}}$ on a message $M\in {\{0,1\}^{n}}$ for the designated receiver B with identity ${\mathit{ID}_{B}}$ by the following steps.
-
(1) Choose an ephemeral secret value ${r_{A}}\in {\mathbb{Z}_{q}^{\ast }}$.
-
(2) Compute ${R_{A}}={r_{A}}\cdot P$.
-
(3) Compute ${\mathit{HID}_{A}}$ = ${H_{1}}(M||{\mathit{ID}_{A}},{R_{A}})$ and ${h_{A}^{(2)}}$ = ${f_{2}}(M||{\mathit{ID}_{A}},{R_{A}})$.
-
(4) Use the private key
${\mathit{SID}_{A}}$ obtained in
Key extract to generate
${V_{A}}$ by
-
(5) Output the signature ${\sigma _{A}}=({\mathit{QID}_{A}^{(1)}},{R_{A}},{V_{A}})$ to the third party with the message M, the identity ${\mathit{ID}_{A}}$, the ephemeral secret value ${r_{A}}$ and the identity ${\mathit{ID}_{B}}$.
-
• Encryption: after receiving the output $({\sigma _{A}},M,{\mathit{ID}_{A}},{r_{A}},{\mathit{ID}_{B}})$ from the sender A, the third party computes ${W_{B}}={H_{3}}(\hat{e}({r_{A}}\cdot {P_{\mathit{pub}}},{\mathit{QID}_{B}^{(2)}}))\oplus ({V_{A}}||{\mathit{QID}_{A}^{(1)}}||{\mathit{ID}_{A}}||M)$, sets the ciphertext ${\mathit{CT}_{B}}=({R_{A}},{W_{B}})$ and transmits it to the receiver B.
-
• Decryption: given the ciphertext ${\mathit{CT}_{B}}=({R_{A}},{W_{B}})$, the receiver B computes ${W_{B}}\oplus {H_{3}}(\hat{e}({R_{A}},{\mathit{DID}_{B}^{(2)}}))$ to obtain $({V_{A}}||{\mathit{QID}_{A}^{(1)}}||{\mathit{ID}_{A}}||M)$. Then B forwards the signature ${\sigma _{A}}$, the identity ${\mathit{ID}_{A}}$ and the message M to the verification phase.
-
• Verification: a signature
${\sigma _{A}}$ on the message
M for the identity
${\mathit{ID}_{A}}$ is verified by the receiver
B in the following manners.
-
(1) Compute ${\mathit{HID}_{A}}={H_{1}}(M,{\mathit{ID}_{A}},{R_{A}})$ and ${\mathit{QID}_{A}^{(2)}}={H_{2}}({\mathit{ID}_{A}})$.
-
(2) Compute ${h_{A}^{(1)}}={f_{1}}({\mathit{ID}_{A}},{\mathit{QID}_{A}^{(1)}})$ and ${h_{A}^{(2)}}={f_{2}}(M,{\mathit{ID}_{A}},{R_{A}})$.
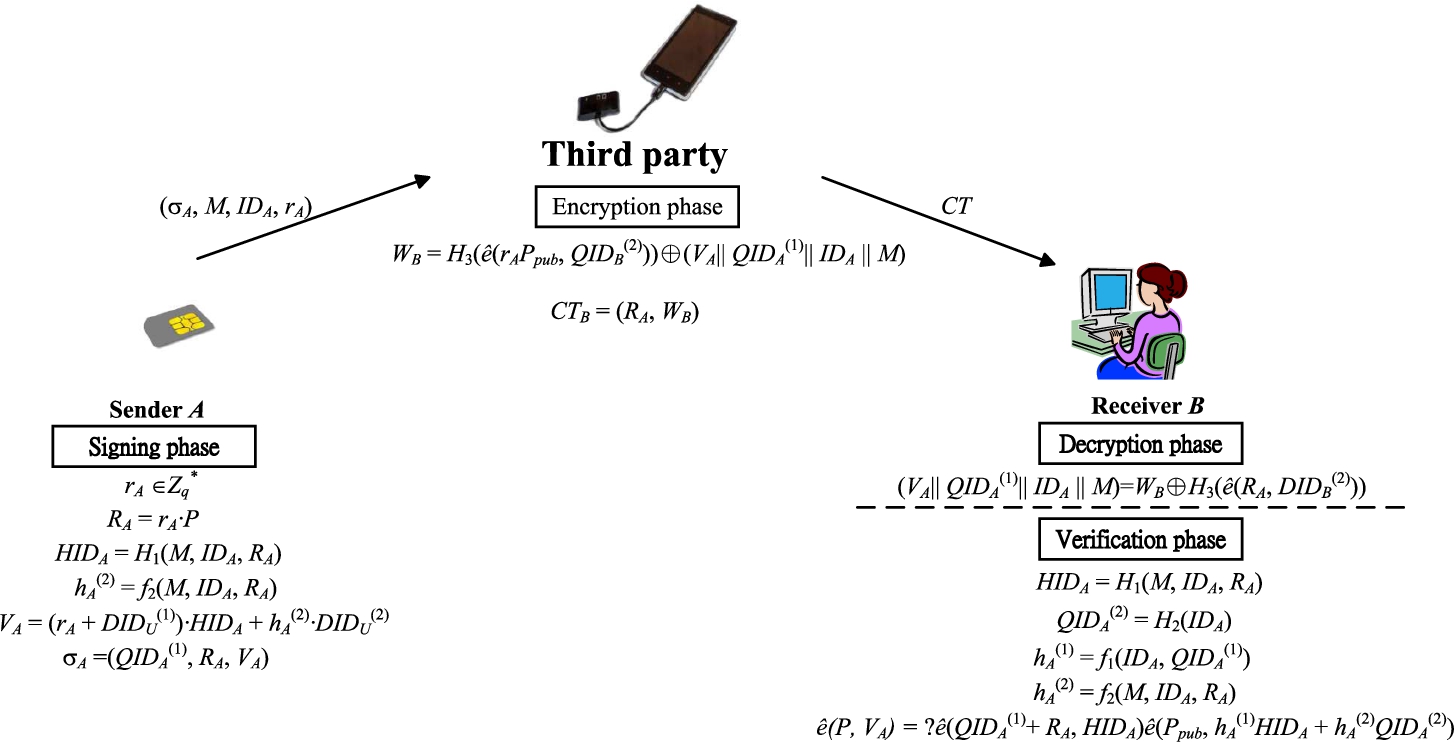
Fig. 3
The relationships of signing, encryption, decryption and verification phases.
-
(3) Check the equality $\hat{e}(P,{V_{A}})=\hat{e}({R_{A}}+{\mathit{QID}_{A}^{(1)}},{\mathit{HID}_{A}})\cdot \hat{e}({P_{\mathit{pub}}},{h_{A}^{(1)}}\cdot {\mathit{HID}_{A}}+{h_{A}^{(2)}}\cdot {\mathit{QID}_{A}^{(2)}})$.
Then the receiver
B outputs “accept” if the last equality holds, and “reject” otherwise.
The signing, encryption, decryption and verification procedures are depicted in Fig.
3. Meanwhile, we present the validity of the equality in (3) above as follows. Since
${V_{A}}=({r_{A}}+{\mathit{DID}_{A}^{(1)}})\cdot {\mathit{HID}_{A}}+{h_{A}^{(2)}}\cdot {\mathit{DID}_{A}^{(2)}}$ with
${\mathit{DID}_{A}^{(1)}}={l_{A}}+{h_{A}^{(1)}}\cdot s$ and
${\mathit{DID}_{A}^{(2)}}=s\cdot {\mathit{QID}_{A}^{(2)}}$, we have
where the last equality follows directly from
${R_{A}}={r_{A}}\cdot P$,
${\mathit{QID}_{A}^{(1)}}={l_{A}}\cdot P$, and
${P_{\mathit{pub}}}=s\cdot P$.
5 Security Analysis
As in Definitions
3 and
4, there are Type I and Type II adversaries in the SIBSC-UF-ACMA and IND-SIBSC-CPA games respectively. In the following, we prove that the proposed SIBSC scheme is secure against Type I and Type II adversaries, respectively, in Theorems
1 and
2. Hence, our SIBSC scheme offers existential unforgeability against adaptive chosen message attacks and is semantically secure against adaptive chosen plaintext attacks.
Theorem 1.
In the random oracle model, the proposed SIBSC scheme is secure against Type I adversary under the CDH assumption. Concretely, suppose that there exists a Type I adversary $\mathcal{A}$ that can break the proposed scheme with a non-negligible advantage ϵ within a running time t. Assume that the hash functions ${f_{1}}$, ${f_{2}}$, ${H_{1}}$, ${H_{2}}$ and ${H_{3}}$ are random oracles, and $\mathcal{A}$ can make ${q_{{f_{i}}}}$ queries to the random oracles ${f_{i}}$ $(i=1,2)$, ${q_{{H_{i}}}}$ queries to the random oracles ${H_{i}}$ $(i=1,2,3)$, ${q_{E}}$ queries to the key extract oracle and ${q_{S}}$ queries to the signing oracle, respectively. Then, we can construct an algorithm $\mathcal{C}$ to solve the CDH problem with an advantage
within a running time
Proof.
We will employ Lemma 1 in Cha and Cheon (
2003) to simplify the security analysis of the proposed scheme. This lemma states that if there is an algorithm with a non-negligible advantage
ϵ within a running time
t to perform ID attacks to an ID-based signature scheme, then there is another algorithm with a non-negligible advantage
${\epsilon ^{\prime\prime }}\geqslant \epsilon (1-1/q)/{q_{{H_{2}}}}$ within a running time
${t^{\prime\prime }}\leqslant t$ to perform a fixed ID attack to the ID-based signature scheme. Suppose that
$\mathcal{A}$ is of Type I adversary that could break the proposed scheme with a non-negligible advantage
ϵ within a running time
t. By Lemma 1 in Cha and Cheon (
2003), there exists another algorithm
$\mathcal{B}$ with the advantage
${\epsilon ^{\prime\prime }}\geqslant \epsilon (1-1/q)/{q_{{H_{2}}}}$ within a running time
${t^{\prime\prime }}\leqslant t$ to perform a fixed attack to the same scheme. Without loss of generality, we choose a fixed identity
${\mathit{ID}_{U}^{\ast }}$ as our target.
Using the algorithm
$\mathcal{B}$, an algorithm
$\mathcal{C}$ will be constructed below to solve the CDH problem. Assume that the algorithm
$\mathcal{C}$ is given a group
${\mathbb{G}_{1}}$ of order
q with a generator
P, and two elements
$aP,bP\in {\mathbb{G}_{1}}$, where
a and
b are unknown to
$\mathcal{C}$. In order to use
$\mathcal{B}$ to compute
$abP$, the algorithm
$\mathcal{C}$ plays a challenger in the following game.
-
• Initial: the challenger $\mathcal{C}$ runs the system setup algorithm and sets ${P_{\mathit{pub}}}=aP$ to create the public parameters $\mathit{PK}=({\mathbb{G}_{1}},{\mathbb{G}_{2}},q,\hat{e},P,{P_{\mathit{pub}}},{f_{1}},{f_{2}},{H_{1}},{H_{2}},{H_{3}})$ of the proposed scheme. Here ${f_{1}}$, ${f_{2}}$, ${H_{1}}$, ${H_{2}}$ and ${H_{3}}$ are random oracles controlled by $\mathcal{C}$. The challenger $\mathcal{C}$ also answers queries of random oracles issued by $\mathcal{B}$ as below.
-
– ${f_{1}}$ queries: at any time, $\mathcal{B}$ can issue queries along with $({\mathit{ID}_{U}},{\mathit{QID}_{U}^{(1)}})$ to the random oracle ${f_{1}}$. To respond to these queries, $\mathcal{C}$ maintains a list ${L_{{f_{1}}}}$ containing tuples of the form $({\mathit{ID}_{U}},{\mathit{QID}_{U}^{(1)}},{\alpha _{U}})$. Initially ${L_{{f_{1}}}}$ is empty. When $\mathcal{B}$ queries the oracle ${f_{1}}$ with a pair $({\mathit{ID}_{U}},{\mathit{QID}_{U}^{(1)}})$, $\mathcal{C}$ responds as follows.
-
(1) If the pair $({\mathit{ID}_{U}},{\mathit{QID}_{U}^{(1)}})$ is already in ${L_{{f_{1}}}}$, the challenger $\mathcal{C}$ responds with the corresponding ${\alpha _{U}}$ to $\mathcal{B}$.
-
(2) Otherwise, the challenger $\mathcal{C}$ randomly selects a value ${\alpha _{U}}\in {\mathbb{Z}_{q}^{\ast }}$, adds the tuple $({\mathit{ID}_{U}},{\mathit{QID}_{U}^{(1)}},{\alpha _{U}})$ in ${L_{{f_{1}}}}$, and responds to $\mathcal{B}$ with ${\alpha _{U}}$.
-
– ${f_{2}}$ queries: at any time, $\mathcal{B}$ can issue queries along with $(M,{\mathit{ID}_{U}},{R_{U}})$ to the random oracle ${f_{2}}$. To respond to these queries, $\mathcal{C}$ maintains a list ${L_{{f_{2}}}}$ containing tuples of the form $(M,{\mathit{ID}_{U}},{R_{U}},{\beta _{U}})$. Initially the list ${L_{{f_{2}}}}$ is empty. When $\mathcal{B}$ queries the oracle ${f_{2}}$ with a tuple $(M,{\mathit{ID}_{U}},{R_{U}})$, $\mathcal{C}$ responds as follows.
-
(1) If the tuple $(M,{\mathit{ID}_{U}},{R_{U}})$ is already in ${L_{{f_{2}}}}$, the challenger $\mathcal{C}$ responds with the corresponding ${\beta _{U}}$ to $\mathcal{B}$.
-
(2) Otherwise, the challenger $\mathcal{C}$ randomly selects a value ${\beta _{U}}\in {\mathbb{Z}_{q}^{\ast }}$, adds the tuple $(M,{\mathit{ID}_{U}},{R_{U}},{\beta _{U}})$ in ${L_{{f_{2}}}}$ and responds to $\mathcal{B}$ with ${\beta _{U}}$.
-
– ${H_{1}}$ queries: at any time, $\mathcal{B}$ can issue queries along with $(M,{\mathit{ID}_{U}},{R_{U}})$ to the random oracle ${H_{1}}$. To respond to these queries, $\mathcal{C}$ maintains a list ${L_{{H_{1}}}}$ containing tuples of the form $(M,{\mathit{ID}_{U}},{R_{U}},{\zeta _{U}},{\zeta _{U}}\cdot bP)$. Initially the list is empty. When $\mathcal{B}$ queries the oracle ${H_{1}}$ with a pair $(M,{\mathit{ID}_{U}},{R_{U}})$, $\mathcal{C}$ responds as follows.
-
(1) If the tuple $(M,{\mathit{ID}_{U}},{R_{U}})$ is already in ${L_{{H_{1}}}}$, the challenger $\mathcal{C}$ responds with the corresponding ${\zeta _{U}}\cdot bP$ to $\mathcal{B}$.
-
(2) Otherwise, the challenger $\mathcal{C}$ randomly selects a value ${\zeta _{U}}\in {\mathbb{Z}_{q}^{\ast }}$, computes ${\zeta _{U}}\cdot bP$, adds the tuple $(M,{\mathit{ID}_{U}},{R_{U}},{\zeta _{U}},{\zeta _{U}}\cdot bP)$ in ${L_{{H_{1}}}}$, and responds to $\mathcal{B}$ with ${\zeta _{U}}\cdot bP$.
-
– ${H_{2}}$ queries: at any time, $\mathcal{B}$ can issue queries with ${\mathit{ID}_{U}}$ to the random oracle ${H_{2}}$. To respond to these queries, $\mathcal{C}$ maintains a list ${L_{{H_{2}}}}$ containing tuples of the form $({\mathit{ID}_{U}},{\mathit{QID}_{U}^{(2)}},{\eta _{U}})$. Initially the list is empty. When $\mathcal{B}$ queries the oracle ${H_{2}}$ with ${\mathit{ID}_{U}}$, $\mathcal{C}$ responds to as follows.
-
(1) If ${\mathit{ID}_{U}}\ne {\mathit{ID}_{U}^{\ast }}$, the challenger $\mathcal{C}$ selects a value ${\eta _{U}}\in {\mathbb{Z}_{q}^{\ast }}$, returns ${\mathit{QID}_{U}^{(2)}}={H_{2}}({\mathit{ID}_{U}})={\eta _{U}}\cdot P$ and stores $({\mathit{ID}_{U}},{\mathit{QID}_{U}^{(2)}},{\eta _{U}})$ in the list ${L_{{H_{2}}}}$.
-
(2) If ${\mathit{ID}_{U}}={\mathit{ID}_{U}^{\ast }}$, the challenger $\mathcal{C}$ selects a value ${\eta _{U}}\in {\mathbb{Z}_{q}^{\ast }}$, returns ${\mathit{QID}_{U}^{(2)}}={H_{2}}({\mathit{ID}_{U}})={\eta _{U}}\cdot P-bP$ and stores $({\mathit{ID}_{U}},{\mathit{QID}_{U}^{(2)}},{\eta _{U}})$ in the list ${L_{{H_{2}}}}$.
-
– ${H_{3}}$ queries: at any time, $\mathcal{B}$ can issue queries along with S to the random oracle ${H_{3}}$. To respond to these queries, the challenger $\mathcal{C}$ maintains a list ${L_{{H_{3}}}}$ containing pairs of the form $(S,T)$. Initially the list is empty. When $\mathcal{B}$ queries the oracle ${H_{3}}$ with S, $\mathcal{C}$ responds as follows.
-
(1) If S already appears in the list ${L_{{H_{3}}}}$, the challenger $\mathcal{C}$ responds with the corresponding T to $\mathcal{B}$.
-
(2) Otherwise, $\mathcal{C}$ randomly selects a string $T\in {\{0,1\}^{k}}$, adds the tuples $(S,T)$ to the list ${L_{{H_{3}}}}$, and responds to $\mathcal{B}$ with T.
-
• Phase 1: the adversary $\mathcal{B}$ may make a number of different queries to the challenger $\mathcal{C}$ in an adaptive manner as follows:
-
– Key extract queries: to respond to these queries, $\mathcal{C}$ maintains a list ${L_{K}}$ containing tuples of the form $({\mathit{ID}_{U}},{\mathit{SID}_{U}})$, where ${\mathit{SID}_{U}}=({\mathit{QID}_{U}^{(1)}},{\mathit{DID}_{U}^{(1)}},{\mathit{DID}_{U}^{(2)}})$. Initially the list is empty. Upon receiving the query along with ${\mathit{ID}_{U}}$, if ${\mathit{ID}_{U}}$ already appears in the list ${L_{K}}$, the challenger $\mathcal{C}$ responds with the associated ${\mathit{SID}_{U}}$ to $\mathcal{B}$. If ${\mathit{ID}_{U}}$ does not appear in ${L_{K}}$, we discuss two cases as follows. If ${\mathit{ID}_{U}}={\mathit{ID}_{U}^{\ast }}$, $\mathcal{C}$ returns nothing because it is forbidden to query the fixed identity ${\mathit{ID}_{U}^{\ast }}$. If ${\mathit{ID}_{U}}\ne {\mathit{ID}_{U}^{\ast }}$, the challenger $\mathcal{C}$ first accesses to the corresponding tuple $({\mathit{ID}_{U}},{\mathit{QID}_{U}^{(2)}},{\eta _{U}})$ in the list ${L_{{H_{2}}}}$. Then, $\mathcal{C}$ chooses two random values ${\alpha _{U}},v\in {\mathbb{Z}_{q}^{\ast }}$ and sets ${\mathit{SID}_{U}}=(vP-{\alpha _{U}}{P_{\mathit{pub}}},v,{\eta _{U}}{P_{\mathit{pub}}})$. However, if the tuple $({\mathit{ID}_{U}},vP-{\alpha _{U}}{P_{\mathit{pub}}},{\alpha _{U}})$ already appears in the list ${L_{{f_{1}}}}$, $\mathcal{C}$ resets the ${\mathit{SID}_{U}}$ by choosing another two random values. Immediately, the challenger $\mathcal{C}$ returns ${\mathit{SID}_{U}}$, and stores $({\mathit{ID}_{U}},vP-{\alpha _{U}}{P_{\mathit{pub}}},{\alpha _{U}})$ and $({\mathit{ID}_{U}},vP-{\alpha _{U}}{P_{\mathit{pub}}},v,{\eta _{U}}{P_{\mathit{pub}}})$ in the lists ${L_{{f_{1}}}}$ and ${L_{K}}$, respectively.
-
– Signing queries: considering such a query for a message M and an identity ${\mathit{ID}_{U}}$, the challenger $\mathcal{C}$ will perform either one of the following two cases.
Case 1. If ${\mathit{ID}_{U}}\ne {\mathit{ID}_{U}^{\ast }}$, the challenger $\mathcal{C}$ first accesses to the tuple $({\mathit{ID}_{U}},{\mathit{QID}_{U}^{(1)}},{\mathit{DID}_{U}^{(1)}},{\mathit{DID}_{U}^{(2)}})$ in the list ${L_{K}}$. Then, $\mathcal{C}$ chooses a random number ${r_{U}}\in {\mathbb{Z}_{q}^{\ast }}$ and computes ${R_{U}}={r_{U}}\cdot P$ and ${V_{U}}=({r_{U}}+{\mathit{DID}_{U}^{(1)}})\cdot {\mathit{HID}_{U}}+{h_{U}^{(2)}}\cdot {\mathit{DID}_{U}^{(2)}}$, where $\mathit{HID}$ and ${h_{U}^{(2)}}$ are obtained by querying ${H_{1}}(M,{\mathit{ID}_{U}},{R_{U}})$ and ${f_{2}}(M,{\mathit{ID}_{U}},{R_{U}})$, respectively. The signature on the message M is ${\sigma _{U}}=({\mathit{QID}_{U}^{(1)}},{R_{U}},{V_{U}})$. It is evident that $(M,{\mathit{ID}_{U}},{\sigma _{U}})$ is valid because it is generated using the real private key ${\mathit{SID}_{U}}=({\mathit{QID}_{U}^{(1)}},{\mathit{DID}_{U}^{(1)}},{\mathit{DID}_{U}^{(2)}})$. The challenger $\mathcal{C}$ then returns ${\sigma _{U}}$ and the ephemeral secret value ${r_{U}}$ to $\mathcal{B}$.
Case 2. If ${\mathit{ID}_{U}}={\mathit{ID}_{U}^{\ast }}$, the challenger $\mathcal{C}$ chooses two values ${l_{U}},{\alpha _{U}}\in {\mathbb{Z}_{q}^{\ast }}$, sets ${\mathit{QID}_{U}^{(1)}}={l_{U}}\cdot P$, ${h_{U}^{(1)}}={f_{1}}({\mathit{ID}_{U}},{\mathit{QID}_{U}^{(1)}})={\alpha _{U}}$ and stores in the list ${L_{{f_{1}}}}$. Immediately, $\mathcal{C}$ accesses to the corresponding tuple $({\mathit{ID}_{U}},{\mathit{QID}_{U}^{(2)}},{\eta _{U}})$ in the list ${L_{{H_{2}}}}$, and selects two random values ${x_{U}},{\zeta _{U}}\in {\mathbb{Z}_{q}^{\ast }}$ to compute ${R_{U}}={\zeta _{U}^{-1}}\cdot {x_{U}}\cdot P-{l_{U}}\cdot P=({\zeta _{U}^{-1}}\cdot {x_{U}}-{l_{U}})\cdot P$ and ${V_{U}}={x_{U}}\cdot bP+{\alpha _{U}}\cdot {\zeta _{U}}\cdot {\eta _{U}}\cdot {P_{\mathit{pub}}}$. It is obvious that the ephemeral secret key ${r_{U}}$ = ${\zeta _{U}^{-1}}\cdot {x_{U}}-{l_{U}}$. The challenger $\mathcal{C}$ then attaches ${\mathit{HID}_{U}}={H_{1}}(M,{\mathit{ID}_{U}},{R_{U}})={\zeta _{U}}\cdot bP$ and ${h_{U}^{(2)}}={f_{2}}(M,{\mathit{ID}_{U}},{R_{U}})={\alpha _{U}}\cdot {\zeta _{U}}$ to their associated tuples in the lists ${L_{{H_{1}}}}$ and ${L_{{f_{2}}}}$, respectively. If neither ${H_{1}}(M,{\mathit{ID}_{U}},{R_{U}})$ nor ${f_{2}}(M,{\mathit{ID}_{U}},{R_{U}})$ is previously stored in the lists ${L_{{H_{1}}}}$ and ${L_{{f_{2}}}}$, respectively, then $\mathcal{C}$ returns ${\alpha _{U}}$ and the ephemeral secret value ${r_{U}}$ to $\mathcal{B}$. Otherwise, $\mathcal{C}$ reselects two random values ${x_{U}},{\zeta _{U}}\in {\mathbb{Z}_{q}^{\ast }}$ and repeats the procedure above.
-
• Forge: assume that the algorithm
$\mathcal{B}$ generates a valid signature tuple
$({M^{\ast }},{\mathit{ID}_{U}^{\ast }},{\sigma _{U}^{\ast }})$, where
${\sigma _{U}^{\ast }}=({{\mathit{QID}_{U}^{\ast }}^{(1)}},{R_{U}^{\ast }},{V_{U}^{\ast }})$, with non-negligible probability
${\epsilon ^{\prime\prime }}$. Following the Forking Lemma in Pointcheval and Stern (
1996,
2000),
$\mathcal{B}$ can output another valid signature tuple
$({M^{\ast }},{\mathit{ID}_{U}^{\ast }},{\sigma ^{\prime }_{U}})$, where
${\sigma ^{\prime }_{U}}=({{\mathit{QID}_{U}^{\ast }}^{(1)}},{R_{U}^{\ast }},{V^{\prime }_{U}})$, with the probability at least
${\epsilon ^{\prime\prime }}/2$. Hence,
and
where
${{h_{U}^{\ast }}^{(2)}}$ and
${{h^{\prime }_{U}}^{(2)}}$ are different hash values from hash queries. Since
${P_{\mathit{pub}}}=aP$,
${{\mathit{QID}_{U}^{\ast }}^{(2)}}={\eta _{U}}\cdot P-bP$ and
${\mathit{HID}_{U}^{\ast }}={\zeta _{U}}\cdot bP$ , we have
and
Therefore, we have
and
Thus, we arrive at
Remember that, at the beginning of the proof, we assume
$\mathcal{A}$ is of Type I adversary that can break the proposed scheme with a non-negligible advantage
ϵ within a running time
t. And then by Lemma 1 in Cha and Cheon (
2003), there exists another algorithm
$\mathcal{B}$ with the advantage
${\epsilon ^{\prime\prime }}\geqslant \epsilon (1-1/q)/{q_{{H_{2}}}}$ within a running time
${t^{\prime\prime }}\leqslant t$ to perform a fixed ID attack to the ID-based signature scheme. Then, by the same probability analysis utilized in Pointcheval and Stern (
1996,
2000), we can conclude that the challenger
$\mathcal{C}$ is able to solve the CDH problem with the probability
${\epsilon ^{\prime }}\geqslant 1/9$ and within the running time
${t^{\prime }}\leqslant 23{q_{{f_{2}}}}{q_{{H_{2}}}}qt/(\epsilon (q-1))$. □
Theorem 2.
In the random oracle model, the proposed SIBSC scheme is secure against Type II adversary under the BDH assumption. Concretely, suppose that there exists a Type II adversary $\mathcal{A}$ that can break the proposed scheme with a non-negligible advantage ϵ. Assume that the hash functions ${f_{1}}$, ${f_{2}}$, ${H_{1}}$, ${H_{2}}$ and ${H_{3}}$ are random oracles, and $\mathcal{A}$ can make ${q_{{f_{i}}}}$ queries to the random oracles ${f_{i}}$ $(i=1,2)$, ${q_{{H_{i}}}}$ queries to the random oracles ${H_{i}}$ $(i=1,2,3)$ and ${q_{E}}$ queries to the key extract oracle, respectively. Then, we can construct an algorithm $\mathcal{C}$ to solve the BDH problem with an advantage ${\epsilon ^{\prime }}\geqslant \frac{2\epsilon }{e(1+{q_{E}}){q_{{H_{3}}}}}$, where e is Euler’s constant, the base of the natural logarithm.
Proof.
Assume that the algorithm
$\mathcal{C}$ is given a group
${\mathbb{G}_{1}}$ of order
q with a generator
P, and three elements
$aP,bP,cP\in {\mathbb{G}_{1}}$, where
a,
b and
c are unknown to
$\mathcal{C}$. In order to compute
$D=\hat{e}{(P,P)^{abc}}$, the algorithm
$\mathcal{C}$ plays a challenger of the adversary
$\mathcal{A}$ in the following game.
-
• Initial: the challenger $\mathcal{C}$ runs the system setup algorithm and sets ${P_{\mathit{pub}}}=aP$ to create the public parameters $\mathit{PK}=({\mathbb{G}_{1}},{\mathbb{G}_{2}},q,\hat{e},P,{P_{\mathit{pub}}},{f_{1}},{f_{2}},{H_{1}},{H_{2}},{H_{3}})$ of the proposed scheme. Here ${f_{1}}$, ${f_{2}}$, ${H_{1}}$, ${H_{2}}$ and ${H_{3}}$ are random oracles controlled by $\mathcal{C}$. The challenger $\mathcal{C}$ also answers queries of random oracles issued by $\mathcal{A}$ as below.
-
– ${f_{1}}$ queries: at any time, $\mathcal{A}$ can issue queries along with $({\mathit{ID}_{U}},{\mathit{QID}_{U}^{(1)}})$ to the random oracle ${f_{1}}$. To respond to these queries, $\mathcal{C}$ maintains a list of tuples denoted by ${L_{{f_{1}}}}$, in which each tuple is of the form $({\mathit{ID}_{U}},{\mathit{QID}_{U}^{(1)}},{\alpha _{U}})$. Initially ${L_{{f_{1}}}}$ is empty. When $\mathcal{A}$ queries the oracle ${f_{1}}$ with a pair $({\mathit{ID}_{U}},{\mathit{QID}_{U}^{(1)}})$, $\mathcal{C}$ responds as follows.
-
(1) If the pair $({\mathit{ID}_{U}},{\mathit{QID}_{U}^{(1)}})$ is already in the list ${L_{{f_{1}}}}$, the challenger $\mathcal{C}$ responds with the corresponding ${\alpha _{U}}$ to $\mathcal{A}$.
-
(2) Otherwise, the challenger $\mathcal{C}$ randomly selects a value ${\alpha _{U}}\in {\mathbb{Z}_{q}^{\ast }}$, adds the tuple $({\mathit{ID}_{U}},{\mathit{QID}_{U}^{(1)}},{\alpha _{U}})$ in ${L_{{f_{1}}}}$, and responds to $\mathcal{A}$ with ${\alpha _{U}}$.
-
– ${f_{2}}$ queries: at any time, $\mathcal{A}$ can issue queries along with $(M,{\mathit{ID}_{U}},{R_{U}})$ to the random oracle ${f_{2}}$. To respond to these queries, $\mathcal{C}$ maintains a list ${L_{{f_{2}}}}$ containing tuples of the form $(M,{\mathit{ID}_{U}},{R_{U}},{\beta _{U}})$. Initially the list is empty. When $\mathcal{A}$ queries the oracle ${f_{2}}$ with a tuple $(M,{\mathit{ID}_{U}},{R_{U}})$, $\mathcal{C}$ responds as follows.
-
(1) If the tuple $(M,{\mathit{ID}_{U}},{R_{U}})$ is already in ${L_{{f_{2}}}}$, the challenger $\mathcal{C}$ responds with the corresponding ${\beta _{U}}$ to $\mathcal{A}$.
-
(2) Otherwise, the challenger $\mathcal{C}$ randomly selects a value ${\beta _{U}}\in {\mathbb{Z}_{q}^{\ast }}$, adds the tuple $(M,{\mathit{ID}_{U}},{R_{U}},{\beta _{U}})$ in ${L_{{f_{2}}}}$ and responds to $\mathcal{A}$ with ${\beta _{U}}$.
-
– ${H_{1}}$ queries: at any time, $\mathcal{A}$ can issue queries along with $(M,{\mathit{ID}_{U}},{R_{U}})$ to the random oracle ${H_{1}}$. To respond to these queries, $\mathcal{C}$ maintains a list ${L_{{H_{1}}}}$ containing tuples of the form $(M,{\mathit{ID}_{U}},{R_{U}},{\zeta _{U}},{\zeta _{U}}\cdot bP)$. Initially the list is empty. When $\mathcal{A}$ queries the oracle ${H_{1}}$ with a pair $(M,{\mathit{ID}_{U}},{R_{U}})$, $\mathcal{C}$ responds as follows.
-
(1) If the tuple $(M,{\mathit{ID}_{U}},{R_{U}})$ already appears in ${L_{{H_{1}}}}$, the challenger $\mathcal{C}$ responds with the corresponding ${\zeta _{U}}\cdot bP$ to $\mathcal{A}$.
-
(2) Otherwise, the challenger $\mathcal{C}$ randomly selects a value ${\zeta _{U}}\in {\mathbb{Z}_{q}^{\ast }}$, computes ${\zeta _{U}}\cdot bP$ and adds the tuple $(M,{\mathit{ID}_{U}},{R_{U}},{\zeta _{U}},{\zeta _{U}}\cdot bP)$ to the list ${L_{{H_{1}}}}$. It responds to $\mathcal{A}$ with ${\zeta _{U}}\cdot bP$.
-
– ${H_{2}}$ queries: at any time, $\mathcal{A}$ can issue queries along with ${\mathit{ID}_{U}}$ to the random oracle ${H_{2}}$. To respond to these queries, $\mathcal{C}$ maintains a list ${L_{{H_{2}}}}$ containing tuples of the form $({\mathit{ID}_{U}},{\mathit{QID}_{U}^{(2)}},{\eta _{U}},\textit{coin})$. Initially the list is empty. When $\mathcal{A}$ queries the oracle ${H_{2}}$ with ${\mathit{ID}_{U}}$, $\mathcal{C}$ responds as follows.
-
(1) If ${\mathit{ID}_{U}}$ already appears in the list ${L_{{H_{2}}}}$, the challenger $\mathcal{C}$ responds with the corresponding ${\mathit{QID}_{U}^{(2)}}$ to $\mathcal{A}$.
-
(2) Otherwise, the challenger $\mathcal{C}$ generates a $\mathit{coin}\in \{0,1\}$ with $\mathrm{Pr}[\mathrm{coin}=0]=\delta $ for some δ that will be determined later. Then $\mathcal{C}$ selects a value ${\eta _{U}}\in {\mathbb{Z}_{q}^{\ast }}$. If $\mathit{coin}=0$, $\mathcal{C}$ computes ${\mathit{QID}_{U}^{(2)}}={H_{2}}({\mathit{ID}_{U}})={\eta _{U}}\cdot P$. If $\mathit{coin}=1$, $\mathcal{C}$ computes ${\mathit{QID}_{U}^{(2)}}={H_{2}}({\mathit{ID}_{U}})={\eta _{U}}\cdot bP$. Finally, $\mathcal{C}$ returns ${\mathit{QID}_{U}^{(2)}}$ to $\mathcal{A}$.
-
– ${H_{3}}$ queries: at any time, $\mathcal{A}$ can issue queries along with S to the random oracle ${H_{3}}$. To respond to these queries, $\mathcal{C}$ maintains a list ${L_{{H_{3}}}}$ containing pairs of the form $(S,T)$. Initially the list is empty. When $\mathcal{A}$ queries the oracle ${H_{3}}$ with S, $\mathcal{C}$ responds as follows.
-
(1) If S already appears in the list ${L_{{H_{3}}}}$, the challenger $\mathcal{C}$ responds with the corresponding T to $\mathcal{A}$.
-
(2) Otherwise, $\mathcal{C}$ randomly selects a string $T\in {\{0,1\}^{k}}$, adds the tuples $(S,T)$ to the list ${L_{{H_{3}}}}$, and responds to $\mathcal{A}$ with T.
-
• Phase 1: the adversary $\mathcal{A}$ may make a number of different queries to the challenger $\mathcal{C}$ in an adaptive manner as follows:
-
– Key extract queries: to respond to these queries, $\mathcal{C}$ maintains a list ${L_{K}}$ containing tuples of the form $({\mathit{ID}_{U}},{\mathit{SID}_{U}})$, where ${\mathit{SID}_{U}}=({\mathit{QID}_{U}^{(1)}},{\mathit{DID}_{U}^{(1)}},{\mathit{DID}_{U}^{(2)}})$. Initially the list is empty. Upon receiving the query along with ${\mathit{ID}_{U}}$, if ${\mathit{ID}_{U}}$ already appears in the list ${L_{K}}$, the challenger $\mathcal{C}$ responds with the associated ${\mathit{SID}_{U}}$ to $\mathcal{B}$. If not, the challenger $\mathcal{C}$ first accesses to the corresponding tuple $({\mathit{ID}_{U}},{\mathit{QID}_{U}^{(2)}},{\eta _{U}},\mathit{coin})$ in the list ${L_{{H_{2}}}}$. In case $\mathit{coin}=0$, $\mathcal{C}$ chooses two random values ${\alpha _{U}},v\in {\mathbb{Z}_{q}^{\ast }}$ and sets ${\mathit{SID}_{U}}=(vP-{\alpha _{U}}{P_{\mathit{pub}}},v,{\eta _{U}}{P_{\mathit{pub}}})$. However, if the tuple $({\mathit{ID}_{U}},vP-{\alpha _{U}}{P_{\mathit{pub}}},{\alpha _{U}})$ already appears in the list ${L_{{f_{1}}}}$, $\mathcal{C}$ resets the ${\mathit{SID}_{U}}$ by choosing another two random values. Immediately, the challenger $\mathcal{C}$ returns ${\mathit{SID}_{U}}$ and stores $({\mathit{ID}_{U}},vP-{\alpha _{U}}{P_{\mathit{pub}}},{\alpha _{U}})$ and $({\mathit{ID}_{U}},vP-{\alpha _{U}}{P_{\mathit{pub}}},v,{\eta _{U}}{P_{\mathit{pub}}})$ in the lists ${L_{{f_{1}}}}$ and ${L_{K}}$, respectively. If $\mathit{coin}=1$, $\mathcal{C}$ reports failure and terminates.
-
• Challenge: the adversary $\mathcal{A}$ outputs $({M_{0}},{M_{1}})$ and ${\mathit{ID}_{U}^{\ast }}$ to the challenger $\mathcal{C}$. Upon receiving them, $\mathcal{C}$ picks a random string $Z\in {\{0,1\}^{k}}$ and defines ${\mathit{CT}_{U}^{\ast }}=(cP,Z)$. The challenger $\mathcal{C}$ then returns ${\mathit{CT}_{U}^{\ast }}$ to the adversary $\mathcal{A}$. Observe that the decryption of ${\mathit{CT}_{U}^{\ast }}$ is indeed $Z\oplus {H_{3}}(\hat{e}(cP,{{\mathit{DID}_{U}^{\ast }}^{(2)}}))$.
-
• Phase 2: the challenger $\mathcal{C}$ responds to key extract queries as in Phase 1. Here ${\mathit{ID}_{U}^{\ast }}$ is forbidden to appear in the key extract queries.
-
• Guess: the adversary $\mathcal{A}$ outputs the guess ${\mathfrak{b}^{\prime }}\in \{0,1\}$. Immediately, the challenger $\mathcal{C}$ randomly picks a pair $(S,T)$ in the list ${L_{{H_{3}}}}$ and outputs ${(S)^{{\eta _{U}^{-1}}}}$ as the solution to the given instance of the BDH problem.
In the following, we discuss the probability that the challenger
$\mathcal{C}$ does not abort.
-
(1) In Phase 1 or 2: suppose that the adversary $\mathcal{A}$ makes a total of ${q_{E}}$ key extract queries. Then the probability that the challenger $\mathcal{C}$ does not abort is ${\delta ^{{q_{E}}}}$.
-
(2) In Challenge: the probability that the challenger $\mathcal{C}$ does not abort is $1-\delta $.
By (1) and (2), the probability that the challenger
$\mathcal{C}$ does not abort is
${\delta ^{{q_{E}}}}(1-\delta )$. Moreover, the maximum value of
${\delta ^{{q_{E}}}}(1-\delta )$ occurs when
$\delta =1-1/({q_{E}}+1)$. By similar techniques of Coron’s analysis of the Full Domain Hash (
2000), we can obtain the probability that the challenger
$\mathcal{C}$ does not abort is at least
$1/e(1+{q_{E}})$, where
e is Euler’s constant. In addition, in the phase of
Guess, the probability that the challenger
$\mathcal{C}$ outputs the correct solution of the BDH problem is at least
$2\epsilon /{q_{{H_{3}}}}$ (Boneh and Franklin,
2001). Hence, the challenger
$\mathcal{C}$ resolves the BDH problem with advantage at least
${\epsilon ^{\prime }}\geqslant \frac{2\epsilon }{e(1+{q_{E}}){q_{{H_{3}}}}}$. □
6 Performance Analysis
To analyse the computational cost and the communication size of the proposed SIBSC scheme, we consider three time consuming operations ${\mathit{TG}_{e}}$, ${\mathit{TG}_{\mathit{mul}}}$ and ${\mathit{TG}_{H}}$, which, respectively, denote the time of executing a bilinear pairing operation $\hat{e}:{\mathbb{G}_{1}}\times {\mathbb{G}_{1}}\to {\mathbb{G}_{2}}$, the time of executing a scalar multiplication in ${\mathbb{G}_{1}}$ and the time of executing a map-to-point hash function.
In our proposed SIBSC scheme, the sender requires
$3{\mathit{TG}_{\mathit{mul}}}+{\mathit{TG}_{H}}$ to generate a signature. For the encryption procedures, the third party requires
${\mathit{TG}_{e}}+{\mathit{TG}_{\mathit{mul}}}+{\mathit{TG}_{H}}$ to generate a ciphertext. Indeed, the execution time of operations
${\mathit{TG}_{e}}$,
${\mathit{TG}_{\mathit{mul}}}$ and
${\mathit{TG}_{H}}$ on the pairing system has been implemented in Scott
et al. (
2006), Liu
et al. (
2014). In Scott
et al. (
2006), the Philips HiPersmart card (smart card) with an 36 MHz processor was used to execute those operations, while in Liu
et al. (
2014) an Inter(R) Pentium IV 3.0 GHz processor (third party) was used to execute those operations. The execution time of operations on smart card and third party was listed in Table
2. Full descriptions of the security level on the pairing system were discussed in Scott
et al. (
2006), Liu
et al. (
2014). According to Table
2, the sender requires less than 490 ms to generate a signature and the third party requires 29.46 ms to generate a ciphertext in our scheme.
On the other hand, in the
Encryption algorithm, a ciphertext is defined by
$({R_{A}},{W_{B}})$, where
${R_{A}}$ is some element in
${\mathbb{G}_{1}}$ and
${W_{B}}$ is bounded to the hash function
${H_{3}}:{\mathbb{G}_{2}}\to {\{0,1\}^{k}}$. Hence, the bit length of a ciphertext is bounded by
$|{\mathbb{G}_{1}}|+k$ in our scheme. Moreover, according to Wander
et al. (
2005), the total message size of the ciphertext is
$64+20$ bytes. Assume that a packet size is 41 bytes which includes 32 bytes for the payload and 9 bytes for the header. Each packet needs additional 8-byte preamble. Therefore, the ciphertext should be
$(32+9)\ast 2+(20+9)\ast 1+8\ast 3=135$ bytes for transmission. Here, transmitting one byte needs 59.2 μ J (Wander
et al.,
2005) so that the ciphertext needs
$135\ast 59.2=7.992\hspace{2.5pt}\hspace{2.5pt}\text{mJ}$ for transmission.
Table 2
Computational cost on the smart card and the third party.
|
${\mathit{TG}_{e}}$ |
${\mathit{TG}_{\mathit{mul}}}$ |
${\mathit{TG}_{H}}$ |
| Smart card |
380 ms |
130 ms |
<100 ms |
| Third party |
20.04 ms |
6.38 ms |
3.04 ms |
Table 3
Comparisons between the proposed scheme and other schemes.
|
Solution 1 |
Solution 2 |
Solution 3 |
Our solution |
| Hired scheme |
CC’s IBS |
CC’s IBS |
CM’s IBSC |
Our SIBSC |
|
(2003) |
(2003) |
(2005) |
|
|
+ BF’s IBE |
+ BF’s IBE |
|
|
|
+ (2001) |
+ (2001) |
|
|
| Computational cost for |
${\mathit{TG}_{e}}$ |
|
${\mathit{TG}_{e}}$ |
|
| smart card |
+ 3${\mathit{TG}_{\mathit{mul}}}$
|
2${\mathit{TG}_{\mathit{mul}}}$
|
+ 3${\mathit{TG}_{\mathit{mul}}}$
|
3${\mathit{TG}_{\mathit{mul}}}$
|
|
+ 2${\mathit{TG}_{H}}$
|
|
+ 2${\mathit{TG}_{H}}$
|
+ ${\mathit{TG}_{H}}$
|
| Execution time of smart card |
< 970 ms |
260 ms |
< 970 ms |
< 490 ms |
| Computational cost for |
|
${\mathit{TG}_{e}}$ |
|
${\mathit{TG}_{e}}$ |
| third party |
– |
+ ${\mathit{TG}_{\mathit{mul}}}$
|
– |
+ ${\mathit{TG}_{\mathit{mul}}}$
|
|
|
+ ${\mathit{TG}_{H}}$
|
|
+ ${\mathit{TG}_{H}}$
|
| Execution time of third party |
– |
29.46 ms |
– |
29.46 ms |
| Communication size (the ciphertext) |
2($|{\mathbb{G}_{1}}|+k$) |
2($|{\mathbb{G}_{1}}|+k$) |
$|{\mathbb{G}_{1}}|+k$ |
$|{\mathbb{G}_{1}}|+k$ |
| Energy consumption for transmitting the ciphertext |
15.984 mJ |
15.984 mJ |
7.992 mJ |
7.992 mJ |
Following Table
1 in the Introduction, the precise comparisons are presented in Table
3. In Solution 1, a smart card takes all computational loads of the hired IBS and IBE schemes to offer authentication and confidentiality. In Solution 2, the IBE scheme is executed by a third party instead of the smart card since it does not require the sender’s private key. It is obvious that Solution 2 aims at reducing the computational cost of the smart card, but not for communication size. On the other hand, Solution 3 employing an IBSC scheme aims at reducing the communication size. As mentioned earlier, since the existing IBSC schemes are inseparable, the smart card takes all computational loads. Table
3 demonstrates that our solution not only reduces the computational cost required by the smart card but also efficiently decreases the total communication size.
7 Conclusions
In this article, the first separable ID-based signcryption (SIBSC) scheme was constructed. In the proposed SIBSC scheme, we aim to employ a semi-trusted third party to assist with expensive pairing computations without endangering the private keys of senders, while retaining communication performance as in IBSC schemes. For security analysis, we demonstrated that our scheme is provably secure to fulfill both authentication and confidentiality by withstanding Type I and Type II adversaries under the computation Diffie–Hellman (CDH) and bilinear Diffie–Hellman (BDH) assumptions, respectively. Indeed, the security analysis was achieved by using random oracles. We believe that to construct a SIBSC scheme without random oracles (in the standard model) is worth studying. It would be an interesting topic for the future work.
Acknowledgements
This research was partially supported by Ministry of Science and Technology, Taiwan, R.O.C., under contract no. MOST103-2221-E-018-022-MY2.
References
Bellare, M., Rogaway, P. (1993). Random oracles are practical: a paradigm for designing efficient protocols. In: Proceedings of CCS’93, pp. 62–73.
Boneh, D., Boyen, X. (2004). Secure identity based encryption without random oracles. In Lecture Notes in Computer Science
: Vol. 3152. Proceedings of Crypto’04, pp. 443–459.
Boneh, D., Franklin, M. (2001). Identity-based encryption from the Weil pairing. In: Proceedings of Crypto’01,
Lecture Notes in Computer Science, Vol. 2139. pp. 213–229.
Boneh, D., Shen, E., Waters, B. (2006). Strongly unforgeable signatures based on computational Diffie–Hellman. In: Proceedings of PKC’06,
Lecture Notes in Computer Science, Vol. 3958, pp. 229–240.
Boyen, X. (2003). Multipurpose identity-based signcryption: a swiss army knife for identity-based cryptography. In: Proceedings of Crypto’03,
Lecture Notes in Computer Science, Vol. 2729. pp. 383–399.
Boyen, X., Waters, B. (2006). Anonymous hierarchical identity-based encryption (without random oracles). In: Proceedings of Crypto’06,
Lecture Notes in Computer Science, Vol. 4117. pp. 290–307.
Canetti, R., Goldreich, O., Halevi, S. (2004). The random oracle methodology, revisited. Journal of ACM, 51(4), 557–594.
Cha, J.C., Cheon, J.H. (2003). An identity-based signature from gap Diffie-Hellman groups. In: Proceedings of PKC’03,
Lecture Notes in Computer Science, Vol. 2567. pp. 18–30.
Chen, L., Malone-Lee, J. (2005). Improved identity-based signcryption. In: Proceedings of PKC’05,
Lecture Notes in Computer Science, Vol. 3386, pp. 362–379.
Chen, L., Cheng, Z., Smart, N.P. (2007). Identity-based key agreement protocols from pairings. International Journal of Information Security, 6(4), 213–241.
Chow, S.S.M., Yiu, S.M., Hui, L.C.K., Chow, K.P. (2004). Efficient forward and provably secure ID-based signcryption scheme with public verifiability and public ciphertext authenticity. In: Proceedings of ICISC’03,
Lecture Notes in Computer Science, Vol. 2971, pp. 352–369.
Coron, J.S. (2000). On the exact security of full domain hash. In: Proceedings of Crypto’00,
Lecture Notes in Computer Science, Vol. 1880, pp. 229–235.
Fahl, S., Harbach, M., Muders, T., Smith, M. (2012). Confidentiality as a service – usable security for the cloud. In: IEEE 11th International Conference on Proceedings of Trust, Security and Privacy in Computing and Communications’12, pp. 153–162.
Jin, Z., Wen, Q., Du, H. (2010). An improved semantically-secure identity-based signcryption scheme in the standard model. Computers & Electrical Engineering, 36(3), 545–552.
Kitagawa, T., Yang, P., Hanaoka, G., Zhang, R., Matsuura, K., Imai, H. (2006). Generic transforms to acquire CCA-security for identity based encryption: the cases of FOPKC and REACT. In: Proceedings of ACISP’06,
Lecture Notes in Computer Science, Vol. 4058. pp. 348–359.
Li, F., Takagi, T. (2013). Secure identity-based signcryption in the standard model. Mathematical and Computer Modelling, 57(11–12), 2685–2694.
Li, F., Liao, Y., Qin, Z. (2011). Analysis of an identity-based signcryption scheme in the standard model. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences E, 94–A(1), 268–269.
Libert, B., Quisquater, J.J. (2003). A new identity based signcryption schemes from pairings. In: Proceedings of IEEE Information Theory Workshop’03, pp. 155–158.
Libert, B., Vergnaud, D. (2009). Adaptive-ID secure revocable identity-based encryption. In: Proceedings of CT-RSA’09,
Lecture Notes in Computer Science, Vol. 5473. pp. 1–15.
Liu, L., Zhang, Z., Chen, X., Kwak, K.S. (2014). Certificateless remote anonymous authentication schemes for wireless body area networks. IEEE Transactions on Parallel and Distributed Systems, 25(2), 332–342.
Ma, R., Li, J., Guan, H., Xia, M., Liu, X. (2015). EnDAS: efficient encrypted data search as a mobile cloud service. IEEE Transactions on Emerging Topics in Computing, 3(3), 372–383.
Malone-Lee, J. (2002).
Identity-based signcryption. Cryptology ePrint Archive, Report 2002/098.
http://eprint.iacr.org/.
Mell, P., Grance, T. (2009). The NIST Definition of Cloud Computing. National Institute of Standards and Technology.
Narayan, S., Parampalli, U. (2008). Efficient identity-based signatures secure in the standard model. IET Information Security, 2(4), 108–118.
Paterson, K.G., Schuldt, J.C.N. (2006). Efficient identity-based signatures secure in the standard model. In: Proceedings of ACISP’06,
Lecture Notes in Computer Science, Vol. 4058, pp. 207–222.
Pointcheval, D., Stern, J. (1996). Security proofs for signature schemes. In: Proceedings of Eurocrypt’96,
Lecture Notes in Computer Science, Vol. 1070. pp. 387–398.
Pointcheval, D., Stern, J. (2000). Security arguments for digital signatures and blind signatures. Journal of Cryptology, 13(3), 361–396.
Scott, M., Costigan, N., Abdulwahab, W. (2006). Implementing cryptographic pairings on smartcards. In: Proceedings of CHES’06,
Lecture Notes in Computer Science, Vol. 4249, pp. 134–147.
Shamir, A. (1984). Identity-based cryptosystems and signature schemes. In: Proceedings of Crypto’84,
Lecture Notes in Computer Science, Vol. 196, pp. 47–53.
Suo, H., Liu, Z., Wan, J., Zhou, K. (2013). Security and privacy in mobile cloud computing. In: Proceedings of Wireless Communications and Mobile Computing Conference’13, 9th International, pp. 655–659.
Tsai, T.T., Tseng, Y.M., Wu, T.Y. (2012). A fully secure revocable ID-based encryption in the standard model. Informatica, 23(3), 481–499.
Tsai, T.T., Tseng, Y.M., Wu, T.Y. (2013). Provably secure revocable ID-based signature in the standard model. Security and Communication Networks, 6(10), 1250–1260.
Tsai, T.T., Tseng, Y.M., Huang, S.S. (2014). Efficient strongly unforgeable ID-based signature without random oracles. Informatica, 25(3), 505–521.
Tseng, Y.M., Huang, S.S., Tsai, T.T., Ke, J.H. (2016). List-free ID-based mutual authentication and key agreement protocol for multiserver architectures. IEEE Transactions on Emerging Topics in Computing, 4(1), 102–112.
Tysowski, P.K., Hasan, M.A. (2013). Hybrid attribute- and re-encryption-based key management for secure and scalable mobile applications in clouds. IEEE Transactions on Cloud Computing, 1(2), 172–186.
Wander, A., Gura, N., Eberle, H., Gupta, V., Shantz, S. (2005). Energy analysis of public-key cryptography for wireless sensor networks. In: Proceedings of 3rd IEEE International Conference Pervasive Computing Commun’05, pp. 324–328.
Waters, B. (2005). Efficient identity-based encryption without random oracles. In: Proceedings of Eurocrypt’05,
Lecture Notes in Computer Science, Vol. 3494. pp. 1–33.
Wu, T.Y., Tseng, Y.M. (2010). An ID-based mutual authentication and key exchange protocol for low-power mobile devices. The Computer Journal, 53(7), 1062–1070.
Zhang, B. (2010). Cryptanalysis of an identity based signcryption scheme without random oracles. Journal of Computational Information Systems, 6(6), 1923–1931.
Zheng, Y. (1997). Digital signcryption or how to achieve cost (signature & encryption) ≪ cost (signature) + cost (encryption). In: Proceedings of Crypto’97,
Lecture Notes in Computer Science, Vol. 1294, pp. 165–179.