Abstract
The Autonomous Vehicle (AV) industry is constantly growing, thus analysing its perspectives is essential. However, for this analysis a sophisticated approach is necessary which considers the ambiguity of decision-makers, and different objectives and criteria related to stakeholders. In this paper a new model is proposed based on Decomposed Fuzzy Sets and the Best-Worst Method to deal with possible non-reciprocity of pairwise comparisons and different preferences of stakeholders in the AV industry. The main advantage of the model is that it is capable of considering optimistic and pessimistic attitudes along with the different objectives and criteria of the involved groups. The results show that users require short travel time, while operators, manufacturers and legislators expect mainly the increase of revenues from the AV implementation. Among the most important criteria, our analysis indicates the need of regulatory and safety issues are the most essential obstacles of expanding the AV industry. The new model can also be applied for evaluating the perspectives of other emerging technologies and industrial sectors.
1 Introduction
Pairwise comparison-based techniques, especially analytic hierarchy process (AHP) and more recently, best-worst method (BWM) are often utilized within multi-criteria decision-making (Kheybari
et al.,
2023). These methods assume that the relation of element A to its pair element B is the reciprocal score of the relation of B to A (Saaty,
1977). This assumption is so strong that during the evaluation process, the decision-makers should not even fill the relations from the other direction since they are automatically determined by the first scores due to their reciprocity (Saenz-Royo
et al.,
2024). In AHP, solely the brackets above the main diagonal of the pairwise comparison matrix (PCM) should be filled by the participants, the rest of the PCM is automatically calculated with the reciprocal values of the given scores. Nevertheless, assuming the reciprocal values is not necessarily adequate for all types of decision-making problems. The following two questions which are related to the creator of the decomposed fuzzy set (DFS) theory should be considered (Cebi
et al.,
2023).
‘If the AV that you use would guarantee security when you travel, how would you feel?’
‘If the AV that you use would not guarantee security when you travel, how would you feel?’
Is it sure that the satisfaction level in the first case is the same as the dissatisfaction level in the second case? Would the given scores be reciprocal to express the preference? We might assume that the dissatisfaction level of not having security is larger at least in scoring of the evaluators.
The same phenomenon occurs when future scenarios and trends of a market or industry are evaluated. If the comparison question is raised positively or negatively, the scores might be different even though most probably there is similarity in evaluating the relations of two criteria or alternatives. The following reasons have led to utilize DFS in evaluating the future perspectives of the AV industry:
Identically, if not all possible pairwise comparisons of a set of criteria are utilized, for the selected comparisons, the same logic of different criteria relations might be applied. So far, this approach has not been investigated, merely models with full evaluations exist in the domain of DFS. In this paper, instead of using purely AHP models, the AHP method is integrated with a technique reducing the necessary number of pairwise comparisons. This reduction is useful to unburden the decision-makers and to increase the consistency of the evaluations (Rezaei,
2015).
Consequently, for investigating the perspectives of the AV industry, a new model that considers the possible vagueness of the comparisons, reduces the effort required from the decision-makers, and provides trustworthy outcomes of ranking the objectives and criteria reflecting the future of AVs is created. Based on the examination of the benchmark, all these criteria are fulfilled in the presented decomposed fuzzy BMW and AHP (DF-BWM-AHP) model. The proposed model provides novel insights in a realistic context, thus augmenting existing body of knowledge in the domain. The novelty of current paper can be listed as follows:
-
• This is the first research that combines DFS with BWM in this field. Since it is not trivial that DFS can be utilized if the pairwise comparisons are not complete as in the case of BWM, a pioneer study in this domain is necessary.
-
• Even though there has been previous research on the perspectives of the AV industry, current paper provides a more sophisticated modelling approach to determine crucial criteria of this new field.
-
• Current paper examines the perspectives considering four different viewpoints, i.e. four stakeholder groups involved in the AV market.
-
• We provide a comparison with previous research on the criteria of the AV market that applied the conventional AHP method and highlight the main differences between the two approaches emphasizing the benefits of the proposed DF-BWM-AHP model.
The paper is structured in the following way. After the introductory part in Section
1, the related literature is reviewed in Section
2, while various DFSs are described in Section
3. The elaborated DF-BWM-AHP integration model is presented as a pseudo-code in Section
4, and the developed model is utilized to evaluate AVs in Section
5. As a validation of the elaborated method, in Section
6, results are compared with a theoretical AHP evaluation and with a real-life Parsimonious AHP (PAHP) survey conducted in the same domain. The study concludes with the presentation of the main outcomes and ideas for future research in Section
7.
2 Literature Review
As a result of the swift pace of technological advancement, AVs are anticipated to become commercially accessible in the near future. AVs possess the potential to alter individuals’ travel behaviour significantly due to the distinct qualities of the new technology compared to the traditional transport modes (Krizsik and Sipos,
2023). The incorporation of AVs into the transportation system has significant implications for various aspects including infrastructure, safety, accessibility, mobility, car ownership, travel patterns, modal share, environment, and land use patterns (Hossaim and Fatmi,
2022). The effects of AVs on individuals (Song
et al.,
2024) can be examined by analysing representative stakeholders who have the power to influence or who are influenced by the presence of AVs. Since the widespread existence of AVs on the market is the matter of future, among the possible stakeholders, the users, legislators, operators, and manufacturers’ attitudes are worth examining (Hamadneh
et al.,
2022).
Preference surveys on AVs often concentrate on user attitudes and choices between cars and AVs (Wang and Zhao,
2019). A common characteristic of these surveys is the use of stated preferences, which is statistically sound but lacks the detection and analysis of uncertain or non-consistent responses, which are very likely in this complex and future-oriented domain.
Several papers cluster the varied groups of users according to their specific characteristics. For example, Kaur and Rampersad (
2018) survey university students to reveal key influencing factors related to the adoption of AVs, but the scholars do not compare the outcomes with less educated groups. Thus, no significant difference could be found between higher and lower educated users. Acheampong
et al. (
2021) did not present any significant difference between the degree of AV acceptance for men and women. Considering the age as an attribute, Fagnant and Kockelman (
2015) emphasize that AVs are more attractive to elder population, Halicka (
2024) connects autonomous driving with the higher quality of life of seniors, while Krueger
et al. (
2016) state that age is an insufficient discriminator of the AV usage. Krueger
et al. stress that the access to private vehicles could not be a solid basis for clustering the users due to the heterogeneity of the user groups. This aspect is confirmed by Becker and Axhausen (
2017), who state that attitudes have most likely more influence on the technological adaptation to AVs than socio-demographic characteristics.
Consequently, in a preference survey on AVs, a sharper borderline is necessary to form groups in the evaluator pattern. This could be done by identifying various stakeholder groups with different motivation and interests (Macharis
et al.,
2009) toward autonomous systems. Moreover, it is obvious that a sustainable approach and development could be reached solely by integrating stakeholders’ preferences (Zavadskas
et al.,
2019; Yamane and Kaneo,
2022; Shrivastava
et al.,
2023). In their related work, Hamadneh
et al. (
2022) identify following four primary stakeholder groups regarding AVs: users, legislators, operators, and manufacturers. The authors thoroughly analyse the stakeholder preferences toward AVs, but they do not consider the possible uncertainty in the responses of the conducted survey; thus, the results are less trustworthy. This could be identified as a gap in the existing body of literature. Such models are necessary that are capable of dealing with different stakeholder approaches and the possible ambiguity of evaluator scoring referring to future perspectives of a new technology.
Regarding the attributes of AV preference surveys, the most popular criteria are the cost, comfort, time, safety, accessibility, reliability, and less driving tension by the utilization of AVs. As Friedrich
et al. intend (
2019), a reduced cost of travelling could be reached by self-driving cars due to car-sharing opportunities, but it is to be examined how significant this attribute is for specific groups of users or stakeholders. Paddeu
et al. (
2020) reveal that comfort in AVs could be especially important for private car owners, and strong correlation is found between attributes of comfort and trust. According to Zhong
et al. (
2020), AVs could decrease the commuters’ travel time by approximately 18–32%, which is an important advantage of using the new technology. This reduction heavily depends on the transportation system and the travelled distance. Furthermore, the value of this travel time reduction differs strongly for the various user and stakeholder groups as some of them are neutral to this amount of time reduction.
The safety of AVs is a multi-layer issue that should be approached in its complexity. Koopman and Wagner (
2017) direct the attention to the hardware fault tolerance, the interaction with the environment, the possible cooperation with humans driving vehicles (i.e. in case of non-fully autonomous transportation systems), and the resilient machine learning. Even though safety might be increased due to the mitigation of human errors, it is still not ultimately decided how safe the use of AVs might be. Meyer
et al. (
2017) assess accessibility attribute of AVs and conclude that autonomous driving might cause a ‘quantum leap’ in accessibility. Apart from the indication of substantial increase in accessibility expected from the utilization of AVs, the researchers point out that the impact heavily depends on the actual capacity of AVs; thus, the growth might be far less than expected in case of non-sufficient AV capacity. Kalra and Paddock (
2016) ask about the value of driven miles that would prove the reliability of AVs. The scholars conclude that even 100 million miles driven with very low fatalities, injuries, and crash rates would leave some uncertainties regarding public use. The question is how different stakeholders cope with this uncertainty bounded to AV traffic. Finally, for some potential users, the less tension on drivers could be an attractive attribute, as stated by Kopelias
et al. (
2020). The strength of this criterion heavily depends on the users’ personal characteristics as well as on the belonging to specific stakeholder groups. Moreover, it is very probable that legislators overestimate while system operators underestimate the relevance of this specific attribute.
The role of stakeholder engagement and the nature of multi-sided approach of AV development is confirmed by many papers in the literature. Fu
et al. (
2023) emphasized the significance of possible international sanctions towards green innovations (e.g. autonomous driving), underlining the power of the legislator participants. Turskis and Šniokienė (
2024) analysed the circular economy efficiency supported by the IoT-driven transformation caused by the AV implementation, stressing the macro-economic consideration by governments or municipalities involved in the AV development. Dabic-Miletic (
2023) pointed out the role of logistics providers as industrial stakeholders connected to AV developments.
Owing to the multi-criteria decision-making (MCDM), and especially AHP models created and utilized in AV domain, the majority of them is connected to risk analysis regarding autonomous vehicle testing (Karasan
et al.,
2020; Zhang and Tak,
2024). Without exception, these models applied a somewhat modified version of AHP keeping the precondition of pairwise reciprocity in prioritizing different scenarios related to AV testing and implementation.
In current study, a recently introduced fuzzy MCDM method is applied that is an extension of intuitionistic fuzzy set (IFS) (Atanassov,
1986; Guo and Song,
2014). IFSs do not require the sum of degree of membership and non-membership to be equal. Introducing this functionality allows for the integration of a supplementary parameter into the membership function, hence enhancing the suitability of IFSs for conveying imprecise and ambiguous information (Alkan and Kahraman,
2023). Several generalizations of the IFSs based on problem types and expert judgments were proposed in the literature. The DFS employs a generalization approach to handle issues related to inconsistency in expert assessments by considering optimistic and pessimistic viewpoints (Li
et al.,
2022). Although MCDM approaches facilitate the resolution of intricate problems that involve many criteria and options, IFSs provide solutions to manage uncertainty (Karuppiah and Sankaranarayanan,
2023). A thorough assessment of the analysed criteria typically depends on the specialized knowledge and subjective assessments of the experts. The level of optimism or pessimism can affect their risk assessments, and the manner in which the questions are formulated (positive or negative) affects precision, creating another difficulty within the process.
As there are some issues regarding the assessment techniques related to uncertainty of judgments in the literature, Cebi
et al. (
2023) elaborate the concept of DFS that aims to represent perceptions of people more comprehensively by using optimistic and pessimistic membership functions. Including these components, DFS offers a more precise method to represent the intricacies of decision-making in situations of uncertainty, thus the replies to both functional and dysfunctional questions are employed. Cebi
et al. (
2023) present DFS-based AHP method to evaluate logistics operators for medical enterprises. To improve overall dependability of AHP evaluations, the approach is expanded by including DFS. This extension considers individual responses to reciprocal questions when they are both unclear and imprecise. Kahraman
et al. (
2023) present a TOPSIS approach combined with DFS that is applied for a supplier selection problem affected by fuzziness. The objective is to assess the accuracy of the judgments. A clear gap can be detected in the relevant literature since so far none of the models deal with a reduced number of pairwise comparisons. It is a relevant trend in MCDM that modellers strive to decrease the evaluation time for the decision-makers while simultaneously increasing the consistency of the evaluations. The two most successful attempts to tackle this problem are the BWM (Liang
et al.,
2020) and parsimonious AHP (PAHP) (Abastante
et al.,
2019; Duleba,
2022; Moslem,
2024). Thus, in this paper combined methods are utilized to enhance the efficiency of evaluations. The elaborated method integrates a pairwise comparison reduction method (BWM) with DFS, while previously referred papers that applied the DFS approach utilized the complete pairwise comparisons of AHP or other MCDM methods. However, in our model a reduced number of these comparisons can be utilized, i.e. the comparisons with the best and worst objective or criteria. In the current paper, we show that the DFS approach can be used even under these conditions, and a feasible outcome can be reached.
To address the gaps detected by the literature review, current study introduces a combined DFS-based MCDM approach to assess the AV industry. First, the criteria weights are determined through by using the extended DF-BWM method. As highlighted previously, the advantage of using the BWM method lies in its ability to comprehensively evaluate the objectives by using less information, which enables more efficient decision-making in complex and uncertain environments. Subsequently, the AHP method is considered by using DFS to identify criteria weights for AVs, where the BWM method is extended with DFSs, where a unique structure is introduced by connecting BWM with DFS-based AHP with the novel aggregation operators.
3 Preliminaries and Definitions
DFS is widely used to tackle lack of consistency in expert opinions by including optimistic and pessimistic perspectives. Thus, it quantifies the dependability of the judgments made by decision-makers to calculate the degree of uncertainty in the decision-making environment. The determination of this is contingent upon the opinions of the decision-makers regarding the functional and dysfunctional questions. Once a judgment is reached, the sum of evaluations should be equal to one. Nevertheless, because of inherent uncertainty of the context, the total of the assessments amounts to less than one. The scarcity in this case signifies the lack of uniformity among the decision-makers. The next part presents the initial findings of DFS, which are derived from the study of Cebi
et al. (
2023).
Definition 3.1.
X is considered as a universe of discourse. A DFS
$\tilde{A}$ is
where function
${\mu _{\tilde{A}}}(\mathrm{x}):\mathrm{X}\to [0,1]$,
${\nu _{\tilde{A}}}(x):X\to [0,1]$ is a degree of membership and non-membership of
x to
$\mathcal{O}$ and
$\mathcal{P}$, where
$\mathcal{O}$ and
$\mathcal{P}$ are optimistic and pessimistic evaluations considering conditions
$0\leqslant {\mu _{\tilde{A}}^{\mathcal{O}}}(x)+{\vartheta _{\tilde{A}}^{\mathcal{O}}}(x)\leqslant 1,\hspace{2.5pt}0\leqslant {\mu _{\tilde{A}}^{\mathcal{P}}}(x)+{\vartheta _{\tilde{A}}^{\mathcal{P}}}(x)\leqslant 1$, and the inconsistency in judgments is
${\mathcal{I}^{A}}=1-({\mu _{\tilde{A}}^{\mathcal{O}}}(x)+{\vartheta _{\tilde{A}}^{\mathcal{O}}}(x)+{\mu _{\tilde{A}}^{\mathcal{P}}}(x)+{\vartheta _{\tilde{A}}^{\mathcal{P}}}(x))$, where
$-1\leqslant {\mathcal{I}^{A}}\leqslant 1$ and
$0\leqslant {\mu _{\tilde{A}}^{\mathcal{O}}}(x)+{\vartheta _{\tilde{A}}^{\mathcal{O}}}(x)+{\mu _{\tilde{A}}^{\mathcal{P}}}(x)+{\vartheta _{\tilde{A}}^{\mathcal{P}}}(x)\leqslant 2$.
Definition 3.2.
Let
$\tilde{\alpha }=\{\mathcal{O}(a,b),\mathcal{P}(c,d)\}$,
${\tilde{\alpha }_{1}}=\{\mathcal{O}({a_{1}},{b_{1}}),\mathcal{P}({c_{1}},{d_{1}})\}$, and
${\tilde{\alpha }_{2}}=\{\mathcal{O}({a_{2}},{b_{2}}),\mathcal{P}({c_{2}},{d_{2}})\}$ be decomposed fuzzy numbers (DFNs) and basic operators given as follows:
can be used as addition operator.
used as multiplication operator.
used for multiplying by a scalar.
λth power of
$\tilde{\alpha }$ can be calculated as in Eq. (
5).
Definition 3.3.
Let
${\tilde{\alpha }_{i}}=\{\mathcal{O}({a_{i}},{b_{i}}),\mathcal{P}({c_{i}},{d_{i}})\}$ be a collection of decomposed weighted arithmetic mean (DWAM) related to
${w_{i}}=({w_{1}},{w_{2}},\dots ,{w_{n}})$ and
${w_{i}}\in [0,1]$ and
${\textstyle\sum _{i=1}^{n}}{w_{i}}=1$, DWAM is introduced in the following manner (Cebi
et al.,
2023):
Example 3.1 (Related to Definition 3.3).
Assume that
${\tilde{\alpha }_{1}}=\{\mathcal{O}(0.50,0.50),\mathcal{P}(0.50,0.50)\}$,
${\tilde{\alpha }_{2}}=\{\mathcal{O}(0.10,0.90),\mathcal{P}(0.90,0.10)\}$, and
${\tilde{\alpha }_{3}}=\{\mathcal{O}(0.75,0.25),\mathcal{P}(0.30,0.70)\}$ are three DFNs, and the weights are equal to each other as
$\frac{1}{3}$. Aggregate the DFNs by utilizing DWAM and decomposed weighted geometric mean (DWGM) operators.
As evidenced by the provided example, the summations of membership and non-membership of the optimistic views are greater than 1. This contradicts the principles of the DFSs. Therefore, the DWAM operator is updated in the following manner:
According to the modified decomposed fuzzy arithmetic mean (MDWAM) operator, Example
3.1 is calculated, and the results are obtained as
$\textit{MDWAM}({\tilde{\alpha }_{1}},{\tilde{\alpha }_{2}},{\tilde{\alpha }_{3}})=\{\mathcal{O}(0.450,0.301),\mathcal{P}(0.673,0.327)\}$.
Definition 3.4.
Let
${\tilde{\alpha }_{i}}=\{\mathcal{O}({a_{i}},{b_{i}}),\mathcal{P}({c_{i}},{d_{i}})\}$ be a collection of DWGM with respect to
${w_{i}}=({w_{1}},{w_{2}},\dots ,{w_{n}})$ and
${w_{i}}\in [0,1]$, DWGM is introduced as follows:
As evidenced by the provided example, the summation of the membership and non-membership of the pessimistic view is greater than 1. This contradicts the principles of the DFSs. Therefore, the DWAM operator is updated in the following manner:
According to the modified decomposed fuzzy geometric mean (MDWGM) operator, Example
3.1 is calculated again, and the results are obtained as
$\textit{MDWAM}({\tilde{\alpha }_{1}},{\tilde{\alpha }_{2}},{\tilde{\alpha }_{3}})=\{\mathcal{O}(0.335,\hspace{2.5pt}0.605\hspace{2.5pt}),\mathcal{P}(0.352,\hspace{2.5pt}0.433)\}$.
Definition 3.5.
The consistency index
$(CI)$ of the DFN
$(\tilde{\alpha }=\{\mathcal{O}(a,b),\mathcal{P}(c,d)\})$ is introduced in the following manner:
If
$CI(\tilde{\alpha })$ is close to 1, the reliability of the decision-maker increases.
Definition 3.6.
The new score index
$(SI)$ of the DFN
$(\tilde{\alpha }=\{\mathcal{O}(a,b),\mathcal{P}(c,d)\})$ is proposed as the following:
where
k represents a multiplier calculated as 0.90 that is equivalent to the max. value of the linguistic scales as shown in Table
1 (Cebi
et al.,
2023).
4 Integrated BWM and AHP Based on DFS
The BWM is a comprehensive MCDM method used to define relative importance of criteria (Rezaei,
2015). The idea behind it is founded upon doing pairwise comparisons between the most favourable and unfavourable factors in addition to other factors. Therefore, a reduced number of evaluations is required compared to the AHP. Ensuring the decision-makers’ consistency becomes challenging when facing high number of criteria or alternatives. The utilization of the BWM as a decision-making tool presents a viable alternative to the AHP in certain scenarios.
The proposed methodology includes three stages. Firstly, BWM is combined with DFS that is proposed for assessing each stakeholder’s objectives. BWM is applied merely for those cases where the total number of pairwise comparisons would be too high, and the evaluation would be too demanding; thus, the risk of getting inconsistent responses and the required time of evaluation are high, as well. After that, decomposed fuzzy AHP (DF-AHP) is utlized for finding criteria weights related to the determined objectives for each stakeholder.
In this case, the total number of required scorings is not too high; thus, complete evaluation is possible. Note that the decomposed fuzzy approach is applied for both MCDM models (i.e. BWM and AHP) regardless of the amount of pairwise comparisons. Finally, the obtained results are analysed and reflected with the reality and the preliminary expectations of the decision-making problem. This can be considered as a validation and verification of outcome in the model. The elaborated stages are provided as a pseudo code.

Table 1
Decomposed fuzzy linguistic scale (Cebi
et al.,
2023).
| Optimistic linguistic terms |
μ |
ν |
Saaty scale |
Pessimistic linguistic terms |
μ |
ν |
| Exactly Equal Important (EEI) |
0 50 |
0 50 |
1 |
Exactly Equal Unimportant (EEU) |
0.50 |
0.50 |
| Slightly More Important {SMI) |
0.55 |
0.45 |
2 |
Slightly More Unimportant (SMU) |
0.45 |
0.55 |
| Weakly More Important (WMI) |
0 60 |
040 |
3 |
Weakly More Unimportant (WMU) |
0.40 |
0.60 |
| More Important (MI) |
0 65 |
0.35 |
4 |
More Unimportant (MU) |
0.35 |
0.65 |
| Strongly More Important (StMI) |
0 70 |
0.30 |
5 |
Strongly More Unimportant (StMU) |
0.30 |
0.70 |
| Very Strongly More Important (VSI) |
0.75 |
0.25 |
6 |
Very Strongly More Unimportant ’(VSU) |
0.25 |
0.75 |
| Absolutely More Important (AMI) |
0.80 |
0.20 |
7 |
Absolutely More Unimportant (AMU) |
0.20 |
0.80 |
| Perfectly More Important (PMI) |
0.85 |
0.15 |
8 |
Perfectly More Unimportant (PMU) |
0.15 |
0.85 |
| Exactly More Important (EMI) |
0.90 |
0.10 |
9 |
Exactly More Unimportant (EMU) |
0.10 |
0.90 |


5 The Application of the Method for the AV Industry
The proposed hybrid DF-BWM-AHP model is applied to address the problem of assessing the AV industry. AV is defined as a commercially available vehicle that operates without a driver and can be offered by a manufacturer as a car-sharing alternative alongside traditional transport modes (Kopelias
et al.,
2020). These AVs are commonly known as privately shared AVs (PSAVs). The selection of PSAVs is justified by its great acceptability among individuals, which is supported by the literature as it indicates a general reluctance among people to engage in ride-sharing activities (Patel
et al.,
2023).
According to Pettigrew and Cronin (2019), eventual implementation of AVs as a form of transportation is expected to have a significant impact on the users. Determining acceptability of AVs is contingent upon stakeholder perspectives since their evaluation may diverge depending on the advantages or disadvantages related to the introduction of AVs for them. In order to conduct an analysis of advantages and disadvantages associated with AVs, it is imperative for stakeholders to assess several criteria in accordance with their perspectives and expectations.
As presented previously (Hamadneh
et al.,
2022), the stakeholders can be categorized into the following four distinct parties: users, legislators, operators, and manufacturers. The users in this context include a wide range of people, such as elderly and disabled travellers, people without driving license, urban and long-distance travellers, as well as individuals with higher incomes. In current study, the involved legislators represent various governments, municipalities, regional authorities, and local authorities. Furthermore, operators encompass public transport operators, infrastructure management organizations, associations, and private transportation operators, as well. Finally, manufacturers serve as representatives for several entities such as technology suppliers, car producers, energy suppliers, and insurance companies.
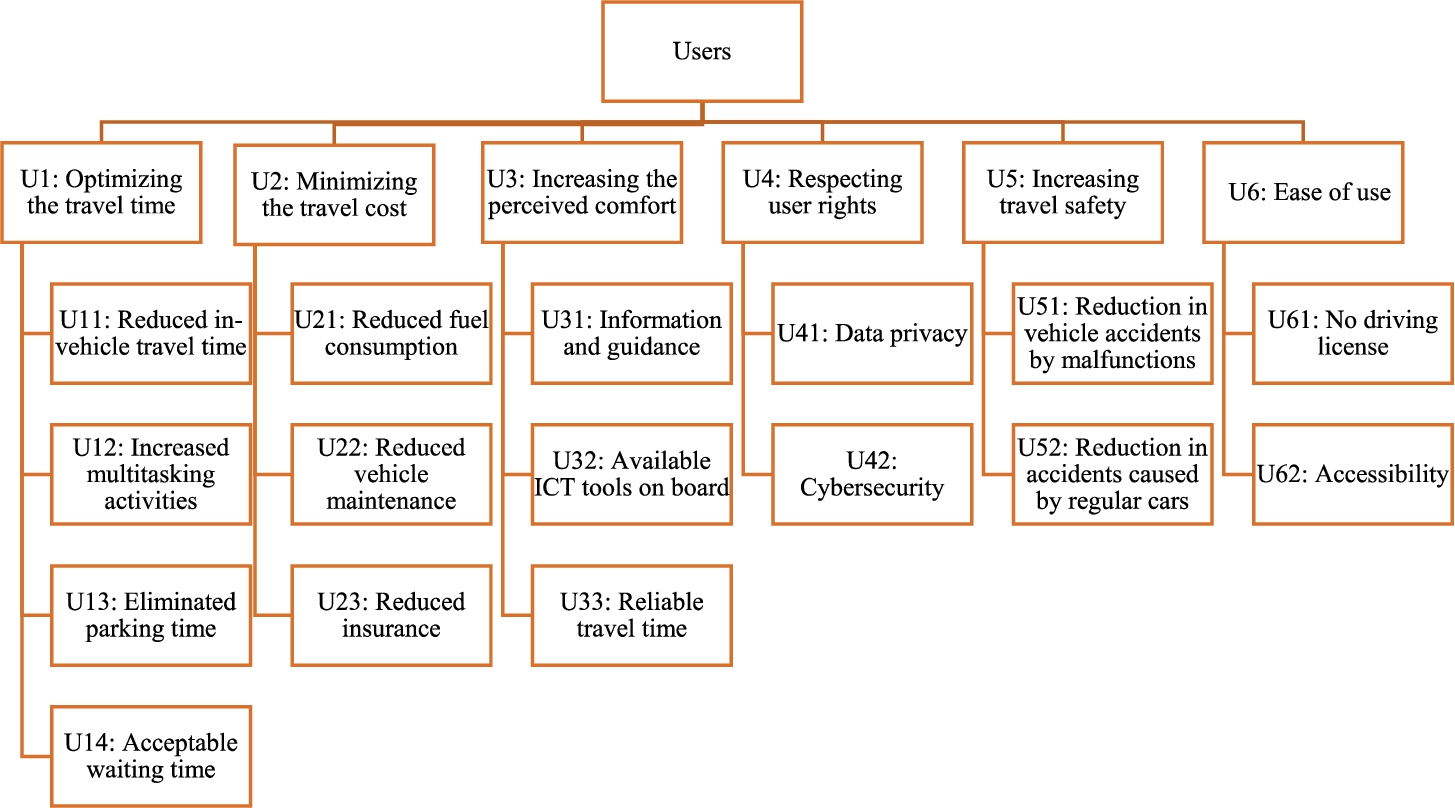
Fig. 1
The problem structure of the AV industry in terms of the users (Hamadneh
et al.,
2022).
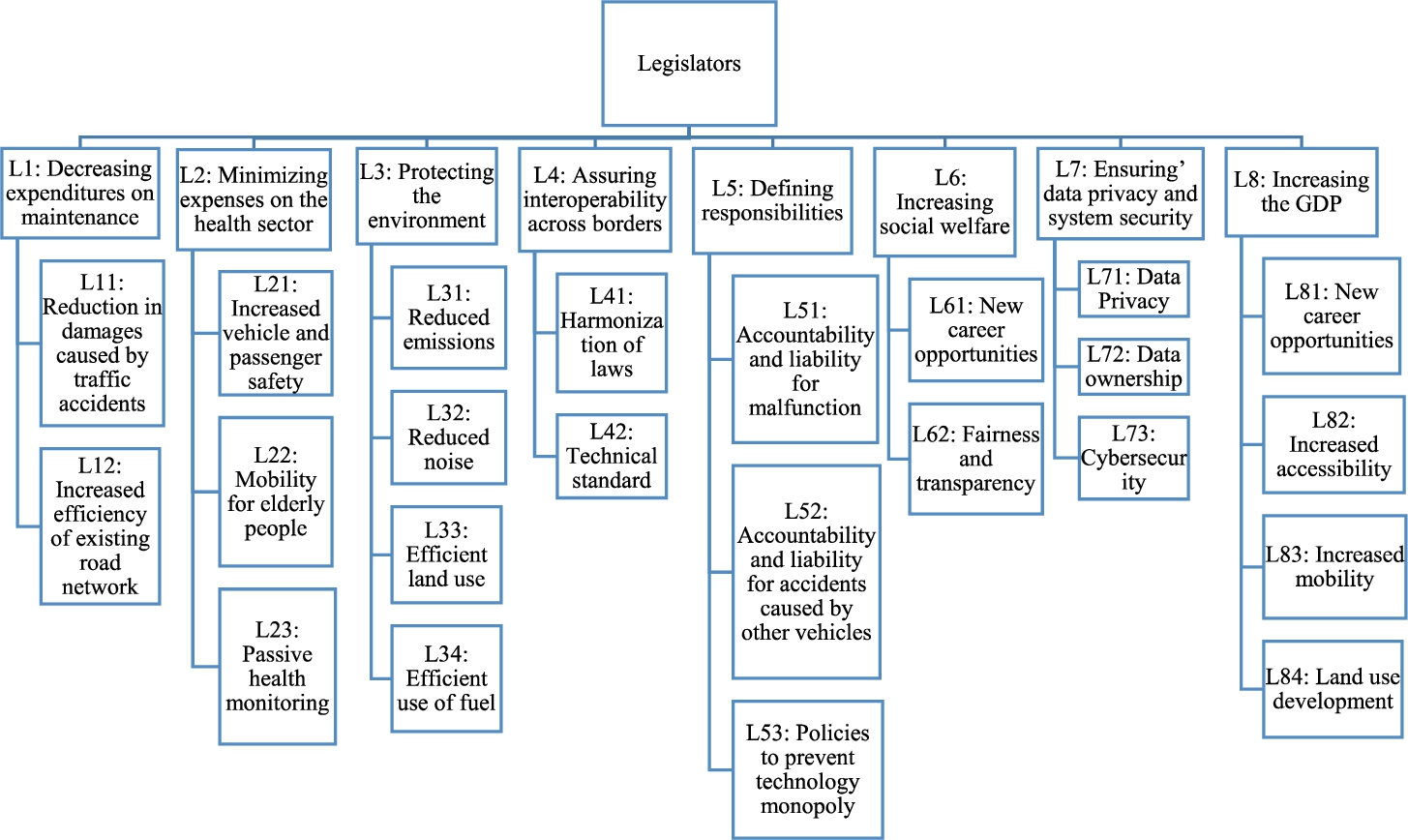
Fig. 2
The problem structure of the AV industry in terms of the legislators (Hamadneh
et al.,
2022).
Figures
1,
2,
3,
4 depict the stakeholders’ aims and criteria upon the adoption of PSAVs as a transport mode. The presented figures illustrate a hierarchical structure aimed at facilitating the adoption of this novel technology by considering stakeholder objectives and establishing specific criteria for evaluating the attainment of these objectives. Note that in case of hierarchical MCDM decision-making, the criteria on the upper level should have approximately the same number of sub-criteria for the sake of appropriate weight allocation (Saaty,
1977). Still, it is important to include all possible objectives and criteria influencing the decision to reflect the decision-making. Finally, the scoring will not be biased if the deviations in the criteria number are not high and the evaluators provide sufficiently consistent scoring. In our research, every stakeholder is provided with a judgment matrix, which contains the relevant objectives and criteria. The evaluation process incorporates the distinction between two objectives or criteria by assigning weights determined by the relative relevance of the criteria, the evaluators’ preferences and needs, as illustrated in the subsequent phase.
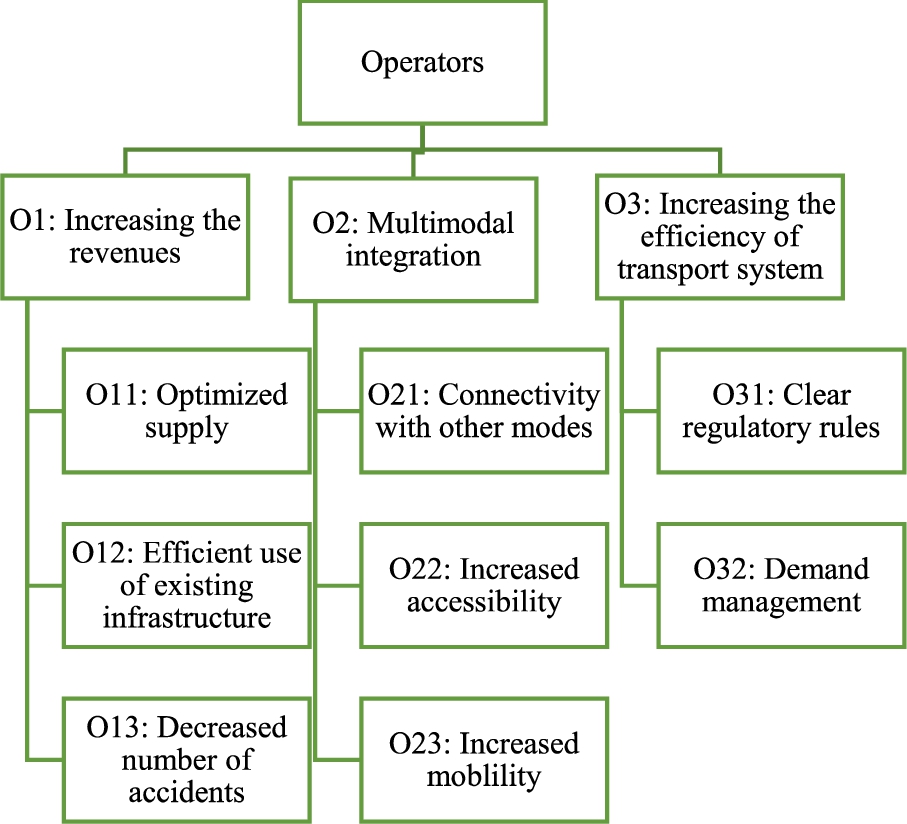
Fig. 3
The problem structure of the AV industry in terms of the operators (Hamadneh
et al.,
2022).
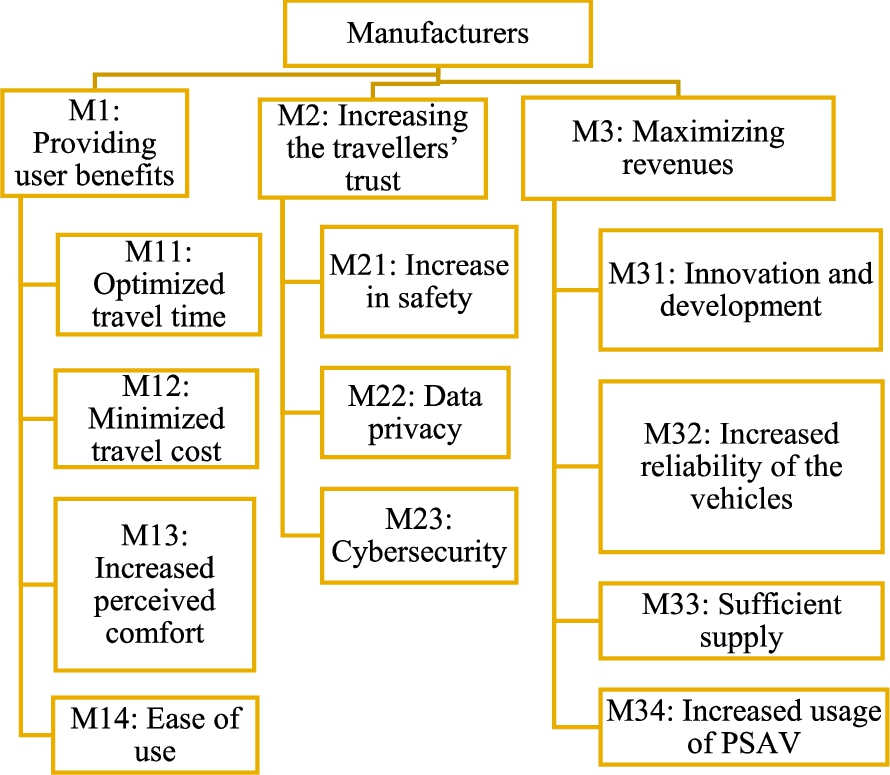
Fig. 4
The problem structure of the AV industry in terms of the manufacturers (Hamadneh
et al.,
2022).
Initially, the DF-AHP technique is employed to ascertain the stakeholders’ relative importance. A total of 61 individuals, i.e. each with distinct occupational backgrounds and varying levels of proficiency, engage in a comparison of stakeholders by assessing them in pairs. During the gathering of the judgments, each question is posed twice encompassing both optimistic and pessimistic perspectives. Table
2 presents a PCM as an illustrative example. As seen in Table
2, in some judgments, the responses to the inquiries characterized by optimism and pessimism do not exhibit a mutually exclusive relationship. The emergence of DFSs can be attributed to this specific reason. The objective is to forecast the impact of the variations in a way that a question is presented to evaluators in their subsequent decision-making process and to incorporate this factor into the computational analyses.
The PCM shown in Table
1 has a calculated CR of 0.05 (i.e. below the 0.1 consistency threshold, thus acceptable) in Stage 1 for the linguistic scale. With this scale the linguistic terms are converted into their corresponding DFSs for each stakeholder.
Table 2
The PCM in terms of the stakeholders according to an arbitrary decision-maker entitled DM1.
| DM 1 |
Users |
Legislators |
Operators |
Manufacturers |
|
O* |
P** |
O* |
P** |
O* |
P** |
O* |
P** |
| Users |
EEI |
EEU |
EMI |
AMU |
WMI |
WMU |
WMU |
WMI |
| Legislators |
EMU |
VSI |
EEI |
EEU |
WMU |
MI |
EMU |
EMI |
| Operators |
WMU |
WMI |
WMI |
WMU |
EEI |
EEU |
StMU |
StMI |
| Manufacturers |
WMI |
WMU |
EMI |
EMU |
StMI |
StMU |
EEI |
EEU |
The responses obtained from a total of 61 individuals are analysed by replicating the procedures outlined in Stage 2 and assessing the level of coherence. After excluding individuals with a CR exceeding 0.1, 44 decision-makers are retained. Subsequently, the decision-makers’ responses are consolidated by using the MDWGM operator, which is followed by the computation of the CIs and score values. For instance, the first decision-maker (DM1) judgments are aggregated as presented in Table
3, where the stakeholders’ importance levels are calculated, which displays the score values. According to this decision-maker, the most important stakeholder is the manufacturers, which is followed by the users.
Table 3
The main stakeholders’ weights according to the first decision-maker (DM1).
|
Respondent 1 |
|
| Stakeholders |
|
$\mathcal{O}({\mu _{ii}^{k}})$ |
$\mathcal{O}({\vartheta _{ii}^{k}})$ |
$\mathcal{P}({\mu _{ii}^{k}})$ |
$\mathcal{P}({\vartheta _{ii}^{k}})$ |
$CI$ |
$SI$ |
| Users |
CR = 0.050 |
0.573 |
0.427 |
0.232 |
0.575 |
0.807 |
6.016 |
| Legislators |
0.211 |
0.789 |
0.566 |
0.300 |
0.806 |
3.287 |
| Operators |
0.436 |
0.564 |
0.449 |
0.450 |
0.891 |
4.955 |
| Manufacturers |
0.659 |
0.341 |
0.111 |
0.675 |
0.777 |
6.756 |
The decision-makers’ judgments are aggregated following the same procedure, and the score values are averaged. The stakeholders’ importance levels are calculated as 0.284, 0.268, 0.232, and 0.216 for the users, legislators, operators, and manufacturers, respectively. DF-AHP could be utilized in cases of uncertainty, which is present in current study. Nevertheless, in light of the considerable quantity of PCMs, the decision is made to apply the BWM method, which depends on the DFSs to mitigate the need for excessive comparisons. Hence, the objectives assigned to each stakeholder are initially ranked by using the BWM, and afterward, the criteria associated with smaller PCMs are evaluated by using the elaborated method.
Instructions are provided to the group of “users” from all groups of stakeholders. A total of 37 users are included in the evaluations, and 24 are included based on their successful completion of the consistency analyses outlined in Stage 2. According to a survey conducted among the participants, it is found that the prevailing consensus regarding the most significant objective is denoted as “U1: Optimizing the travel time”, while the least prioritized objective is identified as “U6: Ease of use”. Table
4 presents linguistic terms that demonstrate superiority of best objective in comparison to the other objectives, whereas Table
5 provides the superiority of other objectives over the worst objective. These linguistic terms are altered into the corresponding DFNs based on Table
1, and they are converted into score values, as well.
Table 4
The PCM for the best objective.
| Consensus judgments |
U1 |
U2 |
U3 |
U4 |
U5 |
U6 |
| O* |
P** |
O* |
P** |
O* |
P* |
P** |
P** |
O* |
P** |
O* |
P** |
| U1 |
EEI |
EEU |
WMI |
WMU |
StMI |
StMU |
PMI |
PMU |
SMI |
SMU |
EMI |
PMU |
| Score values |
5.555 |
6.666 |
7.778 |
9.444 |
6.111 |
8.972 |
Table 5
The PCM for the worst objective.
| Consensus judgments |
U6 |
Score values |
| O* |
P** |
| U1 |
EMI |
PMU |
8.972 |
| U2 |
VSI |
StMU |
7.389 |
| U3 |
MI |
SMU |
5.500 |
| U4 |
SMI |
EEU |
5.278 |
| U5 |
EEI |
WMU |
6.000 |
| U6 |
EEI |
EEU |
5.556 |
The weights of the objectives are computed and presented in Fig.
5. The figure shows that the most significant objective is “U1: Optimizing the travel time”, while the least significant objective is “U4: Respecting user rights” with the weights of 0.214 and 0.126, respectively. Prior to the implementation of the methodology, the objective of the least significance is “U6: Ease of use”. However, subsequent computations lead to a shift in priority resulting in “U4: Respecting the users’ rights” assuming a more prominent position. The primary factor contributing to this phenomenon is the utilization of dual viewpoint inquiries posed to those in positions of authority. To account for inconsistency, decision-makers are presented with a combination of both optimistic and pessimistic questions.
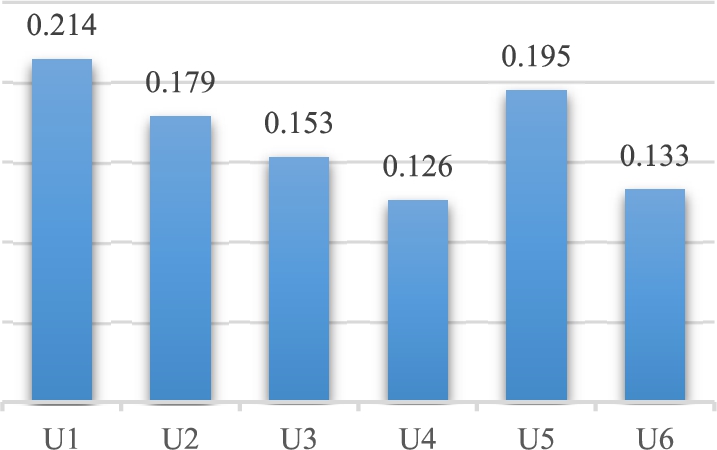
Fig. 5
The users’ objective weights.
An illustrative example of the user judgments regarding objective “U1: Optimizing the travel time” is presented in Table
6 with the aggregated results, which are calculated based on Stage 2. According to User 1, the most important criterion is “U13: No parking time”, while the least important criterion is “U12: Increased onboard multitasking activities”.
Table 6
The PCM example based on the users’ viewpoints for the first objective.
| PCM |
U11: Reduced in-vehicle travel time |
U12: Increased onboard multitasking activities |
U13: No parking time |
U14: Acceptable waiting time |
Aggregated results |
| User 1 |
O* |
P** |
O* |
P** |
O* |
P** |
O* |
P** |
$\mathcal{O}({\mu _{ii}^{k}})$ |
$\mathcal{O}({\vartheta _{ii}^{k}})$ |
$\mathcal{P}({\mu _{ii}^{k}})$ |
$\mathcal{P}({\vartheta _{ii}^{k}})$ |
$CI$ |
$SI$ |
| U11 |
EEI |
EEU |
EMI |
AMU |
EEI |
EEU |
WMU |
WMI |
0.65 |
0.35 |
0.15 |
0.65 |
0.80 |
6.67 |
| U12 |
EMU |
EMI |
EEI |
EEU |
EMU |
EMI |
WMI |
WMU |
0.21 |
0.79 |
0.54 |
0.27 |
0.77 |
3.17 |
| U13 |
EEI |
EEU |
EMI |
EMU |
EEI |
EEU |
EMI |
EMU |
0.67 |
0.33 |
0.04 |
0.70 |
0.72 |
6.68 |
| U14 |
AMU |
AMI |
WMI |
WMU |
StMI |
StMU |
EEI |
EEU |
0.45 |
0.55 |
0.26 |
0.50 |
0.74 |
5.06 |
For each user, the criteria evaluations are collected with the linguistic terms, and they are aggregated. Afterward, the average score values are calculated based on Stage 2 of the proposed methodology. The importance of objectives and criteria from user perspective is presented in Table
7. The criterion of “U52: Reduction in accidents caused by regular cars” is ranked as the most important factor, while the criterion of “U12: Increased onboard multitasking activities” is ranked as the least important based on user perspective.
Table 7
Weights of objectives, criteria, and the rankings based on users’ viewpoints.
| Objectives |
Weights |
Criteria |
Local weights |
Local rankings |
Global weights |
Global rankings |
| U1 |
0.214 |
U11 |
0.304 |
1 |
0.065 |
6 |
|
|
U12 |
0.214 |
4 |
0.046 |
16 |
|
|
U13 |
0.238 |
3 |
0.051 |
12 |
|
|
U14 |
0.244 |
2 |
0.052 |
11 |
| U2 |
0.179 |
U21 |
0.419 |
1 |
0.075 |
3 |
|
|
U22 |
0.306 |
2 |
0.055 |
10 |
|
|
U23 |
0.275 |
3 |
0.049 |
13 |
| U3 |
0.153 |
U31 |
0.309 |
3 |
0.047 |
15 |
|
|
U32 |
0.310 |
2 |
0.047 |
14 |
|
|
U33 |
0.380 |
1 |
0.058 |
9 |
| U4 |
0.126 |
U41 |
0.468 |
2 |
0.059 |
8 |
|
|
U42 |
0.532 |
1 |
0.067 |
5 |
| U5 |
0.195 |
U51 |
0.463 |
2 |
0.090 |
2 |
|
|
U52 |
0.537 |
1 |
0.105 |
1 |
| U6 |
0.133 |
U61 |
0.456 |
2 |
0.060 |
7 |
|
|
U62 |
0.544 |
1 |
0.072 |
4 |
A total of eight legislators take part in the study with one of them being excluded from the analysis due to inconsistency. The DF-BWM-AHP methodology is applied to analyse the data of the remaining seven legislators. The findings of this analysis are presented in Table
8, where the criteria are ranked based on the weights. The results indicate that the objective of “L8: Increasing the GDP” is ranked as the most important one, while objective of “L4: Assuring interoperability across borders” is ranked as the least important. The criterion of “L11: Reduction in damages caused by traffic accidents” is ranked as the most important criterion based on legislator perspectives, while criterion of “L72: Data ownership” is ranked as the least important.
Table 8
Weights of objectives, criteria, and the rankings based on legislators’ viewpoints.
| Objectives |
Weights |
Criteria |
Local weights |
Local rankings |
Global weights |
Global rankings |
| L1 |
0.148 |
L11 |
0.546 |
1 |
0.081 |
1 |
|
|
L12 |
0.454 |
2 |
0.067 |
2 |
| L2 |
0.125 |
L21 |
0.407 |
1 |
0.051 |
5 |
|
|
L22 |
0.326 |
2 |
0.041 |
13 |
|
|
L23 |
0.267 |
3 |
0.033 |
22 |
| L3 |
0.155 |
L31 |
0.289 |
1 |
0.045 |
7 |
|
|
L32 |
0.262 |
2 |
0.041 |
12 |
|
|
L33 |
0.233 |
3 |
0.036 |
17 |
|
|
L34 |
0.215 |
4 |
0.033 |
21 |
| L4 |
0.090 |
L41 |
0.534 |
1 |
0.048 |
6 |
|
|
L42 |
0.466 |
2 |
0.042 |
11 |
| L5 |
0.116 |
L51 |
0.369 |
1 |
0.043 |
10 |
|
|
L52 |
0.327 |
2 |
0.038 |
14 |
|
|
L53 |
0.304 |
3 |
0.035 |
18 |
| L6 |
0.108 |
L61 |
0.524 |
1 |
0.057 |
3 |
|
|
L62 |
0.476 |
2 |
0.052 |
4 |
| L7 |
0.095 |
L71 |
0.352 |
2 |
0.034 |
20 |
|
|
L72 |
0.279 |
3 |
0.027 |
23 |
|
|
L73 |
0.369 |
1 |
0.035 |
19 |
| L8 |
0.162 |
L81 |
0.274 |
1 |
0.044 |
8 |
|
|
L82 |
0.271 |
2 |
0.044 |
9 |
|
|
L83 |
0.229 |
3 |
0.037 |
15 |
|
|
L84 |
0.226 |
4 |
0.037 |
16 |
A total of eight operators fills in the survey, and all operators successfully undergo the consistency analysis. The DF-BWM-AHP methodology is applied to analyse the data of the eight operators. Table
9 indicates the global rankings for objectives and criteria based on operator viewpoints where criteria are ranked based on the weights, as well. The objective of “O1: Increasing the revenues” is ranked as the most significant one, while the objective of “O3: Increasing the efficiency of the transportation system” is ranked as the least significant. The criterion of “O31: Clear regulatory rules” is ranked as the most important criterion, while the criterion of “O23: Increased mobility” is ranked as the least important.
Table 9
Weights of objectives, criteria, and the rankings based on operators’ viewpoints.
| Objectives |
Weights |
Criteria |
Local weights |
Local rankings |
Global weights |
Global rankings |
| O1 |
0.373 |
O11 |
0.352 |
1 |
0.131 |
3 |
|
|
O12 |
0.319 |
3 |
0.119 |
6 |
|
|
O13 |
0.329 |
2 |
0.123 |
4 |
| O2 |
0.339 |
O21 |
0.359 |
1 |
0.122 |
5 |
|
|
O22 |
0.338 |
2 |
0.115 |
7 |
|
|
O23 |
0.304 |
3 |
0.103 |
8 |
| O3 |
0.287 |
O31 |
0.524 |
1 |
0.150 |
1 |
|
|
O32 |
0.476 |
2 |
0.137 |
2 |
A total of eight manufacturers completes the survey, and all manufacturers successfully pass the consistency analysis. The DF-BWM-AHP methodology is used to analyse the data of the manufacturers. Table
10 shows the global rankings for objectives and criteria based on manufacturer responses. The objective of “M2: Increasing the travellers’ trust” is ranked as the most important objective according to manufacturers, while the objective of “M1: Providing user benefits” and “M3: Maximizing the revenues” are ranked as less important factors. The criterion of “M21: Increase in safety” is ranked as the most essential criterion based on manufacturer viewpoints, while the criterion of “M34: Increasing the usage of PSAV” is ranked as the least important.
Table 10
Weights of objectives, criteria, and the rankings based on manufacturers’ viewpoints.
| Objectives |
Weights |
Criteria |
Local weights |
Local rankings |
Global weights |
Global rankings |
| M1 |
0.328 |
M11 |
0.252 |
2 |
0.083 |
7 |
|
|
M12 |
0.304 |
1 |
0.100 |
3 |
|
|
M13 |
0.236 |
3 |
0.078 |
8 |
|
|
M14 |
0.208 |
4 |
0.068 |
10 |
| M2 |
0.343 |
M21 |
0.435 |
1 |
0.149 |
1 |
|
|
M22 |
0.288 |
2 |
0.099 |
4 |
|
|
M23 |
0.277 |
3 |
0.095 |
5 |
| M3 |
0.328 |
M31 |
0.266 |
2 |
0.087 |
6 |
|
|
M32 |
0.316 |
1 |
0.104 |
2 |
|
|
M33 |
0.225 |
3 |
0.074 |
9 |
|
|
M34 |
0.194 |
4 |
0.064 |
11 |
The stakeholders’ importance levels are multiplied by the weights of objectives, and the rankings of objectives considering the perspectives of each stakeholder are obtained, as shown in Fig.
6. The objective of “L4: Assuring interoperability across borders” receives the lowest grade indicating a relatively low level of interest among the respondents in utilizing PSAVs for cross-border travel. Conversely, the highest scores are attributed to the objectives of “O1: Increasing the revenues” and “O2: Multimodal integration”. Policymakers ought to prioritize these two aims while making decisions.
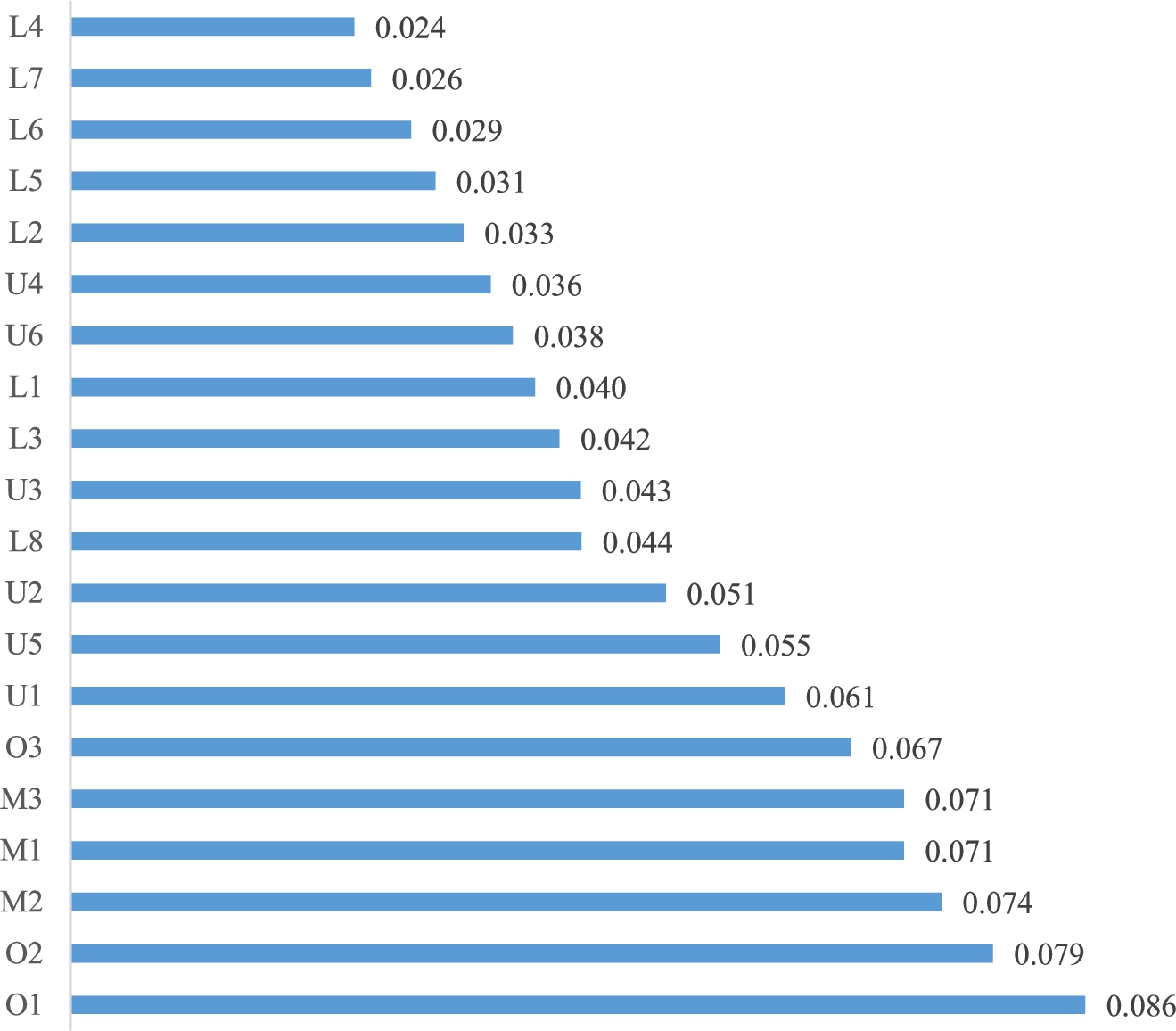
Fig. 6
Rankings of objectives considering stakeholder perspectives.
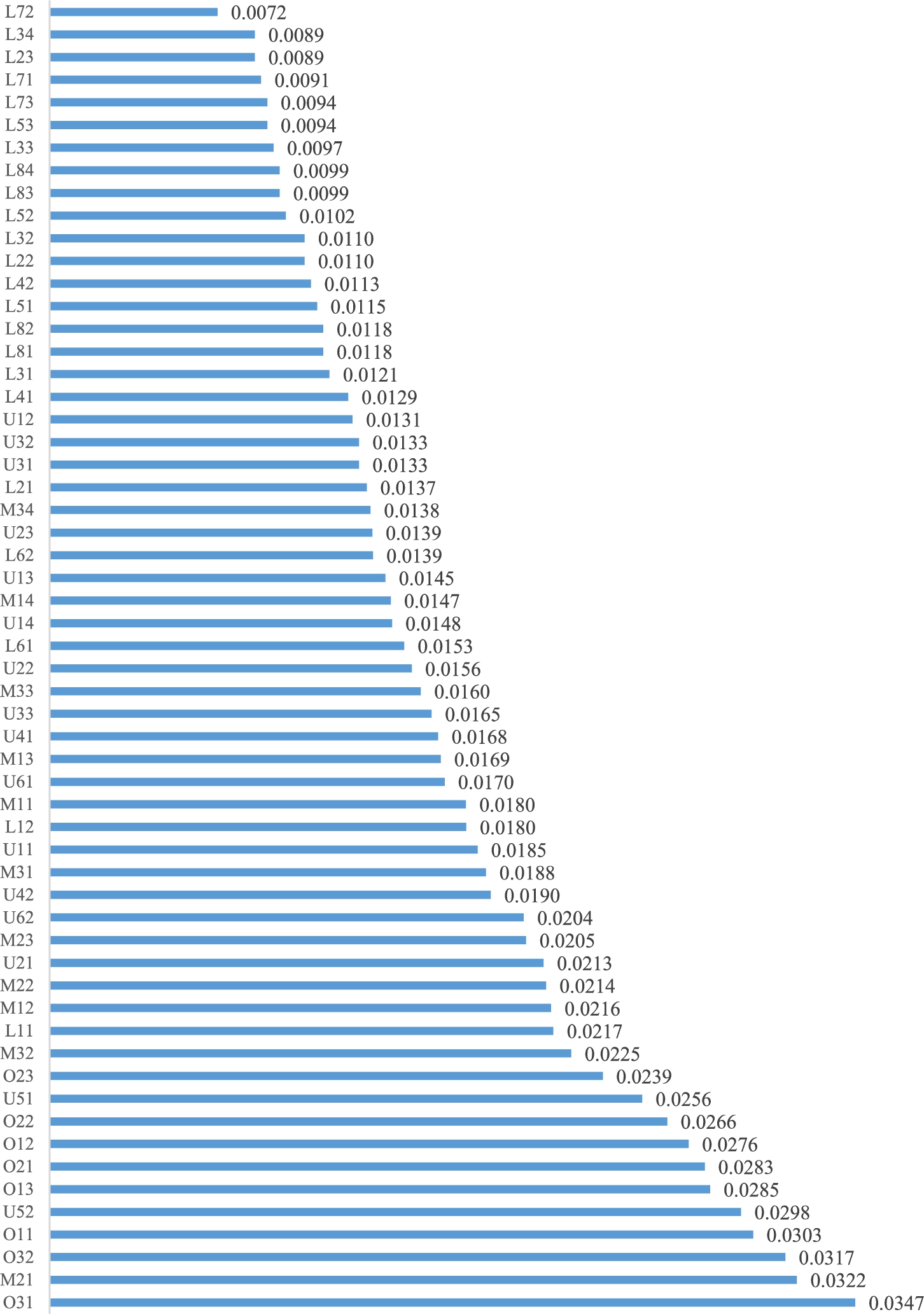
Fig. 7
Ranking of criteria considering stakeholder perspectives.
According to users, legislators, operators, and manufacturers, Fig.
7 shows the rankings of criteria for potential acceptance of PSAV. The concept of “L72: Data ownership” is assigned a relatively low priority suggesting that obtaining PSAVs is not considered to be a challenging task. On the other hand, the category of “O31: Clear regulatory rules” attains the highest value.
6 Discussion
The results of the new DF-BWM-AHP in reflection of the conventional pairwise comparison-based methods, i.e. AHP and PAHP, which is very similar to BWM due to the purpose of reducing the required pairwise comparisons (Duleba,
2022) from the decision-maker, are examined in this section.
Owing to the theory of pairwise comparison-based methods, the preference scores of a pair of preferences are mutually exclusive, which means that in case their relation is evaluated from opposite directions, the scores must be reciprocal. If this rule is followed, the theoretical evaluation (by DM1) of the first level of the case study should be (see Table
1 for reference) as presented in Table
11.
Table 11
Theoretical PCM in terms of stakeholders according to DM1.
| DM1 |
Users |
Legislators |
Operators |
Manufacturers |
|
O* |
P** |
O* |
P** |
O* |
P** |
O* |
P** |
| Users |
EEI |
EEU |
EMI |
EMU |
WMI |
WMU |
WMU |
WMI |
| Legislators |
EMU |
EMI |
EEI |
EEU |
WMU |
WMI |
EMU |
EMI |
| Operators |
WMU |
WMI |
WMI |
WMU |
EEI |
EEU |
StMU |
StMI |
| Manufacturers |
WMI |
WMU |
EMI |
EMU |
StMI |
StMU |
EEI |
EEU |
In contrast, slight but important differences can be detected when comparing the results of Table
11 with the experiential matrix results received from DM1 (Table
12).
Table 12
Experimental PCM in terms of stakeholders according to DM1.
| DM1 |
Users |
Legislators |
Operators |
Manufacturers |
|
O* |
P** |
O* |
P** |
O* |
P** |
O* |
P** |
| Users |
EEI |
EEU |
EMI |
AMU |
WMI |
WMU |
WMU |
WMI |
| Legislators |
EMU |
VSI |
EEI |
EEU |
WMU |
MI |
EMU |
EMI |
| Operators |
WMU |
WMI |
WMI |
WMU |
EEI |
EEU |
StMU |
StMI |
| Manufacturers |
WMI |
WMU |
EMI |
EMU |
StMI |
StMU |
EEI |
EEU |
In the relation of the legislators/users, the optimistic EMU should be paired with the EMI linguistic score; however, DM1 indicates VSI. In the Saaty-scale, it means that instead of 9, merely 6 is scored or in terms of fuzzy sets, not 0.9–0.1 but 0.75–0.25 is indicated. Certainly, the dominance is still expressed, but in the calculation and determination of the final stakeholder weights, there is a significant difference. Without the new DFS approach, this issue would not be considered since all other related methods (AHP, PAHP, or BWM) ignore the possibility of non-reciprocal relations. Moreover, in the Users/Legislators pair, the pessimistic view expresses AMU in the experiential matrix instead of the theoretical EMU. On the Saaty-scale, it means 1/7 substituting 1/9, and for fuzzy sets, it is 0.2–0.8 and not 0.1–0.9. There is a third example of this phenomenon. In case of the Legislators/Operators, DM1 indicates MI instead of WMI; thus, 4 and not 3 is on the Saaty-scale, in fuzzy numbers: 0.65–0.35 and not 0.6–0.4.
None of the mentioned values indicate a large gap between the expected theoretical relation and the experienced relation scores, but in the outcomes of weight determination and prioritization of criteria or alternatives, even small alterations can cause rank reverse. Furthermore, it is emphasized that in case of predictions and trend determination, the occurrence of not perfectly reciprocal preferences is more possible.
To further validate the elaborated method, results are checked with the reference study of Hamadneh
et al. (
2022), which uses the conventional AHP and PAHP techniques, thus not considering the evaluators’ pessimistic and optimistic outlook. According to the findings of current research (Fig.
6), the user group is considered the most important one out of the four stakeholder groups in the decision-making regarding the perspectives of AVs. When all relevant stakeholders are considered, it can be concluded that “O1: Increasing the revenues” is the most essential aim, and “O31: Clear regulatory rules” is the most important aspect in relation to these goals. The dualistic approach in the survey process is satisfactory for both the evaluators (i.e. no time-consuming and demanding survey process) and the analysts (i.e. sufficiently deep and trustworthy final outcomes). The outcome of the reference survey in the same domain of ranking the involved stakeholders’ objectives is presented in Fig.
8.
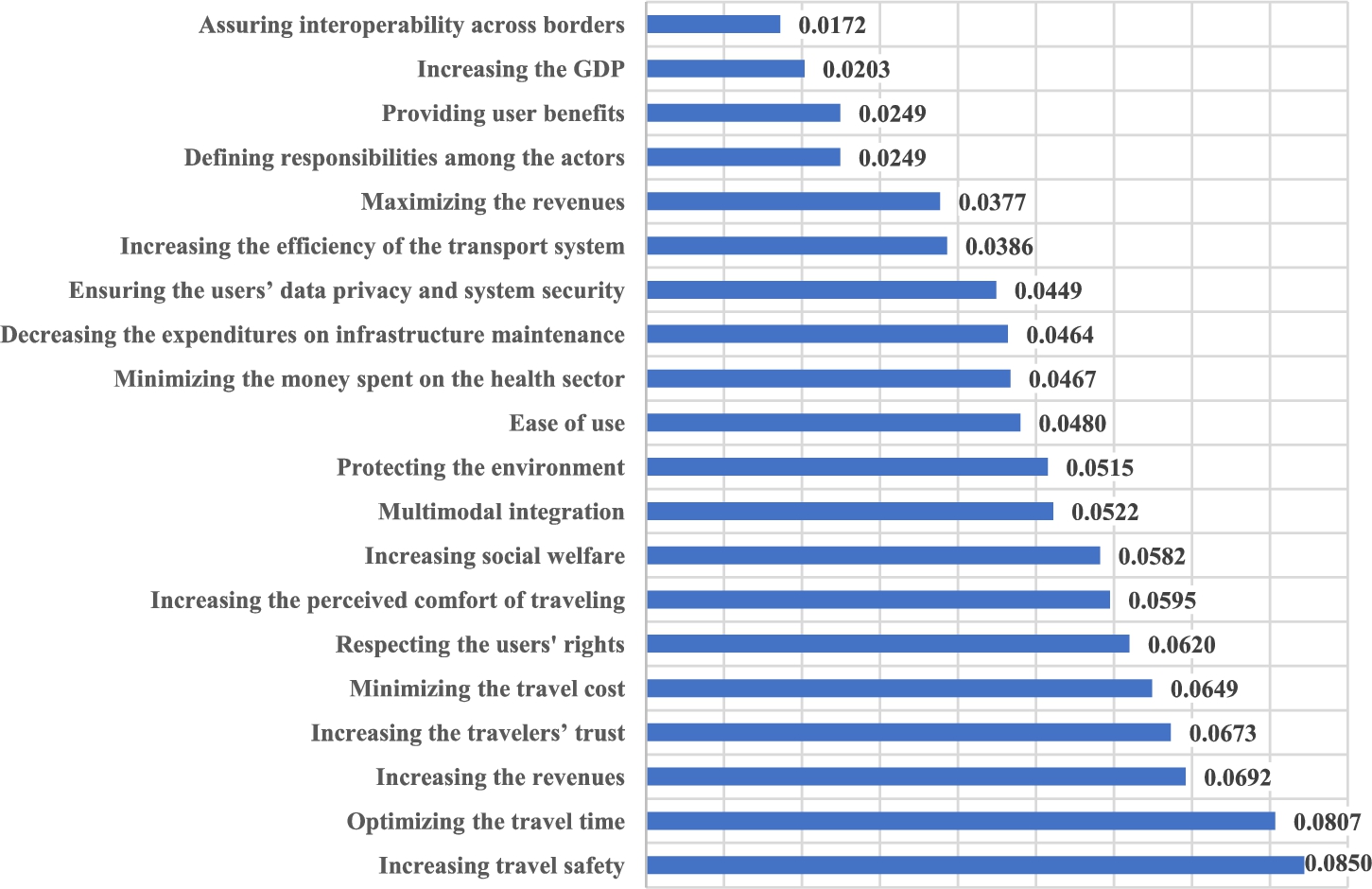
Fig. 8
Rankings of objectives considering stakeholder perspectives in the reference study by Hamadneh
et al. (
2022).
Even though the results are somewhat similar, there are remarkable differences, which suggest higher accuracy in case of the novel DF-BWM-AHP method. In the reference survey, considering all stakeholders’ viewpoints, objective “U5: Increasing travel safety” is ranked as first, and “O1: Increasing the revenues” gets the third position. On the other hand, the new model indicates the dominance of “O1: Increasing the revenues” and “O2: Multimodal integration”, which are clearly the operators’ objectives. This outcome seems more incentive-driven, thus more realistic as the new model takes more possible scenarios into account than the methods applied in the reference study. Motivating the evaluators to contemplate on the optimistic and pessimistic scoring is proven as a powerful tool in terms of self-checking and providing deeper insights into the participants’ way of thinking. This process is similar to the strategic decision-making in companies but in this case, it is at the individual level.
Regarding the criteria, the reference study prioritizes the “U51: Reduction in vehicle accidents” attribute, while in current model “M21: Increase in safety” is significant. However, the results of this study show the primacy of “O31: Clear regulatory rules”, which is not significant in the reference study. It is a relevant difference that could be only found by the application of the elaborated method. If we consider drone technology as an example, the lack of proper regulation has been an obstacle for many years to expand the drone market and reach higher revenues. The same situation occurs for AV industry, and based on the outcome of our analysis, the participants are aware of the need of solid and integrated regulation of the autonomous traffic. Consequently, legislation and setting up rules might be one of the main catalysts of the implementation of AVs. As the second most important criterion of our survey, safety issue is not just a technical problem, even though the primary task is to increase the technical conditions enabling more safe travel. Apart from that, the potential users and other groups of the society should be provided with sufficient information on safety issues of the autonomous traffic, where a targeted campaign might modify the attitude of the public toward the utilization of AVs.
Referring to the objectives, the continuous incentive for ameliorating the PSAVs might result in capability of tackling some unforeseen problems of their implementation and operation. Consequently, considering this attribute (continuous improvement) increases the real-world feature of the results and contributes to the feasibility of the outcome.
Based on results of the case study, there are clear benefits of two-way-directed survey questions for all stakeholders and for society. During the evaluation process, the individuals are inspired to think in a strategic way while taking different aspects into account in their scoring. Additionally, the new method is relevant for experts, municipality officers, and all involved stakeholders when making decisions. In case of long-term, strategic-type decisions, such as the implementation of AVs, this type of consideration is an asset and leads to a more sustainable transportation planning, which is beneficial for the whole society.
It can be stated that the validation through comparisons with a theoretical classical AHP and with a real-world PAHP case study has been successful. The study is limited because asking two-way questions complicates the data collection, still the method generates suitable results by asking optimistic and pessimistic type of questions. When using the BWM method, information is lost by restricting the number of pairwise comparisons because evaluators merely provide their scoring in relation to the best and the worst criteria. However, reduction in time and effort worth more in the process than the loss of information, and without this, the DFS procedure would require much more time, and the inconsistency would significantly grow. Thus, the BWM phase is an inevitable part of the complete model.
Owing to the limitations of our research, the longer and somewhat more complicated survey process has to be mentioned. In case the evaluators are following strict reciprocity in their preference scoring, the two-way questions are redundant, and thus, conventional models of AHP, BWM or other MCDM techniques are recommended. However, in case a certain study refers to future trends or insecure prediction, the proposed new model most likely overperforms all current state-of-the-art MCDM methods. Future research includes the development of interval valued DFS-based processes to further analyse the uncertainty that is present in realistic datasets. Since both the BWM and AHP methods can be combined with other MCDM methods, there are numerous possibilities for creating hybrid decision-making models while keeping the DFS approach.
7 Conclusion
In this study, a DFS-based BWM method is created and integrated with the DF-AHP method. The purpose of this integration is to facilitate the decision-making process in specific cases where the linguistic data are uncertain, and pairwise comparisons are not strictly reciprocal. The analysis showed that in some cases the evaluators provided non-reciprocal scoring when evaluating the perspective of the AV industry, thus it was necessary to apply DFS. The comparative analysis proved that with the proposed model a more realistic and more sophisticated outcome could be gained compared to the conventional AHP and PAHP approaches. Among the benefits, the capability of dealing with optimistic and pessimistic approach, the reduced number of pairwise comparisons (due to the BWM method instead of AHP), the involvement of different stakeholder groups, and the more realistic outcome can be mentioned. Owing to the implementation of the proposed model, users prefer short travel time, while operators, manufacturers and legislators expect increased revenue from AV operations. The two most important criteria have become the clear regulatory rules and the safety of autonomous travel which are realistic as well, since this new transport mode requires solid and integrated regulations. The main concern of multiple involved groups is the safety of the autonomous traffic, while the participants of the market have to cope with mitigating this aversion in order to enhance the acceptance of the AVs. Aiming at the consensual objectives and criteria, the development of the AV market can be boosted, and a more rapid implementation of AVs could be reached.
Conflicts of Interest: The authors declare no conflict of interest.
Data Availability: The data will be provided based on request.