1 Introduction
India experiences numerous earthquakes across its expansive regions annually, highlighting its status as a highly seismically active country due to diverse tectonic conditions. Globally, India is ranked as the sixth most earthquake-prone region, with its geological and climatic factors significantly contributing to the country’s vulnerability to natural disasters, particularly earthquakes. Approximately 56–60% of India’s geographical area is exposed to high seismic hazards (Parvez,
2012). Historically, northeast India has faced at least 17 major earthquakes with their Moment magnitudes (Mw) exceeding 7 during 1869–1988. Notable earthquakes in Assam during this period include the 1869 Cachar earthquake (M
w 7.8), the 1923 southwest Assam earthquake (M
w 7.0), the 1930 Dhubri earthquake (M
w 7.1), the 1931 Assam earthquake (M
w 7.6), the 1943 northeast Assam earthquake (M
w 7.2), and the 1950 Upper Assam earthquake (M
w 8.4) (Parvez,
2012). This history underscores northeast India as a tectonically active region with a predisposition to large-magnitude seismic events.
Previous earthquakes have revealed that structural damage to buildings is primarily due to poor design, substandard construction practices, and inferior materials. Population growth and lifestyle changes in the region have led to a shift from traditional earthquake-resistant Assam-style homes to multi-storied buildings, amplifying vulnerability to seismic risks. The northeast is recognized as one of the world’s most active tectonic regions, and the Bureau of Indian Standards (BIS) places it in Seismic Zone V, indicating a high likelihood of major earthquakes.
Seismic hazard assessment and zonation in India were pioneered by the Geological Survey of India. The country’s first seismic zoning map, created by Tandon in 1956, categorized the region into three zones based on spatiotemporal seismicity statistics (Parvez,
2012). BIS, responsible for developing India’s seismic hazard maps, has periodically updated these maps following significant earthquakes. The seismic map in BIS-1893 (2002) was revised after the 2001 Bhuj earthquake. Earlier versions of the map published in 1962 included six zones, increased to seven in 1966, and later reduced to five in 1970 and 1984. Post-2001, Zone I was merged with Zone II. Furthermore, the Global Seismic Hazard Assessment Program (GSHAP) classifies this region as a high-risk area, with peak ground accelerations ranging between 0.35 g and 0.4 g (Bhatia
et al.,
1999; Thingbaijam
et al.,
2008).
The past few decades have seen rapid infrastructure expansion and unregulated urbanization in the NER. According to the Census of India (2011), the region now includes 14 towns and urban agglomerations, each with a population exceeding 100 000. This population growth has increased vulnerability to earthquakes compared to earlier events. To minimize the effects of future seismic disasters and enhance disaster risk management, it is vital to assess seismic hazards and vulnerabilities at both regional and sub-regional levels. Such assessments can guide authorities in implementing appropriate mitigation and preparedness measures. Seismic risk, which quantifies the potential impacts of earthquakes, is mathematically defined as the product of seismic hazard and vulnerability (D’Amato
et al.,
2022; Frigerio
et al.,
2016).
Seismic hazard assessment (SHA) focuses on estimating ground motion levels at specific sites over defined time periods using deterministic or probabilistic methods. Ground motion is often represented as peak ground acceleration (PGA), spectral acceleration, or other parameters (Dixit
et al.,
2012; Kramer,
1996; Mase
et al.,
2021). Probabilistic seismic hazard assessment (PSHA), grounded in the total probability theorem, accounts for uncertainties related to earthquake magnitude, location, timing, and predictive models—factors often overlooked in deterministic methods (Cornell,
1968; Mase,
2022; McGuire,
2008). Numerous researchers, including Bhatia
et al. (
1999), Nath and Thingbaijam (
2012), NDMA (
2010), Parvez
et al. (
2003), and Sitharam and Kolathayar (
2013), have conducted SHA at a national scale using both probabilistic and deterministic techniques. Regional studies have also been undertaken, such as those by Das
et al. (
2006,
2016), Ghosh and Chakraborty (
2017), Sharma and Malik (
2006), and Ghione
et al. (
2021) for the NER; Sitharam and Sil (
2014) for Tripura; and Baro
et al. (
2018,
2020) for the Shillong Plateau and Meghalaya. Bahuguna and Sil (
2018) explored seismic hazards specific to Assam.
Ground Motion Prediction Equations (GMPEs) provide empirical models that relate earthquake characteristics to ground motion parameters, such as peak ground acceleration (PGA) and spectral acceleration (Sa). In Northeast India, research on GMPE development has been relatively limited, with most equations either based on regional seismic data or derived from simulation-based seismic hazard databases. Key contributions in this area include works by Anbazhagan
et al. (
2013), Bajaj and Anbazhagan (
2019), Gupta (
2010), Singh
et al. (
2016), Nath
et al. (
2012), and NDMA (
2010).
Several studies have applied multiple GMPEs using the logic tree methodology to evaluate seismic hazards in various regions. For instance, Shukla and Choudhury (
2012) focused on Gujarat, examined Goa, Anbazhagan
et al. (
2019) analysed Patna, Borah and Kumar (
2022) worked on Northeast India, and Zahoor
et al. (
2023) investigated the Kashmir region. Despite their significance, these studies often overlooked critical aspects, such as the suitability of selected GMPEs for local geological conditions, their reliability for large-magnitude events, or their applicability over extended distances. Moreover, the weighting schemes used in these approaches generally failed to adequately incorporate the uncertainties associated with PGA estimation.
1.1 Research Gap and Objective of the Study
Northeast India is characterized by a unique and complex tectonic framework, making it one of the most seismically active regions in the world. This region’s tectonic setting, comprising thrusts such as the Main Frontal Thrust (MFT), Main Boundary Thrust (MBT), Main Central Thrust (MCT), (Gupta
et al.,
2022; Kayal,
2008) and faults like the Dauki (Kayal
et al.,
2006), Kopili, and Oldham Faults (England and Bilham,
2015), highlights the necessity for advanced Seismic Hazard Assessment (SHA) techniques. The existing methods, such as the conventional logic tree approach for selecting and weighting Ground Motion Prediction Equations (GMPEs), present significant limitations in addressing the region’s distinctive geological and seismological characteristics.
In recent studies, various methodologies have been applied to assess seismic hazards in Northeast India. Mishra
et al. (
2024) and Kumar
et al. (
2023a) conducted a comprehensive seismic hazard assessment for Guwahati and Silchar city, employing both probabilistic and deterministic approaches to estimate ground motion parameters such as peak ground acceleration (PGA) and spectral acceleration at various probabilities of exceedance. Both studies employed equal weightage to each Ground Motion Prediction Equation (GMPE) to estimate ground motion parameters. Lallawmawma
et al. (
2023) used different areal sources along with multilayer logic tree approach for the computation seismic hazard in Mizoram. Ghione
et al. (
2021) used a hybrid model to compute hazard for Bhutan and Northeast India considering shallow and subduction zone. Kumar
et al. (
2023b) employed a probabilistic approach for the evaluation of seismic hazard for all the capital city of Northeast India. Here, also equal weightage has been given to the two used GMPE without considering the tectonic importance of the different study region of Northeast India. Agrawal
et al. (
2023) added a key factor social vulnerability for the evaluation of risk assessment of Northeast India. In this study, two different GMPE were used for two different focal depths of source zone for the determination of PGA. As factors affecting GMPE are not limited to only focal depth, so the use of GMPE based on focal depth does not lead to accurate measurement of PGA. All the above recent literature puts a serious question on the assigned weights for each of the GMPEs used in various studies.
The traditional logic tree method relies heavily on subjective expert judgment to assign weights to GMPEs, leading to inconsistencies and potential biases. Additionally, it oversimplifies the intricate relationships between key seismic parameters like magnitude, distance, site conditions, and tectonic settings, failing to adequately account for uncertainties (epistemic and aleatory) in peak ground acceleration (PGA) predictions. This gap is particularly critical for Northeast India, where plate interactions at the tri-junction of the Indian, Eurasian, and Burmese plates result in a high degree of crustal deformation and frequent large-magnitude earthquakes along with shallow intra-slab Bengal basin earthquakes. The inability of existing approaches to account for these uncertainties undermines the reliability of seismic hazard models, which are crucial for infrastructure planning and disaster risk mitigation.
The primary objective of this study is to develop and implement a Seismic Hazard Assessment (SHA) framework using Fuzzy Multi-Criteria Decision Making (MCDM) techniques to enhance the accuracy and reliability of Peak Ground Acceleration (PGA) estimates in Northeast India. The study aims to minimize subjectivity in GMPE selection and weighting through a systematic Fuzzy MCDM approach, integrate uncertainties related to site conditions, tectonic settings, magnitude scaling, and distance attenuation, and improve PGA estimation accuracy in the seismotectonically complex region. It tailors the framework to account for the high seismicity of the Indo-Burma Range, Shillong Plateau, Eastern Himalayas, Mishmi Thrust, Naga Thrust, and Bengal Basin while generating robust seismic hazard maps for better infrastructure design, urban planning, and disaster preparedness. Additionally, the study demonstrates the superiority of Fuzzy MCDM over conventional methods in handling uncertainties and providing more reliable hazard estimates, ultimately contributing to a deeper understanding of seismic hazards and improving seismic risk mitigation in Northeast India.
The TrF-FUCOM- Neutrosophic-TOPSIS method is a hybrid MCDM technique used in this work. The TrF-FUCOM approach was first presented by Majumder (
2023a). Saaty created the Analytic Hierarchy Process (AHP), a popular MCDM method, earlier in
1980. AHP assigns suitable weights to several criteria using a defined technique and pairwise comparisons. To address this challenge, Saaty extended the AHP into the Analytic Network Process (ANP) in
1996, with a revised version published in 2001. ANP is particularly effective for complex multi-criteria decision-making (MCDM) problems, as it incorporates feedback and interactions both within and between clusters. This method enables a systematic approach to handling interdependencies in decision-making systems, making it a more generalized form of AHP that accounts for intricate relationships among attributes and decision levels. One of the MCDM methods, Simple Additive Weighting (SAW), was proposed by Zionts and Wallenius (
1983). The Step-wise Weight Assessment Ratio Analysis (SWARA) method, introduced by Keršuliene
et al. (
2010), is a relatively recent and efficient approach for determining subjective weights in multi-criteria decision-making (MCDM) problems. Compared to methods like AHP, SWARA offers a lower computational complexity, making it a more straightforward alternative in certain applications. The weights of alternatives are usually determined via
$n(n-1)/2$ comparisons. Rezaei introduced the Best-Worst Method (BWM), another MCDM technique, in 2015. Rezaei (
2015) claims that BWM overcomes several of AHP’s drawbacks. Because BWM only requires
$2n-3$ comparisons, it is more efficient and consistent than AHP, which requires a greater number of pairwise comparisons. Furthermore, because fewer comparisons are required to produce trustworthy findings, BWM provides more flexibility by getting beyond the restriction of comparing a maximum of nine criteria.
By using vectors like “best-to-others” and “others-to-worst”, the BWM improves reliability and produces more reliable findings than the AHP, which mostly uses pairwise comparisons. However, BWM could have trouble figuring out precise weight coefficient values when large swings affect the consistency level. Interval values should be calculated in these situations, and the average of these intervals should be used to determine the final weight coefficient (Rezaei,
2015). The core region of the interval may or may not contain the required weight coefficients. Interval weight values might not accurately reflect ideal weight coefficients in situations of inconsistency, according research by Pamučar
et al. (
2018a). Pamučar
et al. (
2018b) presented the Full Consistency Method (FUCOM), a technique for establishing criteria weights, in order to overcome these issues. FUCOM tackles the shortcomings of the AHP and BWM models. Pairwise comparisons are made easier while maintaining a balanced number of comparisons
$(n-1)$ that are neither too few nor too many. When determining criteria weights, the FUCOM technique incorporates the subjective preferences of the decision-maker, especially in the first steps where criteria are assessed and compared pairwise. FUCOM is effective, however its criteria weight values vary slightly (Pamučar
et al.,
2018b). By eliminating the requirement for repeated pairwise comparisons of criteria, FUCOM offers a major advantage (Božanic
et al.,
2019; Božanić
et al.,
2020). Linguistic variables are frequently chosen over exact numerical values in circumstances when decision-makers lack information or expertise. Zadeh (
1965) proposed the idea that linguistic variables offer a mathematical framework for dealing with imperfect information. Under ambiguous or imprecise circumstances, fuzzy sets (FSs) have shown themselves to be a useful tool for representing MCDM problems. Triangular or trapezoidal fuzzy numbers can be used to assess the possible results for each criterion (Guha and Chakraborty,
2011). Trapezoidal fuzzy numbers can also be triangular fuzzy numbers, according to Zheng
et al. (
2012). A trapezoidal fuzzy number must take on at least one of its extreme values in order to produce a triangular fuzzy number. In the development of methodologies, researchers have found that trapezoidal fuzzy numbers (TrFNs) provide notable advantages over triangular fuzzy numbers (Majumder,
2023a,
2023b; Majumder
et al.,
2023a). Majumder (
2023a) presented the TrF-FUCOM methodology in light of these discoveries.
Hwang and Yoon first proposed OPSIS, or Technique for Order Preference by Similarity to Ideal Solution, in
1981. Yoon then refined the technique in
1987. Hwang
et al. made more improvements in
1993. The chosen alternative should have the largest distance from the Negative Ideal Solution (NIS) and the shortest distance from the Positive Ideal Solution (PIS), according to the fundamental tenet of TOPSIS. In the year 2023, Neutrosophic-TOPSIS under Single Valued Neutrosophic Set (SVNS) environment was developed by Pramanik
et al. (
2023) to ascertain the ranking of alternatives. In order to facilitate efficient determination, the TrF-FUCOM technique directs the process of allocating criteria weights (Majumder,
2023a). TOPSIS is used in this study because it is easy to use and adaptable to both qualitative and quantitative needs. By comparing the best and worst performance of each alternative, this method improves the trustworthiness of ranking results. TOPSIS is a great option for situations where the interaction between cost and performance is crucial since it also takes cost-benefit parameters into account.
1.2 Novelty of the Study
The Seismic Hazard Assessment (SHA) framework utilizing Fuzzy Multi-Criteria Decision Making (MCDM) techniques is highly relevant to the seismotectonic settings of Northeast India and offers significant novelty and advantages in addressing the region’s complex seismic hazard challenges. Northeast India is one of the most seismically active regions in the world due to its unique tectonic setting, involving the interaction of the Indian Plate with the Eurasian and Burma Plates, resulting in high seismicity across the Indo-Burma Range (IBR), Shillong Plateau (SP), Eastern Himalayas (EH), Mishmi Thrust (MT), Naga Thrust (NT), and Bengal Basin (BB). The conventional Deterministic Seismic Hazard Assessment (DSHA) process often struggles to account for the inherent uncertainties in seismic parameters, such as site conditions, tectonic settings, magnitude scaling, and distance attenuation, which are critical for accurate PGA estimation.
The Fuzzy MCDM framework addresses these challenges by incorporating fuzzy sets and membership functions to quantify uncertainties and reduce subjectivity in weight assignments for Ground Motion Prediction Equations (GMPEs). This approach is particularly advantageous for Northeast India, where the seismotectonic complexity and variability in fault systems demand a more nuanced and flexible hazard assessment methodology. By integrating multiple criteria and fuzzy logic, the framework provides a more reliable and realistic estimation of PGA, capturing the uncertainties associated with seismic events and tectonic settings. This is especially important for regions like the Indo-Burma Range and Mishmi Thrust, where high PGA values are observed due to intense tectonic activity, and the Shillong Plateau, where the Dauki Fault contributes to significant seismic hazard.
2 Methodology
The objective of this study is to develop and implement a Seismic Hazard Assessment (SHA). A hybrid fuzzy-based decision-making technique is used to develop a PGA equation for Seismic Hazard analysis. The methodology is divided into two parts: initial preparation and MCDM-based PGA, which are discussed in Sections
2.1 and
2.2, respectively.
2.1 Initial Preparation
In this study, two different fuzzy-based MCDM techniques are used to determine the score values of the considered alternatives. The initial preparation is divided into two parts: the preliminary analysis of Trapezoidal Fuzzy Numbers (TrFN) and the preliminary analysis of Single-Valued Neutrosophic Sets (SVNS), which are discussed in Sections
2.1.1 and
2.1.2, respectively.
2.1.1 Preliminary of Trapezoidal Fuzzy Number (TrFN)
There have been several varieties of fuzzy numbers created since Zadeh first proposed the idea of fuzzy sets (FS) in 1965, including trapezoidal, Gaussian, and triangular fuzzy numbers. An overview of the most important terms pertaining to fuzzy sets and triangular fuzzy numbers (TrFNs) is provided below.
Definition 1.
A fuzzy set, denoted as $F=\{(f,{\mu _{F}}(f)):f\in R\}$ is characterized by a set of ordered pairs, where $0\leqslant {\mu _{F}}(f)\leqslant 1$ represents the mapping of membership (membership function) of objects g within the FS.
Definition 2.
TrFN is presented by
$\tilde{T}=({t_{1}},{t_{2}},{t_{3}},{t_{4}})$, where
$\tilde{T}$’s membership mapping
${\mu _{\tilde{T}}}$ is presented (Xiao
et al.,
2012).
The parameters are defined by a lower limit
${t_{1}}$, an upper limit
${t_{4}}$, a lower support limit
${t_{2}}$, as well as an upper support limit
${t_{3}}$, where
${t_{1}}\lt {t_{2}}\lt {t_{3}}\lt {t_{4}}$.
A TrFN transitions into a TFN when its two most favourable values coincide. TFNs, therefore, represent specific instances of TrFNs. The latter is used in situations where just a limited segment of the discourse universe is granted exclusive membership, as is seen in conservative or depressing situations. On the other hand, this approach is used in positive or tolerant situations when full membership is available to a far larger segment of the conversation universe. By fostering tolerance and optimism, TrFNs are capable of competently managing events (Berkan and Trubatch,
2000). Based on the assumption that
${\tilde{T}_{1}}=({t_{1}^{/}},{t_{2}^{/}},{t_{3}^{/}},{t_{4}^{/}})$ and
${\tilde{T}_{2}}=({t_{1}^{//}},{t_{2}^{//}},{t_{3}^{//}},{t_{4}^{//}})$ are the two positive TrFNs (Chen and Chen,
2007), the operational principles are as follows:
Definition 3.
The process of turning a fuzzy number into a sharp one is called defuzzification. The output is transformed from the fuzzy domain back into the crisp domain using an inverse transformation. If
${\tilde{T}_{1}}=({t_{1}^{/}},{t_{2}^{/}},{t_{3}^{/}},{t_{4}^{/}})$ is a TrFN, the corresponding crisp value
$R({\tilde{T}_{1}})$ can be generated by the following formula:
2.1.2 Preliminary of Single Valued Neutrosophic Set (SVNS)
Smarandache (
1998) laid the foundation for Neutrosophic Sets in 1998, which was later built upon by Wang
et al. (
2010) with the introduction of Single-Valued Neutrosophic Sets (SVNS). This concept aimed to address situations marked by uncertainty and incomplete data.
The following definition outlines an SVNS
W defined over a specified set
E:
where
${P_{m}}:R\to \{0,1\}\cup (0,1)$,
${Q_{m}}:R\to \{0,1\}\cup (0,1)$,
${S_{m}}:R\to \{0,1\}\cup (0,1)$ and so
$0\leqslant {P_{m}}(x)+{Q_{m}}(x)+{S_{m}}(x)\leqslant 3$. If an SVNS
W over a given set
E,we refer to the triplet
$({P_{m}}(x),{Q_{m}}(x),{S_{m}}(x))$ as a Single-Valued Neutrosophic Number (SVNN).
Mandal and Basu (
2019) proposed a new scoring function designed to tackle Multiple Attribute Decision Making (MADM) challenges within the SVNS framework. The scoring process involves the following steps:
-
(i) Consider a three-dimensional space with the origin represented as O. Within this space, let denote a specific point $U=({a_{\theta }},{b_{\theta }},{c_{\theta }})$, referred to as an SVNN. Perform a translation of this point into U to arrive at $V=({a_{\varpi }},{b_{\varpi }},{c_{\varpi }})$. Here ${a_{\varpi }}={a_{\theta }}+\lambda ,{b_{\varpi }}={b_{\theta }}+\lambda ,{c_{\varpi }}={c_{\theta }}+\lambda ,$ where $\lambda \gt 0$, a real number such that ${c_{\varpi }}$ never equals 1 and remains unique throughout a given problem. Now, let’s consider another point, ${V^{/}}=({a_{\varpi }},-{b_{\varpi }},-{c_{\varpi }})$, resulting from reflecting $V=({a_{\varpi }},{b_{\varpi }},{c_{\varpi }})$ across the x-axis, acting as a mirror.
-
(ii) Locate the score function ${S_{1}}(V)=\cos \theta $, with θ representing the angle between $OV$ and $O{V^{/}}$, and O denoting the origin.
-
(iii) If the score values for two distinct SVNNs, ${V_{1}}=({a_{{\varpi _{1}}}},{b_{{\varpi _{1}}}},{c_{{\varpi _{1}}}})$ and ${V_{2}}=({a_{{\varpi _{2}}}},{b_{{\varpi _{2}}}},{c_{{\varpi _{2}}}})$, denoted as ${S_{1}}({V_{1}})$ and ${S_{1}}({V_{2}})$ respectively, are equal, determine ${V_{1}^{\ast \ast }}=({a_{{\varpi _{1}}}},-{b_{{\varpi _{1}}}},-\sqrt{{c_{{\varpi _{1}}}}}\hspace{0.1667em})$ and ${V_{2}^{\ast \ast }}=({a_{{\varpi _{2}}}},-{b_{{\varpi _{2}}}},-\sqrt{{c_{{\varpi _{2}}}}}\hspace{0.1667em})$ respectively for the corresponding translated points ${V_{1}^{\ast }}=({a_{{\varpi _{1}^{\ast }}}},{b_{{\varpi _{1}^{\ast }}}},{c_{{\varpi _{1}^{\ast }}}})$ and ${V_{2}^{\ast }}=({a_{{\varpi _{2}^{\ast }}}},{b_{{\varpi _{2}^{\ast }}}},{c_{{\varpi _{2}^{\ast }}}})$ where, ${a_{{\varpi _{1}^{\ast }}}}={a_{{\varpi _{1}}}}+\lambda $, ${b_{{\varpi _{1}^{\ast }}}}={b_{{\varpi _{1}}}}+\lambda $, ${c_{{\varpi _{1}^{\ast }}}}={c_{{\varpi _{1}}}}+\lambda $ and ${a_{{\varpi _{2}^{\ast }}}}={a_{{\varpi _{2}}}}+\lambda $, ${b_{{\varpi _{2}^{\ast }}}}={b_{{\varpi _{2}}}}+\lambda $, ${c_{{\varpi _{2}^{\ast }}}}={c_{{\varpi _{2}}}}+\lambda $.
-
(iv) Determine $\cos A$ and $\cos B$, where A represents the angle between $O{V_{1}^{\ast }}$ and $O{V_{1}^{\ast \ast }}$, and B signifies the angle between $O{V_{2}^{\ast }}$ and $O{V_{2}^{\ast \ast }}$, with O denoting the origin.
-
(v) The score mapping ${S_{1}}({V_{1}})=\cos A$, as well as ${S_{1}}({V_{2}})=\cos B$.
2.2 MCDM Based PGA
This study aims to develop and implement a Seismic Hazard Assessment (SHA) framework using Fuzzy MCDM techniques to improve the accuracy and reliability of PGA estimates. The new PGA equation is developed as the average weighted sum of the considered PGA values. The PGA is determined by the formula (
1) with the help of weights of considering PGA and its calculated PGA from ground motion prediction equation (GMPE) The weights are determined with the help of a hybrid MCDM technique. Figure
1 illustrates the computational steps of PGA.
where:
${\textit{PGA}_{f}}=\text{Final PGA}$;
${p_{i}}$ = Calculated Weight for
ith Ground motion Prediction Equation;
$v({\textit{PGA}_{\textit{GMPE}-i}})$ = calculated PGA from
ith No of Ground motion Prediction Equation
$(i=1(1)m)$.
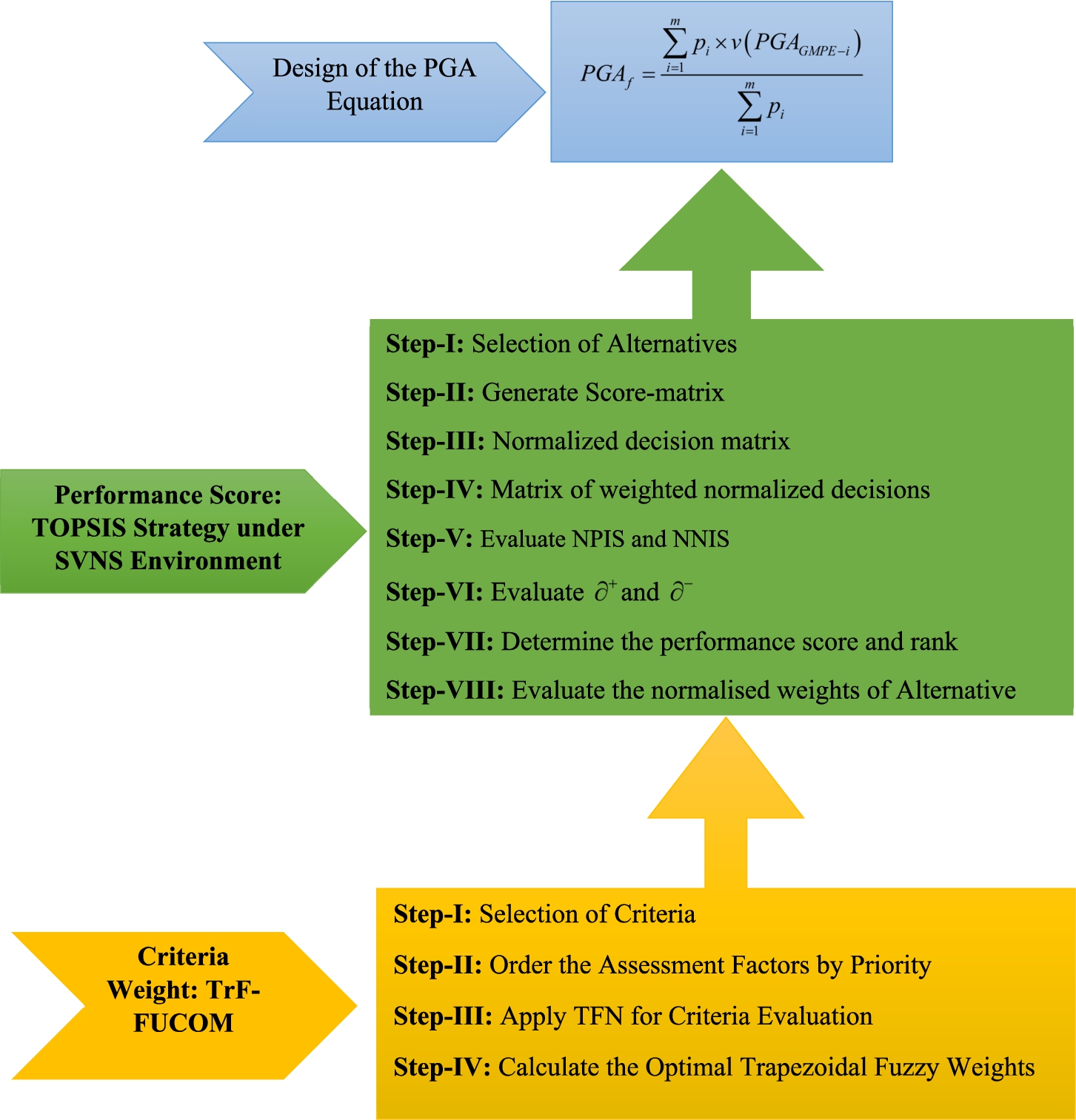
Fig. 1
The comprehensive overview of PGA.
To determine the weights of each GMPE (${\textit{PGA}_{\textit{GMPE}-i}}$), in the present study we use two MCDM techniques, namely Trapezoidal Fuzzy Full Consistency Method (TrF-FUCOM) and Neutrosophic-TOPSIS under Single Valued Neutrosophic Set (SVNS) environment (Neutrosophic-TOPSIS). The TrF-FUCOM is used to determine the weights of criteria and Neutrosophic-TOPIS Strategy within the SVNN used to determine the weights of alternatives. In the Model-I and Model-II, we discuss the computational process of TrF-FUCOM and Neutrosophic-TOPIS Strategy respectively.
Model-I: In this model, we discuss how to determine the weights of criteria with the help of TrF-FUCOM.
Phase-i: Suppose $F=\{{\xi _{r}}:r=1(1)n\}$ is a collection of criteria.
Phase-ii: Decision-makers’ (DMs’) preferences and opinions about the importance of each criterion are used to prioritize them in the first phase. The top rank is given to the factor with the highest weight coefficient, and the lowest weight coefficient factor is ranked last. The most significant factors are listed first, followed by the least significant, in descending order of their weight coefficients. As a result, the qualities are ranked as ${\xi _{r(1)}}\succ {\xi _{r(2)}}\succ \cdots \succ {\xi _{r(\kappa )}}$, and κ represents the rank of a certain factor. An equality symbol in place of ‘≻’ is used to show that two or more components have the same rank.
Phase-iii: By using Table
1, it is possible to compare factors according to their rankings, which are mostly established by the component that is rated first. Determining the trapezoidal fuzzy criterion importance (
${\tilde{\mathrm{\wp }}_{{\xi _{r(\kappa )}}}}$) for each factor is made easier by this procedure. The other components are compared a total of
$n-1$ times because the most significant element is self-compared (its importance is
${\tilde{\mathrm{\wp }}_{{\xi _{r(1)}}}}=EI$). Based on the criteria’s indicated importance, Eq. (
2) is used to compute the fuzzy comparative significance
${\tilde{\chi }_{\kappa /(\kappa +1)}}$.
where the significance of the factor ranked
${\xi _{r(\kappa )}}$ with respect to the factor ranked
${\xi _{r(\kappa +1)}}$ is shown by the symbol
${\tilde{\chi }_{\kappa /(\kappa +1)}}$.
A Trapezoidal Fuzzy vector that represents the relative relevance of choice factors is thus produced by the expression (
3).
Phase-iv: The Trapezoidal Fuzzy weight coefficients of components ${({\tilde{y}_{1}},{\tilde{y}_{2}},\dots ,{\tilde{y}_{n}})^{T}}$ were finally calculated. However, the final values of the weight coefficients must satisfy the following conditions:
Table 1
Evaluating pairs through linguistic measures of significance.
| Providing clear definitions for linguistic terms |
Fuzzy measures with trapezoidal shape of notable significance$({t_{1}},{t_{2}},{t_{3}},{t_{4}})$
|
SI |
| AMI |
$(8,8.5,9,9)$ |
9 |
| Scale of intermediate |
$(\ell -1,\ell -0.5,\ell +0.5,\ell +1)$ |
$2\leqslant \ell \leqslant 8$, $\ell \in N$
|
| EI |
$(1,1,1,1)$ |
1 |
Condition 1.
The weight coefficient ratio (shown in expression (
4)) of the measured components (
${\xi _{r(\kappa )}}$ and
${\xi _{r(\kappa +1)}}$) should correspond to the order of their significance (
${\tilde{\chi }_{\kappa /(\kappa +1)}}$), as suggested by Phase-ii.
Condition 2.
The final values of the weight coefficients must meet the transitivity principle in addition to the requirement stated in expression (
3), that is
${\tilde{\chi }_{\kappa /(\kappa +1)}}\otimes {\tilde{\chi }_{(\kappa +1)/(\kappa +2)}}={\tilde{\chi }_{\kappa /(\kappa +2)}}$, i.e.
$\frac{{\tilde{y}_{\kappa }}}{{\tilde{y}_{\kappa +1}}}\otimes \frac{{\tilde{y}_{\kappa +1}}}{{\tilde{y}_{\kappa +2}}}=\frac{{\tilde{y}_{\kappa }}}{{\tilde{y}_{\kappa +2}}}$. Consequently, the following additional requirement is met by the weight coefficients’ final values (shown in expression (
5)):
Only when the transitivity between the weight coefficients is fully satisfied does the minimum DMC (deviations from the maximum consistency), i.e. $\eta =0$, get satisfied. Therefore, it can be concluded that $\frac{{\tilde{y}_{\kappa }}}{{\tilde{y}_{\kappa +1}}}-{\tilde{\chi }_{\kappa /(\kappa +1)}}=0$, as well as $\frac{{\tilde{y}_{\kappa }}}{{\tilde{y}_{\kappa +2}}}-{\tilde{\chi }_{\kappa /(\kappa +1)}}\otimes {\tilde{\chi }_{(\kappa +1)/(\kappa +2)}}=0$. The DMC for these weight coefficient values is $\eta =0$. Finding the values of the weight coefficients of criteria ${({\tilde{y}_{1}},{\tilde{y}_{2}},\dots ,{\tilde{y}_{n}})^{T}}$ that meet the requirement that $|\frac{{\tilde{y}_{\kappa }}}{{\tilde{y}_{\kappa +1}}}-{\tilde{\chi }_{\kappa /(\kappa +1)}}|\leqslant \eta $ and $|\frac{{\tilde{y}_{\kappa }}}{{\tilde{y}_{\kappa +2}}}-{\tilde{\chi }_{\kappa /(\kappa +1)}}\otimes {\tilde{\chi }_{(\kappa +1)/(\kappa +2)}}|\leqslant \eta $ with the minimization of value η are necessary in order to meet these requirements.
The final nonlinear model for identifying the best fuzzy values for the assessment criteria’s weight coefficients can be set to
${({\tilde{y}_{1}},{\tilde{y}_{2}},\dots ,{\tilde{y}_{n}})^{T}}$ based on the parameters specified.
where
${\tilde{y}_{r}}=({y_{r}^{{t_{1}}}},{y_{r}^{{t_{2}}}},{y_{r}^{{t_{3}}}},{y_{r}^{{t_{4}}}})$ and
${\tilde{\chi }_{\kappa /(\kappa +1)}}=({\chi _{\kappa /(\kappa +1)}^{{t_{1}}}},{\chi _{\kappa /(\kappa +1)}^{{t_{2}}}},{\chi _{\kappa /(\kappa +1)}^{{t_{3}}}},{\chi _{\kappa /(\kappa +1)}^{{t_{4}}}})$.
The requirement that
$\frac{{\tilde{y}_{\kappa }}}{{\tilde{y}_{\kappa +1}}}-{\tilde{\chi }_{\kappa /(\kappa +1)}}=0$, as well as
$\frac{{\tilde{y}_{\kappa }}}{{\tilde{y}_{\kappa +2}}}-{\tilde{\chi }_{\kappa /(\kappa +1)}}\otimes {\tilde{\chi }_{(\kappa +1)/(\kappa +2)}}=0$ meet must be met in order to attain the highest consistency. Thus, a fuzzy linear model, Eq. (
7), can be created from the model provided by Eq. (
6). If it is solved, the ideal fuzzy values of the weight coefficients are
${({\tilde{y}_{1}},{\tilde{y}_{2}},\dots ,{\tilde{y}_{n}})^{T}}$.
where
${\tilde{y}_{r}}=({y_{r}^{{t_{1}}}},{y_{r}^{{t_{2}}}},{y_{r}^{{t_{3}}}},{y_{r}^{{t_{4}}}})$ and
${\tilde{\chi }_{\kappa /(\kappa +1)}}=({\chi _{\kappa /(\kappa +1)}^{{t_{1}}}},{\chi _{\kappa /(\kappa +1)}^{{t_{2}}}},{\chi _{\kappa /(\kappa +1)}^{{t_{3}}}},{\chi _{\kappa /(\kappa +1)}^{{t_{4}}}})$.
Transform optimal weights
${(\tilde{y}{\ast _{1}},\tilde{y}{\ast _{2}},\dots ,\tilde{y}{\ast _{n}})^{T}}$ in which
$\tilde{y}{\ast _{r}}=({y_{r}^{{t_{1}}\ast }},{y_{r}^{{t_{2}}\ast }},{y_{r}^{{t_{3}}\ast }},{y_{r}^{{t_{4}}\ast }})$ (for all
$r=1(1)n$) into crisp value by making use of Eq. (
8).
Model-II: In this model, we discuss how to determine the weights of an alternative with the help of Neutrosophic-TOPSIS.
Consider the set of alternatives $U=\{{u_{i}}:i=1(1)m\}$, $i\geqslant 1$ and $F=\{{\xi _{r}}:r=1(1)n\}$, $r\geqslant 2$ is the set of attributes with weights $R(\tilde{y}{\ast _{r}})$, $r=1(1)n$ respectively.
Decision-makers assign ratings to the ${u_{i}},i=1(1)m$ alternatives based on the attributes ${\xi _{r}},r=1(1)n$, which are represented using an SVNN. Let’s assume the rating for the ${r^{th}}$ attribute concerning the ${i^{th}}$ alternative is presented as follows:
${u_{ir}^{\ast }}=({\xi _{r}},{T_{{u_{i}}}}({\xi _{r}}),{I_{{u_{i}}}}({\xi _{r}}),{F_{{u_{i}}}}({\xi _{r}}))$, $i=1(1)m$, $r=1(1)n$, where $0\leqslant {T_{{u_{i}}}}({\xi _{r}})+{I_{{u_{i}}}}({\xi _{r}})+{F_{{u_{i}}}}({\xi _{r}})\leqslant 3$. Here, $({T_{ir}},{I_{ir}},{F_{ir}})$ is denoted as an SVNN ${u_{ir}^{\ast }}$,($i=1(1)m$ and $r=1(1)n$), where r represents the number of attributes and i represents the number of alternatives. Derive the decision matrix based on the ratings: ${\Omega ^{\ast }}={[{u_{ir}^{\ast }}]_{m\times n}}$
The TOPSIS approach has been summed up as outlined below:
Step 1: The score-matrix $\Omega ={[{u_{ir}}]_{m\times n}}$,($i=1(1)m$ and $r=1(1)n$) is obtained from the decision matrix ${\Omega ^{\ast }}={[{u_{ir}^{\ast }}]_{m\times n}}$ utilizing the methods outlined in the preceding section: i.e. ${u_{ir}}={S_{1}}({u_{ir}^{\ast }})$.
Step 2: Evaluation of the normalized decision matrix
$T={[{t_{ir}}]_{m\times n}}$ using Eq. (
9).
Step 3: Figure out the $\theta ={[{\lambda _{ir}}]_{m\times n}}$ weighted normalized decision matrix, where ${\lambda _{ir}}=R(\tilde{y}{\ast _{r}})\otimes {t_{ir}}$, $i=1(1)m$ and $r=1(1)n$.
Step 4: Find the Neutrosophic Positive Ideal Solution (NPIS) and Neutrosophic Negative Ideal Solution (NNIS), which are degraded by
${\partial ^{+}}$, as well as
${\partial ^{-}}$, respectively.
Step 5: Use the following formulas (
10) and (
11) to determine the distance between each NPIS and NNIS option:
Step 6: Use formula (
12) to calculate each alternative’s performance score:
Step 7: Based on the performance scores, rank the options; they should be in ascending order. Eq. (
13) normalizes the performance score. The normalized performance score is used as a final weighting factor for several GMPE equations in this study.
Putting the value of
${p_{i}}$ in Eq. (
1) to enhance the accuracy and reliability of Peak Ground Acceleration (PGA) estimates.
4 Application of the Model
The objective of the present study is the enhanced seismic hazard evaluation of Northeast India. The application of the proposed model is divided into three parts. Section
4.1 discusses the selection of parameters, Section
4.2 covers the application of MCDM, and Section
4.3 discusses the computational process of the final PGA.
4.1 Selection of Ground Motion Prediction Equation (GMPE)
Ground motion models are designed with a regional perspective, considering distinct tectonic features such as subduction zones, intraplate settings, and plate boundary interactions. These models rely on accelerogram recordings collected from various distances and magnitudes across the study region. A regression analysis is then conducted on peak ground acceleration (PGA) values, incorporating both magnitude and distance parameters to minimize variability and derive region-specific coefficients for different spectral periods. Based on seismic activity and tectonic characteristics, the study area is categorized into two primary zones: shallow crustal intraplate/interplate regions and subduction-related in-slab/interface regions. Accordingly, separate attenuation models are necessary to represent ground motion behaviour accurately in each category.
Several researchers have developed ground motion attenuation relationships specific to different regions of India. Bajaj and Anbazhagan (
2019) introduced an equation tailored to the Himalayan region, calibrated for earthquakes ranging from magnitude 4 to 9 and rupture distances spanning 10–750 km. This model was formulated using an extensive dataset of 4,940 recorded seismic events, facilitating a comprehensive assessment of regional attenuation characteristics. Likewise, Nath
et al. (
2012) derived a ground motion model for Northeast India, utilizing data from 13 earthquakes with magnitudes between Mw 4.8 and Mw 8.1, recorded at distances extending up to 100 km. Atkinson and Boore (
2003) formulated a GMPE for stable continental regions in eastern North America, which, despite its original focus, can be adapted for the Bengal Basin due to its comparable tectonic stability. Raghu Kanth and Iyengar (
2007) proposed a GMPE specifically for Peninsular India, estimating seismic ground motion parameters such as PGA. While developed for a different setting, its application to the Bengal Basin is feasible due to tectonic similarities. Additionally, Singh
et al. (
2016) devised a GMPE for Northeast India, with a focus on seismically active regions influenced by the Indo-Burmese Arc. Given the tectonic similarities between Tripura and the surrounding active zones, this GMPE is considered applicable to the study area, though local geological variations, including soil properties and site conditions, must be accounted for to ensure accurate ground motion predictions.
To validate the five selected attenuation models (Atkinson and Boore,
2003; Raghu Kanth and Iyengar,
2007; Nath
et al.,
2012; Singh
et al.,
2016; Bajaj and Anbazhagan,
2019), strong motion data was sourced from the Cosmos Virtual Data Centre (
http://db.cosmos-eq.org/). Seismic recordings from seven significant earthquakes occurring between 1987 and 1997, captured through the SMART-1 digital network covering the Indo-Burma range and Northeast India, were used for this validation.
Seismic recordings obtained from multiple monitoring stations were utilized to assess the accuracy of the selected ground motion prediction equations (GMPEs). A comparative analysis was performed using peak ground acceleration (PGA) values recorded at the rock level for the India-Bangladesh Border earthquake (1988-02-06, 14:50:45 UTC, Mw = 6), juxtaposing them with the predictions from the chosen GMPEs (Fig.
5). However, due to the proximity between the observed data and the modelled predictions (Fig.
5), along with inherent uncertainties in each equation, selecting the most suitable model presents a challenge. These epistemic uncertainties can be mitigated through the logic tree framework, which enables the incorporation of multiple models into the evaluation process.
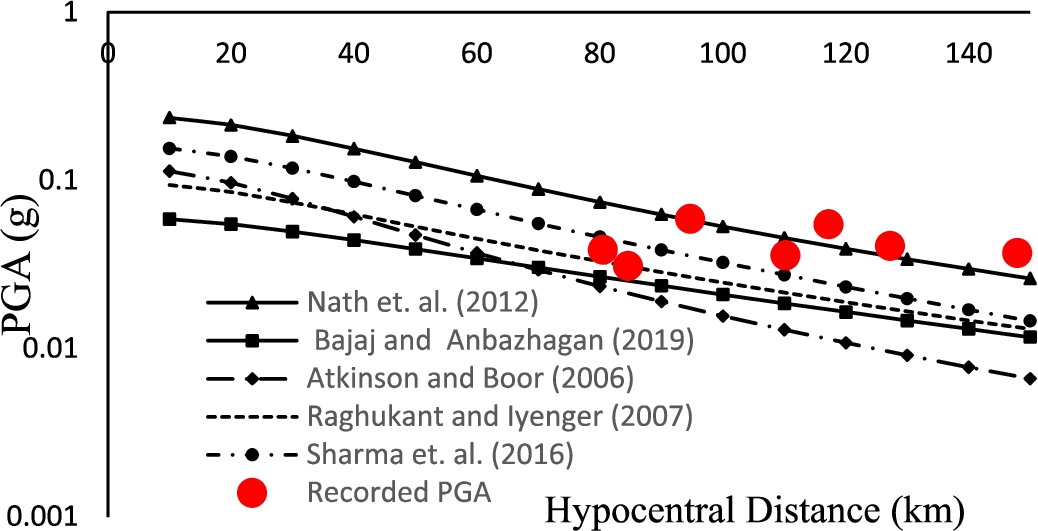
Fig. 5
Comparison of different GMPE with observed Ground Motion data of Mw = 6 on 1988-02-06 in India-Bangladesh Border.
A logic tree structure consists of branches and nodes, where each branch corresponds to a distinct model, and several branches merge at a common node. To refine the decision-making process, an enhanced hybrid trapezoidal neutrosophic-based approach, referred to as the Integrated TrF-FUCOM- Neutrosophic-TOPSIS method, is applied. This technique assigns weightage to each model branch based on its associated uncertainties, ensuring a more robust and objective evaluation. The incorporation of this advanced methodology aids in addressing the uncertainties linked to seismic hazard assessments. Further details regarding the GMPE equations utilized in this study are provided in Table
4. Figure
6 depicts the decision hierarchy in this case.
Table 4
Ground motion attenuation equation used in the study.
|
Authors |
Applicable magnitude |
Applicable distance |
Standard form of equation |
Coefficient for zero period |
| GMPE -1 |
Atkinson and Boore (2003) |
4.5–8 |
1–1000 |
$\operatorname{Log}Y={C_{1}}+{C_{2}}M+{C_{3}}h+{C_{4}}R-g\operatorname{Log}R$ |
${C_{1}}=-0.0471$ |
|
|
|
${C_{2}}=0.6909$ |
|
|
|
$g={10^{(0.301-0.01M)\log (R)}}$ |
${C_{3}}=-0.0113$ |
|
|
|
|
|
${C_{4}}=-0.00202$ |
| GMPE-2 |
Raghu Kanth and Iyengar (2007) |
4–8 |
1–300 |
$\ln Y={C_{1}}+{C_{2}}(M-6)+{C_{3}}{(M-6)^{2}}-\ln R-{C_{4}}R$ |
${C_{1}}=1.6858$ |
|
|
|
${C_{2}}=0.9241$ |
|
|
|
|
${C_{3}}=-0.0760$ |
|
|
|
|
${C_{4}}=-0.0057$ |
| GMPE-3 |
Nath et al. (2012) |
4.6–8.1 |
$\leqslant 100$ |
$\ln Y={C_{1}}+{C_{2}}+{C_{3}}{(10-M)^{3}}+{C_{4}}+\ln ({r_{rup}}+\exp ({C_{6}}M))$ |
${C_{1}}=9.143$ |
|
|
|
${C_{2}}=0.2470$ |
|
|
|
|
${C_{3}}=-0.0140$ |
|
|
|
|
|
${C_{4}}=-2.67$ |
|
|
|
|
|
${C_{5}}=32.9458$ |
|
|
|
|
|
${C_{6}}=0.0663$ |
| GMPE-4 |
Singh et al. (2016) |
4–8.5 |
1–300 |
$\ln Y={C_{1}}+{C_{2}}(M-6)+{C_{3}}{(M-6)^{2}}-\ln R-{C_{4}}R$ |
${C_{1}}=2.082$ |
|
|
|
${C_{2}}=0.8569$ |
|
|
|
|
|
${C_{3}}=-0.0472$ |
|
|
|
|
|
${C_{4}}=-0.0091$ |
| GMPE-5 |
Bajaj and Anbazhagan (2019) |
4.0–9.0 |
1–750 |
$\ln Y={a_{1}}+{a_{2}}(M-6)+{a_{3}}{(9-M)^{2}}-{a_{4}}\ln R-{a_{m}}\ln R(M-6)+{a_{7}}R$ |
${a_{1}}=1.071$ |
|
|
|
${a_{2}}=-0.257$ |
|
|
|
${a_{3}}=-0.184$ |
|
|
|
|
|
${a_{4}}=-0.479$ |
|
|
|
|
|
${a_{m}}=0.078$ |
|
|
|
|
|
${a_{7}}=-0.0085$ |
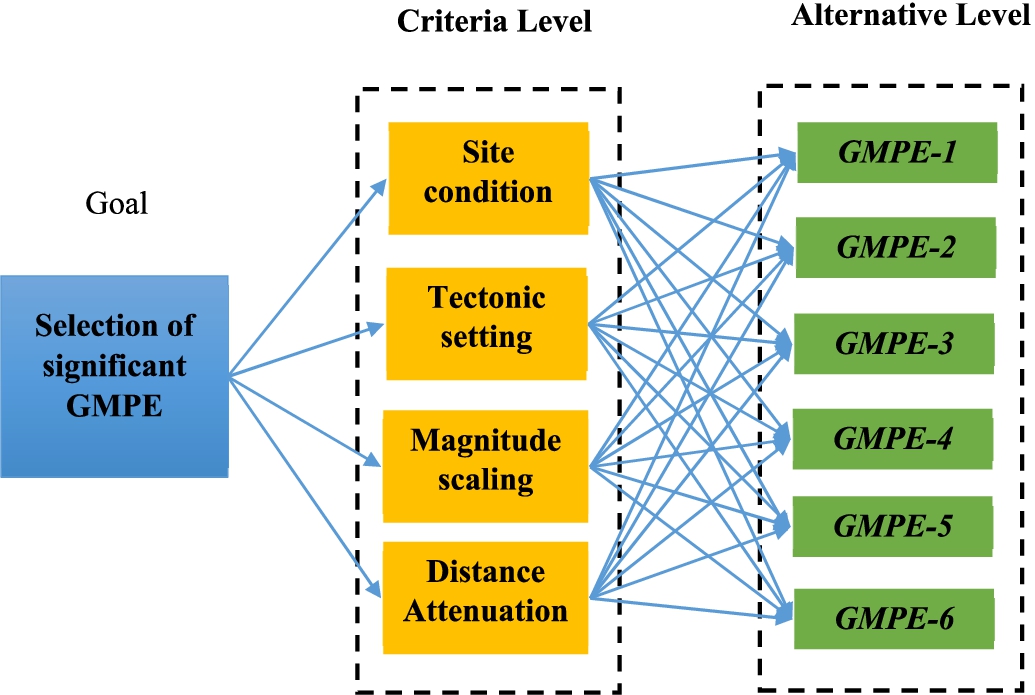
Fig. 6
Decision Hierarchy.
4.2 Application of MCDM
The objective of this study is to develop an improved Seismic Hazard Assessment of Northeast India framework by integrating a fuzzy MCDM technique. From the case study it is clear that in the present study consider six sites, namely Bengal Basin, Indo-Burma, Shillong Plateau, Eastern Himalaya, Mishmi Thrust and Naga Thrust. The behaviour considering criteria and alternatives are changed as per Seismotectonic setting. So, in the present study developed 12 models to determine the score value of alternatives. In this study $\{\textit{Site condition}({\xi _{1}}),\textit{Tectonic setting}({\xi _{2}}),\textit{Magnitude scaling}({\xi _{3}}),\textit{Distance Atten-}\textit{uation}({\xi _{4}})\}$ consider as a set of criteria and $\{\textit{GMPE}-4({u_{1}}),\textit{GMPE}-3({u_{3}}),\textit{GMPE}-4({u_{1}}),\textit{GMPE}-1({u_{4}}),\textit{GMPE}-5({u_{5}})\}$ is consider as a set of alternative.
Model-I: Determine the weights of $\{{\xi _{1}},{\xi _{2}},{\xi _{3}},{\xi _{4}}\}$ for the location Bengal Basin using TrF-FUCOM.
Model-II: Determine the weights of $\{{\xi _{1}},{\xi _{2}},{\xi _{3}},{\xi _{4}}\}$ for the location Indo-Burma using TrF-FUCOM.
Model-III: Determine the weights of $\{{\xi _{1}},{\xi _{2}},{\xi _{3}},{\xi _{4}}\}$ for the location Shillong Plateau using TrF-FUCOM.
Model-IV: Determine the weights of $\{{\xi _{1}},{\xi _{2}},{\xi _{3}},{\xi _{4}}\}$ for the location Eastern Himalaya using TrF-FUCOM.
Model-V: Determine the weights of $\{{\xi _{1}},{\xi _{2}},{\xi _{3}},{\xi _{4}}\}$ for the location Mishmi Thrust using TrF-FUCOM.
Model-VI: Determine the weights of $\{{\xi _{1}},{\xi _{2}},{\xi _{3}},{\xi _{4}}\}$ for the location Naga Thrust using TrF-FUCOM.
Model-VII: Determine the score value of $\{{u_{1}},{u_{2}},{u_{3}},{u_{4}},{u_{5}},{u_{6}}\}$ for the location Bengal Basin using Model I and Neutrosophic-TOPSIS.
Model-VIII: Determine the score value of $\{{u_{1}},{u_{2}},{u_{3}},{u_{4}},{u_{5}},{u_{6}}\}$ for the location Indo-Burma using Model II and Neutrosophic-TOPSIS.
Model-IX: Determine the score value of $\{{u_{1}},{u_{2}},{u_{3}},{u_{4}},{u_{5}},{u_{6}}\}$ for the location Shillong Plateau using Model III and Neutrosophic-TOPSIS.
Model-X: Determine the score value of $\{{u_{1}},{u_{2}},{u_{3}},{u_{4}},{u_{5}},{u_{6}}\}$ for the location Eastern Himalaya using Model IV and Neutrosophic-TOPSIS.
Model-XI: Determine the score value of $\{{u_{1}},{u_{2}},{u_{3}},{u_{4}},{u_{5}},{u_{6}}\}$ for the location Mishmi Thrust using Model V and Neutrosophic-TOPSIS.
Model-XII: Determine the score value of $\{{u_{1}},{u_{2}},{u_{3}},{u_{4}},{u_{5}},{u_{6}}\}$ for the location Naga Thrust using Model VI and Neutrosophic-TOPSIS.
4.2.1 Evaluation Process of Criteria Weights
Model III is used to determine the criteria weights for Shillong Plateau.
Table 5
TrF transformations of evaluations.
| Criteria |
${u_{2}}$ |
${u_{1}}$ |
${u_{3}}$ |
${u_{4}}$ |
| Important fuzzy measures of trapezoidal shape |
$(1,1,1,1)$ |
$(1,1.5,2.5,3)$ |
$(1,1.5,2.5,3)$ |
$(2,2.5,3.5,4)$ |
The initial stage involves establishing the sequence of criteria. Then assign the TrF transformations of evaluations for ordering criteria with the help of Table
1 shown in Table
5.
Hence, the definition of a vector representing comparative significance is as follows:
$\tilde{\chi }=((1,1.5,2.5,3),(0.33,0.6,1.67,3),(0.67,1,2.33,4))$
The constraints arising from the transitivity requirement of the relation are as follows:
Model (
14) was developed to ascertain the optimal values of weight coefficients for the dimensions, incorporating the defined constraints.
Eq. (
14) introduces a fuzzy linear model, which can be resolved to ascertain the optimal values of the criteria.
The fuzzy linear model, as outlined in Eq. (
14), functions as a tool for identifying optimal criteria values. Through the utilization of the Excel solver for linear programming, this model (
14) calculates weight coefficients for the criteria. The weights for TrF criteria are illustrated in Table
6. The defuzzified value of the criteria is determined using Eq. (
8), as depicted in the last column of Table 6.
Table 6
Weights of criteria.
|
${t_{1}}$ |
${t_{2}}$ |
${t_{3}}$ |
${t_{4}}$ |
Weights (defuzzified value) |
| η |
0.116 |
0.116 |
0.116 |
0.116 |
0.116 |
| ${\xi _{1}}$ |
0.184 |
0.199 |
0.199 |
0.298 |
0.213 |
| ${\xi _{2}}$ |
0.182 |
0.182 |
0.613 |
0.667 |
0.407 |
| ${\xi _{3}}$ |
0.087 |
0.175 |
0.254 |
0.254 |
0.200 |
| ${\xi _{4}}$ |
0.035 |
0.081 |
0.291 |
0.305 |
0.180 |
Table 7
Weights of criteria of for different seismotectonic region.
| Model (location) |
Measurement |
Site condition $({\xi _{1}})$
|
Tectonic setting $({\xi _{2}})$
|
Magnitude scaling $({\xi _{3}})$
|
Distance attenuation $({\xi _{4}})$
|
η (Objective function value) |
| Model-I (Bengal Basin) |
Fuzzy measures |
$(1,1,1,1)$ |
$(1,1,1,1)$ |
$(1,1.5,2.5,3)$ |
$(2,2.5,3.5,4)$ |
$(0.068,0.068,0.068,0.068)$ |
| Weights |
0.331 |
0.331 |
0.180 |
0.158 |
0.068 |
| Rank |
1 |
1 |
2 |
3 |
|
| Model-II (Indo-Burma) |
Fuzzy measures |
$(2,2.5,3.5,4)$ |
$(1,1,1,1)$ |
$(1,1,1,1)$ |
$(1,1.5,2.5,3)$ |
$(0.068,0.068,0.068,0.068)$ |
| Weights |
0.158 |
0.331 |
0.331 |
0.180 |
0.068 |
| Rank |
3 |
1 |
1 |
2 |
|
| Model-III (Shillong Plateau) |
Fuzzy measures |
$(1,1.5,2.5,3)$ |
$(1,1,1,1)$ |
$(1,1.5,2.5,3)$ |
$(2,2.5,3.5,4)$ |
$(0.116,0.116,0.116,0.116)$ |
| Weights |
0.213 |
0.407 |
0.200 |
0.180 |
0.116 |
| Rank |
2 |
1 |
2 |
3 |
|
| Model-IV (Eastern Himalaya) |
Fuzzy measures |
$(2,2.5,3.5,4)$ |
$(1,1,1,1)$ |
$(1,1,1,1)$ |
$(1,1.5,2.5,3)$ |
$(0.068,0.068,0.068,0.068)$ |
| Weights |
0.158 |
0.331 |
0.331 |
0.180 |
0.068 |
| Rank |
3 |
1 |
1 |
2 |
|
| Model-V (Mishmi Thrust) |
Fuzzy measures |
$(2,2.5,3.5,4)$ |
$(1,1,1,1)$ |
$(1,1,1,1)$ |
$(1,1.5,2.5,3)$ |
$(0.068,0.068,0.068,0.068)$ |
| Weights |
0.158 |
0.331 |
0.331 |
0.180 |
0.068 |
| Rank |
3 |
1 |
1 |
2 |
|
| Model-VI (Naga Thrust) |
Fuzzy measures |
$(2,2.5,3.5,4)$ |
$(1,1,1,1)$ |
$(1,1,1,1)$ |
$(1,1.5,2.5,3)$ |
$(0.068,0.068,0.068,0.068)$ |
| Weights |
0.158 |
0.331 |
0.331 |
0.180 |
0.068 |
| Rank |
3 |
1 |
1 |
2 |
|
In the similar process in this study evaluate the weights of criteria for different location shown in Table
7.
4.2.2 Evaluation of Score Value of Alternative
Model-IX is used the score value of the considering alternative (GMPE). The decision maker utilizes SVNNs to assess alternatives based on their attributes, leading to the construction of the decision matrix-1.
Matrix-1: Decision Matrix
Matrix Ω is translated by translating the entries of each entry. For each entry in matrix Ω, add 0.01 to all the components, represented in Matrix-2.
Matrix-2: Translation of Ω
The next step is to determine the score matrix using the score function. Matrix-3 represents the score matrix denoted by
$\Omega \ast $. The score value of
Matrix-3: Score Matrix
Determine the Normalized Decision Matrix using Eq. (
8) on matrix
$\Omega \ast $. As shown in matrix-4, the Normalized Decision Matrix decision matrix is denoted by
T.
Matrix-4: Decision Matrix with Normalization
Determine the weighted normalized decision matrix after determining the weights of the criteria. Multiply each criteria weight with the element of the corresponding row of matrix
T to form the matrix. The weighted normalized decision matrix is denoted by matrix
θ and is represented by the matrix-5.
Matrix-5: Weighted Normalized Decision Matrix
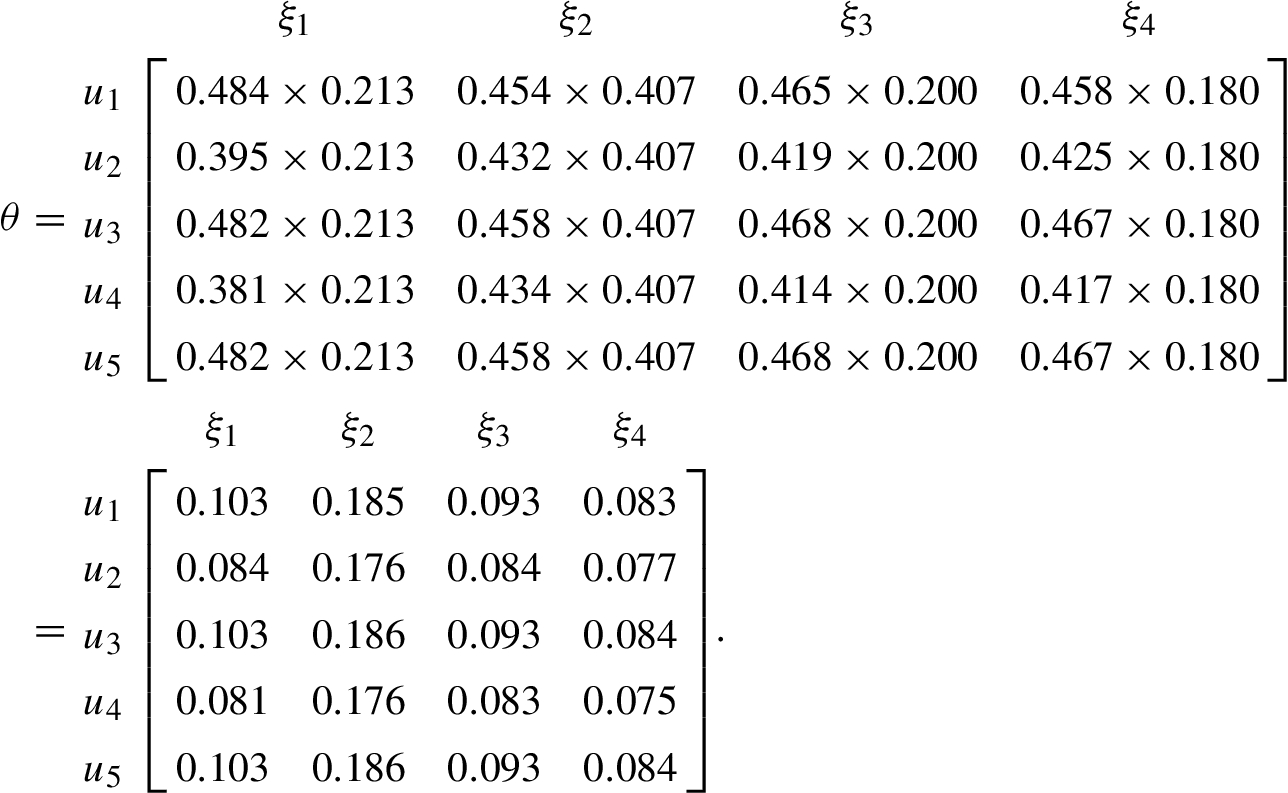
Next, determine NPIS and NNIS using
${\lambda _{r}^{+}}={\max _{r}}{\lambda _{ir}}$,
$r=1(1)5$ and
${\lambda _{r}^{-}}={\min _{r}}{\lambda _{ir}}$,
$r=1(1)5$ respectively.
So,
Next, compute the distance between each alternative between NPIS and NNIS using the formulas (
9) and (
10). Table
8 illustrates the distance between each alternative between NPIS and NNIS.
Table 8
NPIS and NNIS distances from each alternative.
|
Value |
|
Value |
| ${\rho _{1}^{+}}$ |
0.0024 |
${\rho _{1}^{-}}$ |
0.0266 |
| ${\rho _{2}^{+}}$ |
0.0248 |
${\rho _{2}^{-}}$ |
0.0034 |
| ${\rho _{3}^{+}}$ |
0.0003 |
${\rho _{3}^{-}}$ |
0.0276 |
| ${\rho _{4}^{+}}$ |
0.0276 |
${\rho _{4}^{-}}$ |
0.0006 |
| ${\rho _{5}^{+}}$ |
0.0003 |
${\rho _{5}^{-}}$ |
0.0276 |
Table 9
Weights to various GMPEs for PGA computation across different seismotectonic regions (alternative level).
| GMPE |
Site |
Tectonic |
Magnitude |
Distance |
Normalised performance scores |
Rank |
| Model-VII (Bengal Basin) |
| GMPE-1 |
0.7 |
0.2 |
0.1 |
0.7 |
0.15 |
0.1 |
0.75 |
0.2 |
0.05 |
0.7 |
0.2 |
0.1 |
0.067 |
5 |
| GMPE-2 |
0.8 |
0.1 |
0.1 |
0.75 |
0.15 |
0.1 |
0.85 |
0.1 |
0.05 |
0.85 |
0.1 |
0.05 |
0.198 |
3 |
| GMPE-3 |
0.95 |
0.05 |
0.05 |
0.85 |
0.08 |
0.07 |
0.95 |
0.03 |
0.02 |
0.9 |
0.05 |
0.05 |
0.310 |
2 |
| GMPE-4 |
0.75 |
0.15 |
0.1 |
0.7 |
0.2 |
0.1 |
0.8 |
0.15 |
0.05 |
0.75 |
0.15 |
0.1 |
0.098 |
4 |
| GMPE-5 |
0.9 |
0.05 |
0.05 |
0.9 |
0.05 |
0.05 |
0.92 |
0.05 |
0.03 |
0.88 |
0.07 |
0.05 |
0.328 |
1 |
| Model-VIII (Indo Burma Region) |
| GMPE-1 |
0.88 |
0.07 |
0.05 |
0.95 |
0.03 |
0.02 |
0.92 |
0.05 |
0.03 |
0.9 |
0.05 |
0.05 |
0.310 |
1 |
| GMPE-2 |
0.7 |
0.2 |
0.1 |
0.8 |
0.1 |
0.05 |
0.8 |
0.15 |
0.05 |
0.75 |
0.1 |
0.1 |
0.035 |
5 |
| GMPE-3 |
0.8 |
0.1 |
0.1 |
0.9 |
0.05 |
0.05 |
0.85 |
0.1 |
0.05 |
0.9 |
0.05 |
0.1 |
0.218 |
3 |
| GMPE-4 |
0.75 |
0.15 |
0.1 |
0.85 |
0.1 |
0.05 |
0.85 |
0.1 |
0.05 |
0.8 |
0.15 |
0.1 |
0.132 |
4 |
| GMPE-5 |
0.85 |
0.1 |
0.05 |
0.95 |
0.03 |
0.02 |
0.95 |
0.03 |
0.02 |
0.9 |
0.05 |
0.05 |
0.306 |
2 |
| Model-IX (Shillong Plateau) |
| GMPE-1 |
0.8 |
0.1 |
0.1 |
0.85 |
0.15 |
0.05 |
0.8 |
0.1 |
0.1 |
0.8 |
0.1 |
0.1 |
0.007 |
4 |
| GMPE-2 |
0.8 |
0.15 |
0.05 |
0.85 |
0.1 |
0.05 |
0.8 |
0.15 |
0.05 |
0.8 |
0.1 |
0.1 |
0.040 |
3 |
| GMPE-3 |
0.9 |
0.05 |
0.05 |
0.95 |
0.03 |
0.02 |
0.9 |
0.05 |
0.05 |
0.9 |
0.05 |
0.05 |
0.325 |
1 |
| GMPE-4 |
0.9 |
0.05 |
0.05 |
0.92 |
0.05 |
0.03 |
0.9 |
0.05 |
0.03 |
0.88 |
0.07 |
0.05 |
0.302 |
2 |
| GMPE-5 |
0.85 |
0.1 |
0.05 |
0.9 |
0.05 |
0.05 |
0.85 |
0.1 |
0.05 |
0.85 |
0.1 |
0.05 |
0.325 |
1 |
| Model-X (Eastern Himalaya) |
| GMPE-1 |
0.7 |
0.2 |
0.1 |
0.85 |
0.1 |
0.05 |
0.85 |
0.1 |
0.05 |
0.8 |
0.1 |
0.05 |
0.022 |
4 |
| GMPE-2 |
0.7 |
0.1 |
0.1 |
0.8 |
0.1 |
0.05 |
0.8 |
0.1 |
0.05 |
0.75 |
0.1 |
0.05 |
0.140 |
3 |
| GMPE-3 |
0.8 |
0.1 |
0.05 |
0.9 |
0.05 |
0.03 |
0.9 |
0.05 |
0.03 |
0.88 |
0.07 |
0.05 |
0.267 |
2 |
| GMPE-4 |
0.85 |
0.05 |
0.03 |
0.95 |
0.03 |
0.02 |
0.95 |
0.03 |
0.02 |
0.9 |
0.1 |
0.05 |
0.304 |
1 |
| GMPE-5 |
0.8 |
0.1 |
0.05 |
0.9 |
0.05 |
0.03 |
0.9 |
0.05 |
0.03 |
0.88 |
0.07 |
0.05 |
0.267 |
2 |
| Model- XI (Mishmi Thrust) |
| GMPE-1 |
0.7 |
0.2 |
0.1 |
0.85 |
0.1 |
0.05 |
0.85 |
0.1 |
0.05 |
0.8 |
0.1 |
0.05 |
0.022 |
4 |
| GMPE-2 |
0.7 |
0.1 |
0.1 |
0.8 |
0.1 |
0.05 |
0.8 |
0.1 |
0.05 |
0.75 |
0.1 |
0.05 |
0.140 |
3 |
| GMPE-3 |
0.8 |
0.1 |
0.05 |
0.9 |
0.05 |
0.03 |
0.9 |
0.05 |
0.03 |
0.88 |
0.07 |
0.05 |
0.267 |
2 |
| GMPE-4 |
0.85 |
0.05 |
0.03 |
0.95 |
0.03 |
0.02 |
0.95 |
0.03 |
0.02 |
0.9 |
0.1 |
0.05 |
0.304 |
1 |
| GMPE-5 |
0.8 |
0.1 |
0.05 |
0.9 |
0.05 |
0.03 |
0.9 |
0.05 |
0.03 |
0.88 |
0.07 |
0.05 |
0.267 |
2 |
| Model-XII (Naga Thrust) |
| GMPE-1 |
0.7 |
0.2 |
0.1 |
0.85 |
0.1 |
0.05 |
0.85 |
0.1 |
0.05 |
0.8 |
0.1 |
0.05 |
0.022 |
4 |
| GMPE-2 |
0.7 |
0.1 |
0.1 |
0.8 |
0.1 |
0.05 |
0.8 |
0.1 |
0.05 |
0.75 |
0.1 |
0.05 |
0.140 |
3 |
| GMPE-3 |
0.8 |
0.1 |
0.05 |
0.9 |
0.05 |
0.03 |
0.9 |
0.05 |
0.03 |
0.88 |
0.07 |
0.05 |
0.267 |
2 |
| GMPE-4 |
0.85 |
0.05 |
0.03 |
0.95 |
0.03 |
0.02 |
0.95 |
0.03 |
0.02 |
0.9 |
0.1 |
0.05 |
0.304 |
1 |
| GMPE-5 |
0.8 |
0.1 |
0.05 |
0.9 |
0.05 |
0.03 |
0.9 |
0.05 |
0.03 |
0.88 |
0.07 |
0.05 |
0.267 |
2 |
Calculate the performance score for each alternative using the formula (
11). Table
9 displays the performance scores for each alternative in Model IX. Organize the alternatives in ascending order based on their performance scores and assign ranks accordingly.
Similar procedure of Model-IX in this present study calculates the score value of alternatives of different locations. Table
9 represent the results of Model-VII, VIII, IX, X, XI, XII. In this present study normalized performance scores are consider as weights of alternatives.
4.3 Computation of Final PGA
A grid of 0.1-degree x 0.1 degree (11.1 km x 11.1 km) was established to encompass the entire area of Tripura state. Relevant tectonic features that could generate significant ground motions in the vicinity were identified, as shown on the seismotectonic map (see Fig.
2a, b). The maximum earthquake magnitude for each seismic source was determined (refer to Table
4). Distances from each grid point to the corresponding seismic sources were calculated using ArcGIS 10.0 software (ESRI 2011). Ground motion prediction equations (attenuation models) (Table
9) were chosen based on the region’s tectonic characteristics and geology, utilizing magnitudes from the previous step and distances from the calculated data as inputs to estimate ground motion parameters. The magnitudes determined in Table
4 and the distances calculated from ArcGIS 10.0 software serve as inputs for these equations. Subsequently, the computed weightage (Table
9) for each GMPE model was applied to calculate the PGA for all sources using formula 1. The calculated PGA values for all the faults and lines in each scenario are gathered, and the seismic hazard is identified as the maximum ground motion value across all sources. The source responsible for the highest ground motion is designated as the controlling source. PGA has been computed at the centre of each grid points (grid size
$0.{1^{\circ }}\times 0.{1^{\circ }}$). A spatial DSHA map is generated for the entire Northeast India which shows the vulnerable regions in the Northeast.
5 Discussion of the Study
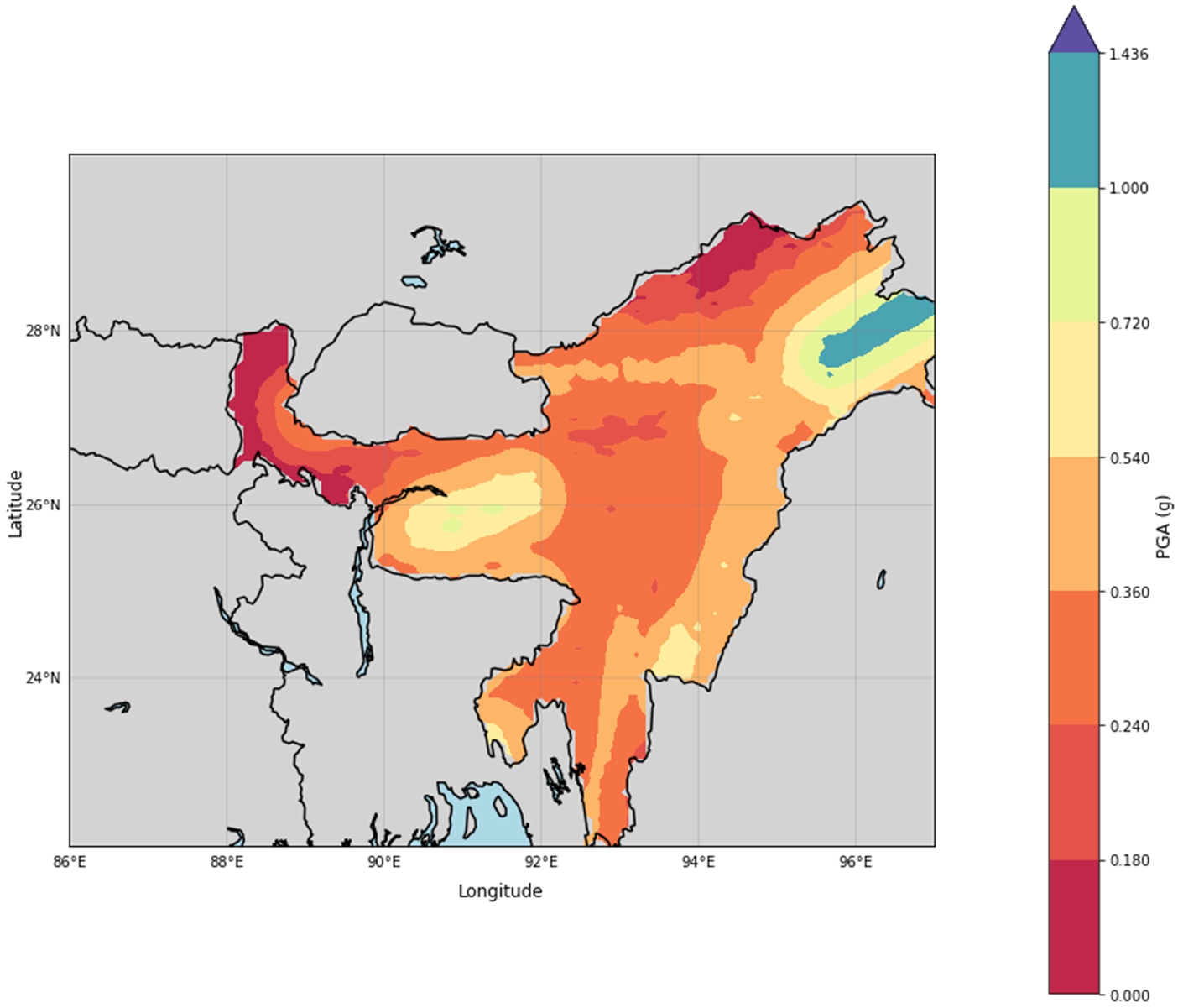
Fig. 7
PGA map of Northeast India.
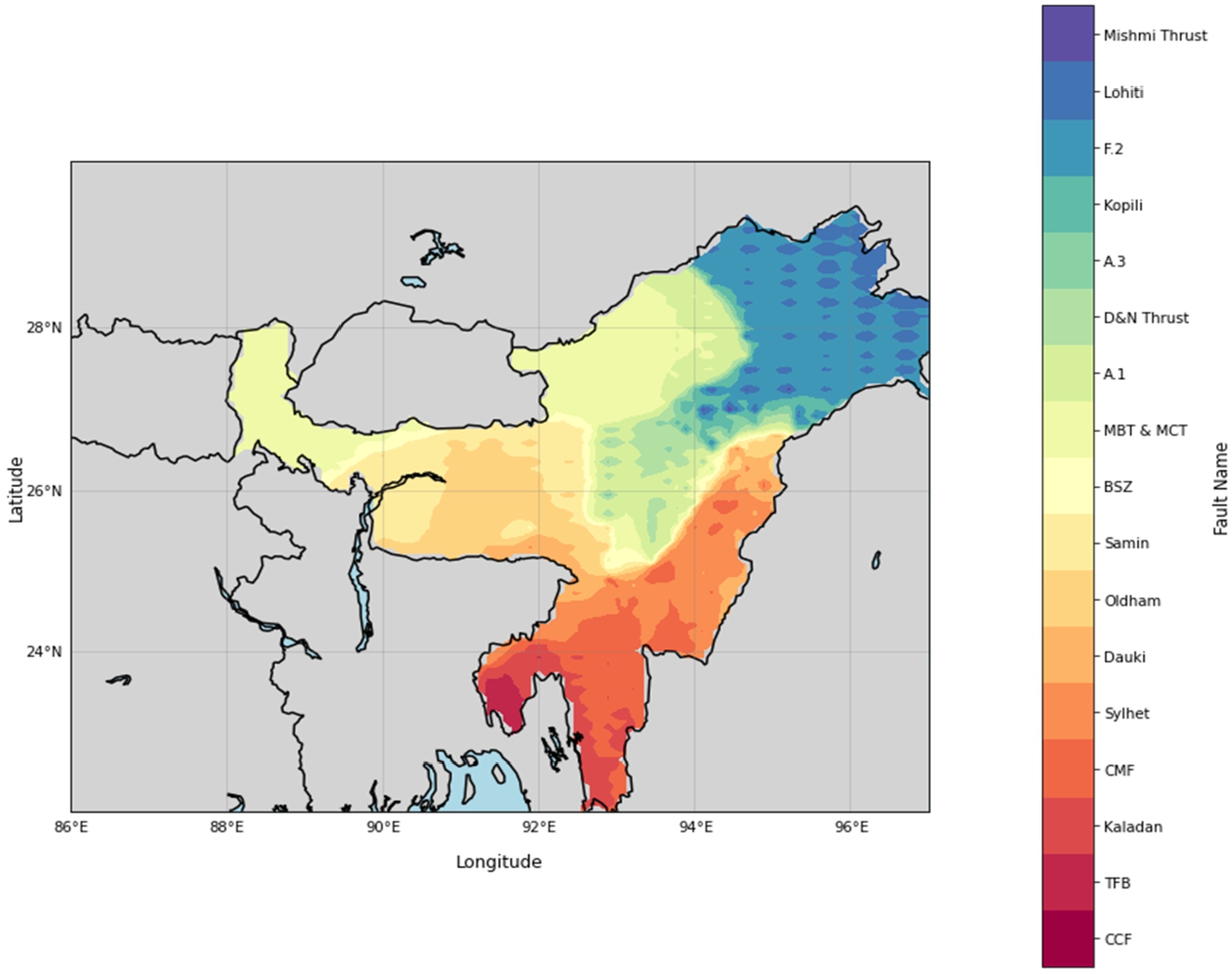
Fig. 8
Spatial map of controlling source across northeast India.
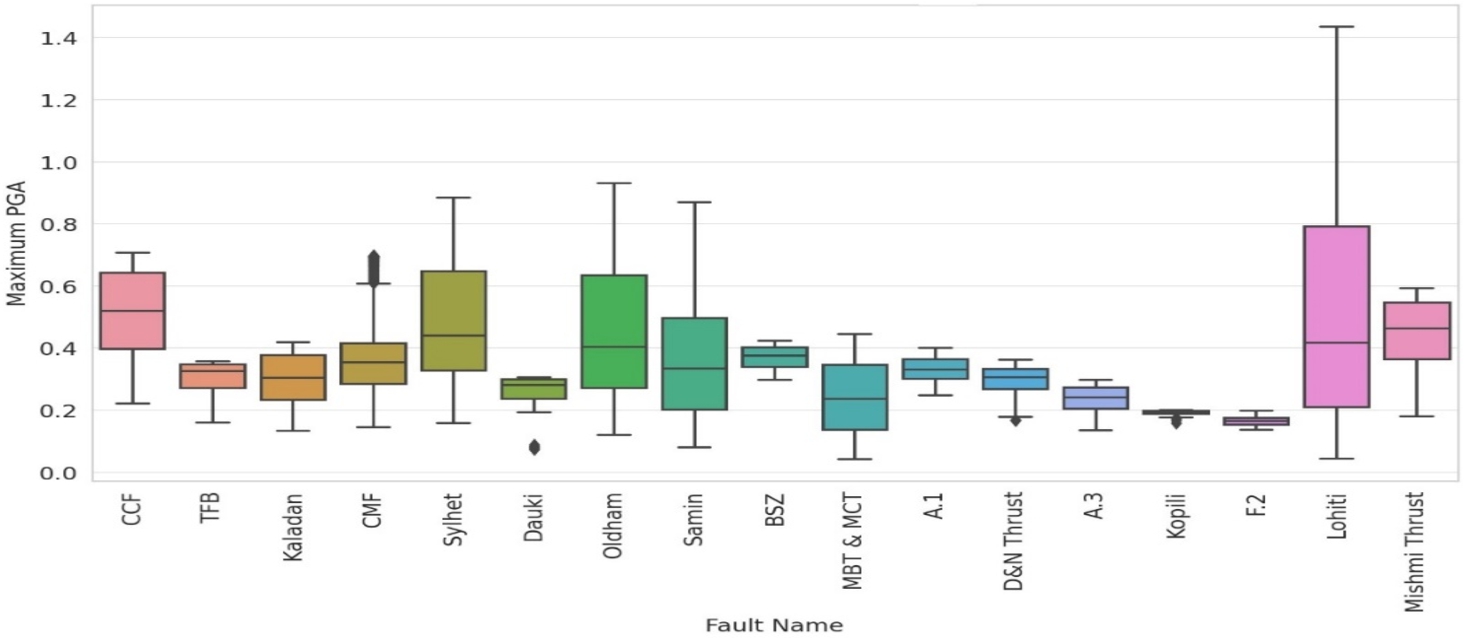
Fig. 9
Box plot of PGA from controlling source.
The results from Fig.
7, Fig.
8 and Fig.
9 provide a comprehensive understanding of the seismic hazard and tectonic behaviour of Northeast India, a region characterized by complex interactions between the Indian, Eurasian, and Burma Plates. Figure
7 represents PGA map of Northeast India with color-coded PGA ranges: (Dark Red: 0.000–0.180 g), (Reddish-Pink: 0.180–0.240 g), (Orange-Red: 0.240–0.360 g), (Orange: 0.360–0.540 g), (Yellow: 0.540–0.720 g), (Light Yellow: 0.720–1.000 g), (Light Blue: 1.000–1.435 g), (Dark Blue: >1.435 g). This figure highlights high PGA zones in the Mishmi Thrust (MT), with values up to 1.436 g, reflecting intense seismic activity due to thrust faulting. The Shillong Plateau (SP), influenced by the Oldham and Dauki Faults, exhibits elevated PGA values up to 0.96 g in Assam, consistent with its history of major earthquakes like the 1897 Great Assam Earthquake. Figure
8 illustrates the spatial distribution of dominant seismic sources across Northeast India, with fault colour codes as follows: Mishmi Thrust (Dark Purple), Lohit (Dark Blue), F2 (Blue), Kopili (Light Blue), A3 (Cyan), D&N Thrust (Light Green), A1 (Yellow-Green), MBT&MCT (Yellow), BSZ (Light Orange), Samim (Orange), Oldham (Reddish Orange), Dauki (Red), Sylhet (Dark Red), CMF (Deep Red), Kaladan (Darker Red), TFB (Brownish Red), and CCF (Dark Brown). The analysis reveals that MBT and MCT serve as the primary controlling sources in most parts of the Eastern Himalayan region, whereas the Lohit Fault dominates the Naga Trust Region, generating the highest recorded PGA of up to 1.43 g. The box plot (Fig.
9) illustrates the maximum PGA distribution across various faults, with the Lohit Fault exhibiting the highest observed PGA (∼1.43 g) and the Kopili Fault showing the lowest observed PGA. As we move to Bengal basin, it is clearly evident that CCF Fault, TFB Fault and Kaladan Fault are the controlling sources around this region which produce PGA up to 0.69 g in this region. So, a detailed discussion is required to understand the variations of PGA and their controlling source in the seven sister Northeastern States of India.
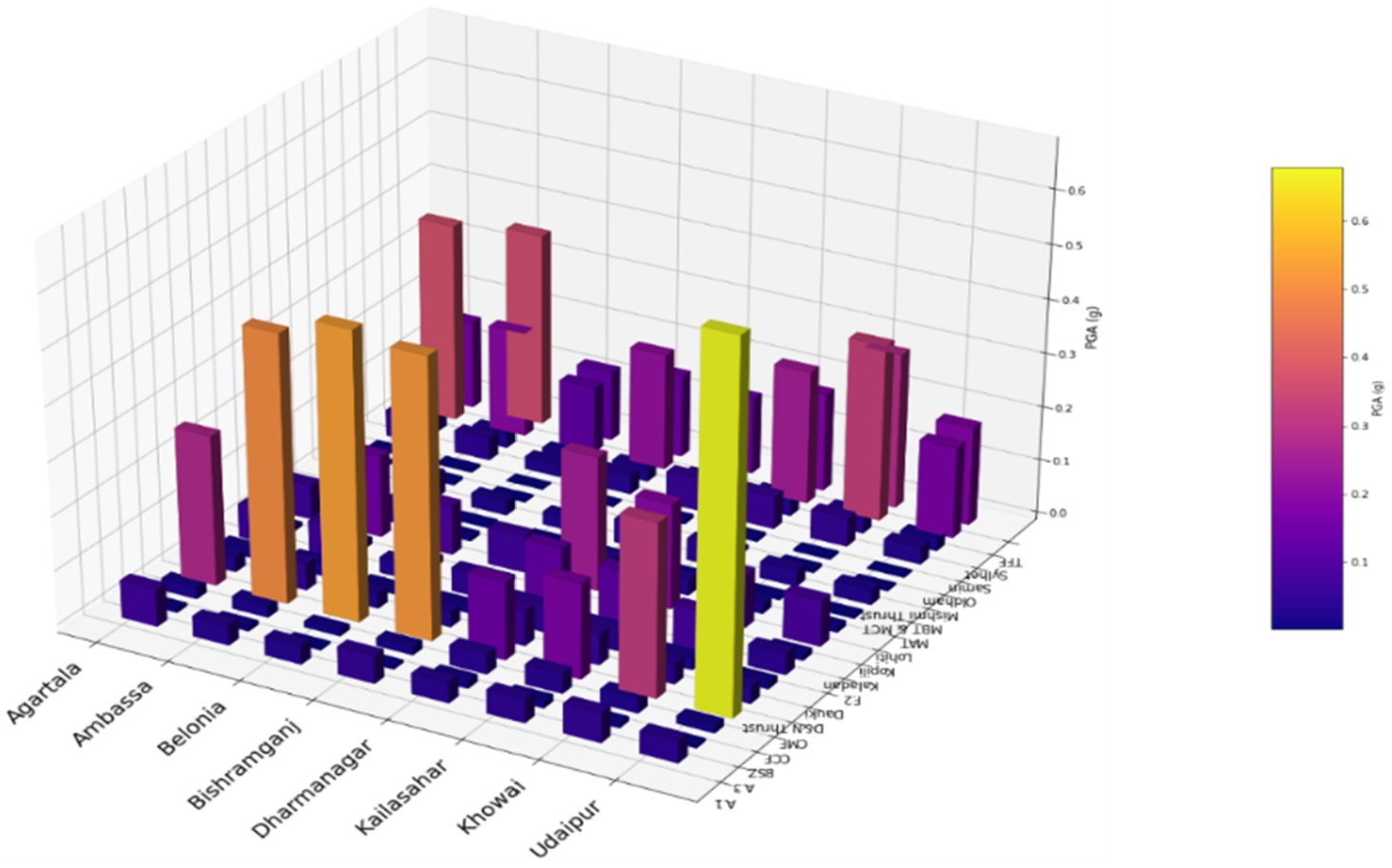
Fig. 10
Variation of PGA across all district headquarters of Tripura considering all seismic sources for their respective maximum earthquake magnitudes.
5.1 PGA across all district headquarters of Tripura
The DSHA (Deterministic Seismic Hazard Assessment) map for Northeast India, presented in Fig.
7, indicates a variation in Peak Ground Acceleration (PGA) values ranging from 0.21 g to 0.69 g. These values are considerably higher than the 0.36 g PGA specified in IS 1893-Part 1 (2002). This higher PGA scenario assumes that all local faults and lineaments are under critical stress, making them capable of triggering earthquakes. The IS 1893-Part 1 (2002) zonation map, based on historical earthquake data, is periodically revised to account for new seismic activity. Figure
10 illustrates the variation in PGA across eight district headquarters in Tripura, considering all seismic sources. Notably, Belonia, the headquarters of South Tripura District, exhibits the highest PGA value among the districts. The greatest PGA in the state is found in the southwestern region of Tripura, near the coordinates 91.4°E and 23.4°N, close to Belonia Subdivision. This area lies approximately 17 km from the Muhuri River, where the PGA ranges between 0.5 g and 0.65 g, indicating a high seismic risk zone. This heightened risk is attributed to the Chittagong Coastal Fault (CCF), which produced a significant earthquake with a magnitude of 6.9 in 1762. In 2009, three earthquakes greater than magnitude 5 (Mw > 5) were recorded in the CCF region, further indicating a substantial earthquake risk. Belonia, with its alluvial soil deposits and classification as Site Class D according to the NEHRP guidelines, faces an increased vulnerability to soil liquefaction. As we move inward towards the central part of Tripura, PGA values on bedrock are observed to range from 0.3 g to 0.37 g, largely due to the proximity of the Sylhet Fault in Bangladesh, which has been seismically active in the past five years. Moving northward towards the Mizoram-Tripura border, the influence of the Kaladan Fault and the Tripura Frontal Fold becomes more prominent, with PGA values reaching up to 0.37 g. This further highlights the varying seismic risk levels across different parts of Tripura.
5.2 PGA Across All District Headquarters of Mizoram
Mizoram, located in the northeastern part of India, comprises 11 districts, including Aizawl, Champhai, and Lunglei, among others. The state is characterized by its hilly terrain, with the Lushai Hills running through the central region, and dense forests that define much of its landscape. The state’s geography is dominated by steep slopes and valleys, drained by numerous rivers such as the Tlawng, Chhimtuipui, and Kaladan. Seismotectonically, Mizoram lies within the eastern Himalayan seismic belt, influenced by active fault zones, including the Kaladan Fault, which runs north-south along the India-Burma plate boundary. The interaction of the Indian and Burma plates, along with various local fault systems, makes Mizoram a seismically active region, with varying earthquake risks across its districts.
The seismic hazard analysis of districts in Mizoram, particularly in relation to the Kaladan Fault, reveals distinct variations in Peak Ground Acceleration (PGA) values across the region, influenced by both fault characteristics and seismotectonic positioning. The Kaladan Fault, a major N-S trending dextral strike-slip fault system, is associated with moderate earthquakes (maximum magnitude of 7.1) and plays a significant role in the seismic activity of the region. Sites located closer to the fault, such as Aizawl, Serchhip, and Lunglei, show relatively higher PGA values, ranging from 0.412 to 0.415, due to their proximity to the Kaladan fault zone, which is a major tectonic feature in the region (Fig.
11). These locations experience a heightened risk of ground shaking due to the fault’s active strike-slip nature, leading to potential earthquakes along the plate boundary between the Indian and Burma plates. As the distance from the fault increases, such as in Mamit and Saitual, the PGA values gradually decrease, with Mamit showing the lowest PGA of 0.210. This drop is justified by the increasing epicentral and hypocentral distances, which reduce the intensity of seismic waves. Additionally, the spatial distribution of PGA results is influenced by the varying geological features of the region. For instance, Champhai, located at a greater distance from the Kaladan Fault, records a PGA of 0.295, reflecting its location within a more stable area of the region, though still within the influence of the fault system. The analysis demonstrates that the closer a district is to the Kaladan Fault, the higher the PGA, which correlates with the fault’s active seismic behaviour and its interaction with regional tectonics. Therefore, the seismic hazard in Mizoram’s districts, as indicated by PGA values, is strongly influenced by proximity to the Kaladan fault, making it a critical factor in seismic risk assessment for the region.
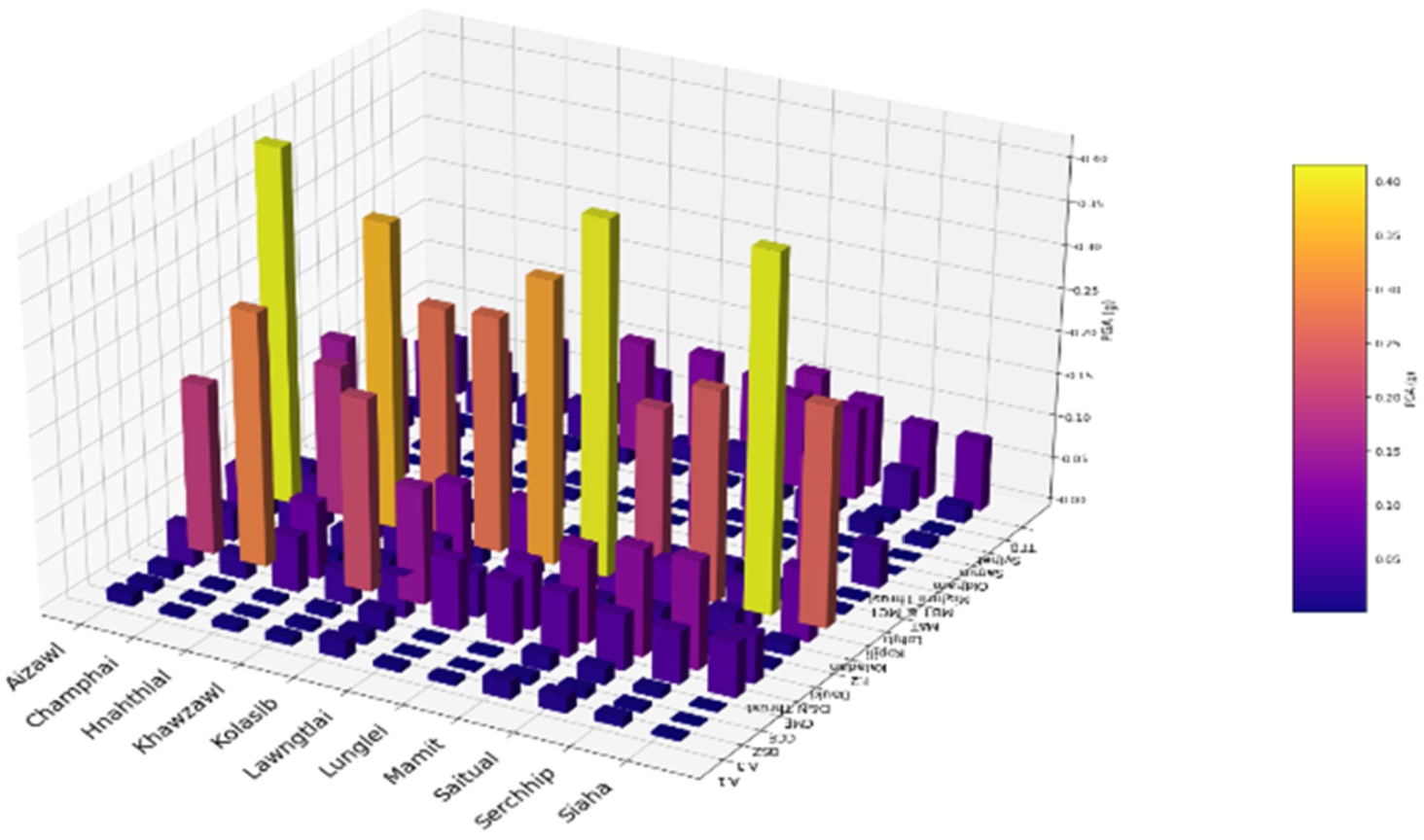
Fig. 11
Variation of PGA across all district headquarters of Mizoram considering all seismic sources for their respective maximum earthquake magnitudes.
5.3 PGA Across all District Headquarters of Assam
Assam, located in northeastern India, consists of 33 districts, each with varying geographical and seismotectonic characteristics. The state is bordered by Bhutan, Bangladesh, and several other northeastern states, with its terrain comprising valleys, hills, and plains. The Brahmaputra River, one of the largest rivers in India, flows through Assam, defining much of its landscape. Seismically, Assam is part of the eastern Himalayan seismic belt, influenced by several active fault zones, such as the Oldham, Samin, Sylhet, and D&N Thrust faults. These tectonic features, particularly the subduction of the Indian plate beneath the Eurasian plate, make the region susceptible to moderate to strong earthquakes. Assam’s geography, combined with its position near major seismic zones, contributes to the varied seismic hazard across its districts. The seismic hazard analysis of the region, based on Peak Ground Acceleration (PGA) values, offers critical insights into the varying levels of seismic risk across different districts, reflecting the influence of fault proximity, seismotectonic positioning, and fault characteristics. The PGA is a key indicator of ground shaking intensity, and this analysis highlights the role of active fault systems in determining the seismic vulnerability of each district. Figure
12 shows PGA values for all districts for all 18 faults for the Assam Region.
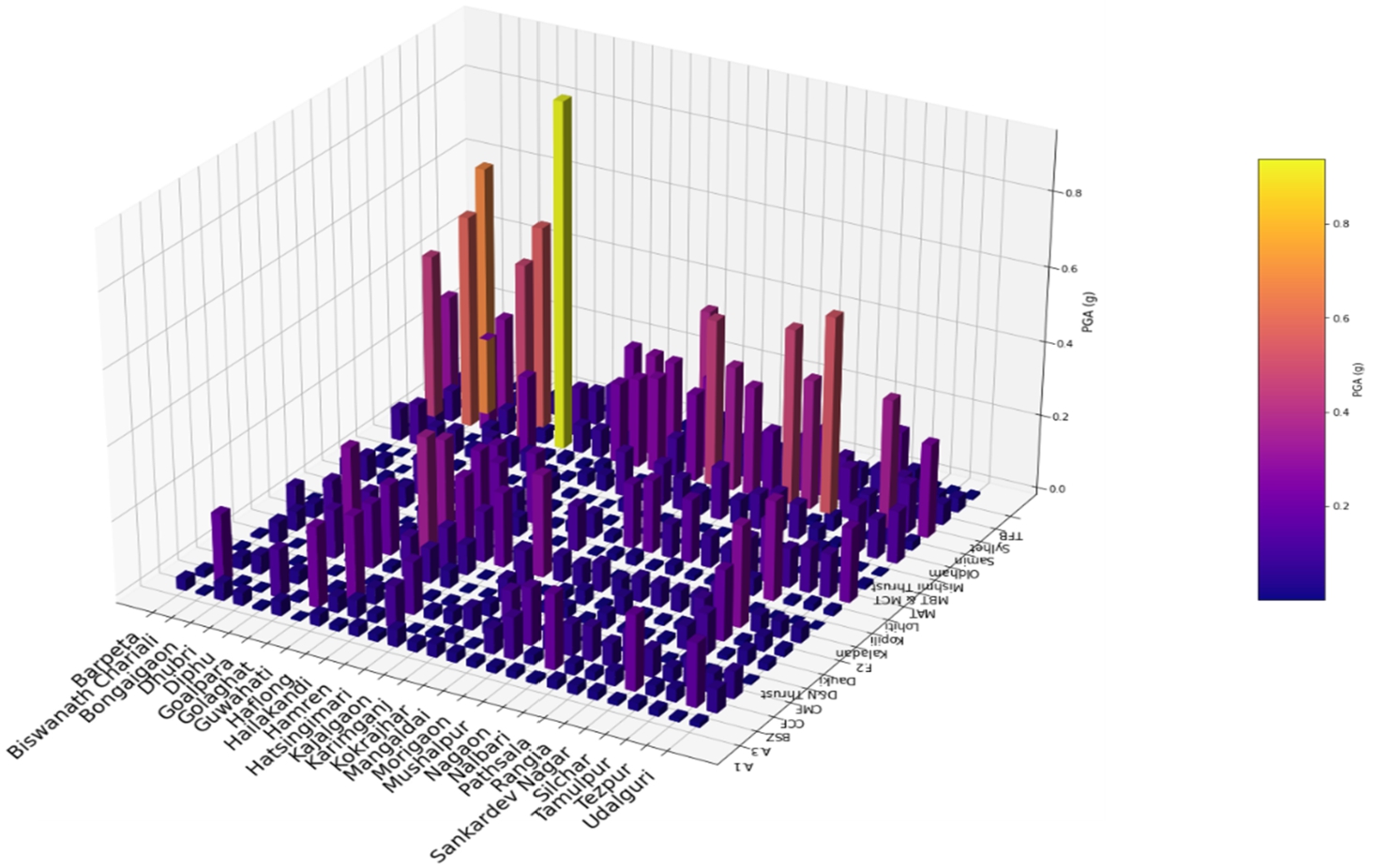
Fig. 12
Variation of PGA across all district headquarters of Assam considering all seismic sources for their respective maximum earthquake magnitudes.
Guwahati, situated near the Oldham fault, exhibits the highest PGA value of 0.9387. The Oldham fault, one of the most active faults in the region, has a significant role in shaping the seismic hazard in Guwahati. With a maximum earthquake magnitude of 8.6 and a depth of 31 km, the fault generates substantial seismic energy, resulting in strong ground shaking in the surrounding areas. The district’s proximity to this fault, combined with its depth, contributes to the high PGA, indicating a higher level of seismic risk. The Oldham fault is known for its historical and ongoing seismic activity, which underlines the need for heightened preparedness and mitigation measures in Guwahati.
In contrast, Bongaigaon (PGA = 0.5741) lies at a greater distance from the Oldham fault, which explains its lower PGA value. Although still influenced by the fault’s seismic activity, Bongaigaon experiences a reduced intensity of ground shaking due to the increased epicentral distance of 35.30 km and hypocentral distance of 46.98 km from the fault. The seismic energy dissipates with distance, leading to a comparatively lower PGA in this district. Despite this, the district is still susceptible to moderate shaking, particularly in the event of a major earthquake along the Oldham fault.
Rangia (PGA = 0.5321) also experiences a notable seismic hazard, though slightly less intense than Bongaigaon. The district’s proximity to the Oldham fault plays a key role, but its PGA value reflects the interaction between fault distance, depth, and earthquake magnitude. The Oldham fault’s influence remains significant but weaker compared to Guwahati due to the increased distance from the fault.
Karimganj (PGA = 0.3859), located near the Sylhet fault, exhibits a lower PGA. The Sylhet fault, with a maximum earthquake magnitude of 8.1 and a depth of 28 km, is a less active seismic source compared to the Oldham fault. The fault generates smaller earthquakes and is located farther from Karimganj. These factors contribute to the reduced seismic hazard in this district, reflected in the relatively low PGA. However, the region is still vulnerable to moderate shaking, especially if a major earthquake occurs along the Sylhet fault.
Goalpara (PGA = 0.5505) also lies near the Samin fault, which has a similar seismic characteristic to the Sylhet fault. The Samin fault, with a magnitude of 8.1 and a depth of 26 km, is associated with moderate seismic activity. The proximity of Goalpara to this fault results in a slightly higher PGA compared to Karimganj, as the district is situated closer to the fault. Despite this, the PGA remains lower than in areas near the Oldham fault, reflecting the fault’s lower seismic intensity.
Haflong (PGA = 0.3457), situated near the D&N Thrust fault, experiences lower PGA values, indicating reduced seismic hazard. The D&N Thrust fault, with a magnitude of 6.7 and a depth of 30 km, produces earthquakes of moderate size, contributing to less intense ground shaking. The district’s distance from the fault and the fault’s moderate seismic activity result in a PGA lower than in areas closer to more active faults like the Oldham fault.
Morigaon (PGA = 0.3355) similarly experiences a relatively low PGA due to its location farther from major fault systems like the Oldham and Samin faults. Although the district is influenced by regional seismicity, the absence of nearby active faults leads to lower seismic intensity and a reduced PGA. The depth of 31 km and the maximum earthquake magnitude of 8.6 for the Oldham fault have minimal effect on this district’s seismic hazard, as it lies outside the most affected zone.
Mushalpur (PGA = 0.2929) exhibits one of the lowest PGAs, which can be attributed to its distance from major fault lines. The district is situated in a region with relatively low seismic activity, and the absence of nearby significant fault sources results in a reduced seismic hazard. The PGA value reflects this lower risk, though it still experiences minor shaking during larger seismic events from distant fault systems.
Diphu (PGA = 0.2657) also exhibits low seismic hazard due to its position relative to the D&N Thrust fault, which is farther from the district. The fault generates moderate earthquakes, but the resulting ground shaking is less intense in Diphu due to the district’s location and the fault’s seismic characteristics.
Sankardev Nagar (PGA = 0.2030) and Nagaon (PGA = 0.2023) show similarly low PGAs. Both districts lie outside the influence of major fault systems like the Oldham and Samin faults and are located in regions of low seismic activity. The low PGAs in these districts reflect minimal seismic risk, though they are still susceptible to distant earthquake shaking.
Udalguri (PGA = 0.2002) and Biswanath Chariali (PGA = 0.1847) experience among the lowest PGAs in the region. These districts are situated far from major fault lines, with minimal seismic activity influencing their ground shaking. The relatively low PGAs in these areas suggest a lower seismic hazard, with shaking likely coming from distant sources.
In conclusion, the seismic hazard in this region is primarily influenced by the proximity to active fault systems like the Oldham, Sylhet, Samin, and D&N Thrust faults, which generate varying levels of seismic activity. Districts closer to these faults, such as Guwahati and Bongaigaon, experience higher PGAs, indicating a higher seismic risk. On the other hand, districts located farther from active fault zones, like Udalguri and Biswanath Chariali, exhibit lower PGAs and are less vulnerable to strong ground shaking. The analysis emphasizes the need for targeted earthquake mitigation strategies, particularly in districts with high PGAs due to their proximity to major active faults.
5.4 PGA Across All District Headquarters of Meghalaya
Meghalaya, located in Seismic Zone V of Northeast India, is one of the most seismically active regions in the country, with several major active faults that significantly influence its vulnerability to earthquakes. The region’s seismic hazard is primarily driven by the Oldham, Dauki, and Samin faults, each contributing to the region’s earthquake potential in distinct ways. The interaction of these faults with the geological features of the Shillong Plateau and surrounding areas amplifies the seismic threat faced by the state.
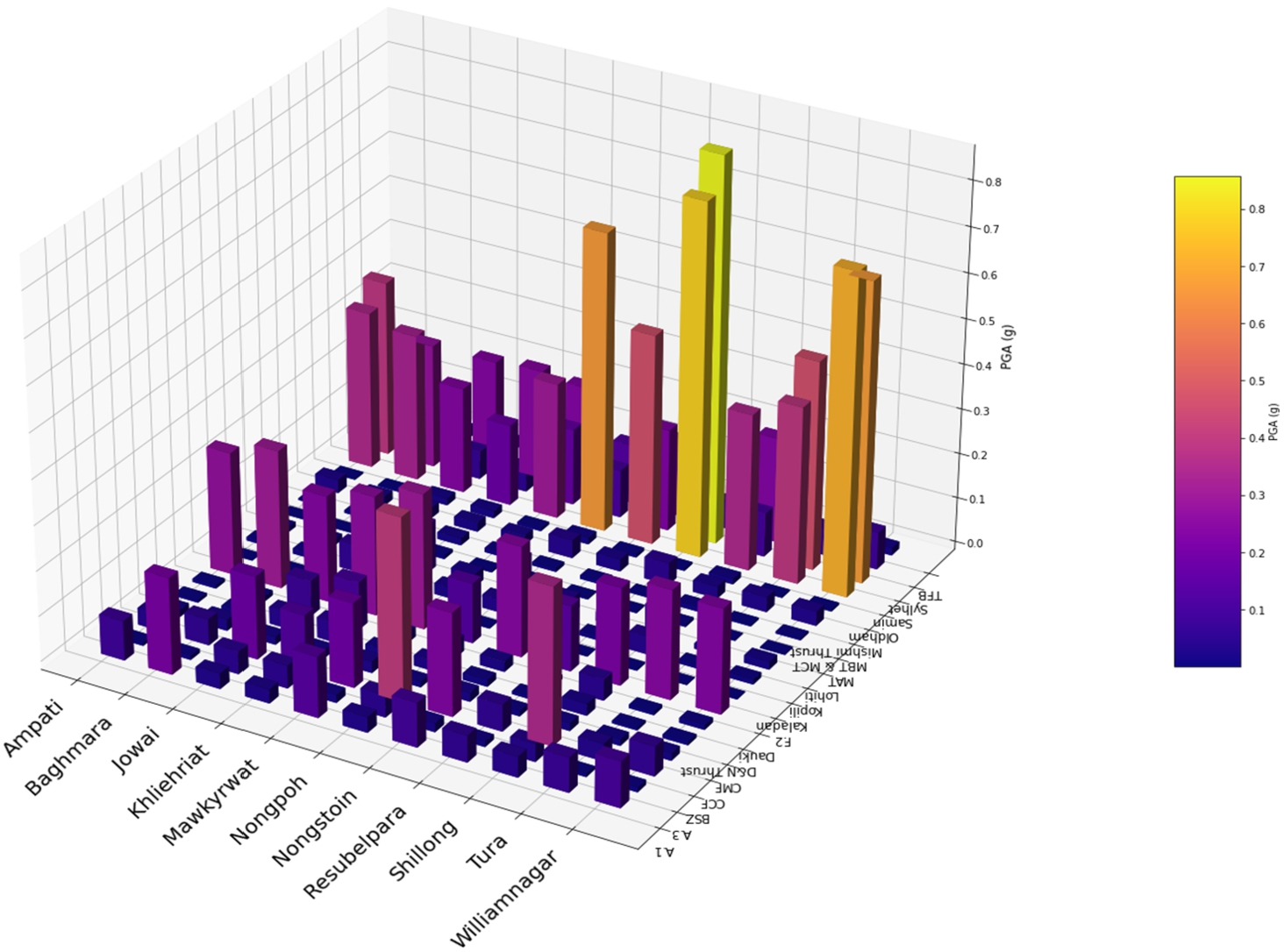
Fig. 13
Variation of PGA across all district headquarters of Meghalaya considering all seismic sources for their respective maximum earthquake magnitudes.
The Oldham Fault, a reverse fault situated to the north of the Shillong Plateau, is a major geological feature in the region. Extending over approximately 110 km, it dips at 57° north and is responsible for the devastating 1897 Assam earthquake (Mw 8.6). This fault has been linked to a slip of 16 m during the earthquake, and studies have shown that the seismic moment generated by this fault during the event was 2.18 × 10
21 Nm, consistent with values obtained from empirical models. Figure
13 shows the PGA values for entire Meghalaya region along with the variations of PGA in District level. The fault marks the northern boundary of the Shillong Plateau and influences several key regions, including Williamnagar, Nongpoh, Ampati, Shillong, Baghmara, Mawkyrwat, Jowai, and Nongstoin. These regions exhibit varying levels of Peak Ground Acceleration (PGA), with Williamnagar and Nongstoin experiencing moderate to high PGAs, indicating the potential for significant ground shaking during an earthquake originating along the Oldham Fault. The fault’s historical activity, especially the 1897 earthquake, underscores its capacity to generate high-magnitude seismic events, making areas in its vicinity particularly vulnerable.
The Dauki Fault, another critical fault in the region, is a 320 km long system that trends east-west and exhibits both reverse and right-lateral strike-slip motion. This fault system runs through Meghalaya, from Brorghat in the west to Leike in Assam to the east, and is composed of multiple fault segments that dip to the north. Studies suggest that the eastern segment of the Dauki Fault, stretching from Brorghat to Leike Assam, forms a single fault. This fault system represents a significant seismic threat, as it is associated with high-stress zones between the Shillong Plateau and the Bengal Basin. Khliehriat, located near the Dauki Fault, is at risk due to the potential for large earthquakes with magnitudes greater than 7.5, which have historically occurred along similar thrust faults. The seismic activity along the Dauki Fault poses a particular danger to the eastern parts of Meghalaya, with the potential for destructive earthquakes that could affect nearby towns and infrastructure.
The Samin Fault, though smaller than the Oldham and Dauki Faults, still plays an important role in the seismic hazard of the region. This fault is approximately 4 km long with a throw of 3 km and has a broader fracture zone of 11 km. Located near the village Samin, it trends in an E30°S–W30°N direction. Although the Samin Fault is not as large as the Oldham or Dauki Faults, its proximity to towns such as Tura and Resubelpara means that it can still generate significant ground shaking. Recorded PGAs of 0.46494 g and 0.856 g in these areas suggest that moderate earthquakes originating from the Samin Fault could lead to substantial ground motion. These areas, while not as vulnerable to large-magnitude earthquakes as those near the Oldham and Dauki Faults, could still experience considerable shaking, especially from smaller to medium-sized seismic events.
The combination of these active faults significantly enhances the seismic hazard faced by Meghalaya. The proximity of these faults to populated areas, coupled with their historical and ongoing seismic activity, underscores the region’s vulnerability to earthquakes. The Oldham Fault, in particular, poses the highest threat, given its association with the 1897 earthquake and its ongoing seismic activity. Regions such as Williamnagar, Shillong, and Nongstoin, which lie within its influence zone, are particularly at risk of strong ground shaking. The Dauki Fault, with its potential for large-magnitude earthquakes, also adds to the region’s seismic risk, particularly in the eastern parts of Meghalaya, including Khliehriat. Meanwhile, the Samin Fault, though smaller, still poses a significant threat to areas like Tura and Resubelpara, with its potential to generate moderate seismic events.
5.5 PGA Across All District Headquarters of Manipur
The seismic hazard analysis of Manipur reveals notable differences in the earthquake risk across various districts in the region, driven largely by their proximity to the active Churachandpur-Manipur Fault (CMF). The CMF, a dextral strike-slip fault located along the boundary between the Indian and Sunda plates, accommodates a significant portion of the relative plate motion (43%) between these two tectonic plates. The seismic hazard, measured in terms of Peak Ground Acceleration (PGA), varies across the districts based on several factors, including their distance from the fault zone, the fault’s characteristics, and their seismotectonic position within the broader regional tectonic setting.
The CMF plays a dominant role in the seismic activity observed in Manipur. This fault is not only a significant structural feature in the region but also an active one, contributing to frequent seismic events due to the ongoing plate motion between the Indian and Sunda plates. As highlighted by Kundu and Gahalaut (2013), a sharp change in the earthquake magnitudes near the longitudes of 93°–95°E corresponds to the location of the CMF, indicating its significant role in the region’s seismicity. This motion along the CMF affects large parts of the Manipur region, with earthquake magnitudes as high as 7.9, and is responsible for a substantial amount of ground shaking that impacts districts in close proximity to the fault.
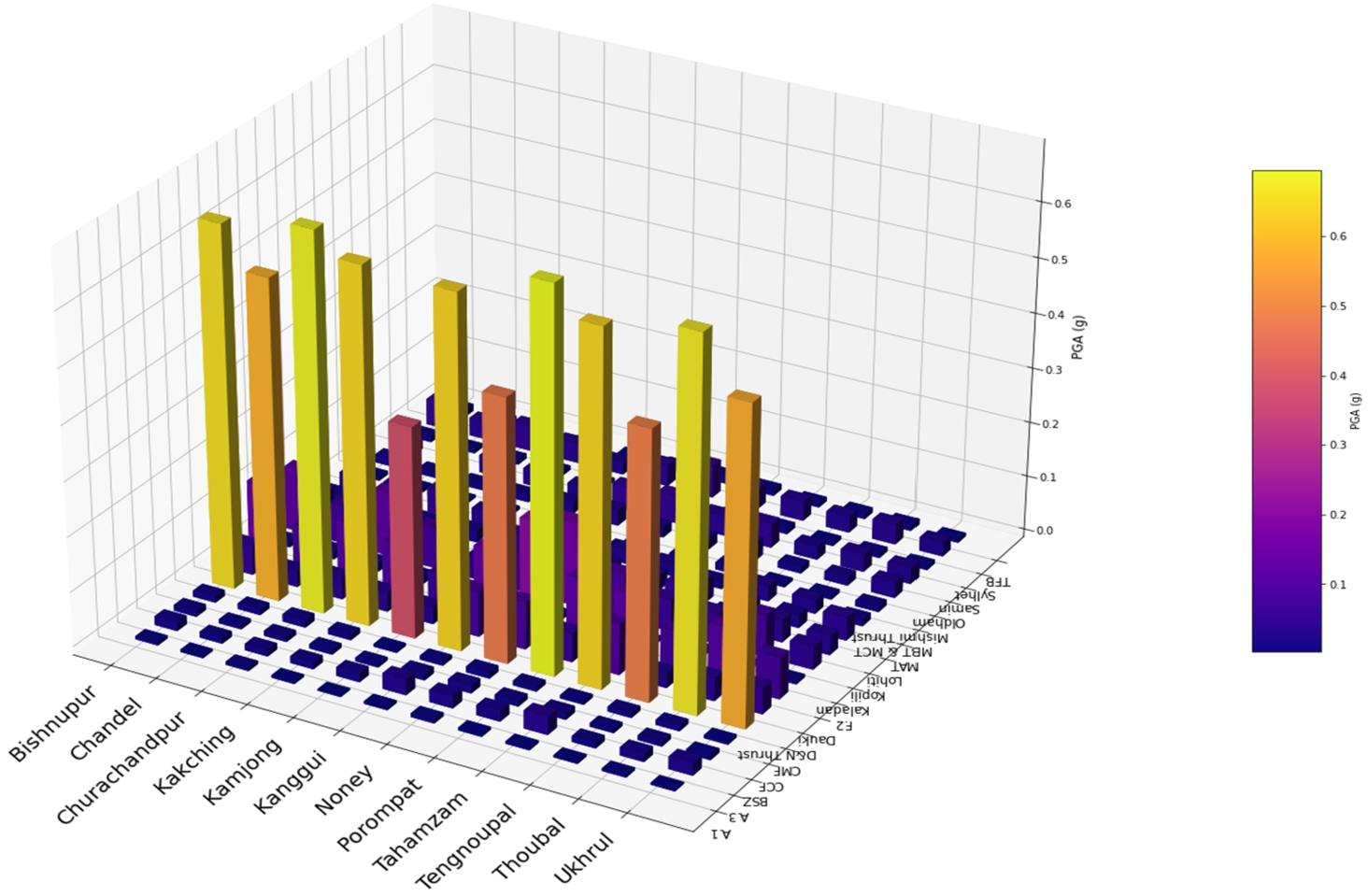
Fig. 14
Variation of PGA across all district headquarters of Manipur considering all seismic sources for their respective maximum earthquake magnitudes.
Figure
14 shows the PGA results for the various districts of Manipur, which indicate a clear spatial gradient in seismic hazard, with districts closer to the CMF Fault experiencing higher levels of ground shaking. For instance, Porompat, situated near the fault, exhibits the highest PGA value of 0.6958. This high level of ground motion is a direct result of its proximity to the CMF Fault, where fault slip and seismic wave propagation from the earthquake source cause strong shaking. In comparison, Churachandpur, although also near the fault, experiences a slightly lower PGA (0.6872), suggesting that while it is similarly exposed to seismic hazard, the ground motion may be somewhat reduced due to minor variations in fault rupture or local site conditions.
As we move further from the fault, such as in Thoubal (PGA: 0.6737) and Bishnupur (PGA: 0.6579), the PGA values begin to decrease, indicating a reduction in seismic hazard. This decrease can be attributed to the attenuation of seismic waves as they travel farther from the earthquake source. Similarly, Kakching (PGA: 0.6465) and Tahamzam (PGA: 0.6426) experience slightly lower PGAs due to their greater distance from the fault. This pattern suggests that the influence of the fault diminishes with increasing distance, as seismic waves lose energy over larger distances.
Moving even farther from the fault, districts such as Chandel (PGA: 0.5838) and Ukhrul (PGA: 0.5752), show a further reduction in PGA. The seismic hazard in these districts is lower, reflecting their more distant location from the CMF. The decrease in ground acceleration is particularly noticeable in these areas, where the seismic waves have significantly attenuated. Similarly, Tengnoupal (PGA: 0.4877) and Noney (PGA: 0.4783), located further from the fault, experience even lower PGAs, indicating a substantially reduced seismic risk.
The lowest PGA value is observed in Kamjong (PGA: 0.3830), which is located at the farthest point from the CMF fault in this study. This very low value further highlights the relationship between seismic hazard and distance from the fault. At this distance, the seismic waves have weakened considerably, leading to minimal ground shaking.
The variations in PGA across Manipur can be explained by several factors, with the most significant being the proximity to the CMF fault. Districts situated closer to the fault experience stronger ground shaking due to their proximity to the earthquake source. This is especially true for Porompat and Churachandpur, where the fault is located relatively nearby. As distance from the fault increases, such as in Kamjong and Tengnoupal, seismic waves lose energy, resulting in lower PGA values and, consequently, reduced seismic hazard.
5.6 PGA Across All District Headquarters of Arunachal Pradesh
The seismic hazard analysis of Arunachal Pradesh reveals significant variation in earthquake risk across the districts, which is primarily influenced by the region’s seismotectonic setting and proximity to active fault systems. This region, located at the junction of the Himalayan Range, the Mishmi Hill Range, and the Naga Hill Range, is seismically active, largely due to the presence of several major fault zones, including the Lohiti Thrust, Mishmi Thrust, and other associated fault structures such as the Po-Chu and Bame Faults. These fault systems, especially the Lohiti and Mishmi Thrusts, play a crucial role in accommodating the tectonic stresses arising from the ongoing collision between the Indian and Eurasian plates. This collision results in high-magnitude seismic events, including the 1950 Assam Earthquake, which occurred due to strike-slip motion along the Po-Chu Fault. The region is characterized by a mixture of thrust and strike-slip faulting, contributing to the complex seismic behaviour observed across the districts.
The seismicity in Arunachal Pradesh is closely linked to the movement along several fault systems that define the region’s seismotectonic framework. The Lohiti Thrust, which runs along the eastern parts of the state, plays a significant role in seismic activity. This thrust extends over 200 km and marks a major tectonic boundary between different geological formations, including the Indo-Burmese mobile belt and the Mishmi formation. The Mishmi Thrust, another key fault in the region, trends WNW–ESE and is particularly important in the Nao Dihing Valley, where it connects with the Main Boundary Thrust (MBT) of the Himalayas. Both these thrusts are associated with significant seismic activity, which is reflected in the ground motion observed across various districts of Arunachal Pradesh. Additionally, the region’s proximity to the convergence of the Himalayan tectonic plate boundary further contributes to the frequent occurrence of large and damaging earthquakes.
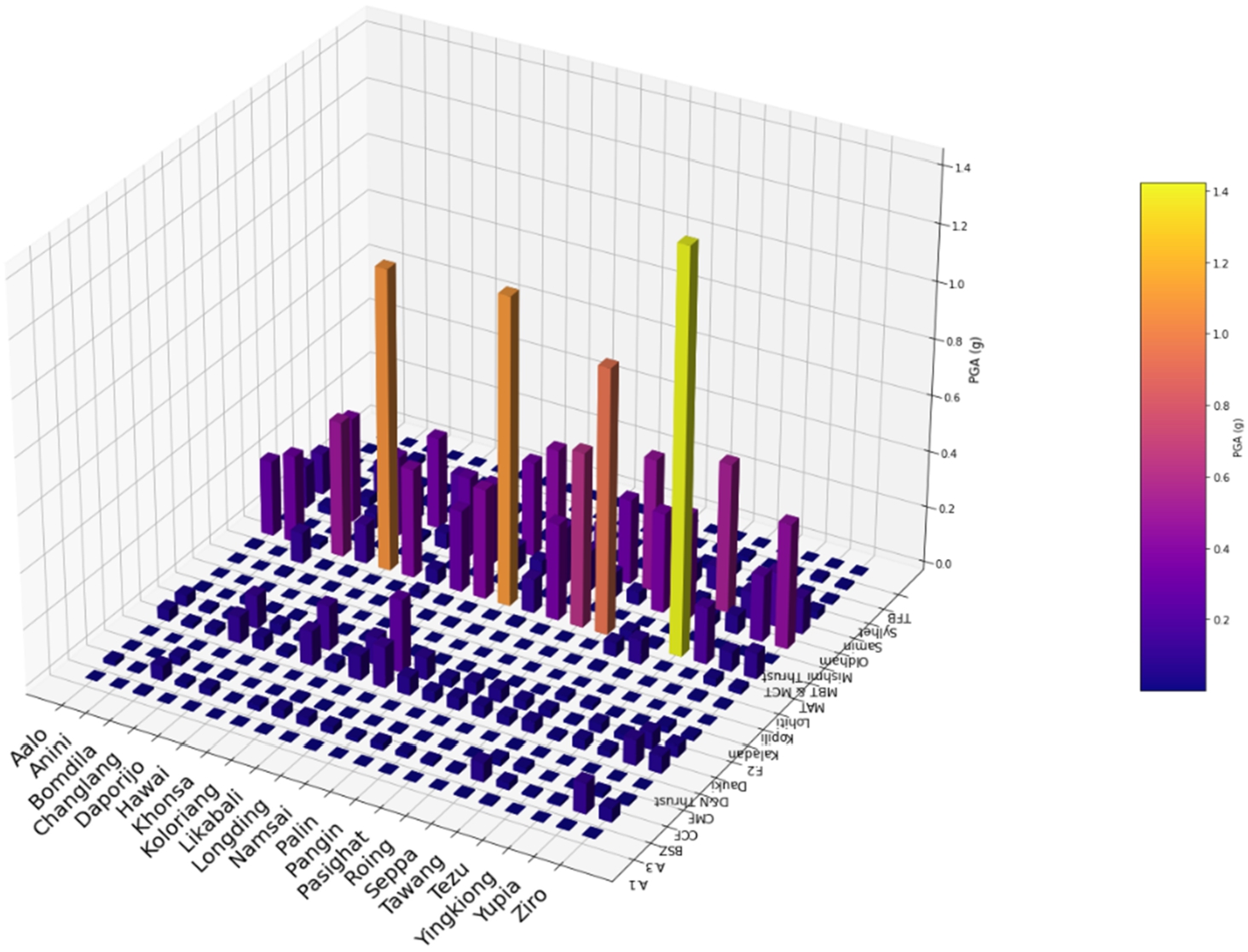
Fig. 15
Variation of PGA across all district headquarters of Arunachal Pradesh considering all seismic sources for their respective maximum earthquake magnitudes.
The Peak Ground Acceleration (PGA) results for various districts in Arunachal Pradesh show a clear pattern of seismic risk that correlates with their proximity to active fault zones (Fig.
15). Districts closer to the Lohiti Thrust, such as Tezu and Namsai, show the highest PGAs, reflecting their immediate proximity to the fault. Tezu, located near the heart of the Lohiti Thrust, exhibits the highest PGA value of 1.423, indicating a very high seismic hazard in the region. This can be attributed to the direct influence of the fault, where tectonic stress is most concentrated and earthquake energy is released. Namsai, situated nearby, experiences a slightly lower PGA of 1.093, still indicating a high seismic risk but slightly reduced compared to Tezu. This decrease in PGA may be due to slight variations in local fault geometry or a difference in the specific fault rupture characteristics in the region.
As we move further away from the Lohiti Thrust, the PGA values gradually decrease. For example, Hawai and Roing, while still near active fault zones, exhibit lower PGA values of 1.071 and 0.939, respectively. This reflects a reduction in seismic hazard as the distance from the fault zone increases. These districts, though still in relatively close proximity to the fault, are less directly impacted by fault movements compared to districts like Tezu and Namsai. The decrease in PGA further supports the notion of seismic wave attenuation with distance from the fault, where the ground shaking diminishes as seismic waves propagate outward.
Districts such as Pasighat and Changlang, which are situated farther from the central fault zone, show a further decrease in PGA values, with Pasighat recording 0.620 and Changlang at 0.484. This reduction can be explained by the increasing distance from the Lohiti Thrust and the reduced intensity of seismic waves as they travel further from the fault source. Although these areas are still within the broader seismic region, the diminished PGA values indicate that they are less exposed to the direct effects of seismic activity. In contrast, districts farther west, such as Ziro, Bomdila, and Tawang, which are located along the Main Boundary Thrust (MBT) and the Mishmi Thrust, display lower PGAs, reflecting their position away from the major active faults in the region. For example, Ziro and Bomdila record PGAs of 0.442 and 0.372, respectively. These lower PGAs are expected as these districts are situated further from the primary fault zones of the Lohiti and Mishmi Thrusts, and the seismic waves have already weakened by the time they reach these locations.
The seismic hazard in Arunachal Pradesh is heavily influenced by its seismotectonic position, with the proximity to active faults like the Lohiti Thrust and Mishmi Thrust determining the level of seismic risk in each district. Districts closer to these faults, such as Tezu and Namsai, experience higher PGAs, indicating a higher seismic hazard, while districts farther from the faults, such as Palin and Yingkiong, exhibit lower PGA.
5.7 PGA Across All District Headquarters of Nagaland
The seismic hazard analysis for Nagaland reveals that the region is seismically active, with notable variations in ground shaking (measured as Peak Ground Acceleration, PGA) across different districts. The seismic hazard in Nagaland is influenced by the region’s tectonic setting, which is characterized by the presence of several major fault systems, including the Churachandpur-Manipur Fault (CMF) and the D&N Thrust. These faults, along with other regional structural features such as the Naga Thrust, contribute to the seismic activity observed in the region. The analysis shows that districts closer to the active faults, particularly the CMF, experience higher levels of ground shaking, while districts farther from these faults experience lower seismic risk. The region’s seismicity, as indicated by past earthquakes, is strongly linked to the movement of the Indian plate, particularly along the plate boundaries that affect the region.
Nagaland is positioned within a tectonically complex zone, influenced by the interaction of multiple active faults. The CMF, a major strike-slip fault that accommodates significant movement between the Indian and Sunda plates, plays a major role in the seismic activity of the region. This fault is responsible for large-scale tectonic motions that produce significant earthquakes in the region. The D&N Thrust, another important fault zone, is located in the southern parts of Nagaland and is also responsible for seismic events, though it generally produces smaller earthquakes compared to the CMF. The tectonic setting in Nagaland is further complicated by the presence of the Naga Thrust, which is a major geological feature in the region. This thrusts, along with other fault systems, generates both thrust and strike-slip earthquakes that contribute to the overall seismic hazard.
The seismicity of the region, including that of Nagaland, is not limited to shallow earthquakes. Earthquakes in the region occur at varying depths, with smaller events typically occurring at depths ranging from 1 to 144.5 km, while higher-magnitude events are generally observed at depths of 4 to 120 km. The depth of these earthquakes plays a crucial role in determining the level of ground shaking, as deeper earthquakes tend to generate less intense surface shaking compared to shallow ones. The occurrence of these deeper seismic events is indicative of the region’s tectonic complexity, where both shallow and deep earthquakes are generated by the interaction of multiple fault systems.
Fig. 16
Variation of PGA across all district headquarters of Nagaland considering all seismic sources for their respective maximum earthquake magnitudes.
The analysis of PGAs across various districts of Nagaland presented in Fig.
16, reveals a clear trend: districts closer to the CMF experience higher PGAs, indicating higher seismic risk. For example, Phek and Meluri, located in proximity to the CMF, exhibit relatively high PGAs of 0.6598 and 0.6556, respectively. These high PGAs are indicative of the significant seismic hazard posed by the CMF, where tectonic movements along the fault lead to substantial ground shaking. The relatively high PGA values in these districts suggest that they are more directly affected by seismic events originating along the CMF. As we move further from the CMF, the PGAs decrease, as observed in districts such as Shamator (PGA: 0.5617) and Noklak (PGA: 0.5046). While these districts are still within the broader influence of the CMF, they are farther from the fault zone, and the seismic waves attenuate as they travel away from the earthquake source. This attenuation results in lower PGAs and reduced seismic hazard in these districts compared to areas like Phek and Meluri. Further decreases in PGA are observed in districts like Kiphire (PGA: 0.4786) and Zünheboto (PGA: 0.4708), which are even farther from the CMF and experience significantly weaker seismic shaking. These districts are still within the region affected by the CMF, but their distance from the fault zone and the attenuation of seismic waves over distance lead to lower PGA values and a reduced seismic risk. As we move to districts such as Longleng (PGA: 0.4487) and Mokokchung (PGA: 0.4434), the PGA continues to decrease, reflecting their more distant location from the CMF and the D&N Thrust. These areas are located farther from the primary seismic sources, and the ground shaking in these districts is further diminished due to both distance and the local geological conditions. The lowest PGAs are observed in districts like Tuensang (PGA: 0.4339) and Kohima (PGA: 0.3579), which are located at even greater distances from the major fault systems. The seismic hazard in these districts is relatively low, as seismic waves lose energy over greater distances, leading to minimal ground shaking at the surface. The variations in PGA across Nagaland can be attributed to several key factors, with proximity to fault zones being the most significant. Districts located closer to the CMF, such as Phek and Meluri, experience higher ground shaking due to their proximity to the fault zone, where the release of tectonic stress results in strong seismic waves. Conversely, districts farther from the fault, such as Tuensang and Kohima, experience much lower PGAs as seismic waves attenuate over distance. The D&N Thrust, although also active in generating earthquakes, produces relatively lower PGA values compared to the CMF. This is likely due to the smaller magnitude and shallower depth of the earthquakes associated with this fault. The shallow nature of earthquakes along the D&N Thrust means that the seismic waves generated may not travel as far or with the same intensity as those generated by the CMF.
7 Conclusion
The research used a trapezoidal neutrosophic-based decision-making approach for seismic hazard analysis in Northeast India, with a specific focus on regions such as Tripura. This innovative methodology addresses the shortcomings of traditional seismic hazard assessment techniques, particularly in the selection and weighting of Ground Motion Prediction Equations (GMPEs). By integrating the TrF-FUCOM and Neutrosophic-TOPSIS methods, the framework effectively tackles uncertainties inherent in seismic hazard analysis, especially in areas with intricate tectonic configurations. The approach incorporates critical factors such as site conditions, tectonic settings, magnitude scaling, and distance attenuation, offering a holistic and robust method for hazard evaluation. This enables the generation of reliable design inputs for earthquake-resistant structures. The study leverages seismic and tectonic data collected within a 300 km radius of Northeast India, ensuring a comprehensive and region-specific analysis. The seismic hazard analysis across various regions in Northeast India reveals significant variations in Peak Ground Acceleration (PGA) values, which correlate with proximity to active fault zones. A total of 28 faults have been identified in Northeast India, with 18 of them being active and capable of generating significant ground motion. Key faults, such as the Oldham, MBT&MCT, Lohiti, CMF, Sylhet, CCF and Kaladan, have been recognized as primary contributors to seismic activity in the capitals of the Northeastern states of India. In Arunachal Pradesh, Tezu shows the highest PGA of 1.423 g, indicating a very high seismic risk near the Lohiti Thrust, while Namsai also exhibits elevated PGAs. In Nagaland, Phek and Meluri near the CMF display PGAs of 0.6598 g and 0.6556 g, respectively. Manipur’s proximity to the CMF is reflected in Porompat’s high PGA of 0.6958 g. Meghalaya sees significant risk due to the Oldham Fault, with Guwahati experiencing the highest PGA of 0.9387 g, while Williamnagar, Shillong, and Nongstoin are also at risk. In Mizoram, Aizawl, Serchhip, and Lunglei have PGAs ranging from 0.412 g to 0.415 g, influenced by the Kaladan Fault. Tripura’s DSHA map shows PGA values from 0.21 g to 0.69 g, with the highest in the southwestern region near Belonia, driven by the Chittagong Coastal Fault (CCF), associated with a significant earthquake in 1762. Peak ground acceleration value obtained for Gangtok city is the least among the entire Northeast India. The results of this study show a reasonable alignment with previous research and the strong-motion accelerogram data recorded during the January 3rd, 2017 earthquake. The seismic hazard analysis findings offer valuable insights for seismic zonation and the earthquake-resistant design of critical infrastructure, such as bridges, buildings, dams, and underground systems like tunnels, drainage, and sewage networks. Additionally, these results will assist in city planning by addressing seismic vulnerabilities and integrating earthquake-resistant design principles into urban development strategies. However, the study could be enhanced by incorporating additional seismic hazard factors, including foreshocks, aftershocks, wave propagation modes, shear wave velocity at bedrock, and more accurate methods for determining the maximum earthquake magnitudes along lineaments, faults, and folds. Future research could focus on developing more efficient algorithms to simplify data handling and interpretation.