1 Introduction
The technological development in the last decades has allowed the creation of many electronic devices used to solve the current problems of humanity. These devices are present in many aspects of human life such as health, agriculture, economy and education. They produce and store huge amounts of digital data, which in turn contain a certain amount of hidden knowledge. Knowledge extraction (Di-Jorio et al., 2009a; Vera et al., 2020; Al-Jammali, 2023) aims to extract useful and understandable hidden knowledge, such as correlation, dependence or co-variation of attributes, from large databases.
A well known data mining task is frequent itemset mining, widely studied by the data mining community. It consists of analysing data to discover frequently co-occurring itemsets (Agrawal and Srikant, 1994; Kenmogne, 2018). It has many applications in many areas such as market basket analysis, e-learning, image classification, activity monitoring, community discovery, malware detection, web mining, chemical and biological analysis, and software bug analysis. Over the past decades, many studies have been devoted to frequent sequence mining (Kenmogne, 2016; Belise et al., 2017, 2018; Kenmogne et al., 2022), which generalizes frequent itemset mining by taking the sequential ordering of itemsets in transactions into account to find frequently co-occurring subsequences in a set of transactions. Recently, gradual patterns that model frequent co-variations between numerical attributes aroused great interest in a multitude of areas. They convey knowledge of the form «the more A, the more B». Examples of gradual patterns extracted from a salary database and a medical database are «the higher the age, the higher the salary» and « patients with high insulin levels, high body mass index and high age have a high probability of having diabetes», respectively. Previous studies have developed two basic algorithms for extracting frequent gradual patterns, namely Graank and Grite. Both algorithms are based on the Apriori principle, which consists in generating candidates and selecting those that are frequent. The difference between them comes from how to calculate the gradual supports. In the Grite algorithm, gradual support is based on the so-called precedence graph approach. In the Graank algorithm, it relies instead on the so-called concordant pairs approach.
Even though the problem of knowledge extraction has been addressed for many years (Frawley et al., 1992; Agrawal and Srikant, 1994; Hüllermeier, 2002; Berzal et al., 2007; Di-Jorio et al., 2009a; Kononenko and Bevk, 2009; Ayouni et al., 2010; Negrevergne et al., 2014; Kenmogne, 2016; Jabbour et al., 2019; Chicco and Jurman, 2020; Lonlac et al., 2020; Lonlac and Nguifo, 2020; Vera et al., 2020; Clémentin et al., 2021; Li and Liu, 2021; Ham et al., 2022), knowledge mining algorithms are well known to be both time and memory intensive for large databases, and the improvements are driven by the need to process more data at faster speed with less cost. This paper follows this trend for the extraction of frequent gradual patterns.
Interesting gradual pattern mining algorithms can be classified into four categories. The first category focuses on the extraction of frequent gradual patterns (Di-Jorio et al., 2009a, 2009b, 2009c; Laurent et al., 2009; Clémentin et al., 2021). The second category focuses on reducing the number of frequent gradual patterns by considering only closed or maximal patterns (Ayouni et al., 2010; Côme and Lonlac, 2021; Belise et al., 2023). The third category focuses on leveraging parallel architectures to speed up the mining process (Laurent et al., 2010, 2012; Negrevergne et al., 2014; Belise et al., 2018). The fourth category concerns the integration of constraints, related to the application context, in the mining process (Belise, 2011; Kenmogne, 2016; Belise et al., 2017; Kenmogne, 2018; Ser et al., 2018; Lonlac et al., 2020). Many algorithms of the four categories are based on the Apriori principle, also known as the test-generation principle, which consists in generating candidate itemsets, calculating their gradual supports and retaining only those candidates whose support is above the minimum threshold. In these algorithms, frequent gradual patterns of size k are used to generate candidates of size $(k+1)$.
The work presented in this paper is related to the first category of algorithms. In this category, performance optimization involves reducing the search space and reducing the costs of fundamental operations used in the mining process, namely support calculation, candidate generation and binary matrix multiplication. In mining algorithms, the search space could be reduced to the lattice of positive gradual patterns, i.e. patterns whose first term is positive. This halves the search space, which in turn results in a halving of the computational load. The reduction of support calculation costs has been studied in the literature in the particular case where the gradual support is based on the so-called precedence graph approach. This paper focuses on reducing the costs of generating and processing candidates, assuming that gradual support relies on the so-called concordant pairs approach. This results in a new approach for extracting frequent gradual patterns. Compared to previous approaches, the cost of candidate generation is significantly reduced by using only frequent gradual itemsets whose size is a power of two to generate all candidates. More precisely, frequent gradual patterns of size ${2^{k}}$ are used to generate all candidates whose size is between ${2^{k}}+1$ and ${2^{(k+1)}}$. Experiments carried out on real and synthetic datasets show a significant gain obtained with the proposed approach compared to the Graank reference approach.
2 State of the Art
This section presents the fundamental concepts of the extraction of the gradual patterns and the methods of extraction of the said patterns.
2.1 Concepts and Definitions
The database described in Table 1 is used to illustrate the concepts and methods for extracting gradual patterns.
Table 1
Example of a numerical database $\mathcal{D}$.
| Id | Age (A) | Salary (S) | Car (C) |
| ${p_{1}}$ | 22 | 1200 | 0 |
| ${p_{2}}$ | 28 | 1850 | 2 |
| ${p_{3}}$ | 24 | 1200 | 3 |
| ${p_{4}}$ | 35 | 2200 | 1 |
For example, in Table 1, A, S and C are items.
Definition 2 (Gradual Item).
A gradual item is of the form ${A^{\ast }}$ where A is an attribute of the database and *$\in \{\gt ,\lt ,\geqslant ,\leqslant \}$ is the variation operator of the values of attribute A.
In database $\mathcal{D}$ in Table 1, ${A^{\gt }}$ is linguistically expressed as “increasing age” and ${A^{\lt }}$ as “decreasing age”.
Definition 3 (Gradual pattern or gradual itemset).
A gradual pattern M, also called gradual itemset, is a concatenation of several gradual items, denoted $M={I_{i}^{\ast i}}$, $i=1..k$, where ${I_{i}^{\ast i}}$ is a gradual item.
M is linguistically interpreted as a conjunction of gradual items. A k-gradual itemsets is an gradual itemset containing k gradual items. For example, the 2-gradual itemset ${A^{\geqslant }}{S^{\geqslant }}$ means “the more the age increases, the more the salary increases”.
Definition 4 (Complementary gradual itemset).
Let $M=({i_{1}^{{\ast _{1}}}},\dots ,{i_{k}^{{\ast _{k}}}})$ be a gradual itemset and c the function defined by $c(\lt )\Rightarrow $ and $c(\gt )=\lt $. The gradual itemset $c(M)=({i_{1}^{c({\ast _{1}})}},\dots ,{i_{k}^{c({\ast _{k}})}})$ is defined as the complement of M.
In the literature, it is often assumed that $c(\geqslant )=\leqslant $, $c(\leqslant )=\geqslant $, $c(\lt )\Rightarrow $ and $c(\gt )=\lt $. However, as in the work of Berzal et al. (2007), in this work, we will only consider strict inequalities. For example, the gradual itemset ${A^{\gt }}{S^{\lt }}$ is the complement of the gradual itemset ${A^{\lt }}{S^{\gt }}$.
Definition 5 (Gradual rule).
A gradual rule, denoted R: ${M_{1}}\to {M_{2}}$, is a causal relationship between two gradual patterns ${M_{1}}$ and ${M_{2}}$. ${M_{1}}$ is called the antecedent or premise of the rule and ${M_{2}}$ the consequent.
The rule ${A^{\geqslant }}\to {S^{\geqslant }}$ means “if the age increases, the salary increases”. The fundamental difference between a gradual rule and a gradual pattern is that the gradual rules reflect the causal trends observed in the dataset while the gradual patterns reflect the co-variation trends.
Definition 6 (Concordant pairs).
A concordant pair with respect to a gradual itemset is a pair of objects in the database that satisfies the order induced by the said itemset.
For example, $\{({p_{1}},{p_{2}}),({p_{1}},{p_{3}}),({p_{1}},{p_{4}}),({p_{2}},{p_{4}}),({p_{3}},{p_{2}}),({p_{3}},{p_{4}})\}$ is the set of concordant pairs with respect to item ${A^{\gt }}$. In contrast to the concordant pairs, we distinguish the discordant pairs.
Definition 7 (Binary matrix of an itemset, Di-Jorio et al., 2009a).
Let $\mathcal{D}$ be a database made up of m attributes and n objects, ${M_{k}}$ a gradual itemset of size k. The binary matrix of gradual itemset ${M_{k}}$ is the square binary matrix of order n such that the inputs are the n objects of the database and for any pair of objects $(o,{o^{\prime }})$ $\in \mathcal{D}X\mathcal{D}$, the entry $(o,{o^{\prime }})$ of the matrix is 1 if the pair is concordant and 0 otherwise.
Table 2 illustrates the notion of binary matrix of a gradual itemset and the calculation of the binary matrix of a concatenation of itemsets. If ${\mathcal{L}_{{M^{\prime }}}}$ and ${\mathcal{L}_{{M^{\prime\prime }}}}$ are respectively the binary matrices of the itemsets ${M^{\prime }}$ and ${M^{\prime\prime }}$, the matrix ${\mathcal{L}_{{M^{\prime }}{M^{\prime\prime }}}}$ of the itemset ${M^{\prime }}{M^{\prime\prime }}$ is ${\mathcal{L}_{{M^{\prime }}{M^{\prime\prime }}}}={\mathcal{L}_{{M^{\prime }}}}\hspace{2.5pt}\textbf{AND}\hspace{2.5pt}{\mathcal{L}_{{M^{\prime\prime }}}}$, where AND is the logical conjunction operator, i.e. ${\mathcal{L}_{{M^{\prime }}{M^{\prime\prime }}}}[i,j]={\mathcal{L}_{{M^{\prime }}}}[i,j]\hspace{2.5pt}\textbf{AND}\hspace{2.5pt}{\mathcal{L}_{{M^{\prime\prime }}}}[i,j]$ for any pair of indexes $(i,j)$.
Table 2
Binary matrices of some itemsets from database $\mathcal{D}$ in Table 1.
| ${\mathcal{L}_{{A^{\gt }}}}$ | ${\mathcal{L}_{{S^{\gt }}}}$ | ${\mathcal{L}_{{C^{\gt }}}}$ | ||||||||||
| ↱ | ${p_{1}}$ | ${p_{2}}$ | ${p_{3}}$ | ${p_{4}}$ | ${p_{1}}$ | ${p_{2}}$ | ${p_{3}}$ | ${p_{4}}$ | ${p_{1}}$ | ${p_{2}}$ | ${p_{3}}$ | ${p_{4}}$ |
| ${p_{1}}$ | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| ${p_{2}}$ | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| ${p_{3}}$ | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| ${p_{4}}$ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| ${\mathcal{L}_{{A^{\gt }}{S^{\gt }}}}$ | ${\mathcal{L}_{{A^{\gt }}{C^{\gt }}}}$ | ${\mathcal{L}_{{A^{\gt }}{S^{\gt }}{C^{\gt }}}}$ | ||||||||||
| ↱ | ${p_{1}}$ | ${p_{2}}$ | ${p_{3}}$ | ${p_{4}}$ | ${p_{1}}$ | ${p_{2}}$ | ${p_{3}}$ | ${p_{4}}$ | ${p_{1}}$ | ${p_{2}}$ | ${p_{3}}$ | ${p_{4}}$ |
| ${p_{1}}$ | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 |
| ${p_{2}}$ | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ${p_{3}}$ | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ${p_{4}}$ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Proposition 1 (Binary matrix of a complementary itemset).
If ${\mathcal{L}_{M}}$ is the binary matrix of the gradual itemset M, the binary matrix of the complementary gradual itemset ${M^{c}}$ can be deduced from that of M by transposing ${\mathcal{L}_{M}}$, i.e. ${\mathcal{L}_{{M^{c}}}}={t_{{\mathcal{L}_{M}}}}$.
The extraction of the relevant gradual patterns and rules is based on quality criteria that are based on the concept of support and the concept of trust. The definition of the support concept varies depending on the extraction method. This paper considers the definition based on the notion of concordant pairs.
Definition 8 (Support of a gradual pattern, Berzal et al., 2007).
The support $\textit{Supp}(M)$ of a gradual pattern $M=\{({A_{j}^{\ast }}{\ast _{j}}),\hspace{2.5pt}j=1..k\}$ is the ratio of the number of concordant pairs with respect to M on the half of the total number of pairs of the database:
Table 3 illustrates the notion of gradual support.
Table 3
Gradual supports of some itemsets from database $\mathcal{D}$ in Table 1.
| Itemset | Complementary itemset | List of concordant pairs | Support |
| ${A^{\gt }}$ | ${A^{\lt }}$ | $\{({p_{1}},{p_{2}})$, $({p_{1}},{p_{3}})$, $({p_{1}},{p_{4}})$, $({p_{2}},{p_{4}})$, $({p_{3}},{p_{2}})$, $({p_{3}},{p_{4}})\}$ | $6/6$ |
| ${S^{\gt }}$ | $S\lt $ | $\{({p_{1}},{p_{2}})$, $({p_{1}},{p_{4}})$, $({p_{2}},{p_{4}})$, $({p_{3}},{p_{2}})$, $({p_{3}},{p_{4}})\}$ | $5/6$ |
| ${C^{\gt }}$ | ${C^{\lt }}$ | $\{({p_{1}},{p_{2}})$, $({p_{1}},{p_{3}})$, $({p_{1}},{p_{4}})$, $({p_{2}},{p_{3}})$, $({p_{4}},{p_{2}})$, $({p_{4}},{p_{3}})\}$ | $6/6$ |
| ${A^{\gt }}{S^{\gt }}$ | ${A^{\lt }}{S^{\lt }}$ | $\{({p_{1}},{p_{2}})$, $({p_{1}},{p_{4}})$, $({p_{2}},{p_{4}})$, $({p_{3}},{p_{2}})$, $({p_{3}},{p_{4}})\}$ | $5/6$ |
| ${A^{\gt }}{C^{\gt }}$ | ${A^{\lt }}{C^{\lt }}$ | $\{({p_{1}},{p_{2}})$, $({p_{1}},{p_{3}})$, $({p_{1}},{p_{4}})\}$ | $3/6$ |
| ${A^{\gt }}{S^{\gt }}{C^{\gt }}$ | ${A^{\lt }}{S^{\lt }}{C^{\lt }}$ | $\{({p_{1}},{p_{2}})$, $({p_{1}},{p_{4}})\}$ | $2/6$ |
2.2 Some Approaches to Extracting Gradual Itemsets
The first approach is based on the notion of linear regression (Hüllermeier, 2002). It only considers fuzzy data and rules whose premise and conclusion have a size less than or equal to two. However, the notion of T-norm makes it possible to overcome the size limitation of the premises and conclusions of the gradual rules. This approach makes it possible to extract the gradual rules.
The second approach evaluates the support of a gradual pattern as a function of the number of concordant pairs and the total number of pairs in the database. The support calculation formula proposed in Berzal et al. (2007), corresponds to that of Definition 1. This definition is implemented in the Graank algorithm (Laurent et al., 2009), which extracts frequent gradual patterns. However, in some works, instead of considering half of the total number of pairs in the database, the total number of pairs in the database is considered instead and the support formula becomes:
The Graank algorithm is based on the Apriori principle, also known as the generate-test principle, which consists of generating candidate itemsets, calculating the gradual support of said candidates and retaining only those candidates whose support is greater than the minimum support threshold. This algorithm performs a breadth-first search of the search space. During the first iteration, it generates candidates of size 1 and retains only those that are frequent. More generally, in the $(k-1)$-th iteration, it generates the candidates of size k and selects those that are frequent. The algorithm stops if none of the candidates of an iteration is frequent.
(3)
\[ \textit{Supp}(M)=\frac{|\{(o,{o^{\prime }})\in \mathcal{D}x\mathcal{D}\mid o{\lt _{M}}{o^{\prime }}\}|}{|\mathcal{D}|(|\mathcal{D}|-1)}.\]The third approach evaluates the support of a gradual pattern based on the longest path of its precedence graph. The nodes of the graph are the objects of the database and the arcs translate variations which are in adequacy with the set of comparison operators of the pattern. The graph of precedence of a gradual pattern is a graphic representation of its binary matrix. The Grite algorithm (Di-Jorio et al., 2009c), which extracts frequent gradual patterns, is based on this approach. Like Graank, Grite is based on the Apriori principle. Its weakness comes from the relatively high cost of calculating the longest path of a precedence graph. Therefore, the computational cost of gradual support is high compared to that of Graank. On the other hand, Graank takes into account the magnitude of the distortion for data that do not satisfy the gradual itemsets. Indeed, the deletion of an object can considerably reduce the value of the support and lead to additional calculations in the Grite algorithm.
3 An Improved Algorithm
3.1 Presentation of Two Versions of the Proposed Algorithms
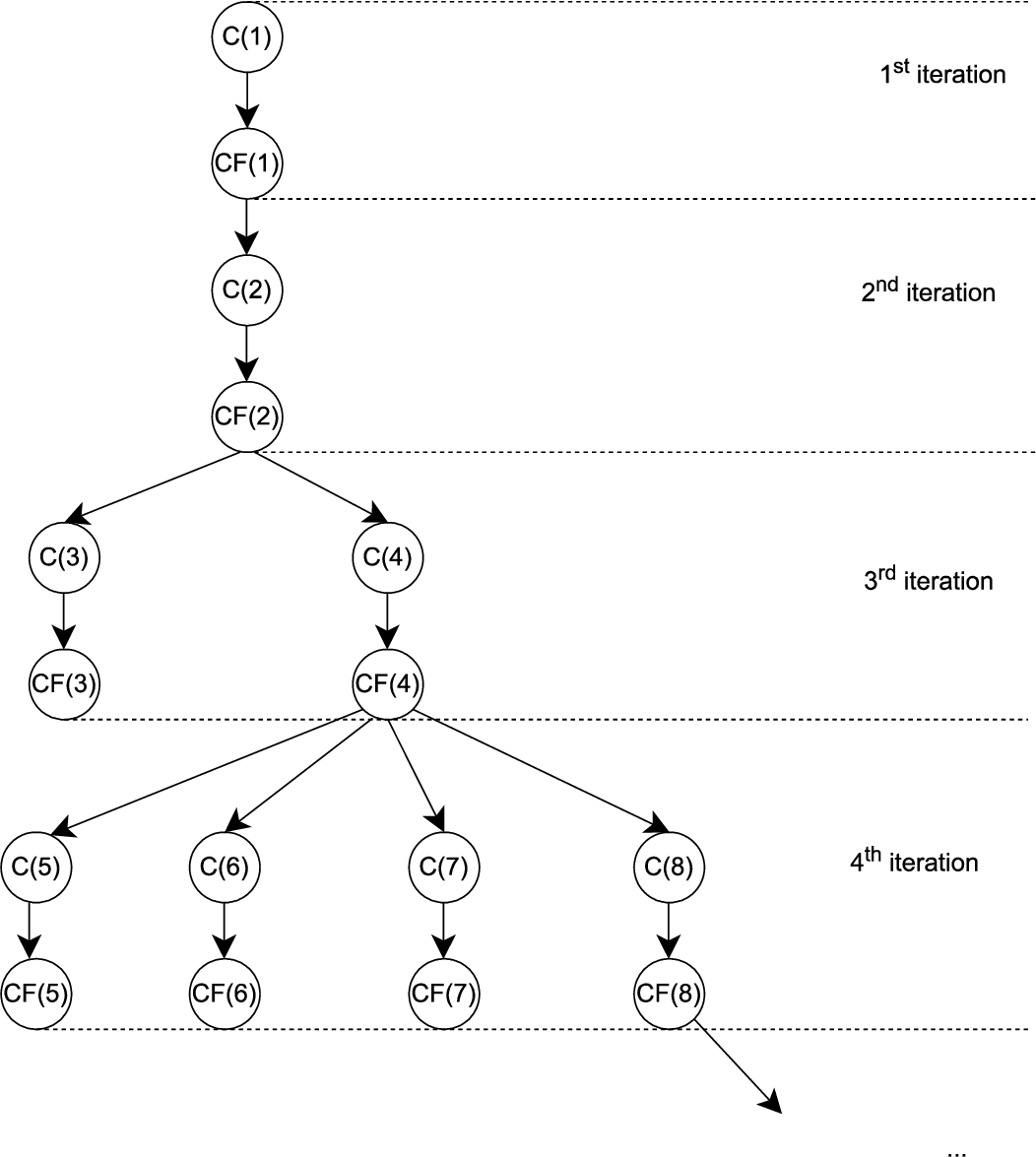
Fig. 1
General principle of the new algorithm. In this figure $\text{C}(i)$ is the set of all candidates itemsets of size i and $\text{CF}(i)$ the set of all frequents itemsets of size i.
Like most pattern discovery algorithms following the Apriori principle, the Graank algorithm performs a breadth-first traversal of the search space to identify frequent gradual itemsets. In this algorithm, the generation of candidate itemsets of size $(k+1)$ is performed by exploiting only gradual and frequent itemsets of size k. To do this, two frequent itemsets of size k are concatenated to form a candidate of size $(k+1)$ if they have $(k-1)$ items in common. The size of a candidate determines his level. For example, if ${A^{+}}{S^{+}}$ and ${A^{+}}{C^{+}}$ are frequent, we concatenate them to obtain the candidate ${A^{+}}{S^{+}}{C^{+}}$ of size 3, i.e. of level 3. At the k-th iteration, the algorithm generates all candidates of size k from the frequent itemsets of size $k-1$, then searches for candidates that are frequent. If $k=1$, the set of candidates is equal to the set of items. The algorithm stops as soon as no frequent itemset is found in an iteration. When $k\geqslant 2$, the k-th iteration requires a memory area to store all frequent itemsets of level $k-1$ with their binary matrix and frequent candidates of level k with their binary matrix. The cost of this storage can be important. The binary matrix of a candidate of size k is obtained as a product of two matrices from two frequent itemsets of size $k-1$. Thus, the binary matrix of a candidate of size k is obtained from $(k-1)$ matrix products. Because of this, the total cost of matrix products can significantly increase the running time of Graank.
The new algorithm presented here attempts to correct Graank’s weaknesses. Compared to Graank, at iteration $k\geqslant 3$, it reduces the memory space needed to store the itemsets used to generate the candidates and the frequent itemsets discovered at iteration k that will be used at iteration $(k+1)$ to generate the candidates. Moreover, it significantly reduces the number of matrix products needed to determine the binary matrix of a candidate. The first difference between Graank and the proposed algorithm concerns the way candidates are generated. All candidates from size $(k+1)$ up to size $2k$ are generated only from gradual and frequent itemsets of size k. In this candidate generation approach, two frequent itemsets of size k and having p items in common make it possible to generate a candidate of size $(2k-p)$, between $2k+1$ and $2k$. The second difference comes from the processing carried out at each iteration as illustrated in Fig. 1. However, we start by searching for all the frequent items before entering the iteration phase. As in Graank, the iterations are numbered starting from 1. However, during iteration $k\geqslant 1$, instead of searching for all the frequent itemsets of level k as in Graank, we rather search for all the frequent itemsets of the levels ${2^{k-1}}+1$ up to ${2^{k}}$. In the first version of the algorithm, at the k-th iteration, the algorithm generates all candidates whose size is between $({2^{k-1}}+1)$ to ${2^{k}}$ only from the frequent itemsets of sizes ${2^{k-1}}$ obtained at the $k-1$ iteration. Then, it goes through all the candidates in ascending order of their level, from level $({2^{k-1}}+1)$ to ${2^{k}}$, to select those who are frequent. Like Graank, the proposed algorithm performs a breadth-first traversal of the search space and stops as soon as it encounters the first level which does not contain a frequent candidate. In the second version of the algorithm, at the k-th iteration, the algorithm does not simultaneously store all the candidates whose level varies from $({2^{k-1}}+1)$ to ${2^{k}}$. It performs an internal iteration which at each step generates a candidate, calculates its binary matrix and determines if it is frequent. The second version of the algorithm stops at the beginning of iteration k if there is no frequent itemset of size ${2^{k-1}}$.
Algorithms 1 and 2 describe two versions of the improved algorithm. They take as input a database and a minimal support provided by the user, and return the set of frequent gradual patterns. Table 4 describes the list of symbols used in the algorithms. As in Graank, both versions of the proposed algorithm exploit the notion of complementarity to reduce the search space by half. To do this, only itemsets with a positive first term are handled. Both versions search and store all frequent itemsets in main memory. Both versions of the algorithm can be modified in the following way to display each frequent itemset immediately after its discovery and in such a way as to reduce the consumption of main memory:
There are two main differences between Algorithms 1 and 2. The first difference comes from the management of the memory space used to store the candidates of an iteration. During an iteration, Algorithm 1 generates the set of all candidates and selects the frequent ones while Algorithm 2 generates the first candidate and keeps it if it is frequent, then generates the second candidate and retains it if it is frequent, and so on. Thus Algorithm 1 requires an additional memory space to store all the candidates of each iteration while Algorithm 2 does not need such memory space. The key idea of Algorithm 2 is to save memory. The second difference comes from their termination criteria. Algorithm 1 could terminate during one iteration without computing the supports of all candidates in said iteration while Algorithm 2 cannot do this because it calculates the supports of all the candidates of an iteration. As a result, Algorithm 1 generally finishes before Algorithm 2.
Table 4
List of symbols.
| Notation | Signification |
| $\mathcal{D}$ | Database |
| ${F_{k}^{+}}$ | Set of frequent itemsets of sizes k whose first term is positive |
| ${C_{k}^{+}}$ | Set of candidate itemsets of size k whose first term is positive |
| m | Number of database attributes |
| Threshold | Minimal support given by the user |
3.2 Complexity Analysis
This section studies the time and memory complexities of Graank and the proposed algorithms.
Consider a candidate c of level $l={2^{k-1}}+p$ for some p and some k, corresponding to the k-th iteration of the new algorithm, such that $1\leqslant p\leqslant {2^{k-1}}$. In Graank, c is derived from the concatenation of two frequent itemsets of size $(l-1)$, which in turn are each derived from the concatenation of two frequent itemsets of size $(l-2)$. By transitivity, c comes from the concatenation of ${2^{p}}$ frequent itemsets of size ${2^{k-1}}$. The matrix of c comes from a product of two matrices of level $(l-1)$, and each of them comes in turn from two matrices of level $(l-2)$ and so on. On the other hand, in both versions of the proposed algorithm, c is derived from the concatenation of two frequent itemsets of size ${2^{k-1}}$. Moreover, the matrix of c is issued from the product of two matrices of frequent itemsets of level ${2^{k-1}}$. The number of matrix products performed between the first and the k-th iteration for the computation of the matrix of c is k. Therefore, generating candidate c requires $(l-1)$ itemset concatenations and $(l-1)$ matrix products in Graank, while k itemset concatenations and k matrix products are needed in the proposed algorithms. This leads to Lemma 1.
Lemma 1.
The generation of a candidate of level $l={2^{k}}+p$, for some p and k, with its matrix requires $(l-1)$ itemset concatenations and $(l-1)$ matrix products in Graank, while k itemset concatenations and k matrix products are needed in the proposed algorithms.
Lemma 1 shows that the CPU cost of generating a candidate and computing its binary matrix is significantly improved.
Lemma 2.
Denote $TC$, $T{C_{1}}$ the time complexity of Graank and Algorithm 1 and 2 respectively. We have
and
where ${C_{l}^{g}}$ (resp. ${C_{l}}$) is the set of candidates of size l generated by Graank (resp. the proposed algorithms).
(4)
\[ TC={\sum \limits_{l=1}^{m}}\big|{F_{l-1}^{+}}\big|\big(\big|{F_{l-1}^{+}}\big|-1\big)2(l-1)+{\sum \limits_{l=1}^{m}}\big|{C_{l}^{g}}\big|{n^{2}}\](5)
\[ T{C_{1}}={\sum \limits_{k=1}^{\lceil {\log _{2}}(m)\rceil }}\big|{F_{{2^{k-1}}}^{+}}\big|\big(\big|{F_{{2^{k-1}}}^{+}}\big|-1\big){2^{k}}+{\sum \limits_{k=1}^{\lceil {\log _{2}}(m)\rceil }}\Big|\bigcup \limits_{{2^{k-1}}+1\leqslant l\leqslant {2^{k}}}{C_{l}}\Big|{n^{2}},\]Lemma 2 shows that, compared to Graank, the overall candidate generation runtime in the proposed algorithms is significantly improved. The overall runtime of the calculation of matrix multiplications is not improved although the execution time for the calculation of the matrix of a single itemset is significantly improved according to Lemma 1.
Denote by $MS(k)$, $M{S_{1}}(k)$ and $M{S_{2}}(k)$ the memory space required by the k-th iteration respectively in Graank, in the first and second versions of the proposed algorithm. $MS(k)$, $M{S_{1}}(k)$ and $M{S_{2}}(k)$ depend on the storage space of candidate itemsets and frequent itemsets. Here, we evaluate $MS(k)$, $M{S_{1}}(k)$ and $M{S_{2}}(k)$. In Graank, at iteration k, after generating a candidate of size k, its gradual support is calculated to know if it is frequent or not before generating the next candidate. Any frequent candidate discovered at iteration k is stored in ${F_{k}^{+}}$. Thus, in Graank, we have:
This is equivalent to:
In (6), the first expression is the memory space required to store all frequent itemsets discovered between levels 1 and $(k-2)$, without storing their matrices. The second expression is the memory space required to store all the frequent itemsets discovered at level $(k-1)$, with their matrices. All frequent itemsets of size $(k-1)$ and their matrices are used to generate all the candidates of size k and their matrices respectively. The third expression is the memory space required to store the current candidate and its matrix, i.e. the one being processed. The fourth expression is the memory space required to store all frequent itemsets of size k and their matrices.
In the first version of the proposed algorithm, iteration k starts by generating and storing all candidates whose size is between ${2^{k-1}}+1$ and ${2^{k}}$. Then, it performs a breadth-search of all candidates, i.e. level by level. The gradual support of the current candidate, i.e. the one being processed, is calculated to know if it is frequent or not. A frequent candidate of size l is stored in ${F_{l}^{+}}$ without its matrix if $l\lt {2^{k}}$ and with its matrix otherwise. Once all the candidates of the same level have been processed, their memory space is freed and used to store frequent itemsets. Thus, in the first version of the proposed algorithm, we have:
(8)
\[\begin{aligned}{}M{S_{1}}(k)& ={\sum \limits_{l=1}^{l={2^{k-1}}-1}}\big(\big|{F_{l}^{+}}\big|l\big)+\big|{F_{{2^{k-1}}}^{+}}\big|\big({2^{k-1}}+{n^{2}}\big)+\big({2^{k}}+{n^{2}}\big)\\ {} & \hspace{1em}+\bigg(\hspace{0.1667em}{\sum \limits_{l={2^{k-1}}+1}^{{2^{k}}}}\big(\big|{C_{l}^{+}}\big|l\big)+{\underset{l={2^{k-1}}+1}{\overset{{2^{k}}}{\max }}}\big(\big|{F_{l}^{+}}\big|l\big)\bigg)+\big|{F_{{2^{k}}}^{+}}\big|{n^{2}}.\end{aligned}\]This is equivalent to:
In (8), the first expression is the memory space required to store all frequent itemsets discovered between levels 1 and ${2^{k-1}}-1$, without storing their matrices. The second expression is the memory space required to store all the frequent itemsets discovered at level ${2^{k-1}}$ with their matrices. All frequent itemsets of size ${2^{k-1}}$ and their matrices are used to generate all candidates whose size is between ${2^{k-1}}+1$ and ${2^{k}}$ with their matrices respectively. The third expression is the memory space required to store the current candidate and its matrix, i.e. the one being processed. The fourth expression is the memory space needed to store all candidates of unprocessed levels and all frequent itemsets whose size is between ${2^{k-1}}+1$ and ${2^{k}}$ without their matrices. The fifth expression is the memory space required to store all the matrices of frequent itemsets of size ${2^{k}}$.
(9)
\[\begin{aligned}{}M{S_{1}}(k)& ={\sum \limits_{l=1}^{l={2^{k-1}}}}\big(\big|{F_{l}^{+}}\big|l\big)+\big|{F_{{2^{k-1}}}^{+}}\big|{n^{2}}+\big({2^{k}}+{n^{2}}\big)\\ {} & \hspace{1em}+\Bigg(\hspace{0.1667em}{\sum \limits_{l={2^{k-1}}+1}^{{2^{k}}}}\big(\big|{C_{l}^{+}}\big|l\big)+{\underset{l={2^{k-1}}+1}{\overset{{2^{k}}}{\max }}}\big(\big|{F_{l}^{+}}\big|l\big)\Bigg)+\big|{F_{{2^{k}}}^{+}}\big|{n^{2}}.\end{aligned}\]In the second version of the proposed algorithm, at iteration k, after generating a candidate whose size is between ${2^{k-1}}+1$ and ${2^{k}}$, its support is calculated to know if it is frequent or not before generating the next candidate. If the current candidate, i.e. the one being processed, is frequent and of size l, it is stored in ${F_{l}^{+}}$ without its matrix if $l\lt {2^{k}}$ and with its matrix otherwise. Thus, in the second version of the proposed algorithm, we have:
This is equivalent to:
(10)
\[\begin{aligned}{}M{S_{2}}(k)& ={\sum \limits_{l=1}^{l={2^{k-1}}-1}}\big(\big|{F_{l}^{+}}\big|l\big)+\big|{F_{{2^{k-1}}}^{+}}\big|\big({2^{k-1}}+{n^{2}}\big)+\big({2^{k}}+{n^{2}}\big)\\ {} & \hspace{1em}+{\sum \limits_{l={2^{k-1}}+1}^{l={2^{k}}-1}}\big(\big|{F_{l}^{+}}\big|l\big)+\big|{F_{{2^{k}}}^{+}}\big|\big({2^{k}}+{n^{2}}\big).\end{aligned}\](11)
\[\begin{aligned}{}M{S_{2}}(k)& ={\sum \limits_{l=1}^{l={2^{k-1}}}}\big(\big|{F_{l}^{+}}\big|l\big)+\big|{F_{{2^{k-1}}}^{+}}\big|{n^{2}}+\big({2^{k}}+{n^{2}}\big)\\ {} & \hspace{1em}+{\sum \limits_{l={2^{k-1}}+1}^{l={2^{k}}}}\big(\big|{F_{l}^{+}}\big|l\big)+\big|{F_{{2^{k}}}^{+}}\big|{n^{2}}.\end{aligned}\]This is equivalent to:
In formula (10), the first, second and third expressions have the same meaning as their counterpart in formula (8). The fourth expression is the memory space needed to store all frequent itemsets whose size is between ${2^{k-1}}+1$ and ${2^{k}}-1$ without their matrices. The fifth expression is the memory space required to store all frequent itemsets of size ${2^{k}}$ and their matrices.
Lemma 3.
We have $M{S_{2}}(k)\lt M{S_{1}}(k)$ and $MS({2^{k}})=M{S_{2}}(k)+(|{F_{{2^{k}}-1}^{+}}|-|{F_{{2^{k-1}}}^{+}}|){n^{2}}$.
Proof.
The first, second, third and fifth expression of formula (9) are respectively equal to their counterpart in formula (11). The fourth expression of formula (11) is less than its counterpart in formula (9). Thus, we have $M{S_{2}}(k)\lt M{S_{1}}(k)$. The calculation of $MS({2^{k}})-MS(k)$ using formulas (12) and (7) leads to $MS({2^{k}})=M{S_{2}}(k)+(|{F_{{2^{k}}-1}^{+}}|-|{F_{{2^{k-1}}}^{+}}|){n^{2}}$. □
Lemma 4.
Denote by ${k_{2}}$, $kg1$ and $kg2$, respectively, the iterations for which $S{M_{2}}(k)$, $SM(k)$and $SM({2^{k}})$ reach their maximum value. Denote by $\textit{SMC}$, ${\textit{SMC}_{1}}$ and ${\textit{SMC}_{2}}$ the spaces memory complexity required by Graank, Algorithm 1 and 2, respectively. We have:
(13)
\[\begin{aligned}{}& \textit{SMC}={\underset{k=1}{\overset{m}{\max }}}\big(MS(k)\big)\end{aligned}\](14)
\[\begin{aligned}{}& {\textit{SMC}_{1}}={\underset{k=1}{\overset{\lceil {\log _{2}}(m)\rceil }{\max }}}\big(M{S_{1}}(k)\big),\end{aligned}\](15)
\[\begin{aligned}{}& {\textit{SMC}_{2}}={\underset{k=1}{\overset{\lceil {\log _{2}}(m)\rceil }{\max }}}\big(M{S_{2}}(k)\big),\end{aligned}\]Proof.
(14) and (15) are straightforward from the respective definitions of $SM(k)$, $SM1(k)$ and $SM2(k)$. (16) is straightforward from equation $MS2(k)\lt MS1(k)$ established in Lemma 3. (17) and (18) are straightforward from equation $MS({2^{k}})=M{S_{2}}(k)+(|{F_{{2^{k}}-1}^{+}}|-|{F_{{2^{k-1}}}^{+}}|){n^{2}}$ established in Lemma 3. □
Lemma 4 shows that the first version of the proposed algorithm consumes more memory space than the second one which in turn can consume less or more memory space than Graank under certain constraints. However, the first version may stop one iteration before the second. Thus, the first version stops faster than the second. The second version stops at the start of an iteration that has no candidate. Such an iteration k implies that there is no frequent itemset of size ${2^{k-1}}$. The first version stop during an iteration whose some level has no frequent itemset. Such iteration k implies that there is no frequent itemset of size ${2^{k-1}}+p$, $1\leqslant p\leqslant {2^{k-1}}$, for some p.
4 Experimentations
This section compares three algorithms: Graank and two versions of the proposed algorithm. Section 4.1 presents datasets. Section 4.2 presents the results of the experimental comparisons.
4.1 Presentation of Datasets
In this section, we present four types of datasets: one agricultural dataset (Islam et al., 2018), three health datasets (Li and Liu, 2021; Chicco and Jurman, 2020), one economic dataset (Clémentin et al., 2021) and three synthetic datasets (Clémentin et al., 2021).
The agricultural dataset (agricultural-dataset-bangladesh) comes from information collected on 28 agricultural areas of Bangladesh. It provides relationships between soil nutrients, types of fertilizers, types of soil and meteorological information. The soil nutrients were collected on 6 different types of land: flooded land at high altitude, flooded land at medium altitude, medium land, medium low land, flood low land, very low flood land and miscellaneous land. We have 4 types of fertilizers (urea, triple superphosphate, diammonium dhosphate, and MP). The types of soils come from 19 different types of soil and 4 different types of soil information. The meteorological data come from the Bangladesh Meteorological Department (BMD), providing information on average rainfall, maximum and minimum temperature, and humidity from 2008–2017. The complete description of the different attributes are given in Islam et al. (2018). The initial database is composed of 44 attributes and 70 transactions. For experimentation purposes, non-numeric attributes and those with missing values were remove, reducing the number of attributes to 32. The acces link to the agricultural dataset is https://www.kaggle.com/tanhim/agricultural-dataset-bangladesh-44-parameters
The three health datasets are described in the following.
-
1. The first health dataset concerns diabetes (diabetes.csv). It comes from the national institute of diabetes and digestive and kidney diseases. It is composed of 9 numeric attributes and 768 transactions. The objective of this dataset is to predict whether a patient is diabetic or not, based on certain diagnostic measures included in the dataset. Several constraints were placed on the selection of these instances from a larger database. In particular, all patients here are females at least 21 years old and of Pima Indian origin. The dataset is composed of several medical predictor variables and a target variable. The predictor variables include the number of pregnancies the patient has had, her BMI, insulin level, age, blood pressure, triceps skinfold thickness and diabetes pedigree function. The acces link to the diabete dataset is https://www.kaggle.com/uciml/pima-indians-diabetes-database
-
2. The second health dataset concerns child mortality (fetal_health.csv) (Li and Liu, 2021). These data come from Larxel Volunteer (São Paulo), It is a set of 22 numerical attributes and 2126 transactions. Due to memory limitations, only 200 transactions were considered in experimentations. The objective of this dataset is to predict fetal health allowing healthcare professionals to take action to prevent infant and maternal mortality. The different attributes in the dataset are based on Fetal Heart Rate (FHR), fetal movements, uterine contractions. The access link to the child mortality dataset is https://www.kaggle.com/andrewmvd/fetal-health-classification
-
3. The third and last health dataset contains medical records of 299 patients with heart failure collected at Faisalabad Heart Institute and Allied Hospital Faisalabad (Punjab, Pakistan), between April and December 2015 (heart_failure_clinical_records.csv) (Chicco and Jurman, 2020). It is a set of 13 numeric attributes and 299 transactions. The access link to this dataset is https://www.kaggle.com/andrewmvd/fetal-health-classification
The economic dataset comes from the Nasdaq Financials dataset (fundamentals.csv) (Clémentin et al., 2021). It contains 35 attributes and 300 transactions. Due to memory limitations, only the first 20 attributes and the first 150 transactions were considered in experimentations. The access link of the economic dataset is https://www.kaggle.com/dgawlik/nyse?select=fundamentals.csv.
The three synthetic datasets are C250-A100-50 (Negrevergne et al., 2014), F20Att00Li (Negrevergne et al., 2014) and test (Negrevergne et al., 2014). The access link to all these datasets is https://github.com/bnegreve/paraminer/tree/master/data/gri
The characteristics of these datasets are summarized in Table 5.
4.2 Experimental Evaluation of Algorithms
This section compares the performance of the Graank algorithm (Laurent et al., 2009) and the two versions of the proposed algorithms. Experiments were performed on a computer with a Intel(R) Core(TM) i7 CPU M 620 @ 2.67 GHz 2.67 GHz with 6 GB RAM, running on Windows 10 Home 64-bit operating system. The different algorithms are implemented in Java. The purpose of experiments is to compare the runtime as depicted on Figs. 2, 3, 4, 5 and the memory consumption as shown in Figs. 6, 7, 8, 9 for different support threshold values on datasets presented on Section 4.1.
4.2.1 Runtime Evaluation of Algorithms
Figure reffig:timeagriculture shows the runtime performance of the three algorithms on the agricultural dataset. The two versions of the proposed algorithm have almost similar execution times and are sometimes at least five times faster than Graank.
Figure 3 shows the runtime performances of the three algorithms on the three medical datasets. The two versions of the proposed algorithm are globally faster than Graank on medical datasets. Moreover, they are sometimes seven times faster than Graank on the diabete dataset and twice as fast as Graank on fetal health and heart failure datasets. However, for some support threshold values, both versions of the proposed algorithm are slightly slower than Graank. This is due to the matrix multiplication times according to Lemma 2. As with the agricultural dataset, the two versions of the proposed algorithm have nearly similar runtimes on medical datasets.
4.2.2 Memory Evaluation of Algorithms
Figure 6 shows the memory consumption on agricultural dataset. The memory consumption of both versions of the proposed algorithm is less than that of Graank for support threshold values which are less than 0.37 and slightly higher otherwise.
Figure 7 shows memory consumption on medical datasets. The memory consumption of both versions of the proposed algorithm is lower than that of Graank. On the other hand, the second version uses less memory than the first one.
Figure 8 shows the memory consumption on the economical dataset. The memory consumption of both versions of the proposed algorithm is lower than that of Graank. Moreover, the second version uses less memory than the first one.
Figure 9 shows the memory consumption on synthetic datasets. The memory consumption of both versions of the proposed algorithm is lower than that of Graank on the first two datasets and slightly higher than that of Graank on the third dataset. As with the economic dataset, the second version consumes less memory than the first one.
In summary, the memory evaluation shows that, in general, Algorithms 1 and 2 outperform Graank in terms of memory consumption and they require sometimes at most half the memory. Between Algorithms 1 and 2, the advantage goes to Algorithm 2 in terms of memory consumption. However, there are marginal cases where Graank consumes less memory than Algorithms 1 and 2. Formula (18) in Lemma 4 characterizes some of the said cases.
4.3 Presentation of Some Interesting Patterns
This section presents some interesting patterns extracted from real datasets.
4.3.1 Case of the Agricultural Dataset
Here some interesting gradual patterns extracted from the agricultural-dataset-bangladesh dataset, with the minimum support threshold $\textit{minSupp}=43\% $: “the more calcareous brown floodplain soil increases, the more calcareous dark grey floodplain soil increases, the more non calcareous grey floodplain soil increases and the more non calcareous dark grey floodplain soil increases” $(\textit{Supp}=51.46\% )$; “the more average rainfall increase, the more minimum temperature increase, the more the boron content increases and the more potato yield increases” $(\textit{Supp}=51.80\% )$.
4.3.2 Case of Health Datasets
Here are some interesting gradual patterns extracted from the diabetes dataset with the minimum support threshold $\textit{minSupp}=4\% $: “the more number of times pregnant increases, the more plasma glucose concentration after 2 hours in an oral glucose tolerance test increases, the more diastolic blood pressure increases, the more body mass index increases and the more age increases” $(\textit{Supp}=16.45\% )$; “the more triceps skin fold thickness increases, the more 2-hour serum insulin level increases, the more body mass index increase and the more diabetes pedigree function increases” $(\textit{Supp}=23.36\% )$.
Here are some interesting gradual patterns extracted from the fetal heart dataset with the minimum support threshold $\textit{minSupp}=6.9\% $ : “the more number of fetal movements per second increases, the more percentage of time with abnormal short term variability decreases, the more width of the histogram made using all values from a record increases and histogram minimum value decreases” $(\textit{Supp}=30.49\% )$; “the more percentage of time with abnormal short term variability increases, the more width of the histogram made using all values from a record decreases, the more histogram minimum value increases and the histogram maximum value decreases and the more histogram variance decreases” $(\textit{Supp}=42.25\% )$.
Here are some interesting gradual patterns extracted from the heart failure dataset with the minimum support threshold $\textit{minSupp}=4\% $: “the more age increases, the more Level of serum creatinine in the blood increases and the more follow-up period (days) decreases” $\textit{Supp}=31.92\% $; “the more percentage of blood leaving the heart at each contraction increases, the more number of platelets in the blood increases and the more follow-up period (days) increases” $(\textit{Supp}=23.97\% )$.
4.3.3 Case of the Economic Dataset
Here are some interesting gradual patterns extracted from the fundamentals dataset, with the minimum support threshold $\textit{minSupp}=5.625\% $: “the more capital expenditure increases, the more earnings before interest and tax decrease, the more earnings before tax decrease and the more fixed asset decreases” $(\textit{Supp}=57.86\% )$; “the more cost of revenue increases, the more earnings before interest and tax increase and the more earnings before tax increase” $(\textit{Supp}=63.49\% )$.
5 Conclusion
In this paper, we have presented a new approach to improve the performance of frequent gradual pattern mining algorithms by reducing the candidate generation and processing costs. The complexity analysis and experimental performances carried out on different databases are to the advantage of the proposed approach compared to the previous ones, which confirms the effectiveness of the new approach. Sometimes, the CPU consumption gain factor is greater than 5 and the memory consumption gain factor is greater than 2. However, the theoretical and experimental studies carried out in this article reveal marginal cases for which Graank requires less memory than the proposed approach. This work opens interesting perspectives. Studying how to reduce the memory space required by Graank for marginal cases is an interesting research question. This may lead to an adaptation or improvement of the candidate generation and processing technique proposed in this paper. It could also lead to the design of a new technique. It is also interesting to study the integration of the proposed candidate generation and processing technique into other data mining algorithms in order to improve their performance. Another research question is to study how to parallelize the algorithms in which the technique proposed in this paper has been integrated in order to take advantage of the benefits offered by parallel computing for processing large datasets.