Abstract
Many confidential multimedia, such as personal privacy, commercial, and military secrets, are transmitted on the Internet. To prevent this confidential multimedia from being eavesdropped on by illegal users, information-hiding technology is a leading research topic nowadays. One of the important research topics of information-hiding technology is coverless information hiding, which utilizes the unchanged property of its multimedia carrier to hide secret information. In this paper, we propose two schemes that employ the average pixel value of an image. The first is an extension of the Coverless Information Hiding Based on the Most Significant Bit (CIHMSB) scheme, referred to as E-CIHMSB. In the E-CIHMSB, we build an extended matrix containing the image fragment’s average pixel value. The second scheme is a combination theory-based CIHMSB, referred to as CB-CIHMSB. In the CB-CIHMSB, we construct the combined matrix. E-CIHMSB and CB-CIHMSB embed the secret bits by changing the most significant bits of the chosen pixel in the matrix. Experimental results show that our schemes achieved higher hiding capacity than previous related schemes. Moreover, the proposed scheme is more robust against steganalysis tools and image quality attacks such as Additive Gaussian White Noise (AWGN), Salt & Pepper noise, low-pass filtering attacks, and JPEG compression attacks than CIHMSB.
1 Introduction
The need for information security in the internet age is inevitable. This is because sensitive information such as military, health care, economic, and personal data is exposed in many applications (Stillman and Defiore,
1980; Liang
et al.,
2020; Oh
et al.,
2019; Iwaya
et al.,
2020; Coleti
et al.,
2020). One solution to this issue is to implement data-hiding techniques. There are two types of data hiding mechanisms: covered and coverless. Covered information hiding is a well-known and widely investigated topic. In a covered information hiding scenario, the sender must provide a cover media to embed secret messages and create stego media. Cover media include images, audio, and video formats (Mahmoud and Elshoush,
2022; Cogranne
et al.,
2022; Yi
et al.,
2019; Liu Y.
et al.,
2022; Mstafa
et al.,
2020; Wang
et al.,
2019). The stego media is then delivered to the recipient. The alteration of the stego media causes distortion and leaves a trace for steganographic analysis tools. Moreover, the hiding capacity of the covered information hiding method has certain limitations due to balancing the stego image quality. Because the greater the hiding capacity, the lower the image quality.
On the other side, the coverless information hiding offers higher hiding capacity without affecting the image quality. The secret messages and cover images are sent as a code stream to the recipient. Furthermore, the coverless information hiding method is more robust against the steganographic analysis tools. The coverless information hiding method utilizes the unchanged property of its multimedia carrier to hide secret information such as pixel value, brightness, and texture. There are several current researches in coverless data hiding (Qin
et al.,
2019; Peng
et al.,
2022; Zhou
et al.,
2019; Wang and Gao,
2019; Luo
et al.,
2021; Zhou
et al.,
2022; Chen
et al.,
2022; Zhang
et al.,
2018; Liu
et al.,
2022; Yang
et al.,
2020; Long
et al.,
2019; Saad
et al.,
2021; Anggriani
et al.,
2023a,
2023b).
In 2020, Peng
et al. (
2022) proposed a coverless information-hiding method based on the Most Significant Bit (MSB) of the cover image (CIHMSB). Their scheme was fragment-based calculation. Begin by segmenting the cover image into several fragments, calculating the average intensity of each fragment, and using the MSB to represent the secret information. As a result, the mapping sequence is used to establish a mapping between the image fragment’s MSB and the confidential data. This process generates a mapping flag sent along with the stego image by the sender.
Yang
et al.’s scheme (
2020) is highly resistant to all steganalysis tool attacks because the cover image is the same as the stego image. This scheme, however, has a lower embedding capacity. This is because each segment only embeds one bit—the larger the fragment, the lower the embedding capacity. To address this issue, we propose a change in which the fragment value is used. In addition, we add more average value of the fragment by implementing the concept of combination theory. We can improve the embedding capacity by conducting this approach. Moreover, the proposed scheme is more robust against steganalysis tools and image attacks.
The remainder of the work is presented: Section
2 presents the criteria for evaluating the information-hiding method’s performance. Section
3 explains our proposed method. Then, Section
4 discusses the experimental results. Finally, Section
5 addresses the conclusions.
2 The Evaluation Criteria
This section presents some of the parameters used to measure the performance of the information-hiding method. Three evaluation criteria are generally used: image quality assessment, hiding capacity assessment, and robustness analysis.
2.1 Image Quality Assessment
The image quality was assessed using the structural similarity (SSIM) index and universal image quality $({Q_{i}})$ index.
The structural similarity (SSIM) index measures the similarity between the cover and stego images. Its value ranges from −1 to +1. When the cover image is the same as the stego image, SSIM is equal to 1, which is also the optimal value of SSIM. It can be expressed by (
1):
where
$\bar{p}$ and
$\bar{q}$ represent the average pixel values of the cover and stego images,
${\sigma _{x}^{2}}$ and
${\sigma _{y}^{2}}$ represent the standard deviation of the cover image and the stego image, respectively. And
${\sigma _{xy}}$ represents the covariance between the cover and stego images. Constant
${c_{1}}=2.55$,
${c_{2}}=7.65$.
The universal image quality index
$({Q_{i}})$ is another important parameter to measure the similarity between the cover and stego images. When the cover image is the same as the stego image,
${Q_{i}}$ can get the optimal value of 1. The definition of
${Q_{i}}$ is as (
2):
where
$\bar{p}$ and
$\bar{q}$ represent the average pixel values of the cover and stego images,
${\sigma _{x}^{2}}$ and
${\sigma _{y}^{2}}$ represent the standard deviation of the cover and stego images. In contrast,
${\sigma _{xy}}$ represents the covariance between the cover and stego images.
2.2 Hiding Capacity Assessment
Hiding capacity is defined as the number of secret bits carried in an image. The measurement is $(\textit{bits}\ast {\textit{carrirer}^{-1}})$.
2.3 Robustness Analysis
Robustness analysis is done by providing an attack on the image. Some commonly used image attacks are Additive Gaussian White Noise (AGWN), salt & pepper noise, Low-pass filtering, and JPEG compression. The attack is done on multiple tests. The final results are averaged over multiple tests.
Bit Error Rate (
BER) is used as the criterion to evaluate the robustness. BER is defined as:
where
${N_{m}}$ represents the number of bits with errors when extracting secret information from the stego image, and
${N_{n}}$ represents the total number of bits of secret information to be hidden. The smaller the BER, the more robust the information-hiding method.
3 The Proposed Method
To address the limitation of hiding capacity in Peng
et al. (
2022), we propose two improvement schemes: An extension of Yang
et al.’s scheme and the combination theory-based scheme. The flowchart of the proposed schemes is depicted in Fig.
1 and Fig.
4, respectively. Furthermore, the proposed schemes can be classified into embedding and extracting procedures explained in the following subsections.
3.1 An Extension of Yang et al.’s Scheme
We extend Yang
et al.’s scheme (
2020) by adding an extra average of the fragments; for convenience, we call it E-CIHMSB. The proposed embedding procedures consist of three main steps: cover image preparation, secret data preparation, and mapping. Firstly, preprocess the cover image into fragment image
${S_{i}}$. Then form an extended matrix that contains the average value of the fragment. Secondly, preprocess the secret data into binary format
${M_{i}}$ so that it can be operated with the MSB of
${V_{i}}$. Finally, a mapping operation between the MSB of
${v_{i}}$ and
${M_{i}}$ is conducted. The embedding procedure is detailed and presented below:
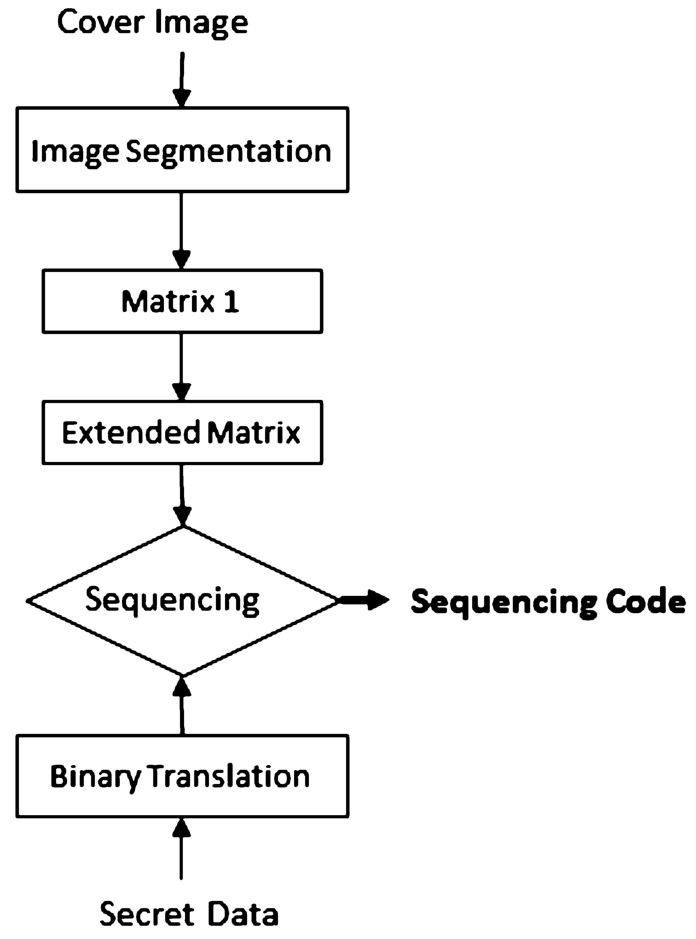
Fig. 1
The flowchart of an extension of Yang et al.’s scheme.
Table 1
The mapping rule of embedding procedure.
| ${M_{i}}$ |
MSB of ${v_{i}}$
|
${Z_{i}}$ |
| 0 |
0 |
1 |
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
1 |
Suppose we have a cover image
I of size 8 × 8 pixels. Firstly, preprocess the cover image into a 4 × 4 non-overlapping fragment, so the number of fragment
${S_{i}}=4$. Then, form a Matrix 1 and extended matrix. The cover image preparation is presented in Fig.
2. Therefore, based on equation (
5), we can embed 5 bits of secret data. Suppose the character of secret data is A (the decimal value is 65). Convert into seven-binary format
${\boldsymbol{M}_{\boldsymbol{i}}}=\mathbf{1},\mathbf{0},\mathbf{0},\mathbf{0},\mathbf{0},\mathbf{0},\mathbf{1}$. Then, the embeddable
${M_{i}}=1,0,0,0,0$. Suppose the mapping key
$\boldsymbol{Q}=\mathbf{2},\mathbf{1},\mathbf{4},\mathbf{3},\mathbf{5}$. Finally, based on the rule in Table
1,
${Z_{i}}=\textbf{0 1 1 1 1}$, as shown in Fig.
3.
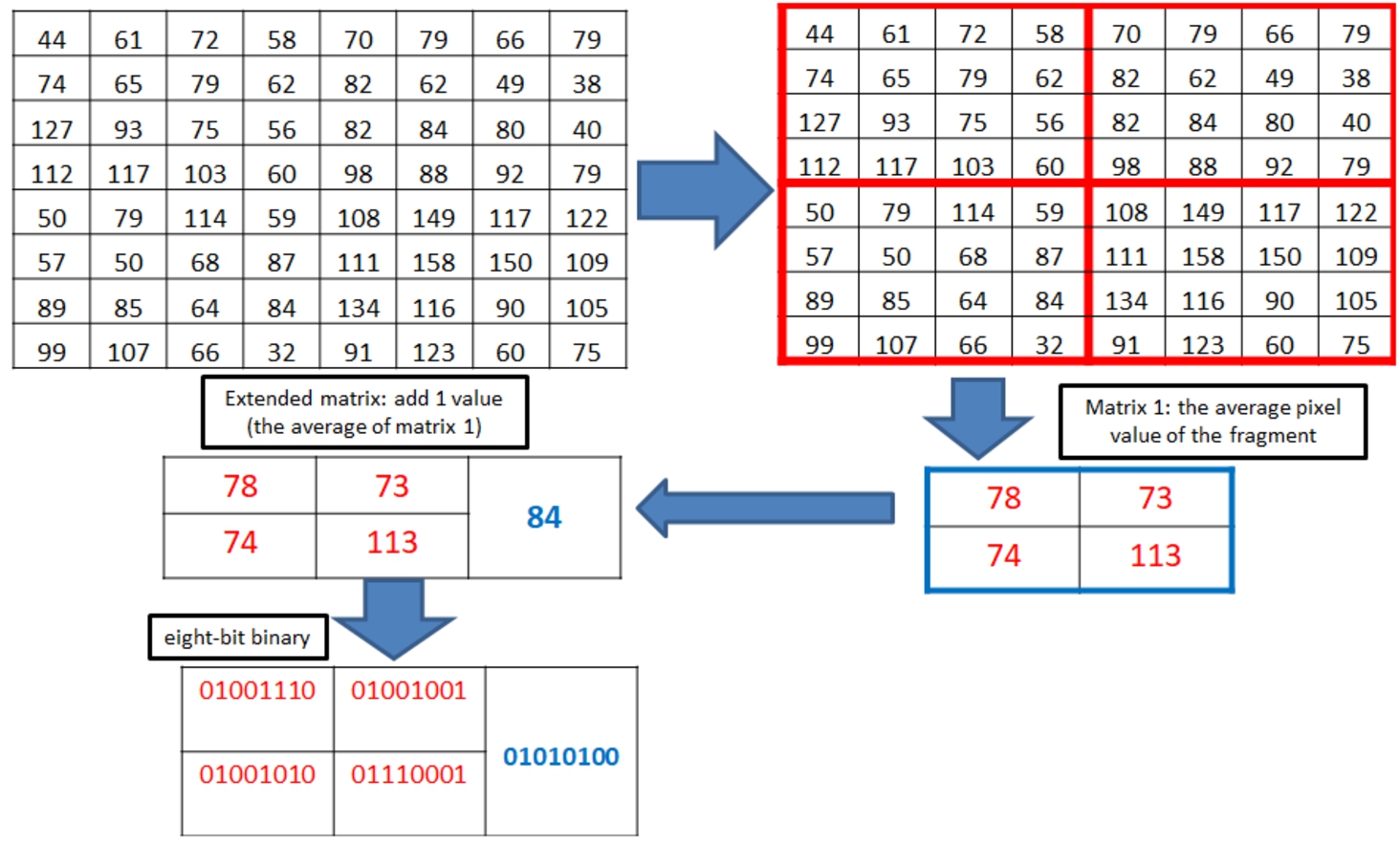
Fig. 2
An example of cover image preparation.
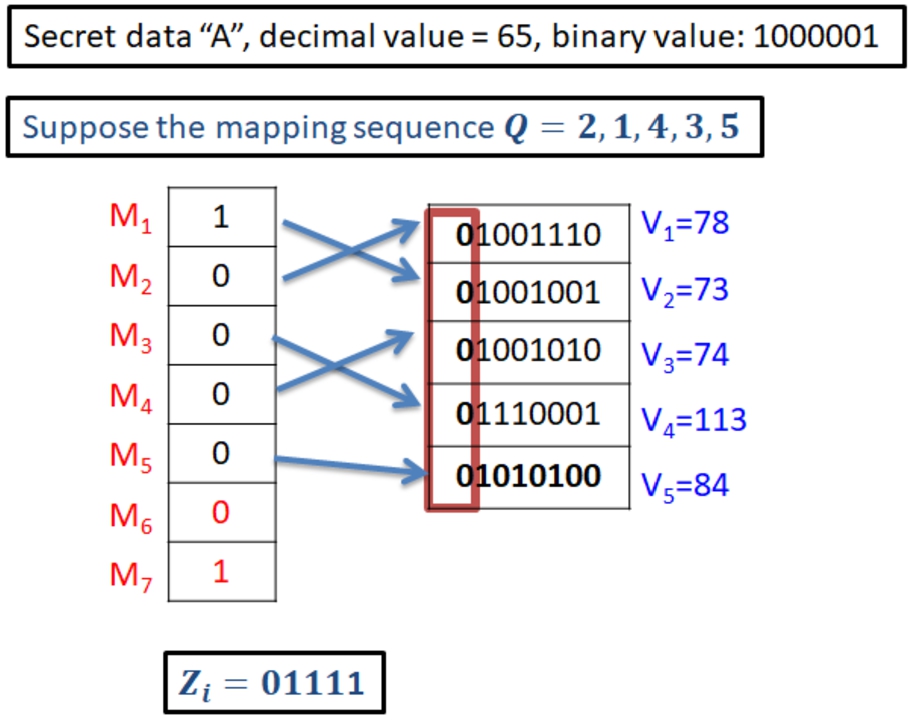
Fig. 3
An example of mapping.
3.2 The Combination Theory-Based Scheme
The combination theory-based scheme adds more averages of the fragments with a combination theory; for convenience, we call it CB-CIHMSB. The proposed embedding procedures consist of three main steps: cover image preparation, secret data preparation, and mapping. Firstly, preprocess the cover image into fragment image ${S_{i}}$. Then form a combined matrix by implementing the concept of combination without repetition. Secondly, preprocess the secret data into binary format ${M_{i}}$ so that it can be operated with the MSB of ${v^{\prime }_{i}}$. Finally, a mapping operation between the MSB of ${v^{\prime }_{i}}$ and ${M_{i}}$ is conducted. The embedding procedure is detailed and presented below:
Firstly, obtain the number of combined matrix (
${\textit{NC}_{r}}$) by (
6):
where
n is the number of things to choose from, we choose
r of them, with no repetition.
Table
2 presents an example of the combination with no repetition under
$n=4$,
$r=1,2,3,4$, and the
${\textit{NC}_{r}}$ value.
Table 2
The example of a combined matrix.
|
$n=4$, $r=1$, $\textit{NC}=4$
|
$n=4$, $r=2$, $\textit{NC}=6$
|
$n=4$, $r=3$, $\textit{NC}=4$
|
$n=4$, $r=4$, $\textit{NC}=1$
|
| ${I_{1}}$ |
${I_{1}}$ ${I_{2}}$
|
${I_{1}}$ ${I_{2}}$ ${I_{3}}$
|
${I_{1}}$ ${I_{2}}$ ${I_{3}}$ ${I_{4}}$
|
| ${I_{2}}$ |
${I_{1}}$ ${I_{3}}$
|
${I_{1}}$ ${I_{2}}$ ${I_{4}}$
|
|
| ${I_{3}}$ |
${I_{1}}$ ${I_{4}}$
|
${I_{1}}$ ${I_{3}}$ ${I_{4}}$
|
|
| ${I_{4}}$ |
${I_{2}}$ ${I_{3}}$
|
${I_{2}}$ ${I_{3}}$ ${I_{4}}$
|
|
Next, calculate the hiding capacity which is the same as the total number of a combined matrix and is defined by (
7):
Finally, form a
Combined Matrix =
$\{{v^{\prime }_{1}},{v^{\prime }_{2}},\dots ,{v^{\prime }_{e}}\}$
where
$e=\text{the number of the}\hspace{2.5pt}\textit{EC}$.
Suppose we have a cover image
I of size
$(8\times 8)$ pixels. Firstly, preprocess the cover image into a
$(4\times 4)$ non-overlapping fragment, so the number of fragment
${S_{i}}=4$. Then form the combined matrix. The cover image preparation is presented in Fig.
5. Therefore, based on (
7), we can embed 15 bits of secret data. Suppose the character of secret data is A, B, and C, and the decimal value is 65, 66, and 67, respectively. Convert into seven-binary format
${M_{i}}=1,0,0,0,0,0,1,\hspace{2.5pt}1,0,0,0,0,1,0,\hspace{2.5pt}1,0,0,0,0,1,1$. The embeddable
${\boldsymbol{M}_{\boldsymbol{i}}}=\mathbf{1},\mathbf{0},\mathbf{0},\mathbf{0},\mathbf{0},\mathbf{0},\mathbf{1},\hspace{2.5pt}\mathbf{1},\mathbf{0},\mathbf{0},\mathbf{0},\mathbf{0},\mathbf{1},\mathbf{0},\mathbf{1}$.
Suppose the mapping key
$Q=7,8,1,2,3,4,6,\hspace{2.5pt}5,10,9,11,12,14,13,15$. Finally, based on the rule in Table
1,
${Z_{i}}=\textbf{0\hspace{0.17em}1\hspace{0.17em}1\hspace{0.17em}1\hspace{0.17em}1\hspace{0.17em}1\hspace{0.17em}0\hspace{0.17em}0\hspace{0.17em}1\hspace{0.17em}1\hspace{0.17em}1\hspace{0.17em}1\hspace{0.17em}0\hspace{0.17em}1\hspace{0.17em}0}$, as shown in Fig.
6.
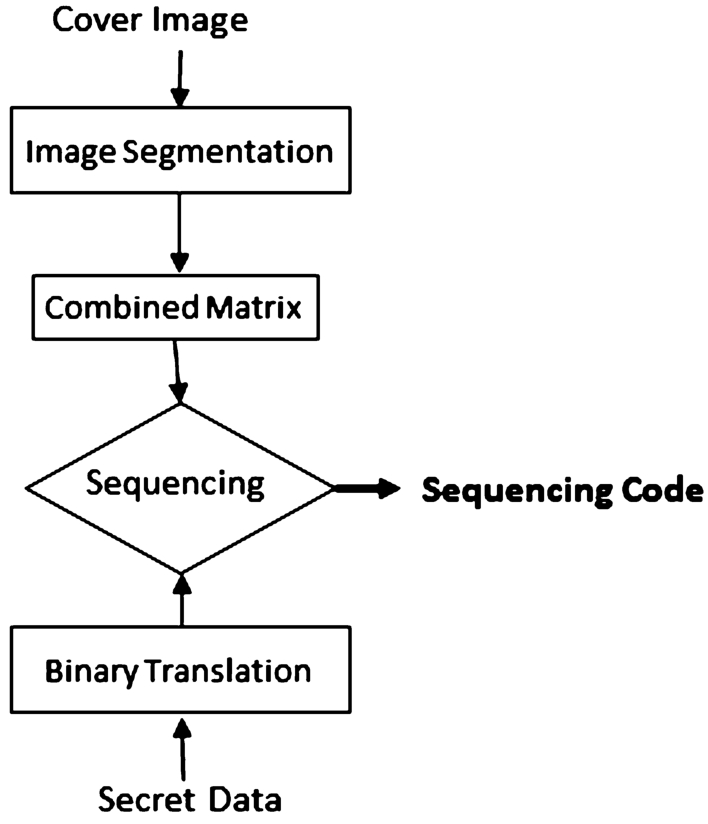
Fig. 4
The flowchart of the proposed combination theory-based scheme.
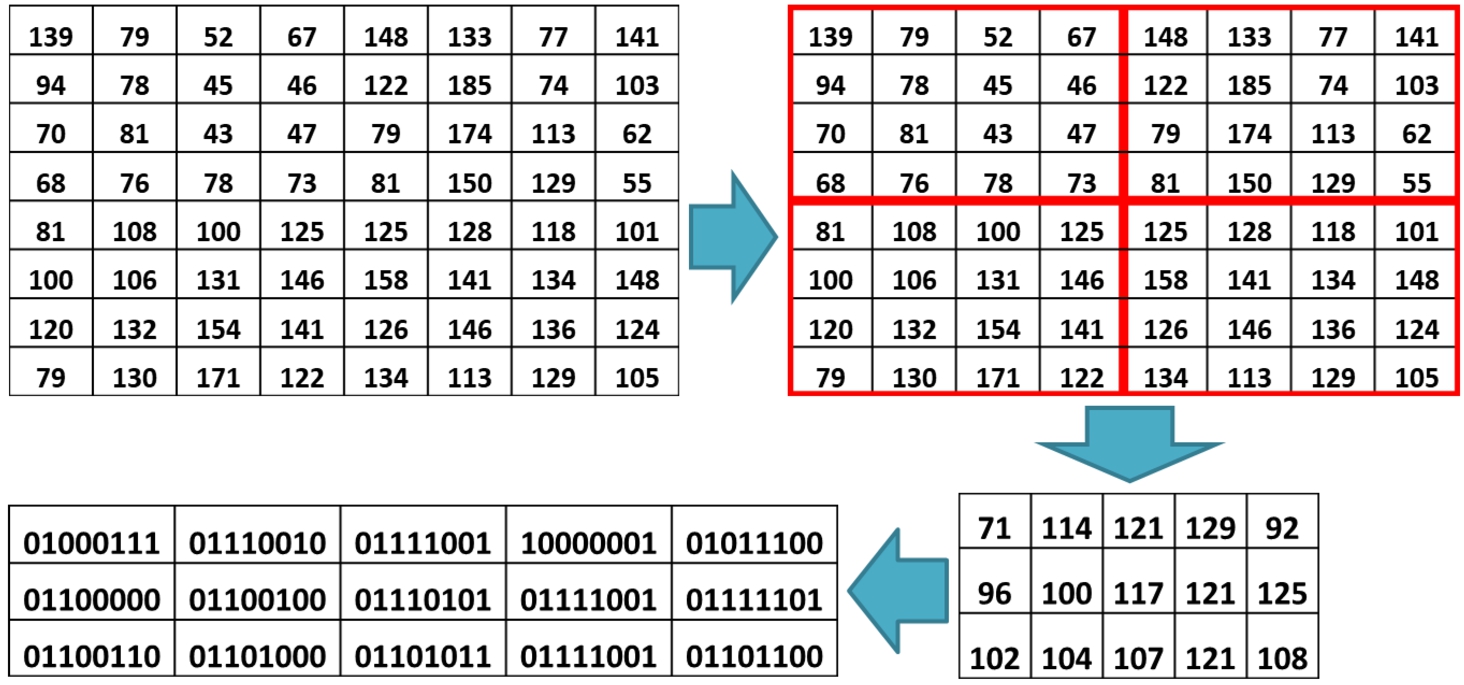
Fig. 5
An example of cover image preparation.
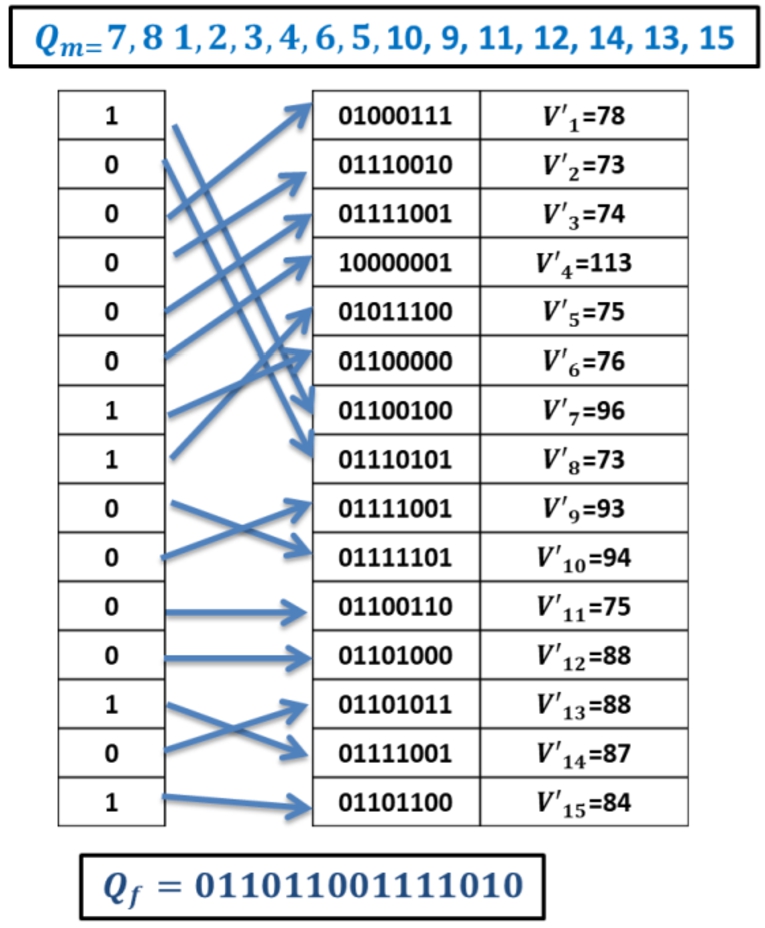
Fig. 6
An example of mapping.
4 Experimental Results
Experimental results were obtained by comparing the performance of CIHMSB (
2022), CIHLHF (
2023b), LMICS (
2022), E-CIHMSB, and CB-CIHMSB. We experimented on the six test grayscale images: Airplane, Baboon, Barbara, Boat, Lena, and Pepper, as shown in Figs.
7(a)–(f), respectively.
4.1 Image Quality Assessment
The image quality assessment is shown in Table
4. As seen in Table
4, the SSIM and
${Q_{i}}$ of CIHMSB, LMICS, the proposed E-CIHMSB, and CB-CIHMSB schemes are equal to 1, which is also the optimal value. Therefore, it means the cover image is the same as the stego image. It indicated the schemes are coverless.
Table 3
The comparison of image quality between CIHMSB, the proposed E-CIHMSB, and CB-CIHMSB schemes.
| Methods |
SSIM |
${Q_{i}}$ |
| CIHMSB (2020) |
1 |
1 |
| LMICS (2022) |
1 |
1 |
| E-CIHMSB |
1 |
1 |
| CB-CIHMSB |
1 |
1 |
4.2 Hiding Capacity Assessment
As seen in Table
4, for cover image size 512 × 512 and the fragment size 8 × 8, the hiding capacity is 16384, 20480, and 61440 for CIHMSB (
2020), CIHLHF (
2023b), E-CIHMSB, and CB-CIHMSB, respectively. Figure
8 presents the hiding capacity comparison of CIHMSB E-CIHMSB and CB-CIHMSB. It can be seen that E-CIHMSB’s capacity is 25% higher than CIHMSB’s. Moreover, CB-CIHMSB’s hiding capacity is 275% higher than CIHMSB and 125% higher than CIHLHF.
Table 4
The comparison of hiding capacity between CIHMSB, the proposed E-CIHMSB, and CB-CIHMSB schemes.
| Methods |
Bits |
carrirer−1
|
Hiding capacity $(\textit{bits}\hspace{0.1667em}\ast \hspace{0.1667em}{\textit{carrirer}^{-1}})$
|
| CIHMSB (2020) |
4 |
$\frac{512\times 512}{8\times 8}=4096$ |
16384 |
| CIHLHF (2023b) |
12 |
49152 |
| E-CIHMSB |
5 |
20480 |
| CB-CIHMSB |
15 |
61440 |
4.3 Robustness Analysis
In the AGWN attack, we define different intensities
${\sigma ^{2}}$ 0.1, 0.5, and 1. In the robustness analysis under salt & pepper noise attack, the noise density increases from 0.001 to 0.005. This experiment uses the average filtering technique to perform a robustness analysis against low-pass filtering attacks. The average filter’s size parameters range 3 × 3 and 5 × 5, with 3 × 3 representing the lowest attack and 5 × 5 representing the highest attack. The compression quality
$(Q$) is used in this experiment to perform a robustness analysis against JPEG compression attacks. The JPEG compression quality
$(Q)$ ranged 50, 70, and 90 in this experiment. Table
5 provides information about the attack type and used parameters.
Table 5
The type of attacks.
| Attack type |
Parameters |
| Additive Gaussian White Noise (AGWN) |
Variance = $\{0.1,0.5,1\}$
|
| Salt & Pepper Noise (SPN) |
Variance = $\{0.001,0.005\}$
|
| Low Pass Filtering: Average Filtering (AF) |
Window size = $\{3\times 3,5\times 5\}$
|
| JPEG Compression |
Quality factor = $\{50,70,90\}$
|
Table
6 presents the BER tendency of the CIHMSB, LMICS, E-CIHMSB, and B-CIHMSB. As shown in Table
6, the higher the noise intensity, the higher the BER.
Table 6
The comparison of attacks performance.
| Attack |
CIHMSB |
LMICS |
E-CIHMSB |
CB-CIHMSB |
| AGWN 0.1 |
10.7583 |
N.A |
9.6700 |
7.9700 |
| AGWN 0.5 |
23.2117 |
N.A |
21.2600 |
18.4400 |
| AGWN 1 |
29.4633 |
N.A |
27.1533 |
24.5517 |
| SPN 0.001 |
0.1333 |
0.0083 |
0.12667 |
0.12500 |
| SPN 0.005 |
0.4450 |
0.0167 |
0.42500 |
0.40667 |
| AF (3 × 3) |
0.9250 |
0.0334 |
0.8367 |
0.6950 |
| AF (5 × 5) |
2.0767 |
0.0520 |
1.8450 |
1.5000 |
| JPEG 50 |
0.4817 |
0.0134 |
0.4517 |
0.3833 |
| JPEG 70 |
0.2983 |
0.0115 |
0.2683 |
0.2400 |
| JPEG 90 |
0.1117 |
0.0074 |
0.1033 |
0.1000 |
Figure
8 shows the BER comparison value between CIHMSB, LMICS, E-CIHMSB, and CB-CIHMSB under AGWN attack. BER tendency of CB-CIHMSB and E-CIHMSB is lower than CIHMSB. It is proven that E-CIHMSB and CB-CIHMSB are more robust than CIHMSB under the AGWN attack.
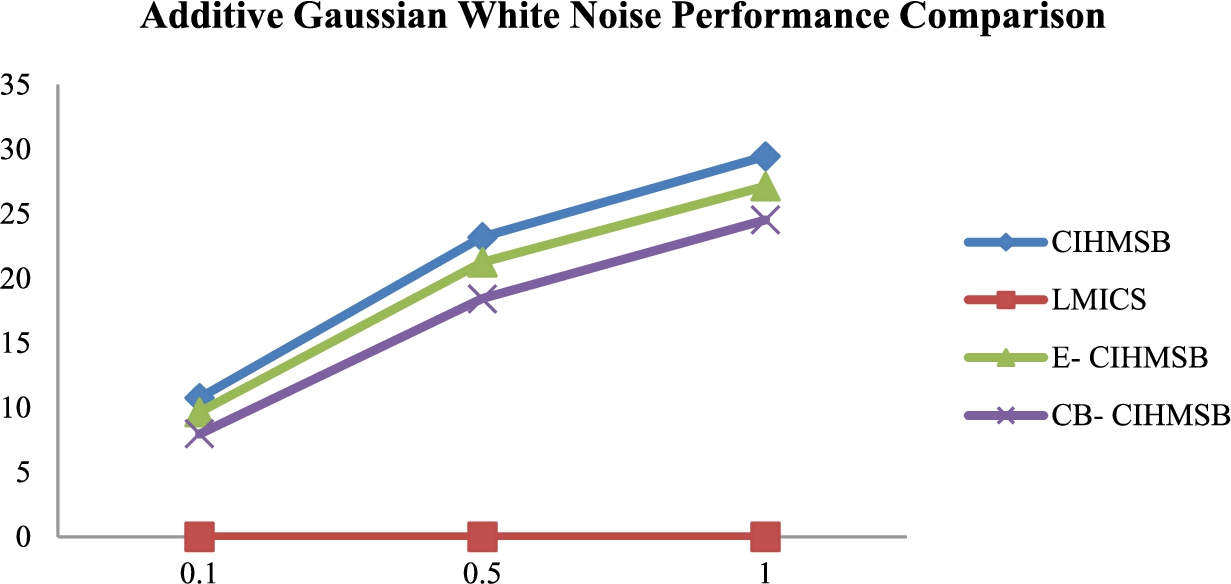
Fig. 8
AGWN performance comparison.
Figure
9 shows the BER comparison value between CIHMSB, LMICS, E-CIHMSB, and CB-CIHMSB under the Salt & Pepper attack. BER tendency of CB-CIHMSB and E-CIHMSB is lower than CIHMSB. Generally, the proposed E-CIHMSB and CB-CIHMSB schemes are more robust than CIHMSB under the Salt & Pepper attack.
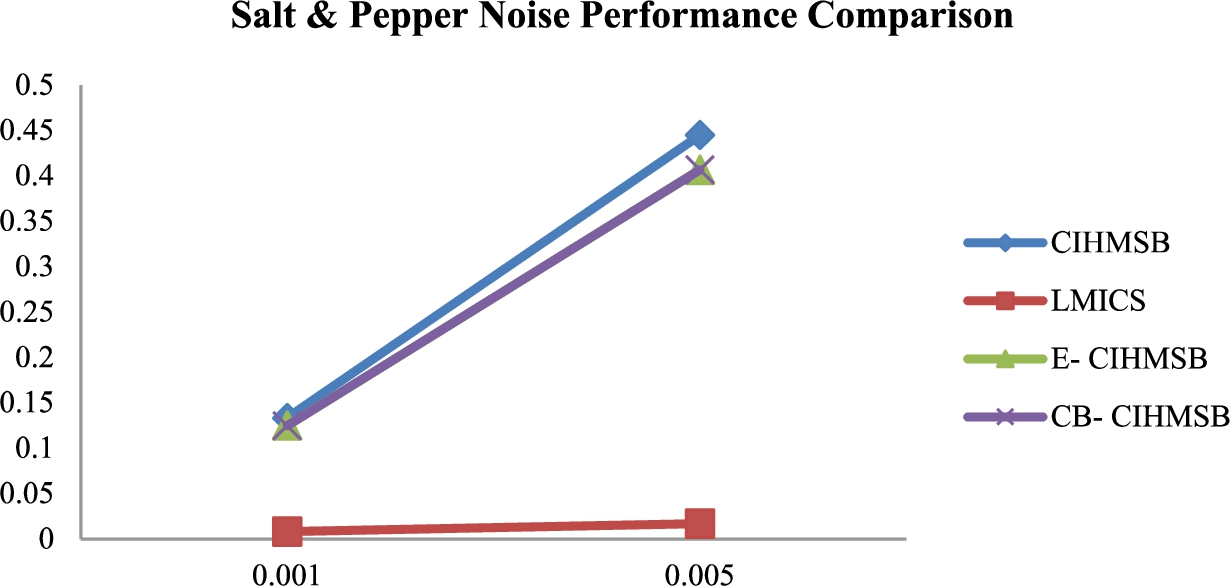
Fig. 9
SPN performance comparison.
Figure
10 shows the BER comparison value between CIHMSB, LMICS, E-CIHMSB, and CB-CIHMSB under a low-filtering attack. Again, the BER increases as the filtering size increases. BER tendency of CB-CIHMSB and E-CIHMSB is lower than CIHMSB. Therefore, the robustness of the proposed E-CIHMSB and CB-CIHMSB schemes under a low-filtering attack is greater than that of CIHMSB.
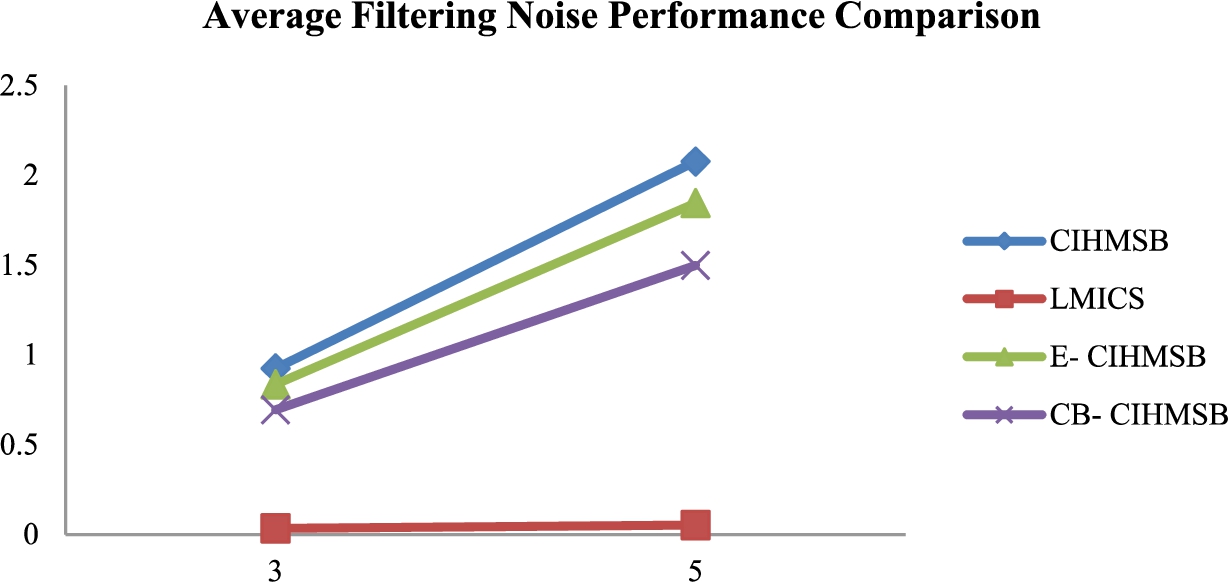
Fig. 10
AF performance comparison.
Figure
11 depicts the BER between CIHMSB, LMICS, E-CIHMSB, and CB-CIHMSB schemes when subjected to a JPEG compression attack with varying
Q. The BER increases as
Q decreases. The proposed E-CIHMSB and CB-CIHMSB schemes are more resistant to JPEG compression than CIHMSB.
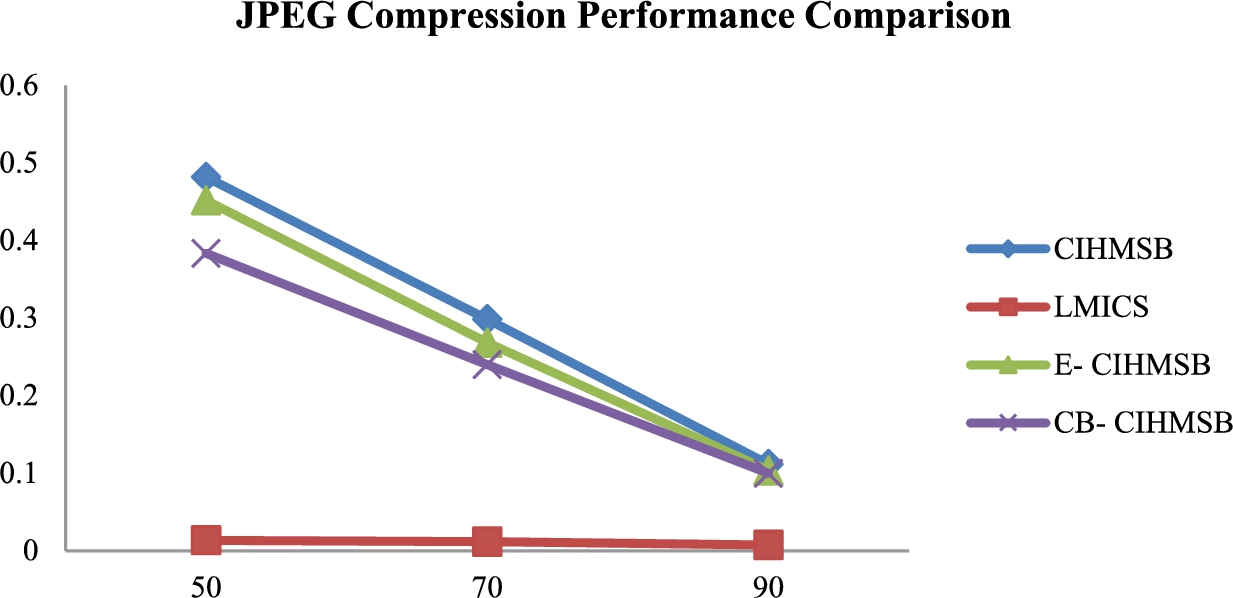
Fig. 11
JPEG compression performance comparison.
5 Conclusion
This study proposed two coverless information hiding methods, E-CIHMSB and CB-CIHMSB, to improve the CIHMSB method’s hiding capacity. The difference between the two methods is in creating the cover image. The first proposed method uses image segmentation to compute each average, after which the extended average value is calculated. The second proposed method, with the combination theory, is used to obtain a higher average value. The greater the number of average value, the greater the hiding capacity. We follow the mapping and sequencing operations for the first and second methods, respectively. We investigate the robustness of the proposed method under AWGN, Salt & Pepper noise, low-pass filtering, and JPEG compression attacks. It has been demonstrated that the proposed method is resistant to steganalysis attacks. The experimental results show that our proposed method’s hiding capacity outperforms CIHMSB.