Algorithms for intersections of different 2D geometric entities have been studied for a long time from various aspects, primarily due to the computation speed, robustness and limited numerical precision of the floating-point representation. The majority of 2D algorithms deal with an intersection of a line or a half-line (ray) or a line segment with 2D geometric entity, e.g. a rectangle, convex polygon (Cyrus and Beck,
1978; Rappoport,
1991), non-convex polygon (Weiler and Atherton,
1977), quadric and cubic curves, parametric curves (Skala,
2021a) and areas with quadratic arcs (Skala,
2015,
1989,
1990a), etc.
3.1 Intersection with a Rectangular Area
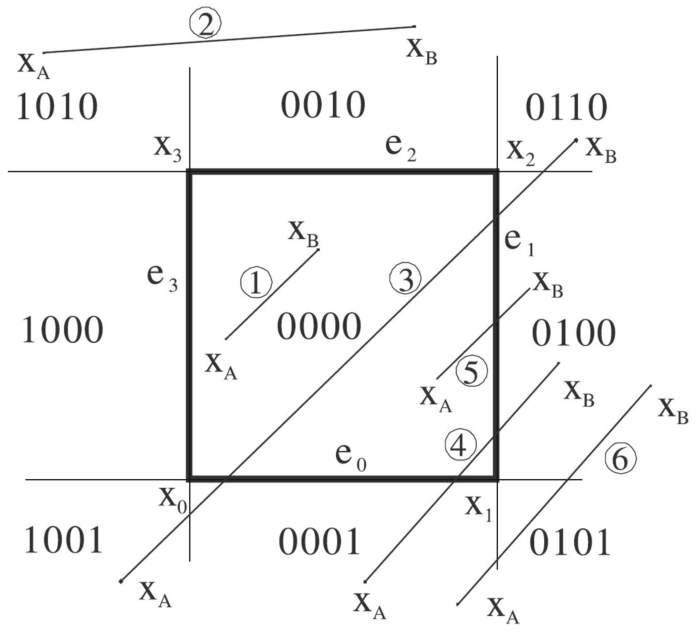
Fig. 2
Cohen-Sutherland coding.
Intersection algorithms with a rectangular area (window) are well known as the line clipping or as the line segment clipping algorithms. The first algorithm was developed and used for the flight simulator project led by Cohen (
1969) in 1967. Efficient coding of the line segment position coding leading to significant computational reduction was introduced in Sproull and Sutherland (
1968) and patented in 1972 (Sutherland,
1972). The Cohen-Sutherland algorithm is described in Newman and Sproull (
1979), Comninos (
2006), Matthes and Drakopoulos (
2019a,
2019b), etc. The Cohen-Sutherland algorithm generates a bit-code LRTB, i.e. [Left, Right, Top, Bottom], for each end-point of the line segment, see Fig.
2. The coding is redundant. However, it enables simple identification of the cases, when the line segment is totally inside or outside as follows:
-
• if $({\mathbf{c}_{A}}\hspace{2.5pt}\mathbf{lor}\hspace{2.5pt}{\mathbf{c}_{B}})=[0000]$ then the line segment is totally inside,
-
• if $({\mathbf{c}_{A}}\hspace{2.5pt}\mathbf{land}\hspace{2.5pt}{\mathbf{c}_{B}})\ne [0000]$ then the line segment is totally outside,
where
land, resp.
or mean bit-wise
and, resp.
or operations.
The ultimately deep classification of all the possible cases using arithmetic operation with the codes was described in Skala (
2021b), see Table
1 and Fig.
3. The
${C_{AB}}$ value is the index to the
array of functions representing each case.
Table 1
Numerical summation codes ${C_{AB}}={C_{A}}+{C_{B}}$, IN – inside area, C – corner area, S – side area, n/a – non-applicable cases or outside case.
|
|
|
IN |
C |
S |
C |
S |
C |
S |
C |
S |
|
${C_{AB}}$ |
${C_{B}}$ |
0 |
5 |
4 |
6 |
2 |
10 |
8 |
9 |
1 |
|
${C_{A}}$ |
|
0000 |
0101 |
0100 |
0110 |
0010 |
1010 |
1000 |
1001 |
0001 |
| IN |
0 |
0000 |
IN |
5 |
4 |
6 |
2 |
10 |
8 |
9 |
1 |
| C |
5 |
0101 |
5 |
n/a |
n/a |
n/a |
7 |
15 |
13 |
n/a |
n/a |
| S |
4 |
0100 |
4 |
n/a |
n/a |
n/a |
6 |
14 |
12 |
13 |
5 |
| C |
6 |
0110 |
6 |
n/a |
n/a |
n/a |
n/a |
n/a |
14 |
15 |
7 |
| S |
2 |
0010 |
2 |
7 |
6 |
n/a |
n/a |
n/a |
10 |
11 |
3 |
| C |
10 |
1010 |
10 |
15 |
14 |
n/a |
n/a |
n/a |
n/a |
n/a |
11 |
| S |
8 |
1000 |
8 |
13 |
12 |
14 |
10 |
n/a |
n/a |
n/a |
9 |
| C |
9 |
1001 |
9 |
n/a |
13 |
15 |
11 |
n/a |
n/a |
n/a |
n/a |
| S |
1 |
0001 |
1 |
n/a |
5 |
7 |
3 |
11 |
9 |
n/a |
n/a |
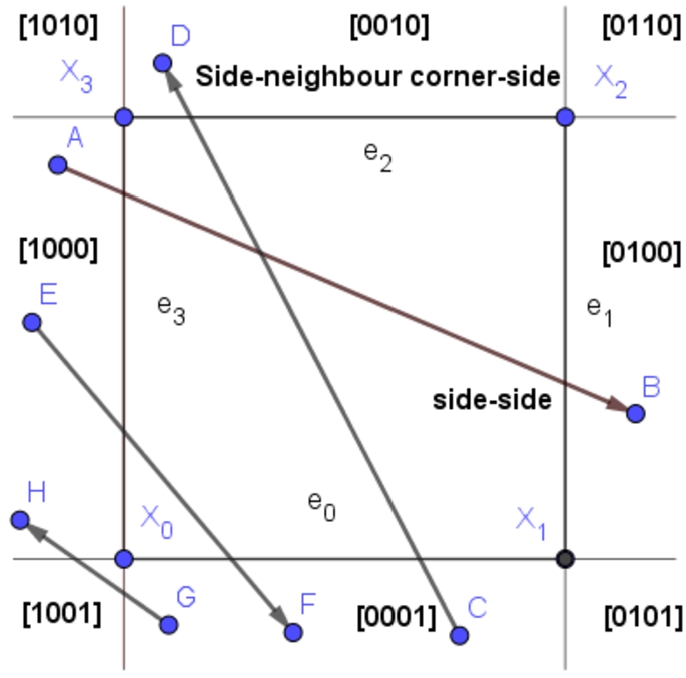
Fig. 3
Two specific situations – SS-SnCS: side-side and side-neighbour corner-side.
Distinguishing all the cases leads to more efficient coding and efficient implementation (Skala,
2021b); specific cases are presented in Table
2.
Table 2
Possible cases: n/a – non-applicable or solved by the C-S coding, C – corner area, S – side area, IN – inside area, End-points: IC – inside-corner, IS – inside-side; Cases: SS – side-side, SnCS – side-near corner-side, SdC – side-distant corner-side, CoC – corner-opposite corner, id – case re-indexing.
|
|
id |
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Case |
|
IN |
C |
S |
C |
S |
C |
S |
C |
S |
|
|
${C_{B}}$ |
0 |
5 |
4 |
6 |
2 |
10 |
8 |
9 |
1 |
|
${C_{A}}$ |
|
0000 |
0101 |
0100 |
0110 |
0010 |
1010 |
1000 |
1001 |
0001 |
| IN |
0 |
0000 |
IN |
IC |
IS |
IC |
IS |
IC |
IS |
IC |
IS |
| C |
5 |
0101 |
IC |
n/a |
n/a |
n/a |
SdC |
CoC |
SdC |
n/a |
n/a |
| S |
4 |
0100 |
IS |
n/a |
n/a |
n/a |
SnCS |
SdC |
SS |
SdC |
SnCS |
| C |
6 |
0110 |
IC |
n/a |
n/a |
n/a |
n/a |
n/a |
SdC |
CoC |
SdC |
| S |
2 |
0010 |
IS |
SdC |
SnCS |
n/a |
n/a |
n/a |
SnCS |
SdC |
SS |
| C |
10 |
1010 |
IC |
CoC |
SdC |
n/a |
n/a |
n/a |
n/a |
n/a |
SdC |
| S |
8 |
1000 |
IS |
SdC |
SS |
SdC |
SnCS |
n/a |
n/a |
n/a |
SnCS |
| C |
9 |
1001 |
IC |
n/a |
SdC |
CoC |
SdC |
n/a |
n/a |
n/a |
n/a |
| S |
1 |
0001 |
IS |
n/a |
SnCS |
SdC |
SS |
SdC |
SnCS |
n/a |
n/a |
The Cohen-Sutherland algorithm can also be extended to the 3D case, i.e. intersection of a line segment with a cube or right-angled parallelepiped.
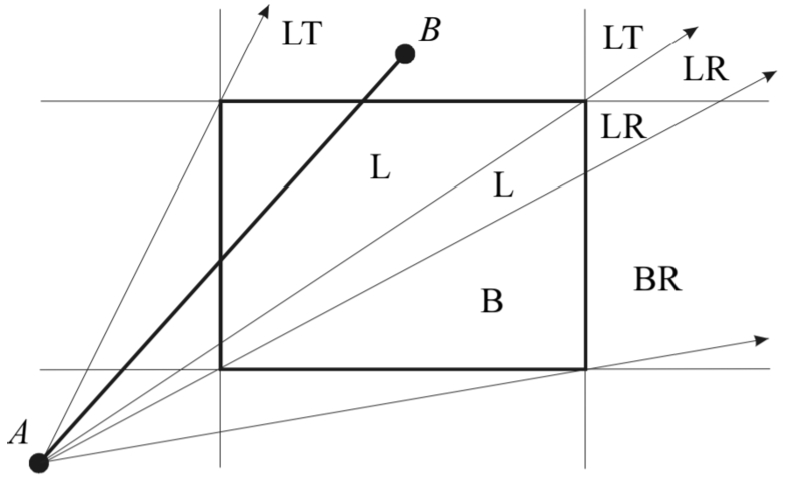
Fig. 4
Nicholl-Lee-Nicholl algorithm – window corners position evaluation.
The Cohen-Sutherland algorithm was improved by Nicholl
et al. (
1987). It uses the window corners position classification in relation to the line segment position, see Fig.
4. The Nicholl-Lee-Nicholl algorithm was improved by Bui and Skala (
1998) using some additional classification of possible cases and extended to the
${E^{3}}$ case in Skala and Bui (
2001).
The algorithms (Liang and Barsky,
1983) and (Dörr,
1990) are based on the direct intersection computation of a line with the polygon edges in the parametric form. Analysis of the Nicholl-Lee-Nicholl and Liang-Barsky algorithms was given in Devai (
2005). Simple and robust line and line segment clipping algorithms in
${E^{2}}$ was described in Skala (
2004,
2005,
2012,
2020). They are based on the projective representation and homogeneous coordinates using a separation of the convex polygon vertices by the given line, see Fig.
5. The sign of the function values
$F(\mathbf{x})$, which represents the given line, for each window corner gives a 4-bit code identifying the edges intersected by the given line. The algorithm can be extended for the convex polygon case.
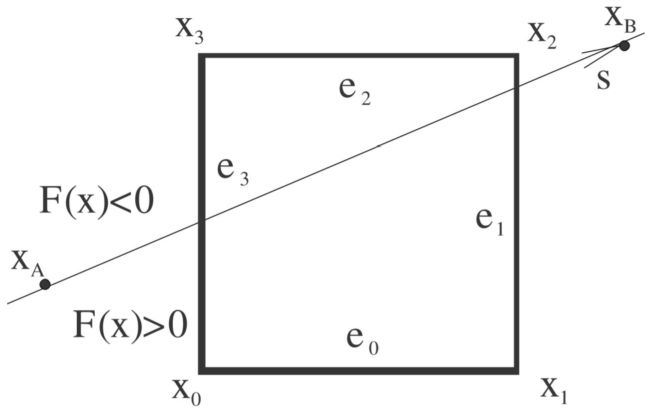
Fig. 5
Clipping against the rectangular window in ${E^{2}}$.
3.2 S-L-Clip Algorithm
Let us consider an implicit function $F(\mathbf{x})={\mathbf{a}^{T}}\mathbf{x}$, where $\mathbf{a}={[a,b:c]^{T}}$ are coefficients of the given line p, $\mathbf{x}={[x,y:w]^{T}}$ means a point on this line. Then the equation $F(\mathbf{x})=0$ represents the given line p in ${E^{2}}$ using the projective extension of the Euclidean space.
The clipping operation should determine the intersection points
${\mathbf{x}_{i}}={[{x_{i}},{y_{i}}:{w_{i}}]^{T}}$,
$i=1,2$ of the given line with the window, if any. The line splits the plane into two parts, see Fig.
5. The corners of the window are split into two groups according to the sign of the function
$F(\mathbf{x})$ value. This results into Smart-Line-Clip (S-L-Clip) algorithm, see Algorithm
1. It means that each corner can be classified by a bit value
${c_{i}}$ as:
where
$\mathbf{a}={[a,b:c]^{T}}$ are coefficients of the given line
p,
$\mathbf{x}={[x,y:w]^{T}}$ means a point on this line. Table
3 shows the codes for all situations (some of those are not possible). The
$\mathbf{TAB}\mathbf{1}$ and
$\mathbf{TAB}\mathbf{2}$ contain indices of edges of the window intersected by the given line (values in the
$\mathbf{MASK}$ is used in the line segment algorithm).
Table 3
All cases; N/A – non-applicable (impossible) cases.
| c |
c |
TAB1 |
TAB2 |
MASK |
| 0 |
0000 |
None |
None |
None |
| 1 |
0001 |
0 |
3 |
0100 |
| 2 |
0010 |
0 |
1 |
0100 |
| 3 |
0011 |
1 |
3 |
0010 |
| 4 |
0100 |
1 |
2 |
0010 |
| 5 |
0101 |
N/A |
N/A |
N/A |
| 6 |
0110 |
0 |
2 |
0100 |
| 7 |
0111 |
2 |
3 |
1000 |
| c |
c |
TAB1 |
TAB2 |
MASK |
| 15 |
1111 |
None |
None |
None |
| 14 |
1110 |
3 |
0 |
None |
| 13 |
1101 |
1 |
01 |
0100 |
| 12 |
1100 |
3 |
1 |
0010 |
| 11 |
1011 |
2 |
1 |
0010 |
| 10 |
1010 |
N/A |
N/A |
N/A |
| 9 |
1001 |
2 |
0 |
0100 |
| 8 |
1000 |
3 |
2 |
1000 |

Algorithm 1
S-L-Clip – line clipping algorithm by the rectangular window
It can be seen, that the S-L-Clip Algorithm
1 is quite simple and easily extensible for the convex polygon clipping case as well. Table
3 can be generated synthetically. It is significantly more straightforward than the algorithm (Liang and Barsky,
1984). It also supports SSE4 and GPU use directly and leads to simple implementations, as the cross-product and dot-product operations, are supported in hardware. It should be noted, that the algorithm is designed for a very general case, as the window corners and the points defining the line, are generally in the projective representation, i.e.
$w\ne 0$. Therefore, the S-L-Clip algorithm has further potential for optimization, especially for the case when the corner points of the window are given in the Euclidean coordinates, i.e.
$w=1$, and clipping is made in the Normalized Device Coordinate (NDC) system (Skala,
2020).
The modification of the S-L-Clip algorithm for a line segment clipping is simple and described in Skala (
2004). The advantage of it is that the end-points and the window corners might be given generally in the projective space, i.e.
$w\ne 0$. The cross-product is used for the intersection computation using SSE4 or GPU acceleration.
Other proposed modifications of algorithms can be found in Bui (
1999), Andreev and Sofianska (
1991), Bao and Peng (
1996), Devai (
2005,
2006,
1998), Duvalenko
et al. (
1990,
1993,
1996), Cai
et al. (
2001), Day (
1992a,
1992b), Evangeline and Anitha (
2014), Kaijian
et al. (
1990), Kodituwakku
et al. (
2013), Kong and Yin (
2001), Maillot (
1992), Wei
et al. (
2013), Slater and Barsky (
1994), Ray (
2012a,
2012b,
2014,
2015), Li (
2016), Singh and Lumar (
2016), Dev and Saharan (
2019).
Some additional modifications of algorithms were published in Brackenbury (
1984), Chao
et al. (
2009), Cheng and Yen (
1989), Dimri (
2015), Dimri
et al. (
2022), Elliriki
et al. (
2019), Hattab and Yusof (
2014), Iraji
et al. (
2011), Jiang and Han (
2013), Jianrong (
2006), Kumar and Awasthi (
2011), Kuzmin (
1995), Li
et al. (
2014), Li and Lei (
2012), Meriaux (
1984), Molla
et al. (
2003), Nisha (
2017b,
2017a), Sobkow
et al. (
1987), Sharma and Manohar (
1993), Wang
et al. (
1998a,
1998b,
2012,
2001), Yang (
1988), Pandey and Jain (
2013), Bhuiyan (
2009). The hardware FPGA implementation was proposed in Dawod (
2011).
Analysis and comparisons of some clipping algorithms were published recently in Krammer (
1992), Skala and Huy (
2000), Skala
et al. (
1995), Nisha (
2017a,
2017b), Matthes and Drakopoulos (
2022), Ray (
2012b).
3.3 Intersection with Polygons
Generic solutions for polygon clipping were developed by Weiler and Atherton (
1977), Rappoport (
1991), Vatti (
1992), Wu
et al. (
2004), Xie
et al. (
2010), Zhang and Sabharwal (
2002), Zhang
et al. (
2022). Boolean operations with polygons were introduced by Rivero and Feito (
2000), Martinez
et al. (
2009).
Algorithms for a line clipping
${E^{2}}$ by a polygon depend on the polygon property, i.e. if the polygon is convex or non-convex. In the case of convex polygons, the convexity property and ordering of vertices enables to decrease complexity from
$O(N)$ to
$O(\lg N)$ (Skala,
1994). It should be noted that a similar complexity decrease is not possible in the
${E^{3}}$ case as there is no ordering.
In the non-convex polygon cases, when the polygon can be self-intersecting, etc., problems with robustness of computation can be expected. Also, in some cases a three-value logic is to be used in order to solve specific cases properly, e.g. a line passes a vertex, a line touches a vertex, a line lies on an edge, etc. (Mccoid and Gander,
2022; Skala,
1989,
1990a).
3.4 Convex Polygons
The Cyrus-Beck’s algorithm (Cyrus and Beck,
1978) is probably the famous algorithm for line-convex polygon clipping. It is based on a computation of the parameter
t of the given line in the parametric form with edges of the given convex polygon, Fig.
6. The algorithm is of
$O(N)$ computational complexity and can be extended for the
${E^{3}}$ case.
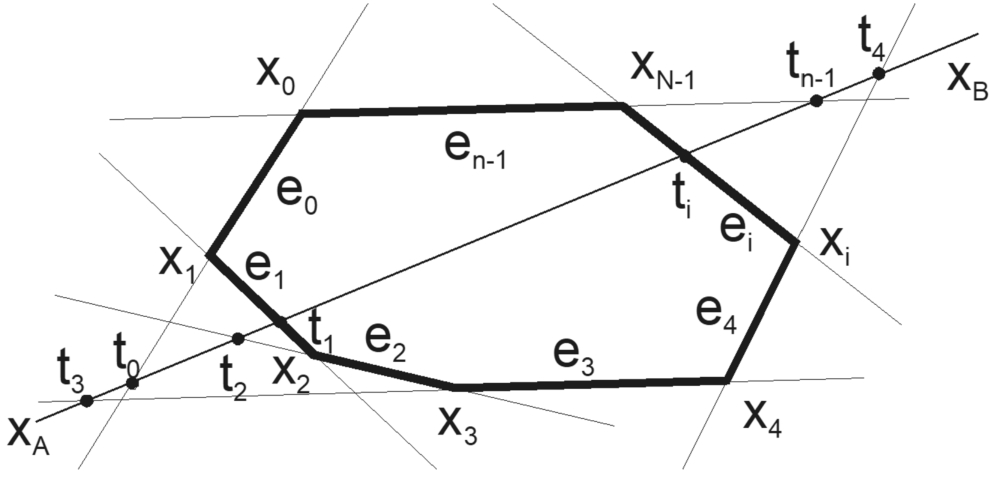
Fig. 6
Cyrus-Beck line clipping algorithm.
The Cyrus-Beck’s algorithm is based on direct intersection computation of the given line
p in the parametric form and a line on which the polygon edge
${e_{i}}$ lies, see Fig.
6, in the implicit form, i.e. on a solution of two linear equations (vector notation is used):
where
${\mathbf{x}_{A}}={[{x_{A}},{y_{A}}]^{T}}$,
$\mathbf{s}={[{s_{x}},{s_{y}}]^{T}}$ is the directional vector of the line
p,
${\mathbf{n}_{i}}={[{n_{x}},{n_{y}}]^{T}}$ is the normal vector of the edge
${e_{i}}$.
Solving those equations, the parameter
t for the intersection point is obtained as:
Then
${t_{i}}$ is the parameter
t value for the intersection of the line
p and the line on which the edge
${e_{i}}$ lies, see Fig.
6.
It can be seen that the algorithm is not robust as if the line
p is parallel or nearly parallel to the edge
${e_{i}}$, the expression
${\mathbf{n}_{i}^{T}}\mathbf{s}\to 0$ and
${t_{i}}\to \pm \infty $. The fraction computation might cause an overflow or high imprecision of the computed parameter
t value, see Fig.
6.
It is hard to detect and solve such cases reliably and programmers usually use a sequence like
which is an incorrect solution as the value
$\textit{eps}$ is the programmer’s choice and the value of
${\mathbf{n}_{i}^{T}}\mathbf{s}$ might also be close to the value of
${\mathbf{n}_{i}^{T}}{\mathbf{x}_{A}}+{c_{i}}$, see Eq. (
12).
However, textbooks do not point out such dangerous construction as far as robustness and computational stability are concerned.
The modification of the Cyrus-Beck’s algorithm using the cross product for more reliable detection of the “close to singular” cases was described by Skala (
1993). Probably the most reliable modification of the Cyrus-Beck’s algorithm is to use:

Algorithm 2
Cyrus-Beck’s line clipping algorithm
The Cyrus-Beck’s algorithm for a line clipping is described by Algorithm
2. It can be easily modified for the line segment clipping just restricting the range of the parameter
t to
$\langle 0,1\rangle $, i.e.
It can be seen that the algorithm complexity is
$O(N)$ and the division operation, which is the most consuming time operation in the floating-point representation, is used
N times.
However, only 2 values (${t_{\min }}$, ${t_{\max }}$) of the parameter t are valid, i.e. $N-2$ computations of the parameter t are lost. Also, reliable detection of the “singular or close to singular” cases is difficult and time-consuming, especially in the ${E^{3}}$ case.
Some improvements and modifications were described by Skala (
1993). As the edges of the convex polygon are ordered, the algorithm with the
$O(\lg N)$ complexity was derived by Skala (
1994). An algorithm based on space subdivision was described in Slater and Barsky (
1994).
Another approach based on the implicit form of the given line and convex polygon vertices classification, the S-Clip algorithm, was developed in Skala (
2021c) and modified by Konashkova (
2014,
2015). Another algorithm based on the S-Clip algorithm was described in Skala (
2021c). An algorithm for a line segment clipping based on the line segment end-points evaluation with the
$O(N)$ complexity was described by Matthes and Drakopoulos (
2022).
The Liang-Barsky algorithm (Liang and Barsky,
1984,
1983) based on direct intersection computation of a line with the convex polygon edges in the parametric form has the
$O(N)$ computational complexity, too.
The algorithm with the run-time
$O(1)$ complexity using pre-computation was developed by Skala (
1996b,
1996d). The algorithm was motivated by the scan-line raster conversion used recently for solving visibility in rendering. The memory requirements depend on the geometrical properties of the given convex polygon. A comparison of the
$O(1)$ algorithm with the Cyrus-Beck algorithm is presented in Skala and Lederbuch (
1996), Skala
et al. (
1996).
Other related algorithms or modifications of existing ones were published by: Li (
2005), Nishita and Johan (
1999), Raja (
2019), Sun
et al. (
2006), Vatti (
1992), Wang
et al. (
2005), Wijeweera
et al. (
2019), Sharma and Kaur (
2016), Sharma and Manohar (
1992) use the affine transformation.
3.5 Non-Convex Polygons
Probably, the first algorithm dealing with the non-convex polygon clipping was published in the Reentrant polygon clipping algorithm paper (Sutherland and Hodgman,
1974), followed by the Weiler-Atherton algorithm for polygon-polygon clipping (Weiler,
1980; Weiler and Atherton,
1977; Rappoport,
1991).
Intersections with arbitrary non-convex polygons were described in Greiner and Hormann (
1998) and solutions of “the singular” (degenerated) cases were described in Foster
et al. (
2019). The algorithm (Skala,
1989) uses a three-value logic.
A robust solution of triangle-triangle intersection in
${E^{2}}$ is described in Mccoid and Gander (
2022). Other algorithms or modifications are described in Dimri (
2015), Evangeline and Anitha (
2014), Lu and Wu (
2002), Lu
et al. (
2002a), Tang and He (
2009). The affine transformations are used in Huang (
2013), Huang and Wangyong (
2009), Huang and Liu (
2002).
Algorithms that also handle arcs and use a three-value logic to handle singular cases properly, including self-intersecting non-convex polygons, were described in Skala (
2015,
1989,
1990a), Wang and Chong (
2016), Tran (
1986).
Non-Polygonal Window
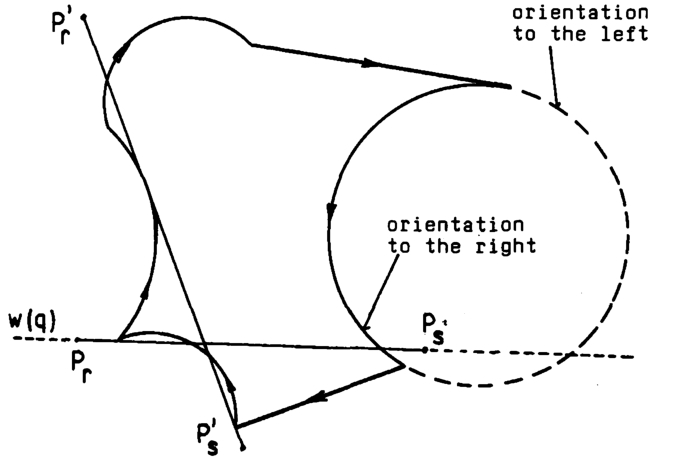
Fig. 7
Line clipping by an area with circular segments (taken from Skala,
1989).
The algorithm for circular arc was described in Van Wyk (
1984), Gupta
et al. (
2016), for overlapping areas by Li
et al. (
2012) and for circular window in Lu
et al. (
2002b), Kumar
et al. (
2018), Wu and Li (
2022), Wu
et al. (
2006), Skala (
1989), see Fig.
7. The above-mentioned algorithms lead to algorithms for set operations with polygons, i.e. union, intersection etc. of polygons described, e.g. Kui Liu
et al. (
2007), Martinez
et al. (
2009).