Abstract
During the COVID-19 pandemic, masks have become essential items for all people to protect themselves from the virus. Because of considering multiple factors when selecting an antivirus mask, the decision-making process has become more complicated. This paper proposes an integrated approach that uses F-BWM-RAFSI methods for antivirus mask selection process with respect to the COVID-19 pandemic. Finally, sensitivity analysis was demonstrated by evaluating the effects of changing the weight coefficients of the criterion on the ranking results, simulating changes in Heronian operator parameters, and comparing the obtained solution to other MCDM approaches to ensure its robustness.
1 Introduction
The COVID-19 pandemic, which is the result of the SARS-CoV-2 virus, has spread around the world in a short time since its emergence in Wuhan, China, mobilized international health authorities and its effect continues to be serious. The studies and reports published by the World Health Organization on the pandemic are followed with interest and concern by the whole world.
Studies examining the effects of the virus on China’s and the world’s economy have revealed that the virus caused a loss of approximately 62 billion dollars to the Chinese economy and more than 280 billion dollars to the world economy in the first quarter (Ayittey
et al.,
2020).
In line with the instructions of the World Health Organization (WHO) against this pandemic that threatens international public health, national administrations also take various measures to protect public health and to get rid of the epidemic with the least damage. However, despite the strictness of the measures, the continuous increase in death cases due to the impact of the epidemic and the epidemic itself causes serious concerns at the international level.
When the reports and scientific studies published by the WHO were examined, it was determined that the demand for healthcare materials such as protective masks and gloves has increased worldwide since the outbreak occurred and that the prices of related healthcare materials also increased significantly due to the increase in demand (Mahase,
2020).
Fuzzy multi criteria decision-making (MCDM) methods are commonly used for decision-making in medical and healthcare fields (Kumar
et al.,
2020; Omrani
et al.,
2018; Otay
et al.,
2017; Reddy
et al.,
2014; Rouyendegh
et al.,
2019; Stević
et al.,
2020; Sumrit,
2020; Thakur and Ramesh,
2017; Zare
et al.,
2019). Yucesan and Gul (
2020) proposed an integrated fuzzy MCDM framework using the Pythagorean fuzzy-AHP and TOPSIS methods to evaluate hospital service quality. Lee
et al. (
2017) aimed to explore a hybrid evaluation model based on fuzzy AHP and fuzzy TOPSIS methods for Taiwan’s medical device manufacturers. Nilashi
et al. (
2019) proposed a hybrid fuzzy MCDM method based on the Decision-Making Trial and Evaluation Laboratory (DEMATEL) and fuzzy Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) to reveal the interrelationships among the factors influencing the development of medical tourism in Malaysia and to find the relative importance of these factors. Abdel-Basset
et al. (
2019) offer a group decision-making approach for estimating the Smart Medical Devices (SMDs) selection process using the TOPSIS method. Gao
et al. (
2020) developed a group decision-making method based on q-rung interval-valued orthopair fuzzy VIse KriterijumsaOptimizacija I Kompromisno Resenje (VIKOR) model for selecting the supplier of medical consumption products. Yang
et al. (
2020) developed the MCDM method based on SpNoF Bonferroni mean operator and the weighted Bonferroni mean operator for selecting an antivirus mask during the COVID-19 pandemic. Torkayesh
et al. (
2021) proposed a combination model based on best-worst method (BWM) and level based weight assessment (LBWA) to estimate the rating of healthcare parameters and integrated compromise solution (CoCoSo) method for selecting the optimal healthcare sector of eastern European countries. Ecer and Pamucar (
2021) suggested a Measurement of Alternatives and Ranking according to the Compromise Solution (MARCOS) approach using intuitionistic fuzzy sets to score healthcare insurance organizations in the COVID-19 period. Ozsahin
et al. (
2021) examined 24 various migraine medicines that help to regulate productive migraine drugs in overall using TOPSIS method.
It can be clearly seen that the integrated MCDM methods based on fuzzy set theory are widely used in the fields of medical and healthcare. However, there are limited studies about the selection of personal protective equipment, especially antivirus masks, during the COVID-19 pandemic.
This paper proposes an integrated approach that uses fuzzy BWM and Ranking of Alternatives through Functional mapping of criterion sub-intervals into a Single Interval (F-BWM-RAFSI) methods for antivirus mask selection process with respect to the COVID-19 pandemic. Due to the vagueness of data and the ambiguity of decision-maker, the involvement of the fuzzy concept into MCDM can obtain much more reliable results in real-life applications. The F-BWM approach which combines the fuzzy set theory and BWM can provide more consistent comparisons. It has been demonstrated that the BWM method performs significantly better than other MCDM methods such as AHP in terms of consistency index, minimum violation, total deviation and conformity (Rezaei,
2015). These advantages are indicated below (Stević
et al.,
2018; Zolfani
et al.,
2019; Ecer and Pamucar,
2020; Luo
et al.,
2020): (i) AHP requires
$\frac{n(n-1)}{2}$ pairwise comparisons, whereas BWM needs
$(2n-3)$ comparisons in general. Because a reduced number of pairwise criterion comparisons has a direct influence on model consistency, BWM yields greater sensitivity findings than AHP, (ii) BWM’s components weights are more realistic than AHP approach, (iii) The data that are more reliable are acquired by the AHP model with a lower number of pairwise comparisons by forming Best-to-Others and Others-to-Worst vectors.
The rest of the paper is presented as follows: Section
2 presents the contribution and novelty of this study. Section
3 introduces the detailed algorithm for hybrid F-BWM-RAFSI methodology. Section
4 gives an illustrative example of antivirus medical mask selection. The sensitivity analysis and the validation of the proposed model are given in Section
5. Finally, Section
6 summarizes the conclusion, limitation and directions for future study.
2 Contribution and Novelty of the Paper
The primary transmission route of COVID-19 is respiratory droplets and contact. During the COVID-19 pandemic, personal protective equipment like antivirus masks has become essential items for medical staff and people to work and travel. Therefore, selection of the personal protective equipment such as antivirus masks are especially important. This paper focuses on the selection process of the antivirus masks under the COVID-19 pandemic situation and aims to address the following research questions (RQs):
-
RQ1: Which criterion is more important for selecting an antivirus mask?
-
RQ2: How to effectively evaluate the antivirus masks through the subjective judgment of group experts in medicine sector?
-
RQ3: How to build a decision-making approach that evaluates the antivirus mask alternatives?
To answer these RQ’s, this study proposes a new hybrid MCDM method that will be addressed here for the first time in order to be applied to a medical mask selection problem. One of the novel MCDM methods, called RAFSI method under a fuzzy environment, can be easily used for solving complex problems. The novelties found in the methodological application of this study are as follows: 1) A new extension of the BWM and RAFSI MCDM model using fuzzy sets is introduced in this paper. The model provides a more objective experts’ evaluation of the criteria and alternatives in a subjective environment. The present methodology enables the evaluation of alternative solutions despite dilemmas in the decision-making process and a lack of quantitative information. 2) Using fuzzy sets in the RAFSI methodology instead of using a crisp value, the structure of the given data is exclusively used. In this way, the uncertainties present in the data are used, thus improving the objectivity of the decision process. According to the authors, the application of fuzzy numbers for the purpose of exploiting the uncertainty that occurs during criteria and alternatives group evaluation using the BWM-RAFSI method has not been considered in the literature so far. Fuzzy numbers allow for the transformation of the uncertainties and inaccuracies present during the evaluation of alternatives and criteria pairwise comparisons.
In sum, the contributions of this paper can be highlighted as follows:
-
• It presents a framework that helps the selection of personal protective equipment such as antivirus masks during COVID-19 pandemic.
-
• It performs a comprehensive evaluation of the antivirus mask selection process through a new MCDM method F-BWM-RAFSI.
-
• Although the RAFSI technique is a powerful decision-making tool, it cannot express fuzziness and ambiguity information. Combined with the fuzzy sets, we posit the fuzzy RAFSI model, which can better describe decision-makers’ evaluation information.
-
• We extend assessments of decision-makers to the fuzzy sets to extract criteria weights and rank the alternatives.
-
• F-BWM-RAFSI approach is suggested to apply to multiple criteria group decision making (MCGDM) problems. It presents a real case study with respect to the evaluation of the antivirus mask alternatives; and
-
• It performs a sensitivity analysis to validate the proposed quantitative evaluation process.
3 Preliminaries
This study proposes a new hybrid MCDM method that will be addressed here for the first time in order to be applied to a medical mask selection problem. Rezaei (
2015) proposed BWM, a newly developed MCDM approach for weighting criteria and alternatives based on pairwise comparisons. The fuzzy logic extension of BWM method proposed by Rezaei (
2015), a newly developed MCDM approach for weighting criteria and alternatives based on pairwise comparisons, can handle uncertainties and vagueness of decision-makers’ opinions in the comparison matrix better. Consequently, this feature of F-BWM which makes the linguistic evaluations of decision-makers more effective and more flexible, makes it superior to other similar methods. RAFSI (Pamučar and Savin,
2020; Žižović
et al.,
2020) is a novel method, which can significantly eliminate rank reversal problems with a simple mathematical formulation. RAFSI in an uncertain environment (RAFSI-F) has been improved and adapted to deal with inaccuracy and uncertainty into antivirus mask selection problem. Consequently, a combined method of F-BWM-RAFSI seems to be an applicable hybrid MCDM model that can increase the validity of the model in the real-life problem. The general framework of the integrated model is demonstrated in Fig.
1.
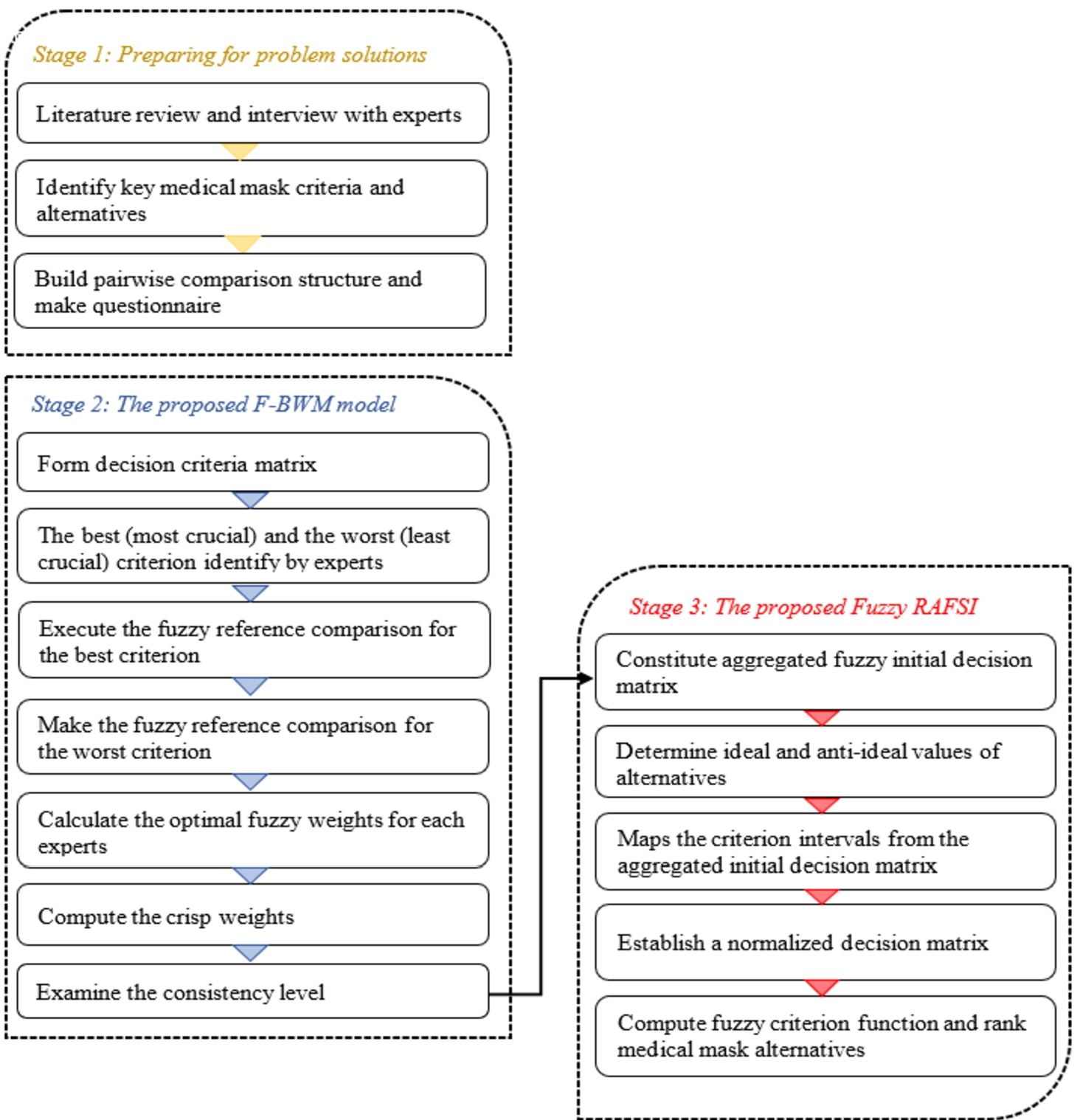
Fig. 1
Systematic steps of the integrated methodology.
3.1 Triangular Fuzzy Numbers
The fuzzy set theory was introduced by Zadeh in 1965 for better reflecting on human judgments and assessment in the decision-making process. Real case decision-making problems include fuzziness and uncertainty, as decision, goals, constraints, decision-maker opinions are not completely known. For that reason, group decision maker problems practically have used fuzzy numbers (Zadeh,
1965). In this study, we prefer to use a triangular fuzzy number that can be defined as
$\tilde{A}=({a_{1}},{b_{1}},{c_{1}})$, where,
${a_{1}}$,
${b_{1}}$ and
${c_{1}}$ denote its lower, medium, and upper number.
Definition 1.
Let
$\tilde{A}=({a_{1}},{b_{1}},{c_{1}})$,
${a_{1}}<{b_{1}}<{c_{1}}$ be a fuzzy set on
$R=(-\infty ,\infty )$. It is called a triangular fuzzy number (Carlsson and Fullér,
2001), if its membership function is illustrated as follows (see in Fig.
2).
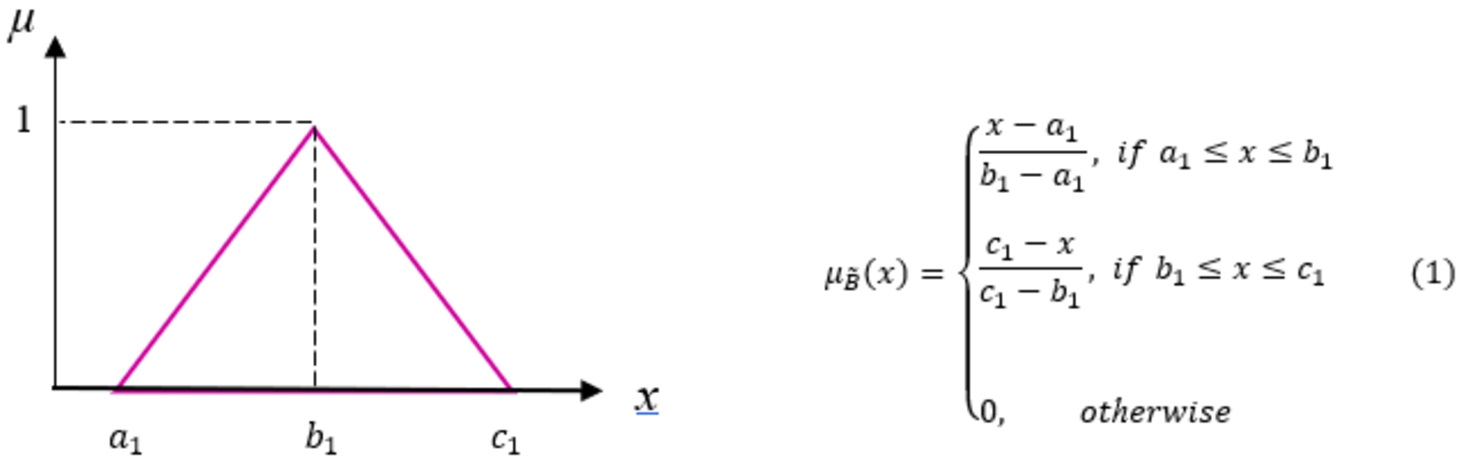
Fig. 2
Triangular fuzzy numbers.
Table 1
Some triangular fuzzy operations (Carlsson and Fullér,
2001).
| Summing operation |
|
| Subtracting operation |
|
| Multiplication operation |
|
| Division operation |
|
Also, the mathematical operations of the triangular fuzzy number are formulated in Table
1.
Assume
$\tilde{A}$ and
$\tilde{B}$ as a triangular fuzzy number as follows:
3.2 Fuzzy Best Worst Method
Fuzzy BWM method have been applied successfully in various areas such as evaluating the sustainable supplier selection criteria (Ecer and Pamucar,
2020; Pamučar and Savin,
2020; Amiri
et al.,
2021), identifying challenges and barriers for development of solar energy (Mostafaeipour
et al.,
2021), evaluating driver behaviour factors (Muravev and Mijic,
2020; Malakoutikhah
et al.,
2021), weighting the risk parameters of FMEA (Tian
et al.,
2018) plant site selection process (Luo
et al.,
2020), environmental performance evaluation (Liu
et al.,
2021; Dwivedi
et al.,
2021), evaluating the green supplier selection criteria (Wu
et al.,
2019), evaluating traffic parameters (Subotić
et al.,
2020) and hospital performance evaluation (Liao
et al.,
2019).
In addition, BWM has been incorporated with a different type of fuzzy sets such as interval type-2 fuzzy number (Wu
et al.,
2019; Qin and Liu,
2019), intuitionistic fuzzy sets (Tian
et al.,
2018; Mou
et al.,
2017), triangular fuzzy numbers (Guo and Zhao,
2017; Hafezalkotob and Hafezalkotob,
2017; Ecer and Pamucar,
2020), Z-numbers (Aboutorab
et al.,
2018), hesitant fuzzy numbers (Mi and Liao,
2019; Yazdani
et al.,
2021; Liao
et al.,
2019), rough-fuzzy approach (Chen and Ming,
2020), Pythagorean hesitant fuzzy sets (Liu
et al.,
2019).
The fuzzy pairwise comparisons are applied based on the linguistic terms given in Table
1. Then, the linguistic evaluations are transformed into triangular fuzzy numbers. The fuzzy comparison matrix (
$\tilde{A})$ can be obtained as follows,
where
${\tilde{x}_{ij}}$ denotes the relative fuzzy preference of criterion
i to criterion
j, which is a triangular fuzzy number;
${\tilde{x}_{ij}}=(1,1,1)$ when
$i=j$. In this study, we prefer to use the steps of F-BWM in Guo and Zhao,
2017. The steps of F-BWM are shown as follows:
Step 1. Build the decision criteria system. The decision criteria system consists of a set of decision criteria. n decision criteria set is presented as follows: $\{{c_{1}},{c_{2}},\dots ,{c_{n}}\}$.
Step 2. Decide the best and the worst criterion. In this step, the best and the worst criterion is decided by experts based on the constructed criteria set in Step 1. The best and the worst criterion are denoted as ${c_{\textit{Best}}}$ and ${c_{\textit{Worst}}}$ for each expert’s team.
Step 3. Implement the fuzzy reference comparisons for the best criterion $({c_{\textit{Best}}})$. In this step, the fuzzy preferences of the best criterion over all the other criteria are decided by experts. Then, the fuzzy comparisons in the linguistic format are converted to triangular fuzzy numbers. The fuzzy Best-to-Other’s vector can be obtained as follows:
where
${\tilde{x}_{Bj}}$ denotes fuzzy comparison of the best criterion
${c_{\textit{Best}}}$ over criterion
j,
$j=\{1,2,\dots ,n\}$.
Step 4. Do the fuzzy reference comparisons for the worst criterion $({c_{\textit{Worst}}})$. In this step, the fuzzy preferences of all the criteria over the worst criterion are determined. The fuzzy Others-to-Worst vector can be obtained as:
where
${\tilde{x}_{jW}}$ denotes the fuzzy comparison of the worst criterion
${c_{\textit{Worst}}}$,
$i=\{1,2,\dots ,n\}$.
Step 5. Determine the optimal fuzzy weights $({\tilde{\boldsymbol{w}}_{1}^{\ast }},{\tilde{\boldsymbol{w}}_{2}^{\ast }},\dots ,{\tilde{\boldsymbol{w}}_{n}^{\ast }})$. The optimal fuzzy weight for each criterion is determined for each fuzzy pair
${\tilde{w}_{B}}/{\tilde{w}_{j}}$ and
${\tilde{w}_{j}}/{\tilde{w}_{W}}$. It should have
${\tilde{w}_{B}}/{\tilde{w}_{j}}={\tilde{x}_{Bj}}$ and
${\tilde{w}_{j}}/{\tilde{w}_{W}}={\tilde{x}_{jW}}$. A solution is obtained that the maximum absolute gaps
$\big|\frac{{\tilde{w}_{B}}}{{\tilde{w}_{j}}}-{\tilde{x}_{Bj}}\big|$ and
$\big|\frac{{\tilde{w}_{j}}}{{\tilde{w}_{W}}}-{\tilde{x}_{jW}}\big|$ for all
j are minimized to satisfy these conditions for all
j.
${\tilde{w}_{B}}$,
${\tilde{w}_{j}}$ and
${\tilde{w}_{W}}$ in fuzzy BWM are triangular fuzzy numbers. In some cases, we prefer to use
${\tilde{w}_{j}}=({a_{j}^{w}},{b_{j}^{w}},{c_{j}^{w}})$ for optimal criteria selection. The triangular fuzzy weight of the criterion
${\tilde{w}_{j}}=({a_{j}^{w}},{b_{j}^{w}},{c_{j}^{w}})$ is transformed into a crisp value using the graded mean integration representation (GMIR) equation in Table
4. Consequently, the constrained optimization problem is constructed for obtaining the optimal fuzzy weights
$({\tilde{\boldsymbol{w}}_{1}^{\ast }},{\tilde{\boldsymbol{w}}_{2}^{\ast }},\dots ,{\tilde{\boldsymbol{w}}_{n}^{\ast }})$ as follows Guo and Zhao (
2017).
where
${\tilde{w}_{B}}=({a_{B}^{w}},{b_{B}^{w}},{c_{B}^{w}})$,
${\tilde{w}_{j}}=({a_{j}^{w}},{b_{j}^{w}},{c_{j}^{w}})$,
${\tilde{w}_{W}}=({a_{W}^{w}},{b_{W}^{w}},{c_{W}^{w}})$,
${\tilde{x}_{Bj}}=({a_{Bj}^{w}},{b_{Bj}^{w}},{c_{Bj}^{w}})$ and Eq. (
6) is transformed to the nonlinearly constrained optimization problem.
where
$\theta =({a^{\theta }},{b^{\theta }},{c^{\theta }})$.
Considering
${a^{\xi }}\leqslant {b^{\xi }}\leqslant {c^{\xi }}$, it is supposed that
${\theta ^{\ast }}=({k^{\ast }},{k^{\ast }},{k^{\ast }})$,
${k^{\ast }}\leqslant {a^{\xi }}$ then Eq. (
7) can be transferred as
Step 6. Compute the crisp weights. After obtaining fuzzy weights, the GMIR is used to alter the fuzzy weight of criterion to crisp weights. Where
$\tilde{a}$ indicates the ranking of triangular fuzzy number (Omrani
et al.,
2018).
The GMIR formula is as follows:
Step 7. Check the consistency level. The consistency ratio is checked in the same way as BWM and through computing the consistency ratio (CR) from the following equation. In this step, the consistency index (CI) for F-BWM is used that is listed in Table
2.
Table 2
Consistency index values for F-BWM (Guo and Zhao,
2017).
| Linguistic terms |
Equally important (EI) |
Weakly important (WI) |
Fairly important (EI) |
Very important (VI) |
Absolutely important (AI) |
| ${\tilde{A}_{BW}}$ |
$(1,1,1)$ |
$(2/3,1,3/2)$ |
$(3/2,2,5/2)$ |
$(5/2,3,7/2)$ |
$(7/2,4,9/2)$ |
| CI |
3 |
3.8 |
5.29 |
6.69 |
8.04 |
3.3 Fuzzy RAFSI Evaluation Method
Ranking of Alternatives through Functional mapping of criterion subintervals Into a Single Interval (RAFSI) method (Žižović
et al.,
2020) is based on defining ideal and anti-ideal reference points and defining the relationship between alternatives concerning defined reference points. The relationships between criterion values and reference points are defined using criterion functions that map criterion sub-intervals into a single criterion interval. This achieves two key advantages of the RAFSI method (Alosta
et al.,
2021; Božanić
et al.,
2021):
i) A data standardization algorithm that allows the translation of data from the initial decision matrix into an interval that is suitable for rational decision making; and
ii) The mathematical formulation of the RAFSI method eliminates the rank reversal problem, as one of the significant shortcomings of many traditional MCDM methods. The following section shows the extension of the RAFSI method to a fuzzy environment (RAFSI-F). By applying fuzzy sets, the RAFSI algorithm has been improved and adapted to handle the inaccuracies and uncertainties that arise when solving real-world problems. The algorithm of the RAFSI-F method is realized through four steps:
Step 1:
Formation of an aggregated fuzzy initial decision matrix. Suppose that the evaluation of alternatives from the set
${A_{i}}$ (
$i=1,2,\dots ,m$) is carried out by
k experts. Experts evaluate alternatives in relation to a defined set of criteria
${C_{j}}$ (
$j=1,2,\dots ,n$) using a predefined fuzzy linguistic scale. Then we can present the judgment of
k expert as a matrix
${X^{(e)}}={[{\tilde{\xi }_{ij}^{(e)}}]_{m\times n}}$, where
$1\leqslant e\leqslant k$.
where
${\tilde{\xi }_{ij}^{(e)}}=({\xi _{ij}^{l(e)}},{\xi _{ij}^{s(e)}},{\xi _{ij}^{u(e)}})$; (
$i=1,\dots ,m$;
$j=1,\dots ,n$) represents the fuzzy value from the fuzzy linguistic scale.
Since we have a group decision-making model, we obtain
k experts’ initial decision-making matrices
${X^{(1)}},{X^{(2)}},\dots ,{X^{(e)}},\dots ,{X^{(k)}}$,
$(1\leqslant e\leqslant k)$. For each expert matrix
${X^{(e)}}={[{\tilde{\xi }_{ij}^{(e)}}]_{m\times n}}$ at position
$(i,j)$ we obtain the fuzzy sequence
${\tilde{\xi }_{ij}^{(e)}}=({\xi _{ij}^{l(e)}},{\xi _{ij}^{s(e)}},{\xi _{ij}^{u(e)}})$. Using the fuzzy Heronian operator (Yu,
2013), Eq. (
12), we obtain the averaged fuzzy number
${\tilde{\xi }_{ij}}=({\xi _{ij}^{l}},{\xi _{ij}^{s}},{\xi _{ij}^{u}})$, where
${\xi _{ij}^{l}}$ and
${\xi _{ij}^{u}}$ respectively represent the lower and upper limits of the fuzzy number interval, while
${\xi _{ij}^{s}}$ represents the value in which the fuzzy number
${\tilde{\xi }_{ij}}$ has the maximum value. The Heronian mean (HM) operator (Yu,
2013) was used to aggregate the values as it allows the representation of the interrelationships between the elements being aggregated.
where
k represents the number of experts participating in the research, while
p,
$q\hspace{2.5pt}\geqslant $ 0 is a set of non-negative numbers. By applying Eq. (
12) we obtain an averaged fuzzy initial decision-matrix
$X={[{\tilde{\xi }_{ij}}]_{m\times n}}$.
Step 2:
Mapping the elements of the initial decision matrix into criterion intervals. For each criterion
${C_{j}}$ $(j=1,2,\dots ,n)$, the decision-maker defines
${\tilde{\xi }_{{I_{j}}}}$ and
${\tilde{\xi }_{{N_{j}}}}$, where
${\tilde{\xi }_{{I_{j}}}}$ represents the ideal value according to the criterion
${C_{j}}$, while
${\tilde{\xi }_{{N_{j}}}}$ represents the anti-ideal value according to the criterion
${C_{j}}$. For each alternative from the set
${A_{i}}$ (
$i=1,2,\dots ,m$), we define a function fi that maps the criterion intervals from the aggregated initial decision matrix (
9) to the criterion interval
$[{n_{1}},{n_{b}}]$, Eq. (
13):
where
${n_{b}}$ and
${n_{1}}$ represent a ratio that shows how much the ideal value is better than the anti-ideal value, while
${\tilde{\xi }_{ij}}$ denotes the value of the
i-th alternative for the
j-th criterion from the aggregated initial decision matrix. It is recommended that the ideal value is at least six times better than the anti-ideal (barely acceptable value), i.e. that
${n_{1}}=1$ and
${n_{b}}=6$.
Thus, we obtain a standardized decision matrix
$T={[{\tilde{\varphi }_{ij}}]_{m\times n}}$ (
$i=1,2,\dots ,m$,
$j=1,2,\dots ,n$) in which all elements of the matrix are translated into the interval
${\tilde{\varphi }_{ij}}\in [{n_{1}},{n_{b}}]$. The elements of the matrix
T are obtained by applying expression (
10), i.e.
${\tilde{\varphi }_{ij}}={f_{{A_{i}}}}({C_{j}})$.
Step 3:
Formation of a normalized decision matrix $N={[{\hat{\varphi }_{ij}}]_{m\times n}}$ (
$i=1,2,\dots ,m$,
$j=1,2,\dots ,n$). By applying Eq. (
14), the normalization of the element of the matrix
T is performed.
where
A and
H represent the arithmetic and harmonic mean of the elements
${n_{1}}$ and
${n_{b}}$, respectively.
Step 4:
Calculation of fuzzy criterion functions of alternatives $\tilde{Q}({A_{i}})$ and ranking of alternatives. By applying Eq. (
15), the criterion functions of alternatives
$\tilde{Q}({A_{i}})$ are calculated and the ranking of alternatives is performed.
From the considered set of alternatives, the alternative that has a higher value of the fuzzy criterion function
$\tilde{Q}({A_{i}})$ is chosen.
4 Case Study of Antivirus Mask Selection
COVID-19 is an infectious disease that primarily spreads out between humans through direct contact with an infected person or their respiratory droplets. Respiratory droplets are generated by breathing, speaking, coughing, and sneezing. Droplet nuclei are respiratory droplets that dry quickly after expiration and shrink to a diameter of less than 5 m. Droplet nuclei remain suspended in air and can travel over long distances. Goggles and respiratory protection are recommended for airborne prevention; a medical mask is needed to avoid COVID-19 infection from spreading via the air (Azap and Erdi˙nç,
2020). To prevent the transmission of COVID-19 infection, wearing masks is one of the most protective measures in order to limit the spread of airborne particles containing the virus (Bir and Widmar,
2021).
This study presents integrated methods that use fuzzy BWM and RAFSI-F approach-based framework for mask selection with respect to COVID-19 disease. We have five experts who are caring for coronavirus patients in the hospital in Istanbul and Bursa which are two cities with the highest population density in Turkey. The details of experts are indicated in Table
3.
Table 3
Expert information.
| Experts |
Profession |
Experience |
Department |
Location |
| EX1 |
Doctor |
5 years |
Public Health |
Istanbul |
| EX2 |
Doctor |
3 years |
Internal Medical |
Istanbul |
| EX3 |
Doctor |
More than 10 years |
Infectious diseases and clinical microbiology |
Istanbul |
| EX4 |
Doctor |
More than 15 years |
Infectious diseases and clinical microbiology |
Bursa |
| EX5 |
Doctor |
More than 15 years |
Infectious diseases and clinical microbiology |
Bursa |
The F-BWM was applied to determine the relative weight scores of the antivirus mask selection criteria and then, the most favoured mask is selected by the RAFSI-F approach using the evaluated weights. For this purpose, the criteria determined in the selection of medical masks and short description were obtained from expert opinions and literature review, mask selection criteria are identified in Table
4.
Table 4
Mask selection criteria.
| Code |
Criteria |
Brief description |
| C1 |
Leak age rate (fitting rate for face) |
Covers the face perfectly, does not stretch or sag |
| C2 |
Quality of raw material |
Manufactured using non-woven fabric material, its pores should be small and it should be made in accordance with health procedure |
| C3 |
Reusability |
Has two or more layer washable |
| C4 |
Breathability |
Allows comfortable breathing |
| C5 |
Use of hypo-allergenic materials |
Contains non-harmful particles and carcinogen substance |
| C6 |
Easy to wear and take off |
Conformity to the face |
| C7 |
Filtration rate |
Preserves the respiratory system against the viruses |
| C8 |
Tear and deformation resistant |
Has a durable and undeformed material |
Six different types of medical masks including basic cloth face mask, surgical face mask, single use face mask, particulate respirators (N95 and above), full face respirator and full-length face shield and their descriptions are also shown in Table
5 (Health,
2021).
4.1 Application of Fuzzy BWM Model
Step 1: Eight criteria for medical selection are shown in Table
3.
Step 2: According to F-BWM, evaluations of experts in linguistic terms are used to obtain the importance weights of antivirus mask criteria, the best criteria, the worst criteria, the best to other comparison matrix, and the other to worst comparison matrix of each expert (EX) are given in Table
6 and Table
7 by using linguistic terms, respectively.
Table 6
Best criteria and Best to Other (BO) vectors identified by experts.
|
${C_{\textit{Best}}}$ |
C1 |
C2 |
C3 |
C4 |
C5 |
C6 |
C7 |
C8 |
| EX 1 |
C7 |
WI |
AI |
FI |
VI |
AI |
AI |
EI |
VI |
| EX 2 |
C7 |
WI |
FI |
VI |
WI |
WI |
AI |
EI |
VI |
| EX 3 |
C7 |
EI |
VI |
FI |
FI |
VI |
FI |
EI |
FI |
| EX 4 |
C7 |
WI |
WI |
WI |
WI |
FI |
AI |
EI |
WI |
| EX 5 |
C7 |
FI |
FI |
AI |
VI |
VI |
FI |
EI |
VI |
Step 3: To take evaluations of Expert 1, as an example, the fuzzy preferences of the best criterion over all the criteria can be obtained with respect to Table
3.
Table 7
Worst criteria and Other to Worst (OW) vectors identified by experts.
|
${C_{\textit{Worst}}}$ |
C1 |
C2 |
C3 |
C4 |
C5 |
C6 |
C7 |
C8 |
| EX 1 |
C6 |
FI |
WI |
FI |
WI |
WI |
EI |
AI |
WI |
| EX 2 |
C6 |
VI |
FI |
WI |
VI |
WI |
EI |
AI |
WI |
| EX 3 |
C5 |
AI |
FI |
FI |
VI |
EI |
FI |
VI |
FI |
| EX 4 |
C6 |
FI |
FI |
FI |
FI |
WI |
EI |
AI |
FI |
| EX 5 |
C3 |
WI |
WI |
EI |
FI |
WI |
WI |
AI |
WI |
Step 4: The fuzzy preferences of all the criteria over the worst criterion can be presented in Table
4.
Step 5: Then, for obtaining the optimal fuzzy weights of all the criteria, the nonlinearly constrained model is established as follows in Eq. (
7).
Step 6: The following nonlinearly constrained optimization problem is obtained using represented by crisp numbers as in Eq. (
8).
Solving above model by using LINGO 18.0 software, the optimal fuzzy weights with regards to EX1 can be calculated, which are:
${\theta ^{\ast }}$ is obtained 0.4494 and the consistency ratio can be computed as:
$\textit{CR}=\frac{0.4494}{8.04}=0.0559$. The CR is lower than 10%, therefore the obtained result is acceptable.
Then, all F-BWM steps have been implemented for each expert. Results of all optimal fuzzy weights and average optimal fuzzy weights (AOFW) of eight criteria are given in Table
8. The average crisp weights of eight criteria are illustrated in Fig.
3, respectively. Heronian function, Eq. (
12) was used for aggregation of fuzzy weight coefficients.
Table 8
Optimal fuzzy weights for five experts.
|
EX1 |
EX2 |
EX3 |
EX4 |
EX5 |
AOFW |
| ${\boldsymbol{w}_{C1}^{\ast }}$ |
$(0.154,0.179,0.215)$ |
$(0.138,0.179,0.179)$ |
$(0.194,0.198,0.227)$ |
$(0.129,0.137,0.142)$ |
$(0.106,0.114,0.143)$ |
$(0.144,0.161,0.181)$ |
| ${\boldsymbol{w}_{C2}^{\ast }}$ |
$(0.064,0.073,0.079)$ |
$(0.074,0.091,0.112)$ |
$(0.059,0.081,0.110)$ |
$(0.129,0.137,0.142)$ |
$(0.098,0.114,0.143)$ |
$(0.085,0.099,0.117)$ |
| ${\boldsymbol{w}_{C3}^{\ast }}$ |
$(0.154,0.167,0.174)$ |
$(0.091,0.099,0.099)$ |
$(0.127,0.127,0.127)$ |
$(0.129,0.137,0.142)$ |
$(0.071,0.076,0.090)$ |
$(0.114,0.121,0.126)$ |
| ${\boldsymbol{w}_{C4}^{\ast }}$ |
$(0.0801,0.0821,0.1)$ |
$(0.138,0.179,0.179)$ |
$(0.127,0.139,0.169)$ |
$(0.129,0.137,0.142)$ |
$(0.095,0.114,0.143)$ |
$(0.114,0.130,0.147)$ |
| ${\boldsymbol{w}_{C5}^{\ast }}$ |
$(0.063,0.073,0.079)$ |
$(0.106,0.122,0.150)$ |
$(0.058,0.058,0.067)$ |
$(0.078,0.084,0.096)$ |
$(0.071,0.081,0.096)$ |
$(0.075,0.084,0.097)$ |
| ${\boldsymbol{w}_{C6}^{\ast }}$ |
$(0.073,0.073,0.079)$ |
$(0.046,0.046,0.051)$ |
$(0.077,0.081,0.110)$ |
$(0.045,0.052,0.061)$ |
$(0.106,0.114,0.143)$ |
$(0.069,0.073,0.088)$ |
| ${\boldsymbol{w}_{C7}^{\ast }}$ |
$(0.241,0.259,0.298)$ |
$(0.219,0.219,0.244)$ |
$(0.209,0.209,0.240)$ |
$(0.219,0.219,0.244)$ |
$(0.286,0.286,0.286)$ |
$(0.235,0.238,0.262)$ |
| ${\boldsymbol{w}_{C8}^{\ast }}$ |
$(0.080,0.082,0.100)$ |
$(0.066,0.068,0.809)$ |
$(0.077,0.081,0.110)$ |
$(0.129,0.137,0.142)$ |
$(0.074,0.081,0.096)$ |
$(0.085,0.089,0.251)$ |
According to the results of the F-BWM model, among the antivirus mask criteria, “Filtration rate (
${w_{C7}}$)” were found to be the most critical criteria related to antivirus mask selection and the next important criteria are “Leakage rate (
${w_{C1}}$)” and “Tear and deformation-resistant (
${w_{C8}}$)”, respectively. On the other hand, “Easy to wear and take off (
${w_{C6}}$)” is the least important criteria to the experts. Ranking from the most important criteria to the least important criteria is as follows:
Step 7: The consistency ratio is an important indicator for calculating the consistency of pairwise comparisons for all experts’ opinions. Its closeness to zero indicates its higher consistency. The consistency ratio is computed for pairwise comparisons that indicate high consistency in paired comparisons, as shown in Table
9. The consistency ratio for each expert is close to zero. Therefore, the weights obtained for the criteria are confirmed.
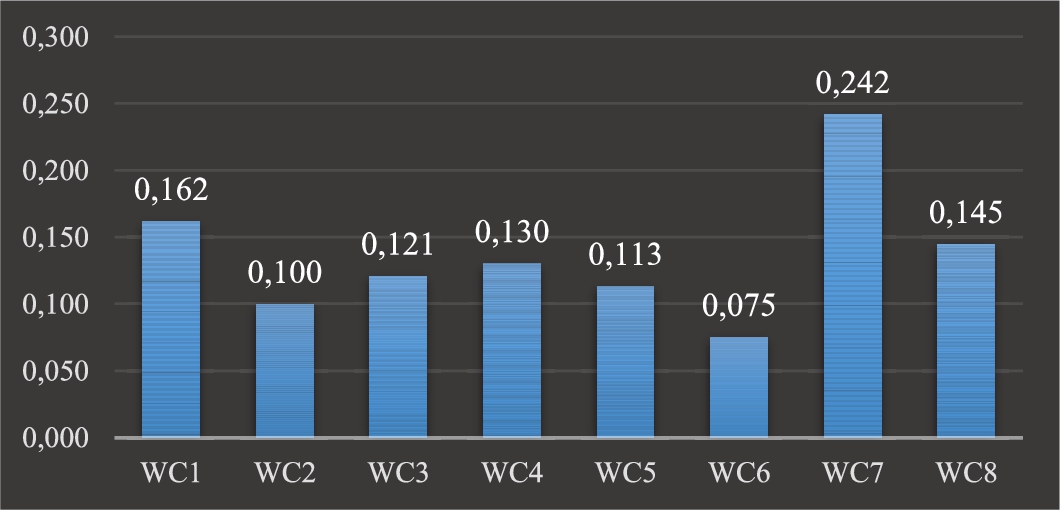
Fig. 3
Average crisp weight for each criterion.
Table 9
Consistency ratio.
|
${\theta ^{\ast }}$ |
CI |
CR |
| EX1 |
0.4494 |
8.040 |
0.055 |
| EX2 |
0.7912 |
8.040 |
0.098 |
| EX3 |
0.6093 |
6.690 |
0.091 |
| EX4 |
0.6232 |
8.040 |
0.077 |
| EX5 |
0.5000 |
8.040 |
0.062 |
4.2 Application of Fuzzy RAFSI Model
After defining the weight coefficients of the criteria, five experts evaluated the alternatives
${A_{i}}$ $(i=1,2,\dots ,6)$ in relation to the eight criteria
${C_{j}}$ $(j=1,2,\dots ,8)$ that were defined in the previous part of the paper. Criteria belongs to the group of
max criteria, while the criterion
${C_{1}}$ belongs to the group of
min criteria. To evaluate the evaluation of alternatives, the experts used the fuzzy linguistic scale shown in Table
10.
Table 10
Fuzzy linguistic scale.
| Linguistic terms |
Membership function |
| Very Poor (VP) |
(1, 1, 1) |
| Poor (P) |
(1, 2, 3) |
| Medium Poor (MP) |
(2, 3, 4) |
| Medium (M) |
(3, 4, 5) |
| Medium High (MH) |
(4, 5, 6) |
| High (H) |
(5, 6, 7) |
| Very High (VH) |
(6, 7, 8) |
| Extremely High (EH) |
(7, 8, 9) |
| Absolutely High (AH) |
(8, 9, 9) |
After evaluating the alternatives, the experts’ correspondence matrices were obtained and are shown in Table
11.
Table 11
The experts’ correspondence matrices.
| Criteria |
${A_{1}}$ |
${A_{2}}$ |
${A_{3}}$ |
| ${C_{1}}$ |
VP; P; M; P; MH |
VP; P; MP; MH; M |
VP; P; M; H; M |
| ${C_{2}}$ |
MH; MH; MP; MP; P |
H; M; M; MH; VH |
MP; MP; MP; MP; VH |
| ${C_{3}}$ |
H; MH; VP; AH; EH |
VP; VP; VP; VP; VP |
VP; VP; VP; VP; VP |
| ${C_{4}}$ |
H; MH; VH; MH; EH |
M; M; VH; MP; VH |
MH; MH; VH; MP; VH |
| ${C_{5}}$ |
M; MH; MH; M; M |
VH; M; EH; VH; EH |
MH; M; EH; MP; EH |
| ${C_{6}}$ |
EH; VH; EH; EH; VH |
VH; M; EH; EH; AH |
H; M; MH; VH; AH |
| ${C_{7}}$ |
MP; MP; P; P; MP |
EH; M; MP; MH; VH |
VP; P; P; MH; VH |
| ${C_{8}}$ |
H; M; P; H; EH |
MP; MP; P; MP; MH |
MP; MP; VP; MP; MH |
| Criteria |
${A_{4}}$ |
${A_{5}}$ |
${A_{6}}$ |
| ${C_{1}}$ |
VP; VP; VP; P; P |
VP; P; VP; P; P |
VP; MP; P; VH; MH |
| ${C_{2}}$ |
MH; M; EH; EH; EH |
H; MH; EH; AH; EH |
VP; VP; H; MP; EH |
| ${C_{3}}$ |
M; M; M; MH; VP |
EH; VH; EH; AH; VH |
VP; M; VH; MP; VH |
| ${C_{4}}$ |
M; M; H; MP; M |
P; VP; MH; P; MH |
VP; M; H; M; AH |
| ${C_{5}}$ |
MH; MH; EH; VH; EH |
MH; P; H; VH; EH |
VP; VP; H; H; EH |
| ${C_{6}}$ |
MP; M; H; P; VH |
MP; VP; MP; P; VH |
VP; MH; M; MP; AH |
| ${C_{7}}$ |
EH; H; VH; EH; AH |
EH; EH; VH; EH; EH |
VP; VP; M; P; VH |
| ${C_{8}}$ |
MH; M; H; MH; VH |
EH; H; EH; EH; EH |
VP; P; H; MP; VP |
By applying expression (
12) we get an aggregated initial decision matrix, Table
12. When calculating the initial rank of alternatives, it is recommended that decision-makers choose the values
$p=q=1$, since the adoption of the value
$p=q=1$ simplifies the decision-making process.
Table 12
The aggregated initial decision matrix.
| Criteria |
${A_{1}}$ |
${A_{2}}$ |
${A_{3}}$ |
${A_{4}}$ |
${A_{5}}$ |
${A_{6}}$ |
| ${C_{1}}$ |
$(2.57,3.4,4.24)$ |
$(2.37,3.21,4.05)$ |
$(2.55,3.39,4.23)$ |
$(1.00,1.35,1.70)$ |
$(1.00,1.51,2.04)$ |
$(3.25,4.08,4.92)$ |
| ${C_{2}}$ |
$(2.38,3.21,4.05)$ |
$(4.02,5.02,6.02)$ |
$(2.57,3.55,4.54)$ |
$(5.87,6.86,7.86)$ |
$(6.35,7.35,8.18)$ |
$(2.97,3.64,4.31)$ |
| ${C_{3}}$ |
$(4.45,5.14,5.64)$ |
$(1,10.180,1.36)$ |
$(1.00,1.00,1.00)$ |
$(3.20,4.04,4.88)$ |
$(6.51,7.51,8.34)$ |
$(3.57,4.41,5.25)$ |
| ${C_{4}}$ |
$(4.56,5.40,6.24)$ |
$(3.88,4.87,5.86)$ |
$(4.20,5.20,6.19)$ |
$(3.18,4.18,5.18)$ |
$(2.23,3.06,3.89)$ |
$(4.25,5.08,5.74)$ |
| ${C_{5}}$ |
$(3.02,3.87,4.71)$ |
$(5.37,6.37,7.36)$ |
$(4.40,5.39,6.38)$ |
$(5.20,6.2,70.19)$ |
$(4.24,5.23,6.22)$ |
$(4.09,4.78,5.46)$ |
| ${C_{6}}$ |
$(6.02,7.02,8.02)$ |
$(5.72,6.71,7.53)$ |
$(4.88,5.87,6.69)$ |
$(3.39,4.38,5.37)$ |
$(2.42,3.24,4.08)$ |
$(3.60,4.43,5.08)$ |
| ${C_{7}}$ |
$(1.51,2.35,3.19)$ |
$(4.22,5.21,6.20)$ |
$(2.45,3.27,4.09)$ |
$(6.35,7.35,8.17)$ |
$(6.51,7.51,8.50)$ |
$(2.28,2.79,3.32)$ |
| ${C_{8}}$ |
$(4.06,5.05,6.04)$ |
$(2.36,3.35,4.35)$ |
$(2.04,2.87,3.71)$ |
$(4.51,5.51,6.51)$ |
$(6.34,7.34,8.34)$ |
$(2.24,2.91,3.59)$ |
The element at position
${A_{1}}$–
${C_{1}}$, by applying expression (
12), we obtain as follows:
The remaining elements of the aggregated initial decision matrix (Table
12) are aggregated similarly.
Step 2: The experts defined the ideal and anti-ideal points,
${\tilde{\xi }_{{I_{j}}}}=(10,10,10)$ and
${\tilde{\xi }_{{N_{j}}}}=(0.5,0.5,0.5)$, by consensus for each criterion
${C_{j}}$ $(i=1,2,\dots ,8)$. Based on the defined ideal and anti-ideal points, criterion intervals are formed. Using expression (
13), the functions for standardization of criteria are defined. Since all the values of the criteria in the initial decision matrix are defined using the same linguistic scale, the same function
${\tilde{f}_{{A_{i}}}}({C_{j}})$ was used to map all the criteria
${C_{j}}$ (
$j=1,2,\dots ,8$):
By applying the function
${\tilde{f}_{{A_{i}}}}({C_{j}})$, we obtain a standardized initial decision matrix (
$T={[{\tilde{\varphi }_{ij}}]_{6\times 8}}$,
$i=1,2,\dots ,6$,
$j=1,2,\dots ,8$), given in Table
13.
Table 13
The standardized initial decision matrix.
| Criteria |
${A_{1}}$ |
${A_{2}}$ |
${A_{3}}$ |
${A_{4}}$ |
${A_{5}}$ |
${A_{6}}$ |
| ${C_{1}}$ |
$(2.75,3.44,4.15)$ |
$(2.58,3.28,3.99)$ |
$(2.73,3.43,4.14)$ |
$(1.42,1.71,2.01)$ |
$(1.42,1.85,2.29)$ |
$(3.32,4.02,4.72)$ |
| ${C_{2}}$ |
$(2.58,3.29,3.99)$ |
$(3.97,4.81,5.64)$ |
$(2.75,3.57,4.4)$ |
$(5.52,6.36,7.2)$ |
$(5.93,6.77,7.47)$ |
$(3.08,3.64,4.21)$ |
| ${C_{3}}$ |
$(4.33,4.9,5.33)$ |
$(1.42,1.57,1.73)$ |
$(1.42,1.42,1.42)$ |
$(3.27,3.98,4.69)$ |
$(6.06,6.9,7.6)$ |
$(3.59,4.29,5)$ |
| ${C_{4}}$ |
$(4.42,5.12,5.83)$ |
$(3.85,4.68,5.52)$ |
$(4.12,4.95,5.79)$ |
$(3.26,4.1,4.94)$ |
$(2.45,3.15,3.86)$ |
$(4.16,4.86,5.42)$ |
| ${C_{5}}$ |
$(3.13,3.84,4.55)$ |
$(5.1,5.94,6.78)$ |
$(4.28,5.11,5.95)$ |
$(4.96,5.8,6.63)$ |
$(4.15,4.98,5.82)$ |
$(4.02,4.6,5.18)$ |
| ${C_{6}}$ |
$(5.65,6.49,7.33)$ |
$(5.39,6.23,6.92)$ |
$(4.69,5.52,6.21)$ |
$(3.44,4.27,5.1)$ |
$(2.62,3.31,4.01)$ |
$(3.61,4.31,4.86)$ |
| ${C_{7}}$ |
$(1.85,2.56,3.27)$ |
$(4.13,4.97,5.8)$ |
$(2.64,3.33,4.03)$ |
$(5.92,6.76,7.46)$ |
$(6.06,6.9,7.74)$ |
$(2.5,2.93,3.37)$ |
| ${C_{8}}$ |
$(4,4.83,5.67)$ |
$(2.57,3.4,4.24)$ |
$(2.29,3,3.7)$ |
$(4.38,5.22,6.06)$ |
$(5.92,6.76,7.6)$ |
$(2.46,3.03,3.6)$ |
By substituting the values from the aggregated initial decision matrix into the function
${\tilde{f}_{{A_{i}}}}({C_{j}})$, expression (
13), we obtain the elements of the standardized initial decision matrix. The fuzzy value at position
${A_{1}}$–
${C_{1}}$ is obtained by applying the function
${\tilde{f}_{{A_{i}}}}({C_{j}})$:
In the same way, we get the remaining elements of the standardized initial decision matrix. Applying the function
${\tilde{f}_{{A_{i}}}}({C_{j}})$ defines the relationship between the elements of the aggregate matrix and the ideal/anti-ideal values. At the same time, the introduction of a standardized initial decision matrix eliminates the rank reversal problem that in dynamic decision-making conditions can lead to inconsistent decisions.
Step 3: By applying expression (
14), the normalization of the matrix element of the standardized initial decision matrix is performed. As shown in expression (
14), the arithmetic mean
$(A=5)$ is used to normalize the
max criterion (
${C_{2}},{C_{3}},\dots ,{C_{8}}$), while the harmonic mean
$(H=1.8)$ is used to normalize the min criterion (
${C_{1}}$). Thus, we obtain a new matrix
$N={[{\hat{\varphi }_{ij}}]_{6\times 8}}$ (
$i=1,2,\dots ,6$,
$j=1,2,\dots ,8$) as shown in Table
14.
Step 4: By applying expression (
15), the criterion functions of alternatives are calculated. Based on the
$\tilde{Q}({A_{i}})$ ranking of the alternatives is performed, so it is preferable that the alternative has a higher
$\tilde{Q}({A_{i}})$ value. The ranking of alternatives is shown in Table
15.
Table 14
Normalized initial decision matrix.
| Criteria |
${A_{1}}$ |
${A_{2}}$ |
${A_{3}}$ |
${A_{4}}$ |
${A_{5}}$ |
${A_{6}}$ |
| ${C_{1}}$ |
$(0.22,0.26,0.33)$ |
$(0.23,0.27,0.35)$ |
$(0.22,0.26,0.33)$ |
$(0.45,0.53,0.63)$ |
$(0.39,0.49,0.63)$ |
$(0.19,0.22,0.27)$ |
| ${C_{2}}$ |
$(0.26,0.33,0.4)$ |
$(0.4,0.48,0.56)$ |
$(0.27,0.36,0.44)$ |
$(0.55,0.64,0.72)$ |
$(0.59,0.68,0.75)$ |
$(0.31,0.36,0.42)$ |
| ${C_{3}}$ |
$(0.43,0.49,0.53)$ |
$(0.14,0.16,0.17)$ |
$(0.14,0.14,0.14)$ |
$(0.33,0.4,0.47)$ |
$(0.61,0.69,0.76)$ |
$(0.36,0.43,0.5)$ |
| ${C_{4}}$ |
$(0.44,0.51,0.58)$ |
$(0.38,0.47,0.55)$ |
$(0.41,0.5,0.58)$ |
$(0.33,0.41,0.49)$ |
$(0.25,0.32,0.39)$ |
$(0.42,0.49,0.54)$ |
| ${C_{5}}$ |
$(0.31,0.38,0.45)$ |
$(0.51,0.59,0.68)$ |
$(0.43,0.51,0.59)$ |
$(0.5,0.58,0.66)$ |
$(0.42,0.5,0.58)$ |
$(0.4,0.46,0.52)$ |
| ${C_{6}}$ |
$(0.57,0.65,0.73)$ |
$(0.54,0.62,0.69)$ |
$(0.47,0.55,0.62)$ |
$(0.34,0.43,0.51)$ |
$(0.26,0.33,0.4)$ |
$(0.36,0.43,0.49)$ |
| ${C_{7}}$ |
$(0.19,0.26,0.33)$ |
$(0.41,0.5,0.58)$ |
$(0.26,0.33,0.4)$ |
$(0.59,0.68,0.75)$ |
$(0.61,0.69,0.77)$ |
$(0.25,0.29,0.34)$ |
| ${C_{8}}$ |
$(0.4,0.48,0.57)$ |
$(0.26,0.34,0.42)$ |
$(0.23,0.3,0.37)$ |
$(0.44,0.52,0.61)$ |
$(0.59,0.68,0.76)$ |
$(0.25,0.3,0.36)$ |
Table 15
The ranking of alternatives.
| Alt. |
Fuzzy value ($\tilde{Q}({A_{i}})$) |
Crisp value ($Q({A_{i}})$) |
Rank |
| ${A_{1}}$ |
$(0.295,0.387,0.516)$ |
0.3930 |
4 |
| ${A_{2}}$ |
$(0.322,0.418,0.559)$ |
0.4255 |
3 |
| ${A_{3}}$ |
$(0.265,0.351,0.474)$ |
0.3569 |
6 |
| ${A_{4}}$ |
$(0.425,0.54,0.703)$ |
0.5477 |
2 |
| ${A_{5}}$ |
$(0.448,0.564,0.733)$ |
0.5726 |
1 |
| ${A_{6}}$ |
$(0.278,0.356,0.463)$ |
0.3611 |
5 |
Based on the obtained results, we can single out the antivirus mask A5 as the dominant solution, i.e. the following ranking of alternatives is proposed: ${A_{5}}>{A_{4}}>{A_{2}}>{A_{1}}>{A_{6}}>{A_{3}}$.
5 Validation and Discussion of Results
To verify the proposed solution, the sensitivity analysis of the fuzzy BWM-RAFSI model is presented in the following section. After obtaining the initial results in the MCDM framework, the question arises as to how subjectively defined input parameters influence decision making and what solutions are obtained by applying other multi-criteria techniques (Muhammad
et al.,
2021). Therefore, in the next section of the paper, the robustness check and sensitivity analysis of the obtained results to the change of the input parameters of the MCDM model were performed. The input parameters of the MCDM model mean the parameters that are defined based on the subjective preferences of the decision-maker (Biswas,
2020). In the following section, sensitivity analysis and validation of results were performed through four sections. In the first section, the analysis of the influence of the change of the weight coefficients of the criteria on the ranking results was performed. In the second and third sections, the analysis of the influence of the change of the parameters
p and
q in the Heronian operator on the ranking results was performed. In the fourth section, the robustness of the obtained solution was checked by comparison with other MCDM techniques.
5.1 Influence of Change of Criterion Weight Coefficients on Ranking Results
It is indisputable that the results of multi-criteria models largely depend on the values of the weight coefficients of the criteria. In this study, experts’ preferences were used to determine the weight coefficients of the criteria, which were processed using fuzzy BWM. Since this is a subjective model for determining the weights of the criteria, the question arises as to how these subjective assessments affect the final results of the research. Since the greatest influence on the final decision has the criterion that has the highest value of the criteria weight
$({C_{7}})$, an experiment was conducted in which the change of the value of the criteria weight
${\tilde{w}^{\prime }_{7}}=({w_{7}^{{l^{\prime }}}},{w_{7}^{{s^{\prime }}}},{w_{7}^{{u^{\prime }}}})$ in the interval
${w_{7}^{{l^{\prime }}}}\in [0.024,0.233]$ was simulated;
${w_{7}^{{s^{\prime }}}}\in [0.024,0.236]$ and
${w_{7}^{{u^{\prime }}}}\in [0.026,0.259]$. The left limit value of the interval is defined by reducing the value of criterion
${\tilde{w}_{7}}$ by 99%, while the right limit value is defined by reducing the value of criterion
${\tilde{w}_{7}}$ by 1%. The intervals are divided into 50 scenarios, while at the same time the values of the remaining criteria are corrected by applying the expression
${\tilde{w}^{\prime }_{n}}=\frac{{\tilde{w}_{n}}(1-{\tilde{w}_{7}})}{(1-{\tilde{w}^{\prime }_{7}})}$, where
${\tilde{w}_{n}}$ represents the original value of the considered criterion, while
${\tilde{w}^{\prime }_{7}}$ represents the corrected value of the most influential criterion. Thus, 50 new vectors of criteria weights were formed and their influence on the change of criterion functions of alternatives
$\tilde{Q}({A_{i}})$ was analysed in Fig.
4.
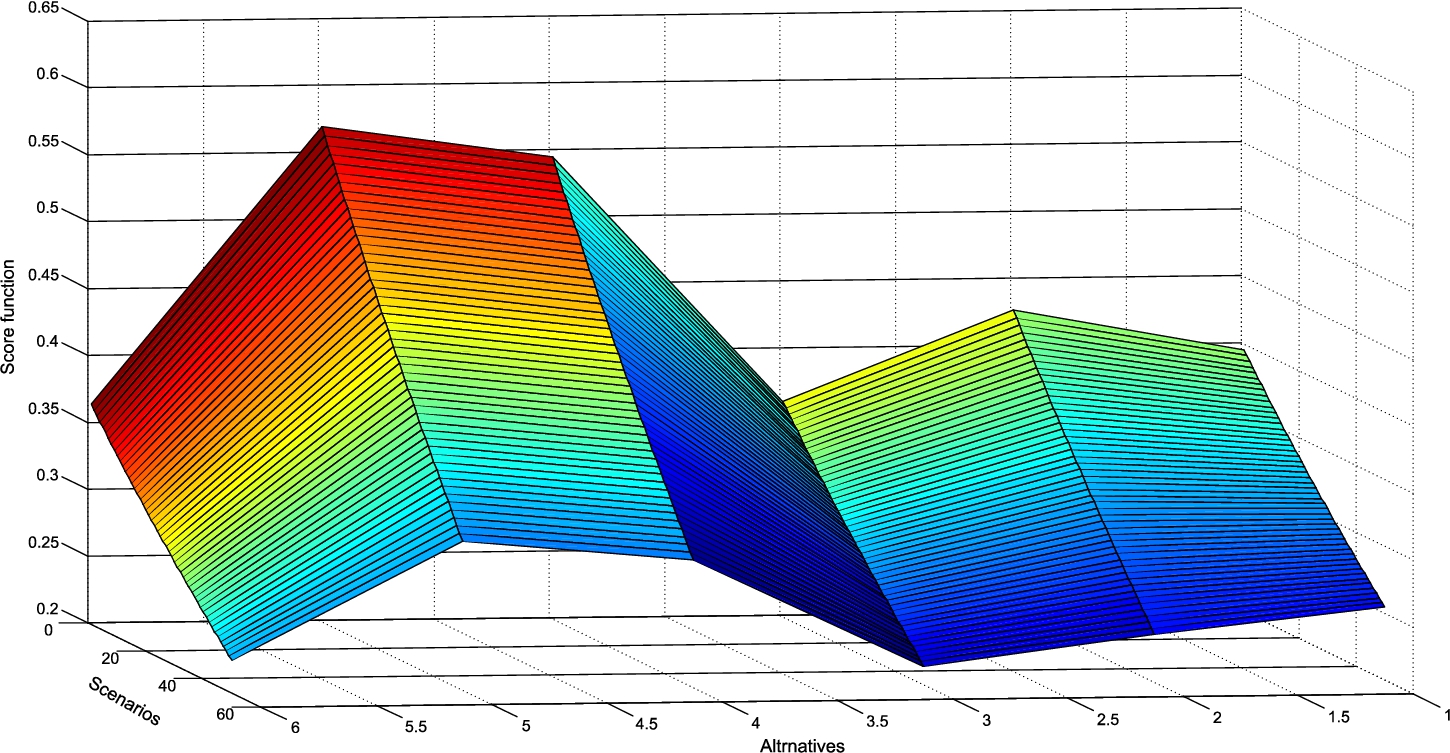
Fig. 4
Influence of change of criteria weights on change of criterion functions of alternatives $\tilde{Q}({A_{i}})$.
The analysis shown in Fig.
4 shows that the new vectors of the weight coefficients of the criteria affect the change in the values of the criterion functions of the alternative, which shows that the model is sensitive to changes in the input parameters. Also, it was shown that through the first 31 scenarios, the initial rank
${A_{5}}>{A_{4}}>{A_{2}}>{A_{1}}>{A_{6}}>{A_{3}}$ was confirmed. In the next 29 scenarios, for the values of the weighting coefficients
${w_{7}^{{l^{\prime }}}}\in [0.024,0.087]$;
${w_{7}^{{s^{\prime }}}}\in [0.024,0.088]$ and
${w_{7}^{{u^{\prime }}}}\in [0.026,0.097]$, the third-ranked alternative (A2) and the fourth-ranked alternative
$({A_{1}})$ switched places, while the ranking of the remaining alternatives was confirmed. Based on the presented analysis, we can conclude that the first-ranked alternative
$({A_{5}})$ remained dominant through all 50 scenarios and that it represents the best solution regardless of the changes in the values of the criteria weights. Also, alternative
${A_{4}}$ (second-ranked alternative) retained its position in the set of dominant alternatives, as it remained second-ranked through 50 scenarios. At the same time, it was confirmed that alternatives
${A_{6}}$ and
${A_{3}}$ represent the worst solutions through all 50 scenarios.
5.2 Influence of Change of Values of Parameters p and q on Change of Weight Coefficients of Criteria
By changing the values of the parameters
p and
q in the Heronian function, the calculation of the aggregate values of the criteria weights becomes more complicated, since a larger number of mutual relations between the attributes is considered at the same time. Therefore, it is necessary to perform an analysis of the influence of changes in the parameters
p and
q on the change of the criteria weights, and indirectly on the change in the ranks of the alternative. The change of the parameters
p and
q was performed through three experiments:
Experiment I: The influence of the change of the parameter
$p\in [1,300]$ on the change of utility function of alternatives was analysed, while the value of the parameter
$q=1$ remained unchanged through all 300 scenarios;
Experiment II: In this experiment, the effect of changing the parameter
$q\in [1,300]$ was analysed in a similar way, while the value of the parameter
$p=1$ remained unchanged; and
Experiment III: The influence of the change of both parameters simultaneously was analysed, which implied the change of
p and
q in the interval
$p\in [1,300]$ and
$q\in [1,300]$. Limit values of parameters
p and
q are defined based on a large number of simulations, which showed that for higher values of parameters
p and
q of 300 has no significant changes in the values of weight coefficients of the criteria. The influence of the change of the parameters
p and
q on the change of the aggregated values of the weight coefficients of the criteria and indirectly on the change of the criterion functions of the alternatives
$\tilde{Q}({A_{i}})$ shown in Fig.
5.
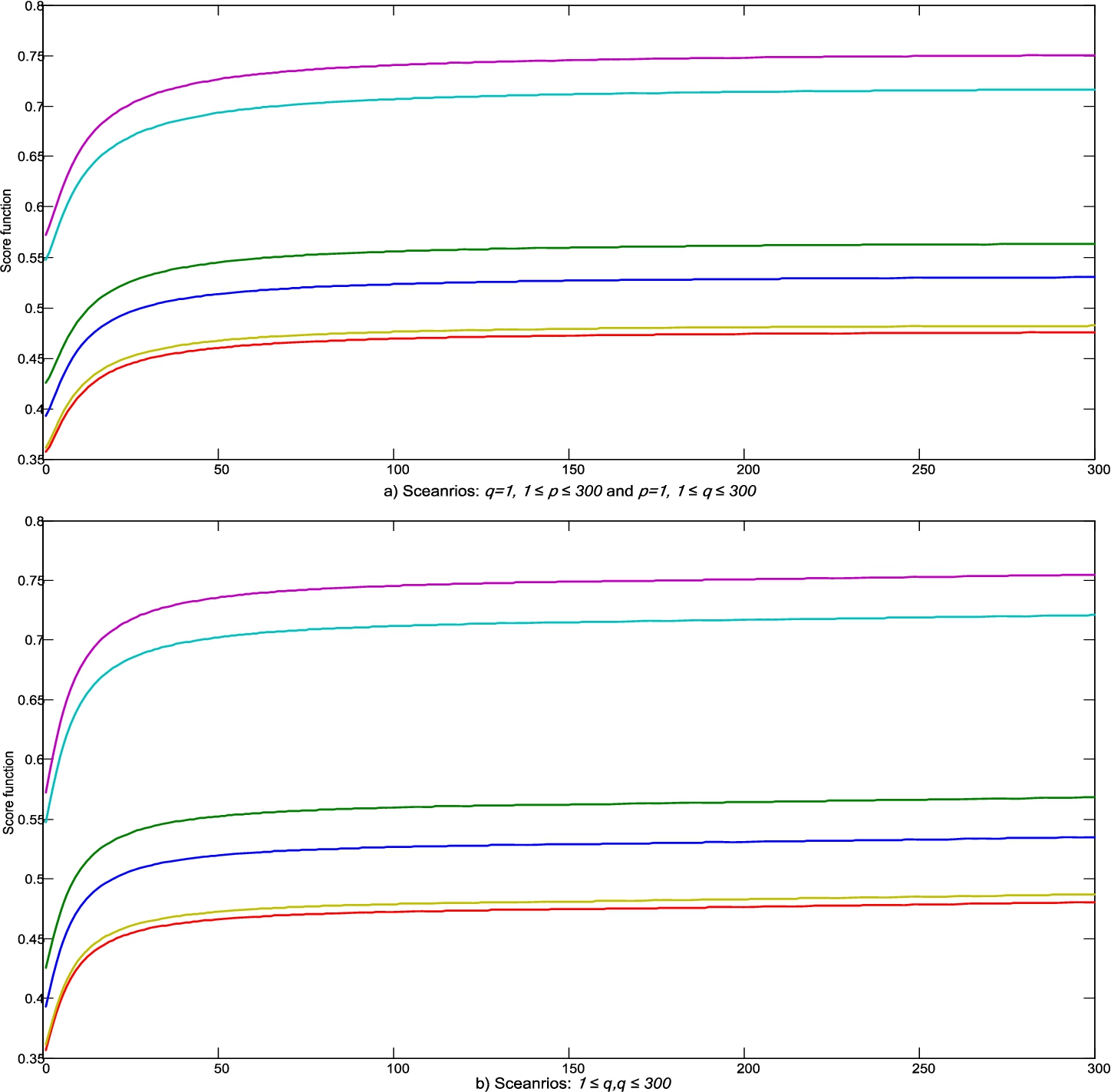
Fig. 5
Influence of parameters p and q on change of weight coefficients and change of criterion functions of alternatives.
The presented experiments showed that changes in the values of the parameters p and q affect the change in the values of the weight coefficients of the criteria and the change in the criterion functions of the alternative. Through 900 scenarios that were divided into three experiments, there were no changes in the ranks of the alternative, despite changes in the values of the criterion functions. Through all scenarios, the initial rank ${A_{5}}>{A_{4}}>{A_{2}}>{A_{1}}>{A_{6}}>{A_{3}}$ was confirmed, so we can conclude that alternative ${A_{5}}$ is the dominant alternative in the considered set of alternatives.
5.3 Influence of Change of the Value of Parameters p and q on Change of Value in the Initial Decision Matrix
Since the Heronian function was used to aggregate values from experts’ initial decision matrices into an aggregated initial decision matrix, this section analyses the impact of changing the
p and
q parameters on the change in the value of the aggregated initial decision matrix. As in the previous section, three experiments were performed here during which the influence of the change of the parameters
p and
q in the interval
$p,q\in [1,300]$ was considered. The influence of changing the parameters
p and
q on the change of aggregate values in the initial decision matrix is shown in Fig.
6.
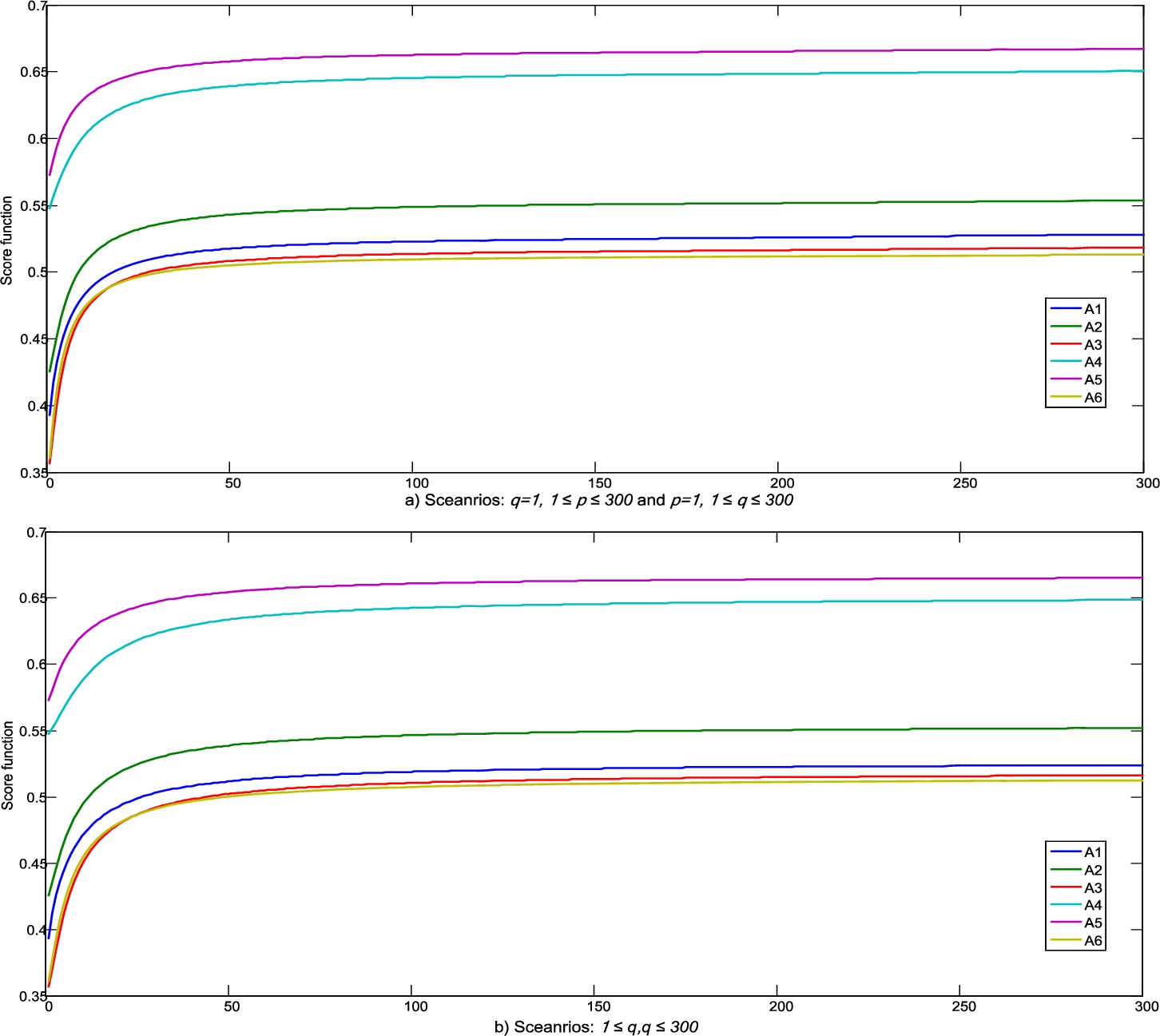
Fig. 6
Influence of parameters p and q on the change of aggregate values in the initial decision matrix.
The values of the criterion functions of the alternatives (Fig.
6) show that changes in the values of the parameters
p and
q lead to changes in the aggregate initial decision matrix. In the presented simulation, it is noticed that there is a change only in the ranks of the worst-ranked alternatives, i.e. alternatives
${A_{6}}$ and
${A_{3}}$. In the first two experiments, for the values of the parameters
$p,q\in [12,300]$, alternatives
${A_{6}}$ and
${A_{3}}$ switched their places, while in the third experiment, for the values of the parameters
$p,q\in [13,300]$, alternatives
${A_{6}}$ and
${A_{3}}$ changed their ranks. In all three experiments, there were no changes in the ranks of the remaining alternatives, which confirmed their initial rank. From the presented analysis (through all 900 simulations) we can conclude that there is a satisfactory advantage of the first-ranked alternative
$({A_{5}})$ in relation to the remaining alternatives from the considered set.
5.4 Comparison with Fuzzy MCDM Methodologies
Since fuzzy sets were used for uncertainty processing in this paper, four fuzzy multicriteria techniques were chosen to compare the results: fuzzy COPRAS (Complex Proportional Assessment) technique (Fouladgar
et al.,
2012) method, fuzzy MABAC (Multi-Attributive Border Approximation area Comparison) method (Božanić
et al.,
2021), fuzzy MAIRCA (Multi-Attributive Ideal-Real Comparative Analysis) method (Gul and Ak,
2020) and fuzzy MARCOS (Measurement Alternatives and Ranking according to the Compromise Solution) method (Stanković
et al.,
2020; Arsu and Ayçin,
2021).
A comparative overview of the application of these fuzzy MCMD methodologies is shown in Fig.
7.
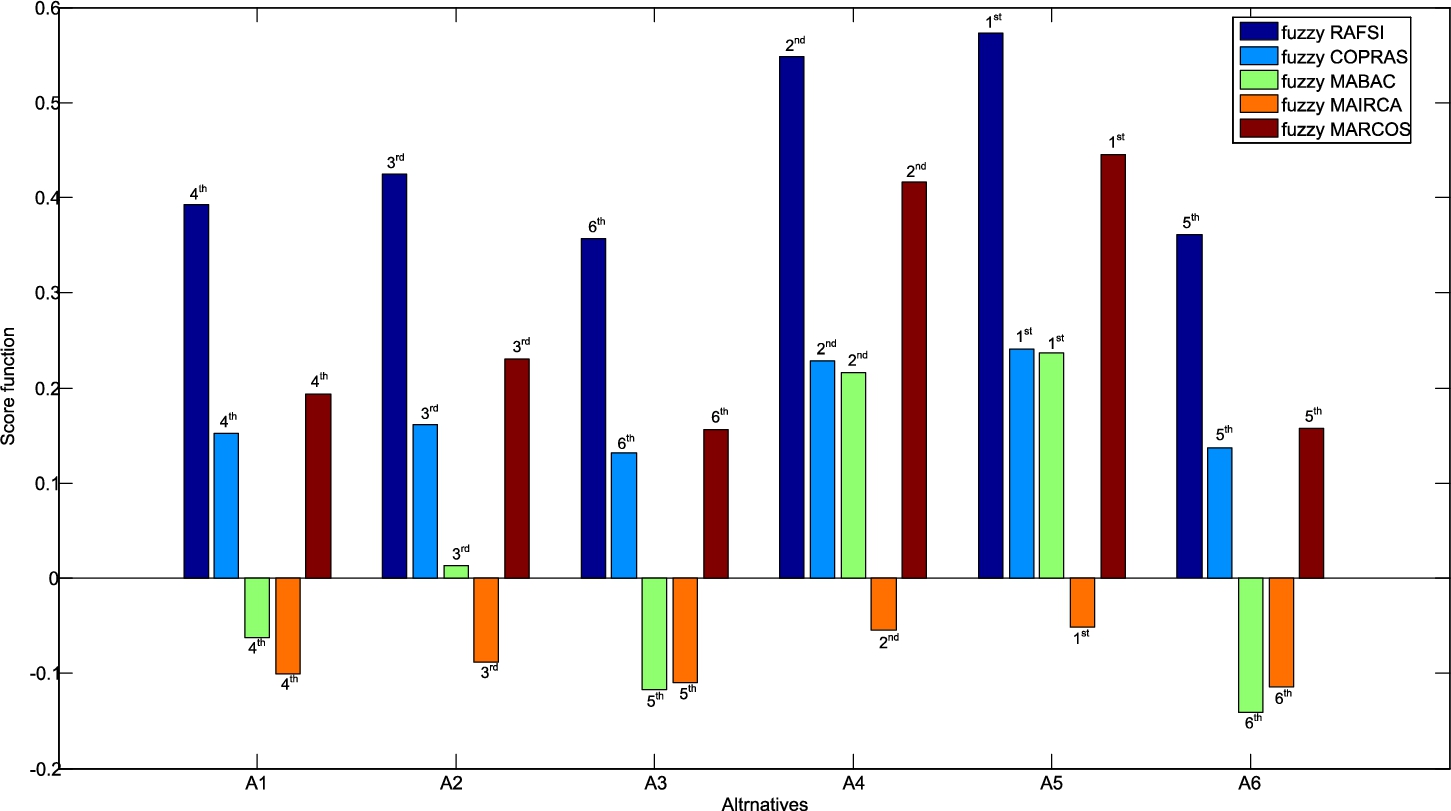
Fig. 7
Ranks of the alternatives based on the different fuzzy methodology.
Based on the obtained results, it was confirmed that alternative ${A_{5}}$ represents the best solution according to all MCDM methodologies. The results showed that using the fuzzy MARCOS and fuzzy COPRAS methods the same rank was obtained. Ranking differences occurred in the fuzzy MABAC and fuzzy MAIRCA methods and they are reflected in the different ranks of the last two worst alternatives (${A_{6}}$ and ${A_{3}}$). The presented analysis proves the robustness of the fuzzy BWM-RAFSI methodology proposed in this paper and that the proposed choice of alternative ${A_{5}}$ is credible.
6 Conclusion
COVID-19 has spread more like most other common respiratory diseases, mainly through respiratory droplet transmission without physical contact. Therefore, wearing a face mask is one of the most effective ways to prevent the spread of the virus. Especially, health workers are the most likely to be exposed to COVID-19 because they are in close contact with patients with suspected, probable or confirmed COVID-19. During the COVID-19 epidemic, face masks have become a highly effective item for health care staff and ordinary people. Different types of masks have been suggested throughout the COVID-19 pandemic. However, some masks are more effective than others. In order to determine what types of face mask work best to prevent the spread of COVID-19, this paper proposes a combined approach that uses F-BWM and fuzzy RAFSI methods for the mask selection process for healthcare personnel with respect to the COVID-19 pandemic to fill the gap in the literature.
There are two main advantages of the proposed fuzzy BWM-RAFSI methodology: 1) fuzzy BWM-RAFSI method has a new mathematical treatment for data normalization that enables transferring data from the initial decision making matrix into any interval which is adequate for making rational decisions and 2) resistance of fuzzy BWM-RAFSI method to rank reversal problem (Žižović
et al.,
2020). This paper offers some important contributions to the literature: (i) A novel integrated MCDM approach was used to select an appropriate medical face mask for preventing COVID-19 in healthcare workers, (ii) Antivirus mask selection criteria were considered under the fuzzy environment to make a more accurate decision, (iii) The proposed MCDM methodology can evaluate alternatives, although it is inaccurate and lacks quantitative information, (vi) The combination of two model BWM-RAFSI under fuzzy environment enables a more flexible decision-making process in the healthcare sector during COVID-19 pandemic, (v) This proposed model was compared with other MCDM methods with sensitivity analysis and validation of this model was demonstrated.
One of the possible limitations of the fuzzy BWM-RAFSI multi-criteria methodology is the mathematical complexity that requires the knowledge of nonlinear mathematical programming and fuzzy theory. This feature may be a limiting factor for a broader application in the multi-criteria decision-making field. To overcome this limitation, it is recommended that future research be directed towards developing a decision support system based on the application of the fuzzy BWM-RAFSI methodology. Also, a major source of limitation is that due to the over-intensity and high workload during the pandemic process, the opinions of healthcare workers such as nurses, medical technicians, dentists and etc. were not considered in this evaluation process.
Further research can benefit from the perspectives of healthcare workers from other professions and occupations. Furthermore, this proposed model can be performed for the same problem under newly released fuzzy extensions such as Pythagorean fuzzy sets, cubic picture fuzzy sets and spherical fuzzy sets for the future work. By doing this way, the validity of this hybrid model can be tested with the results obtained from several fuzzy sets. Finally, this new integrated model may be used in a variety of healthcare domains, including the development of an optimum COVID-19 diagnostic system, wearable health devices, and treatment techniques.
Compliance with ethical standards
Conflict of interest: The authors declare that they have no conflict of interest.
Ethical approval: This article does not contain any studies with human participants or animals performed by any of the authors.
Informed consent: N/A.