Abstract
There exist various types of similarity measures for intuitionistic fuzzy sets in the literature. However, in many studies the interactions among the elements are ignored in the construction of the similarity measure. This paper presents a cosine similarity measure for intuitionistic fuzzy sets by using a Choquet integral model in which the interactions between elements are considered. The proposed similarity measure is applied to some pattern recognition problems and the results are compared with some existing results to demonstrate the effectiveness of this new similarity measure.
1 Introduction
Zadeh (
1965) introduced the concept of fuzzy set by using a membership function and Atanassov (
1986) expanded this concept to the concept of intuitionistic fuzzy set (IFS) by using both a membership function and a non-membership function. The theory of intuitionistic fuzzy sets has been extensively studied by many authors (see e.g. Szmidt and Kacprzyk,
2000,
2003; Xu and Yager,
2006; Ye,
2009,
2010,
2018; Xu,
2010; Melo-Pinto
et al.2013; Balasubramaniam and Ananthi,
2014; Mani and Jerome,
2014; Lu and Ye,
2016; Das
et al.,
2016; Luo and Zhao,
2018). The concept of similarity measure is one of these study areas. A similarity measure is an important tool for measuring the degree of similarity between two IFSs and various versions of the concept of the similarity measure have been applied to various fields such as pattern recognition, medical diagnosis, decision making, face recognition systems, clustering (see e.g. De
et al.,
2001; Hung and Yang,
2004; Liu,
2005; Vlachos and Sergiadis,
2007; Li
et al.,
2007; Xu and Chen,
2008; Ye,
2012; Luo and Ren,
2016; Ngan,
2016; Hwang et al.,
2018; Song
et al.,
2019). Many similarity measures of IFSs have been investigated in the literature and the concept of cosine similarity measure is one of them. The concept of cosine similarity measure for fuzzy sets is defined as the inner product of two vectors divided by the product of their lengths, that is, the cosine of the angle between the vector representations of fuzzy sets and it has been investigated by many researchers (Gerstenkorn and Manko,
1991; Ye,
2011,
2016; Garg,
2018; Wei,
2018; Wei and Wei,
2018; Wei
et al.,
2019; Wang
et al.,
2019).
The concepts of fuzzy measure (or capacity or non-additive measure) and the Choquet integral were introduced by Choquet (
1953). Since that time, fuzzy measures and integrals have been studied on a rather mathematical point of view, especially in multi criteria decision making field. The purpose of the multi criteria decision making field is to order alternatives based on multiple contradictory criteria and choose the best alternative (see e.g. Grabisch,
1996; Ünver
et al.,
2018). Actually a fuzzy integral is a generalization of weighted mean. Yang and Ha (
2008) introduced a similarity measure for IFSs by using a Choquet integral model where a generalized fuzzy measure was used to characterize interactions among elements of IFSs. Also, the Choquet integral model instead of a weighted average model was used to compute this similarity measure.
The purpose of a pattern recognition problem is to decide whether an object belongs to a set or a class. Many studies have been made to solve such a problem and many similarity measures have been proposed by several researchers (see e.g. Dengfeng and Chuntian,
2002; Liang and Shi,
2003; Mitchell,
2003; Liu,
2005; Wei and Ye,
2010; Hwang and Yang,
2013; Zhu and Ye,
2013; Song
et al.,
2014; Boran and Akay,
2014; Chen and Chang,
2015; Jiang
et al.,
2019).
In this study, we provide a new cosine similarity measure for IFSs by considering the Choquet integral, inspired by a weighted cosine similarity measure for IFSs which has been given by Ye (
2011). First of all, we give the basic definitions that are used throughout the study, and then we recall the concepts of fuzzy measure and Choquet integral. Then we propose a new cosine similarity measure based on the Choquet integral for IFSs. To demonstrate the effectiveness of the new similarity measure, we apply it to a pattern recognition and a medical diagnosis problem. We also compare the results of the proposed cosine similarity measure with some previous results in the literature.
2 Preliminaries
In this section we recall some definitions of fuzzy set theory, correlation coefficient, some cosine similarity measures and some weighted cosine similarity measures for IFSs.
Definition 1 (Zadeh, 1965).
A fuzzy set
A of a given set
X is defined with a function which is called the membership function of
A and is denoted by
The value
${\mu _{A}}(x)$ is said to be the grade of membership of the element
x to the set.
In the following definition we recall the concept of IFS that was introduced by Atanassov (
1986).
Definition 2 (Atanassov, 1986).
An IFS
A in
X is given by
where
${\mu _{A}}:X\to [0,1]$ is a function which is called the membership function and
${\nu _{A}}:X\to [0,1]$ is a function which is called the non-membership function with
${\mu _{A}}(x)+{\nu _{A}}(x)\leqslant 1$, for any
$x\in X$. The values
${\mu _{A}}(x)$ and
${\nu _{A}}(x)$ are the grade of membership and the grade of non-membership of the element
x to the set
A, respectively.
It is clear that each fuzzy set is an intuitionistic fuzzy set, but the converse is not true in general. Now, we recall a correlation coefficient between IFSs which is actually the motivation of the cosine similarity measure between two IFSs.
Definition 3 (Gerstenkorn and Manko, 1991).
Let
$X=\{{x_{1}},\dots ,{x_{n}}\}$ be a finite set and
A and
B be two IFSs of
X. A correlation coefficient between
A and
B is defined by
where the correlation of
A and
B is given by
and the informational intuitionistic energies of
A and
B are
and
respectively.
The correlation coefficient
k satisfies the following properties (Gerstenkorn and Manko,
1991):
-
$\mathbf{({P_{1}})}$ $0\leqslant k(A,B)\leqslant 1$;
-
$\mathbf{({P_{2}})}$ $k(A,B)=k(B,A)$;
-
$\mathbf{({P_{3}})}$ If $A=B$ then $k(A,B)=1$.
Various similarity measures were defined to quantify the degree of similarity between IFSs. Chen (
1995) proposed a similarity measures between vague sets. Hong and Kim (
1999) and Fan and Zhangyan (
2001) pointed out limitations of the similarity measure of Chen (
1995) and proposed a new similarity measure for IFSs. Later, Li
et al. (
2007) proposed a new similarity measure and Dengfeng and Chuntian (
2002) generalized their similarity measure of IFSs by using Minkowski distance and applied this measure to the pattern recognition. Then, Mitchell (
2003) modified this similarity measure. Later, Hung and Yang (
2004) proposed simple and well suited similarity measures for IFSs by using Hausdorff distance and applied it to the pattern recognition. Now, we recall some cosine similarity measures from the literature.
Definition 4 (Salton and McGill, 1983).
Let
$X=\{{x_{1}},\dots ,{x_{n}}\}$ be a finite set and let
and
be two fuzzy sets of a set
X. A cosine similarity measure based on Bhattacharya’s distance (Bhattacharya,
1946) between
A and
B is defined by
It is clear that $0\leqslant {C_{F}}(A,B)\leqslant 1$.
Definition 5 (Ye, 2011).
Let
$X=\{{x_{1}},\dots ,{x_{n}}\}$ be a finite set and let
and
be two IFSs of
X. A cosine similarity measure between IFSs
A and
B is defined by
For
$n=1$ the cosine similarity measure
${C_{\textit{IFS}}}$ is equivalent to the correlation coefficient
k, that is
${C_{\textit{IFS}}}(A,B)=k(A,B)$. The cosine similarity measure also satisfies
${P_{1,2,3}}$.
Definition 6 (Ye, 2011).
Let
$X=\{{x_{1}},\dots ,{x_{n}}\}$ be a finite set and let
A and
B be two IFSs of
X. A weighted cosine similarity measure between IFSs
A and
B is defined by
where
$w=({w_{1}},\dots ,{w_{n}})$ is the weight vector with
${w_{i}}\in [0,1]$ for all
$i=1,\dots ,n$ and
${\textstyle\sum _{i=1}^{n}}{w_{i}}=1$. In particular, if
$w=(1/n,1/n,\dots ,1/n)$, then the weighted cosine similarity measure is reduced to the cosine similarity measure between IFSs
A and
B, i.e.
${W_{\mathit{IFS}}}(A,B)={C_{\mathit{IFS}}}(A,B)$. Obviously, the weighted cosine similarity measure of two IFSs
A and
B also satisfies
${P_{1,2,3}}$.
The concept of Choquet integral is a generalization of the concept of weighted mean. Yang and Ha (
2008) proposed a similarity measure between IFSs by considering the Choquet integral. Now, we recall the concepts of fuzzy measure and Choquet integral.
Definition 7 (Choquet, 1953).
Let
$X\ne \varnothing $ be a finite set and let
$P(X)$ be the power set of
X. If
-
(i) $\sigma (\varnothing )=0$,
-
(ii) $\sigma (X)=1$,
-
(iii) $\sigma (A)\leqslant \sigma (B)$ for any $A,B\subset X$ such that $A\subseteq B$ (monotonicity),
then the set function
$\sigma :P(X)\to [0,1]$ is called a fuzzy measure on
X.
Definition 8 (Choquet, 1953).
Let
$X\ne \varnothing $ be a finite set and let
σ be a fuzzy measure on
X. The Choquet integral of a function
$f:X\to [0,1]$ with respect to
σ is defined by
where the sequence
${\{{x_{(k)}}\}_{k=0}^{n}}$ is a permutation of the sequence
${\{{x_{k}}\}_{k=0}^{n}}$ such that
$0:=f({x_{(0)}})\leqslant f({x_{(1)}})\leqslant f({x_{(2)}})\leqslant \cdots \leqslant f({x_{(n)}})$ and
${E_{(k)}}:=\{{x_{(k)}},{x_{(k+1)}},\dots ,{x_{(n)}}\}$.
Definition 9 (Yang and Ha, 2008).
Let
$X=\{{x_{1}},\dots ,{x_{n}}\}$ be a finite set and let
A and
B are two given IFSs in
X and let
σ be a fuzzy measure on
X. A similarity measure between
A and
B is given with
where
$f({x_{i}})=\alpha |{\mu _{A}}({x_{i}})-{\mu _{B}}({x_{i}}){|^{p}}+\beta |{\nu _{A}}({x_{i}})-{\nu _{B}}({x_{i}}){|^{p}}+\gamma |{\pi _{A}}({x_{i}})-{\pi _{B}}({x_{i}}){|^{p}}$ and
$\alpha ,\beta ,\gamma \in [0,1]$,
$\alpha +\beta +\gamma =1$ and
$1<p<+\infty $.
3 Choquet Cosine Similarity Measure
In this section, by considering the Choquet integral we construct a new cosine similarity measure.
Definition 10.
Let
$X=\{{x_{1}},\dots ,{x_{n}}\}$ be a finite set and let
A and
B be two IFSs in
X and let
σ be a fuzzy measure on
X. A Choquet cosine similarity measure between
A and
B is given with
where
Proposition 1.
Let $X=\{{x_{1}},\dots ,{x_{n}}\}$ be a finite set, let A and B be two IFSs in X. The Choquet cosine similarity measure ${W_{\mathit{IFS}}^{(C,\hspace{0.1667em}\sigma )}}$ satisfies the following properties:
-
$\mathbf{({P_{1}})}$ $0\leqslant {W_{\mathit{IFS}}^{(C,\sigma )}}(A,B)\leqslant 1$;
-
$\mathbf{({P_{2}})}$ ${W_{\mathit{IFS}}^{(C,\sigma )}}(A,B)={W_{\mathit{IFS}}^{(C,\sigma )}}(B,A)$;
-
$\mathbf{({P_{3}})}$ If $A=B$ then ${W_{\mathit{IFS}}^{(C,\sigma )}}(A,B)=1$.
Proof.
$\mathbf{({P_{1}})}$ Since ${f_{A,B}}({x_{i}})\in [0,1]$ and for any $i=1,\dots ,n$ and the Choquet integral is monotone, we have $0\leqslant {W_{\mathit{IFS}}^{(C,\sigma )}}(A,B)\leqslant 1$.
$\mathbf{({P_{2}})}$ It is trivial that since ${f_{A,B}}({x_{i}})={f_{B,A}}({x_{i}})$ for any $i=1,\dots ,n$.
$\mathbf{({P_{3}})}$ If $A=B$, then ${\mu _{A}}({x_{i}})={\mu _{B}}({x_{i}})$ and ${\nu _{A}}({x_{i}})={\nu _{B}}({x_{i}})$ for $i=1,\dots ,n$. We have ${f_{A,B}}({x_{i}})=1$ and so ${W_{\mathit{IFS}}^{(C,\sigma )}}(A,B)=1$. Thus, the proof is completed. □
4 Applications
The proposed cosine similarity measure can be used to evaluate the degree of similarity between two IFSs. Therefore, it can be applied to pattern recognition problems with the intuitionistic fuzzy information. It is more delicate than the cosine similarity measures in the literature since it considers interactions between criteria.
Let $X=\{{x_{1}},\dots ,{x_{n}}\}$ be a finite set of attributes and let $C=\{{C_{1}},\dots ,{C_{m}}\}$ be a finite set of alternatives. Here, Q needs to be classified in one of ${C_{i}}$, $i=1,\dots ,m$. Now, we give the implementation steps of the promised Choquet integral model.
Step 1. Since the model is a fuzzy integral model, it is necessary to establish a fuzzy measure on a given set before we can use the model. The decision maker determines which fuzzy measure will be used according to the situation and the number of elements of the set is mostly effective in making this determination. The thing to note here is that if the weights of the singletons in the set are given, these weights could be equal to the fuzzy measure of the singletons with the condition that the sum of fuzzy measure of singletons is equal to one. Otherwise, we may use decision making methods such as analytic hierarchy process (AHP), analytic network process (ANP) to determine fuzzy measure of singletons. For example, in sets with at least 3 elements, the decision maker establishes a hypothetical measure that will be effective in relieving the decision-making process as it can directly see the interaction between the criteria. Let
X be a finite set with at least 3 elements, and let
σ be a fuzzy measure on
X. If
-
(i) $\sigma (\{{x_{i}},{x_{j}}\})=\sigma (\{{x_{i}}\})+\sigma (\{{x_{j}}\})$, then no interaction ${x_{i}}$ between ${x_{j}}$,
-
(ii) $\sigma (\{{x_{i}},{x_{j}}\})>\sigma (\{{x_{i}}\})+\sigma (\{{x_{j}}\})$, then ${x_{i}}$ and ${x_{j}}$ are positively interactive,
-
(iii) $\sigma (\{{x_{i}},{x_{j}}\})<\sigma (\{{x_{i}}\})+\sigma (\{{x_{j}}\})$, then
${x_{i}}$ and
${x_{j}}$ are negatively interactive, for all
${x_{i}},{x_{j}}\in X$ (Grabisch,
1997).
Moreover, the decision maker can also use measures such as
λ-fuzzy measures (Larbani
et al.,
2011),
k-additive fuzzy measures (Grabisch,
1997),
p-symmetric fuzzy measures (Miranda
et al.,
2002) in the measurement determination process in order to ease the decision making process. Here, we use hypothetical fuzzy measure and a
λ-fuzzy measure in the process of solving the pattern recognition and the medical diagnosis problem, respectively.
Step 2. The function
${f_{Q,C}}({x_{i}})$ is calculated by using Definition
10.
Step 3. We choose the best alternative by using the recognition principle of maximum degree of similarity between IFSs.
4.1 Pattern Recognition Problem
We consider a pattern recognition problem which is adapted from Ye (
2011).
Example 1.
Let
${C_{1}}$,
${C_{2}}$ and
${C_{3}}$ be three patterns which are represented by following IFSs in a given finite set
$X=\{{x_{1}},{x_{2}},{x_{3}}\}$:
Let
$Q=\{\langle {x_{1}},0.5,0.3\rangle ,\langle {x_{2}},0.6,0.2\rangle ,\langle {x_{3}},0.8,0.1\rangle \}$ be a pattern that needs to be classified in one of three classes
${C_{1}}$,
${C_{2}}$, and
${C_{3}}$.
Consider the following hypothetical fuzzy measure
σ on
X:
$\sigma (\{{x_{1}}\})=0.5$,
$\sigma (\{{x_{2}}\})=0.3$,
$\sigma (\{{x_{3}}\})=0.2$,
$\sigma (\{{x_{1}},{x_{2}}\})=0.7$,
$\sigma (\{{x_{1}},{x_{3}}\})=0.8$,
$\sigma (\{{x_{2}},{x_{3}}\})=0.6$,
$\sigma (\{{x_{1}},{x_{2}},{x_{3}}\})=1$. For the sake of completeness, the weights used in Example 5.1 of Ye (
2011) are considered here as the measures of singletons.
| ${f_{{C_{1}},Q}}({x_{1}})=0.8574$ |
${f_{{C_{1}},Q}}({x_{2}})=0.9486$ |
${f_{{C_{1}},Q}}({x_{3}})=0.9998$ |
| ${f_{{C_{2}},Q}}({x_{1}})=0.9146$ |
${f_{{C_{2}},Q}}({x_{2}})=0.9486$ |
${f_{{C_{2}},Q}}({x_{3}})=0.9922$ |
| ${f_{{C_{3}},Q}}({x_{1}})=0.9761$ |
${f_{{C_{3}},Q}}({x_{2}})=0.9486$ |
${f_{{C_{3}},Q}}({x_{3}})=0.9922$ |
The cosine values are given in Table
1 and the results of similarity are given in the Table
2. For example, for
${C_{3}}$ pattern we have
${f_{{C_{3}},Q}}({x_{2}})\leqslant {f_{{C_{3}},Q}}({x_{1}})\leqslant {f_{{C_{3}},Q}}({x_{3}})$ and so we get
Table 2
Comparison of classification results of Example
1.
| Similarity measure |
Similarity scores |
| $({C_{1}},Q)$ |
$({C_{2}},Q)$ |
$({C_{3}},Q)$ |
|
W (for $\alpha =\beta =\gamma =1/3$ and $p=2$, with respect to σ), (Yang and Ha, 2008) |
0.7219 |
$\mathbf{0.8248}$ |
0.6294 |
| ${W_{\mathit{IFS}}^{(C,\hspace{0.1667em}\sigma )}}$ |
0.9223 |
0.9437 |
$\mathbf{0.9738}$ |
|
${W_{\mathit{IFS}}}$ (Ye2011) |
0.9133 |
0.9404 |
$\mathbf{0.9712}$ |
According to the recognition principle of maximum degree of similarity between IFSs, the process of assigning the pattern
Q to
${C_{i}}$ is described by
Therefore, we obtain
$t={C_{3}}$ from (
1) for the proposed cosine similarity measure
${W_{\mathit{IFS}}^{(C,\hspace{0.1667em}\sigma )}}$. Namely,
Q pattern belongs to the class
${C_{3}}$. This result is in agreement with the result of Ye (
2011). Moreover, we obtain again
$t={C_{3}}$, when we solve this problem for
W (Definition
9) by using the same fuzzy measure
σ.
4.2 Medical Diagnosis Problem
Medical diagnosis is the process of determining which disease explains the symptoms of a patient. In this process, patterns of symptoms are compared with patterns of disease. We take the medical diagnosis problem which is discussed by Ye (
2011).
Example 2.
Let us consider a set of diagnosis and symptoms as follow.
Suppose that a patient, with respect to all the symptoms, is represented by the following IFS:
Moreover, assume that each diagnosis
${Q_{i}}$ for
$i=1,2,3,4,5$ is given as an IFSs with respect to all the symptoms as follow.
The goal is to classify
P into one of the diagnosis
${Q_{i}}$ $(i=1,2,3,4,5)$ with respect to all symptoms. For this purpose we need a fuzzy measure. We calculate the measures of singletons by Analytic Hierarchy Process (AHP) (Saaty,
1980). In AHP we use the following Standard Preference (Table
3).
Table 3
Standard preference table.
| Importance scale |
Definition |
| 1 |
Equal importance |
| 3 |
Moderate importance of one over another |
| 5 |
Essential or strong importance |
| 7 |
Very strong importance |
| 9 |
Extreme importance |
| 2, 4, 6 and 8 |
Intermediate values between two adjacent judgments |
Table
4 depends on the expert view and it is giving the consistent reciprocal comparison matrix with consistency index 0.0941903 used in (AHP).
Table 4
Reciprocal comparison matrix.
|
${s_{1}}$ |
${s_{2}}$ |
${s_{3}}$ |
${s_{4}}$ |
${s_{5}}$ |
| ${s_{1}}$ |
1 |
3 |
2 |
7 |
8 |
| ${s_{2}}$ |
0.333333 |
1 |
0.333333 |
6 |
6 |
| ${s_{3}}$ |
0.5 |
3 |
1 |
4 |
5 |
| ${s_{4}}$ |
0.142857 |
0.166667 |
0.25 |
1 |
3 |
| ${s_{5}}$ |
0.125 |
0.166667 |
0.2 |
0.333333 |
1 |
The weights that are calculated by (AHP) are given in Table
5.
Table 5
Weight of singletons.
| ${W_{{s_{1}}}}=0.428156$ |
${W_{{s_{2}}}}=0.191606$ |
| ${W_{{s_{3}}}}=0.280161$ |
${W_{{s_{4}}}}=0.062917$ |
| ${W_{{s_{5}}}}=0.0371593$ |
|
Now, we are ready to construct a fuzzy measure which is a
λ-fuzzy measure (see, Takahagi,
2000). By taking
$\lambda =0.75$ we construct the fuzzy measure
σ given in Table
6.
| $\eta (\varnothing )=0$ |
$\eta (\{{s_{1}}\})=0.685876$ |
$\eta (\{{s_{2}}\})=0.386562$ |
| $\eta (\{{s_{3}}\})=0.51713$ |
$\eta (\{{s_{4}}\})=0.145252$ |
$\eta (\{{s_{5}}\})=0.0882035$ |
| $\eta (\{{s_{1}},{s_{2}}\})=0.836764$ |
$\eta (\{{s_{1}},{s_{3}}\})=0.887728$ |
$\eta (\{{s_{1}},{s_{4}}\})=0.742572$ |
| $\eta (\{{s_{1}},{s_{5}}\})=0.720304$ |
$\eta (\{{s_{2}},{s_{3}}\})=0.726001$ |
$\eta (\{{s_{2}},{s_{4}}\})=0.481904$ |
| $\eta (\{{s_{2}},{s_{5}}\})=0.444458$ |
$\eta (\{{s_{3}},{s_{4}}\})=0.595614$ |
$\eta (\{{s_{3}},{s_{5}}\})=0.564789$ |
| $\eta (\{{s_{4}},{s_{5}}\})=0.222067$ |
$\eta (\{{s_{1}},{s_{2}},{s_{3}}\})=0.969258$ |
$\eta (\{{s_{1}},{s_{2}},{s_{4}}\})=0.873979$ |
| $\eta (\{{s_{1}},{s_{2}},{s_{5}}\})=0.859362$ |
$\eta (\{{s_{1}},{s_{3}},{s_{4}}\})=0.918363$ |
$\eta (\{{s_{1}},{s_{3}},{s_{5}}\})=0.906331$ |
| $\eta (\{{s_{1}},{s_{4}},{s_{5}}\})=0.772556$ |
$\eta (\{{s_{2}},{s_{3}},{s_{4}}\})=0.777517$ |
$\eta (\{{s_{2}},{s_{3}},{s_{5}}\})=0.757284$ |
| $\eta (\{{s_{2}},{s_{4}},{s_{5}}\})=0.532325$ |
$\eta (\{{s_{3}},{s_{4}},{s_{5}}\})=0.637119$ |
$\eta (\{{s_{1}},{s_{2}},{s_{3}},{s_{4}}\})=0.989366$ |
| $\eta (\{{s_{1}},{s_{2}},{s_{3}},{s_{5}}\})=0.981468$ |
$\eta (\{{s_{1}},{s_{2}},{s_{4}},{s_{5}}\})=0.893659$ |
$\eta (\{{s_{1}},{s_{3}},{s_{4}},{s_{5}}\})=0.934564$ |
| $\eta (\{{s_{2}},{s_{3}},{s_{4}},{s_{5}}\})=0.80476$ |
$\eta (\{{s_{1}},{s_{2}},{s_{3}},{s_{4}},{s_{5}}\})=1$ |
|
We calculate the Choquet cosine similarity measure of the IFSs. For this purpose we need the cosine values obtained in Table
7.
| ${f_{{Q_{1}},P}}({s_{1}})=0.9922$ |
${f_{{Q_{1}},P}}({s_{2}})=0.6484$ |
${f_{{Q_{1}},P}}({s_{3}})=0.9946$ |
${f_{{Q_{1}},P}}({s_{4}})=0.8877$ |
| ${f_{{Q_{1}},P}}({s_{5}})=0.9997$ |
${f_{{Q_{2}},P}}({s_{1}})=0.9922$ |
${f_{{Q_{2}},P}}({s_{2}})=0.4678$ |
${f_{{Q_{2}},P}}({s_{3}})=0.9701$ |
| ${f_{{Q_{2}},P}}({s_{4}})=0.9863$ |
${f_{{Q_{2}},P}}({s_{5}})=0.9991$ |
${f_{{Q_{3}},P}}({s_{1}})=0.7893$ |
${f_{{Q_{3}},P}}({s_{2}})=1$ |
| ${f_{{Q_{3}},P}}({s_{3}})=0.9994$ |
${f_{{Q_{3}},P}}({s_{4}})=0.4678$ |
${f_{{Q_{3}},P}}({s_{5}})=0.9985$ |
${f_{{Q_{4}},P}}({s_{1}})=0.2631$ |
| ${f_{{Q_{4}},P}}({s_{2}})=0.5881$ |
${f_{{Q_{4}},P}}({s_{3}})=0.2425$ |
${f_{{Q_{4}},P}}({s_{4}})=0.4290$ |
${f_{{Q_{4}},P}}({s_{5}})=0.9936$ |
| ${f_{{Q_{5}},P}}({s_{1}})=0.2461$ |
${f_{{Q_{5}},P}}({s_{2}})=0.1643$ |
${f_{{Q_{5}},P}}({s_{3}})=1$ |
${f_{{Q_{5}},P}}({s_{4}})=0.3987$ |
| ${f_{{Q_{5}},P}}({s_{5}})=0.2824$ |
|
|
|
The results of the cosine similarity measure are given in Table
8. For example, for
${Q_{4}}$ symptom we obtain
${f_{{Q_{4}},P}}({s_{3}})\leqslant {f_{{Q_{4}},P}}({s_{1}})\leqslant {f_{{Q_{4}},P}}({s_{4}})\leqslant {f_{{Q_{4}},P}}({s_{2}})\leqslant {f_{{Q_{4}},P}}({s_{5}})$ and so we have
Therefore, we obtain
$t={Q_{1}}$ from (
1) for the proposed cosine similarity measure
${W_{\mathit{IFS}}^{(C,\hspace{0.1667em}\eta )}}$. Namely,
P patient has viral fever. This result is in agreement with the one obtained in Ye (
2011). Moreover, we obtain again
$t={Q_{1}}$, when we solve this problem for
W (Definition
9) by using the proposed fuzzy measure
η.
Table 8
Comparison of classification results of Example
2.
| Similarity measure |
Similarity scores |
| $({Q_{1}},P)$ |
$({Q_{2}},P)$ |
$({Q_{3}},P)$ |
$({Q_{4}},P)$ |
$({Q_{5}},P)$ |
|
W (for $\alpha =\beta =\gamma =1/3$ and $p=2$, with respect to η), (Yang and Ha, 2008) |
0.6579 |
$\mathbf{0.7420}$ |
0.6855 |
0.4544 |
0.4692 |
| ${W_{\mathit{IFS}}^{(C,\hspace{0.1667em}\eta )}}$ |
$\mathbf{0.9685}$ |
0.9546 |
0.9426 |
0.4557 |
0.6441 |
|
${C_{\mathit{IFS}}}$ (Ye, 2011) |
$\mathbf{0.9046}$ |
0.0.8602 |
0.8510 |
0.5033 |
0.4542 |
The numerical results presented in Table
2 and Table
8 show that the result of the proposed cosine similarity measure is consistent with Ye (
2011). The difference of this cosine similarity measure from the existing similarity measures is that it is established by considering the interaction between the criteria. Indeed, in both similarity measures proposed by Yang and Ha (
2008) and the cosine similarity measure algorithms proposed in this study, the interaction between the criteria using the fuzzy measure is considered. However, as the variables
α,
β,
γ and
p change, the result may change and the decision maker has to explain what he/she pays attention to when choosing these variables. When these variables are independent of special selection, both ordering of their
$f({x_{i}})$ values and the calculation of the Choquet integral become difficult and as the number of elements of the set increases, it becomes very hard to make comparisons between these calculations. In the Choquet cosine similarity measure proposed in this paper
${f_{A,B}}({x_{i}})$ is equal to
$\cos {\theta _{i}}$ for any
$i=1,\dots ,n$. In this case, the decision maker will not have difficulty while ordering functions and calculating the proposed cosine similarity measure.
Figure
1 illustrates the calculation of the Choquet integral of
${f_{{Q_{4}},P}}$ in Example
2. Choquet integral value is the sum of 5 rectangle areas.
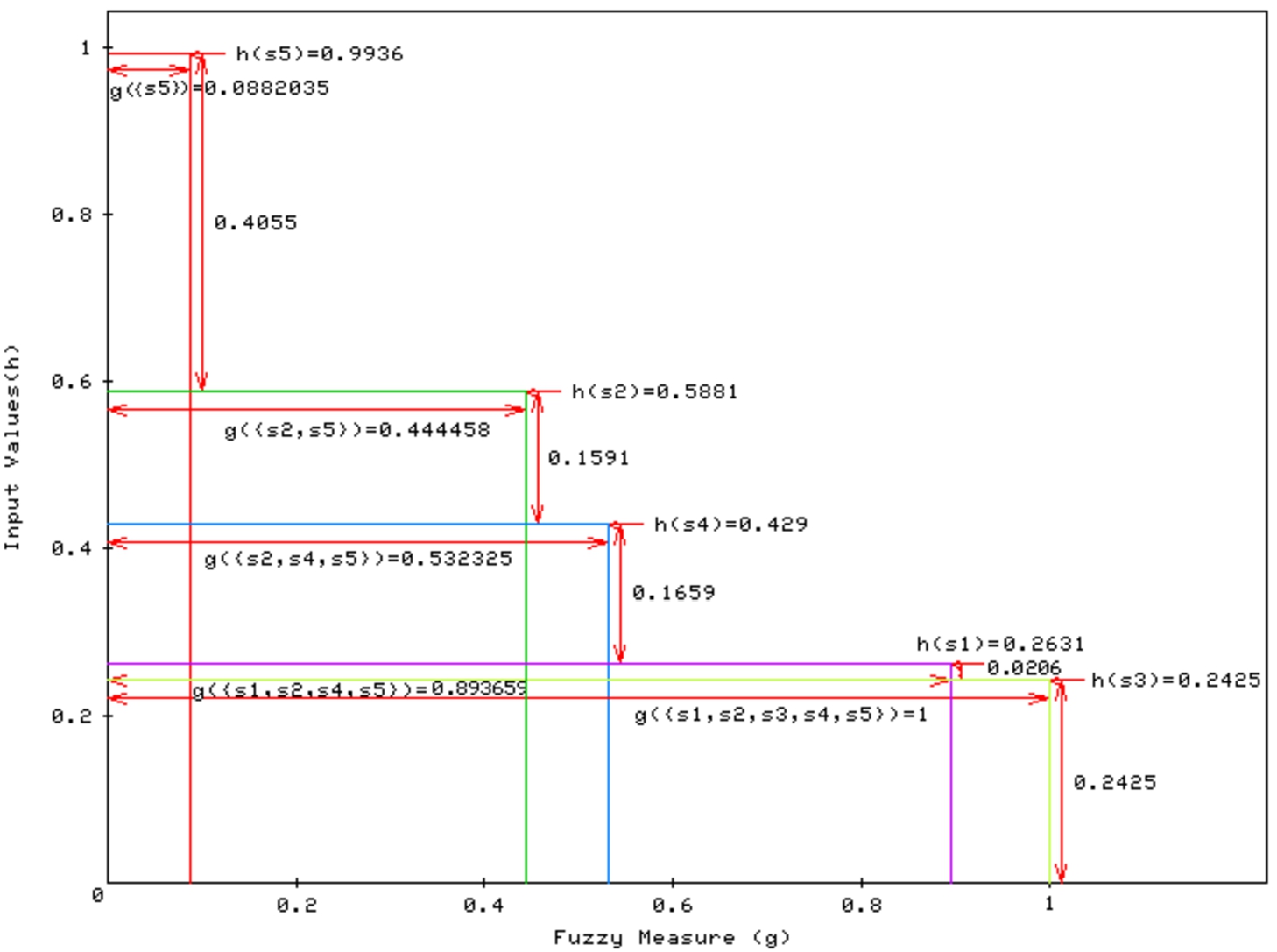
Fig. 1
Choquet integral of ${f_{{Q_{4}},P}}$.
5 Conclusion
In this paper, we propose a new cosine similarity measure based on the Choquet integral, inspired by the cosine similarity measure given for intuitionistic fuzzy sets in the literature. In addition, we apply this new similarity measure to a pattern recognition and a medical diagnosis problem and we obtain results that are consistent with the results obtained in the past. If we consider the sensitivity of Choquet integral compared with the weighted mean, we can say that the similarity measure proposed in this paper is more sensitive than the one proposed in the past. In the future, different kind of similarity measures and fuzzy sets can be considered. The applications can be extended to some other real life areas such as face recognition systems and classification.
Acknowledgements
Figure 1 was created in Multipurpose Fuzzy Measure and Fuzzy Integrals calculation software by CGI by Dr. Eiichiro Takahagi (takahagi@isc.senshu-u.ac.jp).
The authors are grateful to the Referees for carefully reading the manuscript and for offering substantial comments and suggestions which enabled them to improve the paper.
References
Atanassov, K.T. (1986). Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 20, 87–96.
Balasubramaniam, P., Ananthi, V.P. (2014). Image fusion using intuitionistic fuzzy sets. Information Fusion, 20, 21–30.
Bhattacharya, A. (1946). On a measure of divergence of two multinomial populations. Sankhya, 7, 401–406.
Boran, F.E., Akay, D. (2014). A biparametric similarity measure on intuitionistic fuzzy sets with applications to pattern recognition. Information Sciences, 255, 45–57.
Chen, S.M. (1995). Measures of similarity between vague sets. Fuzzy Sets Systems, 74, 217–223.
Chen, S.M., Chang, C.H. (2015). A novel similarity measure between Atanassov’s intuitionistic fuzzy sets based on transformation techniques with applications to pattern recognition. Information Sciences, 291, 96–114.
Choquet, G. (1953). Theory of capacities. Annales de L’Institut Fourier, 5, 131–295.
Das, S., Guha, D., Dutta, B. (2016). Medical diagnosis with the aid of using fuzzy logic and intuitionistic fuzzy logic. Applied Intelligence, 45, 850–867.
De, S.K., Biswas, R., Roy, A.R. (2001). An application of intuitionistic fuzzy sets in medical diagnosis. Fuzzy Sets and Systems, 117, 209–213.
Dengfeng, L., Chuntian, C. (2002). New similarity measures of intuitionistic fuzzy sets and application to pattern recognitions. Pattern Recognition Letters, 23, 221–225.
Fan, L., Zhangyan, X. (2001). Similarity measures between vague sets. J. Software (in Chinese), 12, 922–927.
Garg, H. (2018). An improved cosine similarity measure for intuitionistic fuzzy sets and their applications to decision-making process. Hacettepe Journal of Mathematics and Statistics, 47, 1578–1594.
Gerstenkorn, T., Manko, J. (1991). Correlation of intuitionistic fuzzy sets. Fuzzy Sets and Systems, 44, 39–43.
Grabisch, M. (1996). The application of fuzzy integrals in multi criteria decision making. European Journal of Operational Research, 89, 445–456.
Grabisch, M. (1997).
k-Order additive discrete fuzzy measures and their represantation. Fuzzy Sets and Systems, 92, 167–189.
Hong, D.H., Kim, C. (1999). A note on similarity measures between vague sets and between elements. Information Sciences, 115, 83–96.
Hung, W.L., Yang, M.S. (2004). Similarity measures of intuitionistic fuzzy sets based on Hausdorff distance. Pattern Recognition Letters, 25, 1603–1611.
Hwang, C.M., Yang, M.S. (2013). New construction for similarity measures between intuitionistic fuzzy sets based on lower, upper and middle fuzzy sets. International Journal of Fuzzy Systems, 15, 371–378.
Hwang, C.M., Yang, M.S., Hung, W.L. (2018). New similarity measures of intuitionistic fuzzy sets based on the Jaccard index with its application to clustering. International Journal of Intelligent Systems, 33, 1672–1688.
Jiang, Q., Jin, X., Lee, S.J., Yao, S (2019). A new similarity/distance measure between intuitionistic fuzzy sets based on the transformed isosceles triangles and its applications to pattern recognition. Expert Systems with Applications, 116, 439–453.
Larbani, M., Huang, C., Tzeng, G. (2011). A novel method for fuzzy measure identification. International Journal of Fuzzy Systems, 13, 24–34.
Li, Y., Olson, D.L., Qin, Z. (2007). Similarity measures between intuitionistic fuzzy (vague) sets: a comparative analysis. Pattern Recognition Letters, 28, 278–285.
Liang, Z., Shi, P. (2003). Similarity measures on intuitionistic fuzzy sets. Pattern Recognition Letters, 24, 2687–2693.
Liu, H.W. (2005). New similarity measures between intuitionistic fuzzy sets and between elements. Mathematical and Computer Modelling, 42, 61–70.
Lu, Z., Ye, J. (2016). Decision-making method for clay-brick selection based on subtraction operational aggregation operators of intuitionistic fuzzy values. The Open Cybernetics Systemics Journal, 10, 283–291.
Luo, L., Ren, H. (2016). A new similarity measure of intuitionistic fuzzy set and application in MADM problem. Advances in Modelling and Analysis A, 53, 204–223.
Luo, R., Zhao, R., (2018). A distance measure between intuitionistic fuzzy sets and its application in medical diagnosis. Artificial Intelligence in Medicine, 89, 34–39.
Mani, G., Jerome, J. (2014). Intuitionistic fuzzy expert system based fault diagnosis using dissolved gas analysis for power transformer. Journal of Electrical Engineering and Technology, 9, 2058–2064.
Melo-Pinto, P., Couto, P., Bustince, H., Barrenechea, E., Pagola, M., Fernandez, J. (2013). Image segmentation using Atanassov’s intuitionistic fuzzy sets. Expert Systems with Applications, 40, 15–26.
Miranda, P., Grabisch, M., Gıl, P. (2002).
p-symmetric fuzzy measures. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 10, 105–123.
Mitchell, H.B. (2003). On the Dengfeng–Chuntian similarity measure and its application to pattern recognition. Pattern Recognition Letters, 24, 3101–3104.
Ngan, S.C. (2016). An activation detection based similarity measure for intuitionistic fuzzy sets. Expert Systems with Applications, 60, 62–80.
Saaty, T.L. (1980). The Analytic Hierarchy Process. McGraw-Hill Book Company, New York.
Salton, G., McGill, M.J. (1983). Introduction to Modern Information Retrieval. McGraw-Hill Book Company, New York.
Song, Y., Wang, X., Lei, L., Xue, A. (2014). A new similarity measure between intuitionistic fuzzy sets and its application to pattern recognition.
Abstract and Applied Analysis,
Song, Y., Wang, X., Quan, W., Huang, W. (2019). A new approach to construct similarity measure for intuitionistic fuzzy sets. Soft Computing, 23, 1985–1998.
Szmidt, E., Kacprzyk, J. (2000). Distances between intuitionistic fuzzy sets. Fuzzy Sets and Systems, 114, 505–518.
Szmidt, E., Kacprzyk, J. (2003). An intuitionistic fuzzy set based approach to intelligent data analysis: an application to medical diagnosis. In: Abraham, A., Jain, L.C., Kacprzyk, J. (Eds.), Recent Advances in Intelligent Paradigms and Applications. Studies in Fuzziness and Soft Computing, Vol. 113. Physica, Heidelberg, pp. 57–70.
Takahagi, E. (2000). On identification methods of
λ-fuzzy measures using weights and
λ. Japanese Journal of Fuzzy Sets and Systems, 12, 665–676.
Ünver, M., Özçelik, G., Olgun, M. (2018). A fuzzy measure theoretical approach for multi criteria decision making problems containing sub-criteria. Journal of Intelligent Fuzzy System, 35, 6461–6468.
Vlachos, I.K., Sergiadis, G.D. (2007). Intuitionistic fuzzy information—application to pattern recognition. Pattern Recognition Letters, 28, 197–206.
Wang, P., Wang, J., Wei, G., Wei, C. (2019). Similarity measures of
q-rung orthopair fuzzy sets based on cosine function and their applications. Mathematics, 7, 340.
Wei, G. (2018). Some similarity measures for picture fuzzy sets and their applications. Iranian Journal of Fuzzy Systems, 15, 77–89.
Wei, G., Wei, Y. (2018). Similarity measures of Pythagorean fuzzy sets based on the cosine function and their applications. International Journal of Intelligent Systems, 33, 634–652.
Wei, G., Wang, J., Lu, M., Wu, J., Wei, C. (2019). Similarity measures of spherical fuzzy sets based on cosine function and their applications. IEEE Access, 7, 159069–159080.
Wei, P., Ye, J. (2010). Improved intuitionistic fuzzy cross-entropy and its application to pattern recognitions. In: IEEE International Conference on Intelligent Systems and Knowledge Engineering, Hangzhou, China, pp. 114–116.
Xu, Z., Yager, R.R. (2006). Some geometric aggregation operators based on intuitionistic fuzzy sets. International Journal of General Systems, 35, 417–433.
Xu, Z.S. (2010). A deviation-based approach to intuitionistic fuzzy multiple attribute group decision making. Group Decision and Negotiation, 19, 57–76.
Xu, Z.S., Chen, J. (2008). An overview of distance and similarity measures of intuitionistic fuzzy sets. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 16, 529–555.
Yang, L., Ha, M. (2008). A new similarity measure between intuitionistic fuzzy sets based on a Choquet integral model. In: Fifth International Conference on Fuzzy Systems and Knowledge Discovery, Jinan, China, pp. 116–121.
Ye, J. (2009). Multicriteria fuzzy decision-making method based on the intuitionistic fuzzy cross-entropy. In: Proceedings in International Conference on Intelligent Human-Machine Systems and Cybernetics. IEEE Computer Society, Hangzhou, Zhejiang, pp. 59–61.
Ye, J. (2010). Fuzzy decision-making method based on the weighted correlation coefficient under intuitionistic fuzzy environment. European Journal of Operational Research, 205, 202–204.
Ye, J. (2011). Cosine similarity measures for intuitionistic fuzzy sets and their applications. Mathematical and Computer Modelling, 53, 91–97.
Ye, J. (2012). Multicriteria group decision-making method using vector similarity measures for trapezoidal intuitionistic fuzzy numbers. Group Decision and Negotiation, 21, 519–530.
Ye, J. (2016). Similarity measures of intuitionistic fuzzy sets based on cosine function for the decision making of mechanical design schemes. Journal of Intelligent and Fuzzy Systems, 30, 151–158.
Ye, J. (2018). Generalized Dice measures for multiple attribute decision making under intuitionistic and interval-valued intuitionistic fuzzy environments. Neural Computing and Applications, 30, 3623–3632.
Zadeh, L.A. (1965). Fuzzy sets. Information and Control, 8, 338–353.
Zhu, L., Ye, J. (2013). Intuitionistic fuzzy and interval-valued intuitionistic fuzzy cosine similarity measures for pattern recognitions. International Journal of Advancements in Computing Technology, 5, 751–758.