1 Introduction
Since their discovery, e-cash systems have drawn attention of many scientific minds in cryptography. Developments in this branch of cryptography led to most famous cryptocurrency in the world – Bitcoin. Nowadays authors tend to propose transactions based on e-cash system, rather than focusing on check transactions. The following challenges for e-cash systems were pointed out by many authors (Pfitzmann and Köhntopp,
2001; Rosenberg,
2010; Eng and Okamoto,
1994; Chaum
et al.,
1988; Chaum and Pedersen,
1992; Kreft and Adi,
2006; Muleravičius
et al.,
2016):
-
1. Security against money laundering;
-
2. Double spending prevention;
-
3. Loss of e-wallet;
-
4. Preservation of customers’ anonymity;
-
5. Minimization of online operations on a large database;
-
6. Security against e-coin forgery.
Since e-cash is now considered a digital analogue of regular money, any proposed system of this type should satisfy the following main properties:
-
1. Anonymity: The customer using his e-cash to pay for a product must remain anonymous against the recipient of the money as well as the bank.
-
2. Unreusability: E-cash cannot be copied or double spent. This implies that the e-wallet system has to minimize the risks for forgery and/or provide ways for the identification of a dishonest user.
-
3. Unforgeability: Only authorized parties (i.e. the bank) can produce e-cash.
-
4. Off-line Payment: The payment transaction must be performed offline, i.e. no communication with the bank should be necessary during the payment protocol.
-
5. Transferability: Received e-cash can be applied for other payments among customers, regardless of whether transactions are online or offline.
-
6. Divisibility: E-cash must be divisible, i.e. the customer should be able to divide it into smaller amounts.
One of the crucial drawbacks of an e-cash system is the rapid growth of the data throughout its transfers. The latter point plays a major role in the effectiveness of the e-cash system. However, for a long time it was ignored by many proposed systems. According to Chaum and Pedersen (
1992), the amount of data transferred among users through any divisible, offline and anonymous e-cash system is growing in size due to the information needed to store in order to ensure double spending prevention, divisibility and other properties.
Nevertheless, some alternative e-cash systems were proposed that managed to avoid the growth of the e-cash data (D’Amiano and Di Crescenzo,
1994; Okamoto,
1995). However, as mentioned in Chan
et al. (
1998), Tsiounis (
1997), those e-schemes had other issues such as the limit of the total size of payments or lack of efficiency of e-cash protocols. In Fuchsbauer (
2009) an attempt was made to construct a transferable e-cash scheme without the aforementioned data growth problem. However, it was later outlined in Waters (
2005), Fuchsbauer (
2009) that there was still a dramatic increase in the size of the public key.
A new direction in the development of offline e-cash systems without the data growth drawback was established when Brand first presented an e-wallet scheme using observers in Brands (
1993). He proposed the idea of bank’s trustee for the purchaser (e.g. a chip implemented in a purchaser’s mobile device) which allows to perform payments without the online connection to the bank. However, the cryptographic security of Brand’s e-cash system was never proven and hence the system was never initiated.
Another problem that often takes place in divisible, anonymous, offline e-cash systems is the lack of proof of the security of a complex cryptographic system. According to Rosenberg (
2010), the majority of divisible e-cash systems to this day “use proofs about double-discrete logarithms and require similar sequences of primes in their setup”. It was noted in Brands (
1993) and Cramer and Shoup (
2003), the decisional Diffie–Hellman (DDH) assumption is needed to prove the cryptographic security of a number of previously proposed protocols. This comes from the fact that the Diffie-Hellman key exchange (Diffie and Hellman,
1976) cannot be proved secure in any reasonable and standard way just based on the computational Diffie–Hellman (CDH) assumption: the DDH assumption is required.
In Petersen and Poupard (
1997) an efficient payment system with anonymity revocation and trusted third party (TTP) was presented. It was the first scheme that managed to achieve an offline prevention of all possible extortion attacks. Due to the system’s scalable security and efficiency, secure realizations for an internet payment scheme as well as a highly efficient payment scheme for electronic purse applications were developed on the basis of this scheme. The system also incorporated a possible way to revoke anonymity using the collaboration of a judge and the bank if a malicious purchaser was to be detected (Stadler
et al.,
1995). The judge could be implemented in a Purchaser’s smart device. However, it should be protected to ensure Purchaser’s anonymity.
This paper considers an offline, divisible, anonymous and transferable e-cash system with observers operating in the environment with TTP (the bank), which was previously presented in Sakalauskas
et al. (
2018). Detailed description of our scheme is presented in Sections
2.1–
2.3. The analysed e-money system does not possess the data growth problem addressed above due to the utilization of observers. We also perform analysis of several attack scenarios, which include existential forgery of data by both parties (Purchaser and Vendor) of our system in Section
3. In Section
4 we show that both parties can trust each other. This analysis relies on the so-called BAN logic presented in Burrows
et al. (
1989) (hence it was named after the authors).
2 Offline E-Cash System with Observers
In this section we present a novel e-cash system with observers based on Schnorr identification and modified ElGamal e-signature. These cryptographic primitives are often implemented due to their provable security. Our e-cash system satisfies such e-cash system properties as divisibility, anonymity, offline payment, transferability and double-spending prevention requirements. To provide offline payment property and bypass the growth of the transferred e-cash data the implemented cryptographic bank’s trustee Observer (i.e. cryptographic chip) is used.
Presented e-cash system is executed between the following parties: the Bank (
B), the Purchaser (
P), the Vendor (
V) and their Observers (
${\mathbf{O}_{\mathbf{P}}}$ and
${\mathbf{O}_{\mathbf{V}}}$ respectively). Our e-cash system operates using withdrawal, payment and deposit protocols described in detail in Sections
2.1–
2.3.
The general parameters and functions used in the proposed e-cash scheme are presented in Table
1 below:
Table 1
E-cash system notations.
| Parameter/functions |
Description |
| $q,p$ |
Large prime numbers, such that $p=2q+1$
|
| G |
Generator of multiplicative group ${\mathbf{Z}_{p}^{\ast }}$
|
| ${h_{i}}$ |
Value of hash function |
| ${\mathit{Sig}_{\mathit{ElG}}^{X}}(m)$ |
ElGamal signature function, where m and X correspond to the message to be signed on and the ElGamal private key of the signer |
| ${\mathit{Ver}_{\mathit{ElG}}^{A}}(s,m)$ |
ElGamal signature verification function, where $m,s$ and X correspond to the message, signature on the message and the ElGamal public key of the signer |
| i |
Serial number of the transaction |
|
${\mathit{PrK}_{P}}={x_{P}}$, ${\mathit{PuK}_{P}}=\{G,{A_{P}}={G^{{x_{P}}}}\}$
|
Purchaser’s temporary private and public keys
It is important to note that in the proposed scheme, the purchaser generates random temporary private and public keys for each transaction, which ensures the anonymity property of the proposed e-cash scheme |
|
${\mathit{PrK}_{O}}={x_{O}}$, ${\mathit{PuK}_{O}}=\{G,{A_{O}}={G^{{x_{O}}}}\}$
|
Observer’s private and public keys |
| ${\mathit{Id}_{P}},{\mathit{Id}_{V}}$ |
Unique identification number of the Purchaser’s and Vendor’s Observer chips respectively |
| ${m_{i}}$ |
Sum of money to be spent by the Purchaser |
| ${\tilde{m}_{i}}$ |
Actual price of the products to be bought by the purchaser |
| ${t_{i}}$ |
Time instance of the e-cash withdrawal |
| ${m_{i}}||{t_{i}}$ |
Concatenation of the sum and the time instance |
| ${t_{w0}},{t_{p0}},{t_{d0}}$ |
Time instance of the last e-cash withdrawal (payment, deposit) protocol |
| ${m_{\max }^{P}},{m_{\max }^{V}}$ |
The amount of money in the e-wallet of Purchaser and Vendor respectively |
| ${\xi _{i}^{(1)}},{\xi _{i}^{(2)}}$ |
Random values of ${\mathrm{Z}_{q}^{\ast }}$ for Schnorr interactive identification protocol |
Our e-cash system consists of Withdrawal, Payment and Deposit protocols. These protocols are presented below and are executed in order of presentation.
2.1 Withdrawal Protocol
Assume that the Purchaser is interested in acquiring some goods from the Vendor. Let the total price of these goods be ${m_{i}}$, where i denotes the number of the transaction. He initializes the purchase deal by requesting Vendor’s identity indicator ${\mathit{Id}_{V}}$, which is sent to him via secure channel. We consider it the zeroth step of our scheme.
Execution of our e-cash system starts by performing the following steps of the Withdrawal protocol:
-
1. The Purchaser sends a request to his Observer to provide him with the desired sum ${m_{i}}$. He generates his temporary keys ${\mathit{PrK}_{P}}={x_{P}}$ and ${\mathit{PuK}_{P}}=\{G,{A_{P}}={G^{{x_{P}}}}\}$ and sends his public key${A_{P}}$ to the observer together with the desired sum, the time of request ${t_{i}}$ and Vendor’s identity indicator ${\mathit{Id}_{V}}$. Hence, the Purchaser’s observer receives the following information:
-
2. Observer
${\mathbf{O}_{\mathbf{P}}}$ checks if the Purchaser possesses the desired sum and verifies if the request takes place in the current time and if time instance
${t_{i}}$ is greater than the time instance
${t_{w0}}$ of a previous request:
The protocol is aborted if any failures occur at this step. Purchaser receives an error message indicating the problem.
-
3. Observer
${\mathbf{O}_{\mathbf{P}}}$ generates private data for the Purchaser – random values
${\xi _{i}^{(1)}}$,
${\xi _{i}^{(2)}}$, which he will later use for Shnorr identification during the Payment protocol:
-
4. Using the generator
G, the Observer
${\mathbf{O}_{\mathbf{P}}}$ computes public data for the Purchaser, which Vendor will later use during the Payment protocol to identify him:
-
5. Using pre-generated public data as well as data generated at previous steps of this protocol the Observer
${\mathbf{O}_{\mathbf{P}}}$ calculates the following public data for the Purchaser:
During this step the Observer
${\mathbf{O}_{\mathbf{P}}}$ also generates the following El-Gamal signatures to prevent existential forgery of data:
-
6. Observer
${\mathbf{O}_{\mathbf{P}}}$ renews a time instance of the last request:
-
7. Observer
${\mathbf{O}_{\mathbf{P}}}$ renews Purchaser’s e-wallet balance:
-
8. Observer ${\mathbf{O}_{\mathbf{P}}}$ sends all generated data and signatures during this protocol to the Purchaser thus completing the request:
As a result of this protocol the Purchaser can now spend the desired sum as he wishes using the data and signatures, obtained from his Observer.
2.2 Payment Protocol
After Withdrawal protocol has completed, the Purchaser initializes the Payment protocol. The steps of this protocol are as follows:
-
1. The Purchaser sends public data pre-generated by his Observer ${\mathbf{O}_{\mathbf{P}}}$ to the Vendor together with the total price of the goods ${m_{i}}$ and the time instance ${t_{i}}$ of the transaction:
-
2. The Vendor verifies if the total price of the goods
${m_{i}}$ is correct and if the time instance
${t_{i}}$ is greater than the time of the last purchase
${t_{p0}}$:
Note that the Vendor does not verify if the transaction takes place at the current time, since the Purchaser can initialize this protocol at any time after receiving data from his Observer. The protocol is aborted if any failures occur at this step. The Purchaser receives an error message indicating the problem.
-
3. The Vendor verifies signatures to ensure that the received data was not forged in any way:
The protocol is aborted if any failures occur at this step, since the Vendor found forgery of the received data. The Purchaser receives an error message indicating the problem. The Purchaser can no longer use the data of this transaction to execute any new payments.
-
4. The Vendor generates a random challenge
${h_{i}}$ for the Purchaser to ensure that he is not dealing with an attacker:
-
5. The Vendor initializes Shnorr identification protocol by sending a random challenge
${h_{i}}$ to the Purchaser:
-
6. Using his private data
${\xi _{i}^{(1)}},{\xi _{i}^{(2)}}$ pre-generated by the Observer
${\mathbf{O}_{\mathbf{P}}}$, the Purchaser calculates the response values
${r_{i}^{(1)}}$ and
${r_{i}^{(2)}}$ in a following way:
He forwards the response values
${r_{i}^{(1)}}$ and
${r_{i}^{(2)}}$ to the Vendor:
-
7. Using Purchaser’s public data
${w_{i}^{(1)}}$,
${w_{i}^{(2)}}$ the Vendor verifies the validity of the received response values in the following way:
The protocol is aborted if any failures occur at this step. The Purchaser receives an error message indicating the identification problem. He may retry to initialize the Payment protocol if the Vendor allows this possibility. Otherwise the data of this transaction can no longer be used.
If no failures during these steps occurred, then the payment has been made. However, the Vendor now has to confirm that the payment took place.
-
8. The Vendor turns to his Observer for signature generation by sending the received payment sum ${m_{i}}$ and time instance ${t_{i}}$, i.e. he confirms that the Purchaser has paid the sum ${m_{i}}$ for the goods at the time ${t_{i}}$:
-
9. The Vendor’s Observer confirms the validity of the received data by verifying the signature
${S_{i}^{(3)}}$:
If this verification fails, then the Observer blocks the transaction for deposit, i.e. the Vendor is no longer able to deposit the sum
${m_{i}}$ to his e-wallet.
-
10. The Vendor’s Observer generates a signature ${S_{V}}={\mathit{Sig}_{\mathit{ElG}}^{{x_{O}}}}({\mathit{Id}_{V}^{{m_{i}}\| {t_{i}}}})$ and sends it to the Vendor:
-
11. The Vendor sends the following data to the Purchaser for verification:
-
12. The Purchaser performs the following actions to ensure that he is not dealing with a Malicious Vendor:
If verification is successful, then the deal is made and both parties receive messages of this result. Otherwise, the deal is off and the Purchaser may turn to the Bank in electronic or physical form to restore his wallet balance. Both parties receive error messages.
-
13. The Vendor
V renews a time instance of the last purchase by the Purchaser
P:
Upon successful completion of this protocol the Vendor has received the total price of the goods and can send them to the Purchaser in electronic or physical form. Otherwise, if any errors occurred, the culprit is reported to the Bank.
2.3 Deposit Protocol
To complete the execution of our e-cash system, the Vendor has to deposit the received sum
${m_{i}}$. Hence he initializes the following protocol:
3 Security Against Existential Forgery Analysis
In this section we consider security of our scheme against adaptive inside adversary, i.e. we assume that an attacker is a legitimate user (Purchaser or Vendor) of the proposed system and hence has his own mobile device with an Observer and pre-generated data as described above. We consider the following attack scenarios:
-
1. Attack of a Malicious Purchaser (MP):
-
(a) Double spending, i.e. using the same data to purchase goods more than once from the Vendor;
-
(b) Forgery of transaction data, i.e. faking payment sum, time instance and any data sent to the Vendor. There are two alternatives to this attack: spend less money than demanded by the Vendor (forging payment sum) or present a previous transaction as a new one (forging time instance), i.e. perform double spending by forgery.
-
2. Man in the Middle Attack (MitM):
-
(a) Purchaser impersonation by faking identity ${\mathit{Id}_{P}}$, i.e. using the e-wallet of another legitimate Purchaser to acquire goods for yourself;
-
(b) Vendor impersonation by faking identity ${\mathit{Id}_{V}}$, i.e. acquire and deposit money, meant for another legitimate Vendor.
-
3. Attack of a Malicious Vendor (MV):
-
(a) Double deposit, i.e. using the same data to increase the balance of Vendor’s e-wallet more than once;
-
(b) Deny of payment and refusing goods shipment, i.e. keep Purchaser’s money for yourself without delivering the goods;
-
(c) Forgery of transaction data, i.e. faking payment sum, time instance and any data received from an honest the Purchaser. There are two alternatives to this attack: deposit more money than received from the Purchaser (forging payment sum) or present a previous transaction as a new one (forging time instance), i.e. perform double deposit by forgery.
To start our analysis we first focus on the Attack of MP scenario, i.e. actions, which can be executed by a dishonest Purchaser to benefit from the deal with an honest Vendor.
The prevention of double spending is guaranteed by Shnorr identification, i.e. upon receiving the same transaction twice the Vendor can recover the Purchaser’s identity by calculating the following expression:
where responses
${r_{i}^{(1)}}$ and
${r_{i}^{(2)}}$ were received during the first sending whereas responses
${r^{\prime (1)}_{i}}$ and
${r^{\prime (2)}_{i}}$ were received during the second sending of the same transaction. The validity of (
1) is proven in Sakalauskas
et al. (
2018). Note that expression (
1) is calculated modulo
q.
To consider forgery of the data by MP we recall the data sent during Payment protocol to the Vendor:
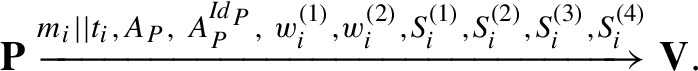
Since this data involves signatures, in order to fake his identity the Purchaser may try to forge signatures sent during this step. However, since he is not able to generate signatures by himself (only the Purchaser’s Observer can do this), forgery of any ElGamal signature requires him to deal with discrete logarithm problem (DLP) as stated in Theorem 20 of Pointcheval and Stern (
2000) considering modified ElGamal signature scheme security against an adaptive adversary. Based on the result of Poicheval and Stern we claim the following:
Proposition 1.
If Purchaser can forge any signature during Payment protocol, then he is able to recover Purchaser Observer’s private ElGamal key ${x_{O}}$ in reasonable time.
Hence we focus on the data signed by these signatures, i.e. we assume that the adversary aims to alter this data to obtain a valid signature on a fake data.
Formally, the security of the Purchaser’s identity relies on the uniqueness of signature
as stated in Pointcheval and Stern (
2000). To prove this let us consider the data signed, i.e.
Since
G is a generator of the multiplicative group
${Z_{p}^{\ast }}$, the value of
${A_{P}}$ is unique and hence we assume that it is some other generator of the same group. In this case the private key
${x_{P}}$ is relatively prime with group characteristic
p. Due to
${A_{P}}$ being a generator of the multiplicative group, the value of
${A_{P}^{{\mathit{Id}_{P}}}}$ is unique as well and hence if
${A_{P}^{{\mathit{Id}_{P}}}}={A_{P}^{{\mathit{Id}_{{P^{\prime }}}}}}$, where
${\mathit{Id}_{{P^{\prime }}}}$ is some forged identity, then
${\mathit{Id}_{P}}={\mathit{Id}_{{P^{\prime }}}}$. Furthermore, if
${A_{P}^{{\mathit{Id}_{P}}}}={A_{{P^{\prime }}}^{{\mathit{Id}_{{P^{\prime }}}}}}$, then
${x_{{P^{\prime }}}}\cdot {\mathit{Id}_{{P^{\prime }}}}={x_{P}}\cdot {\mathit{Id}_{P}}$, where data with index
${P^{\prime }}$ is fake. However, for randomly chosen values
${x_{P}}$,
${\mathit{Id}_{P}}$,
${x_{{P^{\prime }}}}$,
${\mathit{Id}_{{P^{\prime }}}}$, the probability
is negligible if the value of characteristic
p is large enough. Assume that the adversary is in possession of
${A_{P}^{{\mathit{Id}_{P}}}}$ and
${\mathit{Id}_{{P^{\prime }}}}$. In order to switch
${\mathit{Id}_{P}}$ to a fake identity
${\mathit{Id}_{{P^{\prime }}}}$ the adversary has to solve the following problem:
for some unknown value of
${x_{{P^{\prime }}}}$, which is a private key of the fake Purchaser’s
${\mathbf{P}^{\prime }}$ Observer. Hence we obtain the DLP as stated above.
The correctness of time instance
${t_{i}}$, payment sum
${m_{i}}$ and Vendor’s identity
${\mathit{Id}_{V}}$ follows from the structure of
${N_{i}^{(1)}}$ and signature
Analogously the DLP to be solved in case of successful forgery is as follows:
for some unknown value of
${x_{{P^{\prime }}}}$, where
${N^{\prime (1)}_{i}}$ is some garbage data.
Hence, the Vendor will discover any altering of data on the Purchaser’s side by verifying signatures on step 3 of Payment protocol.
Valid signatures
${S_{i}^{(1)}}$ and
${S_{i}^{(2)}}$ ensure correct values of
${w_{i}^{(1)}}$ and
${w_{i}^{(2)}}$, which are required for successful Shnorr identification. This comes from the fact that the unaltered data
${A_{P}^{{N_{i}^{(1)}}}}$ and
${A_{P}^{{N_{i}^{(2)}}}}$ is invertible and hence
Since identities (
4) and (
5) hold, Vendor will discover forgery of these values on step 8 of Payment protocol. We now claim the following:
Proposition 2.
Purchaser cannot forge any data sent during Payment protocol.
Hence the following corollary is true:
Corollary 1.
All unfair actions of MP adversary will be discovered by the Vendor.
We now consider the scenarios of
MitM attacks. Let us assume that an inside adversary
MP has intercepted the Payment protocol and has acquired the data sent by another legitimate Purchaser. His objective is to obtain the goods using the victim’s e-wallet. To achieve this goal, he has to forge victim’s personal data by replacing it with his own. However, in this case he has to deal with the following DLP:
for some unknown variable
${\tilde{m}_{i}}||{\tilde{t}_{i}}$, where
${A_{\mathit{MP}}}$ is the attacker’s public key. Furthermore, since an attacker cannot affect any of the signatures acquired, due to Proposition
1, he has to forge the value of
${w_{i}^{(2)}}$. Hence, he has to solve the following equation:
for some unknown value of
${\tilde{w}_{i}^{(2)}}$. This equation by itself does not pose any advantage for an attacker. However, to pass Schnorr identification phase an attacker lacks private values
${\xi _{i}^{(1)}},{\tilde{\xi }_{i}^{(2)}}$ and thus has to solve the following equations:
Based on these facts we claim, that:
Proposition 3.
If MP can purchase goods using legitimate Purchaser’s e-wallet, then he is able to solve the DLPs (
6)
, (
8)
and (
9)
in reasonable time.
Let us now assume that an inside adversary MV has intercepted the Payment protocol and has acquired the data sent by an honest Purchaser. His objective is to deposit money meant for another legitimate Vendor. To achieve this goal an adversary has to forge victim’s identity by switching it with his own. This is not possible, since the data sent to the Observer does not have this information. Furthermore, MV’s Observer can use only identity ${\mathit{Id}_{\mathit{MP}}}$ and MV can in no way affect this. Hence the Observer discovers that the stolen transaction is not meant for MV on step 3 of the Deposit protocol by verifying signature ${S_{i}^{(3)}}$ and blocks the deposit.
Based on these results we claim that the following proposition holds:
Proposition 4.
Our system is resistant against Purchaser impersonation and Vendor impersonation MitM attack scenarios.
To complete our analysis we consider Attack of MV scenario, i.e. actions, which can be executed by a dishonest Vendor to benefit from the deal with an honest Purchaser.
Double deposit is prevented by the fact that the Vendor is not able to forge time instance due to Proposition
2 which is also valid for him. Hence, his Observer discovers this attempt at step 2 of the Deposit protocol.
Deny of payment is prevented by writing a check during steps 8–11 of the Payment protocol since during steps 9 and 10 the Observer verifies signature
${S_{i}^{(3)}}$ and hence confirms that the payment took place by generating a signature
${S_{V}}$. Due to Proposition
1, which is also valid for the Vendor, honest Purchaser discovers a fake check
$({\mathit{Id}_{V}^{{m_{i}}||{t_{i}}}},{S_{V}})$ at step 12 of the Payment protocol.
The main goal or manipulation of data received by the Vendor is increasing the e-wallet balance disproportionately by affecting the payment sum. These manipulations may also involve forging other parameters, such as
${A_{P}}$. Note, however, that the Vendor is incapable to affect any of the signatures received due to Proposition
1, which is also valid for him. Any attempts to forge the value
${A_{P}}$ result in a solution of discrete logarithm problem since
${A_{P}}={G^{{x_{P}}}}$ and hence:
Due to the latter identity, forgery of the payment sum would imply the following equation:
for some unknown
x, where
${\tilde{m}_{i}}$ is the forged payment sum and
${\tilde{t}_{i}}$ is the forged time instance. Hence, we state that:
Proposition 5.
If Vendor can manipulate the payment sum, then he is able to solve the discrete logarithm problem (
10)
in reasonable time.
Remark 1.
The latter proposition is also valid for Purchaser.
Due to validity of signatures received, the Vendor’s Observer discovers any forgery by the Vendor on step 3 of Deposit protocol.
Based on the presented results we state that:
Proposition 6.
Any unfair actions of MV will be discovered.
Hence relying on Propositions
1,
4 and
6 we conclude that:
Proposition 7.
Our e-money system is secure against active inside attacks.
4 Trustworthiness Analysis
Trustworthiness of the proposed e-cash system is analysed using Burrows–Abadi–Needham (BAN) logic. BAN logic was first presented in Burrows
et al. (
1989) and is a set of rules that can be used to define and analyse the trustworthiness of a cryptographic protocol. BAN logic seeks to determine whether the exchanged information between different parties is trustworthy from malicious insiders such as malicious bank, vendor, purchaser or others. BAN logic starts with a set of goals that are to be proven, and relies on the assumptions which should be made and used as a basis for the proof. The main BAN logic notations are presented below.
Table 2
BAN logic notation.
| Notation |
Description |
|
A|$\equiv X$
|
A trusts X
|
|
A |$\Rightarrow X$
|
A has jurisdiction over X, in other words A is the authority on X and is to be trusted on it; |
| $P\stackrel{k}{\leftrightarrow }V$ |
Shared key k between P and V
|
| $\mathrm{\# }X$ |
X is fresh |
| $A\lhd X$ |
A sees X
|
|
A|$\sim X$
|
A said X(without implying that this utterance was recent or not) |
| $(X,Y)$ |
X or Y is one part of $(X,Y)$
|
| ${\langle X\rangle _{k}}$ |
X is combined with k
|
| ${\{X\}_{k}}$ |
X is encrypted with k
|
| $A\ni M$ |
A possesses M |
| $\stackrel{K}{\to }P$ |
P has a public key. |
Firstly, as mentioned above, the proposed scheme uses the following parameters:
Purchaser’s parameters: ${\mathit{PrK}_{p}}={x_{P}}$, ${\mathit{PuK}_{p}}=\{G,{A_{P}}={G^{{x_{P}}}}\}$.
Purchaser Observer’s parameters: ${\mathit{PrK}_{O}}={x_{O}}$, ${\mathit{PuK}_{O}}=\{G,{A_{O}}={G^{{x_{O}}}}\}$.
We are going to keep original notation for parameters ${\xi _{i}^{(1)}},{\xi _{i}^{(2)}},{A_{P}^{{\mathit{Id}_{P}}}},{w_{i}^{(1)}},{w_{i}^{(2)}},$ ${N_{i}^{(1)}},{N_{i}^{(2)}},{S_{i}^{(1)}},{S_{i}^{(2)}},{S_{i}^{(3)}},{S_{i}^{(4)}}\hspace{0.2778em}$ in order to provide clarity for further analysis.
In order to check the correctness and security of our payment protocol, we will set the following goals:
-
G1: The Vendor believes in the validity of the received payment:
-
G2: The Vendor trusts the Purchaser:
-
G3: The Purchaser trusts the Vendor:
We use the following assumptions as a base for proving the correctness of these goals:
E-cash withdrawal and payment protocols involve sending the following parameters:
-
M1: Data, generated by the Purchaser’s Observer, is sent to the Purchaser:
-
M2: The Purchaser sends the transaction data to the Vendor:
-
M3: The Vendor sends Shnorr identification challenge to the Purchaser:
-
M4: The Purchaser sends response parameters to authenticate himself to the Vendor:
-
M5: The Vendor sends response parameters to authenticate himself to the Purchaser:
It follows from M2 that the Vendor receives the following data from the Purchaser:
The application of message seeing rule results in the fact that the Vendor sees the data, received from the Purchaser:
The application of message meaning and belief rules and the use of Purchaser Observer‘s public key results in the fact that the Vendor believes in the validity of data, generated by the Purchaser’s Observer:
It follows from the belief rule that:
Since
${A_{P}}$ is a public key, the Vendor believes in the fact, that the received transaction is meant for him and that the sum
${m_{i}}$ and the time instance
${t_{i}}$ are approved by the Bank:
Subsequently the Vendor believes in the validity of these parameters:
The application of nonce-verification rule, jurisdiction and control, and the assumption that the Observer is trusted by all parties’ results in the proof of the goal G1:
Now we consider the second goal. The Vendor sees the following information received from the Purchaser:
By applying the message meaning rule and assumption A3 we obtain:
i.e. the Vendor believes that it was the Purchaser, who sent him the specified data. Moreover, it follows from assumption A3 and concatenation rules that, due to correct values of total price
${m_{i}}$ and the time instance
${t_{i}}$, it is the Purchaser, who is interested in acquiring the goods:
We now apply the nonce-verification rule:
and hence the Vendor trusts that the Purchaser obtained the desired sum
${m_{i}}$ from the Bank at the time
${t_{i}}$, i.e. the Purchaser has jurisdiction to spend this sum of money. Furthermore, the Vendor also believes that the Bank has the jurisdiction over the Purchaser via his representative (Observer
${\mathbf{O}_{\mathbf{P}}}$). Furthermore, the Vendor believes that the Purchaser knows his identity:
Finally, using jurisdiction, control and referencing to the rules above, the Vendor trusts the Purchaser’s identity:
The second goal
$\mathbf{V}|\equiv \mathbf{P}$ now follows from the proven results
$\mathbf{V}|\equiv {\mathit{Id}_{p}}$ and
$\mathbf{V}|\equiv {m_{i}}$, since Vendor trusts the Purchaser‘s identity and fairness (the sum
${m_{i}}$ is not forged).
Now we consider the third goal. Due to M5, the Purchaser sees the following information received from the Vendor:
Note that the Vendor received this data from his Observer, implying that:
By applying the message meaning rule, concatenation rule, and assumption A4 we obtain:
i.e. the Purchaser believes that it was the Vendor’s Observer, who generated the signature. Moreover, it follows from assumptions A4 and concatenation rules that, due to correct values of total price
${m_{i}}$ and the time instance
${t_{i}}$, the Purchaser is dealing with an honest Vendor:
We now apply the nonce-verification rule:
Hence, the Purchaser believes that the Vendor’s Observer has jurisdiction over the Vendor. Furthermore, due to this fact, the Purchaser trusts that the Vendor knows his identity since his Observer possesses this information:
Finally, using jurisdiction, control and referencing to the rules above, the Purchaser trusts the Vendor’s identity:
Hence, the validity of the third goal
$\mathbf{P}|\equiv \mathbf{V}$ now follows from the proven results.
5 Investigation of Execution Time
Since the considerable amount of payment operations is performed in Observer having restricted computation resources, the effectivity of proposed e-wallet system depends on the estimation of the operation time.
The computation time is directly related with the processor’s clock frequency. If processor is running at 1 GHz clock frequency, then its clock cycle takes ${10^{-9}}\hspace{2.5pt}\text{s}=1ns$ time.
The arithmetic operations required to perform a payment protocol is multiplication and addition together with shifting operation all performed in the registers of Observer. We name those operations as elementary operations.
We assume that 32 bits’ microprocessor is used in Observer. It is far less than the bit length of variables used in payment protocol represented by 2048 bit integers. Without the loss of generality, we assume that all elementary operations take one clock cycle.
The most time consuming operation is the exponentiation modulo p of length in 2048 bits. For the assessment of computation time, firstly, we must estimate the number of elementary operations required for the calculation of the modular exponent function $r={g^{k}}\hspace{0.2778em}\text{mod}\hspace{0.2778em}p$.
According to Knuth (
1981), Hwang
et al. (
2005), the modular exponent function is computed using
addition chain method (Knuth,
1981). The formulas to find the number of those operations are the following:
where:
-
1. ${\mathit{MOD}_{E}}(k,p)$ – denotes an operation of modular exponentiation $r={g^{k}}\hspace{0.2778em}\text{mod}\hspace{0.2778em}p$;
-
2. $M(w),\hspace{0.2778em}A(w),\hspace{0.2778em}\mathit{Mod}(w)$ – denote operations of multiplication, addition and modulus with the bit length of operand is w;
-
3. $l(w)$ – denotes the bit length of w;
-
4. S denotes the shift operator.
The bit lengths of the variables in our scheme are presented in Table
3.
Table 3
Bit length of variables.
| Variable |
Bit length |
| $p,q,{x_{P}},{x_{O}}\hspace{0.2778em}{A_{P}},{A_{O}},\hspace{0.2778em}G,\hspace{0.2778em}{\mathit{Id}_{P}},{h_{i}},\hspace{0.2778em}R$ |
2048 bits |
| ${\xi _{i}^{(1)}},{\xi _{i}^{(2)}},{w_{i}^{(1)}},{w_{i}^{(2)}},{N_{i}^{(1)}},{N_{i}^{(2)}},{S_{i}^{(1)}},{S_{i}^{(2)}},{S_{i}^{(3)}},{r_{i}^{(1)}},{r_{i}^{(2)}}$ |
2048 bits |
| $m,t$ |
∼18 bits |
| ${m_{i}}||{t_{i}}$ |
∼ 36 bits |
| $H(m)$ |
∼256 bits |
By default, we take 82 clock cycles for SHA-2 computation (Guilford
et al.,
2012).
After the number N of clock cycles is found, the operation time can be estimated in the following way: $\mathit{Time}=N\cdot T$, where $T=1/F$ and F is a clock frequency. We assume $F=1.6$ GHz in further steps for the demonstration of calculations results.
By Hinterwälder
et al. (
2013,
2015) all Brands e-cash protocols take about 2966 ms in all protocols generated in cards. By Au
et al. (
2007) the computational time of CHL e-cash protocol in single payment is 30 modular exponentiations and takes about 2111 ms by Juang (
2010) approximations, but it’s cost of each operation is somehow hard to compute because it depends of how many transactions have been made before and how many coins will be used. The comparison of our system with Brands and CHL systems is presented in Table
4.
Table 4
Computation time comparisons in ms.
| Protocol |
Our system |
Brands |
CHL |
| Withdrawal |
665 |
– |
– |
| Payment |
1241 |
– |
– |
| Deposit |
629 |
– |
– |
| Total |
2535 |
2996 |
2111 |
Hence, our system requires approximately the same computation time, while its functionality has a significant advantage with respect to others.
In Table
5 we present a comparison of some offline payment e-cash systems and explore such properties as: transferability, traceability, data growth and anonymity (against Vendor and Bank). However, each of these systems possesses the flaw of money growth in size when transferred. Furthermore, any previously presented e-cash system, which eliminates this flaw, also loses anonymity against Vendor or other offline payment properties.
Table 5
Comparison of e-money schemes.
| E-money systems |
Year |
Transf. |
Trace. |
Data grows |
Anon. against V. |
Anon. against B. |
| CHL |
2005 |
Yes |
No |
Yes |
Yes |
Yes |
| fairCASH |
2006 |
Yes |
No |
Yes |
Yes |
Yes |
| Endorsed |
2007 |
Yes |
Yes |
Yes |
Yes |
Yes |
| Secret splitting |
2009 |
Yes |
Yes |
Yes |
Yes |
Yes |
| GS proof e-cash |
2011 |
Yes |
Yes |
Yes |
Yes |
Yes |
| Baldimtsi |
2015 |
Yes |
Yes |
Yes |
Yes |
Yes |
| Canard e-cash |
2015 |
No |
No |
Yes |
No |
No |
| Märtens |
2015 |
No |
Yes |
Yes |
Yes |
Yes |
| Scalable e-cash |
2015 |
Yes |
No |
Yes |
Yes |
Yes |
| Dissertation |
2018 |
Yes |
No |
No |
Yes |
No |
As it can be seen, our e-cash system has the following functional advantages: anonymity against Vendor, offline payment, divisibility, transferability and double-spending prevention requirements, and most important one – data does not grow in size when transferred.
Based on the presented comparison we conclude that our system stands out from the other systems since it possesses similar characteristics as those schemes while also avoiding a drawback of growing in size. Furthermore, it has better or approximate computation time if compared to other schemes presented in Table
5.