Abstract
The evolution of Wireless Sensor Networks has led to the development of protocols that must comply with their new restrictions while being efficient in terms of energy consumption and time. We focus on a collision resolution protocol, the so-called Two Cell Sorted (2CS-WSN). We propose three different ways to improve its performance by minimizing the collision resolution time or the energy consumption. After evaluating these proposals and carrying out the comparison with the original protocol, we recommend an improvement to the protocol which reduces the elapsed time by early $8\% $ and the number of retries and conflicts more than $40\% $.
1 Introduction
In recent years, we have witnessed a growth of interconnected devices. With the advent of Internet of Things (IoT), houses and factories will be populated with tens of devices and sensors to monitor some variables or conditions, and taking automatic actions according to them. In this growing and challenging environment, Wireless Sensor Networks (WSNs) are a first class passenger and, therefore, it is crucial to define protocols that reduce the amount of consumed resources. WSNs are composed of small spatially distributed nodes, where each of them is provided with a sensor to monitor physical or environmental conditions such as temperature, motion, and, normally, they collaborate in a common task. Among these tasks are monitoring rooms or manufacturing processes, measuring pollution and so on.
This prominent era poses new challenges to normal deployments (wired networks). In the specific case of MAC layer protocols for WSNs and IoT, designers must pay special attention in the definition and configuration of new protocols in this highly-constrained and continuously changing scenario. For instance, resources are very limited and, therefore, one must evaluate each step in order not to waste them. In design phase, time and energy saving must be taken especially into account since it will influence the reliability and performance in a real case. Additionally, the nodes communicate through a wireless medium and it adds extra complexity to protocol definition, since it is not easy to infer if other nodes are transmitting at the same time. When this happens it appears what is known as a collision. Avoiding and resolving collisions is highly related with time/energy saving and performance. The way transmissions are sorted has led to many proposals in this area, where a good decision-making protocol can reduce the number of colliding nodes and, as a consequence, impact the two constraints presented previously.
In this way, a new MAC layer protocol for collision resolution called Two Cells Sorted Wireless Sensor Network protocol (2CS-WSN) was proposed by in Royo
et al. (
2009). This work was an adaptation of 2-Cell (2C) protocol (Paterakis and Papantoni-Kazakos,
1989) to the particular setting of wireless networks. The authors used simulation in a well-known wireless sensor networks simulator called Castalia (Boulis
et al.,
2011) to evaluate the performance of this new proposal.
Besides simulation, there are other techniques (e.g. testing and formal methods) that can be used for protocol validation and/or verification. On the one hand, simulations or tests are typically useful for a quick assessment of design, but sometimes they can hide the presence of some errors such as deadlocks, livelocks and so on. The main difference between formal methods and other techniques such as testing or simulation is the exhaustive study of all the paths in the system, that is, simulation or testing focus normally on a set of cases trying to express certain behaviours, whereas formal methods study all the possible cases in order to identify unexpected behaviour not covered by other methods. Thus, formal methods can be used to prove some important correctness criteria. In Mateo
et al. (
2015), we presented a rigorous formal study of 2CS-WSN using probabilistic model checking, an automated technique that, given a finite-state model of a probabilistic system and a formal property, systematically checks whether this property holds for that model with its probability.
Moreover, probabilistic model checking allows to assess the performance of the system. For instance, we can evaluate the expected time to resolve a collision in different scenarios or study properties of great interest to designers such as “the probability that a certain number of nodes have successfully managed to transmit within a certain time” or “the probability that all nodes have transmitted before a certain time”. Finally, let us comment that we used it to evaluate energy consumption of 2CS-WSN in Ruiz
et al. (
2016).
In this paper, we go one step further. By using probabilistic model checking and the well-known model checker PRISM (Kwiatkowska
et al.,
2011; Klein
et al.,
2017) we have specified 2CS-WSN with a different approach, proposing a new model that allows the investigation of the behaviour of each node, which has allowed us to propose new variants to 2CS-WSN to improve the decision making in case of collision. The results obtained have been compared with the obtained in our previous work. In the original algorithm of Royo
et al. nodes in the transmission cell (only in the first one) can decide to transmit or not using the same probability. Our proposal studies the impact of a wide range of possibilities. We have analysed the system performance using different probabilities and also changing the behaviour of the participants in the collision in the different cells (not only in the first one). In terms of energy and time consumption, we proposed an improvement in the algorithm which improves significantly the results obtained in the original protocol.
To sum up, our contribution is the proposal and study of new improvements for 2CS-WSN protocol using Probabilistic Model Checking as a formal technique and PRISM as a computer tool. Thus, the main contributions stated by this paper:
-
• to present a novel formal model of 2CS-WSN in PRISM.
-
• to validate our model versus Castalia simulator.
-
• to present novel modifications of the original protocol: 2CS-Down, 2CS-Up and 2CS-Hybrid.
-
• to check correctness properties and performance evaluation of each new alternative.
-
• to compare each new alternative with 2CS-WSN.
-
• to obtain the best parameters in each scenario.
-
• to choose the best option in terms of energy and time consumption defining a new MAC layer protocol.
The paper is organized as follows. Section
2 presents a brief background about the formalism and the software tool used in this work. A description of the 2CS-WSN protocol is presented in Section
3 and its specification in PRISM in Section
4. Section
5 studies the appropriate modifications to improve the protocol 2CS-WSN. Finally, Section
6 presents some related works and in Section
7 we provide some conclusions and lines of future work.
2 Background
We are going to do a brief introduction of the mathematical and computational background used in this work. For more details, about stochastic processes you can see Ross (
1996) and the website of PRISM (PRISM,
2017) for probabilistic model checking.
2.1 Discrete Time Markov Chain
A stochastic process $\mathbf{X}=\{X(t),\hspace{2.5pt}t\in T\}$ is a collection of random variables. If t represents the time, then $X(t)$ shows the state of the process at time t. Moreover, if the index set T is a countable set, that is, $T=\{0,1,2,\dots \}$, then X is a discrete time stochastic process and it can be represented as ${X_{n}}$, $n=0,1,2,\dots $ Besides, if we denote the set of possible values considering the set of nonnegative integers $0,1,2,\dots $ , then ${X_{n}}=i$ will indicate that the process is in the state i at time n.
Roughly, a (homogeneous) Discrete Time Markov Chain (DTMC) is a discrete time stochastic process with the memoryless or Markov property, that is, the state of the system at time
$n+1$ depends only on the state at time
n and the probabilities do not change with time, that is, they are independent of time,
for all states
${i_{0}},{i_{1}},\dots ,i,j$ and all
$n\geqslant 0$. In this way, Eq. (
1) may be interpreted as stating that the conditional probability of any future state
${X_{n+1}}$ given the past states
${X_{0}},{X_{1}},\dots ,{X_{n-1}}$ and the present state
${X_{n}}$, is independent of the past states and depends only on the present state. The value
${p_{ij}}$ represents the probability that the process will, when in state
i, make next a transition to state
j, and consequently it follows:
and we denote by
P the matrix of one-step transition probabilities
${p_{ij}}$
Alternatively, a DTMC can also be defined as a tuple $(S,{s_{0}},P)$ where:
-
– S is the set of states;
-
– ${s_{0}}\in S$ is the initial state;
-
– $P:S\times S\to [0,1]$ is the one-step transition probability matrix where ${\textstyle\sum _{{s^{\prime }}\in S}}P(s,{s^{\prime }})=1$, $\forall s\in S$.
We can also define the
n-step transition probability ${p_{ij}^{n}}$ of a DTMC as a conditional probability. Given that the process is currently in state
i, it will be in the state
j after
n additional transitions, that is,
and according to
Chapman–Kolmogorov equations
and denoting by
${\mathbf{P}^{(n)}}$ the matrix of
n-step transition probabilities
${p_{ij}^{n}}$, then we have that
and
meaning that the
n-step transition probability matrix may be obtained by multiplying the matrix
P by itself
n times, it is, the probability to move from the state
i to the state
$j\hspace{0.1667em}$ in
n time-steps (component
$(i,j)$ of
${P^{(n)}}$ ) can be easily calculated by the component
$(i,j)$ of the
${P^{n}}$ (
n power of
P).
A DTMC can also be represented as a directed graph, where each node is a state, and there is an arc from the state i to j, labelled by ${p_{ij}}$, if ${p_{ij}}>0$.
2.2 Probabilistic Model Checking. PRISM
The Model Checking formal technique (Clarke
et al.,
2001) is used with the purpose of proving the correctness of a system, and for that all possible executions of the system are explored. In the case the system had a stochastic behaviour, Probabilistic Model Checking is used to prove its correctness, that is, Probabilistic Model Checking provides a tool for establishing if (or with what probability) a desired property holds. It is based on the study of stochastic mathematical models, being DTMC in our model. The desired property is expressed using logics, we use Probabilistic Computation Tree Logic (PCTL) (Hansson and Jonsson,
1994).
PRISM is a probabilistic model checker developed initially at the University of Birmingham and now it is maintained at the University of Oxford. Our models are specified using the PRISM modelling language, a single high-level language for model description based on guarded command notation. Moreover, the fundamental components of the PRISM language are modules and variables. A model is composed of a number of modules which can interact with each other. A module contains a number of local variables. The values of these variables at any given time constitute the state of the module. The global state of the whole model is determined by the local state of all modules. The behaviour of each module is described by a set of commands. A command takes the form:
where the guard is a predicate over all the variables in the model (including those belonging to other modules). Each update describes a transition the module can make if the guard is true. A transition is specified by giving the new values of the variables in the module, possibly as a function of other variables. Each update is also assigned a probability which will be assigned to the corresponding transition.
PRISM also supports the specification and analysis of properties based on rewards (real values associated with certain states or transitions of the model). These rewards can be used to reason about the probability that a model behaves in a certain fashion and also to obtain a wider range of quantitative measures relating to model behaviour.
More details about the tool and different case studies, some of them in the area of sensors technology, can be found in PRISM (
2017).
3 2CS-WSN: A Stack Protocol with Random Access
In this section, we will introduce informally the 2CS-WSN protocol. A more detailed information can be found in Royo
et al. (
2009).
2CS-WSN was designed as an alternative to the Self-stabilizing Adaptive MAC protocol (SA-MAC) (Zheng and Jamalipour,
2009), which is a power-aware synchronous MAC (Medium Access Control) protocol that takes into account some important design principles, e.g. power saving, synchronization and transmission scheduling. This protocol is based on the fact that, in order to limit the waste of power due to channel overhearing, it is necessary to synchronize the ON/OFF periods of senders and receivers. In this way, the operation of the SA-MAC protocol can be divided into two phases: neighbour discovery and synchronization/data transmission.
Due to simultaneous channel access, it is possible to have conflicts during the neighbour discovery phase, requiring a conflict resolution mechanism. To this end, 2-Cell (2C) protocol (Paterakis and Papantoni-Kazakos,
1989) was introduced. This 2C protocol is called a stack protocol because its time evolution can be easily visualized as a group of stations moving up and down in a cell stack as their counters decrease or increase, respectively. In this context, contending stations may be either transmitting or waiting and the two states can be represented using only two cells in a stack. The transmission cell (
$\mathit{TC}$) represents the group of transmitting stations and the waiting cell (
$\mathit{WC}$) represents the group of stations that have deferred transmission. The station must do a random choice between the transmission (which means to remain in
$\mathit{TC}$) or joining to the
$\mathit{WC}$ (waiting group).
Although this 2C protocol has many desirable features it may incur in significant access delays when a large number of stations contend for channel access. As a consequence, an extended version of the 2C protocol where $\mathit{WC}$ consists of several ordered stages was developed: 2CS-WSN. In this approach, there is more than one waiting cell where the stations that expect to transmit will be located depending on the value of their counter.
Moreover, no specific transmission medium has been considered in the original description of stack protocols, so that it is necessary to adapt the protocol to the particularities of wireless communications. Originally, a central station is continuously monitoring the channel and providing feedback messages, but it cannot be assumed in self-configuring wireless ad-hoc networks. Consequently, in this new version, the nodes are responsible for monitoring the transmission medium and reacting accordingly. Therefore, in this extended version of the 2C protocol, network nodes infer that a collision has happened, instead of detecting a collision, when the reply to their requests does not arrive.
Furthermore, 2CS-WSN protocol assumes that the time is slotted and stations are allowed to transmit only at the beginning of a time slot. Moreover, a time slot is basically equal to the time that it takes to transmit a packet and receive a feedback message from a central station. Since there are only two possibilities for this feedback message: detected collision (C Collision message) and no detected collision ($\mathit{NC}$ No Collision message), we can consider that this feedback message is binary.
When only one station transmitted, then its corresponding packet will be successfully transmitted. On the other hand, when there were several transmission attempts in the same slot, then there will be a collision and its resolution will begin in the following slot. This collision resolution procedure is finished when all stations that had collided have successfully transmitted their packets. This collision resolution interval is called $\mathit{CRI}$. In a $\mathit{CRI}$, each participating station provides a counter that controls its channel access.
At the beginning of a slot i, we denote by ${c_{i}}$ the value of this counter and only when ${c_{i}}=0$ a station is allowed to attempt channel access in slot i. Let consider ${f_{i}}\in \{C,\mathit{NC}\}$ as the feedback message corresponding to the transmission in slot i which is received at the end of the same time slot. Then, if the transmission was unsuccessful ${f_{i}}=C$, otherwise the feedback message is ${f_{i}}=\mathit{NC}$. If $\mathit{CRI}$ is not in progress, that is, the channel is sensed to be free, stations with new transmission requests will set their counter to 0 and will attempt channel access in the following slot t. Each station updates its counter depending on the feedback messages, and it is as follows:
-
• If ${c_{t}}=1$ and ${f_{t}}=\mathit{NC}$, then ${c_{t+1}}={c_{t}}-1$.
-
• If ${c_{t}}\geqslant 1$ and ${f_{t}}=C$, then ${c_{t+1}}={c_{t}}+1$.
-
• If ${c_{t}}=0$ and ${f_{t}}=C$, then ${c_{t+1}}$ will change to 1 with probability 0.5.
In Fig.
1 we present the basic idea of the algorithm to help the reader in the following steps where we will delve deeply into it.
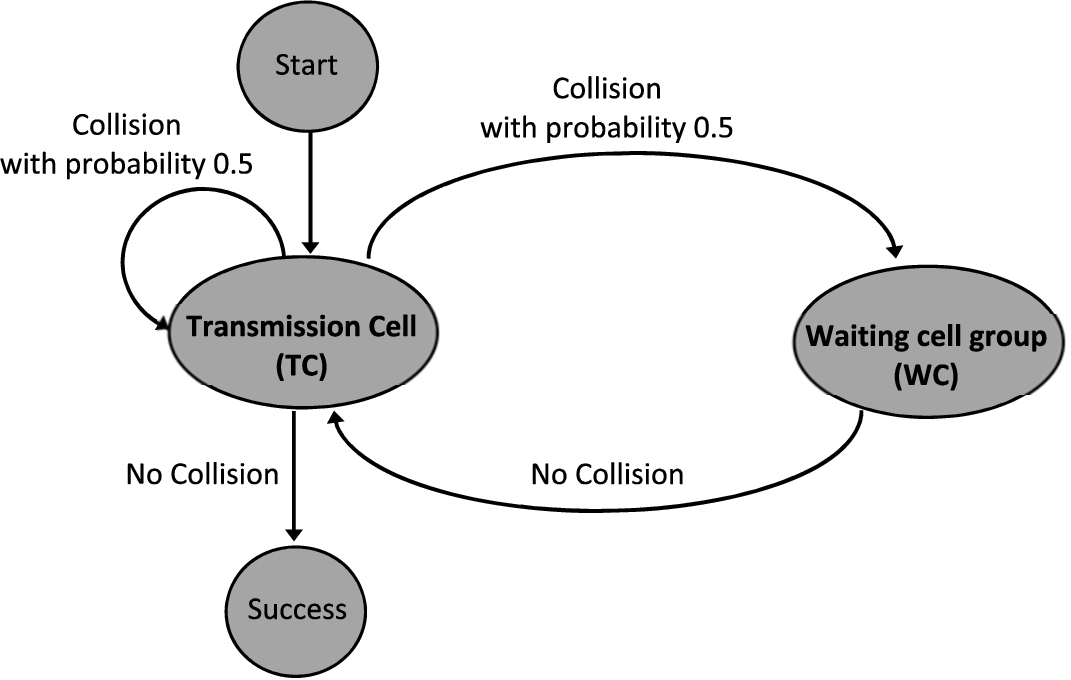
Fig. 1
Basic idea of the original algorithm at a glance.
Figure
2 shows the flow chart of the 2CS-WSN protocol and, for the sake of clarity, we introduce a brief and intuitive small example with only four nodes and two waiting cells. Let us consider the scenario presented in the collision resolution example depicted in Fig.
3, where a collision has occurred and four nodes (A, B, C, D) are involved. There is one transmission cell, denoted by
$\mathit{TC}$, at the beginning with four nodes, and two waiting cells, denoted by
${\mathit{WC}_{1}}$ and
${\mathit{WC}_{2}}$, respectively. We denote by
${p_{\mathit{TC}}}$ the probability of a node to remain in
$\mathit{TC}$ and by
${p_{{\mathit{WC}_{1}}}}$ the probability of entering into the first waiting group (with the obvious condition that
${p_{{\mathit{WC}_{1}}}}=1-{p_{\mathit{TC}}}$). All nodes in
$\mathit{TC}$ have the same probability. In this way, each node in
$\mathit{TC}$ decides randomly, with probability 0.5 (
${p_{\mathit{TC}}}=0.5$), either to retransmit or move to
${\mathit{WC}_{1}}$. In the last case, if the node moves from
$\mathit{TC}$ to
${\mathit{WC}_{1}}$ then the nodes in
${\mathit{WC}_{1}}$ move to
${\mathit{WC}_{2}}$. When only one node remains in
$\mathit{TC}$, then it can successfully transmit. Then, the nodes in
${\mathit{WC}_{1}}$ move to
$\mathit{TC}$ and the nodes in
${\mathit{WC}_{2}}$ move to
${\mathit{WC}_{1}}$. Finally, if all nodes can successfully transmit, the initial collision is considered solved.
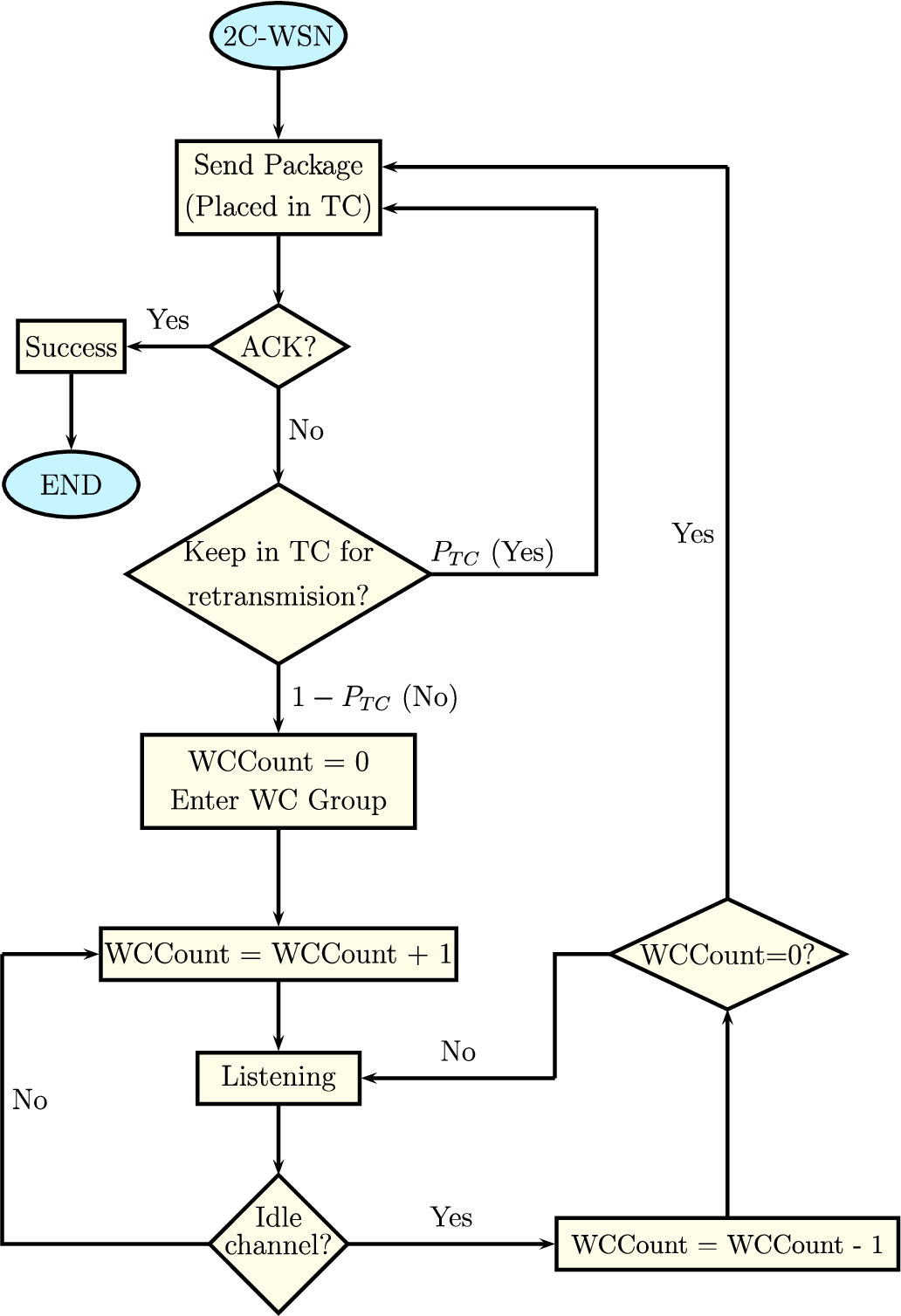
Fig. 2
The 2CS-WSN algorithm.
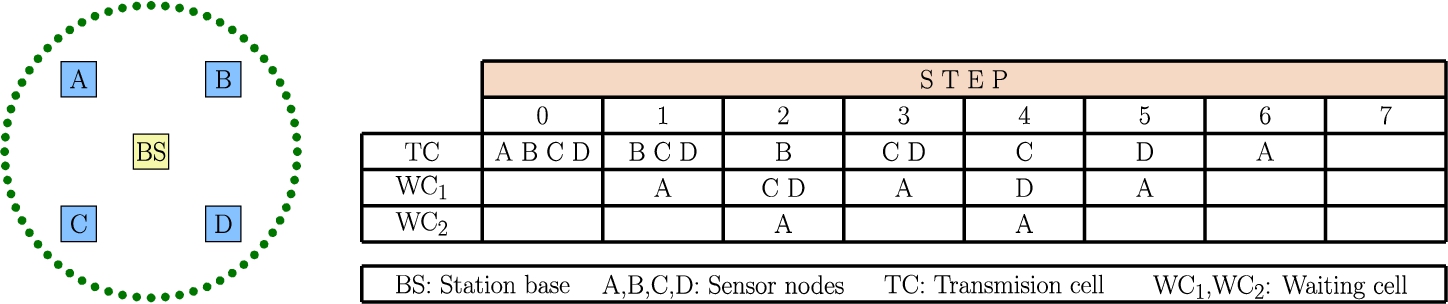
Fig. 3
Collision resolution example using 2CS-WSN with 4 nodes in collision and 2 waiting cells.
In particular, Fig.
3 shows the following case: initially all four nodes (A, B, C, D) attempt transmission and, therefore, a collision occurs. As a result of this collision, node A randomly decides to enter the waiting cell
${\mathit{WC}_{1}}$ whereas nodes B, C and D, also randomly, decide to remain in the transmission cell
$\mathit{TC}$. Therefore, in the following transmission opportunity, nodes B, C and D try to transmit and collide again. As a result of the second collision, nodes C and D randomly decide to enter the waiting group
${\mathit{WC}_{1}}$ whereas node A moves from
${\mathit{WC}_{1}}$ to
${\mathit{WC}_{2}}$. At this time only node B randomly decided to remain in
$\mathit{TC}$ thus achieving a successful transmission in the following transmission opportunity. This successful transmission causes nodes in
${\mathit{WC}_{1}}$ (i.e. nodes C and D) to move to the
$\mathit{TC}$ and nodes in
${\mathit{WC}_{2}}$ (i.e. node A) move to
${\mathit{WC}_{1}}$ (i.e. node A). This algorithm repeats until all nodes that participated in the initial collision can successfully transmit their packets.
4 2CS-WSN Model in PRISM
In our first proposals to model the 2CS-WSN algorithm in terms of DTMCs using PRISM (Mateo
et al.,
2015; Ruiz
et al.,
2016), we modelled the behaviour of the system as a whole taking into account the number of nodes in
$\mathit{TC}$ and
${\mathit{WC}_{i}}$ and showing the evolution in next time step. That is, we used DTMCs to represent all the possible states of the system (computing the probabilities to evolve from one state to its possible successors in each time-step). Mainly, in Mateo
et al. (
2015) our aim was to to check some correctness properties, such as the absence of deadlock, and also to study different operating modes collecting some performance measures taking into account, mainly, collision resolution time. The obtained results were according to the conformity with the former implementation in Castalia. This study was extended in Ruiz
et al. (
2016) where we focused on the energy consumption of the system.
These studies fulfilled our expectations, but there was one important point that our previous model of the system did not allow us to do: to study the behaviour of each node individually. This aspect becomes important because with this new vision of the system we are able to model certain variants of the behaviour of the system that may improve it.
Now, we face the protocol from a completely different perspective and we propose a novel model to specify the protocol focusing on the evolution of each node. We study the behaviour of the system by modelling the particular behaviour of each node, and then the system comprises all nodes. We use DTMCs to represent every possible state of the system by computing the probabilities to evolve from one state to another state according to the behaviour of each node.
It is worthwhile to mention that all the nodes in the network have not to be taken into account, but only the nodes in collision. This means that the scalability of these protocols has not to be considered in terms of total number of nodes in the network, it is enough to consider the maximum number of nodes in collision that the algorithm is able to manage in a reasonable time. The probability that a certain number of nodes are involved in a collision depends on several factors such as the collision avoidance algorithm, the size of the network and especially the application that is intended for the network of sensors.
To frame our work, according to the study presented in Rajbal and Rajba (
2012), assuming up to 10 nodes involved in the collision, the results are valid for networks with 572 nodes. Furthermore, these studies have been always done under saturated traffic condition (with a traffic load of 0.6) which is not a usual load situation but taken to be the worst situation. For a standard load, the percentage of collisions decreases considerably.
In short, in this paper, we consider 10 nodes in collision in the system, being aware that this number exceeds the average number of collisions per unit of time in real systems, which we have been able to verify in different real systems, among which we highlight the ones presented in Hortelano
et al. (
2017) or the ones related to body area networks (i.e. Prabh
et al. (
2016)), where the number of nodes in collision is smaller.
Therefore, the model can be defined as follows: considering
n as the number of nodes in collision and
m, the number of waiting cells, and also a variable
${x_{i}}$ is defined for each node with
$i\in [1..n]$, where
${x_{i}}$ can take the following values:
Then, a state is defined as a tuple $({x_{1}},{x_{2}},\dots ,{x_{n}})$ where the initial state (all nodes are involved in a collision) is $(1,1,\dots ,1)$ and the state of the system when the collision has been solved is $(0,0,\dots ,0)$.
A module is used to model each node. Moreover, all commands are prefixed with the action
a in order to force the modules to make transitions simultaneously (i.e. to synchronize). For the sake of clarity, Fig.
4 shows the PRISM code considering just 4 nodes (4 modules) and 2 waiting cells, but it is easily scalable to any number of nodes and waiting cells.

Fig. 4
PRISM code for 4 nodes and 2 WCs.
Here, the formula $qt$ is used to know how many nodes attempt to transmit, that is, the number of nodes whose state variables have value 1. Likewise, to know how many nodes have completed the transmission successfully the formula $ht$ counts the number of nodes whose state variables have value 0. Moreover, each module consists of the following commands:
-
• $[a]$ ${x_{i}}$ = 1 & $qt$ = 1 $\to ({x^{\prime }_{i}}=0)$;
If the node i attempts to transmit (placed in $\mathit{TC}$) and there is only one node trying to access the channel, it transmits and changes the value of its state variable to 0 (successful transmission).
-
• $[a]$ ${x_{i}}>1$ & $qt>1\to ({x^{\prime }_{i}}=\min ({x_{i}}+1,m));$
If the node i is waiting to transmit (placed in a $\mathit{WC}$) and there is more than one node trying to transmit (in $\mathit{TC}$) (there is a conflict), the node i moves to the next waiting cell, provided that the node is not already in the last one.
-
• $[a]$ ${x_{i}}=1$ & $qt>1\to 0.5:({x^{\prime }_{i}}=2)+0.5:({x^{\prime }_{i}}=1)$;
If the node i attempts to transmit (in $\mathit{TC}$) and more than one node also tries to do it, the node i can retry the transmission (remaining in $\mathit{TC}$) with a probability 0.5 or move to the first waiting cell $({\mathit{WC}_{1}})$.
-
• $[a]$ ${x_{i}}>1$ & $qt\leqslant =1\to ({x^{\prime }_{i}}=\max (0,{x_{i}}-1))$;
If the node i is waiting to transmit (in a $\mathit{WC}$), and there is no node transmitting or there is just one node trying it, the node i moves up to the previous waiting cell.
-
• $[a]$ ${x_{i}}=0\to ({x^{\prime }_{i}}=0)$;
A node that has already transmitted has nothing else to do until the next transmission.
Tables
1 and
2 show the scalability of the model (states and transitions, respectively) for different sizes of networks. It can be observed that an increase in the number of waiting cells involves a greater increase in the number of states and transitions than when the number of nodes is increased and maintaining fixed the number of waiting cells. For example, for an 8-node network with two waiting cells, the model has 63,241 states while for an 8-node network with three waiting cells there are 350,097 states, representing an increase of 286,856 states. However, if there are 9 nodes in collision and two waiting cells, the model has 257,034 states, i.e. there is a smaller increase (193,793 states) but this is not the case when considering the number of transitions.
Table 1
2CS-WSN model scalability (states).
|
States |
| NS |
1 WC |
2 WC |
3 WC |
4 WC |
| 3 |
24 |
36 |
57 |
78 |
| 4 |
77 |
181 |
361 |
630 |
| 5 |
238 |
838 |
2,153 |
4,598 |
| 6 |
723 |
3,655 |
12,173 |
31,751 |
| 7 |
2,180 |
15,368 |
66,181 |
211,382 |
| 8 |
6,553 |
63,241 |
350,097 |
1,369,615 |
| 9 |
19,674 |
257,034 |
1,187,649 |
8,695,374 |
| 10 |
59,039 |
1,037,323 |
9,318,037 |
54,372,463 |
| 11 |
177,136 |
4,169,740 |
47,363,165 |
336,185,534 |
| 12 |
531,429 |
16,723,981 |
239,382,233 |
2,061,471,527 |
| 13 |
1,594,310 |
66,994,190 |
1,205,344,585 |
12,564,294,278 |
| 14 |
4,782,955 |
268,189,711 |
6,054,206,301 |
76,239,017,143 |
| 15 |
14,348,892 |
1,073,217,552 |
30,559,985,909 |
461,129,956,134 |
Table 2
2CS-WSN model scalability (transitions).
|
Transitions |
| NS |
1 WC |
2 WC |
3 WC |
4 WC |
| 3 |
49 |
70 |
100 |
130 |
| 4 |
220 |
442 |
776 |
1236 |
| 5 |
939 |
2,534 |
5,524 |
10,504 |
| 6 |
3,898 |
13,726 |
37,060 |
83,994 |
| 7 |
15,929 |
72,006 |
239,200 |
645,614 |
| 8 |
64,504 |
370,834 |
1,508,016 |
4,829,800 |
| 9 |
259,831 |
1,888,966 |
9,352,396 |
35,455,660 |
| 10 |
1,043,446 |
9,557,542 |
57,397,148 |
256,850,286 |
| 11 |
4,183,029 |
45,154,022 |
349,797,760 |
1,843,293,346 |
| 12 |
16,572,628 |
241,961,626 |
2,121,692,296 |
13,140,028,892 |
| 13 |
67,055,603 |
1,213,679,718 |
12,827,231,668 |
93,218,782,544 |
| 14 |
268,320,754 |
6,080,949,358 |
77,375,330,676 |
659,008,082,146 |
| 15 |
1,703,496,049 |
30,445,309,318 |
466,000,860,250 |
4,646,953,747,126 |
Based on these results we proceed to choose the parameters that will define the scenario in which we will work in the rest of this study. In choosing the scenario there are two important parameters to consider; the number of nodes in collision (enough to reflect the behaviour of real systems) and the number of waiting cells (infinite in the original algorithm). In order to choose the number of nodes in collision, we remark, given its importance, that we do not work with the total number of nodes in the network, but only with those nodes that have collided in the same unit of time. As mentioned above, assuming 10 nodes in collision, we are covering the study of networks with more than 500 nodes, which includes a large part of real networks. Regarding the number of waiting cells to be considered, by analysing Tables
1 and
2 we note that the size of the state space/transitions grows exponentially so that a well-known disadvantage of model checking may arise: the state explosion problem. Although there are new researches looking for efficient ways to deal with it even including new emerging trends as Big Data (Camilli,
2015). In Probabilistic Model Checking, some recent advances in the area can be found (Kwiatkowska
et al.,
2017) and, surely, in the future the state explosion problem can be reduced significantly, but at the moment in some cases it is a problem. Therefore, due to the current restrictions, we have decided to work with four waiting cells.
5 2CS-WSN Improvements
Once the new model has been developed, we take advantage of it to study a set of features that are of particular interest in wireless sensor networks, namely, the time needed to resolve the conflict, the number of conflicts that arise in the resolution, the number of transmission retries, and finally, the fragmentation produced in the transmission cell. Then, we used PCTL logic for expressing significant properties. Moreover, to carry out this study we extended our model with “rewards” so that certain transitions of the model were associated to a reward (real value). Basically, a
reward can be considered a real value which is associated with certain states or transitions of the model. Moreover, the rewards are accumulated over paths that fulfil predetermined conditions and allow us to calculate expected values. So that, we include in our model the rewards shown in Fig.
5.

Fig. 5
Rewards structure.
In particular, the reward
time allows us to obtain the time it takes to resolve the conflict. Each time slot in the 2CS-WSN protocol assumes 1.6 ms, therefore, every action of the protocol takes the value of 1.6. To obtain this time, we use the property
${\phi _{1}}$.
The reward
conflicts computes the number of conflicts that are expected to appear. Keep in mind that a conflict involving five nodes is counted as a single conflict, so the value of 1 is assigned each time to more than one node’s attempt to transmit. We use the property
${\phi _{2}}$ to study the number of conflicts.
Another important measure is the number of
retries needed until all nodes are able to transmit. In this case, if 5 nodes are trying to transmit (where it is considered as an only one conflict), then there will be 5 retries, so we assign the value
$qt$ to this reward. This value is obtained by evaluating the property
${\phi _{3}}$.
Finally, it is also useful to assess how many time slots in which a node could transmit are empty. To do this, we assign the value of 1 whenever any node wants to transmit but they are in a waiting cell. To calculate it, the property
${\phi _{4}}$ associated to the reward
gaps is used.
As stated above, the protocol uses, by default, a probability of 0.5 for retrying transmission and 0.5 for the node moving down to the first waiting cell. Using the model presented in the previous section, we have obtained the results for the properties
${\phi _{1}}$,
${\phi _{2}}$,
${\phi _{3}}$ and
${\phi _{4}}$ varying the probability from 0.1 to 0.9 with increments of 0.1 (Table
3). The scenario in which the study have been conducted consists of 10 nodes in conflict and 4 waiting cells. We can appreciate that the best configuration for the protocol is
${p_{\mathit{TC}}}=0.5$.
Finally, in order to verify that our model fits the real system, the results have been validated with those offered by the Castalia simulator.
Table 3
Results obtained varying the probability from 0.1 to 0.9 in 2CS-WSN protocol.
| Probabilities |
Time (ms) |
Conflicts |
Retries |
Gaps |
| 0.1 |
119.78 |
58.78 |
222.43 |
6.08 |
| 0.2 |
68.48 |
28.02 |
104.66 |
7.78 |
| 0.3 |
52.74 |
18.93 |
68.91 |
4.03 |
| 0.4 |
46.36 |
15.28 |
54.02 |
3.70 |
| 0.5 |
44.40 |
13.94 |
48.28 |
3.82 |
| 0.6 |
45.64 |
14.02 |
48.24 |
4.51 |
| 0.7 |
50.49 |
15.40 |
3.51 |
6.16 |
| 0.8 |
61.80 |
18.87 |
67.61 |
9.75 |
| 0.9 |
94.84 |
26.16 |
112.55 |
20.11 |
Once the protocol has been studied in depth according to the novel specification in PRISM, our next goal is to find the appropriate modifications to improve the protocol 2CS-WSN, that is, to make it more efficient.
Before introducing the improvement proposals, it is worth remembering that the protocol uses probabilities when there is a collision only to decide if the node retries to transmit in the next time slot (remains in TC) or goes to the first waiting cell but all nodes located in the waiting cells move without any probability depending on whether there has been a collision or not. Thus:
-
• If ${c_{t}}\geqslant 1$ and ${f_{t}}=\mathit{NC}$, then ${c_{t+1}}={c_{t}}-1$.
-
• If ${c_{t}}\geqslant 1$ and ${f_{t}}=C$, then ${c_{t+1}}=min({c_{t}}+1,n)$.
-
• If ${c_{t}}=0$ and ${f_{t}}=C$, then ${c_{t+1}}={c_{t}}$ with probability ${p_{\mathit{TC}}}$ and ${c_{t+1}}=1$ with probability $1-{p_{\mathit{TC}}}$.
Now, we present and study three different proposals. All of them are based on the concept of using probabilities to decide whether a node should move to another waiting cell or remain. We have called these proposals: 2CS-Down, 2CS-Up and 2CS-Hybrid. Here, we analyse them individually and compare them with the original protocol 2CS-WSN in a scenario with 10 nodes in collision and 4 waiting cells. To make this comparison, the parameters evaluated are:
-
• Expected time, meaning how long it takes all sensors to transmit.
-
• Number of conflicts that arise, a conflict is understood as having more than one sensor is in the TC.
-
• Number of retries, which has a direct influence on energy consumption.
-
• Number of unused timed slots (gaps), it means the use of the waiting cells.
5.1 2CS-Down
We propose to apply the policy used in the transmission cell to the waiting cells, i.e. if there is a collision and there are nodes in the waiting cell ${W_{i}}$, they decide if they move down ${W_{i+1}}$ or remain in the cell ${W_{i}}$ with probability ${p_{\mathit{TC}}}$.
-
• If ${c_{t}}\geqslant 1$ and ${f_{t}}=\mathit{NC}$, then ${c_{t+1}}={c_{t}}-1$.
-
• If ${c_{t}}\geqslant 1$ and ${f_{t}}=C$, then ${c_{t+1}}={c_{t}}$ with probability ${p_{\mathit{TC}}}$ and ${c_{t+1}}=\min ({c_{t}}+1,n)$ with probability $1-{p_{\mathit{TC}}}$.
-
• If ${c_{t}}=0$ and ${f_{t}}=C$, then ${c_{t+1}}={c_{t}}$ with probability ${p_{\mathit{TC}}}$ and ${c_{t+1}}=1$ with probability $1-{p_{\mathit{TC}}}$.
In the same scenario stated above, we carry out the study for the four defined parameters modifying the probability
${p_{\mathit{TC}}}$ from 0.1 to 0.9. The results are shown in Fig.
6.
According to the results, it seems that the expected improvement has not occurred in all cases. Specifically, if we focus our attention when the system works with probabilities equal to 0.5 (${p_{\mathit{TC}}}=0.5$) which proved to achieve the best results in the original 2CS protocol, three of the four parameters studied have gotten worse, namely the time needed to resolve the collision and the number of conflicts and retries. Just an improvement with respect to the use of the waiting cells, that is, the number of unused timed slots (gaps), is obtained in 2CS-Down proposal considering probabilities greater or equal than 0.5. Although this alternative seems promising, it only improves the use of the waiting cells and, in this case, it does not have a direct correlation with the time required to solve the collision.
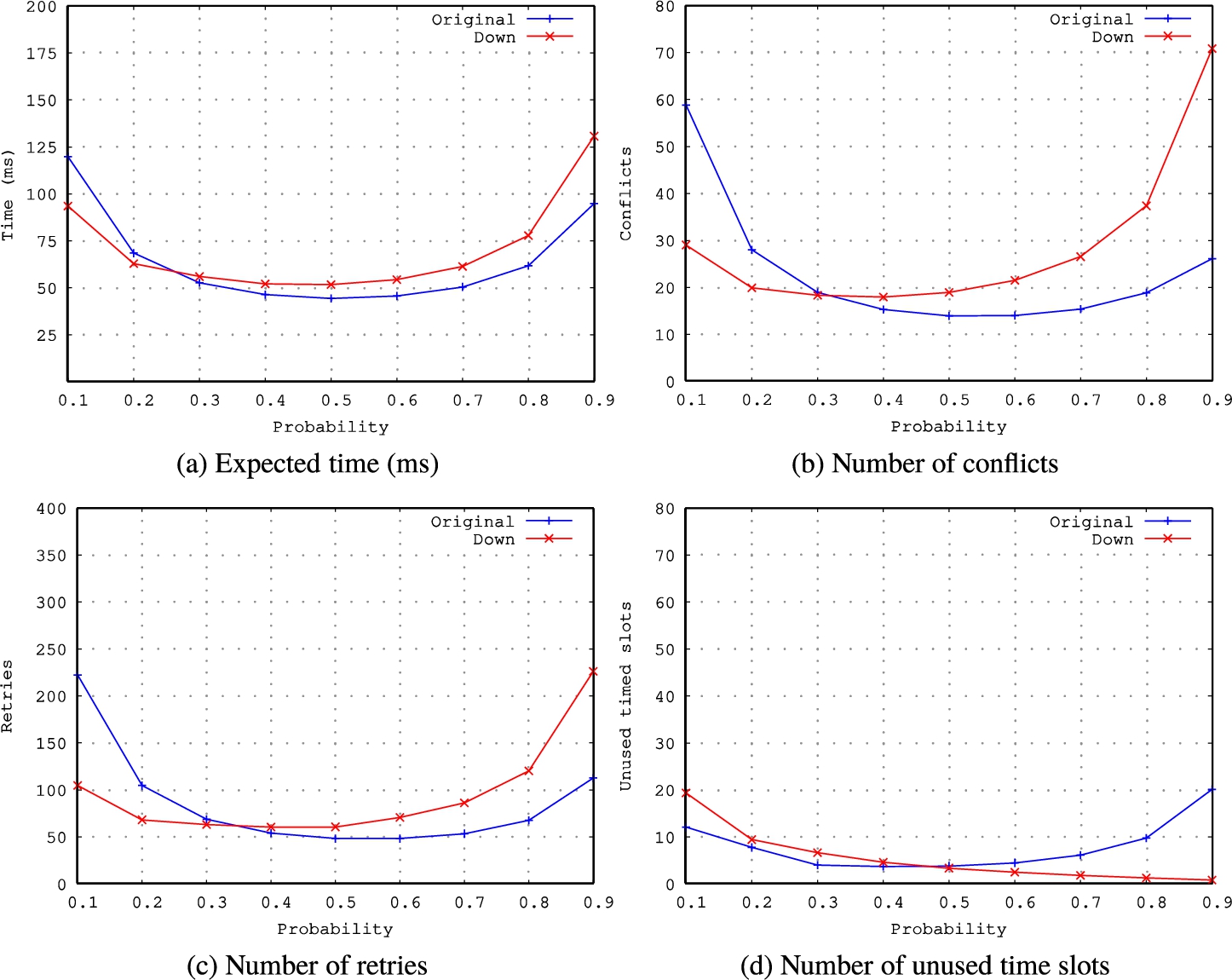
Fig. 6
Comparative 2CS vs 2CS-Down.
5.2 2CS-Up
This new alternative is based on the idea that when a node has transmitted (TC is empty), nodes that are in the cell ${W_{i}}$ go up to the cell ${W_{i-1}}$ with probability ${p_{\mathit{TC}}}$. It should improve the results as fewer nodes are involved in the conflict. Let us see if it is true. The behaviour of the protocol is modified as follows:
-
• If ${c_{t}}\geqslant 1$ and ${f_{t}}=\mathit{NC}$, then ${c_{t+1}}={c_{t}}$ with probability ${p_{\mathit{TC}}}$ and ${c_{t+1}}=\min ({c_{t}}-1,n)$ with probability $1-{p_{\mathit{TC}}}$.
-
• If ${c_{t}}\geqslant 1$ and ${f_{t}}=C$, then ${c_{t+1}}={c_{t}}+1$.
-
• If ${c_{t}}=0$ and ${f_{t}}=C$, then ${c_{t+1}}={c_{t}}$ with probability ${p_{\mathit{TC}}}$ and ${c_{t+1}}=1$ with probability $1-{p_{\mathit{TC}}}$.
Once again, we perform the study for the four parameters. The results obtained can be seen in Fig.
7 and they are now much more encouraging. It can be observed that this modification of the protocol significantly improves the values in the two most important parameters, that is, the time needed to solve the collision and the number of retries performed (remember that the latter has a direct relation with the energy consumption). This improvement in time appears only for probabilities less than 0.5, but the number of retries decreases for any probability. Obviously, the number of conflicts has also a decrease similar to the number of retries.
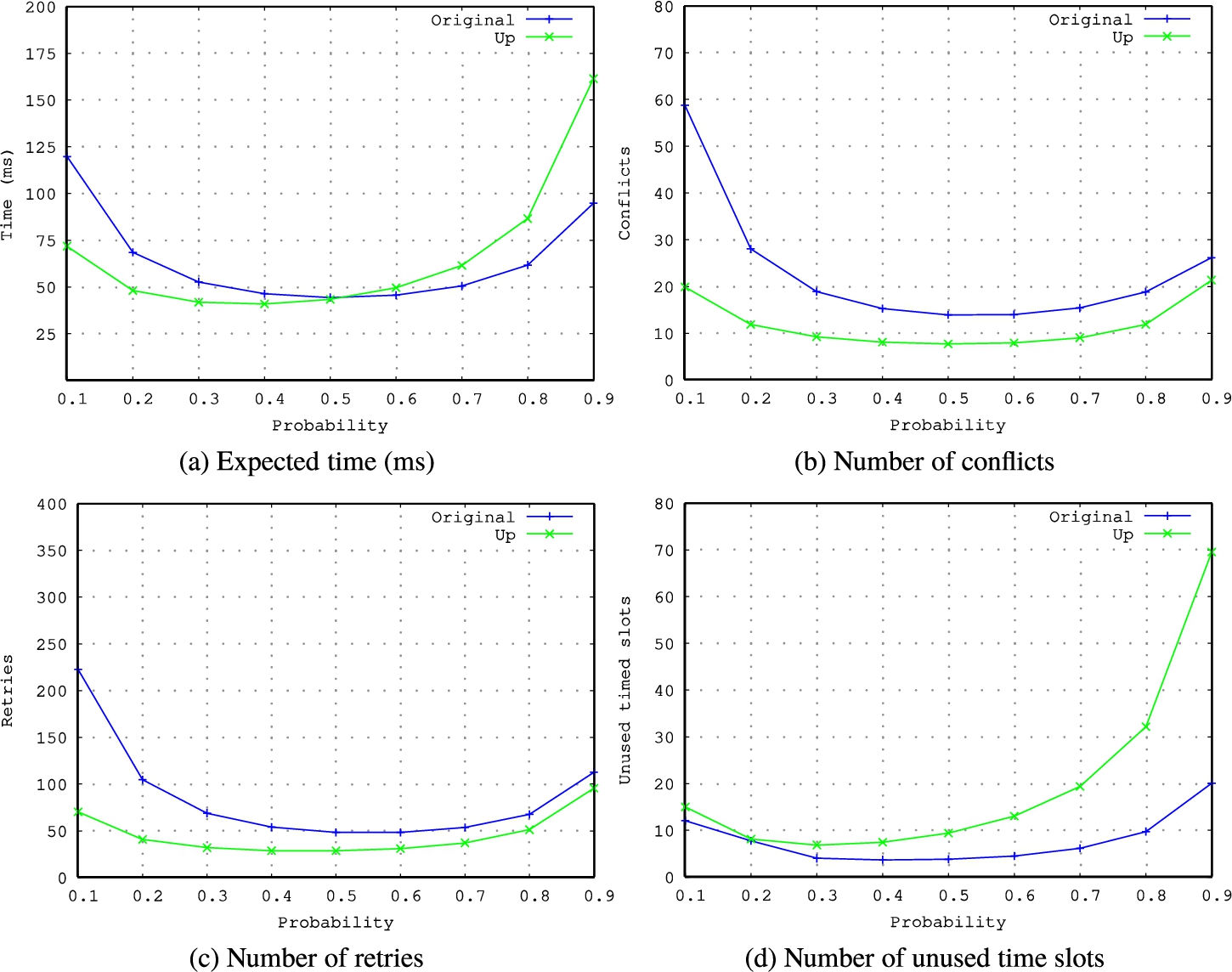
Fig. 7
Comparative 2CS vs 2CS-Up.
In this new proposal, the best result with respect to expected time is obtained considering ${p_{\mathit{TC}}}=0.4$, whereas the best result with respect to number of conflicts or retries is obtained considering ${p_{\mathit{TC}}}=0.5$. However, the number of gaps increases for all probabilities, but does not have an impact on the time required to end the collision.
It seems that we have found a way to improve the protocol, but we still have to evaluate one more alternative.
5.3 2CS-Hybrid
Once it has been found that the version 2CS-Up improves the protocol thanks to the inclusion of new probabilities, we wonder what would happen if we join the two modifications presented previously. The result is the version called 2CS-Hybrid. This proposal is a hybrid of the two previous ones, so that probability is applied in both cases, when the node moves up and when it moves down. The protocol works as follows:
-
• If ${c_{t}}\geqslant 1$ and ${f_{t}}=\mathit{NC}$, then ${c_{t+1}}={c_{t}}$ with probability ${p_{\mathit{TC}}}$ and ${c_{t+1}}=min({c_{t}}-1,n)$ with probability $1-{p_{\mathit{TC}}}$;
-
• If ${c_{t}}\geqslant 1$ and ${f_{t}}=C$, then ${c_{t+1}}={c_{t}}$ with probability ${p_{\mathit{TC}}}$ and ${c_{t+1}}=min({c_{t}}+1,n)$ with probability $1-{p_{\mathit{TC}}}$;
-
• If ${c_{t}}=0$ and ${f_{t}}=C$, then ${c_{t+1}}={c_{t}}$ with probability ${p_{\mathit{TC}}}$ and ${c_{t+1}}=1$ with probability $1-{p_{\mathit{TC}}}$.
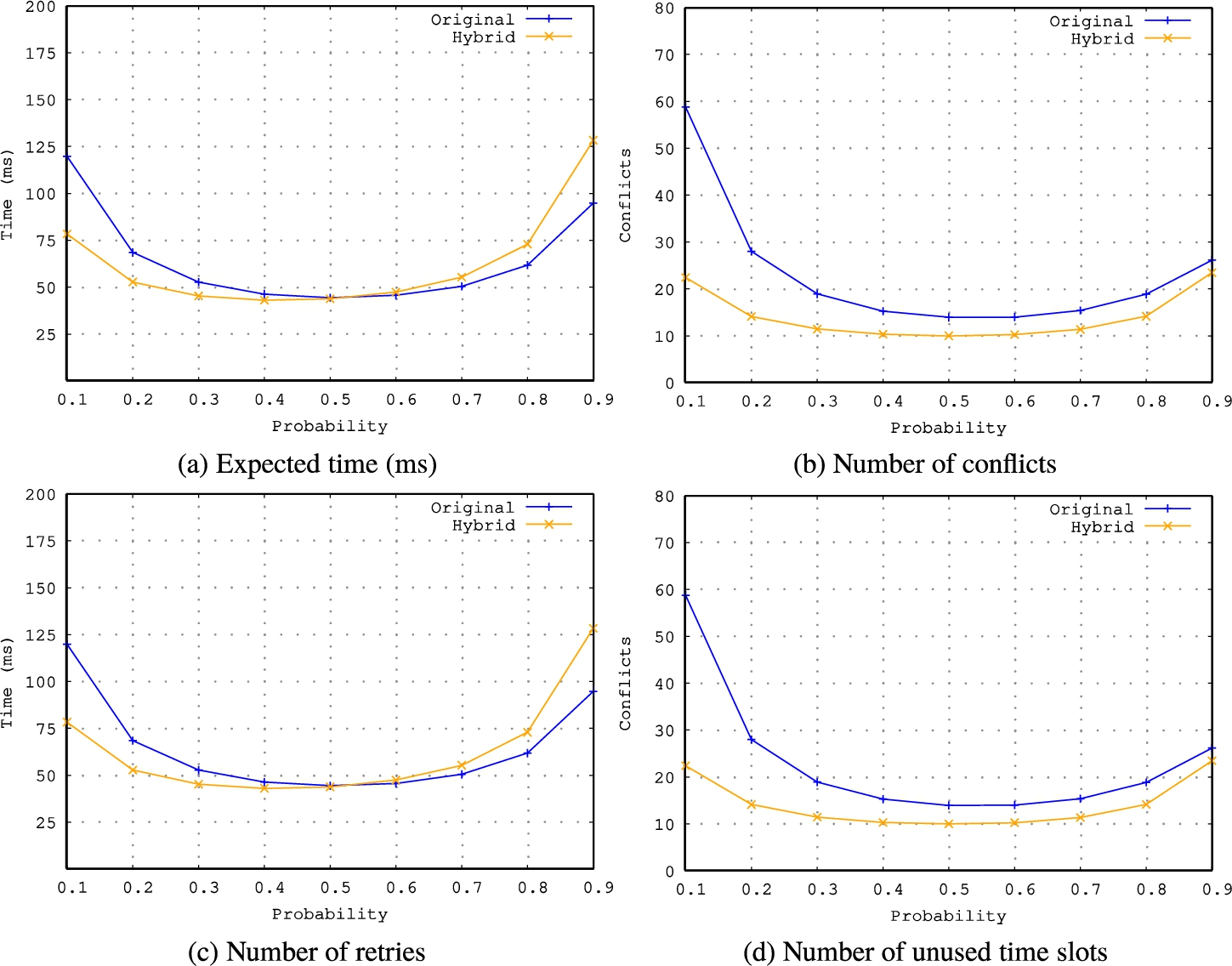
Fig. 8
Comparative 2CS vs 2CS-Hybrid.
Analysing the results shown in Fig.
8, we can see that 2CS-Hybrid proposal improves the same parameters as 2CS-Up improved but unfortunately this improvement is lower in all cases. This makes sense because it reduces the gain obtained thanks to the inclusion of the probability to decide to go up with the loss that we have observed by including the probability in the decision to go down.
5.4 Discussion
Before starting this session and intending to summarize and make more understandable the proposals, Fig.
9 presents a summary of the variations made in the 2CS-WSN protocol in this paper.

Fig. 9
Summary of the different alternatives to the protocol.
Up to now, the three alternatives presented have been compared against the original algorithms. In order to appreciate clearly the improvements, Table
4 shows the numeric values of the different alternatives where the best results, in the original 2CS protocol and in the corresponding proposal, are annotated in black. Moreover, Fig.
10 presents a global vision with the comparison among the three alternatives and the original algorithm summering all the results.
Table 4
Results of the different alternatives to the protocol.
| Time (ms) |
| Prob. |
2CS-Orig |
2CS-Down |
2CS-Up |
2CS-Hybrid |
| 0.1 |
119.78 |
93.50 |
71.84 |
78.38 |
| 0.2 |
68.48 |
62.96 |
48.05 |
52.80 |
| 0.3 |
52.74 |
56.00 |
41.82 |
45.29 |
| 0.4 |
46.36 |
52.12 |
40.92 |
43.06 |
| 0.5 |
44.40 |
51.72 |
43.43 |
43.82 |
| 0.6 |
45.64 |
54.38 |
49.58 |
47.43 |
| 0.7 |
50.49 |
61.37 |
61.54 |
55.33 |
| 0.8 |
61.80 |
77.84 |
86.58 |
72.93 |
| 0.9 |
94.84 |
130.68 |
161.41 |
128.35 |
| Conflicts |
| Prob. |
2CS-Orig |
2CS-Down |
2CS-Up |
2CS-Hybrid |
| 0.1 |
58.78 |
29.04 |
19.88 |
22.43 |
| 0.2 |
28.02 |
19.91 |
11.89 |
14.14 |
| 0.3 |
18.93 |
18.36 |
9.26 |
11.46 |
| 0.4 |
15.28 |
17.94 |
8.11 |
10.33 |
| 0.5 |
13.94 |
18.96 |
7.72 |
10.00 |
| 0.6 |
14.02 |
21.51 |
7.96 |
10.28 |
| 0.7 |
15.40 |
26.55 |
9.06 |
11.38 |
| 0.8 |
18.86 |
37.36 |
11.92 |
14.18 |
| 0.9 |
26.16 |
70.82 |
21.36 |
23.46 |
| Retries |
| Prob. |
2CS-Orig |
2CS-Down |
2CS-Up |
2CS-Hybrid |
| 0.1 |
222.43 |
104.78 |
70.29 |
104.74 |
| 0.2 |
104.66 |
68.23 |
40.76 |
68.23 |
| 0.3 |
68.91 |
63.20 |
31.88 |
63.20 |
| 0.4 |
54.02 |
60.52 |
28.74 |
60.52 |
| 0.5 |
48.28 |
60.64 |
28.59 |
63.02 |
| 0.6 |
48.24 |
70.64 |
31.03 |
70.64 |
| 0.7 |
53.51 |
86.29 |
37.15 |
86.29 |
| 0.8 |
67.61 |
120.34 |
51.24 |
120.34 |
| 0.9 |
112.55 |
226.20 |
95.69 |
226.20 |
| Unused slots |
| Prob. |
2CS-Orig |
2CS-Down |
2CS-Up |
2CS-Hybrid |
| 0.1 |
6.08 |
19.40 |
15.03 |
16.56 |
| 0.2 |
7.78 |
9.44 |
8.15 |
8.88 |
| 0.3 |
4.03 |
6.65 |
6.87 |
6.86 |
| 0.4 |
3.70 |
4.63 |
7.46 |
6.58 |
| 0.5 |
3.82 |
3.36 |
9.42 |
7.39 |
| 0.6 |
4.51 |
2.48 |
13.03 |
9.36 |
| 0.7 |
6.16 |
1.81 |
19.41 |
13.20 |
| 0.8 |
9.75 |
1.28 |
32.19 |
21.40 |
| 0.9 |
20.11 |
0.85 |
69.52 |
46.76 |
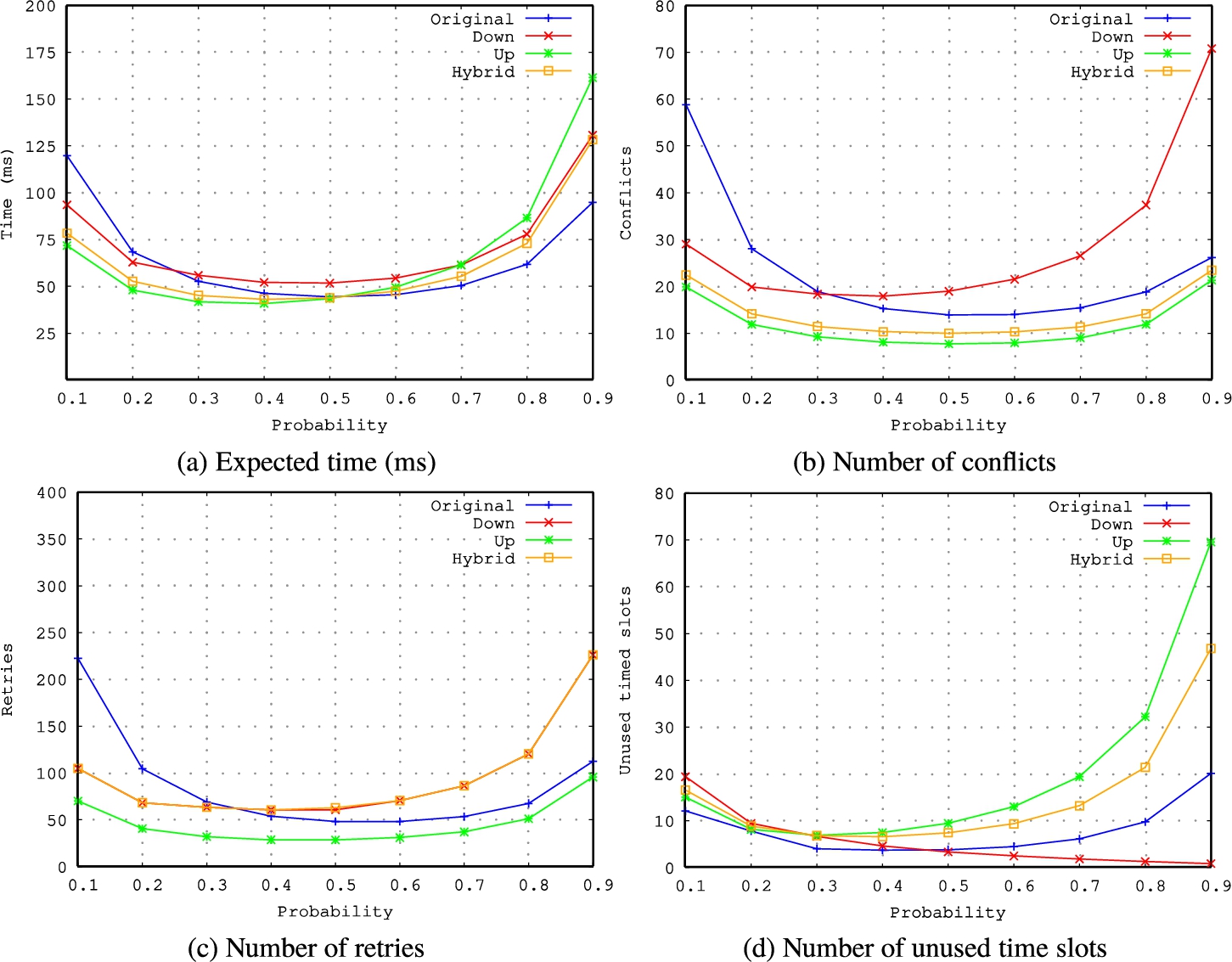
Fig. 10
Comparative among new proposals.
The original algorithm of Royo
et al. works with
${p_{\mathit{TC}}}=0.5$ and we proved in our previous work that this probability achieved the best results. With the new model of the protocol presented in this paper, as expected, the conclusion is confirmed and the
${p_{\mathit{TC}}}=0.5$ is again the best option in the original algorithm as we can see in Table
3. Moreover, by analysing Fig.
10 and Table
4 we can obtain important conclusions for each parameter evaluated:
-
(a) Expected time: The version 2CS-Up (with priorities from 0.3 to 0.5) and the version 2CS-Hybrid (with priorities 0.4 and 0.5) show better results than those obtained in the original 2CS protocol using its best priority (${p_{\mathit{TC}}}=0.5$). The best result (40.92 ms) is obtained in the version 2CS-Up with ${p_{\mathit{TC}}}=0.4$. This decreases by $7.85\% $ the result obtained in the original 2CS protocol.
-
(b) Number of conflicts: Both, the version 2CS-Up (with priorities from 0.2 to 0.8) and the version 2CS-Hybrid (with priorities from 0.3 to 0.7) minimize the number of conflicts that happened in the original version using its best priority (${p_{\mathit{TC}}}=0.5$). The best result of expected conflicts (7.72) is obtained in the version 2CS-Up using a probability ${p_{\mathit{TC}}}=0.5$. This decreases by $44.60\% $ the result obtained in the original 2CS protocol.
-
(c) Number of retries: Note that the graphics of version 2CS-Down and 2CS-Hybrid show very close results so that only one of them can be seen in Fig.
10. Only working with the version 2CS-Up with probabilities from
${p_{\mathit{TC}}}=0.2$ to
${p_{\mathit{TC}}}=0.7$ obtain better results with the original 2CS protocol using its best priority in this case (
${p_{\mathit{TC}}}=0.6$). The best result of retries (28.59) is obtained in the version 2CS-Up using a probability
${p_{\mathit{TC}}}=0.5$. This decreases by
$40.74\% $ the result obtained in the original 2CS protocol.
-
(d) Number of unused time slots: This parameter is improved with the version 2CS-Down with probabilities higher than 0.5, increasing as the probability increases.
According to this information, we finally analyse the version 2CS-Up with
${p_{\mathit{TC}}}=0.4$ and with
${p_{\mathit{TC}}}=0.5$ in order to choose the best option based on the time and energy consumption and comparing the results with respect to the original 2CS protocol (with
${p_{\mathit{TC}}}=0.5$):
-
• 2CS-Up, ${p_{\mathit{TC}}}=0.4$: it decreases the time by $7.85\% $, the conflicts by $41.79\% $ and the retries by $40.47\% $.
-
• 2CS-Up, ${p_{\mathit{TC}}}=0.5$: it decreases the time by $2.19\% $, the conflicts by $44.60\% $ and the retries by $40.78\% $.
Therefore, we must recommend the version 2CS-Up with
${p_{\mathit{TC}}}=0.4$, which reduces the elapsed time by early
$8\% $ and the number of retries and conflicts more than
$40\% $ compared to the original 2CS version.
The fact that the alternative with the best results is 2CS-Up gives us information about the behaviour of the algorithm of great importance: its best behaviour is achieved by two actions, namely distributing the nodes as much as possible and forcing them to go up quickly (small probability ${p_{\mathit{TC}}}$). In addition, with a higher distribution of the nodes in the waiting cells, the time to resolve the conflict may not always improve, but the reduction in the number of conflicts and in the number of retries is significant, which helps us achieve one of our main objectives: to reduce energy consumption by reducing these two parameters.
Although we have managed to find an alternative that improves the protocol, we continue to look for better options, but with less satisfactory results. Firstly, we tried to work with random probabilities, but this option quickly found the problem of the state space explosion problem, so we could not get results. Secondly, we proposed to include adaptive probabilities in the model. In this alternative, each node was able to adapt its probability according to the number of nodes that are in its situation, that is, the probability that a node decides to move or remain in a cell depends on the number of nodes that are currently in the cell where that node is located. This proposal seemed promising but when we tried to implement it we found a problem that we could not solve: a node is not aware of the activity of the other nodes, therefore, it knows neither where the nodes are located nor how many nodes are in a cell. Consequently, we were finally forced to discard this alternative because although our system can model it, it is not in line with the situation of the real system.
6 Related Work
First, it is worthwhile to mention the original paper (Paterakis and Papantoni-Kazakos,
1989) and the work of Royo
et al. (
2009). In this paper, the authors gather the main advantages of a protocol for wired networks (2-CS) and they adapt it to the particularities of a wireless medium. Starting from it, we modelled in Mateo
et al. (
2015), Ruiz
et al. (
2016) 2CS-WSN by using Discrete Time Markov chains. In those papers, we evaluated the system as a whole, that is, in our formal model, we studied each cell in particular and the probabilities of moving between cells. In this paper, the approach is totally different. Here, we do not model the system as a whole, but, on the contrary, we consider here each node in the collision which allows the investigation of the behaviour of each node. Only with this new perspective it is possible to propose the new alternatives presented in this paper. A quantitative study of the original protocol with this perspective, using Markov Decision Processes (MDP), can be found in Patel and Patel (
2015). This work is based on our previous works (Mateo
et al.,
2015; Ruiz
et al.,
2016), following the same lines to describe and analyse the protocol. The main difference of our work is that this work focus on studying properties of an individual node and uses on-the-fly symmetry reduction approach to prevent the state space explosion, but it does not propose new alternatives to improve the protocol.
Due to the probabilistic behaviour of algorithms (or protocols) used in any of the layers of wireless sensor networks stack, probabilistic model checking and Markov chains have been used to study and analyse a wide range of them. For instance, in Gallina
et al. (
2012), a framework to automatically evaluate the performance of Mobile Ad-hoc Networks in terms of different kinds of metrics, such as throughput and energy consumption, is presented. Using a probabilistic process calculus called PEBUM, Markov Decision Processes (MDPs) and PRISM, they evaluate the network performance in terms of time and energy costs. In Duflot
et al. (
2010), Duflot
et al. focus on the applicability of these techniques to the analysis of communication protocols. In this chapter of book, they advocate the use of formal methods and, in particular, probabilistic model checking due to the presence of concurrency, real-time constraints and randomization. They study the IEEE 802.3 (CSMA/CD) protocol as a case study. Yüksel
et al. (
2012) apply stochastic model checking in an area not widely explored such as security. In particular, they propose a new method for the process of key update in Zigbee and, using stochastic model checking, they find the optimal strategy in this process. Finally, let us remark a complete PhD Thesis in this topic (Fruth,
2011) where a big spectrum in the analysis of wireless sensor networks is covered showing the suitability of this approach in real scenarios. More recently, in Kapus (
2017) shows how PRISM is applied successfully for the validation of the analytical performance model derived in the work of Buratti and Verdone (
2009), where analytical model for the non beacon-enabled mode of the IEEE 802.15.4 medium access control protocol is provided.
Other related works include (Kauer
et al.,
2016), where Kauer
et al. perform a formal analysis of the DSME GTS reservation process and propose means to detect inconsistencies faster. The UPPAAL tool environment for verification of systems of timed automata is used to model the allocation and deallocation of GTSs. This model is used to prove that DSME resolves all inconsistencies in a bounded time span. Since in Dombrowski
et al. (
2016), Dombrowski
et al. advocate the use of probabilistic model checking in the design phase for safety critical systems. Here, they use Probabilistic Timed Automata (PTA) for the analysis of an ultra-reliable low-latency wireless protocol called EchoRing. Finally, in Siddique
et al. (
2017), the authors formally study network dependability, providing a formal specification of double-rings with dual attachments (DRDA) topologies of optical networks using Continuous-Time Markov Chains.
Furthermore, as related work about IoT and PRISM, in Mohsin
et al. (
2017) we can find a framework for formally quantifying risk in Internet of Things applications, using PRISM as the underlying probabilistic model checker.
7 Conclusions and Future Work
It is a fact that the massive use of IoT has brought a revolution in the use of the WSNs and the need to design new protocols. In spite of how fast these changes take place, these protocols must not only be correct, but they also must fulfil the new constraints, therefore, studying them in depth becomes a necessity. Specifically, in this work, we have studied a MAC layer protocol for WSN, 2CS-WSN, and we have presented new different proposals to improve this protocol in terms of energy and time consumption. We have used Probabilistic Model Checking in our study and analysis.
We have taken advantage of the utility of model checking as a perfect help to conventional analysis methods that rely on simulators. We have used model checking to study performance profiles which exhaustively ranges over worst- and best-case behaviour and perfectly complements the analysis carried out by simulators. Specifically, we show the use of probabilistic model checking in the sensor networks through the study of 2CS-WSN, a collision resolution protocol for them. Concretely, we have modelled 2CS-WSN protocol in terms of Probabilistic Model Checking using PRISM tool, but taking into account the behaviour of the system by modelling the particular behaviour of each node in contrast to our previous works where we consider the behaviour of the system as a whole. This new perspective has allowed to analyse three new alternatives to the protocol studied: 2CS-Down, 2CS-Up and 2CS-Hybrid. All of them have been studied in detail and compared with the original protocol finding that the best proposal is 2CS-Up with ${p_{\mathit{TC}}}=0.4$, which reduces the elapsed time by early $8\% $ and the number of retries more than $40\% $ compared to the original 2CS version. The possibility of adding adaptive and/or random probabilities to the model has also been analysed, but these alternatives had to be discarded by the characteristics of the system.
The success of this work lies mainly in the close relationship with the designers of the 2CS protocol, in two directions, initially thanks to their collaboration to validate our model and, finally, with our contribution by proposing an alternative (2CS-Up with ${p_{\mathit{TC}}}=0.4$) which will improve the protocol.
This methodology can be also applied in other algorithms/protocols relative to sensors where the probability has a crucial role. Due to the uncertainties underlying wireless communication which relies as much on the random faults intrinsic to the wireless medium as on the internal algorithms, it is a suitable field to continue our work. Specifically, we intend to use this methodology to study the protocols emerged in Novel communication standards like Bluetooth Low Energy (BLE), also known as Bluetooth Smart (BS) (Townsend
et al.,
2014) which is experiencing a significant growth by means of deploying networks based on low-cost and low-power. BLE standard offers the possibility to perform communication under such a wide range of configurations, being its selection criteria typically dependant on the final application purpose, therefore, it seems interesting to be able to carry out evaluations with different configurations before its implementation.
Acknowledgements
This study was funded in part by the Spanish Ministry of Science and Innovation and the European Union FEDER Funds under Grant TIN2015-65845-C3-2-R and also by the JCCM regional project SBPLY/17/180501/000276, which is also co-financed by the European Union FEDER Funds.
References
Boulis, A. et al. (2011). Castalia: a simulator for wireless sensor networks and body area networks.
NICTA: National ICT Australia,
83.
Buratti, C., Verdone, R. (2009). Performance analysis of IEEE 802.15.4 non beacon-enabled mode. IEEE Transactions on Vehicular Technology, 58(7), 3480–3493.
Camilli, M. (2015).
Coping with the State Explosion Problem in Formal Methods: Advanced Abstraction Techniques and Big Data Approaches. Thesis of Deptartment of Computer Science, Universita degli Studi di Milano.
Clarke, E.M., Grumberg, O., Peled, D.A. (2001). Model Checking. MIT Press.
Dombrowski, C., Junges, S., Katoen, J.-P., Gross, J. (2016). Model-checking assisted protocol design for ultra-reliable low-latency wireless networks. In: 2016 IEEE 35th Symposium on Reliable Distributed Systems (SRDS). IEEE, pp. 307–316.
Duflot, M., Kwiatkowska, M., Norman, G., Parker, D., Peyronnet, S., Picaronny, C., Sproston, J. (2010). FMICS Handbook on Industrial Critical Systems. In: Practical Applications of Probabilistic Model Checking to Communication Protocols. IEEE Computer Society Press, pp. 133–150.
Fruth, M. (2011).
Formal Methods for the Analysis of Wireless Network Protocols. PhD thesis, Oxford University.
Gallina, L., Han, T., Kwiatkowska, M.Z., Marin, A., Rossi, S., Spanò, A. (2012). Automatic energy-aware performance analysis of mobile ad-hoc networks. In: Proceedings of the IFIP Wireless Days Conference 2012, Ireland, November 21–23, 2012, pp. 1–6.
Hansson, H., Jonsson, B. (1994). A logic for reasoning about time and reliability. Formal Aspects of Computing, 6(5), 512–535.
Hortelano, D., Olivares, T., Ruiz, M.C., Garrido-Hidalgo, C., López, V. (2017). From sensor networks to internet of things. Bluetooth low energy, a standard for this evolution.
Sensors,
17(2).
Kapus, T. (2017). Using PRISM model checker as a validation tool for an analytical model of IEEE 802.15.4 networks. Simulation Modelling Practice and Theory, 77, 367–378.
Kauer, F., Köstler, M., Lübkert, T., Turau, V. (2016). Formal analysis and verification of the IEEE 802.15.4 dsme slot allocation. In: Proceedings of the 19th ACM International Conference on Modeling, Analysis and Simulation of Wireless and Mobile Systems, pp. 140–147.
Klein, J., Baier, C., Chrszon, P., Daum, M., Dubslaff, C., Märcker, S.K.S., Müller, D. (2017). Advances in probabilistic model checking with prism: variable reordering, quantiles and weak deterministic Büchi automata. International Journal on Software Tools for Technology Transfer, 20(2), 179–194.
Kwiatkowska, M., Norman, G., Parker, D. (2011). PRISM 4.0: verification of probabilistic real-time systems. In Proceedings of the 23rd International Conference on Computer Aided Verification (CAV’11),
LNCS, Vol. 6806. Springer, pp. 585–591.
Kwiatkowska, M., Norman, G., Parker, D. (2017). Probabilistic model checking: advances and applications. In: Formal System Verification, pp. 73–121.
Mateo, J.A., Macià, H., Ruiz, M.C., Calleja, J.L., Royo, F. (2015). Probabilistic model checking: one step forward in wireless sensor networks simulation. IJDSN, 11, 285396:1–285396:11.
Mohsin, M., Sardar, M.U., Hasan, O., Anwar, Z. (2017). oTRiskAnalyzer: A Probabilistic Model Checking Based Framework for Formal Risk Analytics of the Internet of Things.
IEEE Access, IEEE.
Patel, R., Patel, D. (2015). A quantitative analysis of collision resoluction protocol for wireless sensor network.
Journal of Software Engineering and Applications, 361–371.
Paterakis, M., Papantoni-Kazakos, P. (1989). A simple window random access algorithm with advantageous properties. IEEE Transactions on Information Theory, 35, 1124–1130.
Prabh, K.S., Royo, F., Tennina, S., Olivares, T. (2016). A MAC protocol for reliable communication in low power body area networks. Journal of Systems Architecture – Embedded Systems Design, 66–67, 1–13.
Rajbal, S., Rajba, T. (2012). The probability of collisions in wireless sensor network with random sending. Przegląd Elektrotechniczny, 88, 243–246.
Ross, S. (1996). Stochastic Processes. Wiley Series in Probabiliy and Mathematical Statistics.
Royo, F., López-Guerrero, M., Orozco-Barbosa, L., Olivares, T. (2009). 2C-WSN: a configuration protocol based on TDMA communications over WSN. In: Global Telecommunications Conference, GLOBECOM. IEEE, pp. 1–6.
Ruiz, M.C., Macià, H., Mateo, J.A., Calleja, F.J. (2016). Formal analysis of an energy-aware collision resolution protocol for wireless sensor networks. In: International Conference on Computational Science 2016, ICCS 2016, 6–8 June 2016. San Diego, California, USA, pp. 1191–1201.
Siddique, U., Hoque, K.A., Johnson, T.T. (2017). Formal specification and dependability analysis of optical communication networks. In: Design, Automation & Test in Europe Conference & Exhibition, DATE 2017, Lausanne, Switzerland, March 27–31, 2017, pp. 1564–1569.
Townsend, K., Cufí, C., Davidson, R. (2014). Getting Started with Bluetooth Low Energy: Tools and Techniques for Low-Power Networking.
Oreilly & Associates Incorporated.
Yüksel, E., Nielson, H.R., Nielson, F., Fruth, M., Kwiatkowska, M.Z. (2012). Optimizing zigbee security using stochastic model checking.
CoRR. abs/1205.6675.
Zheng, J., Jamalipour, A. (2009). Wireless Sensor Networks: A Networking Perspective. John Wiley & Sons.