1 Introduction
High mortality from cardiovascular diseases (CVD) is a major health problem in the Lithuanian male population. During the last decades, an increasing trend of CVD mortality was observed in Lithuanian men, reaching 728.9 deaths per 100000 population in 2015 and being one of the highest in Europe (Lithuanian Ministry of Health,
2016). Epidemiological studies have demonstrated that the prevalence of conventional CVD risk factors is also very high in the Lithuanian population (Rėklaitienė
et al.,
2012). Prognostic values of these risk factors for the development of CVD in Lithuania have been found to be comparable to those in other populations (Tamošiūnas
et al.,
2014; Kuzmickienė
et al.,
2013). However, the impact of specific lifestyle and biological risk factors on the prediction of mortality from CVD – and especially the prediction of the risk of CVD morbidity – is still underestimated not only in Lithuania, but in other Baltic countries as well.
Regression analysis and classification can be performed using a popular statistical learning method called recursive partitioning (Kerdprasop and Kittisak,
2011; Strobl
et al.,
2009; Hothorn
et al.,
2006). Problems related to the analysis of data on health and the risk of mortality and morbidity could also be solved by other modern methods of statistical analysis, such as artificial neural networks, support vector machines, ensemble methods employing bagging and boosting algorithms – but recursive partitioning has a distinct feature. In contrast to many “black box” methods in which the internal logic can be difficult to work out, recursive partitioning offers a result as a simple human readable representation having a shape of a tree (Jing,
2013; Breiman
et al.,
1984; Zhao
et al.,
2016). Therefore, these methods are also called
decision trees. Statistical data analysis techniques usually put some restrictions on the sample: normality, homoscedasticity, independence, etc. Hypothesis testing is a common step performed before the application of some statistical methods. The model is considered valid if these assumptions are satisfied.
This approach is not used in data mining and machine learning algorithms. Nevertheless, there is a need to validate the results using these techniques as well. Cross-validation (CV) is a common accuracy assessment technique for machine learning algorithms (Han
et al.,
2012). CV is used to estimate the precision of the models.
Logistic regression is the most common method used to model CVD. The main purpose of this article was to compare the traditional binary logistic regression (LR) analysis with the decision tree (DT) analysis for the evaluation of the risk of CVD in adult men living in the city. For this purpose, we selected the conditional inference tree method which is not often used for comparison.
2 Materials and Methods
2.1 Study Population
In our study, we used data from the Multifactorial Ischemic Heart Disease Prevention Study (MIHDPS). In the MIHDPS study, a random sample of male inhabitants of Kaunas city (Lithuania) aged 40–59 years was examined (between 1977 and 1980). The initial survey included 5933 men (participation rate – 69.8%). We excluded 307 men because of duplicates or incomplete information on variables used in the current analysis. The final number of participants included in the current analysis was 5626. The same sample was used for both logistic regression and decision tree models.
This study was based on voluntary, informed participation. The participants did not provide written consent prior to the baseline examination, as this was not required in the former Soviet Union. The participants’ records and information were anonymized and de-identified prior to the analysis.
In this article, the conditional inference tree implemented in the party package of R statistical software will be used. Men with ischemic heart disease (IHD) (previous myocardial infarction (MI), angina pectoris, and ischemic changes in the electrocardiogram) or cardiovascular disease (IHD + stroke and intermittent claudication) were assigned to the case group, and the remaining subjects were assigned to the control group (men without IHD or CVD).
2.2 Measurements
Data were collected using a standard protocol and uniform methods of measurement. All participants underwent physical examination (total cholesterol level, blood pressure (BP), height, and weight measurements). BP was measured on the right brachial artery using a mercury sphygmomanometer and appropriately sized arm cuffs in the sitting position after 5 minutes of rest. The measurements were performed to the nearest 2 mmHg. The first Korotkoff phase was recorded as systolic BP, and the fifth Korotkoff phase was used to determine diastolic BP. The average of two measurements was used in the analysis. The height of the participants was measured with a stadiometer, approximating the measurements to the nearest centimeter. Weight was measured with standardized medical scales, with the patient wearing no shoes or heavy clothes, and the measurements were approximated to the nearest 0.1 kg. The body mass index (BMI) was calculated as weight in kilograms divided by height in meters squared (kg/m${^{2}}$).
Fasting serum samples were analyzed in the Laboratory of the Institute of Cardiology, the Lithuanian University of Health Sciences. Total serum cholesterol concentration was measured by applying the method proposed by Huang
et al. (
1961). Fasting glucose concentration was directly determined in serum by using the ortho-toluidine technique (Glasunov
et al.,
1981).
A standard questionnaire was applied to obtain data on the respondents age, physical activity, smoking status, alcohol consumption, the use of antihypertensive, lipid-lowering, or antidiabetic medications, and family history of CVD. Physical activity was assessed by hours spent for moderate physical activity (walking, standing, and sitting) per working day and hours per week spent for this activity during the leisure-time. The respondents were categorized into two groups according to their level of physical activity during working days and during leisure time: active (⩾10 hours/week) and inactive (<10 hours/week). According to the frequency of alcohol consumption, the respondents were classified into six groups: never or former drinkers, those consuming alcoholic beverages less frequently than once per month, 1–3 times per month, once per week, 2–3 times per week, several times per week, or daily. We also grouped the participants into two groups according to the reported frequency of alcohol: never-drinkers or former drinkers, and drinkers. According to the smoking habits, the participants were categorized as never-smokers, those smoking sometimes but not every day, daily smokers and quitters.
IHD at baseline was determined by: 1) a documented history of MI and/or ischemic changes on electrocardiogram (ECG) coded by Minnesota codes (MC) 1-1 or 1-2 (Prineas
et al.,
1982); 2) angina pectoris as defined by G. Rose’s questionnaire (without MI and/or MC 1-1 or 1-2) (Rose
et al.,
1982); 3) ECG findings coded by MC 1-3, 4-1, 4-2, 4-3, 5-1, 5-2, 5-3, 6-1, 6-2, 7-1, or 8-3 (without MI and/or MC 1-1, 1-2 and without angina pectoris). Previous stroke was determined on the basis of the documented history of stroke.
The information on family history MI, stroke, and sudden death was evaluated among first-degree relatives only: parents (father and mother) and siblings (brothers and/or sisters). The following questions were asked: “Did your father ever experience MI (stroke or sudden death)?”, “Did your mother ever experience MI (stroke or sudden death)?”, “Did your brother ever experience MI (stroke or sudden death)?”, and “Did your sister ever experience MI (stroke or sudden death)?” We also used a combined family history variable – family history of CVD – which included a history of MI and/or stroke and/or sudden death in at least one of the parents or siblings. According to the family history variable, the participants were categorized as having one or more parents or siblings with CVD and those without any first-degree relatives with CVD.
2.3 Statistical Analysis
Firstly, we calculated descriptive statistics of the variables. Quantitative variables were described as median, minimum, and maximum because variable distributions did not satisfy the normality assumption (Kolmogorov–Smirnov Test). Nonparametric Mann-Whitney U test was used to determine differences in the distributions of continuous variables between control (men without IHD or CVD) and case (men with IHD or CVD) groups. Qualitative variables were described using frequencies. The Chi-squared test was used to determine differences in categorical variables between the control and the case groups. Univariate and multivariate binary logistic regression analysis were used.
2.4 Logistic Regression
Binary logistic regression analysis is a non-linear regression technique that assumes that the expected probability of a binary outcome is:
where the
${X_{n}}$ are variables with numeric values (if binary, they are zero for control and one for case) and the
${\beta _{n}}$ are the regression coefficients that quantify their contribution to the probability (Long
et al.,
1993). Univariate binary logistic regression analysis was performed to identify the impact of clinical and lifestyle factors on the prevalence of IHD and CVD. Multiple logistic regression analysis was used to build the final model. Variable selection for multiple logistic regression model was performed using bidirectional
stepwise procedure based on Akaike information criterion (AIC) (Akaike,
1973).
Comparisons were expressed as odds ratios and 95% confidence intervals (95% CI) and Akaike information criterion:
$\mathit{AIC}=2k-2\ln (L)$, where
L – the value of the maximum likelihood function and
k – number of the estimated parameters in the model (Akaike,
1973).
A nonparametric receiver operating characteristic curve (ROC) was used to determine the discriminatory power of the represented model. A probability level of p-value < 0.05 was taken as statistically significant.
2.5 Decision Tree and Cross-Validation
Recursive partitioning is a greedy algorithm that splits data into partitions based on the values of a single variable. The splitting process is repeated recursively until some stop condition is satisfied, thus producing a tree-shaped model. If the number of the covariates is large enough, they also allow for producing a full-length tree, ending with a tree that contains a single class observation in each leaf. These trees have overfitting problems. An additional pruning procedure is necessary (Strobl
et al.,
2009).
Many recursive partitioning methods have a selection bias towards covariates with many possible splits and the problem of overfitting. The latter problem could be solved by using the tree pruning procedure. We used recursive partitioning (implemented in the
party package of R statistical software) based on conditional inference procedures. The selected method is based on a well-defined theory. It performs unbiased splitting selection and implements stop conditions based on the significance of the association between covariates and the response, thus eliminating overfitting and the need for tree pruning (Hothorn
et al.,
2006). In this regard, selected conditional inference tree method is superior to other DT methods (ex. CART, C4.5, C5.0, ID3).
There are many descriptions of the decision tree structure. Presented in short, the decision tree structure is the following. The topmost decision node in a tree is called the
root node; it corresponds to the best predictor. The final nodes are called
terminal nodes or
leaves. Every node, except for terminal nodes, contains a test condition and splits data into two or mode subsets based on the result of the test condition. Conditions are selected for the maximum separation of positive and negative classes in branches of the node. This procedure is applied recursively, thus creating possibly a good separation of the classes in the terminal nodes. The numbers after the predicted class for the terminal node indicate the probabilities of each class and allow to see
the probability of the winning class, that is, the factor that determines the final classification (WebFOCUS RStat,
2011).
The basic idea of cross-validation (e.g. Stone (
1974); Geisser (
1975)) is splitting data into subsets, where some subsets are used for fitting the model, and the rest of the data are used for the estimation of the prediction error. Statistical properties CV are then analysed – e.g. leave-one-out CV is asymptotically equivalent to the Akaike Information Criterion (Akaike,
1973). Leave-one-out CV splits the data into smallest subsets containing a single observation. One observation is used for model error estimation, and the rest of the data are used for fitting the model. This procedure is repeated for every observation. Leave-one-out CV is a computationally intensive method. Another popular CV algorithm is
k-fold CV. Data are split into equal-size
k subsets (folds). A single subset is used for error estimation, and the rest are used for fitting the model. Leave-one-out CV can be considered a special case of
k-fold CV in which the number of folds is equal to the sample size (Schneider,
1997). In this paper, 10-fold CV is used to estimate the prediction error for both logistic regression and decision tree models. Value
$k=10$ is a common choice recommended by a number of authors (e.g. Han
et al. (
2012); Witten
et al. (
2011)).
3 Results
Clinical characteristics of the patients are presented in Table
1. Glucose level after a 2-hour load did not differ significantly between patients with and without CVD (
p-value = 0.074). Smoking at present and physical activity in the summer did not differ significantly between patients with and without IHD (
p-values: 0.114 and 0.069, respectively). The proportions of MI and diabetes in the subjects’ mothers did not differ significantly between patients with and without CVD (
p-values: 0.066 and 0.167, respectively) or IHD (
p-values: 0.062 and 0.195, respectively) either. All the remaining variables differed statistically significantly between the case and the control groups (all
p-values were smaller than 0.05).
Table 1
Clinical characteristics of the patient with IHD or CVD and without IHD or CVD.
|
Ischemic heart disease (IHD) |
Cardiovascular disease (CVD) |
| Variable |
Yes $(N=612)$
|
No $(N=5014)$
|
p-value |
Yes $(N=674)$
|
No $(N=4952)$
|
p-value |
| Systolic blood pressure (SBP), mm Hg, median (min; max) |
141 (93; 240) |
133 (88; 236) |
<0.001${^{a}}$
|
141 (93; 240) |
133 (88; 236) |
<0.001a
|
| Diastolic blood pressure (DBP), mm Hg, median (min; max) |
90 (56;150) |
86 (47; 142) |
<0.001a
|
90 (56; 150) |
86 (47; 142) |
<0.001a
|
| Skinfold thickness – triceps (STT), mm, median (min; max) |
10.2 (1; 38.2) |
9.8 (1; 39.4) |
0.006a
|
10.2 (1; 38.2) |
9.8 (1; 39.4) |
0.004a
|
| Skinfold thickness – scapula (STS), mm, median (min; max) |
17.2 (2.4; 40) |
15.4 (1.6; 40) |
<0.001a
|
17.2 (2.4; 40) |
15.4 (1.6; 40) |
<0.001a
|
| Serum cholesterol (Cholesterol), mmol/L, median (min; max) |
6.1 (2.8; 10.2) |
5.9 (1.4; 13.2) |
0.014a
|
6.1 (2.8; 12.7) |
5.9 (1.4; 13.2) |
0.002a
|
| Glucose level after 2-hour load (Glucose), mmol/L, |
| median (min; max) |
7.5 (2.4; 19.3) |
7.2 (1.8; 19.9) |
0.010a
|
7.4 (2.4; 19.3) |
7.2 (1.8; 19.9) |
0.074a
|
| Mother alive (MA), n (%): No
|
351 (57.35) |
2522 (50.30) |
|
388 (57.57) |
2485 (50.18) |
|
| Yes |
257 (41.99) |
2454 (48.94) |
0.004b
|
282 (41.84) |
2429 (49.05) |
0.002b
|
| I don’t know |
4 (0.65) |
38 (0.76) |
|
4 (0.59) |
38 (0.77) |
|
| Mother’s myocardial infarction (MMI), n (%): No
|
569 (92.97) |
4747 (94.67) |
|
628 (93.18) |
4688 (94.67) |
|
| Yes |
26 (4.25) |
130 (2.59) |
0.062b
|
28 (4.15) |
128 (2.58) |
0.066b
|
| I don’t know |
17 (2.78) |
137 (2.73) |
|
18 (2.67) |
136 (2.75) |
|
| Number of brothers and sisters at present (NBSP), |
| median (min; max) |
2 (0; 12) |
2 (0; 16) |
<0.001a
|
2 (0; 12) |
2 (0; 16) |
<0.001a
|
| Increased blood pressure (IBP), n (%): No
|
414 (67.65) |
4095 (81.67) |
<0.001b
|
458 (67.95) |
4051 (81.81) |
<0.001b
|
| Yes |
198 (32.35) |
919 (18.33) |
|
216 (32.05) |
901 (18.19) |
<0.001b
|
| Blood pressure-lowering medicine (MLBP), n (%): No
|
505 (82.52) |
4709 (93.92) |
<0.001b
|
555 (82.34) |
4659 (94.08) |
<0.001b
|
| Yes |
107 (17.48) |
305 (6.08) |
|
119 (17.66) |
293 (5.92) |
| Last intake of medicine (LMWA), weeks ago, |
| median (min; max) |
0 (0; 9) |
0 (0; 9) |
<0.001a
|
0 (0; 9) |
0 (0;9) |
<0.001a
|
| Disability group (Disability), n (%):No
|
536 (87.58) |
4797 (95.67) |
<0.001b
|
582 (86.35) |
4751 (95.94) |
<0.001b
|
| Yes |
76 (12.42) |
217 (4.33) |
|
92 (13.65) |
201 (4.06) |
|
| Smoking habits (Smoking), n (%): Never smoked
|
161 (26.31) |
1516 (30.24) |
|
173 (25.67) |
1504 (30.37) |
|
| Not every day |
15 (2.45) |
135 (2.69) |
0.114b
|
16 (2.37) |
134 (2.71) |
0.032b
|
| Regular smokers and quitters |
436 (71.24) |
3363 (67.07) |
|
485 (71.96) |
3314 (66.92) |
|
| Alcohol drinking (Alcohol), n (%): No
|
89 (14.54) |
385 (7.68) |
<0.001b
|
106 (15.73) |
368 (7.43) |
<0.001b
|
| Yes |
523 (85.46) |
4629 (92.32) |
|
568 (84.27) |
4584 (92.57) |
|
| Number of working days per week (NWDPW), |
| median (min; max) |
5 (0; 7) |
5 (0; 7) |
<0.001a
|
5 (0; 7) |
5 (0; 7) |
<0.001a
|
| Walking in summer (WSHPW), hours per week, |
| median (min; max) |
6 (0; 30) |
4 (0; 32) |
0.004a
|
5.5 (0; 30) |
4 (0; 32) |
0.002a
|
| Walking in winter (WWHPW), hours per week, |
| median (min; max) |
4 (0; 30) |
3 (0; 30) |
0.002a
|
4 (0; 30) |
3 (0;30) |
0.001a
|
| Physical activity in summer (PASHPW), |
| hours per week, median (min; max) |
7 (0; 30) |
7 (0; 32) |
0.069a
|
7 (0; 30) |
7 (0; 32) |
0.024a
|
| BMI, kg/${m^{2}}$, median (min; max) |
28.2 (17.6; 42.9) |
27.1 (17; 47.6) |
<0.001a
|
28.2 (17.6; 42.9) |
27.1 (14; 47.6) |
<0.001a
|
| Age, years, median (min; max) |
51.6 (39.7;62.8) |
49.1 (38.6; 61.9) |
<0.001a
|
51.8 (39.7; 62.8) |
49.1 (38.6; 61.9) |
<0.001a
|
| Intermittent claudication (Claudication), n (%): No
|
596 (97.39) |
4976 (99.24) |
<0.001b
|
– |
– |
|
| Yes |
16 (2.61) |
38 (0.76) |
|
|
|
|
| Diabetes, n (%): No
|
602 (98.37) |
4965 (99.02) |
0.195b
|
663 (98.37) |
4904 (99.03) |
0.167b
|
| Yes |
10 (1.63) |
49 (0.97) |
|
11 (1.63) |
48 (0.97) |
|
Table 2
One variable binary logistic regression analysis for the identification of clinically important factors for ischemic heart disease.
| Variable |
Coef. |
OR (95% CI) |
AIC |
AUC |
p-value |
| Systolic blood pressure (SBP), mm Hg |
0.022 |
1.022 (1.018; 1.026) |
3751 |
0.615 |
<0.001 |
| Diastolic blood pressure (DBP), mm Hg |
0.032 |
1.032 (1.025; 1.039) |
3788 |
0.596 |
<0.001 |
| Skinfold thickness – triceps (STT), mm |
0.029 |
1.029 (1.011; 1.047) |
3864 |
0.534 |
0.001 |
| Skinfold thickness – scapula (STS), mm |
0.039 |
1.040 (1.027; 1.053) |
3836 |
0.576 |
<0.001 |
| Serum cholesterol (Cholesterol), mmol/L |
0.101 |
1.107 (1.028; 1.191) |
3867 |
0.530 |
0.007 |
| Glucose level after 2-hour load |
| (Glucose), mmol/L |
0.036 |
1.037 (1.006; 1.068) |
3869 |
0.532 |
0.017 |
| Mother alive (MA) |
| MA = Yes
|
−0.284 |
0.752 (0.634; 0.892) |
3865 |
0.536 |
0.001 |
| MA = I don’t know
|
−0.279 |
0.756 (0.226; 1.896) |
|
|
0.597 |
| Mother’s myocardial infarction (MMI) |
| MMI = Yes
|
0.512 |
1.669 (1.063; 2.521) |
3871 |
0.509 |
0.012 |
| MMI = I don’t know
|
0.035 |
1.035 (0.599; 1.677) |
|
|
0.894 |
| Number of brothers and sisters |
| at present (NBSP) |
−0.069 |
0.933 (0.893; 0.973) |
3864 |
0.542 |
0.002 |
| Increased blood pressure (IBP) |
| IBP = Yes
|
0.757 |
2.131 (1.771; 2.558) |
3814 |
0.570 |
<0.001 |
| Blood pressure-lowering medicine (MLBP) |
| BPLM = Yes
|
1.185 |
3.271 (2.568; 4.140) |
3793 |
0.557 |
<0.001 |
| Last intake of medicine |
| (LMWA), weeks ago |
0.092 |
1.096 (1.053; 1.139) |
3856 |
0.533 |
<0.001 |
| Disability group (Disability) |
| Disability = Yes
|
1.142 |
3.134 (2.366; 4.113) |
3819 |
0.540 |
<0.001 |
| Smoking habits (Smoking) |
| Smoking = Not every day
|
0.045 |
1.046 (0.576; 1.772) |
3872 |
0.521 |
0.874 |
| Smoking = Regular smokers and quitters
|
0.199 |
1.221 (1.011; 1.481) |
|
|
0.040 |
| Alcohol drinking (Alcohol) |
| Alcohol = Yes
|
−0.716 |
0.489 (0.383; 0.629) |
3846 |
0.534 |
<0.001 |
| Number of working (NWDPW), days/week |
−0.252 |
0.777 (0.726; 0.834) |
3831 |
0.533 |
<0.001 |
| Walking in summer (WSHPW), hours/week |
0.019 |
1.019 (1.006; 1.032) |
3866 |
0.535 |
0.004 |
| Walking in winter (WWHPW), hours/week |
0.021 |
1.021 (1.006; 1.035) |
3866 |
0.537 |
0.004 |
| Physical activity in summer, |
| (PASHPW) hours/week |
−0.008 |
0.992 (0.981; 1.002) |
3872 |
0.522 |
0.110 |
| BMI, kg/m${^{2}}$
|
0.076 |
1.079 (1.056; 1.103) |
3828 |
0.582 |
<0.001 |
| Age, years |
0.070 |
1.073 (1.056; 1.089) |
3791 |
0.611 |
<0.001 |
| Intermittent claudication (Claudication) |
| Claudication = Yes
|
1.257 |
3.515 (1.896; 6.226) |
3860 |
0.509 |
<0.001 |
| Diabetes |
| Diabetes = Yes
|
0.521 |
1.683 (0.800; 3.199) |
3872 |
0.503 |
0.136 |
A binary logistic regression model was used to identify risk factors related to IHD and CVD. From a set of variables (Tables
2,
4), the following variables remained as independent variables in the final model (multiple analysis) (Tables
3,
5): systolic blood pressure (SBP), the number of brothers and sisters at present (NBSP), usage of blood pressure-lowering medicines (MLBP), disability group (Disability), alcohol drinking (Alcohol), body mass index (BMI), the patient’s age (Age), and intermittent claudication (Claudication) for IHD, and systolic blood pressure (SBP), serum cholesterol (Cholesterol), number of brothers and sisters at present (NBSP), usage of blood pressure-lowering medicines (MLBP), disability group (Disability), alcohol drinking (Alcohol), smoking habits (Smoking), number of working days per week (NWDPW), time for walking in winter (WWHPW), body mass index (BMI), and the patient’s age (Age) for CVD.
Taking BPLM, disability, intermittent claudication, regular smoking, and higher value of BMI, SBP, age, serum cholesterol, and walking in winter were associated with a higher probability of IHD or CVD (equations (
1) and (
2) are binary logistic regression equations, where
$\widehat{P}$ is the estimate of probability). However, a higher number of brothers and sisters and alcohol drinking were associated with a lower probability of these diseases.
Our binary logistic regression models showed the power (IHD – AUC = 0.688 and CVD – AUC = 0.696) to discriminate IHD or CVD in the Lithuanian sample of middle-aged men (Tables
3,
5).
Conditional inference tree, calculated using R function ctree package party, method was used to build a decision tree. This method performs variable selection for tree splitting based on statistical criterion. A typical significance level value $\alpha =0.05$ was used.
Table 3
Multiple binary logistic regression analysis for the identification of clinically important factors for ischemic heart disease.
| Variable |
Coef. |
OR |
Lower |
Upper |
p-value |
| Systolic blood pressure (SBP), mm Hg |
0.012 |
1.012 |
1.008 |
1.017 |
<0.001 |
| Number of brothers and sisters at present (NBSP) |
−0.065 |
0.937 |
0.896 |
0.979 |
0.004 |
| Blood pressure-lowering medicine (MLBP) |
| MLBP = Yes
|
0.847 |
2.333 |
1.611 |
3.346 |
<0.001 |
| Disability group (Disability) |
| Disability = Yes
|
0.673 |
1.959 |
1.394 |
2.722 |
<0.001 |
| Alcohol drinking (Alcohol) |
| Alcohol = Yes
|
−0.461 |
0.631 |
0.482 |
0.834 |
0.001 |
| BMI, kg/m${^{2}}$
|
0.046 |
1.047 |
1.023 |
1.071 |
<0.001 |
| Age, years |
0.050 |
1.051 |
1.035 |
1.069 |
<0.001 |
| Intermittent claudication (Claudication) |
| Claudication = Yes
|
0.805 |
2.236 |
1.150 |
4.144 |
0.013 |
Table 4
One variable binary logistic regression analysis for the identification of clinically important factors for cardiovascular disease.
| Variable |
Coef. |
OR (95% CI) |
AIC |
AUC |
p-value |
| Systolic blood pressure (SBP), mm Hg |
0.021 |
1.021 (1.017; 1.025) |
4008 |
0.609 |
<0.001 |
| Diastolic blood pressure (DBP), mm Hg |
0.030 |
1.031 (1.024; 1.037) |
4044 |
0.594 |
<0.001 |
| Skinfold thickness– triceps (STT), mm |
0.029 |
1.029 (1.012; 1.046) |
4117 |
0.534 |
0.001 |
| Skinfold thickness – scapula (STS), mm |
0.038 |
1.039 (1.026; 1.051) |
4090 |
0.575 |
<0.001 |
| Serum cholesterol (Cholesterol), mmol/L |
0.124 |
1.132 (1.055; 1.214) |
4116 |
0.536 |
0.001 |
| Glucose level after 2-hour load, |
| (Glucose) mmol/L |
0.025 |
1.025 (0.996; 1.055) |
4125 |
0.521 |
0.093 |
| Mother alive (MA) |
| MA = Yes
|
−0.296 |
0.744 (0.631; 0.875) |
4117 |
0.537 |
<0.001 |
| MA = I don’t know
|
−0.394 |
0.674 (0.201; 1.689) |
|
|
0.456 |
| Mother myocardial infarction (MMI) |
| MMI = Yes
|
0.490 |
1.633 (1.056; 2.440) |
4125 |
0.508 |
0.962 |
| MMI = I don’t know
|
−0.012 |
0.988 (0.581; 1.583) |
|
|
0.962 |
| Number of brothers and sisters at present |
| (NBSP) |
−0.059 |
0.942 (0.904; 0.981) |
4120 |
0.538 |
0.004 |
| Increased blood pressure (IBP) |
| IBP = Yes
|
0.752 |
2.120 (1.774; 2.526) |
4064 |
0.569 |
<0.001 |
| Blood pressure-lowering medicine (MLBP) |
| MLBP = Yes
|
1.227 |
3.409 (2.670; 4.283) |
4035 |
0.559 |
<0.001 |
| Last intake of medicine |
| (LMWA) weeks ago |
0.104 |
1.109 (1.067; 1.151) |
4103 |
0.536 |
<0.001 |
| Disability group (Disability) |
| Disability = Yes
|
1.318 |
3.736 (2.867; 4.838) |
4045 |
0.548 |
<0.001 |
| Smoking habits (Smoking) |
| Smoking = Not every day
|
0.037 |
1.038 (0.583; 1.734) |
4123 |
0.525 |
0.893 |
| Smoking = Regular smokers and quitters
|
0.241 |
1.272 (1.061; 1.533) |
|
|
0.013 |
| Alcohol drinking (Alcohol) |
| Alcohol = Yes
|
−0.844 |
0.430 (0.342 ;0.545) |
4084 |
0.541 |
<0.001 |
| Number of working (NWDPW), days/week |
−0.285 |
0.752 (0.704; 0.804) |
4066 |
0.541 |
<0.001 |
| Walking in summer (WSHPW), hours/week |
0.020 |
1.020 (1.008; 1.033) |
4118 |
0.537 |
0.001 |
| Walking in winter (WWHPW), hours/week |
0.023 |
1.024 (1.010; 1.038) |
4117 |
0.540 |
0.001 |
| Physical activity in summer |
| (PASHPW), hours/week |
−0.010 |
0.990 (0.980; 1.000) |
4124 |
0.526 |
0.046 |
| BMI, kg/m${^{2}}$
|
0.075 |
1.078 (1.056; 1.100) |
4079 |
0.581 |
<0.001 |
| Age, years |
0.072 |
1.075 (1.060; 1.091) |
4032 |
0.615 |
<0.001 |
| Diabetes |
| Diabetes = Yes
|
0.528 |
1.695 (0.832; 3.158) |
4126 |
0.503 |
0.117 |
Table 5
Multiple binary logistic regression analysis for the identification of clinically important factors for cardiovascular disease.
| Variable |
Coef. |
OR |
Lower |
Upper |
p-value |
| Systolic blood pressure (SBP), mm Hg |
0.011 |
1.001 |
1.007 |
1.016 |
<0.001 |
| Serum cholesterol (Cholesterol), mmol/L |
0.112 |
1.119 |
1.039 |
1.204 |
0.003 |
| Number of brothers and sisters at present (NBSP) |
−0.055 |
0.947 |
0.907 |
0.987 |
0.011 |
| Blood pressure-lowering medicine (MLBP) |
| MLBP = Yes
|
0.7103 |
2.035 |
1.554 |
2.648 |
<0.001 |
| Disability group (Disability) |
| Disability = Yes
|
0.830 |
2.294 |
1.665 |
3.133 |
<0.001 |
| Smoking habits (Smoking) |
| Smoking = Regular smokers and quitters
|
0.237 |
1.267 |
1.047 |
1.540 |
0.016 |
| Alcohol drinking (Alcohol) |
| Alcohol = Yes
|
−0.618 |
0.539 |
0.417 |
0.702 |
<0.001 |
| Number of working days per week (NWDPW) |
−0.097 |
0.908 |
0.839 |
0.984 |
0.018 |
| Walking in winter (WWHPW), hours per week |
0.016 |
1.016 |
1.000 |
1.031 |
0.036 |
| BMI, kg/m${^{2}}$
|
0.051 |
1.052 |
1.029 |
1.076 |
<0.001 |
| Age, years |
0.531 |
1.055 |
1.038 |
1.071 |
<0.001 |
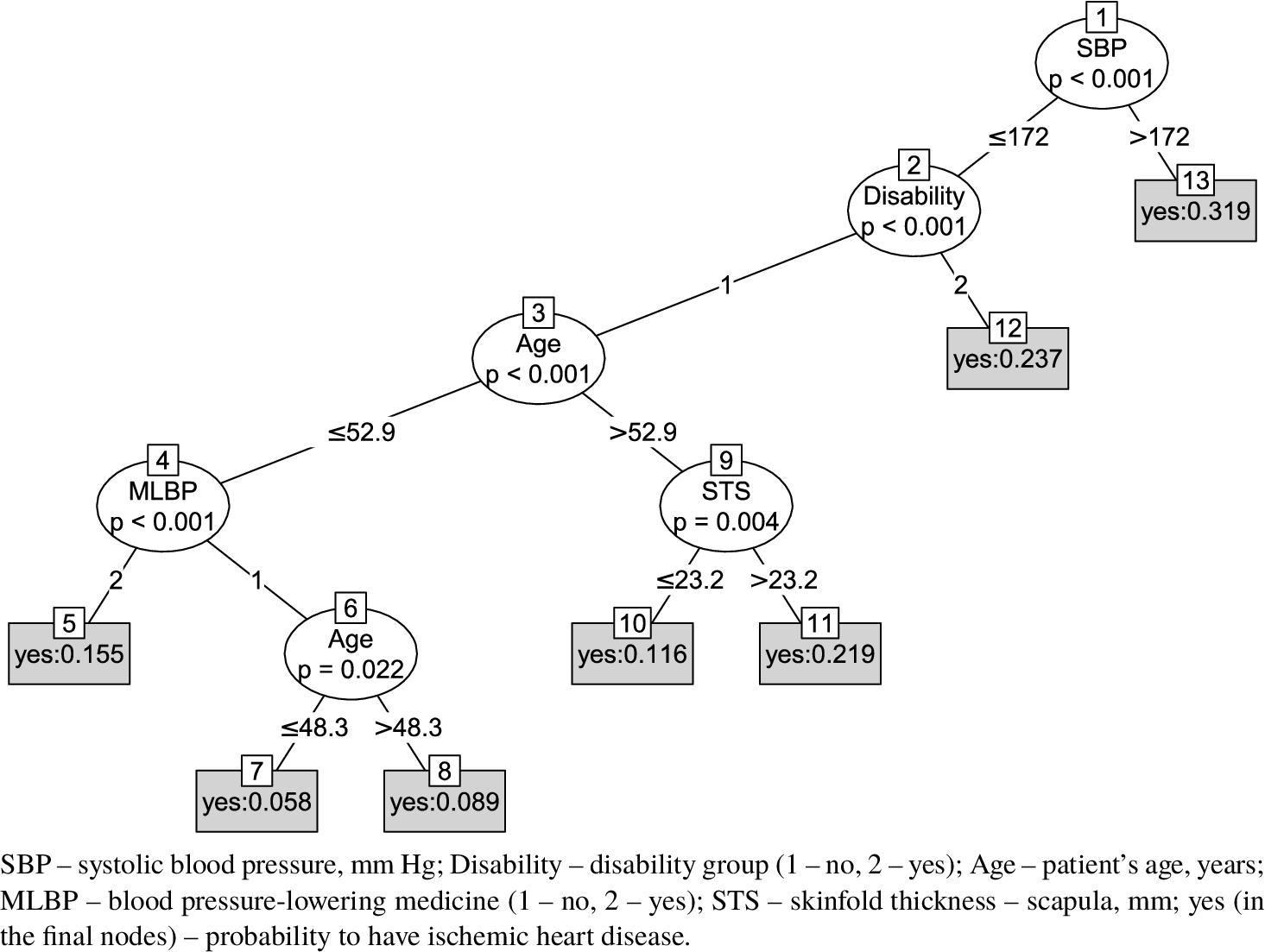
Fig. 1
Decision tree model for the prediction of ischemic heart disease.
Table 6
Errors of binary logistic regression and decision tree.
|
In-Sample |
10-fold CV |
|
MAE |
EER |
AUC |
MAE |
EER |
AUC |
|
IHD |
| Logistic regression |
0.18080 |
0.36993 |
0.68751 |
0.18213 |
0.38070 |
0.67438 |
| Decision tree |
0.18445 |
0.38424 |
0.66725 |
0.18592 |
0.40394 |
0.63402 |
|
CVD |
| Logistic regression |
0.19411 |
0.36650 |
0.69632 |
0.19514 |
0.37392 |
0.68277 |
| Decision tree |
0.19686 |
0.35762 |
0.69233 |
0.20089 |
0.38991 |
0.64624 |
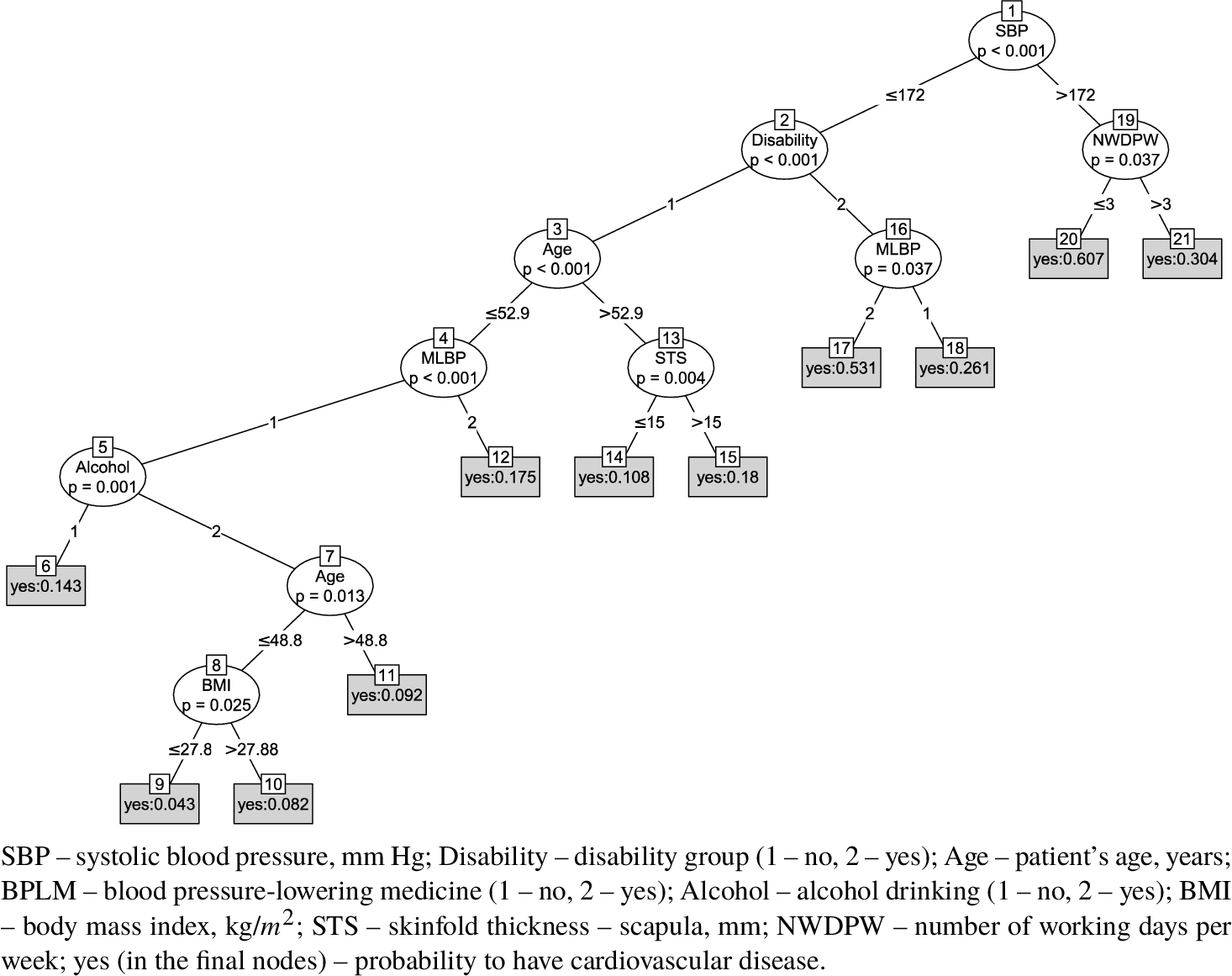
Fig. 2
Decision tree model for the prediction of cardiovascular disease.
Figures
1 and
2 show decision tree models for IHD (the number of nodes is 13) and CVD (the number of nodes is 21). For IHD and CVD, the root node performs branching based on SBP. It has two branches: ⩽172 mmHg and >172 mmHg. Terminal nodes 5, 7, 8, 10, 11, 12, and 13 are for IHD with the probability of the winning class: 0.155, 0.058, 0.089, 0.116, 0.219, 0.237, and 0.319, respectively. For CVD, the terminal nodes are 6, 9, 10, 11, 12, 14, 15, 17, 18, 20, and 21, and the probability of the winning class is 0.143, 0.043, 0.082, 0.092, 0.175, 0.108, 0.18, 0.531, 0.261, 0.607, and 0.304, respectively. Thus, the highest probability (0.319) to have IHD is when a person has high SBP (more than 172 mmHg and nodes 1 and 13). If a person’s data corresponds to nodes 1, 19, and 20, he or she has the a highest probability (0.607) to have CVD. The lowest probability (0.058) to have IHD is indicated by nodes 1, 2, 3, 4, 6, and 7, and the lowest probability to have CVD – by the presence of nodes 1, 2, 3, 4, 5, 7, 8, and 9 (the probability is 0.043).
The decision tree (Fig.
1) can be rewritten into equivalent set of IF-THEN decision rules (Han
et al.,
2012):
The probability of IHD is less than 0.5 for all terminal nodes of the decision tree. We present probabilities of IHD in IF-THEN rules to avoid using strict classification into IHD=yes and IHD=no classes. We assume that the decision tree visual representation is easier to understand than decision rules for humans, thus we will not present a full set of decision rules. If preferred, the decision rules can be obtained by traversing of all decision tree paths from root to terminal nodes.
The major aim of this article was to compare the errors of binary logistic regression and the decision tree and to determine which method was superior (Table
6). We found that 10-fold CV mean absolute error of classification probability in the binary logistic regression (MAE = 0.18213) was lower only by 2.04%, compared to the error in the decision tree (MAE = 0.18592) for IHD; 2.86% for CVD. Similar results were obtained for in-sample mean absolute errors, where logistic regression error was 1.40–1.98% lower than decision tree error. The difference between equal error rates for both methods, LR and DT, was small 2.48–5.75%. In all cases errors for LR were lower, except for in-sample CVD case, where EER for DT is 2.48% smaller than for LR.
Difference between in-sample and 10-fold CV errors was also small – 0.79–2.00%. This indicates that selected methods were not overfitting.
4 Discussion
It is important not only to consider the risks of developing CVD, but also to choose the appropriate statistical method that allows for the closest assessment of these risks and produces the fewest errors. In this study, the most popular binary logistic regression model was applied to assess the impact of various factors on the risk of CVD, and the results were compared with those of the decision tree model. These methods were chosen because these two techniques have often been used for very similar tasks (Long
et al.,
1993). The decision tree is easily interpretable by the consumer. In addition, decision tree models are robust to outliers, do not depend on distribution assumptions or parametric dependencies, and can easily handle missing data (Song and Lu,
2015). Node condition testing and tree traversing from root to leaves can be performed without the need for mathematical calculations.
The decision tree also provides insight and understanding into the predictive structure of the data (Breiman
et al.,
1984). The root node test condition variable is the most influential variable in the classification of observations. The other nodes contain most influential variables for subsets of the data.
The results produced by the logistic regression model are a little more complicated to read and understand as compared to those produced by the decision tree. Another reason is the scarcity of scientific studies that use decision trees for CVD data analysis. Soni
et al. indicated that, compared to other classification methods such as a neural network or Naive Bayes, the decision tree algorithm was the most accurate in CVD prediction (Soni
et al.,
2011). Many popular algorithms have selection bias towards covariates with many possible splits (Hothorn
et al.,
2006).
There are not many articles in domain of medicine that compare logistic regression to decision tree. All of them compare logistic regression to the most common decision tree algorithms (based on heuristic criterion): CART, ID3, C4.5, C5.0. In this article we compare classical statistical logistic regression method to decision tree method also based on a well-defined statistical theory.
We found that alcohol drinking was associated with a lower probability of IHD or CVD. This was unexpected because the relationship is inverse in most studies. However, this question was relevant earlier as well. Renaud and Lorgeril (
1992) presented findings showing that the consumption of alcohol at the level of intake in France (20–30 g per day) can reduce the risk of coronary heart disease (CHD) by at least 40%. The researchers suggested that alcohol may protect from CHD by preventing atherosclerosis through the action of high-density-lipoprotein cholesterol, but serum concentrations of this factor are not higher in France than in other countries.
Mukamal
et al. (
2005) indicated that consuming moderate amounts of alcohol 3 to 4 days per week was associated with a lower relative risk of ischemic stroke (0.68; 95% CI = (0.44; 1.05)).
Fernandez-Scola (
2015) presented the results of epidemiological case-control studies and meta-analyses showing a U-type bimodal relationship – i.e. that low-to-moderate alcohol consumption (particularly of wine or beer) was associated with a decrease in cardiovascular events and mortality, compared with abstention.
Gaziano (
2016) indicated that alcohol was associated with an increase in HDL cholesterol and a lower risk of diabetes. He stated that this seems to be one important mechanism by which alcohol could lower the risk of heart disease. We have one more possible explanation: if people feel healthy, they allow themselves to drink more alcohol.
5 Conclusion
Both methods, the binary logistic regression and the decision tree, applied for assessing the risk of IHD and CVD in middle-aged men revealed which factors were statistically significant variables to predict these diseases. For the risk of IHD, these factors were the following: systolic blood pressure, the number of brothers and sisters at present, using blood pressure-lowering medicine, disability group, alcohol drinking, body mass index, age, and intermittent claudication. For the risk of CVD, these factors were systolic blood pressure, serum cholesterol level, the number of brothers and sisters at present, using blood pressure-lowering medicine, disability group, alcohol drinking, smoking habits, the number of working days per week, time for walking in the winter, the body mass index, and age.
The binary logistic regression method showed a very slightly lower level of mean absolute errors than the decision tree did (the difference was 2.04% for IHD and 2.86% for CVD), but for consumers, the results of the decision tree are easier to understand and to interpret. Khemphila and Boonjing (
2010) presented a similar problem for classifying heart disease patients using the logistic regression and the decision tree. Error rates for these methods (0.22 – for logistic regression and 0.21 – for decision tree) were also similar. Both methods are appropriate for the analysis of data on cardiovascular disease.