This section introduces the methodology used in this study for solving green supplier selection problems. Some concepts of IFSs are presented, followed by the developed methodology and steps.
3.2 Steps of the Integrated Methodology
This subsection presents an integrated methodology for green supplier selection on the basis of BWM and improved TOPSIS. Figure
1 shows the flowchart of the proposed approach.
For convenience, let $M=\{1,2,\dots ,m\}$, $N=\{1,2,\dots ,n\}$ and $T=\{1,2,\dots ,t\}$. The MCGDM problem concerned is described as follows.
Let $A=\{{a_{1}},{a_{2}},\dots ,{a_{m}}\}$ be a set of m alternatives, $C=\{{c_{1}},{c_{2}},\dots ,{c_{n}}\}$ be a set of n criteria, and $E=\{{e_{1}},{e_{2}},\dots ,{e_{t}}\}$ be a set of t DMs. Assume that ${w_{j}}$ $(j\in N)$ is the weight value of ${c_{j}}$, where ${w_{j}}\geqslant 0$ and ${\textstyle\sum _{j=1}^{n}}{w_{j}}=1$. Suppose that ${r_{ij}^{k}}$ ($i\in M$, $j\in N$, $k\in T$) represents the rating of alternative ${a_{i}}$ with respect to criterion ${c_{j}}$ provided by DM ${e_{k}}$. Thus, the individual decision matrix provided by DM ${e_{k}}$ can be expressed as ${R^{k}}={({r_{ij}^{k}})_{m\times n}}$. Denote the weight vector of criteria by $w=({w_{1}},{w_{2}},\dots ,{w_{n}})$, and the weight vector of DMs by $\omega =({\omega _{1}},{\omega _{2}},\dots ,{\omega _{t}})$.
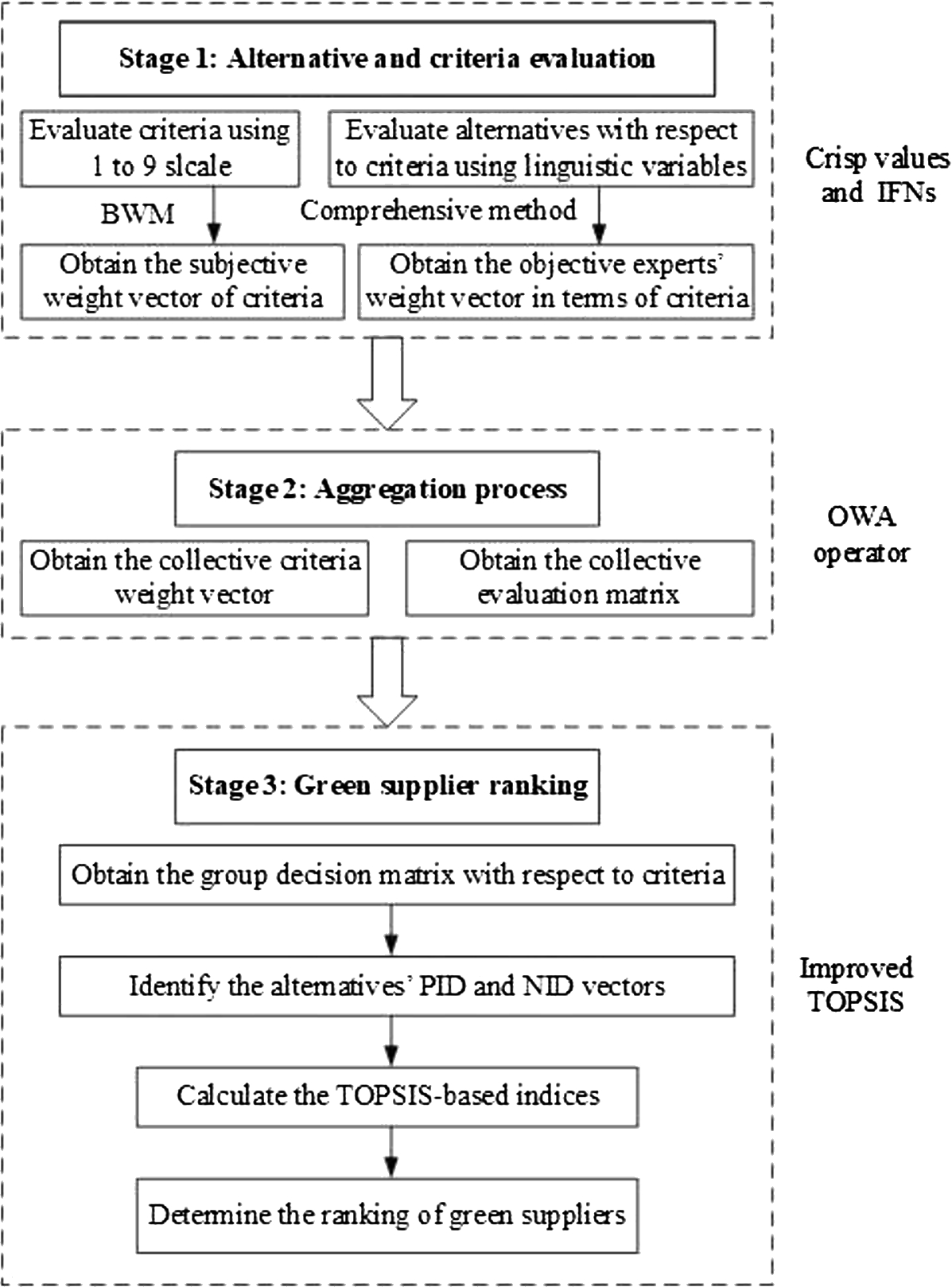
Fig. 1
Assessment framework of the proposed approach.
The focus is how to rank alternatives on the basis of individual decision matrices ${R^{k}}$ $(k\in T)$ associated with weight information. To solve this type of MCGDM problem, a methodology integrated with intuitionistic fuzzy TOPSIS and BWM is introduced. The main steps of the proposed approach are briefly presented as follows.
-
Step 1: Define the overall goal, criteria, sub-criteria and associated alternatives for decision-making problems, and then establish the hierarchy of the considered problem.
-
Step 2: Design and select the evaluation scale of IFS.
The study by Aloini
et al. (
2014) is employed to assign the evaluation values of alternatives by using the scale, as shown in Table
2.
Table 2
Rating alternatives with linguistic terms (Aloini
et al.,
2014).
| Linguistic terms |
IFNs |
| Absolutely good (AG)/absolutely high (AH) |
$\langle 0.9,0.05,0.05\rangle $ |
| Very good (VG)/very high (VH) |
$\langle 0.8,0.1,0.1\rangle $ |
| Good (G)/high (H) |
$\langle 0.7,0.2,0.1\rangle $ |
| Medium good (MG)/medium high (MH) |
$\langle 0.6,0.3,0.1\rangle $ |
| Fair (F)/medium (M) |
$\langle 0.45,0.4,0.15\rangle $ |
| Medium poor (MP)/medium low (ML) |
$\langle 0.4,0.5,0.1\rangle $ |
| Poor (P)/low (L) |
$\langle 0.3,0.6,0.1\rangle $ |
| Very poor (VP)/very low (VL) |
$\langle 0.2,0.7,0.1\rangle $ |
| Absolutely poor (AP)/absolutely low (AL) |
$\langle 0.05,0.9,0.05\rangle $ |
-
Step 3: Determine the weight vectors of criteria and sub-criteria.
In accordance with the principle of BWM developed by Rezaei (
2015,
2016), DMs firstly select the best (e.g. most important and desirable) and the worst (e.g. least important and desirable) criteria.
Secondly, DMs determine the preferences of the best criterion over all the other criteria by using a number from 1 to 9 (1 means equally important and 9 signifies extremely important). The result is presented as a ‘best-to-others (BO)’ vector as follows:
where
${u_{Bj}}$ indicates the preference of the best criterion
B over criterion
j, and
${u_{BB}}=1$.
Thirdly, DMs determine the preferences of the other criteria over the worst criterion by using a number from 1 to 9 (1 means equally important and 9 signifies extremely important). The result is presented as an ‘others-to worst (OW)’ vector as follows:
where
${v_{jW}}$ indicates the preference of criterion
j over the worst criterion
W, and
${v_{WW}}=1$.
Lastly, establish a mathematical model and derive the optimal weights
$({w_{1}^{\ast }},{w_{2}^{\ast }},\dots ,{w_{n}^{\ast }})$. For each pair of
${w_{B}}/{w_{j}}$ and
${w_{j}}/{w_{W}}$, the optimal weight should satisfy the conditions
${w_{B}}/{w_{j}}={u_{Bj}}$ and
${w_{j}}/{w_{W}}={v_{jW}}$. To meet these requirements, the maximum absolute differences
$|\frac{{w_{B}}}{{w_{j}}}-{u_{Bj}}|$ and
$|\frac{{w_{j}}}{{w_{W}}}-{v_{jW}}|$ for all
j should be minimized. Thus, the following model can be constructed by considering the sum condition and non-negativity of weights.
Here, Model (4) can be transformed into the following linear programming model:
The optimal weights
$({w_{1}^{\ast }},{w_{2}^{\ast }},\dots ,{w_{n}^{\ast }})$ and consistency index
${\xi ^{\ast }}$ can be derived by solving Model (5). Furthermore, calculating the consistency level of comparisons is required. Rezaei (
2015) defined the consistency index as follows.
Definition 7 (See Rezaei, 2015).
A comparison is fully consistent when ${v_{Bj}}\times {v_{jW}}={v_{BW}}$ for all j, in which ${v_{Bj}}$, ${v_{jW}}$ and ${v_{BW}}$ indicate the preference of the best criterion over criterion j, the preference of criterion j over the worst criterion and the preference of the best criterion over the worst criterion, respectively.
Table 3
Consistency index of BWM (Rezaei,
2015).
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| Consistency index |
0.00 |
0.44 |
1.00 |
1.63 |
2.33 |
3.00 |
3.73 |
4.47 |
5.23 |
The consistency ratio (CR) of the BWM can be calculated, combining the obtained
${\xi ^{\ast }}$ and its corresponding consistency index (Table
3) as follows:
where
$\mathit{CR}\in [0,1]$. The closer the
$\mathit{CR}$ is to zero, the more consistent the obtained vector will be, and vice versa. Generally,
$\mathit{CR}\leqslant 0.1$ shows that the obtained vector is acceptable.
As every DM is skilled in only some specific fields, it is more appropriate to allocate different weight values of each DM on different criteria.
For each criterion ${c_{j}}$, the criterion value expressed by DM ${e_{k}}$ is transformed into an IFN vector ${r_{j}^{k}}=({r_{1j}^{k}},{r_{2j}^{k}},\dots ,{r_{mj}^{k}})$. Let ${\omega _{j}^{k}}$ be the weight of ${e_{k}}$ with respect to ${c_{j}}$. To determine the criterion weight ${\omega _{j}^{k}}$, two aspects should be considered simultaneously. One aspect is the closeness coefficient that captures the similarity between the individual decision matrix provided by DM ${e_{k}}$ and the collective one by the group of DMs. The other aspect is the proximity degree that measures the proximity between the individual decision matrix provided by DM ${e_{k}}$ and those matrices provided by all other DMs.
In accordance with the previous analysis,
${\omega _{j}^{k}}$ (
$j\in N$;
$k\in T$) can be derived from two aspects. On one hand, an improved TOPSIS method inspired by the idea of TOPSIS (Hwang and Yoon,
1981; Wang
et al.,
2017; Yue,
2014) is developed to calculate the closeness coefficient. On the other hand, the proximity degree can be calculated on the basis of distance measure.
(1) Calculate the closeness coefficient on the basis of the improved TOPSIS.
The PID vector
${r_{j}^{\ast }}$ on criterion
${c_{j}}$ is defined as the arithmetic average of all individual decision vectors
${r_{j}^{k}}$ $(k\in T)$ on the basis of Eq. (
1), that is,
${r_{j}^{\ast }}=({r_{1j}^{\ast }},{r_{2j}^{\ast }},\dots ,{r_{mj}^{\ast }})$, where
where
${\varpi _{k}}$ is the associated weight value of the IFOWA operator, and its value can be determined in accordance with the normal distribution-based method (Xu,
2005).
The NID vectors consist of the individual negative ideal decision (INID) vector, left individual negative ideal decision (LINID) vector and right individual negative ideal decision (RINID) vector. The INID, LINID and RINID vectors on criterion
${c_{j}}$ are denoted by
${r_{j}^{c}}=({r_{1j}^{c}},{r_{2j}^{c}},\dots ,{r_{mj}^{c}})$,
${r_{j}^{l-}}=({r_{1j}^{l-}},{r_{2j}^{l-}},\dots ,{r_{mj}^{l-}})$ and
${r_{j}^{r-}}=({r_{1j}^{r-}},{r_{2j}^{r-}},\dots ,{r_{mj}^{r-}})$, respectively. In accordance with the complement operation in Definition
2,
-
(iii) Calculate distances
$d({r_{j}^{k}},{r_{j}^{\ast }})$,
$d({r_{j}^{k}},{r_{j}^{c}})$,
$d({r_{j}^{k}},{r_{j}^{l-}})$ and
$d({r_{j}^{k}},{r_{j}^{r-}})$ by using Eq. (
3).
Subsequently, an extended closeness coefficient of each individual decision vector
${r_{j}^{k}}$ with respect to the ideal decision vectors, including
${r_{j}^{\ast }}$,
${r_{j}^{c}}$,
${r_{j}^{l-}}$ and
${r_{j}^{r-}}$, is defined as follows:
(2) Calculate the average proximity degree on the basis of distance measure.
The proximity degree between
${r_{ij}^{k}}$ and
${r_{ij}^{l}}$ is denoted by
${\gamma _{ij}^{lk}}$ and can be calculated as:
where
$d({r_{ij}^{l}},{r_{ij}^{k}})$ is the distance between
${r_{ij}^{k}}$ and
${r_{ij}^{l}}$ on the basis of Eq. (
2).
Furthermore, on the basis of Eq. (
12), the average proximity degree
${\eta _{j}^{k}}$ between DM
${e_{k}}$ and all the other DMs
${e_{l}}$ (
$l\in T$,
$l\ne k$) on criterion
${c_{j}}$ can be calculated as follows:
where
$d({r_{ij}^{l}},{r_{ij}^{k}})$ is the distance between
${r_{ij}^{k}}$ and
${r_{ij}^{l}}$ on the basis of Eq. (
2).
(3) Derive the weights of DMs with respect to different criteria.
To comprehensively consider the closeness coefficient and proximity degree, a control parameter
θ $(0\leqslant \theta \leqslant 1)$ is employed to construct the unified criterion weight
${\lambda _{j}^{k}}$ of DM
${e_{k}}$ on criterion
${c_{j}}$, as shown as follows:
The unified criterion weight ${\lambda _{j}^{k}}$ can tradeoff the closeness efficient versus the proximity degree by altering the values of parameter θ. Particularly, ${\lambda _{j}^{k}}$ will only depend on the closeness efficient if $\theta =1$, and it will only depend on the proximity degree if $\theta =0$. Without loss of generality, a default control parameter $\theta =0.5$ can be set in practical application.
The unified criterion weights
${\lambda _{j}^{k}}$ $(k\in T)$ are normalized, and the weight
${\omega _{j}^{k}}$ of DM
${e_{k}}$ with respect to criterion
${c_{j}}$ can be obtained as follows:
Let
${\hat{R}^{k}}={({\hat{r}_{ij}^{k}})_{m\times n}}$ be the weighted individual decision matrix. Then, the following result can be obtained:
where
${\hat{\mu }_{ij}^{k}}=1-{(1-{\mu _{ij}^{k}})^{{\omega _{j}^{k}}}}$ and
${\hat{\nu }_{ij}^{k}}={({\nu _{ij}^{k}})^{{\omega _{j}^{k}}}}$ on the basis of the operations in Definition
2.
${\omega _{j}^{k}}$ denotes the obtained weight of DM
${e_{k}}$ using Eq. (
15).
In the following, the target is to rank all the alternatives on the basis of the improved TOPSIS method.
(1) Obtain the group decision matrix with respect to criteria.
For each alternative
${a_{i}}$ $(i\in M)$, the weighted individual decision matrix in Eq. (
16) is transformed into a group decision matrix of DMs with respect to the following criteria:
where the element
${h_{kj}^{i}}$ in
${H^{i}}$ is the same as the element
${\hat{r}_{ij}^{k}}$ in
${\hat{R}^{k}}$ in Eq. (
16). Similar to the individual decision matrix
${R^{k}}$, the matrix
${H^{i}}$ is called the alternative decision matrix. For each criterion
${c_{j}}$, the weighted criterion values of alternative
${a_{i}}$ expressed by all the DMs
${e_{k}}$ $(k\in T)$ are denoted as an IFN vector
${h_{j}^{i}}=({h_{1j}^{i}},{h_{2j}^{i}},\dots ,{h_{tj}^{i}})$.
(2) Determine the alternatives’ PID vector ${h_{j}^{\ast }}$ and the NID vectors ${h_{j}^{c}}$ and ${h_{j}^{-}}$ on criterion ${c_{j}}$.
Similar to the procedures in Step 4, let
${h_{j}^{\ast }}=({h_{1j}^{\ast }},{h_{2j}^{\ast }},\dots ,{h_{tj}^{\ast }})$ denote the alternatives’ PID vector. The alternatives’ PID vector should be the best decision of all
${H^{i}}$ $(i\in M)$ in Eq. (
17). The elements in the alternatives’ PID vector can be calculated as follows:
Similar to the individual NID decision vectors, the alternatives’ NID vector should have maximum separation from the alternatives’ PID vector
${h_{j}^{\ast }}$. It can naturally consider the complement
${({h_{j}^{\ast }})^{c}}$ of
${h_{j}^{\ast }}$, which shows the maximum separation from
${h_{j}^{\ast }}$. Let
${h_{j}^{c}}=({h_{1j}^{c}},{h_{2j}^{c}},\dots ,{h_{tj}^{c}})$ denote the complement
${({h_{j}^{\ast }})^{c}}$ of
${h_{j}^{\ast }}$, where
Moreover, the following alternatives’ decision vector also shows the maximum separation from the alternatives’ PID vector
${h_{j}^{\ast }}$. Let
${h_{j}^{-}}=({h_{1j}^{-}},{h_{2j}^{-}},\dots ,{h_{tj}^{-}})$ denote one of the alternatives’ NID vectors, where
(3) Calculate the TOPSIS-based index ${\mathit{CI}_{kj}^{i}}$ and the comprehensive TOPSIS-based index $\mathit{CI}({a_{i}})$.
The distances between each alternative’s decision value
${h_{kj}^{i}}$ and
${h_{kj}^{\ast }}$,
${h_{kj}^{c}}$ and
${h_{kj}^{-}}$ are calculated on the basis of Eq. (
2) and are denoted as
$d({h_{kj}^{i}},{h_{kj}^{\ast }})$,
$d({h_{kj}^{i}},{h_{kj}^{c}})$ and
$d({h_{kj}^{i}},{h_{kj}^{-}})$, respectively.
Furthermore, an improved TOPSIS-based index is developed to measure the discrimination of
${h_{kj}^{i}}$ with respect to
${h_{kj}^{\ast }}$,
${h_{kj}^{c}}$ and
${h_{kj}^{-}}$ and is defined as:
The improved TOPSIS-based index
${\mathit{CI}_{kj}^{i}}$ can be employed to evaluate the performance of alternative
${a_{i}}$ with respect to criterion
${c_{j}}$. By coupling the criterion weight
${w_{j}^{k}}$ in terms of DM
${e_{k}}$, the comprehensive TOPSIS-based index
$\mathit{CI}({a_{i}})$ of the characteristics for alternative
${a_{i}}$ is expressed as follows:
Significantly, the closer the alternatives’ decision value ${h_{kj}^{i}}$ is to alternatives’ PID value ${h_{kj}^{\ast }}$, and the farther ${h_{kj}^{i}}$ is from the alternatives’ NID values ${h_{kj}^{c}}$ and ${h_{kj}^{-}}$, the closer the $\mathit{CI}({a_{i}})$ is to 1. Thus, the comprehensive TOPSIS-based index $\mathit{CI}({a_{i}})$ can be used to rank the preference order of all alternatives. A larger $\mathit{CI}({a_{i}})$ indicates a better alternative ${a_{i}}$.